A Simple GIS-Based Model for Urban Rainstorm Inundation Simulation
Abstract
1. Introduction
2. Methodology
2.1. Model Development
2.1.1. SCS Runoff Model
2.1.2. Combining the Surface Runoff Model and Drainage Model
- Data input module. Provide spatial data input, including rainfall pattern editing, land use classification, sub-catchment division, and pipe network connectivity editing.
- SCS rainfall-runoff module. Provide surface runoff calculation based on the raster grid, the Thiessen partition of a sub-catchment, and calculation of for each sub-catchment.
- Surface flow module. Extract hydrological parameters, such as the elevation, slope, aspect, and flow direction. Simulate surface runoff by calculating the flow path, flow speed, and the maximum weighted distance to the manhole for each sub-catchment.
- Drainage flow module. Establish the feature database of the directed pipe-network with spatial topological relationships. Build the attribute database with attributes, such as pipe caliber, material, elevation, and so on, and relate the attribute database to the feature database.
2.2. Model Application
2.2.1. Study Area
2.2.2. Data Used
3. Results
3.1. Model Performance and Validation
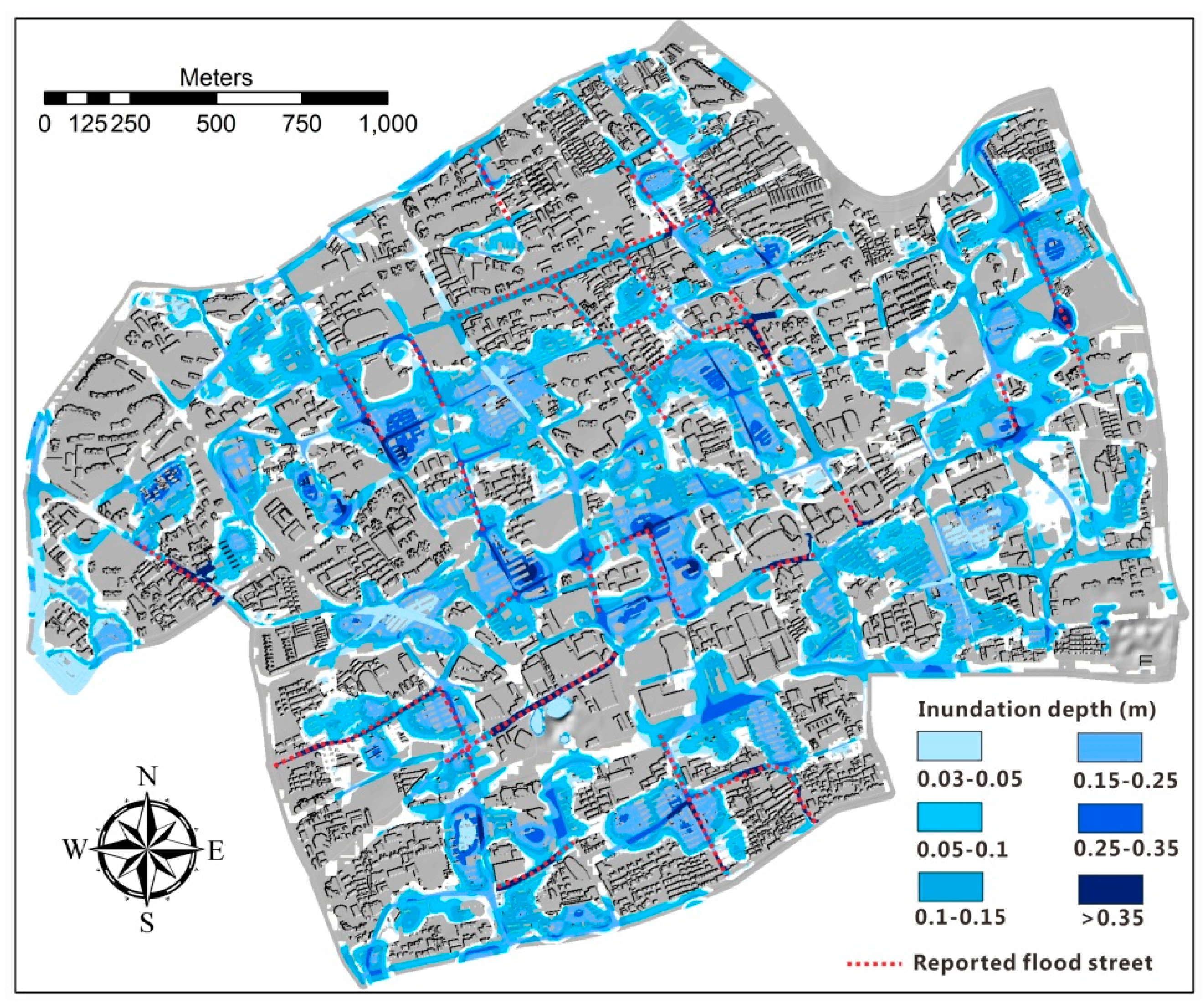
3.2. Urban Surface Flooding
3.3. Drainage Discharge
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, J.Y.; Wang, Y.T.; He, R.M. Discussion on the urban flood and waterlogging and causes analysis in China. Adv. Water Sci 2016, 27, 485–491. (In Chinese) [Google Scholar]
- Li, G.F.; Tong, Y.Y.; Wang, H.M. Impact assessment of urbanization on flood risk in the Yangtze River Delta. Stoch. Environ. Res. Risk Assess. 2013, 27, 1683–1693. [Google Scholar] [CrossRef]
- Jha, A.; Lamond, J.; Bloch, R. Five Feet High and Rising Cities and Flooding in the 21st Century; Social Science Electronic Publishing: New York, NY, USA, 2011. [Google Scholar]
- Yu, H.F.; Zhao, Y.L.; Fu, Y.H. Spatiotemporal Variance Assessment of Urban Rainstorm Waterlogging Affected by Impervious Surface Expansion: A Case Study of Guangzhou, China. Sustainability 2018, 10, 3761. [Google Scholar] [CrossRef]
- Mike Urban. Available online: https://www.mikepoweredbydhi.com/products/mike-urban (accessed on 23 March 2019).
- InfoWorks CS. Available online: http://www.hrwallingford.com/ (accessed on 23 March 2019).
- SOBEK. Available online: https://www.deltares.nl/en/software/sobek/ (accessed on 23 March 2019).
- Storm Water Management Model (SWMM). Available online: http://www.epa.gov/ednnrmrl/models/swmm/ (accessed on 23 March 2019).
- Gironás, J.; Roesner, L.A.; Rossman, L.A.; Davis, J. A new applications manual for the Storm Water Management Model (SWMM). Environ. Model. Softw. 2010, 25, 813–814. [Google Scholar] [CrossRef]
- Chen, J.; Hill, A.A.; Urbano, L.D. A GIS-based model for urban flood inundation. J. Hydrol. 2009, 373, 184–192. [Google Scholar] [CrossRef]
- Zhang, S.H.; Pan, B.Z. An urban storm-inundation simulation method based on GIS. J. Hydrol. 2014, 517, 260–268. [Google Scholar] [CrossRef]
- Huang, C.; Chen, Y.; Wu, J.P. Mapping spatio-temporal flood inundation dynamics at large river basin scale using time-series flow data and MODIS imagery. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 350–362. [Google Scholar] [CrossRef]
- Yu, D.P.; Coulthard, T.J. Evaluating the importance of catchment hydrological parameters for urban surface water flood modelling using a simple hydro-inundation model. J. Hydrol. 2015, 524, 385–400. [Google Scholar] [CrossRef]
- Massari, C.; Tarpanelli, A.; Moramarco, T. A fast simplified model for predicting river flood inundation probabilities in poorly gauged areas. Hydrol. Process. 2015, 29, 2275–2289. [Google Scholar] [CrossRef]
- Heimhuber, V.; Tulbure, M.G.; Broich, M. Modeling multidecadal surface water inundation dynamics and key drivers on large river basin scale using multiple time series of Earth observation and river flow data. Water Resour. Res. 2017, 53, 1251–1269. [Google Scholar] [CrossRef]
- Xu, Z.X.; Cheng, L. Progress on studies and applications of the distributed hydrological models. J. Hydraul. Eng. 2008, 39, 1009–1017. (In Chinese) [Google Scholar]
- Sayama, T.; Tatebe, Y.; Iwami, Y. Hydrologic sensitivity of flood runoff and inundation: 2011 Thailand floods in the Chao Phraya River basin. Nat. Hazards Earth Syst. 2015, 15, 1617–1630. [Google Scholar] [CrossRef]
- Rosa, P.D.; Andrea, F.; Annalisa, M. Automatic Web Procedure for Calculating Flood Flow Frequency. Water 2019, 11, 14. [Google Scholar] [CrossRef]
- Flood Modeller. Available online: https://www.floodmodeller.com/ (accessed on 23 March 2019).
- Zhang, S.H.; Wang, T.W.; Zhao, B.H. Calculation and visualization of flood inundation based on a topographic triangle network. J. Hydrol. 2014, 509, 406–415. [Google Scholar] [CrossRef]
- Zhang, S.H.; Xia, Z.X.; Yuan, R. Parallel computation of a dam-break flow model using OpenMP on a multi-core computer. J. Hydrol. 2014, 512, 126–133. [Google Scholar] [CrossRef]
- Cho, Y.; Engel, B.A. Spatially distributed long-term hydrologic simulation using a continuous SCS CN method-based hybrid hydrologic model. Hydrol Process. 2018, 32, 904–922. [Google Scholar] [CrossRef]
- Mishra, S.K.; Pandey, R.P.; Jain, M.K.; Singh, V.P. A Rain Duration and Modified AMC-dependent SCS-CN Procedure for Long Duration Rainfall-runoff Events. Water Resour. Manag. 2008, 22, 861–876. [Google Scholar] [CrossRef]
- Soulis, K.X.; Valiantzas, J.D. Identification of the SCS-CN Parameter Spatial Distribution Using Rainfall-Runoff Data in Heterogeneous Watersheds. Water Resour. Manag. 2013, 27, 1737–1749. [Google Scholar] [CrossRef]
- Ajmal, M.; Waseem, M.; Ahn, J.H.; Kim, T.W. Improved Runoff Estimation Using Event-Based Rainfall-Runoff Models. Water Resour. Manag. 2015, 29, 1995–2010. [Google Scholar] [CrossRef]
- Geetha, K.; Mishra, S.K.; Eldho, T.I.; Rastogi, A.K.; Pandey, R.P. SCS-CN-based Continuous Simulation Model for Hydrologic Forecasting. Water Resour. Manag. 2008, 22, 165–190. [Google Scholar] [CrossRef]
- Suribabu, C.R.; Bhaskar, J. Evaluation of urban growth effects on surface runoff using SCS-CN method and Green-Ampt infiltration model. Earth. Sci. Inform. 2015, 8, 609–626. [Google Scholar] [CrossRef]
- Li, L.L. Hydrological Analysis and Calculation Research of Un-Gauged Basins. J. Henan Sci. Technol. 2016, 19, 59–60. (In Chinese) [Google Scholar]
- Razafison, U.; Stéphane, C.; Delestre, O. A Shallow Water model for the numerical simulation of overland flow on surfaces with ridges and furrows. Eur. J. Mech. B-Fluid 2012, 31, 44–52. [Google Scholar] [CrossRef]
- Huang, J.B.; Wen, J.W.; Wang, B.; Zhu, S. Numerical analysis of the combined rainfall-runoff process and snowmelt for the Alun River Basin, Heilongjiang, China. Environ. Earth. Sci. 2015, 74, 6929–6941. [Google Scholar]
- Kumar, T.; Jhariya, D.C. Identification of Rainwater Harvesting Sites using SCS-CN Methodology, Remote Sensing and Geographical Information System Techniques. Geocarto Int. 2017, 32, 1367–1388. [Google Scholar] [CrossRef]
- Tiwari, K.; Goyal, R.; Sarkar, A. GIS-based Methodology for Identification of Suitable Locations for Rainwater Harvesting Structures. Water Resour. Manag. 2018, 32, 1811–1825. [Google Scholar] [CrossRef]
- Pantelakis, D.; Zissis, T.; Anastasiadou-Partheniou, E.; Baltas, E. Numerical Models for the Simulation of Overland Flow in Fields Within Surface Irrigation Systems. Water Resour. Manag. 2012, 26, 1217–1229. [Google Scholar] [CrossRef]
- Chen, P.; Zhang, J.; Zhang, L.; Sun, Y.; Rudatsikira, E. Evaluation of resident evacuations in urban rainstorm waterlogging disasters based on scenario simulation: Daoli district (Harbin, China) as an example. Int. J. Environ. Res. Public Health 2014, 11, 9964. [Google Scholar] [CrossRef]
- Dang, A.T.N.; Kumar, L. Application of remote sensing and GIS-based hydrological modelling for flood risk analysis: A case study of District 8, Ho Chi Minh city, Vietnam. Geomat. Nat. Hazards Risk 2017, 8, 1792–1811. [Google Scholar] [CrossRef]
- Yin, J.; Yu, D.P.; Yin, Z.; Liu, M.; He, Q. Evaluating the impact and risk of pluvial flash flood on intra-urban road network: A case study in the city center of Shanghai, China. J. Hydrol. 2016, 537, 138–145. [Google Scholar] [CrossRef]
- Rizeei, H.M.; Pradhan, B.; Saharkhiz, M.A. Surface runoff prediction regarding LULC and climate dynamics using coupled LTM, optimized ARIMA, and GIS-based SCS-CN models in tropical region. Arab. J. Geosci. 2018, 11, 53. [Google Scholar] [CrossRef]
- Yin, Z.E.; Yin, J.; Xu, S.Y. Community-based scenario modelling and disaster risk assessment of urban rainstorm waterlogging. Acta Geogr. Sin. 2011, 21, 274–284. [Google Scholar] [CrossRef]
- Huang, Q.Y.; Wang, J.; Li, M.Y.; Fei, M.; Dong, J. Modeling the influence of urbanization on urban pluvial flooding: A scenario-based case study in Shanghai, China. Nat. Hazards 2017, 87, 1035–1055. [Google Scholar] [CrossRef]
- Fan, F.L.; Deng, Y.B.; Hu, X.F. Estimating Composite Curve Number Using an Improved SCS-CN Method with Remotely Sensed Variables in Guangzhou, China. Remote Sens. 2013, 5, 1425–1438. [Google Scholar] [CrossRef]
- Xu, J.H.; Zhao, Y.; Zhong, K.W. Coupling Modified Linear Spectral Mixture Analysis and Soil Conservation Service Curve Number (SCS-CN) Models to Simulate Surface Runoff: Application to the Main Urban Area of Guangzhou, China. Water 2016, 8, 550. [Google Scholar] [CrossRef]
- Bouvier, C.; Bouchenaki, L.; Tramblay, Y. Comparison of SCS and Green-Ampt Distributed Models for Flood Modelling in a Small Cultivated Catchment in Senegal. Geosciences 2018, 8, 122. [Google Scholar] [CrossRef]
- Cronshey, R.G.; McCuen, R.H.; Miller, N. Urban Hydrology for Small Watersheds; USDA, Soil Conservation Service: Washington, DC, USA, 1986; p. 164.
- McCuen, R.H. A Guide to Hydrologic Analysis Using SCS Methods; The National Agricultural Library: Beltsville, MD, USA; Washington, DC, USA, 1982.
- Ponce, V.M.; Hawkins, R.H. Runoff Curve Number: Has It Reached Maturity? J. Hydrol. Eng. 1996, 1, 11–19. [Google Scholar] [CrossRef]
- Lunasin, E.; Titi, E.S. Finite determining parameters feedback control for distributed nonlinear dissipative systems—A computational study. Math 2015, 3, 1–23. [Google Scholar] [CrossRef][Green Version]
- Gildas, B.; Georges, D.; Benayache, Z. Towards nonlinear delay-based control for convection-like distributed systems: The example of water flow control in open channel systems. Netw. Heterog. Media 2017, 4, 211–221. [Google Scholar]
- Shen, H.B.; Xu, Z.X.; Zhang, S.H. Review on the simulation of overland flow in hydrological models. Adv. Water Sci. 2016, 27, 467–475. (In Chinese) [Google Scholar]
- Athol, D.A.; Gary, L.; Anthony, J.P. Rill hydraulics on a semiarid hillslope, southern Arizona. Earth. Surf. Proc. Land 2015, 21, 35–47. [Google Scholar]
- Seo, Y.; Hwang, J.; Noh, S.J. Analysis of Urban Drainage Networks Using Gibbs’ Model: A Case Study in Seoul, South Korea. Water 2015, 7, 4129–4143. [Google Scholar] [CrossRef]
- Konsoer, K.; Zinger, J.; Parker, G. Bankfull hydraulic geometry of submarine channels created by turbidity currents: Relations between bankfull channel characteristics and formative flow discharge. J. Geophys. Res.-Earth 2013, 118, 216–228. [Google Scholar] [CrossRef]
- Strupczewski, W.G.; Szymkiewicz, R. Analysis of paradoxes arising from the Chezy formula with constant roughness: I. Depth-discharge curve. Hydrol. Sci. J. 1997, 41, 659–673. [Google Scholar] [CrossRef]
- Wang, C.X.; Du, S.Q.; Wen, J.H.; Zhang, M.; Gu, H.; Shi, Y.; Xu, H. Analyzing explanatory factors of urban pluvial floods in Shanghai using geographically weighted regression. Stoch. Environ. Res. Risk Assess. 2017, 31, 1777–1790. [Google Scholar] [CrossRef]
- Quan, R.S. Rainstorm waterlogging risk assessment in central urban area of Shanghai based on multiple scenario simulation. Nat. Hazards 2011, 73, 1569–1585. [Google Scholar] [CrossRef]
- Yin, J.; Yin, Z.; Zhong, H.D.; Xu, S.; Hu, X.; Wang, J.; Wu, J. Monitoring urban expansion and land use/land cover changes of Shanghai metropolitan area during the transitional economy (1979–2009) in China. Environ. Monit. Assess. 2011, 177, 609. [Google Scholar] [CrossRef]
- Yu, H.L.; Wang, H.C.; Yang, S.S.; Hang, S.J.; Zhang, J.P.; Zhang, S.F.; Yang, K.; Zhang, F.J.; Cha, M.P. Code for Design of Outdoor Wastwater Engineering; China Planning Press: Beijing, China, 2006. [Google Scholar]
- Ning, J. Study on the Short-Term Rainstorm Intensity Formula and Design Rain Pattern in Shanghai. Master’s Thesis, Tongji University, Shanghai, China, 2006. (In Chinese). [Google Scholar]
- Du, S.Q.; Gu, H.H.; Wen, J.H.; Chen, K.; Van Rompaey, A. Detecting Flood Variations in Shanghai over 1949–2009 with Mann-Kendall Tests and a Newspaper-Based Database. Water 2015, 7, 1808–1824. [Google Scholar] [CrossRef]
- Yin, J.; Yu, D.P.; Wilby, R. Modelling the impact of land subsidence on urban pluvial flooding: A case study of downtown Shanghai, China. Sci. Total Environ. 2016, 544, 744–753. [Google Scholar] [CrossRef]
- Bathrellos, G.D.; Skilodimou, H.D.; Chousianitis, K.; Youssef, A.M.; Pradhan, B. Suitability estimation for urban development using multi-hazard assessment map. Sci. Total Environ. 2017, 575, 119–134. [Google Scholar] [CrossRef]
- Skilodimou, H.D.; Bathrellos, G.D.; Chousianitis, K. Multi-hazard assessment modeling via multi-criteria analysis and GIS: A case study. Environ. Earth. Sci. 2019, 78, 47. [Google Scholar] [CrossRef]
- Chen, A.S.; Evans, B.; Djordjevi, S.; Savić, D.A. A coarse-grid approach to representing building blockage effects in 2D urban flood modelling. J. Hydrol. 2012, 426–427, 1–16. [Google Scholar] [CrossRef]
- Yu, D.P. Parallelization of a two-dimensional flood inundation model based on domain decomposition. Environ. Model. Softw. 2010, 25, 935–945. [Google Scholar] [CrossRef]
- Meenar, M.; Fromuth, R.; Soro, M. Planning for watershed-wide flood-mitigation and stormwater management using an environmental justice framework. Environ. Pract. 2018, 20, 55–67. [Google Scholar] [CrossRef]
- Ernst, J.; Dewals, B.J.; Detrembleur, S.; Archambeau, P.; Erpicum, S.; Pirotton, M. Micro-scale flood risk analysis based on detailed 2D hydraulic modelling and high resolution geographic data. Nat. Hazards 2010, 55, 181–209. [Google Scholar] [CrossRef]
- Sarhadi, A.; Soltani, S.; Modarres, R. Probabilistic flood inundation mapping of ungauged rivers: Linking GIS techniques and frequency analysis. J. Hydrol. 2012, 458–459, 68–86. [Google Scholar] [CrossRef]
- Chang, L.C.; Shen, H.Y.; Wang, Y.F.; Huang, J.-Y.; Lin, Y.-T. Clustering-based hybrid inundation model for forecasting flood inundation depths. J. Hydrol. 2010, 385, 257–268. [Google Scholar] [CrossRef]

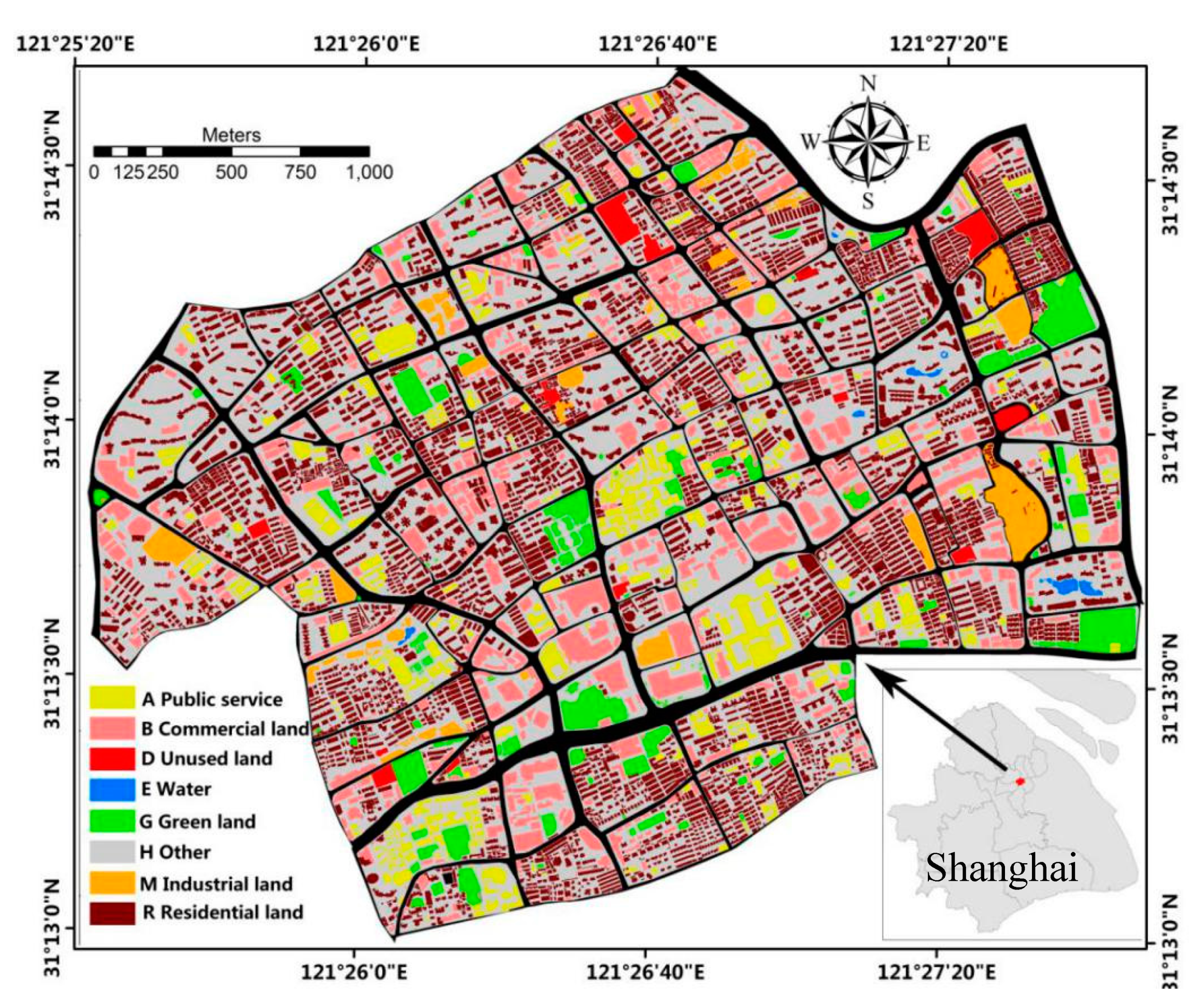
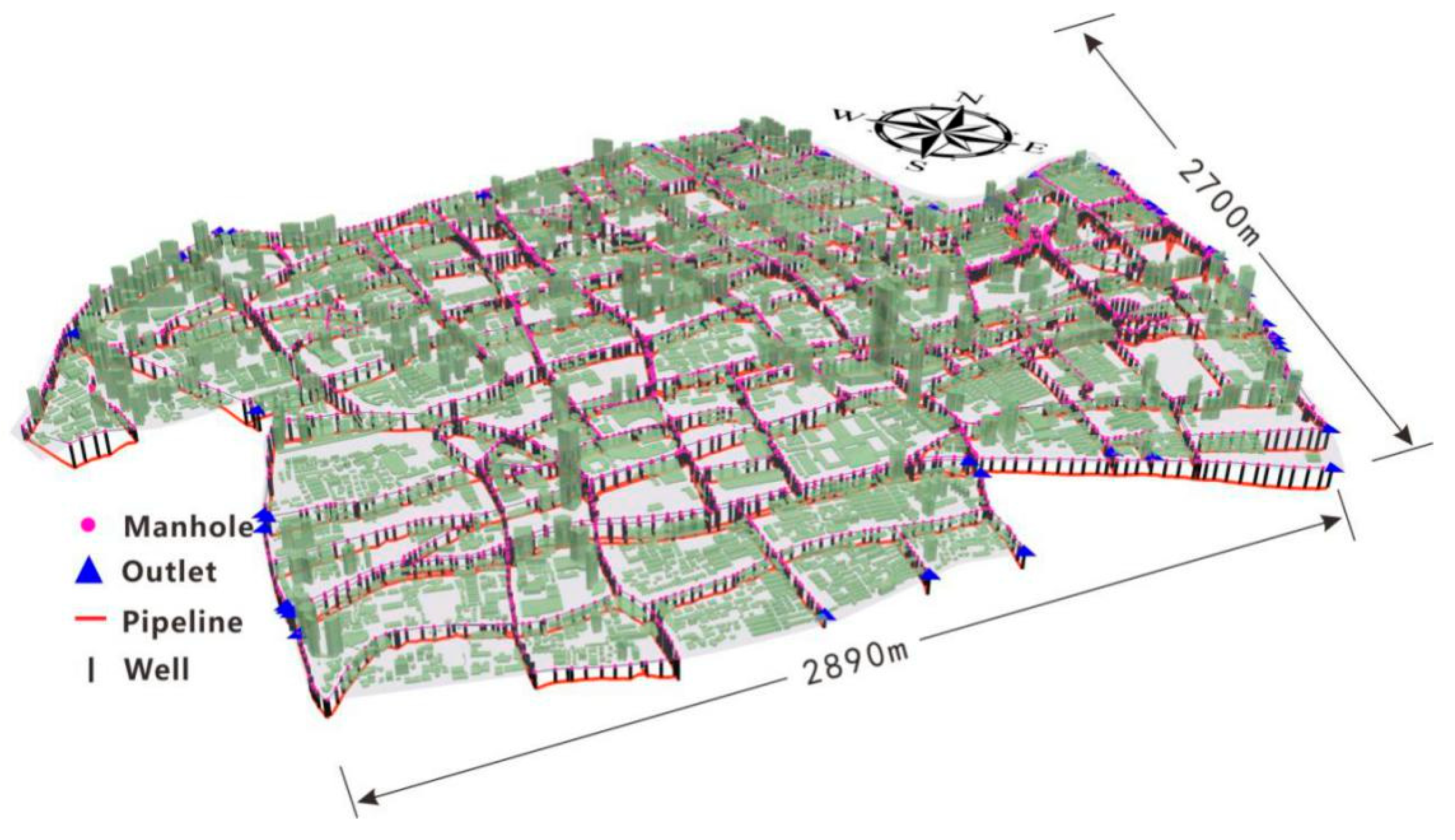
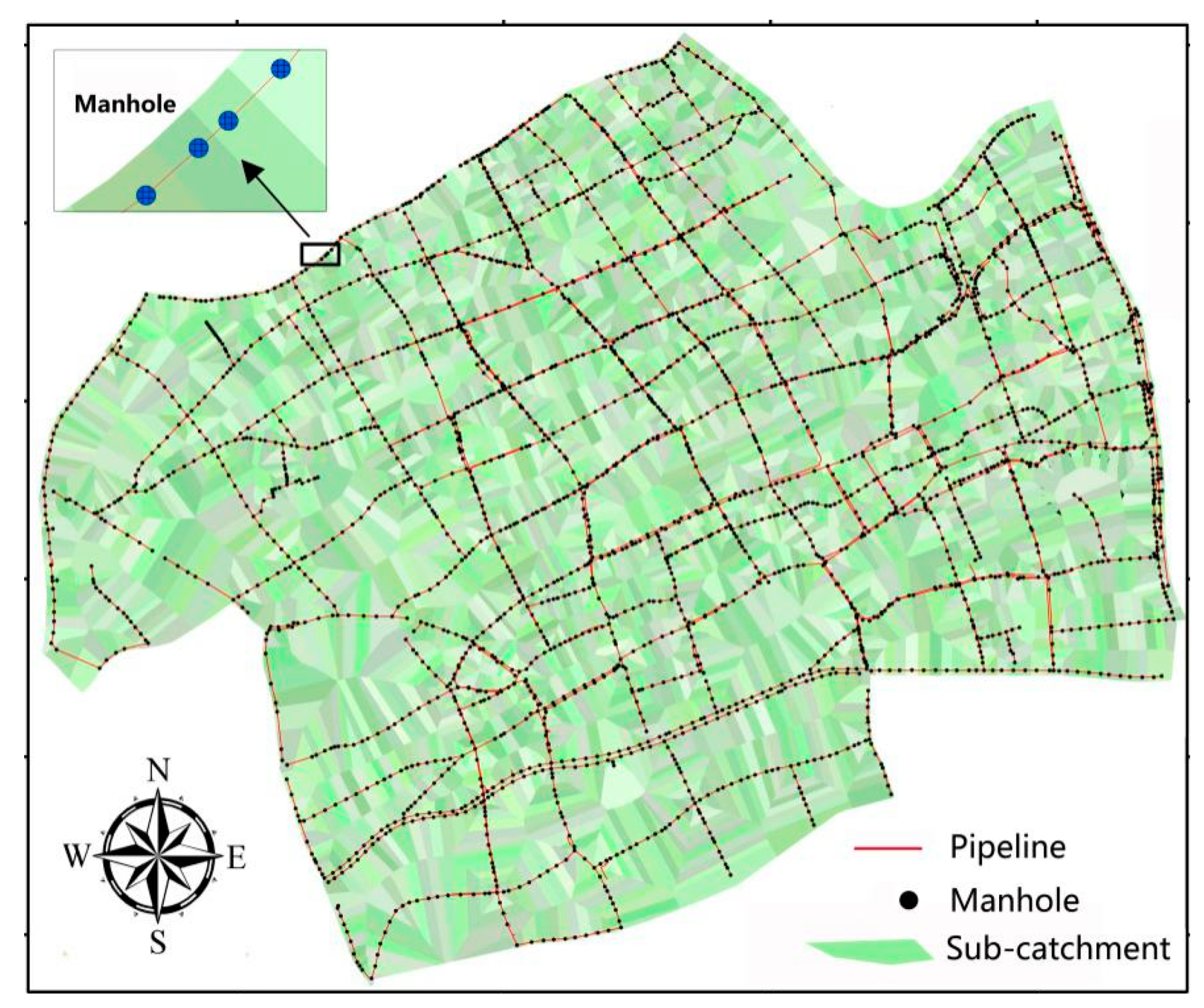
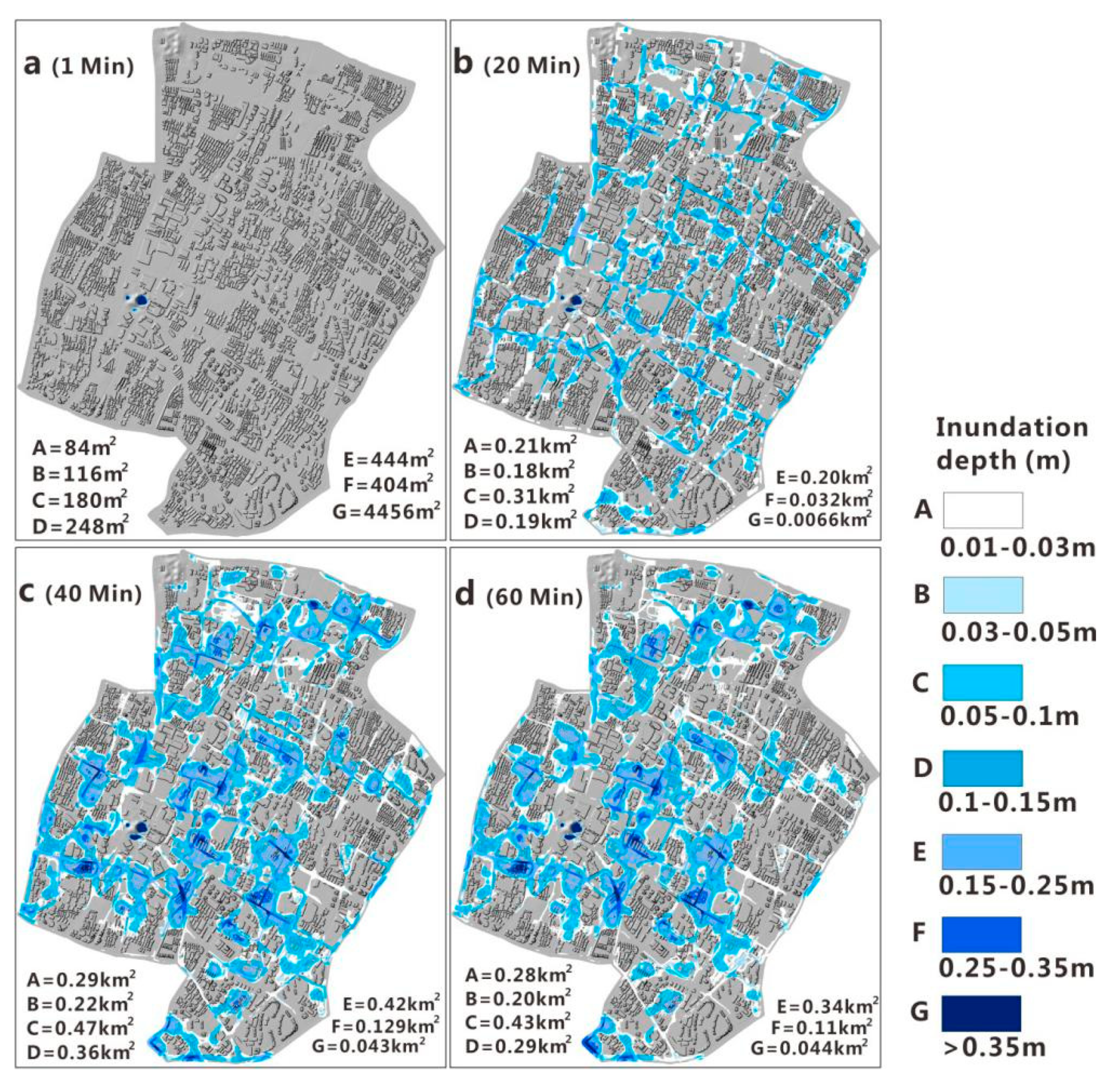
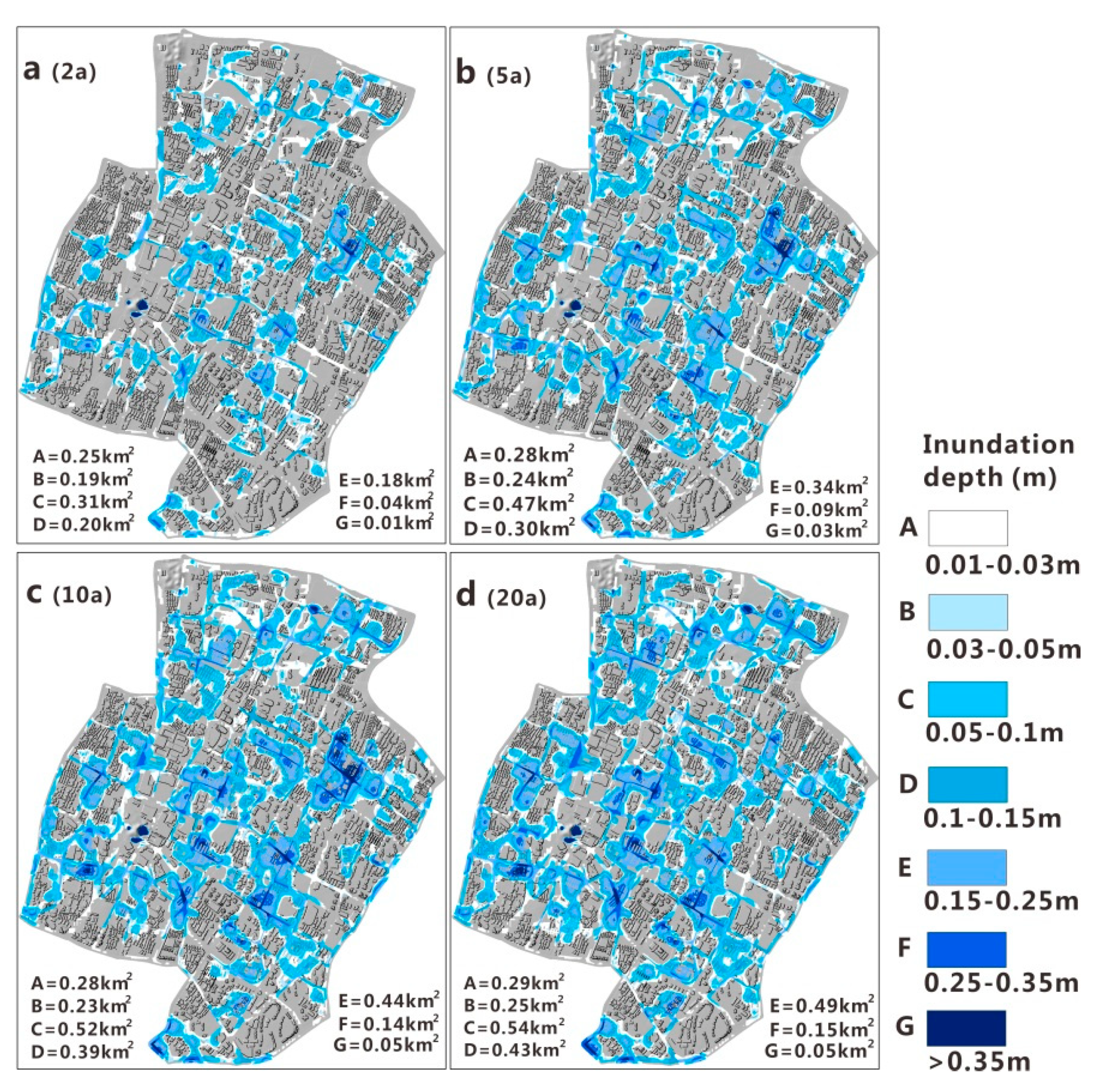
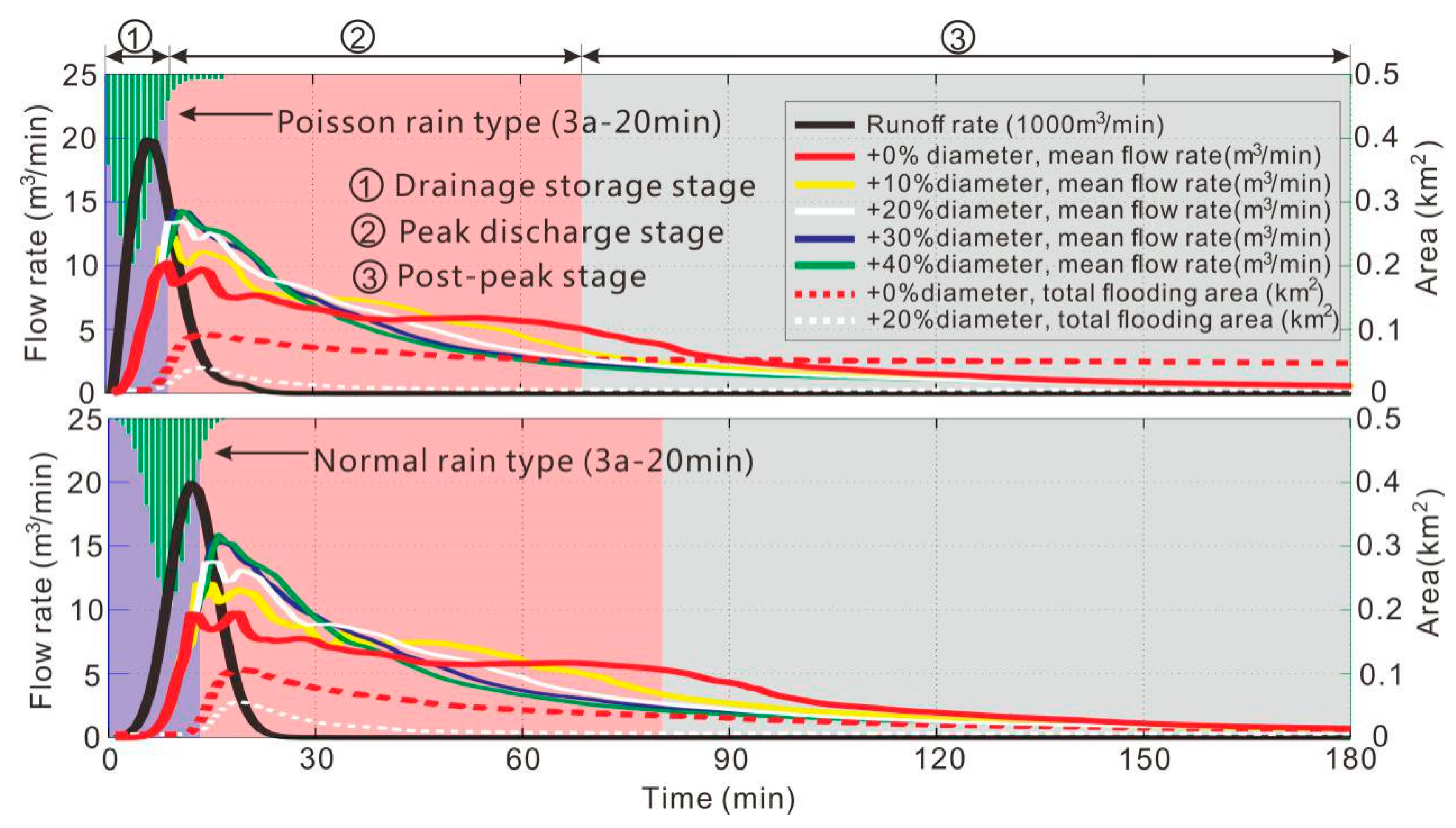
| Land Use Classification | Soil Permeability | ||||
|---|---|---|---|---|---|
| A | B | C | D | ||
| Residential land (R) | 77 | 85 | 90 | 92 | |
| Commercial land (B) | 88 | 91 | 93 | 95 | |
| Industrial land (M) | 86 | 89 | 91 | 93 | |
| Public facilities (A) | 85 | 89 | 92 | 95 | |
| Square land (G) | Green space (G1) | 30 | 55 | 74 | 80 |
| Squares (G2) | 80 | 90 | 95 | 98 | |
| Other land (G3) | 67 | 76 | 80 | 87 | |
| Water surface (E) | 100 | 100 | 100 | 100 | |
| Road (R) | 85 | 89 | 95 | 97 | |
| Pipeline Length | Pipeline Diameter | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Length (m) | 10–20 | 20–30 | 30–50 | 50–100 | >100 | Diameter Range: 0.2–3.6 m | |||
| Diameter (m) | ≤0.5 | 0.6–1 | >1 | ||||||
| Number | 738 | 835 | 1054 | 221 | 24 | Percentage (%) | 23 | 58 | 19 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, X.; Zhang, M.; Wen, J.; Du, S.; Xu, H.; Wang, L.; Yang, Y. A Simple GIS-Based Model for Urban Rainstorm Inundation Simulation. Sustainability 2019, 11, 2830. https://doi.org/10.3390/su11102830
Meng X, Zhang M, Wen J, Du S, Xu H, Wang L, Yang Y. A Simple GIS-Based Model for Urban Rainstorm Inundation Simulation. Sustainability. 2019; 11(10):2830. https://doi.org/10.3390/su11102830
Chicago/Turabian StyleMeng, Xianhong, Min Zhang, Jiahong Wen, Shiqiang Du, Hui Xu, Luyang Wang, and Yan Yang. 2019. "A Simple GIS-Based Model for Urban Rainstorm Inundation Simulation" Sustainability 11, no. 10: 2830. https://doi.org/10.3390/su11102830
APA StyleMeng, X., Zhang, M., Wen, J., Du, S., Xu, H., Wang, L., & Yang, Y. (2019). A Simple GIS-Based Model for Urban Rainstorm Inundation Simulation. Sustainability, 11(10), 2830. https://doi.org/10.3390/su11102830






