The Underground Economy and Carbon Dioxide (CO2) Emissions in China
Abstract
1. Introduction
2. Literature Review
2.1. EKC Hypothesis
2.2. The Underground Economy and Its Environmental Impacts
3. Theoretical Framework
3.1. EKC Model
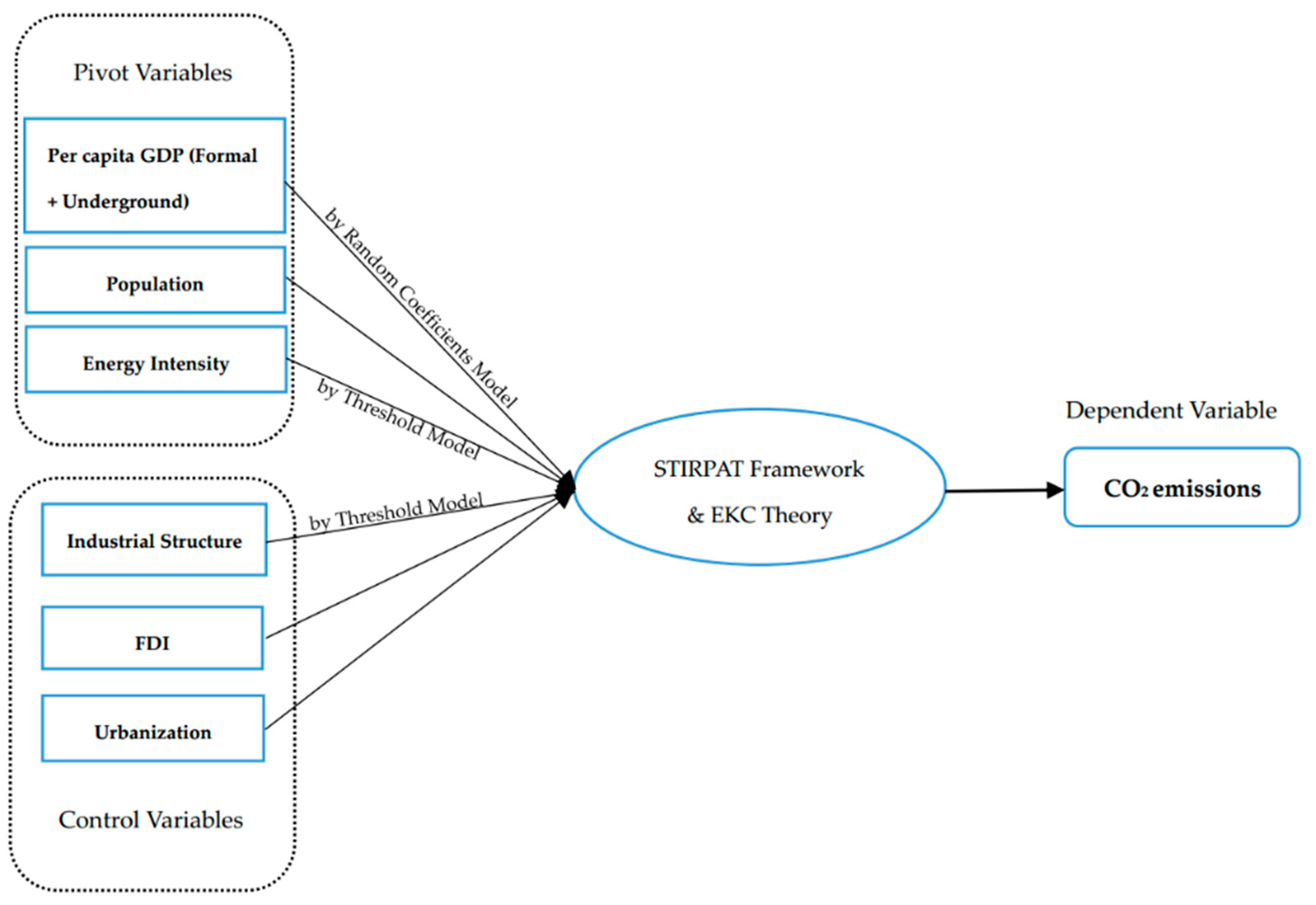
3.2. STIRPAT Model
4. Methodology and Data (Variables)
4.1. Measuring the Underground Economy Scale
4.2. The Random Coefficients Model
4.3. The Threshold Regression
4.4. Measuring CO2 Emissions from Energy Consumption
4.5. Variables and Data Resource
5. Results
5.1. The EKC Estimation
5.2. Driving Forces and the Underground Economic Impacts
5.3. Robustness Check
6. Discussion
6.1. Income-Carbon Dioxides Nexus
6.2. Underground Economy’s Impacts on CO2 Emissions
6.3. Structural and Technological Effects
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| lnGDPT | (lnGDPT)2 | (lnGDPT)3 | lnGDPT | (lnGDPT)2 | (lnGDPT)3 | ||
|---|---|---|---|---|---|---|---|
| Beijing | −9.211 ** | 1.282 * | −0.059 | Henan | −1.066 | 0.388 | −0.037 |
| (−2.27) | (1.87) | (−1.54) | (−0.19) | (0.34) | (−0.47) | ||
| Tianjin | −0.127 | 0.138 | −0.012 | Hubei | −7.089 | 1.510 | −0.100 |
| (−0.04) | (0.24) | (−0.38) | (−1.39) | (1.47) | (−1.45) | ||
| Hebei | −16.347 ** | 3.232 ** | −0.206 ** | Hunan | −0.761 | 0.151 | −0.006 |
| (−2.41) | (2.43) | (−2.36) | (−0.14) | (0.14) | (−0.08) | ||
| Shanxi | −2.352 | 0.552 | −0.041 | Guangdong | −8.852 ** | 1.647 ** | −0.099 ** |
| (−0.41) | (0.47) | (−0.53) | (−1.96) | (2.14) | (−2.27) | ||
| Inner Mongolia | −9.219 ** | 1.836 ** | −0.110 ** | Guangxi | 3.374 | −0.591 | 0.037 |
| (−2.12) | (2.17) | (−2.04) | (0.68) | (−0.58) | (0.54) | ||
| Liaoning | −40.051 *** | 7.308 *** | −0.442 *** | Hainan | −13.229 ** | 2.440 * | −0.141 * |
| (−7.48) | (7.74) | (−7.94) | (−1.95) | (1.87) | (−1.69) | ||
| Jilin | −14.965 *** | 2.894 *** | −0.183 *** | Chongqing | −20.888 *** | 3.913 *** | −0.239 *** |
| (−2.59) | (2.62) | (−2.62) | (−3.16) | (3.12) | (−2.99) | ||
| Heilongjiang | −6.408 | 1.219 | −0.071 | Sichuan | −1.644 | 0.385 | −0.030 |
| (−0.84) | (0.85) | (−0.79) | (−0.31) | (0.36) | (−0.41) | ||
| Shanghai | −0.920 | 0.157 | −0.008 | Guizhou | −6.496 | 1.605 * | −0.115 * |
| (−0.39) | (0.44) | (−0.42) | (−1.52) | (1.73) | (−1.78) | ||
| Jiangsu | −8.606 * | 1.460 * | −0.076 * | Yunnan | −7.414 | 1.779 | −0.133 |
| (−1.94) | (1.88) | (−1.68) | (−1.21) | (1.45) | (−1.64) | ||
| Zhejiang | −13.700 *** | 2.454 *** | −0.141 *** | Shaanxi | −16.758 *** | 3.414 *** | −0.230 *** |
| (−3.60) | (3.81) | (−3.89) | (−4.68) | (4.61) | (−4.54) | ||
| Anhui | −10.857 ** | 2.231 ** | −0.148 ** | Gansu | 11.129 *** | −2.469 *** | 0.185 *** |
| (−2.44) | (2.45) | (−2.45) | (3.38) | (−3.34) | (3.40) | ||
| Fujian | −14.921 ** | 2.670 ** | −0.154 ** | Qinghai | −20.965 *** | 4.178 *** | −0.267 *** |
| (−2.48) | (2.49) | (−2.42) | (−3.85) | (3.76) | (−3.58) | ||
| Jiangxi | 5.052 | −1.151 * | 0.085 * | Ningxia | −2.108 | 0.711 | −0.060 |
| (1.56) | (−1.66) | (1.73) | (−0.35) | (0.59) | (−0.74) | ||
| Shandong | −11.244 ** | 2.187 *** | −0.138 *** | Xinjiang | −36.255 *** | 7.051 *** | −0.449 *** |
| (−2.39) | (2.62) | (−2.75) | (−5.01) | (4.98) | (−4.85) |
| lnGDPT | (lnGDPT)2 | (lnGDPT)3 | lnGDPT | (lnGDPT)2 | (lnGDPT)3 | ||
|---|---|---|---|---|---|---|---|
| Beijing | −21.546 *** | 3.648 *** | −0.203 *** | Henan | −12.340 *** | 2.821 *** | −0.199 *** |
| (−3.73) | (3.85) | (−3.92) | (−2.71) | (3.02) | (−3.12) | ||
| Tianjin | −9.420 ** | 1.725 ** | −0.099 *** | Hubei | −22.595 *** | 4.496 *** | −0.286 *** |
| (−1.99) | (2.33) | (−2.57) | (−4.52) | (4.54) | (−4.37) | ||
| Hebei | −22.232 *** | 4.483 *** | −0.290 *** | Hunan | −9.703 ** | 2.000 ** | −0.125 ** |
| (−4.35) | (4.42) | (−4.33) | (−2.47) | (2.50) | (−2.31) | ||
| Shanxi | −10.704 ** | 2.234 ** | −0.147 ** | Guangdong | −18.273 *** | 3.251 *** | −0.185 *** |
| (−2.38) | (2.49) | (−2.46) | (−3.02) | (3.18) | (−3.21) | ||
| Inner Mongolia | −12.738 *** | 2.517 *** | −0.152 *** | Guangxi | −9.817 ** | 2.107 ** | −0.136 ** |
| (−4.45) | (4.55) | (−4.28) | (−2.33) | (2.42) | (−2.28) | ||
| Liaoning | −21.762 *** | 4.009 *** | −0.241 *** | Hainan | −8.142 | 1.630 | −0.098 |
| (−3.77) | (3.99) | (−4.11) | (−1.27) | (1.34) | (−1.28) | ||
| Jilin | −23.774 *** | 4.638 *** | −0.292 *** | Chongqing | −21.708 *** | 4.213 *** | −0.262 *** |
| (−3.80) | (3.90) | (−3.87) | (−4.22) | (4.41) | (−4.43) | ||
| Heilongjiang | −17.118 *** | 3.336 *** | −0.207 *** | Sichuan | −9.628 ** | 2.164 ** | −0.148 ** |
| (−2.73) | (2.93) | (−2.98) | (−2.01) | (2.23) | (−2.27) | ||
| Shanghai | −6.193 | 0.936 | −0.046 | Guizhou | −8.481 *** | 2.116 *** | −0.157 *** |
| (−1.55) | (1.55) | (−1.51) | (−2.66) | (3.02) | (−3.13) | ||
| Jiangsu | −7.806 | 1.350 | −0.071 | Yunnan | −17.281*** | 3.598 *** | −0.240 *** |
| (−1.58) | (1.57) | (−1.43) | (−3.49) | (3.63) | (−3.58) | ||
| Zhejiang | −22.920 *** | 4.001 *** | −0.226 *** | Shaanxi | −26.105 *** | 5.143 *** | −0.323 *** |
| (−4.32) | (4.49) | (−4.55) | (−5.44) | (5.32) | (−4.99) | ||
| Anhui | −22.480 *** | 4.618 *** | −0.306 *** | Gansu | −5.924 * | 1.403 * | −0.097 * |
| (−8.91) | (9.13) | (−9.01) | (−1.8) | (1.95) | (−1.85) | ||
| Fujian | −33.054 *** | 5.914 *** | −0.342 *** | Qinghai | −31.678 *** | 6.416 *** | −0.419 *** |
| (−5.25) | (5.38) | (−5.31) | (−7.05) | (7.14) | (−7.02) | ||
| Jiangxi | −3.271 | 0.783 | −0.053 | Ningxia | −10.398 * | 2.404 ** | −0.168 ** |
| (−0.85) | (0.97) | (−0.96) | (−1.93) | (2.23) | (−2.34) | ||
| Shandong | −14.839 *** | 2.863 | −0.170 | Xinjiang | −26.038 *** | 4.764 *** | −0.280 *** |
| (−3.07) | (3.35) | (−3.38) | (−4.14) | (3.96) | (−3.62) |
References
- Ballantyne, A.G.; Wibeck, V.; Neset, T.-S. Images of climate change—A pilot study of young people’s perceptions of ICT-based climate visualization. Clim. Chang. 2016, 134, 73–85. [Google Scholar] [CrossRef]
- Karl, T.R.; Trenberth, K.E. Modern Global Climate Change. Science 2003, 302, 1719–1723. [Google Scholar] [CrossRef]
- Stern, D.I.; Zha, D. Economic growth and particulate pollution concentrations in China. Environ. Econ. Policy Stud. 2016, 18, 327–338. [Google Scholar] [CrossRef]
- Lewis, J.I. China’s strategic priorities in international climate change negotiations. Wash. Q. 2007, 31, 155–174. [Google Scholar] [CrossRef]
- Biswas, A.K.; Farzanegan, M.R.; Thum, M. Pollution, shadow economy and corruption: Theory and evidence. Ecol. Econ. 2012, 75, 114–125. [Google Scholar] [CrossRef]
- Edgar, E.L. THE underground economy and the currency enigma. Public Financ. Financ. Publiques 1994, 49, 119–136. [Google Scholar]
- Schneider, F. Measuring the Size and Development of the Shadow Economy. Can the Causes be Found and the Obstacles be Overcome? In Essays on Economic Psychology; Springer: Berlin, Germany, 1994. [Google Scholar]
- Huang, P.C.C. China’s Neglected Informal Economy Reality and Theory. Mod. China 2009, 35, 405–438. [Google Scholar] [CrossRef]
- Wang, X. Grey Income and Resident Income Gap. Tax. China 2007, 48–49. (in Chinese). [Google Scholar] [CrossRef]
- Li, J. Measuring the Unobservable Economy Based on National Accounts. J. Cent. Univ. Financ. Econ. 2008, 28, 24–28. (in Chinese). [Google Scholar]
- Mazhar, U.; Elgin, C. Environmental regulation, pollution and the informal economy. SBP Res. Bull. 2013, 9, 62–81. [Google Scholar]
- Yu, C.; Gao, H. The effect of environmental regulation on environmental pollution in China—Based on the hidden economy perspective. China Ind. Econ. 2015, 32, 21–35. [Google Scholar]
- Elgin, C.; Oztunali, O. Pollution and informal economy. Econ. Syst. 2014, 38, 333–349. [Google Scholar] [CrossRef]
- Grossman, G.M.; Krueger, A.B. Economic Growth and the Environment. Nber Work. Pap. 1995, 110, 353–377. [Google Scholar] [CrossRef]
- Stern, D.I. Innovation and spillovers in regions: Evidence from European patent data. Glob. Environ. Chang. 2006, 16, 207–220. [Google Scholar] [CrossRef]
- Holtz-Eakin, D.; Selden, T.M. Stoking the fires? CO2 emissions and economic growth. J. Public Econ. 1995, 57, 85–101. [Google Scholar] [CrossRef]
- Zhang, C.; Lin, Y. Panel estimation for urbanization, energy consumption and CO2 emissions: A regional analysis in China. Energy Policy 2012, 49, 488–498. [Google Scholar] [CrossRef]
- Kaika, D.; Zervas, E. The Environmental Kuznets Curve (EKC) theory—Part A: Concept, causes and the CO2 emissions case. Energy Policy 2013, 62, 1392–1402. [Google Scholar] [CrossRef]
- Kaika, D.; Zervas, E. The environmental Kuznets curve (EKC) theory. Part B Critical issues. Energy Policy 2013, 62, 1403–1411. [Google Scholar] [CrossRef]
- Yin, J.; Zheng, M.; Chen, J. The effects of environmental regulation and technical progress on CO2 Kuznets curve: An evidence from China. Energy Policy 2015, 77, 97–108. [Google Scholar] [CrossRef]
- Taskin, F.; Zaim, O. Searching for a Kuznets curve in environmental efficiency using kernel estimation. Econ. Lett. 2000, 68, 217–223. [Google Scholar] [CrossRef]
- Maddison, D. Environmental Kuznets curves: A spatial econometric approach. J. Environ. Econ. Manag. 2006, 51, 218–230. [Google Scholar] [CrossRef]
- Zheng, X.; Yu, Y.; Wang, J.; Deng, H. Identifying the determinants and spatial nexus of provincial carbon intensity in China: A dynamic spatial panel approach. Reg. Environ. Chang. 2014, 14, 1651–1661. [Google Scholar] [CrossRef]
- Kang, Y.-Q.; Zhao, T.; Yang, Y.-Y. Environmental Kuznets curve for CO2 emissions in China: A spatial panel data approach. Ecol. Indic. 2016, 63, 231–239. [Google Scholar] [CrossRef]
- Zhou, Z.; Ye, X.; Ge, X. The Impacts of Technical Progress on Sulfur Dioxide Kuznets Curve in China: A Spatial Panel Data Approach. Sustainability 2017, 9, 674. [Google Scholar] [CrossRef]
- Ge, X.; Zhou, Z.; Zhou, Y.; Ye, X.; Liu, S. A Spatial Panel Data Analysis of Economic Growth, Urbanization, and NOx Emissions in China. Int. J. Environ. Res. Public Health 2018, 15, 725. [Google Scholar] [CrossRef]
- Xu, B.; Zhong, R.; Liu, Y. Comparison of CO2 emissions reduction efficiency of household fuel consumption in China. Sustainability 2019, 11, 979. [Google Scholar] [CrossRef]
- Haseeb, A.; Xia, E.; Baloch, M.A.; Abbas, K. Financial development, globalization, and CO2 emission in the presence of EKC: Evidence from BRICS countries. Environ. Sci. Pollut. Res. 2018, 25, 31283–31296. [Google Scholar] [CrossRef]
- Levinson, A. The ups and downs of the environmental Kuznets curve. Recent Adv. Environ. Econ. 2002, 119–139. [Google Scholar] [CrossRef]
- Millimet, D.L.; List, J.A.; Stengos, T. The Environmental Kuznets Curve: Real Progress or Misspecified Models? Rev. Econ. Stat. 2003, 85, 1038–1047. [Google Scholar] [CrossRef]
- List, J.A.; Gallet, C.A. The environmental Kuznets curve: Does one size fit all? Ecol. Econ. 1999, 31, 409–423. [Google Scholar] [CrossRef]
- Stern, D.I. Progress on the Environmental Kuznets Curve? Environ. Dev. Econ. 1998, 3, 173–196. [Google Scholar] [CrossRef]
- Unruh, G.C.; Moomaw, W.R. An alternative analysis of apparent EKC-type transitions. Ecol. Econ. 1998, 25, 221–229. [Google Scholar] [CrossRef]
- Franklin, R.S.; Ruth, M. Growing Up and Cleaning Up: The Environmental Kuznets Curve Redux. Appl. Geogr. 2012, 32, 29–39. [Google Scholar] [CrossRef]
- Bradford, D.F.; Schlieckert, R.; Shore, S.H. The Environmental Kuznets Curve: Exploring a Fresh Specification. Contrib. Econ. Anal. Policy 2000, 4, 1073. [Google Scholar]
- Cole, M.A.; Neumayer, E. Examining the Impact of Demographic Factors on Air Pollution. Popul. Environ. 2004, 26, 5–21. [Google Scholar] [CrossRef]
- Perman, R.; Stern, D.I. Evidence from panel unit root and cointegration tests that the Environmental Kuznets Curve does not exist. Aust. J. Agric. Resour. Econ. 2003, 47, 325–347. [Google Scholar] [CrossRef]
- Poumanyvong, P.; Kaneko, S. Does urbanization lead to less energy use and lower CO2 emissions? A cross-country analysis. Ecol. Econ. 2010, 70, 434–444. [Google Scholar] [CrossRef]
- Dinda, S.; Coondoo, D. Income and emission: A panel data-based cointegration analysis. Mpra Pap. 2006, 57, 167–181. [Google Scholar] [CrossRef]
- Wagner, M. The carbon Kuznets curve: A cloudy picture emitted by bad econometrics? Resour. Energy Econ. 2008, 30, 388–408. [Google Scholar] [CrossRef]
- Kostakis, I. The impact of shadow economy and/or corruption on private consumption: Further evidence from selected Eurozone economies. Eurasian Econ. Rev. 2017, 7, 411–434. [Google Scholar] [CrossRef]
- Hajilee, M.; Stringer, D.Y.; Metghalchi, M. Financial market inclusion, shadow economy and economic growth: New evidence from emerging economies. Q. Rev. Econ. Financ. 2017, 66, S1062976916301600. [Google Scholar] [CrossRef]
- Blackman, A.; Shih, J.-S.; Evans, D.; Batz, M.; Newbold, S.; Cook, J. The benefits and costs of informal sector pollution control: Mexican brick kilns. Environ. Dev. Econ. 2006, 11, 603–627. [Google Scholar] [CrossRef]
- Baksi, S.; Bose, P. Environmental Regulation in the Presence of An Informal Sector, University of Winnipeg Department of Economics Working Paper; University of Winnipe: Winnipeg, MB, Canada, 2010; Volume 3. [Google Scholar]
- Croitoru, L.; Sarraf, M. Benefits and costs of the informal sector: The case of brick kilns in Bangladesh. J. Environ. Prot. 2012, 3, 476–484. [Google Scholar] [CrossRef]
- Martínez-Zarzoso, I.; Bengochea-Morancho, A.; Morales-Lage, R. The impact of population on CO2 emissions: Evidence from European countries. Environ. Resour. Econ. 2007, 38, 497–512. [Google Scholar] [CrossRef]
- Dinda, S. Environmental Kuznets Curve Hypothesis: A Survey. Ecol. Econ. 2004, 49, 431–455. [Google Scholar] [CrossRef]
- Dietz, T.; Rosa, E.A. Effects of Population and Affluence on CO2 Emissions. Proc. Natl. Acad. Sci. USA 1997, 94, 175–179. [Google Scholar] [CrossRef]
- York, R.; Rosa, E.A.; Dietz, T. STIRPAT, IPAT and ImPACT: Analytic tools for unpacking the driving forces of environmental impacts. Ecol. Econ. 2003, 46, 351–365. [Google Scholar] [CrossRef]
- Cheung, K.-Y.; Ping, L. Spillover effects of FDI on innovation in China: Evidence from the provincial data. China Econ. Rev. 2004, 15, 25–44. [Google Scholar] [CrossRef]
- Wang, H.; Jin, Y. Industrial Ownership and Environmental Performance: Evidence from China; The World Bank: Washington, DC, USA, 2002. [Google Scholar]
- Bao, Q.; Chen, Y.; Song, L. Foreign direct investment and environmental pollution in China: A simultaneous equations estimation. Environ. Dev. Econ. 2011, 16, 71–92. [Google Scholar] [CrossRef]
- Dean, J.M.; Lovely, M.E.; Wang, H. Are Foreign Investors Attracted to Weak Environmental Regulations? Evaluating the Evidence from China; The World Bank: Washington, DC, USA, 2005. [Google Scholar]
- Stern, D.I. The Rise and Fall of the Environmental Kuznets Curve. World Dev. 2004, 32, 1419–1439. [Google Scholar] [CrossRef]
- Parikh, J.; Shukla, V. Urbanization, energy use and greenhouse effects in economic development. Angew. Chem. 1995, 54, 3932–3936. [Google Scholar] [CrossRef]
- Chen, H.; Jia, B.; Lau, S.S.Y. Sustainable urban form for Chinese compact cities: Challenges of a rapid urbanized economy. Habitat Int. 2008, 32, 28–40. [Google Scholar] [CrossRef]
- Li, J.; Xu, G. Investigation for the Unobserved Economy in China. Stat. Res. 2005, 22, 21–26. (In Chinese) [Google Scholar]
- Liu, H.; Xia, F. Estimate the Informal Economic Size in China: The Production Factor Method. Financ. Res. 2004, 25, 16–19. (In Chinese) [Google Scholar]
- Cole, M. Re-examining the pollution-income relationship: A random coefficients approach. Econ. Bull. 2005, 14, 1–7. [Google Scholar]
- Hansen, B.E. Threshold effects in non-dynamic panels: Estimation, testing, and inference. J. Econom. 1999, 93, 345–368. [Google Scholar] [CrossRef]
- Hansen, B.E. Inference When a Nuisance Parameter Is Not Identified Under the Null Hypothesis. Econometrica 1996, 64, 413–430. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Synthesis Report; Cambridge University Press: Cambridge, UK, 2007.
- Wang, P.; Wu, W.; Zhu, B.; Wei, Y. Examining the impact factors of energy-related CO2 emissions using the STIRPAT model in Guangdong Province, China. Appl. Energy 2013, 106, 65–71. [Google Scholar] [CrossRef]
- Qiang, W.; Wu, S.D.; Zeng, Y.E.; Wu, B.W. Exploring the relationship between urbanization, energy consumption, and CO 2 emissions in different provinces of China. Renew. Sustain. Energy Rev. 2016, 54, 1563–1579. [Google Scholar]
- National Statistics Bureau of China. Available online: http://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 10 October 2018).
- Perman, R.; Ma, Y.; Mcgilvray, J. Natural Resource and Environmental Economics; Pearson Education: London, UK, 2003. [Google Scholar]
- Cole, M.A. Limits to growth, sustainable development and environmental Kuznets curves: An examination of the environmental impact on economic development. Sustain. Dev. 2015, 7, 87–97. [Google Scholar] [CrossRef]
- Canas, Â.; Ferrão, P.; Conceição, P. A new environmental Kuznets curve? Relationship between direct material input and income per capita: Evidence from industrialised countries. Ecol. Econ. 2003, 46, 217–229. [Google Scholar] [CrossRef]
- Rothman, D.S. Environmental Kuznets curves—Real progress or passing the buck? A case for consumption-based approaches. Ecol. Econ. 1998, 25, 177–194. [Google Scholar] [CrossRef]
- Torras, M.; Boyce, J.K. Income, inequality, and pollution: A reassessment of the environmental Kuznets Curve. Ecol. Econ. 1998, 25, 147–160. [Google Scholar] [CrossRef]
- Ai, H.; Deng, Z.; Yang, X. The effect estimation and channel testing of the technological progress on China’s regional environmental performance. Ecol. Indic. 2015, 51, 67–78. [Google Scholar] [CrossRef]
- Blackman, A.; Bannister, G.J. Community pressure and clean technology in the informal sector: An econometric analysis of the adoption of propane by traditional mexican brickmakers. J. Environ. Econ. Manag. 1998, 35, 1–21. [Google Scholar] [CrossRef]
- Syrquin, M.; Chenery, H.B. Patterns of Development, 1950 to 1983; The World Bank: Washington, DC, USA, 1989; p. e867. [Google Scholar]
- Suri, V.; Chapman, D. Economic growth, trade and energy: Implications for the environmental Kuznets curve. Ecol. Econ. 1998, 25, 195–208. [Google Scholar] [CrossRef]
- Wang, Y.; Han, R.; Kubota, J. Is there an Environmental Kuznets Curve for SO2 emissions? A semi-parametric panel data analysis for China. Renew. Sustain. Energy Rev. 2016, 54, 1182–1188. [Google Scholar] [CrossRef]
- REN21 Secretariat. Renewables 2014: Global Status Report; REN21 Secretariat: Paris, France, 2014. [Google Scholar]
- He, X.; Zhang, Y. Influence Factors and Environmental Kuznets Curve Relink Effect of Chinese Industry’s Carbon Dioxide Emission—Empirical Research Based on STIRPAT Model with Industrial Dynamic Panel Data. China Ind. Econ. 2012, 26–35. (In Chinese) [Google Scholar] [CrossRef]
| Energy Type | Raw Coal | Coke | Fuel Oil | Diesel | Kerosene | Gasoline | Electricity |
|---|---|---|---|---|---|---|---|
| Emission factor | 0.7559 | 0.8550 | 0.6185 | 0.5921 | 0.5714 | 0.5538 | 0.2720 |
| Conversion coefficient (tce/t) | 0.7143 | 0.9714 | 1.4286 | 1.4571 | 1.4714 | 1.4714 | - |
| Variable | Definition (unit) | Mean | Std. Dev. | Min | Max |
|---|---|---|---|---|---|
| lnGDPT | Total (underground + formal) per capita GDP (100 yuan) | 5.435 | 0.845 | 3.354 | 7.596 |
| lnGDPN | Underground per capita GDP (100 yuan) | 4.188 | 0.981 | 1.286 | 6.762 |
| fdi | Ratio of FDI to GDP (%) | 2.765 | 2.698 | 0.001 | 21.188 |
| str | Proportion of secondary industry (%) | 45.325 | 7.853 | 19.262 | 59.045 |
| lnPOP | Total Population (10 thousand) | 8.143 | 0.763 | 6.221 | 9.306 |
| urb | Proportion of urban population (%) | 47.414 | 15.621 | 21.890 | 89.600 |
| lnEI | Energy intensity (tons of coal equivalent/billion yuan) | 9.639 | 0.506 | 8.669 | 10.928 |
| lnCO2 | Carbon dioxides emissions (10,000 tons) | 10.155 | 0.894 | 6.904 | 12.030 |
| Dependent Variable: lnCO2 | Cubic Model | Quadratic Model | Linear Model |
|---|---|---|---|
| lnGDPT | −9.430 *** | 0.249 | 0.329 *** |
| (−2.92) | (0.76) | (4.68) | |
| (lnGDPT)2 | 1.819 *** | 0.008 | |
| (2.90) | (0.24) | ||
| (lnGDPT)3 | −0.113 *** | ||
| (−2.77) | |||
| fdi | −0.016 * | −0.01 | −0.008 |
| (−1.74) | (−0.78) | (−0.60) | |
| str | 0.014 *** | 0.018 *** | 0.016 *** |
| (3.43) | (4.26) | (3.69) | |
| lnPOP | 0.631 | 0.410 | 0.386 |
| (0.82) | (0.42) | (0.45) | |
| urb | 0.040 *** | 0.037 *** | 0.037 *** |
| (3.91) | (3.65) | (4.27) | |
| lnEI | 0.379 *** | 0.431 *** | 0.466 *** |
| (3.02) | (3.46) | (4.39) | |
| Test of parameter constancy (χ2) | 17,749.03 *** | 15,448.34 *** | 14,487.28 *** |
| Observations | 570 | 570 | 570 |
| . | Economic Structure (str) As the Regime Dependent Variable | Technology (lnEI) as the Regime Dependent Variable |
|---|---|---|
| Test for single threshold | ||
| F1 | 46.73 | 66.86 |
| P-value | 0.038 | 0.006 |
| (10%, 5%, 1% critical values) | 36.9721, 44.2496, 61.4470 | 34.212, 40.132, 65.269 |
| Test for double threshold | ||
| F2 | 36.79 | 45.70 |
| P-value | 0.048 | 0.018 |
| (10%, 5%, 1% critical values) | 32.426, 36.044, 49.296 | 29.862, 37.052, 52.730 |
| Test for triple-threshold | ||
| F3 | 28.56 | 41.19 |
| P-value | 0.608 | 0.656 |
| (10%, 5%, 1% critical values) | 63.668, 73.516, 92.938 | 93.692, 105.639, 148.572 |
| Threshold estimates (γ1, γ2) | 4.782, 5.635 | 4.796, 5.633 |
| Economic Structure (str) as the Regime Dependent Variable | Technology (lnEI) as the Regime Dependent Variable | ||||||
|---|---|---|---|---|---|---|---|
| lnGDPN | 0.168 *** | lnPOP | 1.302 *** | lnGDPN | 0.159 *** | lnPOP | 1.249 *** |
| (8.47) | (11.36) | (8.16) | (11.13) | ||||
| fdi | –0.016 *** | urb | 0.036 *** | fdi | −0.017 *** | urb | 0.034 *** |
| (−3.88) | (14.45) | (−4.07) | (14.11) | ||||
| lnEI | 0.350 *** | str1(β1) | 0.006 *** | str | 0.010 *** | lnEI1(β1) | 0.323 *** |
| (7.56) | (2.62) | (5.46) | (7.15) | ||||
| str2(β2) | 0.010 *** | lnEI2(β2) | 0.343 *** | ||||
| Observations | 570 | (5.23) | Observations | 570 | (7.59) | ||
| R2 | 0.917 | str3(β3) | 0.013 *** | R2 | 0.921 | lnEI3(β3) | 0.363 *** |
| Adjusted-R2 | 0.911 | (7.29) | Adjusted-R2 | 0.915 | (7.99) | ||
| aic | −587.6 | aic | −612.5 | ||||
| bic | −548.5 | bic | −573.4 | ||||
| Variables | M1 | M2 | M3 | M4 |
|---|---|---|---|---|
| lnGDPT | −15.737 *** | −9.912 *** | −16.970 *** | −16.266 *** |
| (−5.94) | (−3.06) | (−6.09) | (−6.05) | |
| (lnGDPT)2 | 3.071 *** | 1.953 *** | 3.324 *** | 3.186 *** |
| (6.28) | (3.16) | (6.25) | (6.42) | |
| (lnGDPT)3 | −0.191 *** | −0.120 *** | −0.212 *** | −0.199 *** |
| (−6.20) | (−3.00) | (−6.13) | (−6.32) | |
| lnPOP | 1.722 * | 1.811 | 0.818 | 1.908 * |
| (1.90) | (1.52) | (0.92) | (1.89) | |
| lnEI | 0.430 *** | 0.308 ** | 0.480 *** | 0.420 *** |
| (3.96) | (2.38) | (5.32) | (4.23) | |
| fdi | −0.008 | |||
| (−0.70) | ||||
| str | 0.013 *** | |||
| (3.07) | ||||
| urb | 0.039 *** | |||
| (4.33) |
| Variables | Economic Structure (str) as the Regime Dependent Variable | Technology (lnEI) as the Regime Dependent Variable | |||||
|---|---|---|---|---|---|---|---|
| M1 | M2 | M3 | M4 | M5 | M6 | M7 | |
| lnGDPN | 0.347 *** | 0.321 *** | 0.175 *** | 0.329 *** | 0.320 *** | 0.179 *** | 0.308 *** |
| (18.02) | (16.23) | (8.80) | (16.80) | (16.57) | (9.03) | (15.58) | |
| lnPOP | 1.518 *** | 1.295 *** | 1.379 *** | 1.290 *** | 1.068 *** | 1.269 *** | 1.432 *** |
| (11.75) | (9.57) | (12.57) | (10.37) | (8.16) | (11.96) | (11.44) | |
| lnEI | 0.161 *** | 0.103 ** | 0.385 *** | ||||
| (3.06) | (2.03) | (8.12) | |||||
| fdi | −0.024*** | −0.023 *** | |||||
| (−4.83) | (−4.70) | ||||||
| urb | 0.040 *** | 0.036 *** | |||||
| (16.61) | (14.52) | ||||||
| str | 0.011 *** | ||||||
| (5.36) | |||||||
| Thresholds (γ1 γ2) | 4.954 | 4.796 | 5.308 | 4.796 | 4.796 | 4.782 | 4.769 |
| 5.670 | 5.633 | 6.048 | 5.566 | 5.566 | 5.651 | 5.635 | |
| str1(β1) | 0.005 ** | 0.004 | 0.011 *** | ||||
| str2(β2) | 0.011 *** | 0.011 *** | 0.014 *** | ||||
| str3(β3) | 0.016 *** | 0.016 *** | 0.017 *** | ||||
| lnEI1(β1) | 0.176 *** | 0.161 *** | 0.439 *** | 0.098 ** | |||
| lnEI2(β2) | 0.208 *** | 0.196 *** | 0.461 *** | 0.126 ** | |||
| lnEI3(β3) | 0.244 *** | 0.232 *** | 0.484 *** | 0.160 *** | |||
| Observations | 570 | 570 | 570 | 570 | 570 | 570 | 570 |
| R2 | 0.879 | 0.884 | 0.914 | 0.882 | 0.887 | 0.915 | 0.887 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z. The Underground Economy and Carbon Dioxide (CO2) Emissions in China. Sustainability 2019, 11, 2802. https://doi.org/10.3390/su11102802
Zhou Z. The Underground Economy and Carbon Dioxide (CO2) Emissions in China. Sustainability. 2019; 11(10):2802. https://doi.org/10.3390/su11102802
Chicago/Turabian StyleZhou, Zhimin. 2019. "The Underground Economy and Carbon Dioxide (CO2) Emissions in China" Sustainability 11, no. 10: 2802. https://doi.org/10.3390/su11102802
APA StyleZhou, Z. (2019). The Underground Economy and Carbon Dioxide (CO2) Emissions in China. Sustainability, 11(10), 2802. https://doi.org/10.3390/su11102802





