Optimal Design and Application of a Multiple Tuned Mass Damper System for an In-Service Footbridge
Abstract
:1. Introduction
2. Parametric Study and Optimal Design
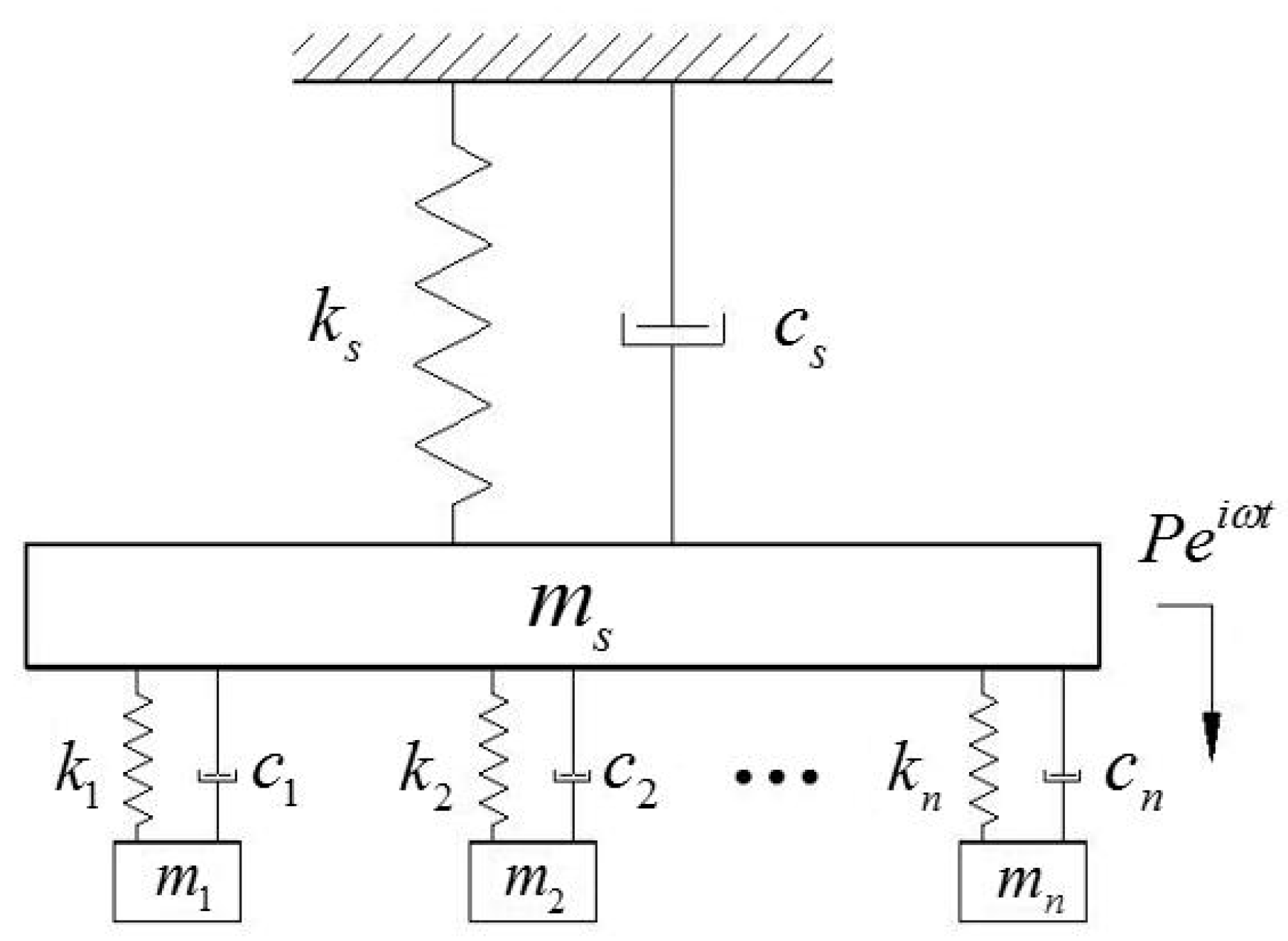
2.1. Schematic Diagram and Dynamic Analysis
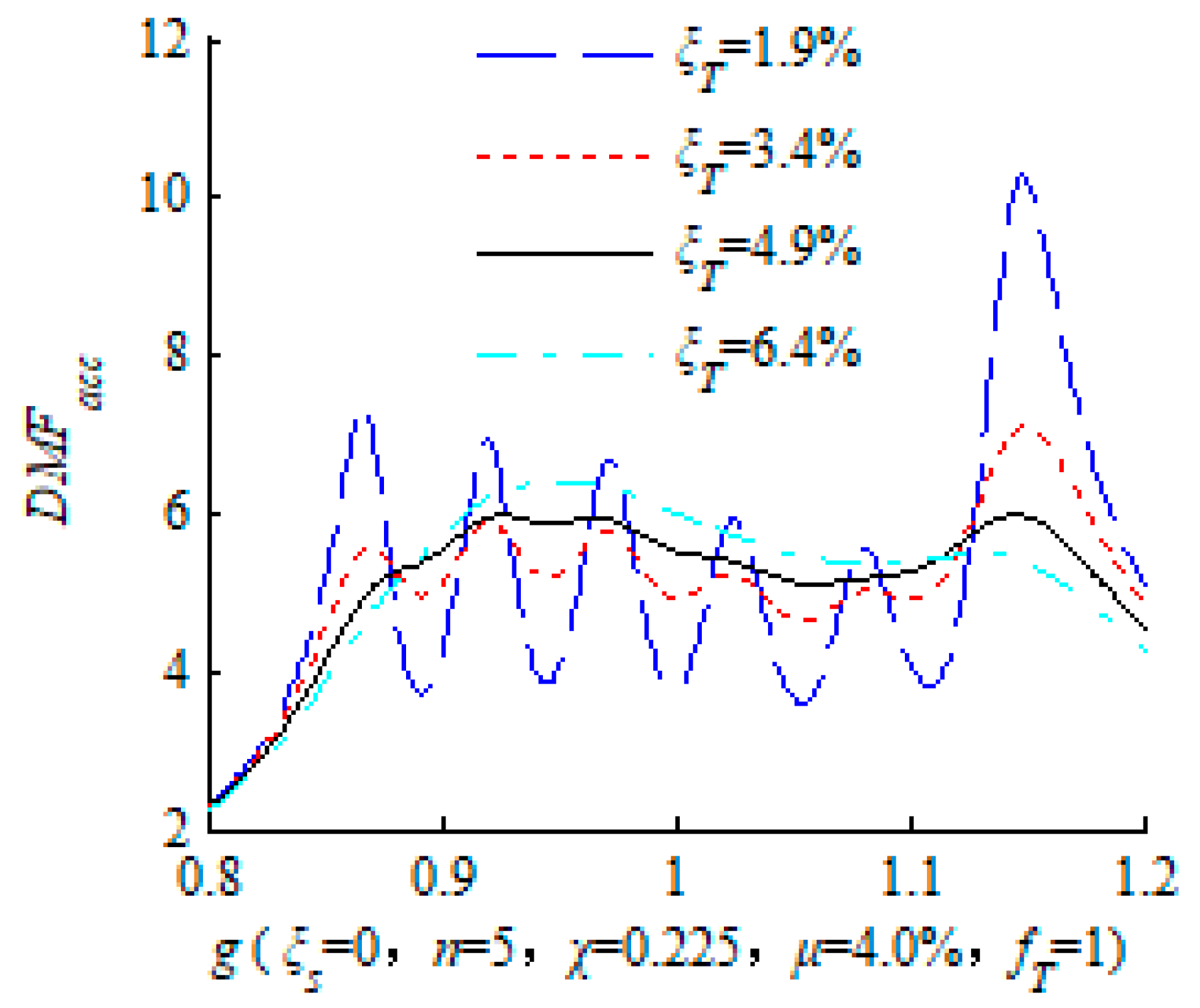
2.2. Discussion on the Frequency Bandwidth and TMD Damping Ratio
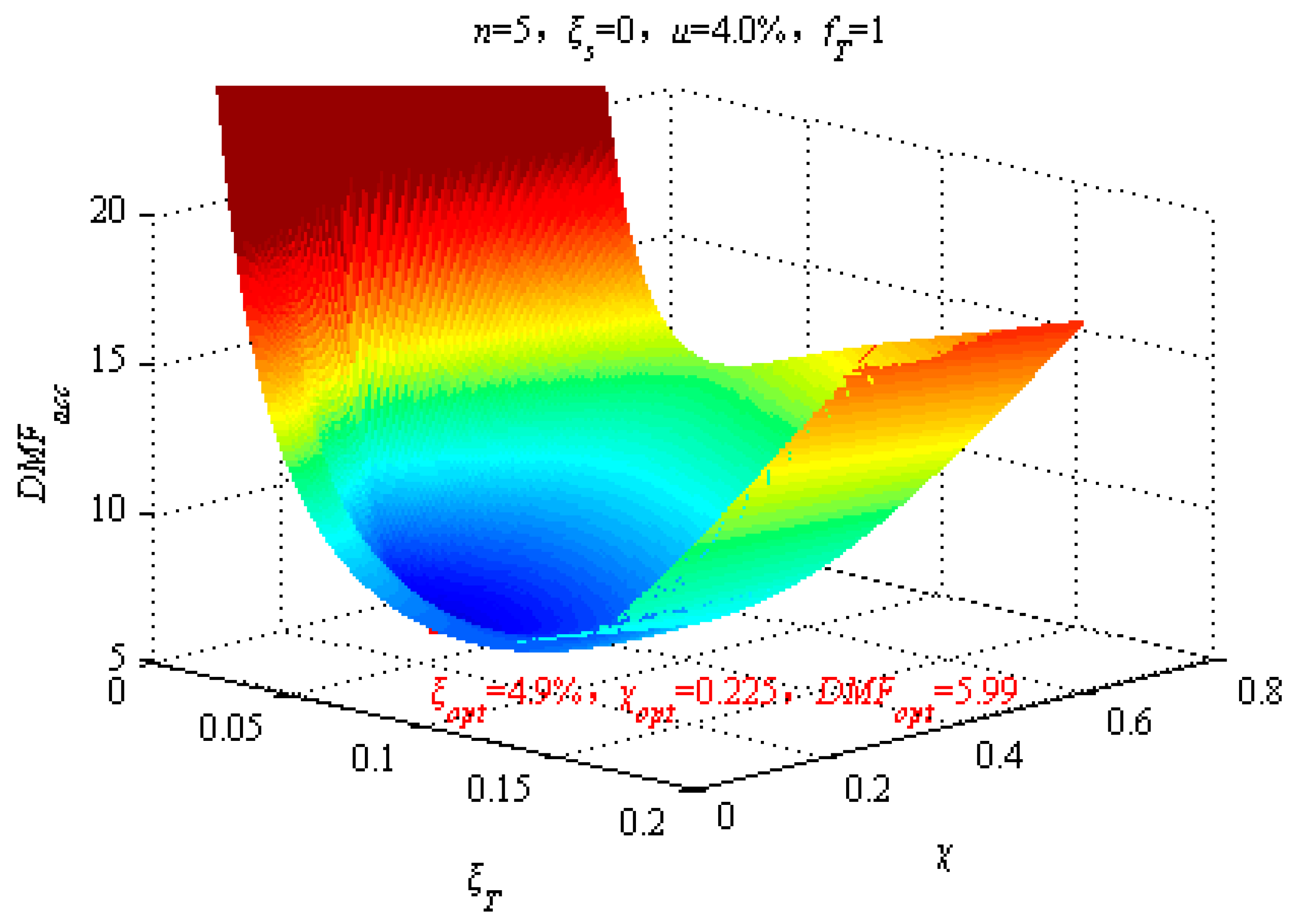
2.3. Optimal Design of the Frequency Bandwidth and TMD Damping Ratio
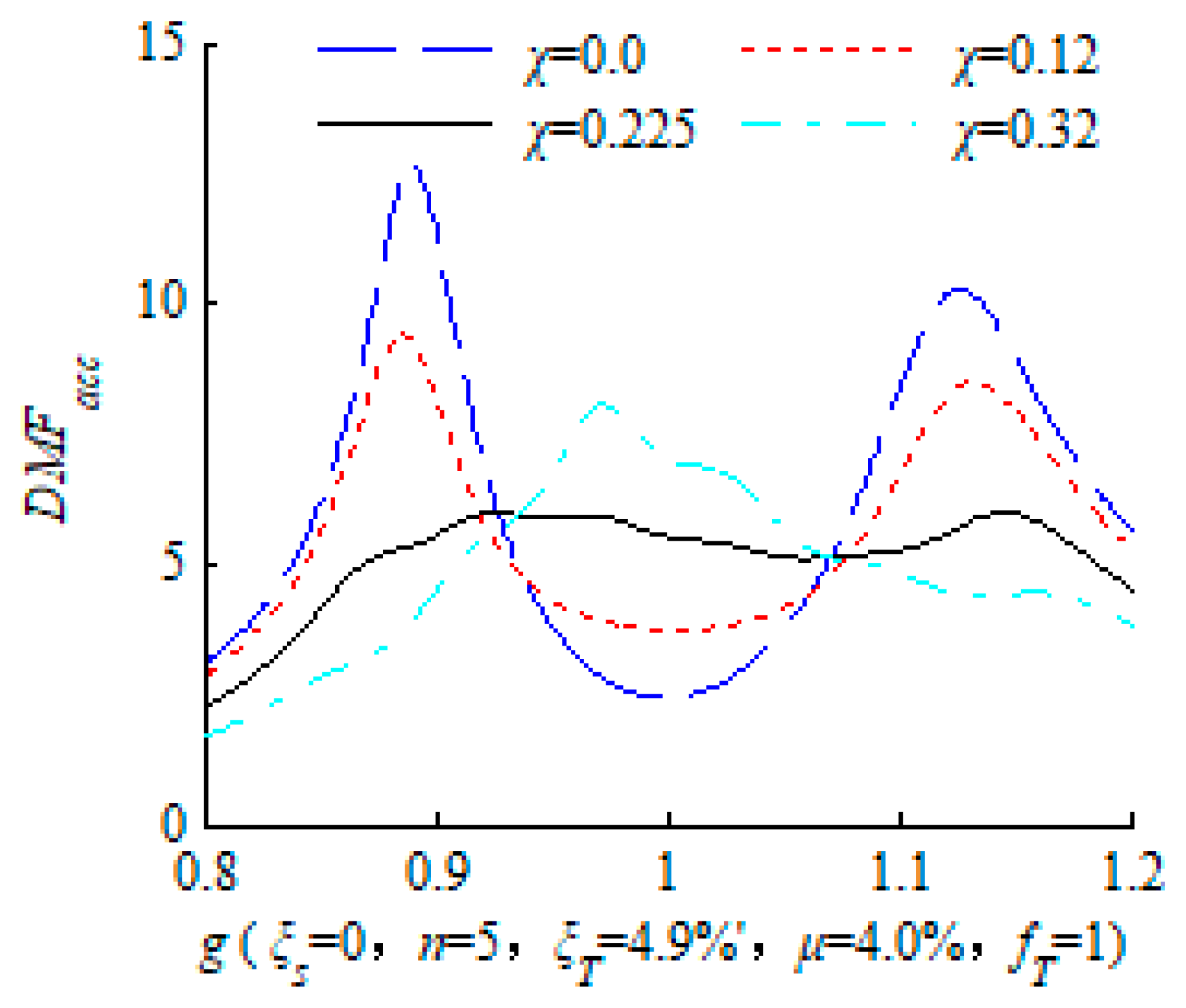
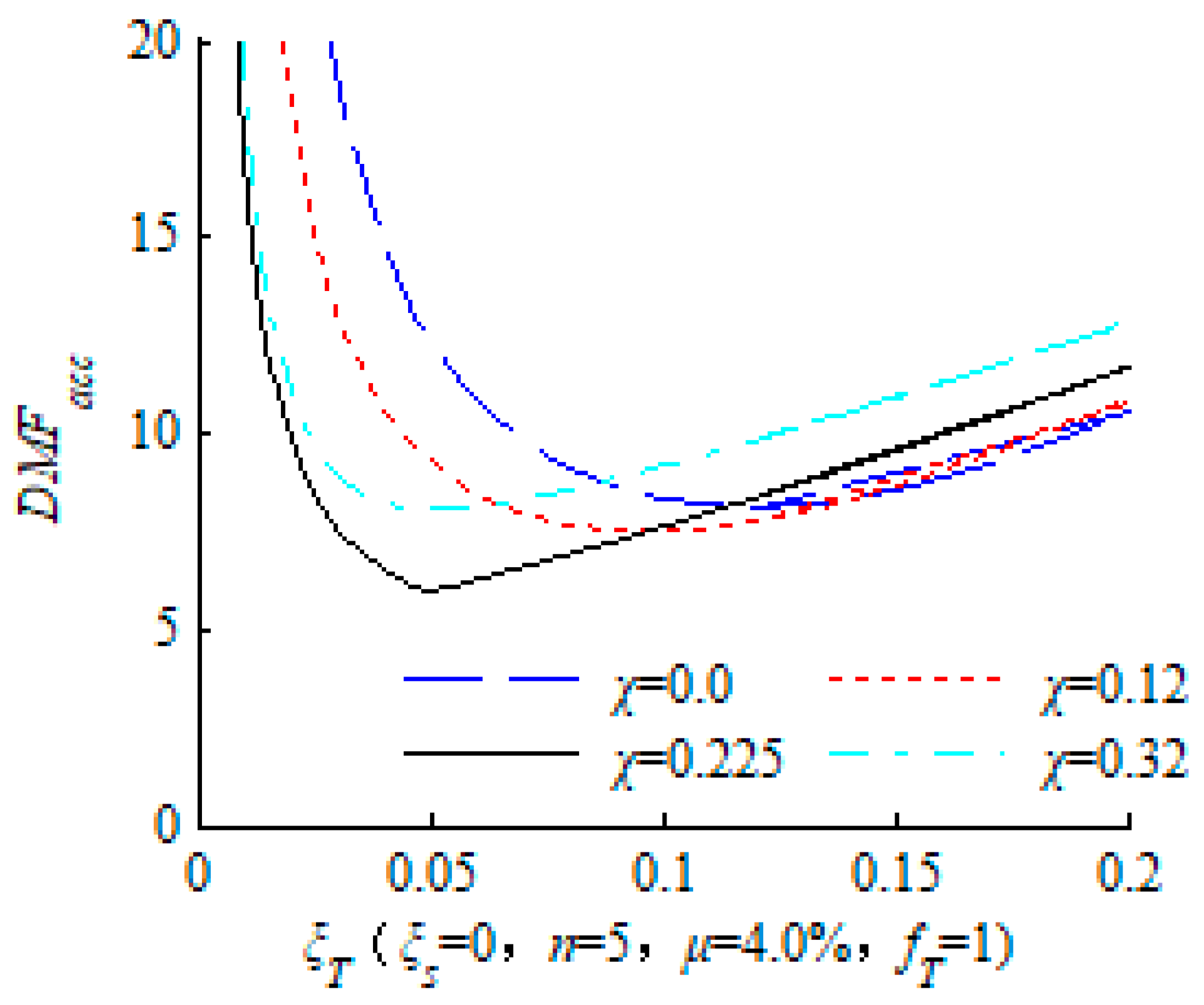
2.4. Discussion on the Central Frequency Ratio
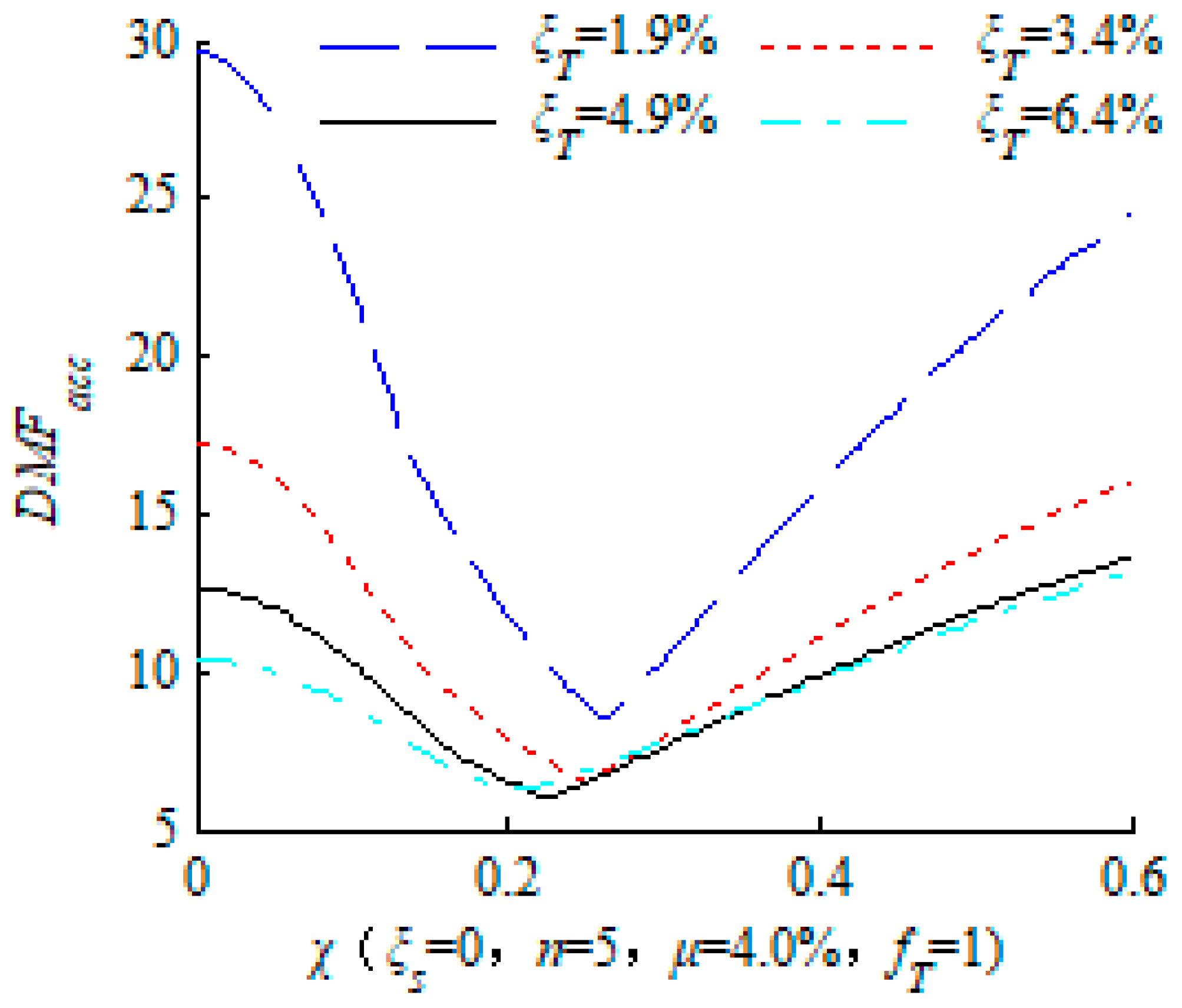
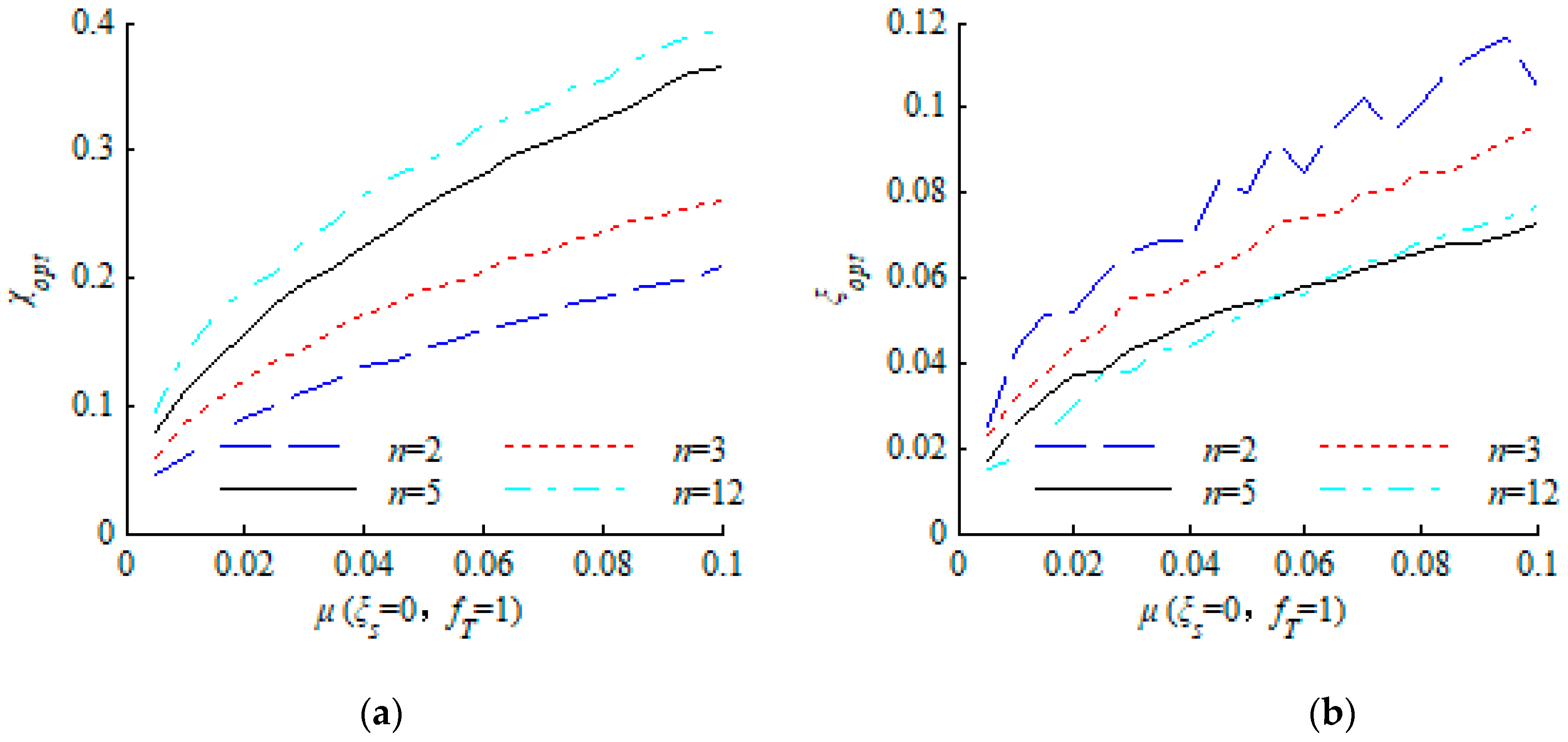
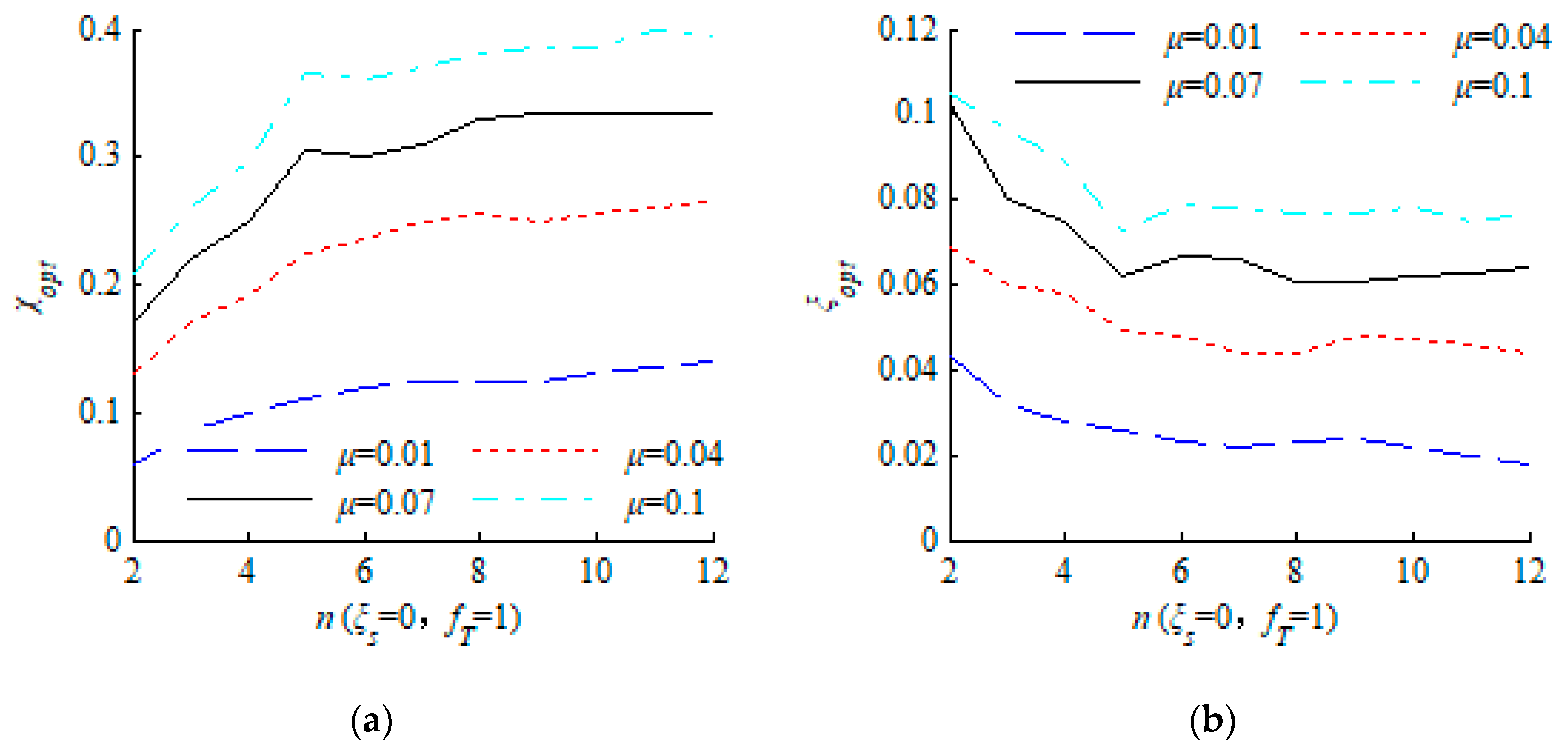
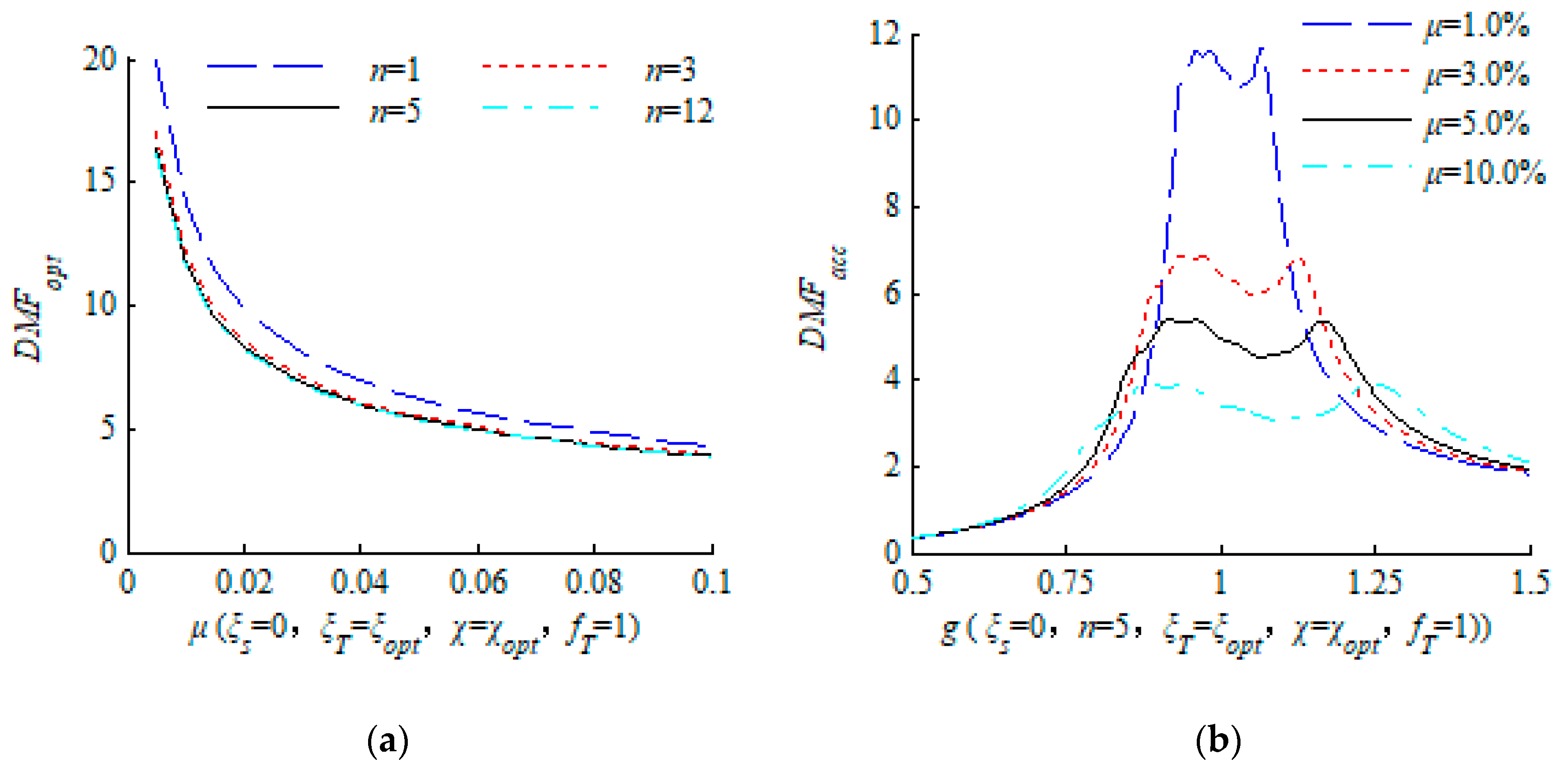
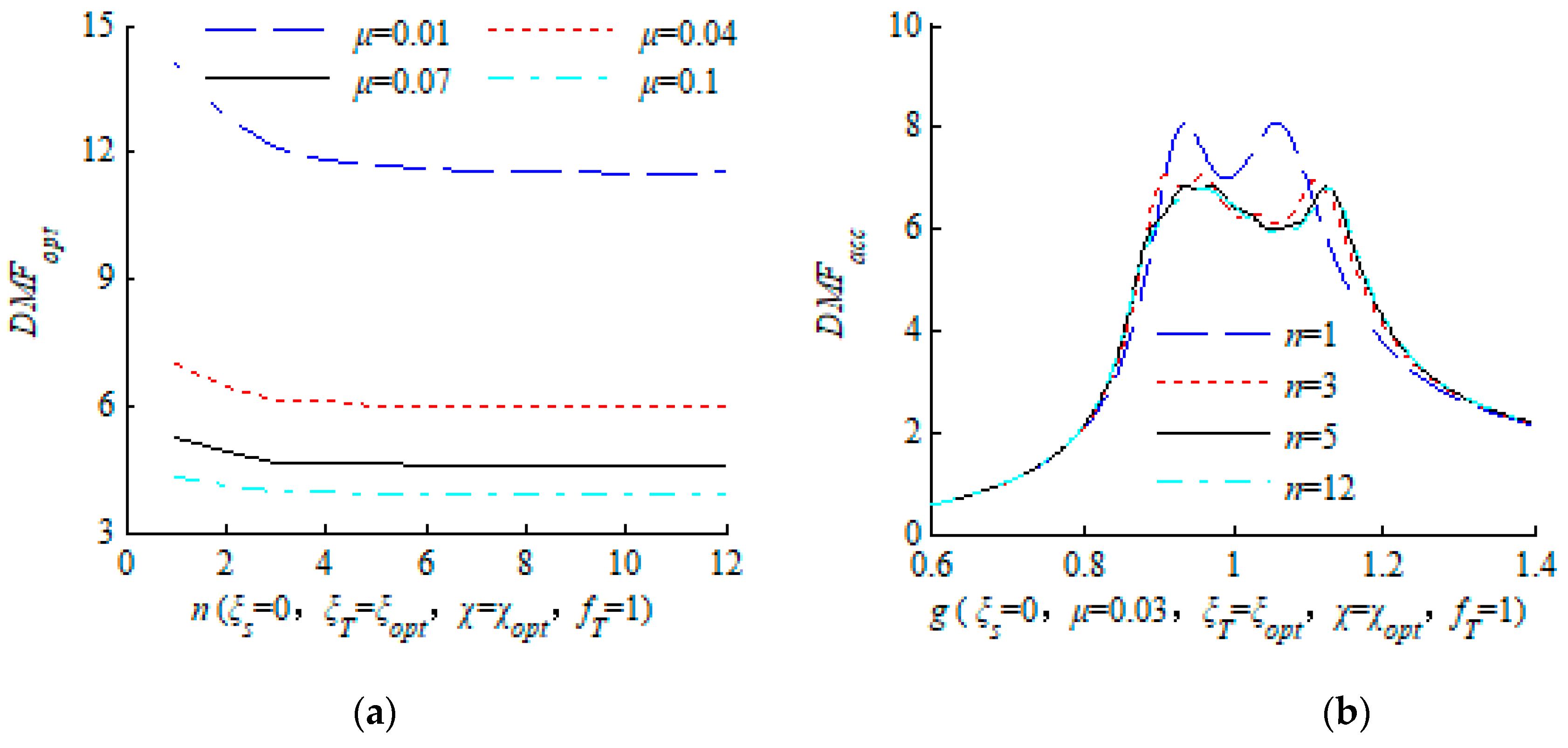
2.5. Discussion on the Mass Ratio
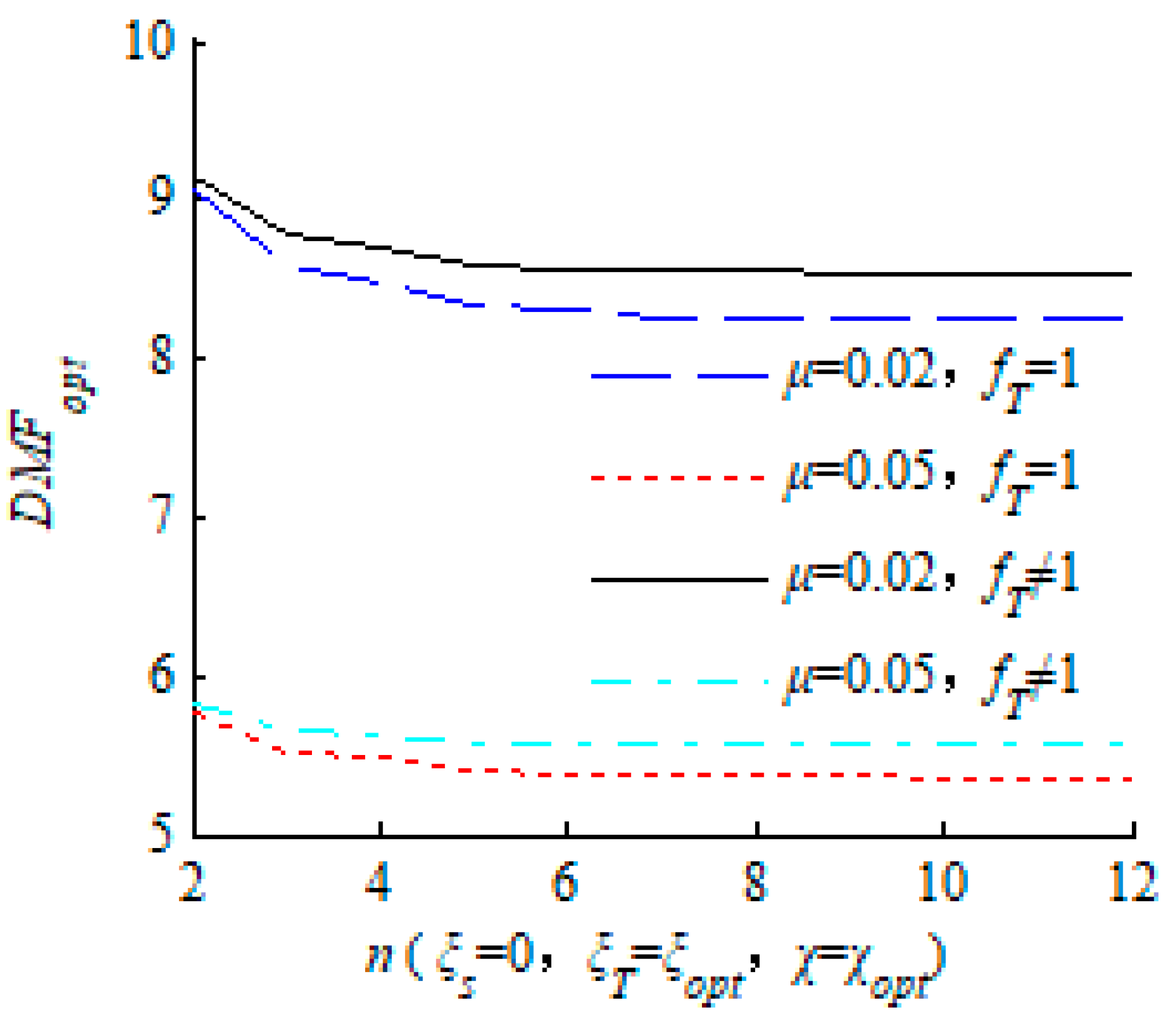
2.6. Discussion on the Number of TMDs
2.7. Design Process of an MTMD System
3. Optimal Design of an MTMD System for a Footbridge
3.1. Model Analysis and In Situ Test
3.2. Optimal Design of an MTMD System
4. Implementation of the MTMD System and Vibration Test
5. Conclusions
- 1)
- According to the parametric study, the central frequency ratio was suggested to be 1; a larger mass ratio would get a better control effect, but it also should be reasonable; the number of TMDs was suggested to be 3~5.
- 2)
- The frequency bandwidth and damping ratio of the MTMD system could be calculated through the proposed optimization formulas.
- 3)
- A slender steel footbridge was analyzed through the finite element model and an in situ test, and an MTMD system was designed based on the proposed optimal design formulas.
- 4)
- The vibration control effect of the MTMD system was verified through a series of in situ comparison tests. The results showed that under walking, running and jumping excitations with different frequencies, the MTMD system always had an excellent vibration control effect, and the footbridge with an MTMD system could meet the acceleration limit requirement. The analysis result agreed well with the in situ test.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shi, W.; Wang, L.; Lu, Z. Study on self-adjustable tuned mass damper with variable mass. Struct. Control Health Monit. 2018, 25, e2114. [Google Scholar] [CrossRef]
- Shi, W.; Wang, L.; Lu, Z.; Gao, H. Study on adaptive-passive and semi-active eddy current tuned mass damper with variable damping. Sustainability 2018, 10, 99. [Google Scholar] [CrossRef]
- Shi, W.; Wang, L.; Lu, Z.; Zhang, Q. Application of an artificial fish swarm algorithm in an optimum tuned mass damper design for a pedestrian bridge. Appl. Sci. 2018, 8, 175. [Google Scholar] [CrossRef]
- Casciati, F.; Casciati, S.; Faravelli, L. A contribution to the modelling of human induced excitation on pedestrian bridges. Struct. Saf. 2017, 66, 51–61. [Google Scholar] [CrossRef]
- Domaneschi, M.; Martinelli, L.; Po, E. Control of wind buffeting vibrations in a suspension bridge by TMD: Hybridization and robustness issues. Comput. Struct. 2015, 155, 3–17. [Google Scholar] [CrossRef]
- Li, Z.; Li, D.; Lu, Y.; Tang, C. Analysis on Vibration Control of a Large–Span Pedestrian Suspension Bridge Based on a Multiple Tuned Mass Damper System; Noise & Vibration Worldwide—SAGE Publications Ltd.: London, UK, 2019; Volume 50, pp. 56–63. [Google Scholar]
- Wang, D.; Wu, C.; Zhang, Y.; Li, S. Study on vertical vibration control of long-span steel footbridge with tuned mass dampers under pedestrian excitation. J. Constr. Steel Res. 2019, 154, 84–98. [Google Scholar] [CrossRef]
- Ferreira, F.; Moutinho, C.; Cunha, Á.; Caetano, E. Use of semi-active tuned mass dampers to control footbridges subjected to synchronous lateral excitation. J. Sound Vib. 2019, 446, 176–194. [Google Scholar] [CrossRef]
- Casciati, S. Human induced vibration vs. cable-stay footbridge deterioration. Smart Struct. Syst. 2016, 18, 17–29. [Google Scholar] [CrossRef]
- Narasimhan, S.; Caetano, E.; Fujino, Y. Special issue on load modeling and experimental studies on lively pedestrian bridges. J. Bridge Eng. 2016, 21, C2016001. [Google Scholar] [CrossRef]
- Nimmen, K.; Lombaert, G.; Roeck, G.; Broeck, P. Vibration serviceability of footbridges: Evaluation of the current codes of practice. Eng. Struct. 2014, 59, 448–461. [Google Scholar] [CrossRef] [Green Version]
- Zivanovic, S.; Pavic, A.; Reynolds, P. Vibration serviceability of footbridges under human-induced excitation: A literature review. J. Sound Vib. 2005, 279, 1–74. [Google Scholar] [CrossRef]
- Brownjohn, J.M.W.; Paivc, A. Experimental methods for estimating modal mass in footbridges using human-induced dynamic excitation. Eng. Struct. 2007, 29, 2833–2843. [Google Scholar] [CrossRef]
- García-Diéguez, M.; Zapico-Valle, J.L. Sensitivity of the vertical response of footbridges to the frequency variability of crossing pedestrians. Vibration 2018, 1, 290–311. [Google Scholar] [CrossRef]
- Jiménez-Alonso, J.F.; Pérez-Aracil, J.; Díaz, H.; Mateo, A.; Sáez, A. Effect of Vinyl flooring on the modal properties of a steel footbridge. Appl. Sci. 2019, 9, 1374. [Google Scholar] [CrossRef]
- Spencer, N.S., Jr. State of the art of structural control. J. Struct. Eng. 2003, 129, 845–856. [Google Scholar] [CrossRef]
- Shi, W.; Wang, L.; Lu, Z.; Wang, H. Experimental and numerical study on adaptive-passive variable mass tuned mass damper. J. Sound Vib. 2019, 452, 97–111. [Google Scholar] [CrossRef]
- Sun, C.; Nagarajaiah, S.; Dick, A.J. Family of smart tuned mass damper with variable frequency under harmonic excitation and ground motions: Closed-form evaluation. Smart Struct. Syst. 2014, 13, 319–341. [Google Scholar] [CrossRef]
- Moutinho, C.; Cunha, Á.; Caetano, E.; de Carvalho, J.M. Vibration control of a slender footbridge using passive and semiactive tuned mass dampers. Struct. Control. Health Monit. 2018, 25, e2208. [Google Scholar] [CrossRef]
- Lievens, K.; Lombaert, G.; Roeck, G.; Broeck, P. Robust design of a TMD for the vibration serviceability of a footbridge. Eng. Struct. 2016, 123, 408–418. [Google Scholar] [CrossRef]
- Caetano, E.; Cunha, Á.; Moutinho, C.; Magalhães, F. Studies for controlling human-induced vibration of the Pedro e Inês footbridge, Portugal. Part 2: Implementation of tuned mass dampers. Eng. Struct. 2010, 32, 1082–1091. [Google Scholar] [CrossRef]
- Casado, C.; Díaz, I.; Sebastián, J.; Poncela, A.; Lorenzana, A. Implementation of passive and active vibration control on an in-service footbridge. Struct. Control. Health Monit. 2013, 20, 70–87. [Google Scholar] [CrossRef]
- Tubino, F.; Piccardo, G. Tuned mass damper optimization for the mitigation of human-induced vibrations of pedestrian bridges. Meccanica 2015, 50, 809–824. [Google Scholar] [CrossRef]
- Huang, H.; Chang, W.S.; Mosalam, K.M. Feasibility of shape memory alloy in a tuneable mass damper to reduce excessive in-service vibration. Struct. Control. Health Monit. 2017, 24, e1858. [Google Scholar] [CrossRef]
- Rathi, A.; Chakraborty, A. Reliability-based performance optimization of TMD for vibration control of structures with uncertainty in parameters and excitation. Struct. Control. Health Monit. 2017, 24, e1857. [Google Scholar] [CrossRef]
- Lievens, K.; Lombaert, G.; Van Nimmen, K.; De Roeck, G.; Van den Broeck, P. Robust vibration serviceability assessment of footbridges subjected to pedestrian excitation: Strategy and applications. Eng. Struct. 2018, 171, 236–246. [Google Scholar] [CrossRef]
- Rezaei Rad, A.; Banazadeh, M. Probabilistic risk-based performance evaluation of seismically base-isolated steel structures subjected to far-field earthquakes. Buildings 2018, 8, 128. [Google Scholar] [CrossRef]
- Tajammolian, H.; Khoshnoudian, F.; Rezaei Rad, A.; Loghman, V. Seismic fragility assessment of asymmetric structures supported on TCFP bearings subjected to near-field earthquakes. Struct. 2018, 13, 66–78. [Google Scholar] [CrossRef]
- Wang, L.; Shi, W.; Zhou, Y. Study on self-adjustable variable pendulum tuned mass damper. Struct. Des. Tall Spec. Build. 2019, 28, e1561. [Google Scholar] [CrossRef]
- Wang, L.; Shi, W.; Li, X.; Yheng, L. An adaptive-passive retuning device for a pendulum tuned mass damper considering mass uncertainty and optimum frequency. Struct. Control. Health Monit. 2019, e2377. [Google Scholar] [CrossRef]
- Nagarajaiah, S. Adaptive passive, semi-active, smart tuned mass dampers: Identification and control using empirical mode decomposition, Hilbert transform, and short-term Fourier transform. Struct. Control. Health Monit. 2009, 16, 800–841. [Google Scholar] [CrossRef]
- Varadarajan, N.; Nagarajaiah, S. Wind response control of building with variable stiffness tuned mass damper using empirical mode decomposition/Hilbert transform. J. Eng. Mech. 2004, 130, 451–458. [Google Scholar] [CrossRef]
- Sun, C.; Nagarajaiah, S. Study on semi-active tuned mass damper with variable damping and stiffness under seismic excitations. Struct. Control. Health Monit. 2014, 21, 890–906. [Google Scholar] [CrossRef]
- Ferreira, F.; Moutinho, C.; Cunha, Á.; Caetano, E. Proposal of optimum tuning of semiactive TMDs used to reduce harmonic vibrations based on phase control strategy. Struct. Control. Health Monit. 2018, 25, e2131. [Google Scholar] [CrossRef]
- Carpineto, N.; Lacarbonara, W.F. Mitigation of pedestrian-induced vibrations in suspension footbridges via multiple tuned mass dampers. J. Vib. Control 2010, 16, 749–776. [Google Scholar] [CrossRef]
- Li, Q.; Fan, J.; Nie, J.; Li, Q.; Chen, Y. Crowd-induced random vibration of footbridge and vibration control using multiple tuned mass dampers. J. Sound Vib. 2010, 329, 4068–4092. [Google Scholar] [CrossRef]
- Lu, X.; Ding, K.; Shi, W.; Weng, D. Tuned mass dampers for human-induced vibration control of the Expo Culture Centre at the World Expo 2010 in Shanghai, China. Struct. Eng. Mech. 2012, 43, 607–621. [Google Scholar] [CrossRef]
- Gaspar, C.M.R.; de Santos, S.J.G.; Costa-Neves, L.F. Multimode vibration control of building steel–concrete composite floors submitted to human rhythmic activities. Comput. Struct. 2016, 165, 107–122. [Google Scholar] [CrossRef]
- Daniel, Y.; Lavan, O.; Levy, R. Multiple-tuned mass dampers for multimodal control of pedestrian bridges. J. Struct. Eng. 2012, 138, 1173–1178. [Google Scholar] [CrossRef]
- Jokic, M.; Stegic, M.; Butkovic, M. Reduced-order multiple tuned mass damper optimization: A bounded real lemma for descriptor systems approach. J. Sound Vib. 2011, 330, 5259–5268. [Google Scholar] [CrossRef]
- Roman, L.; Justyna, G. Dynamic analysis of structures with multiple tuned mass dampers. J. Civ. Eng. Manag. 2009, 15, 77–86. [Google Scholar]
- Hoang, N.; Warnitchai, P. Design of multiple tuned mass dampers by using a numerical optimizer. Earthq. Eng. Struct. Dyn. 2005, 34, 125–144. [Google Scholar] [CrossRef]
- Nakhorn, P.; Sopak, K.; Pennung, W. Application of non-linear multiple tuned mass dampers to suppress man-induced vibrations of a pedestrian bridge. Earthq. Eng. Struct. Dyn. 2010, 32, 1117–1131. [Google Scholar]
- Den Hartog, J.P. Mechanical Vibrations; McGraw-Hill/Dover: New York, NY, USA, 1985. [Google Scholar]
- Occhiuzzi, A.; Spizzuoco, M.; Ricciardelli, F. Loading models and response control of footbridges excited by running pedestrians. Struct. Control. Health Monit. 2008, 15, 349–368. [Google Scholar] [CrossRef]
- Magalhaes, F.; Cunha, A.; Caetano, E.R. Damping estimation using free decays and ambient vibration tests. Mech. Syst. Signal. Process. 2010, 24, 1274–1290. [Google Scholar] [CrossRef] [Green Version]
- Carroll, S.P.; Owen, J.S.; Hussein, M.F.M. A coupled biomechanical/discrete element crowd model of crowd–bridge dynamic interaction and application to the Clifton Suspension Bridge. Eng. Struct. 2013, 49, 58–75. [Google Scholar] [CrossRef]
- Murray, T.M.; Allen, D.E.; Ungar, E.E. Floor Vibrations Due to Human Activity-Steel Design Guide Series; American Institute of Steel Construction: Chicago, IL, USA, 1997. [Google Scholar]
- ISO 2631–2—Evaluation of Human Exposure to Whole-Body Vibration—Part 2: Human Exposure to Continuous and Shock-Induced Vibrations in Buildings (1 to 80 Hz); International Organization for Standardization: Geneve, Switzerland, 1989.
- Wyatt, T.A. Design Guide on the Vibration of Floors; The Steel Construction Institute: Berkshire, UK, 1989. [Google Scholar]
- Computer & Structures Inc. Structure Analysis Program 2000 (SAP2000) [Software], Computer & Structures Inc.: Berkeley, CA, USA, 2011.
- Ferreira, F.; Simões, L. Optimum design of a controlled cable-stayed footbridge subject to a running event using semiactive and passive mass dampers. J. Perform. Constr. Facil. 2019, 33, 04019025. [Google Scholar] [CrossRef]
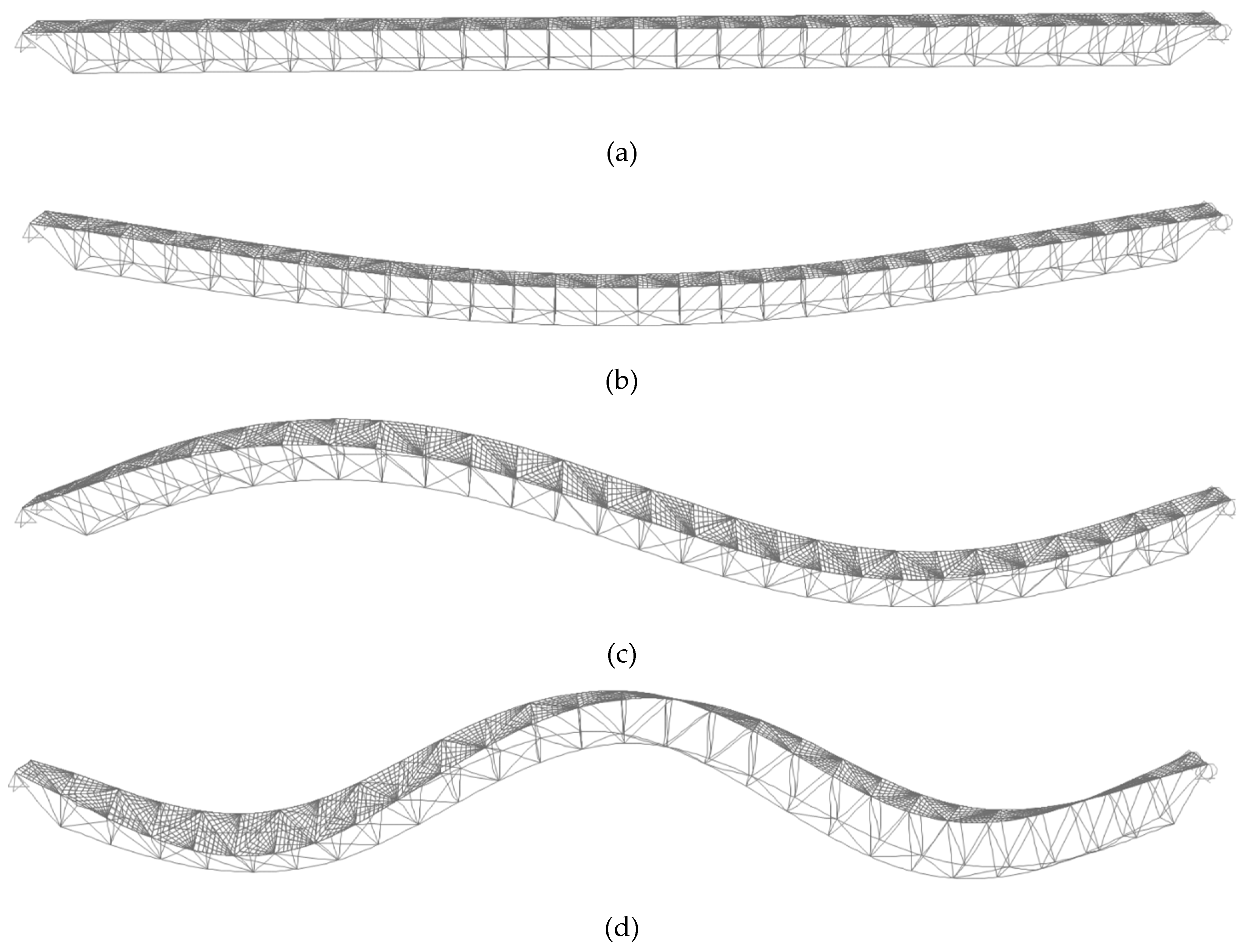

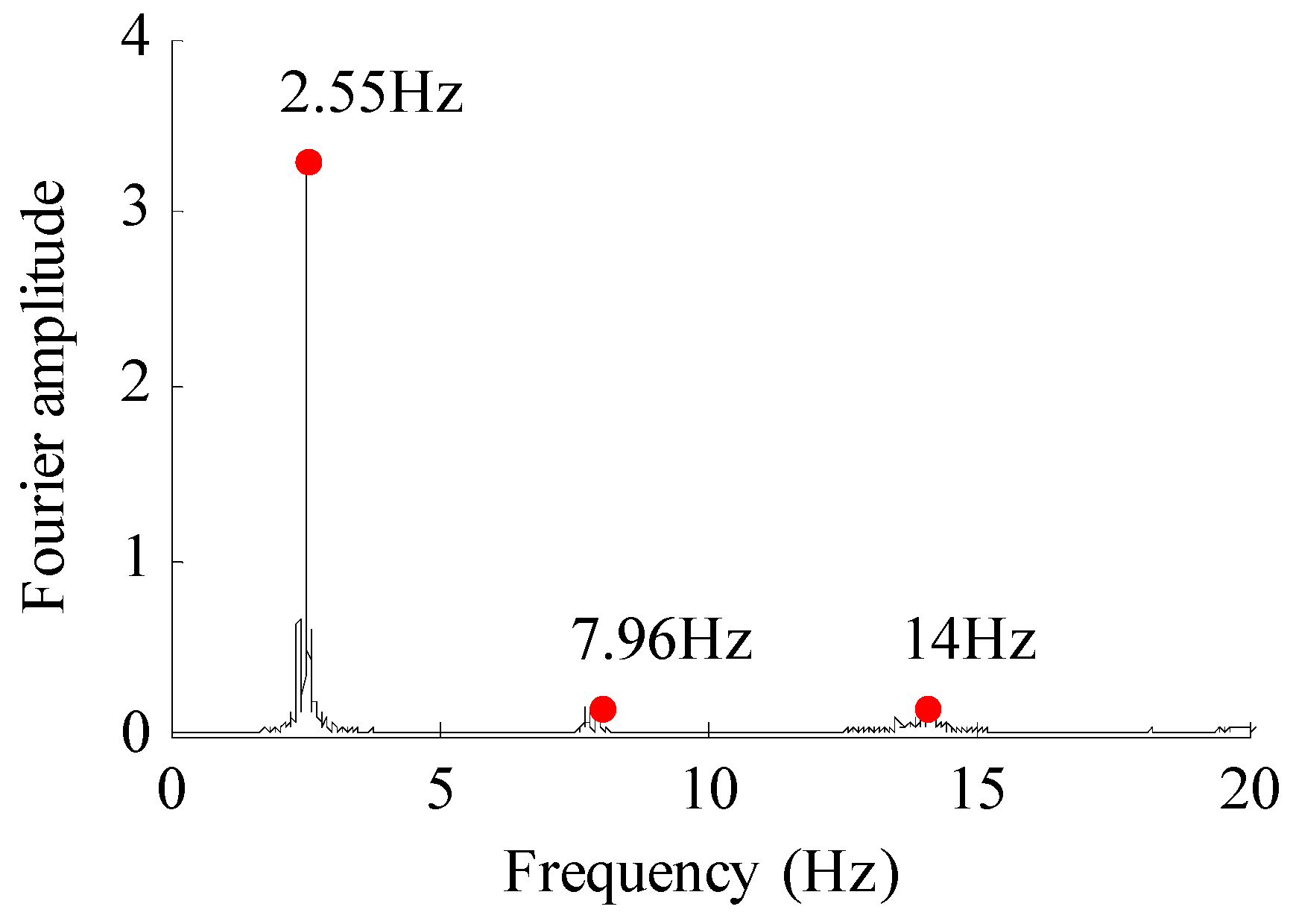
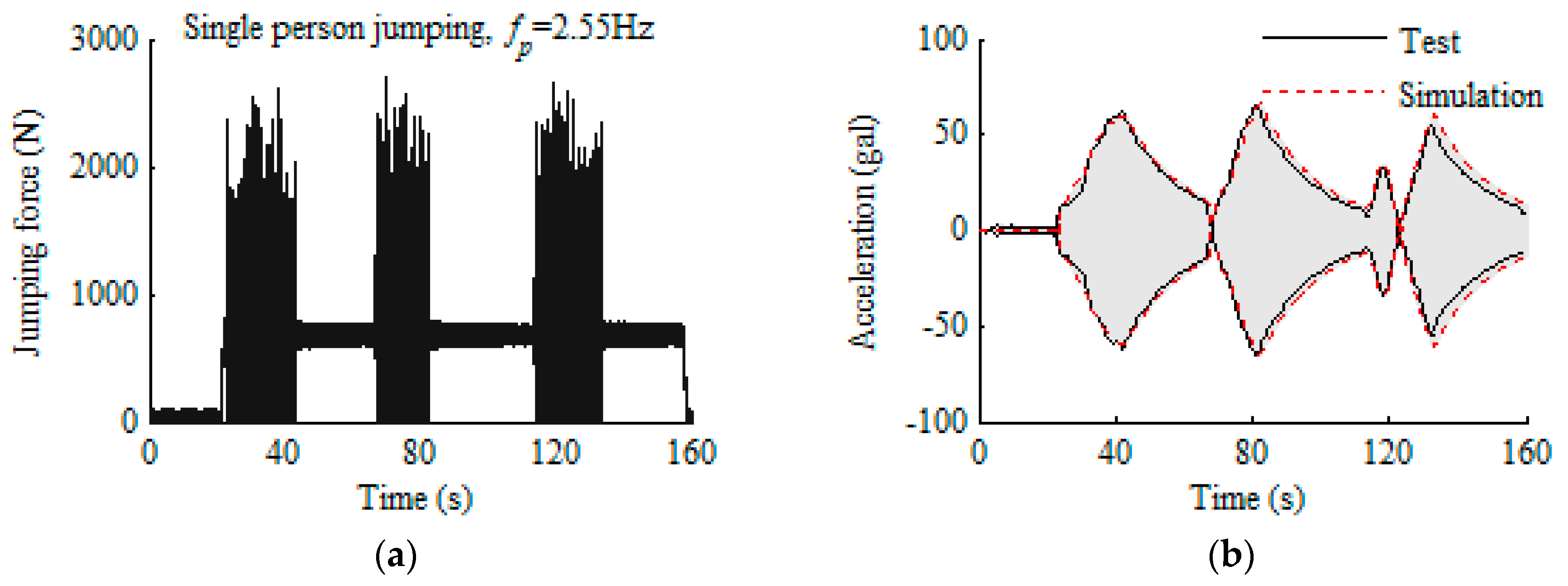
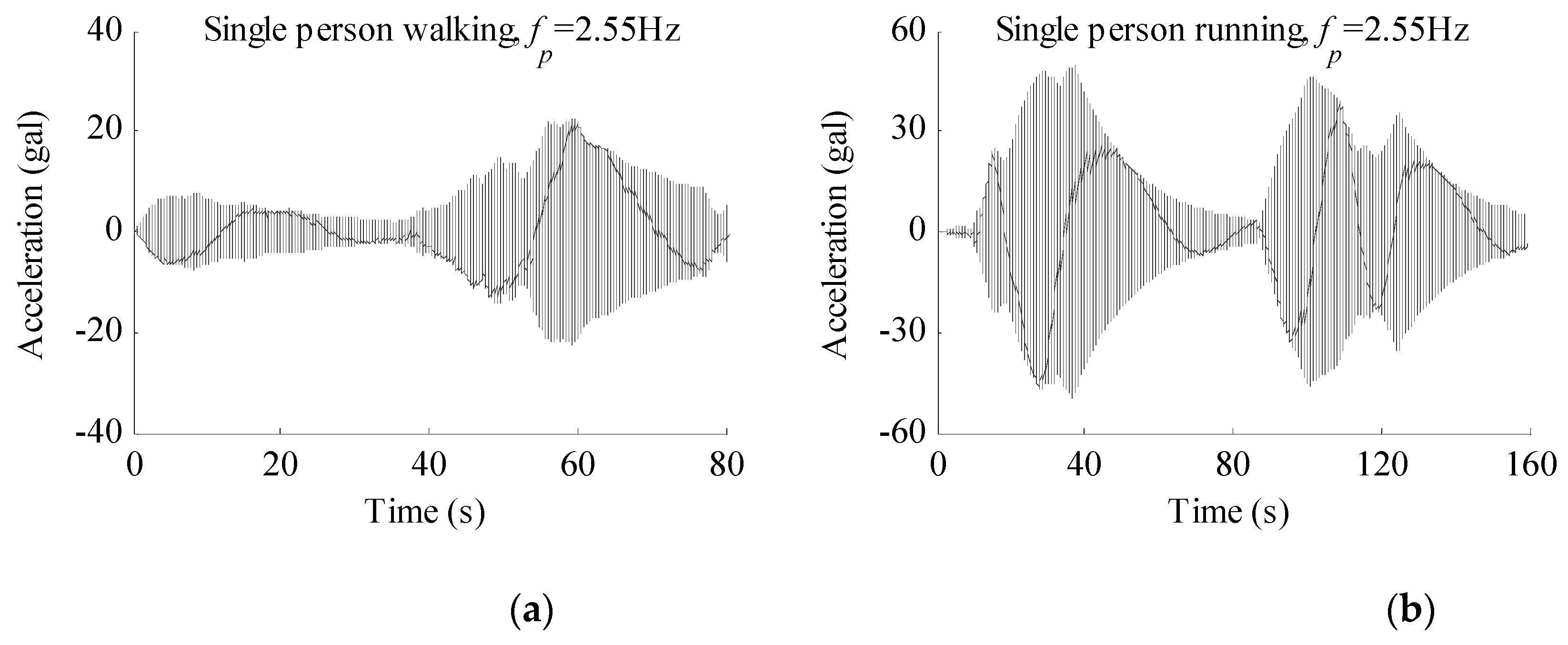

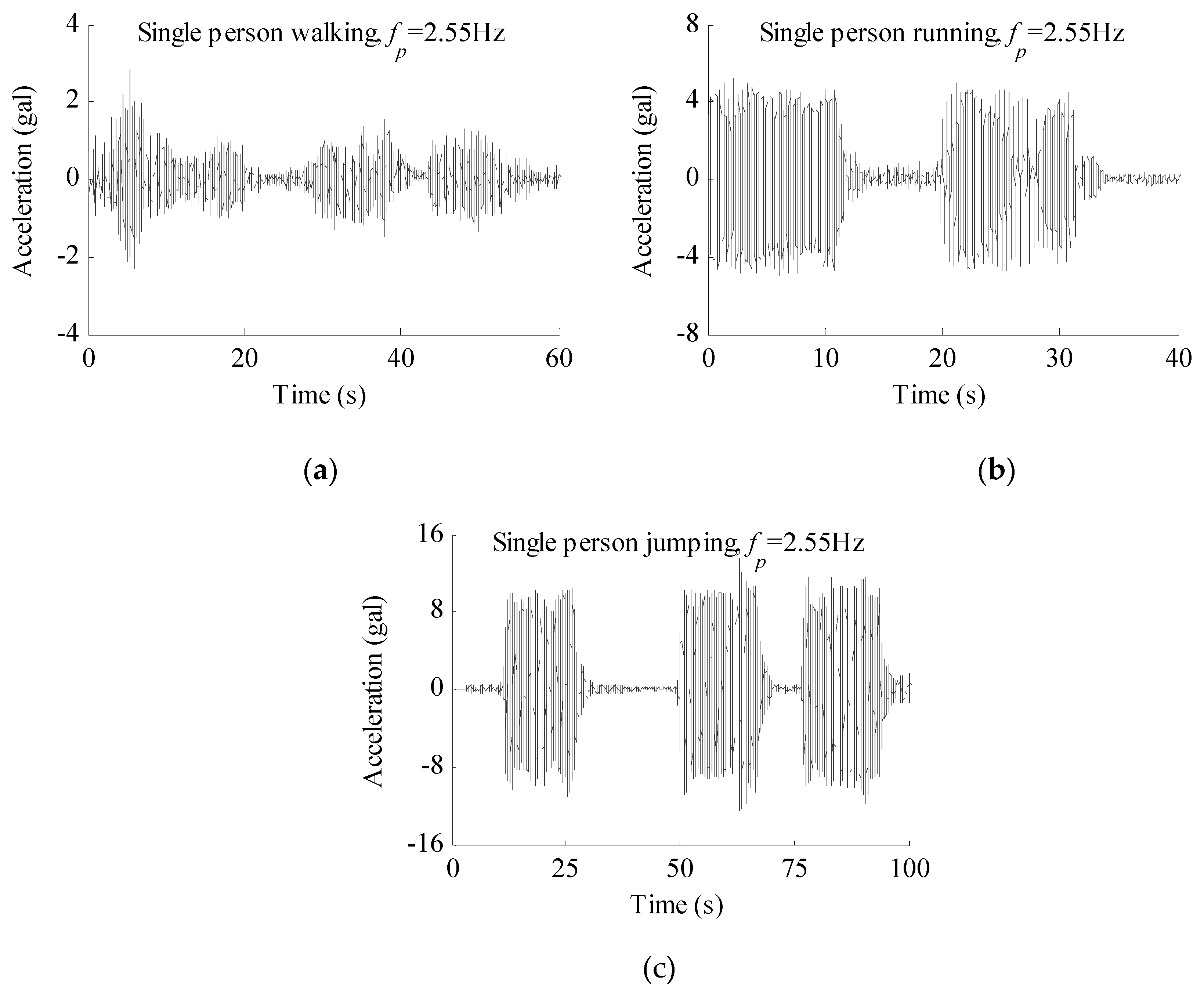
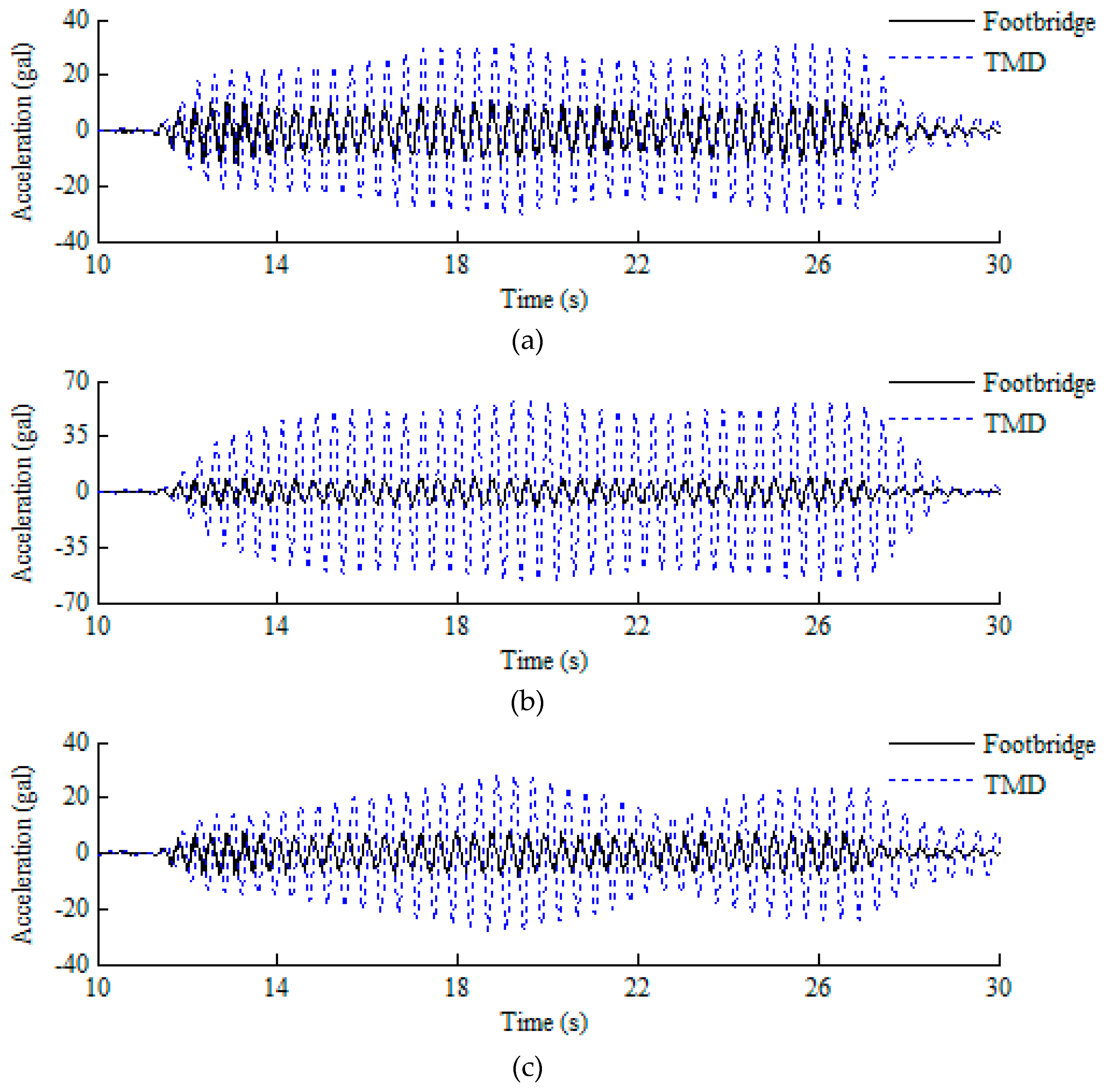
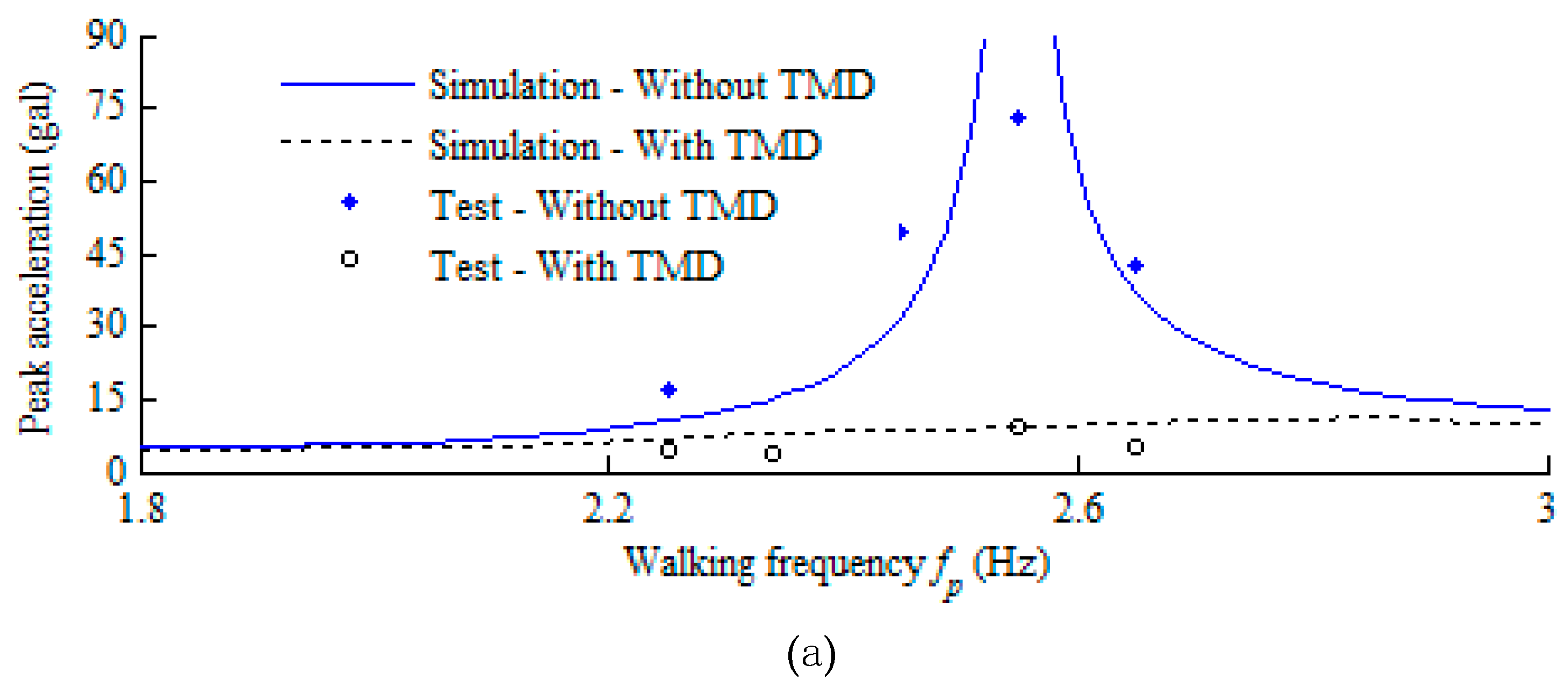
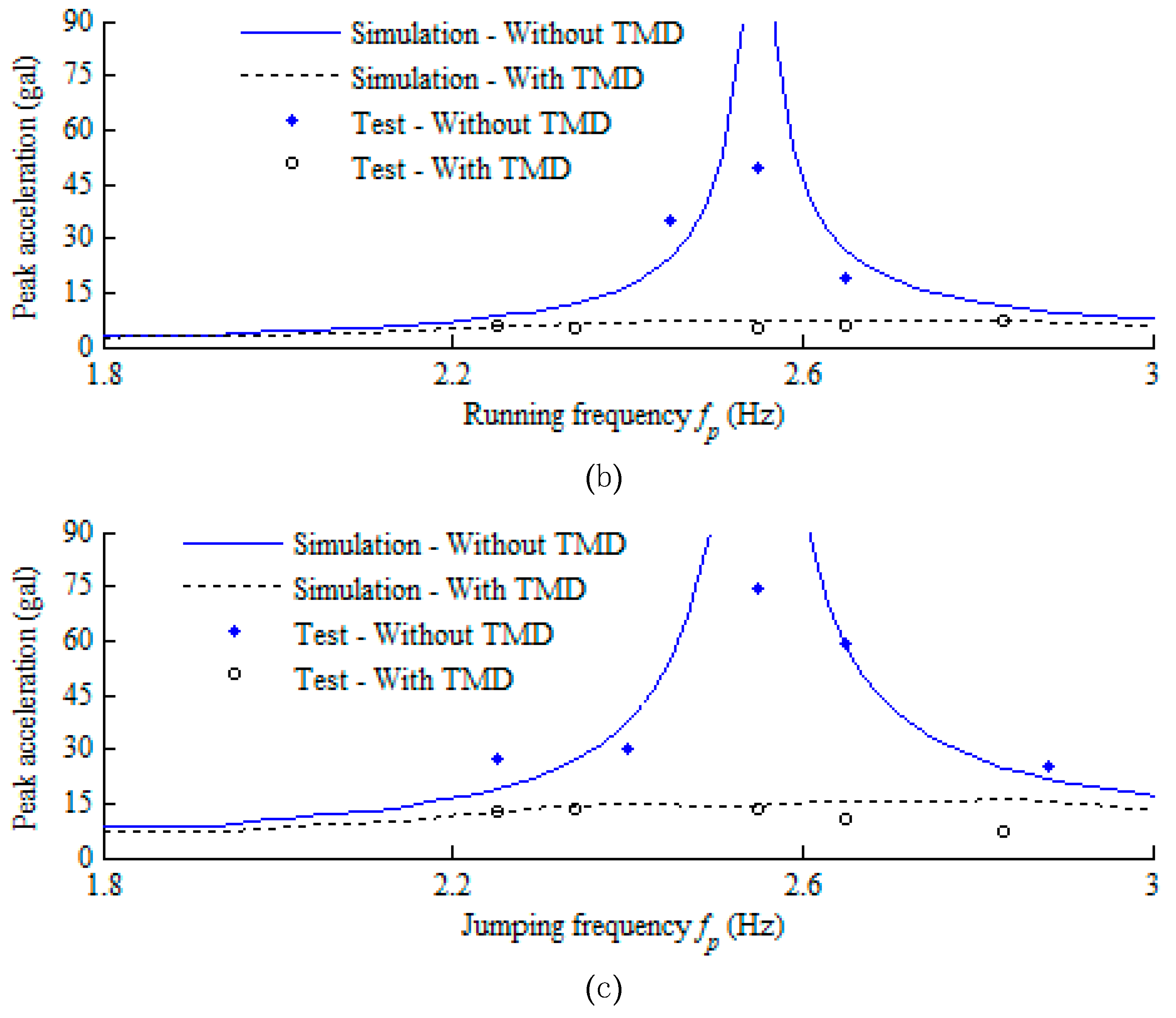

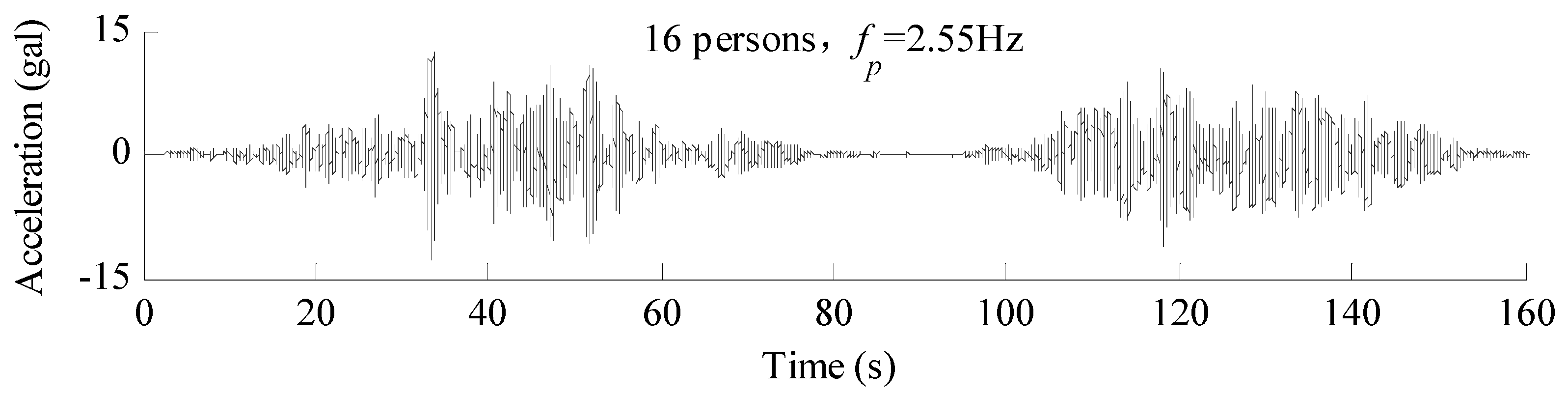
| Type | Component | Size (mm) | Number | Input Loads |
|---|---|---|---|---|
| Crossbar | Beam element | 150 × 150 × 8 | 56 | Walking, running and jumping excitations, which are measured from the in situ test, are input in the midspan node. |
| Longitudinal bar | Beam element | 550 × 550 × 20 | 108 | |
| Vertical bar | Beam element | 550 × 550 × 20 | 54 | |
| Diagonal bar | Beam element | 350 × 350 × 16 | 108 | |
| Bridge deck | Shell element | 55181 × 1450 × 100 | 1 |
| Order | Test Frequency/Hz | Analysis Frequency/Hz | Deviation | Damping Ratio |
|---|---|---|---|---|
| First | 2.55 | 2.55 | 0.00% | 0.35% |
| Second | 7.96 | 7.18 | –9.80% | |
| Third | 14.00 | 13.86 | –1.00% |
| Structural frequency | 2.55 Hz | ||
| Structural modal mass | 83.3 t | ||
| Total number of TMD | 3 | ||
| Order of TMD | A1 | A2 | A3 |
| Mass of TMD | 1.0 t | 1.0 t | 1.0 t |
| MTMD mass ratio | 3.6% | ||
| Optimal frequency bandwidth | 0.16 | ||
| Central frequency ratio | 1.00 | ||
| Central frequency | 2.55 Hz | ||
| TMD frequency | 2.35 Hz | 2.55 Hz | 2.75 Hz |
| Optimal damping ratio | 6.0% | ||
| Case | Without Control/gal | With the MTMD System/gal | Reduction/% |
|---|---|---|---|
| Walking excitation | 72.9 | 9.1 | 87.5% |
| Running excitation | 49.5 | 5.2 | 89.5% |
| Jumping excitation | 74.5 | 13.5 | 81.9% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Shi, W. Optimal Design and Application of a Multiple Tuned Mass Damper System for an In-Service Footbridge. Sustainability 2019, 11, 2801. https://doi.org/10.3390/su11102801
Wang C, Shi W. Optimal Design and Application of a Multiple Tuned Mass Damper System for an In-Service Footbridge. Sustainability. 2019; 11(10):2801. https://doi.org/10.3390/su11102801
Chicago/Turabian StyleWang, Chao, and Weixing Shi. 2019. "Optimal Design and Application of a Multiple Tuned Mass Damper System for an In-Service Footbridge" Sustainability 11, no. 10: 2801. https://doi.org/10.3390/su11102801
APA StyleWang, C., & Shi, W. (2019). Optimal Design and Application of a Multiple Tuned Mass Damper System for an In-Service Footbridge. Sustainability, 11(10), 2801. https://doi.org/10.3390/su11102801




