Secondary Development and Application of Bio-Inspired Isolation System
Abstract
1. Introduction
2. Biomechanism of the New Isolation System
2.1. Biomechanism
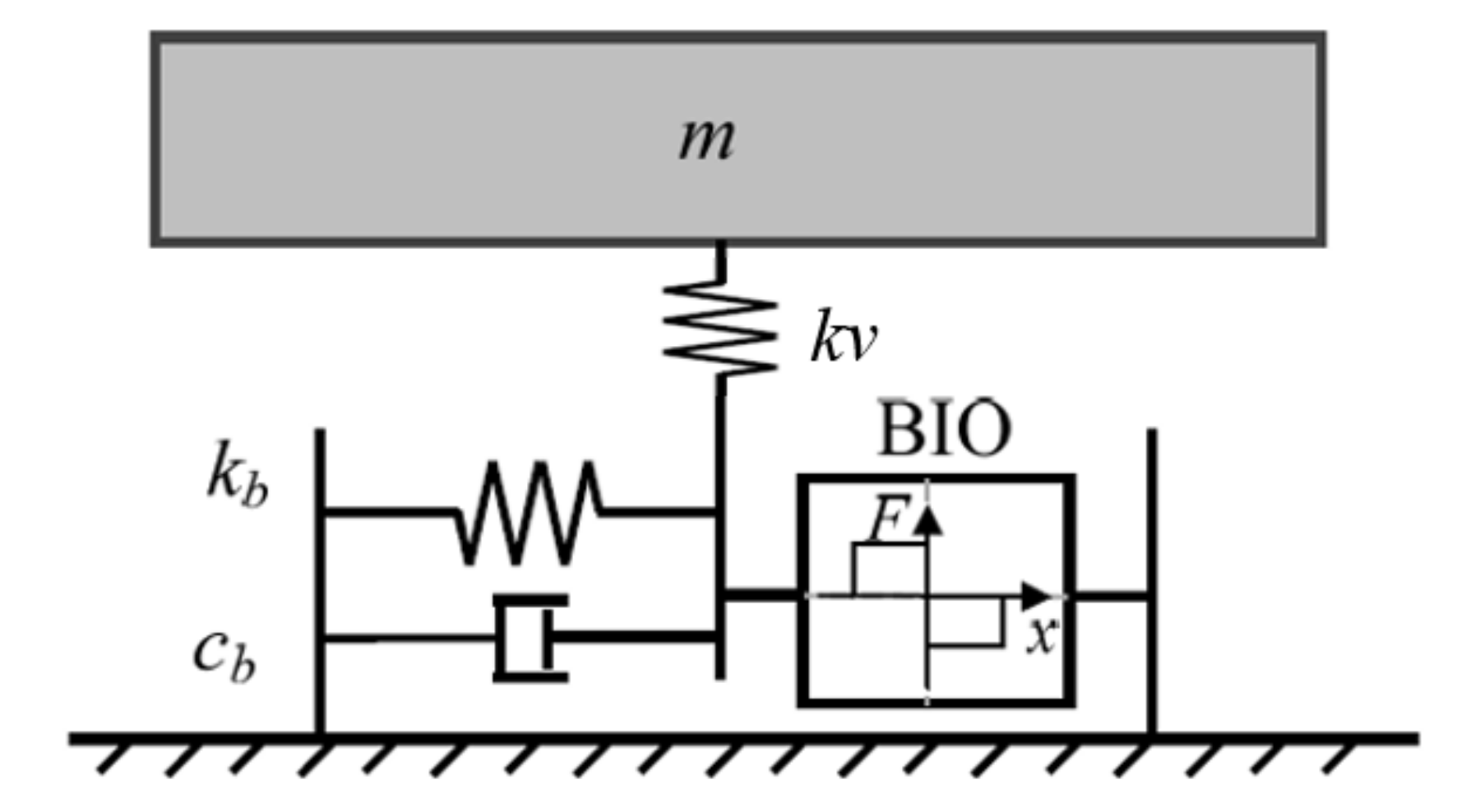
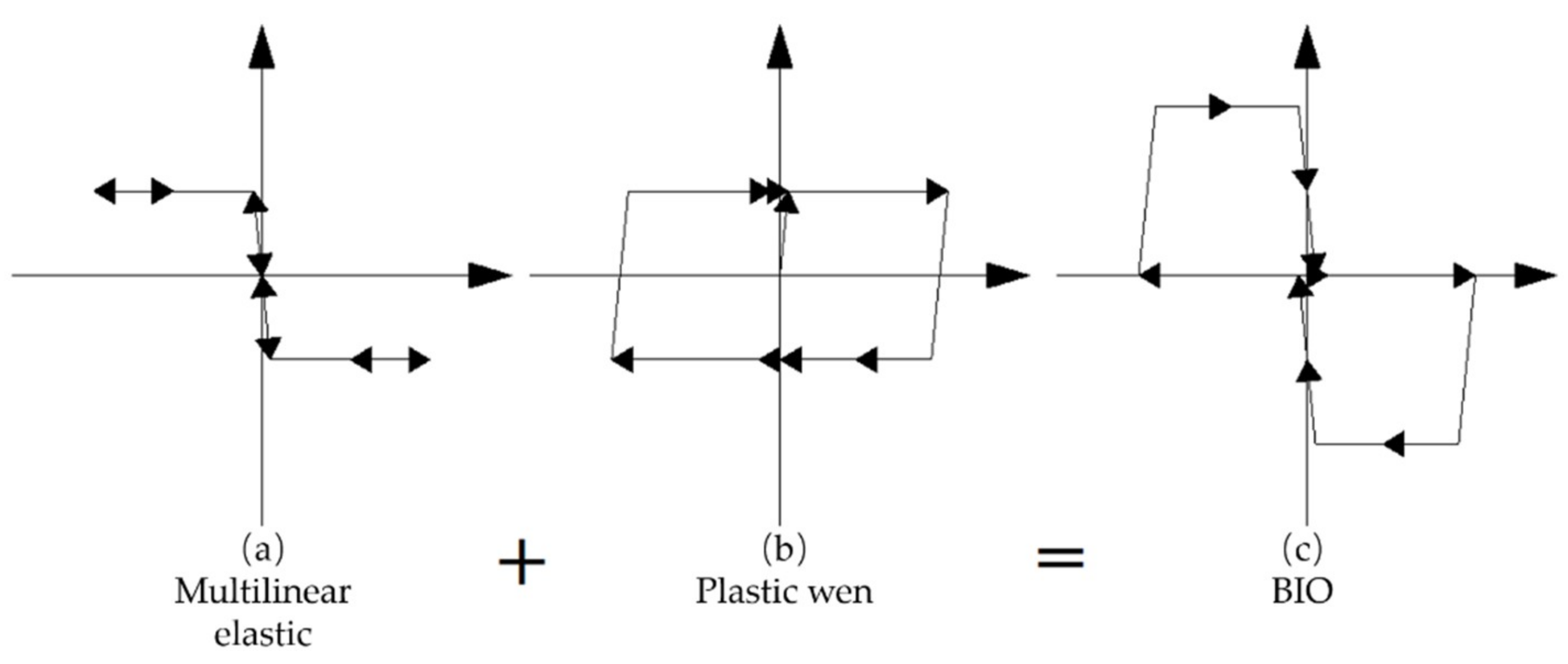
2.2. Restoring Force Model
3. Development of User Subroutine
3.1. Secondary Development in Abaqus
- (1)
- Abaqus offers a large selection of structural elements, analysis procedures, and modeling tools;
- (2)
- Abaqus offers preprocessing and postprocessing. Many third-party vendors offer preprocessing and postprocessors with interfaces for Abaqus;
- (3)
- Maintaining and porting subroutines is much easier than maintaining and porting a complete finite element program.
3.2. Simulation in SAP2000
4. Verification of User Subroutine
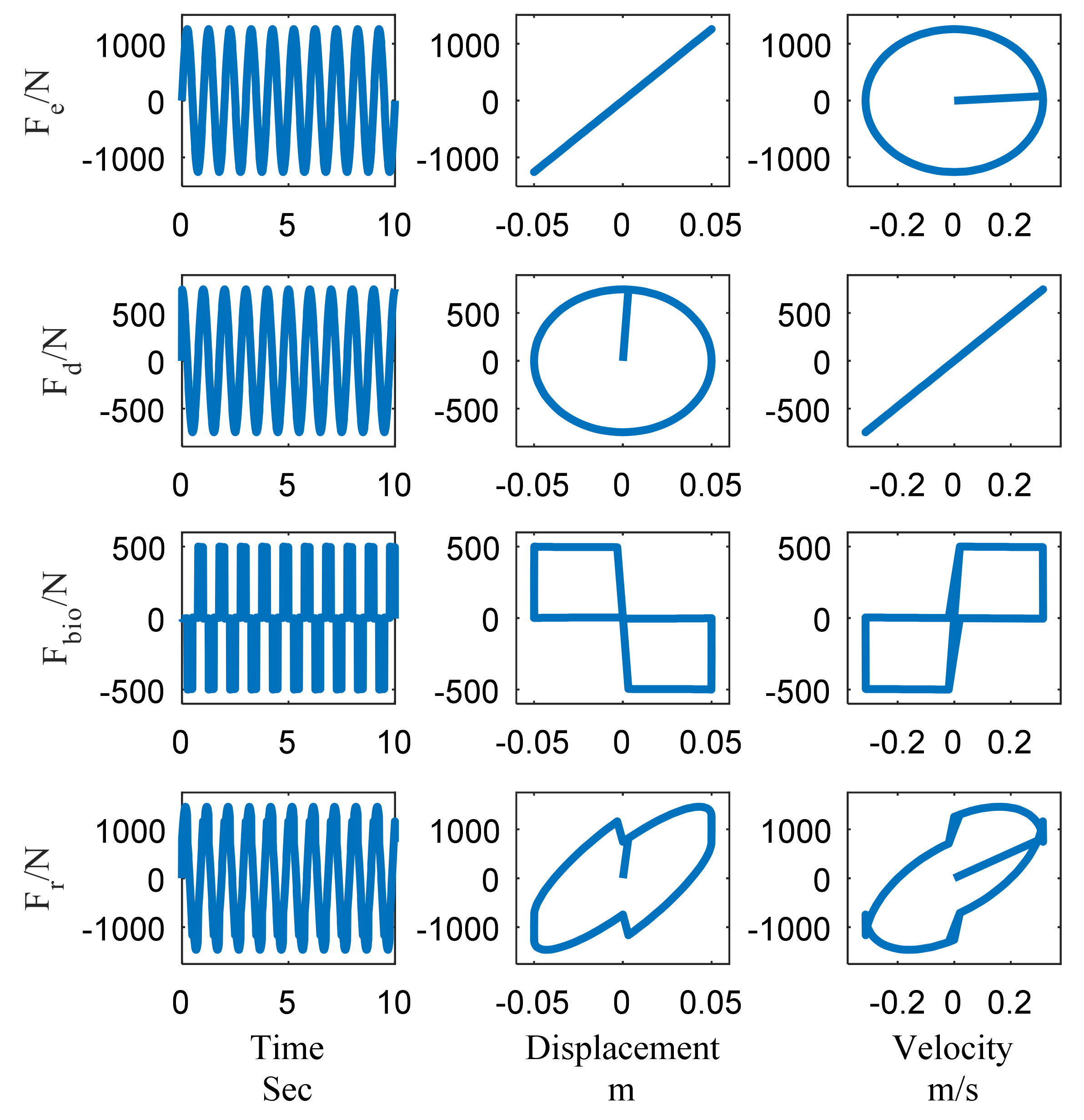
4.1. Verification of Restoring Force Model
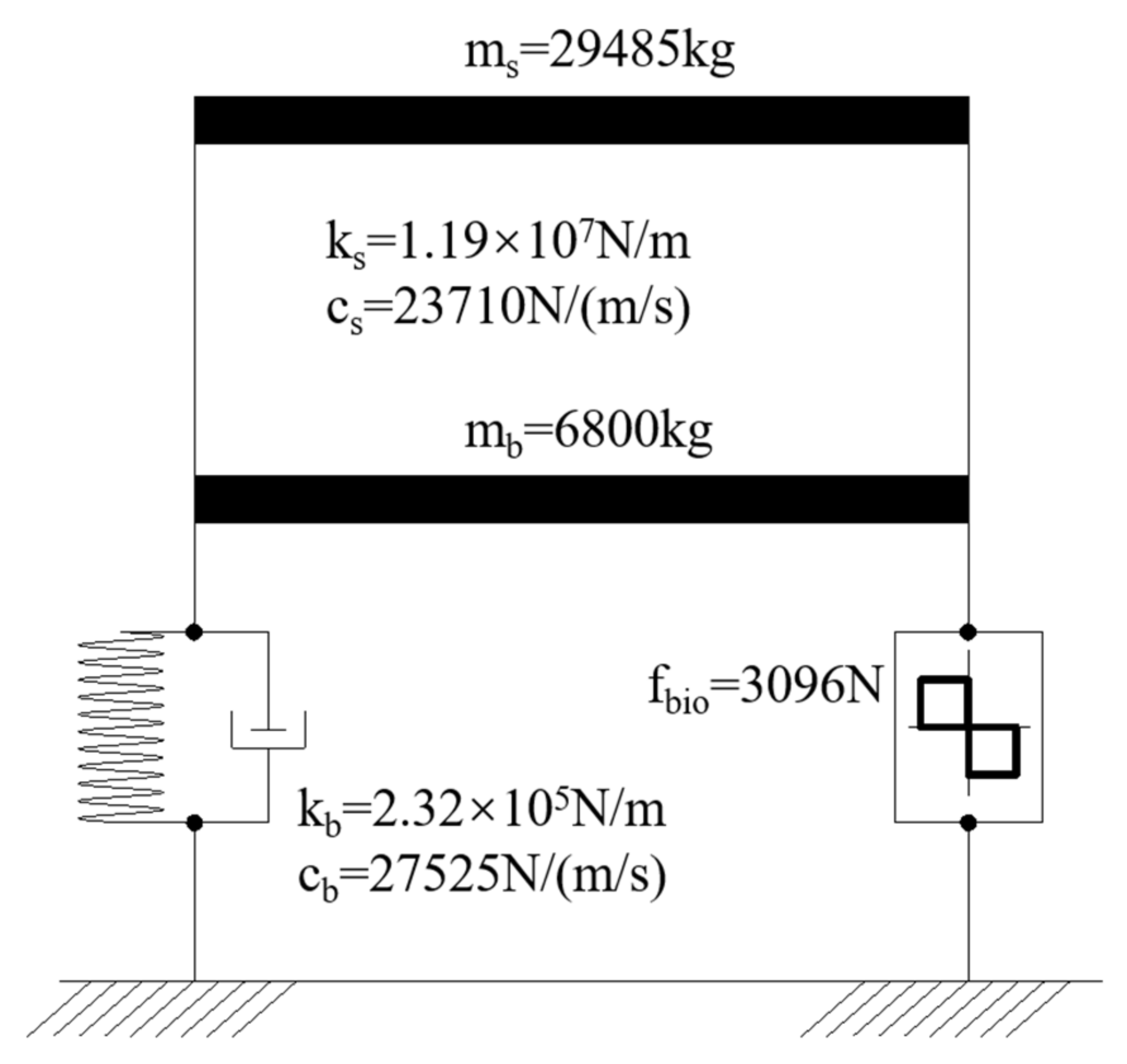
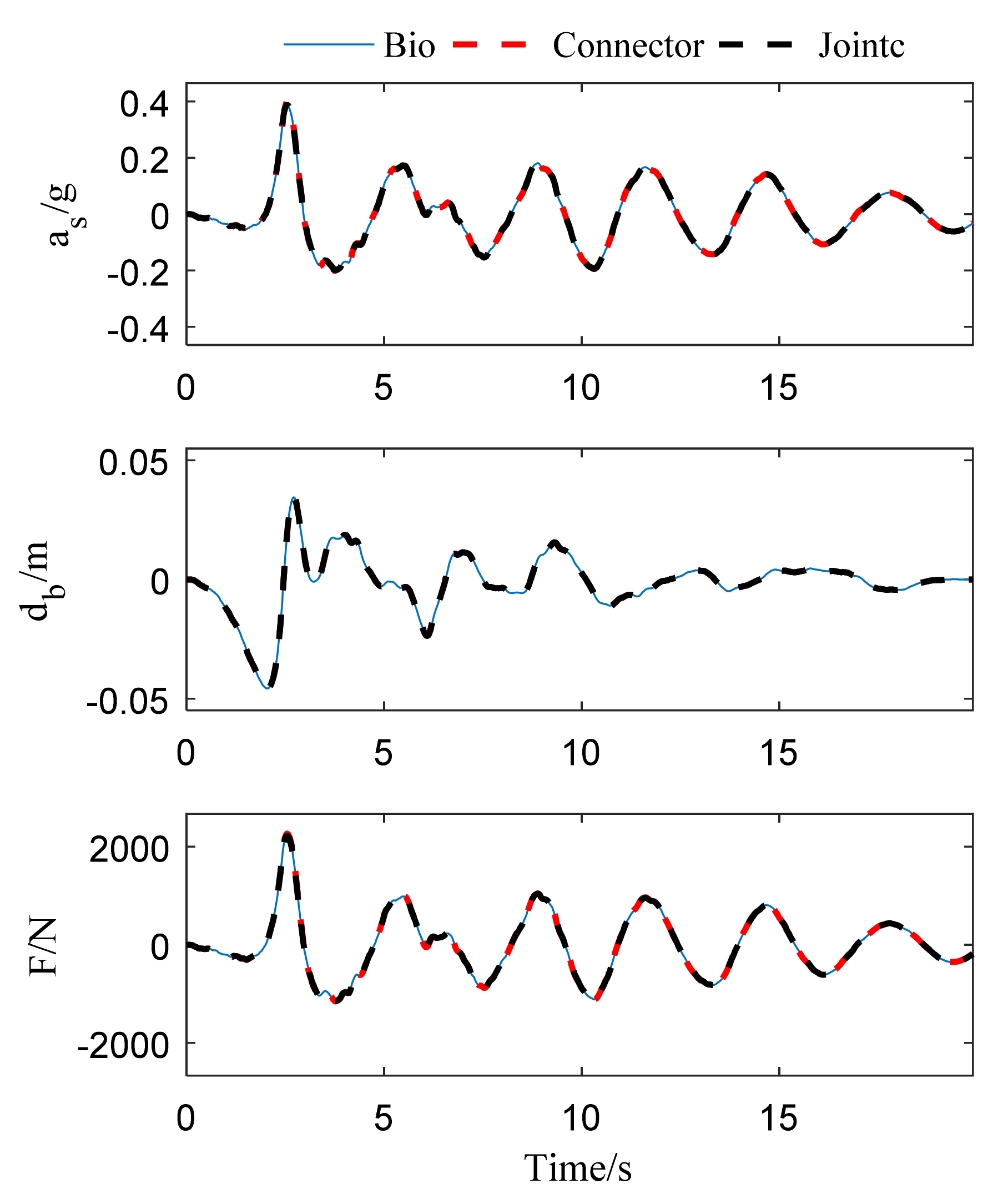
4.2. Verification of Bio-Inspired Isolator User Subroutine in Lumped Mass Model
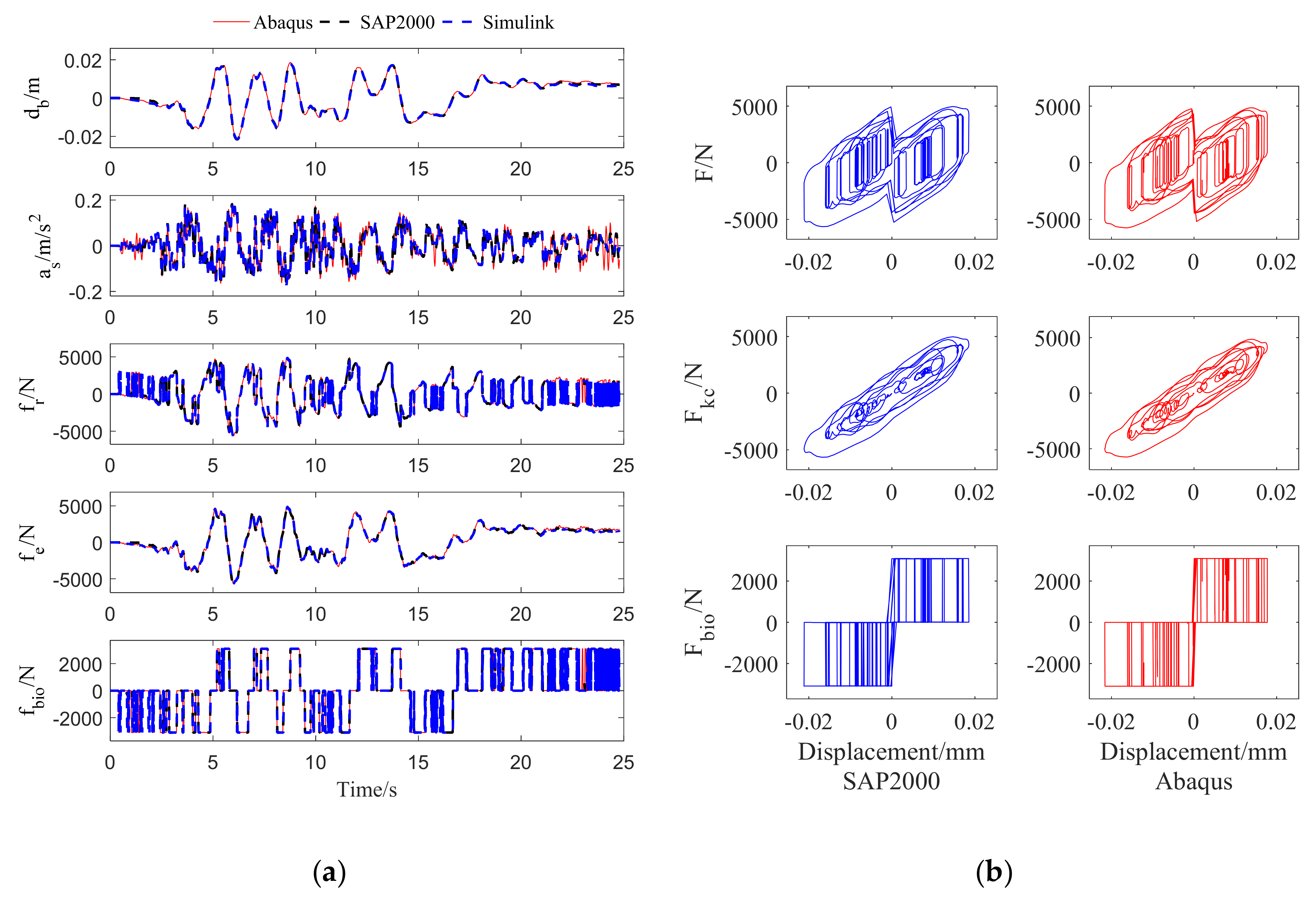
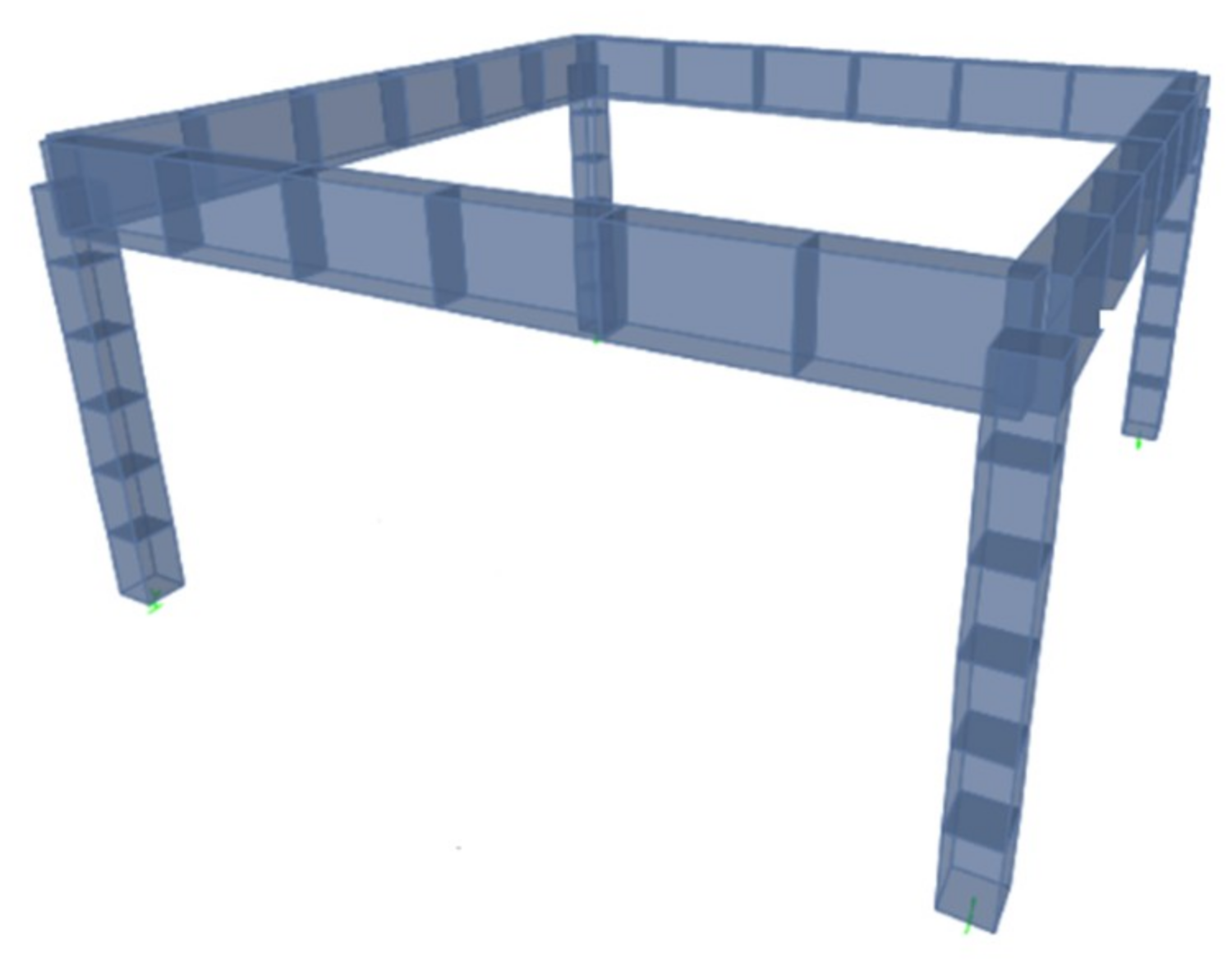
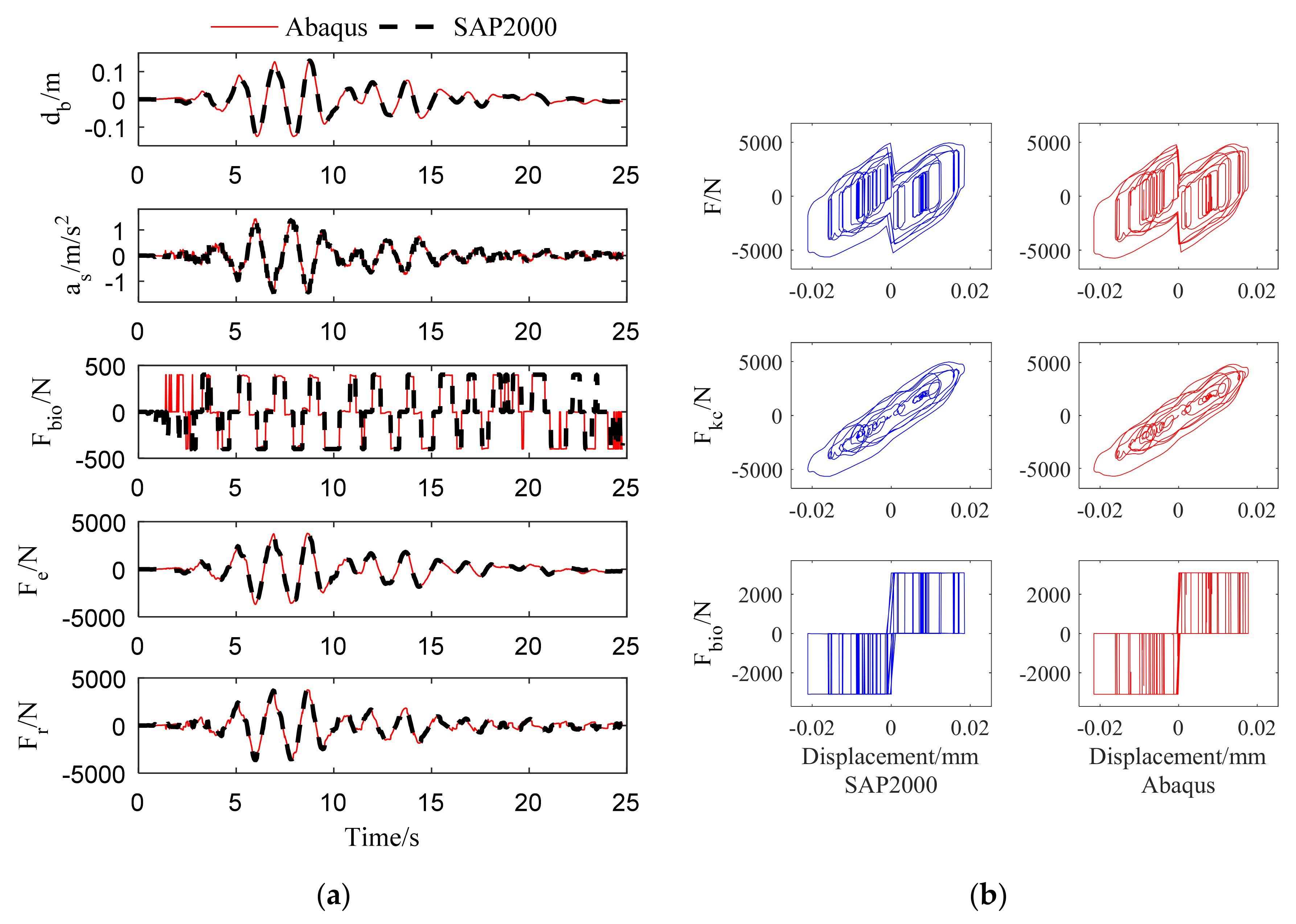
4.3. Verification of 3D Simple Model
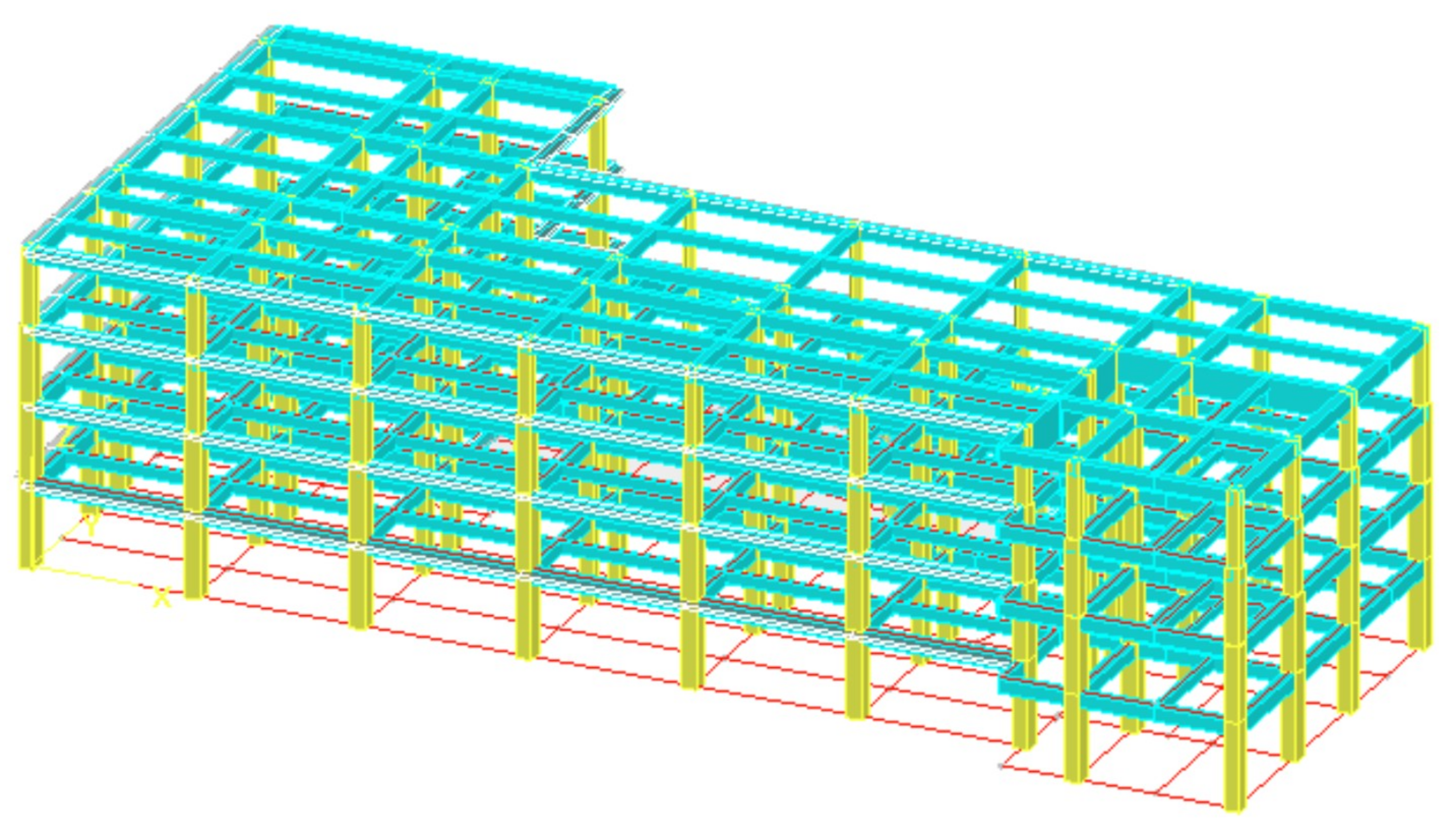
5. Verification of 3D Complex Structural Model
Control Algorithm
6. Conclusions
- (1)
- In the lumped mass model, the restoring force model of the user subroutine is verified by comparing it to the theoretical restoring force model under sinusoidal load;
- (2)
- It can be concluded from the comparison of the UEL subroutine in Abaqus and Matlab/Simulink or SAP2000 that the user subroutine can meet the demand of scientific research in the lumped mass model;
- (3)
- By comparing the response of the structure with the UEL subroutine, joint/connector, and SAP2000, the user subroutine can reach a satisfying computational accuracy in the 3D model;
- (4)
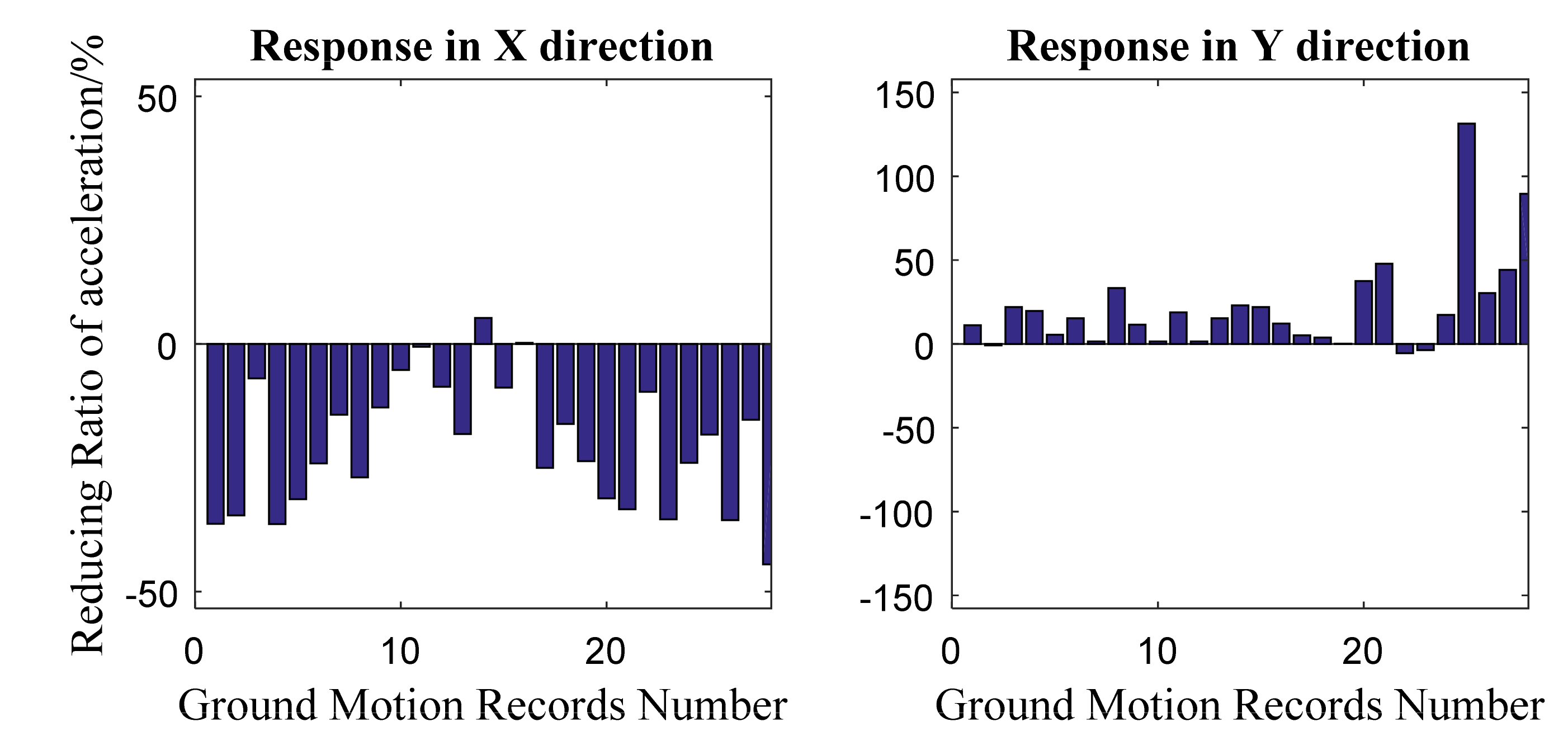
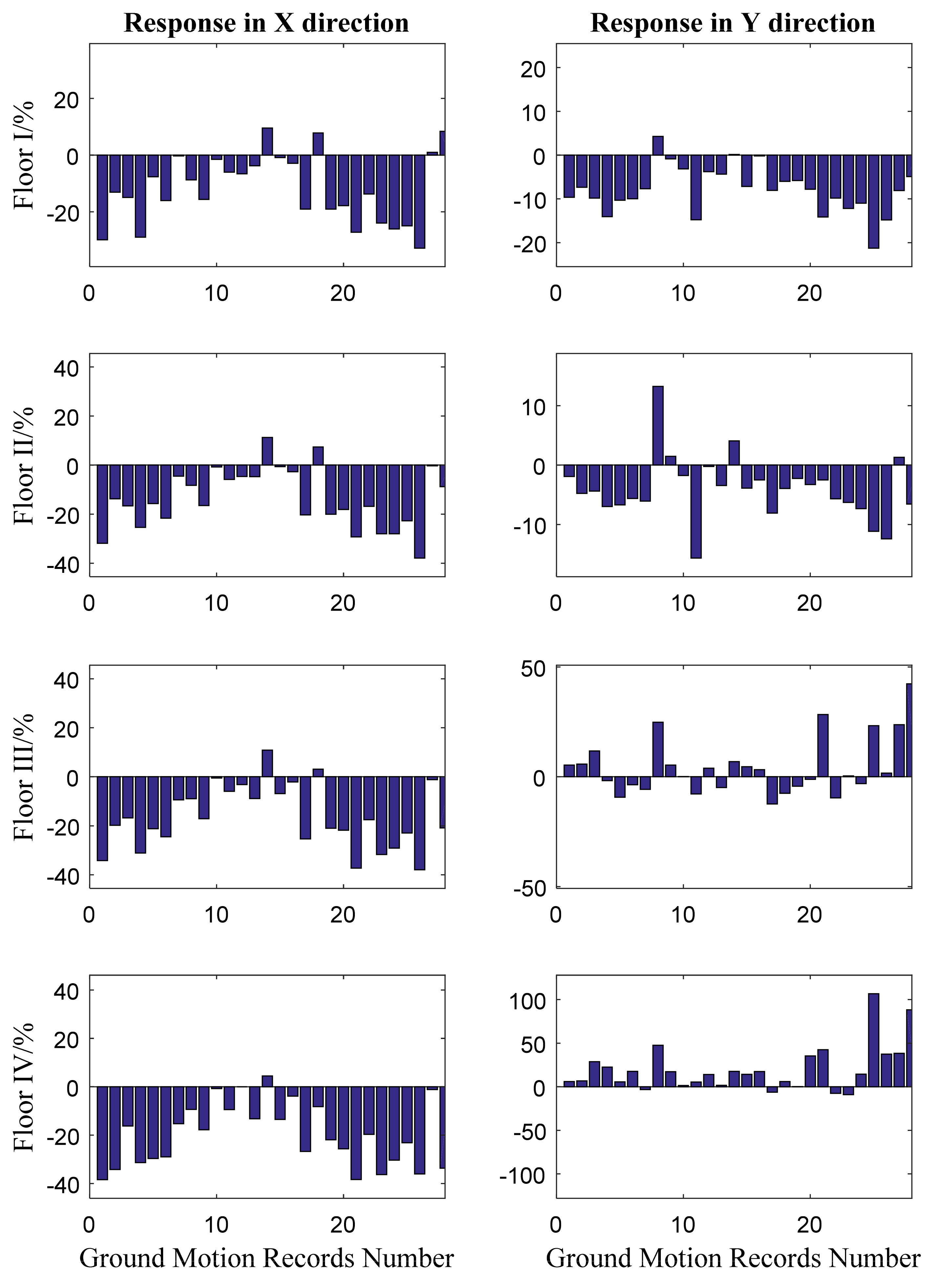
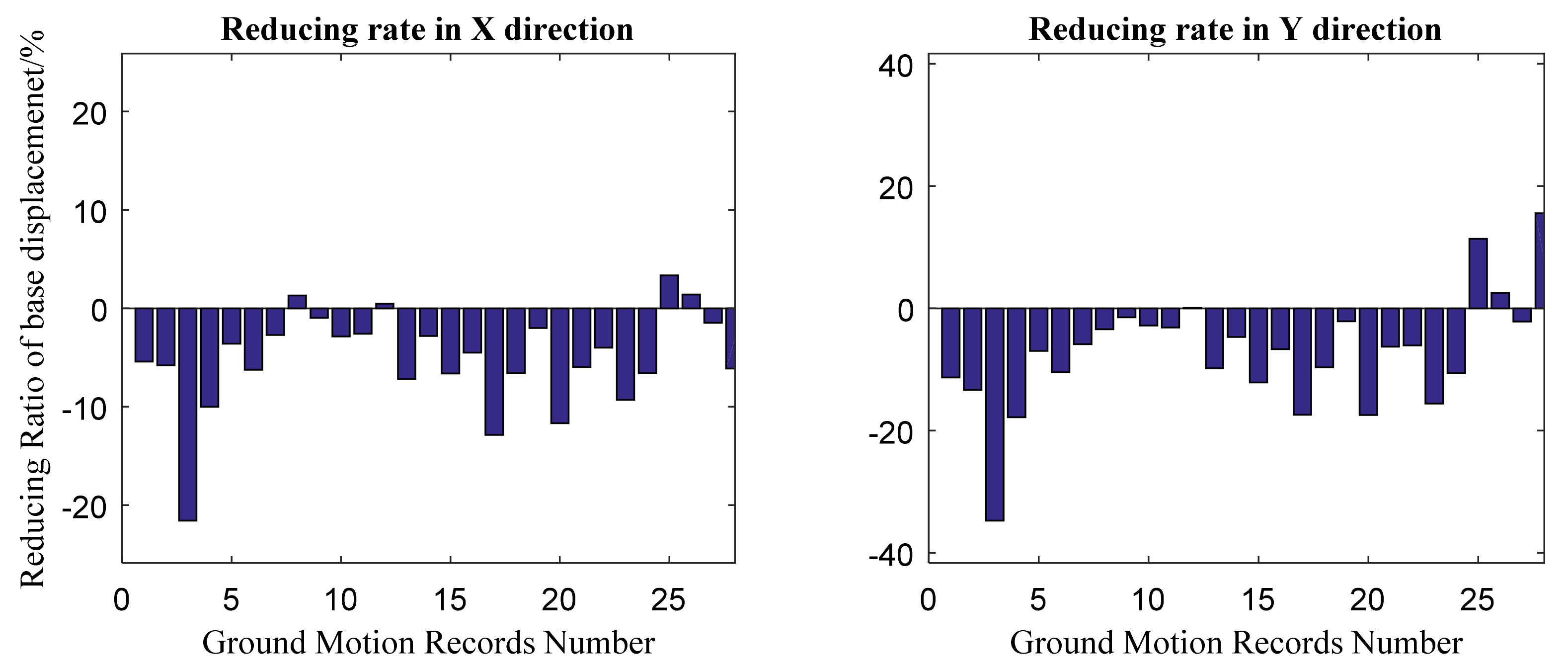
- The user subroutine can be applied in the real complex 3D structural model to simulate the bio-inspired isolation system. In the case study, the bio-inspired isolation system performs much better in the X direction than the traditional isolated system. In the Y direction, compared to the response of the traditional isolated system, the base displacement and the shear force of floor I and floor II (response below floor II) are smaller, while the acceleration at the top story and shear force of floor III and floor IV (response above floor III) are larger. It can be concluded that the bio-inspired isolated system is sensitive to the aspect ratio of the structure and will perform differently in two directions. Despite this, the response of low floors will always benefit from the bio-inspired system. The response of the high floors may be larger than that of traditional isolated results, but is still acceptable.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shi, W.; Wang, L.; Lu, Z. Study on self-adjustable tuned mass damper with variable mass. Struct. Control Health Monit. 2017, 25, e2114. [Google Scholar] [CrossRef]
- Shi, W.; Wang, L.; Lu, Z.; Gao, H. Study on adaptive-passive and semi-active eddy current tuned mass damper with variable damping. Sustainability 2018, 10, 99. [Google Scholar] [CrossRef]
- Shi, W.; Wang, L.; Lu, Z.; Zhang, Q. Application of an artificial fish swarm algorithm in an optimum tuned mass damper design for a pedestrian bridge. Appl. Sci. 2018, 8, 175. [Google Scholar] [CrossRef]
- Wang, L.; Shi, W.; Zhou, Y. Study on self-adjustable variable pendulum tuned mass damper. Struct. Des. Tall Spec. Build. 2018, e1561. [Google Scholar] [CrossRef]
- Cancellara, D.; De Angelis, F. Assessment and dynamic nonlinear analysis of different base isolation systems for a multi-storey RC building irregular in plan. Comput. Struct. 2017, 180, 74–88. [Google Scholar] [CrossRef]
- Lewandowski, R.; Łasecka-Plura, M. Design sensitivity analysis of structures with viscoelastic dampers. Comput. Struct. 2016, 164, 95–107. [Google Scholar] [CrossRef]
- Kvåle, K.; Sigbjörnsson, R.; Øiseth, O. Modelling the stochastic dynamic behavior of a pontoon bridge: A case study. Comput. Struct. 2016, 165, 123–135. [Google Scholar] [CrossRef]
- Lee, T.; Kawashima, K. Semi-active control of nonlinear isolated bridges with time delay. J. Struct. Eng. 2007, 133, 235–241. [Google Scholar] [CrossRef]
- Sayani, P.; Ryan, K. Comparative evaluation of base-isolated and fixed-base buildings using a comprehensive response index. J. Struct. Eng. 2009, 135, 698–707. [Google Scholar] [CrossRef]
- Hu, J. Response of Seismically Isolated Steel Frame Buildings with Sustainable Lead-Rubber Bearing (LRB) Isolator Devices Subjected to Near-Fault (NF) Ground Motions. Sustainability 2014, 7, 111–137. [Google Scholar] [CrossRef]
- Halldórsson, B.; Mavroeidis, G.; Papageorgiou, A. Near-fault and far-field strong ground-motion simulation for earthquake engineering applications using the specific barrier model. J. Struct. Eng. 2010, 137, 433–444. [Google Scholar] [CrossRef]
- Foti, D. Local ground effects in near-field and far-field areas on seismically protected buildings. Soil Dyn. Earthq. Eng. 2015, 74, 14–24. [Google Scholar] [CrossRef]
- Tirca, L.D.; Foti, D.; Diaferio, M. Response of middle-rise steel frames with and without passive dampers to near-field ground motions. Eng. Struct. 2003, 25, 169–179. [Google Scholar] [CrossRef]
- Foti, D. On the Seismic Response of Protected and Unprotected Middle-Rise Steel Frames in Far-Field and Near-Field Areas. Shock Vib. 2014, 2014, 393870. [Google Scholar] [CrossRef]
- Buratti, N.; Stafford, P.; Bommer, J. Earthquake accelerogram selection and scaling procedures for estimating the distribution of drift response. J. Struct. Eng. 2010, 137, 345–357. [Google Scholar] [CrossRef]
- Kalpakidis, I.; Constantinou, M.; Whittaker, A.S. Effects of large cumulative travel on the behavior of lead-rubber seismic isolation bearings. J. Struct. Eng. 2009, 136, 491–501. [Google Scholar] [CrossRef]
- Symans, M.; Constantinou, M. Semi-active control systems for seismic protection of structures: A state-of-the-art review. Eng. Struct. 1999, 21, 469–487. [Google Scholar] [CrossRef]
- Bitaraf, M.; Ozbulut, O.E.; Hurlebaus, S.; Barroso, L. Application of semi-active control strategies for seismic protection of buildings with MR dampers. Eng. Struct. 2010, 32, 3040–3047. [Google Scholar] [CrossRef]
- Kannan, S.; Uras, H.; Aktan, H. Active control of building seismic response by energy dissipation. Earthq. Eng. Struct. Dyn. 2010, 24, 747–759. [Google Scholar] [CrossRef]
- Rodellar, J.; Barbat, A. Active control of building structures under measured seismic loads. Eng. Comput. 2018, 2, 128–134. [Google Scholar] [CrossRef]
- Nguyen, X.B.; Komatsuzaki, T.; Iwata, Y.; Asanuma, H. Modeling and semi-active fuzzy control of magnetorheological elastomer-based isolator for seismic response reduction. Mech. Syst. Signal Process. 2018, 101, 449–466. [Google Scholar] [CrossRef]
- Zhao, D.; Li, Y.; Li, H.; Qian, H. Seismic reductions investigation of semi-active base-isolated structure based on multi-level fuzzy control. Shock Vib. 2016, 35, 78–84. [Google Scholar]
- Cha, Y.; Agrawal, A. Seismic retrofit of MRF buildings using decentralized semi-active control for multi-target performances. Earthq. Eng. Struct. Dyn. 2017, 46, 409–424. [Google Scholar] [CrossRef]
- Kappos, A.; Gkatzogias, K. Semi-Active Control Systems in Bridge Engineering: A Review of the Current State of Practice. Struct. Eng. Int. 2016, 26, 290–300. [Google Scholar]
- Yang, J.N.; Wu, J.C.; Kawashima, K.; Unjoh, S. Hybrid control of seismic-excited bridge structure. Earthq. Eng. Struct. Dyn. 2010, 24, 1437–1451. [Google Scholar] [CrossRef]
- Park, K.; Jung, H.; Lee, I. Hybrid control strategy for seismic protection of a benchmark cable-stayed bridge. Eng. Struct. 2003, 25, 405–417. [Google Scholar] [CrossRef]
- Yang, H.T.Y.; Lin C-Hung Bridges, D.; Randall, C.J.; Hansma, P.K. Bio-inspired passive actuator simulating an abalone shell mechanism for structural control. Smart Mater. Struct. 2010, 19, 105011. [Google Scholar] [CrossRef]
- Chen, X.; Yang, H.T.Y.; Shan, J.; Hansma, P.K.; Shi, W. Bio-Inspired Passive Optimized Base-Isolation System for Seismic Mitigation of Building Structures. J. Eng. Mech. 2015, 142, 04015061. [Google Scholar] [CrossRef]
- Shan, J.; Shi, Z.; Hu, F.; Yu, J.; Shi, W. Stochastic optimal design of novel nonlinear base isolation system for seismic-excited building structures. Struct. Control Health Monit. 2016, 25, e2168. [Google Scholar] [CrossRef]
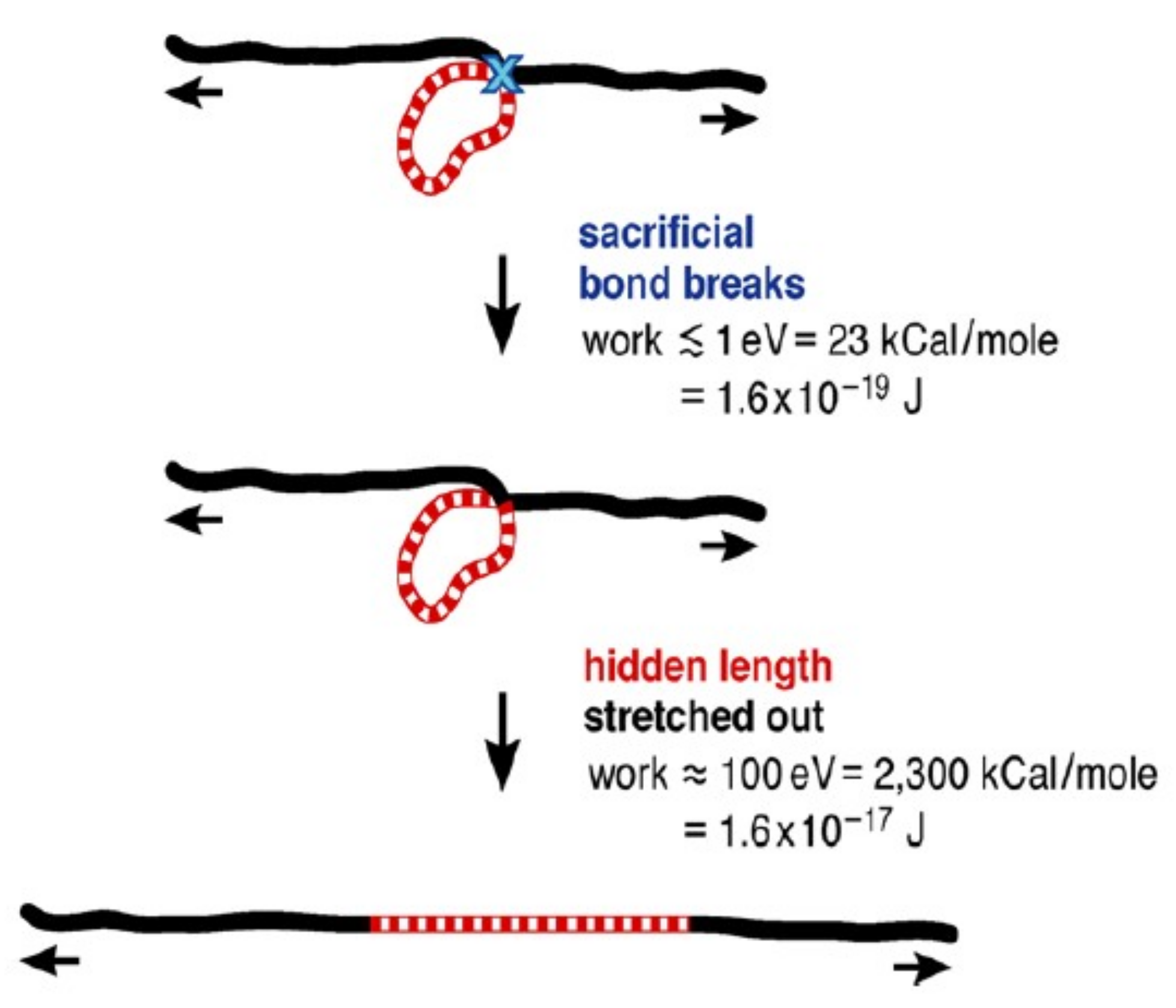
- Thurner, P.J.; Erickson, B.; Jungmann, R.; Schriock, Z.; Weaver, J.C.; Fantner, G.E.; Schitter, G.; Morse, D.E.; Hansma, P.K. High-speed photography of compressed human trabecular bone correlates whitening to microscopic damage. Eng. Fract. Mech. 2007, 74, 1928–1941. [Google Scholar] [CrossRef]
- Hansma, P.K.; Fantner, G.E.; Kindt, J.H.; Thurner, P.J.; Schitter, G.; Turner, P.J.; Udwin, S.F.; Finch, M.M. Sacrificial bonds in the interfibrillar matrix of bone. J. Musculoskelet. Neuronal Interact. 2005, 5, 313. [Google Scholar] [PubMed]
- Fantner, G.E.; Oroudjev, E.; Schitter, G.; Golde, L.S.; Thurner, P.; Finch, M.M.; Turner, P.; Gutsmann, T.; Morse, D.E.; Hansma, H.; et al. Sacrificial bonds and hidden length: Unraveling molecular mesostructures in tough materials. Biophys. J. 2006, 90, 1411–1418. [Google Scholar] [CrossRef] [PubMed]
- Becker, N.; Oroudjev, E.; Mutz, S.; Cleveland, J.P.; Hansma, P.K.; Hayashi, C.Y.; Makarov, D.E.; Hansma, H.G. Molecular nanosprings in spider capture-silk threads. Nat. Mater. 2003, 2, 278–283. [Google Scholar] [CrossRef] [PubMed]
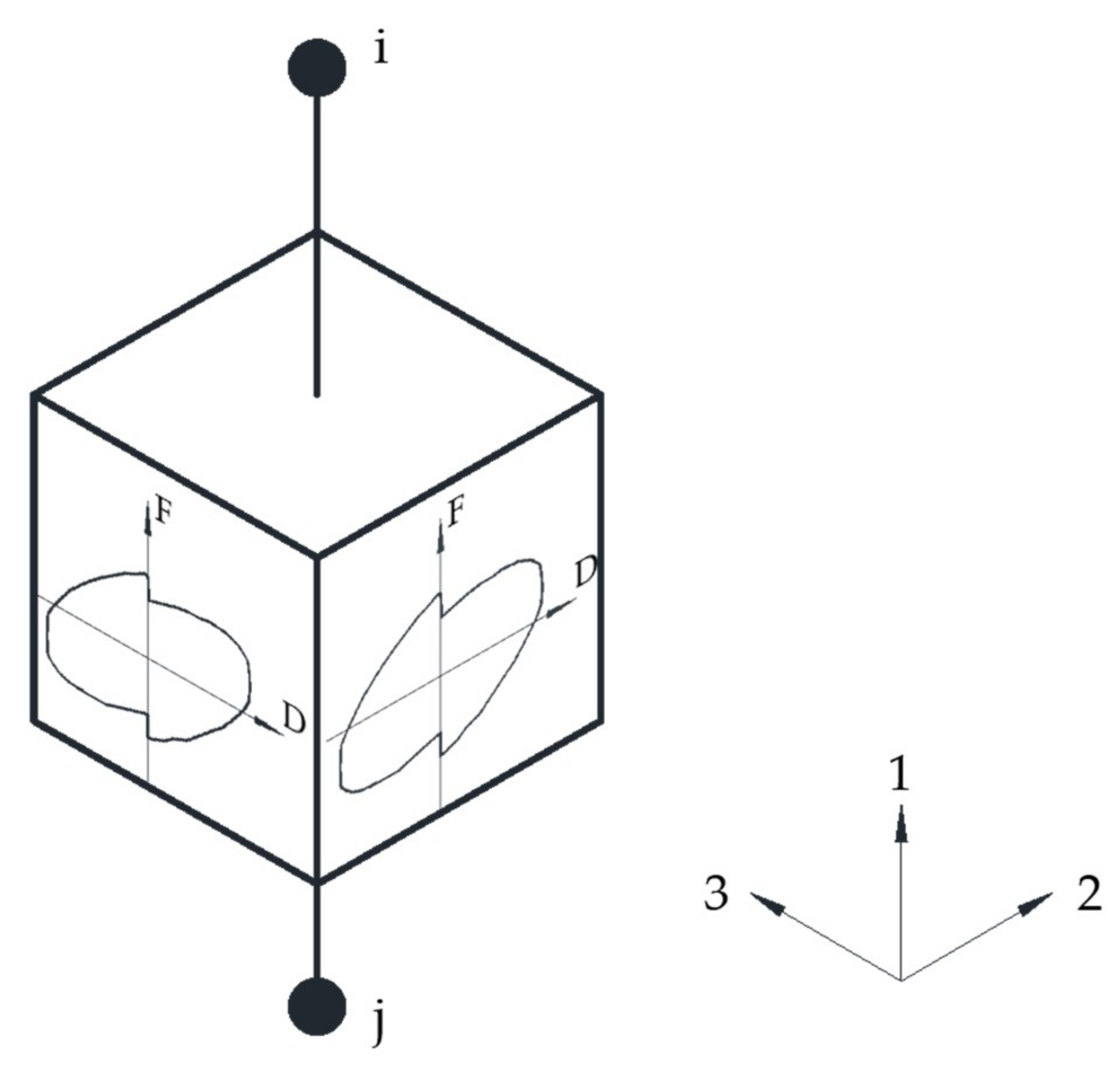
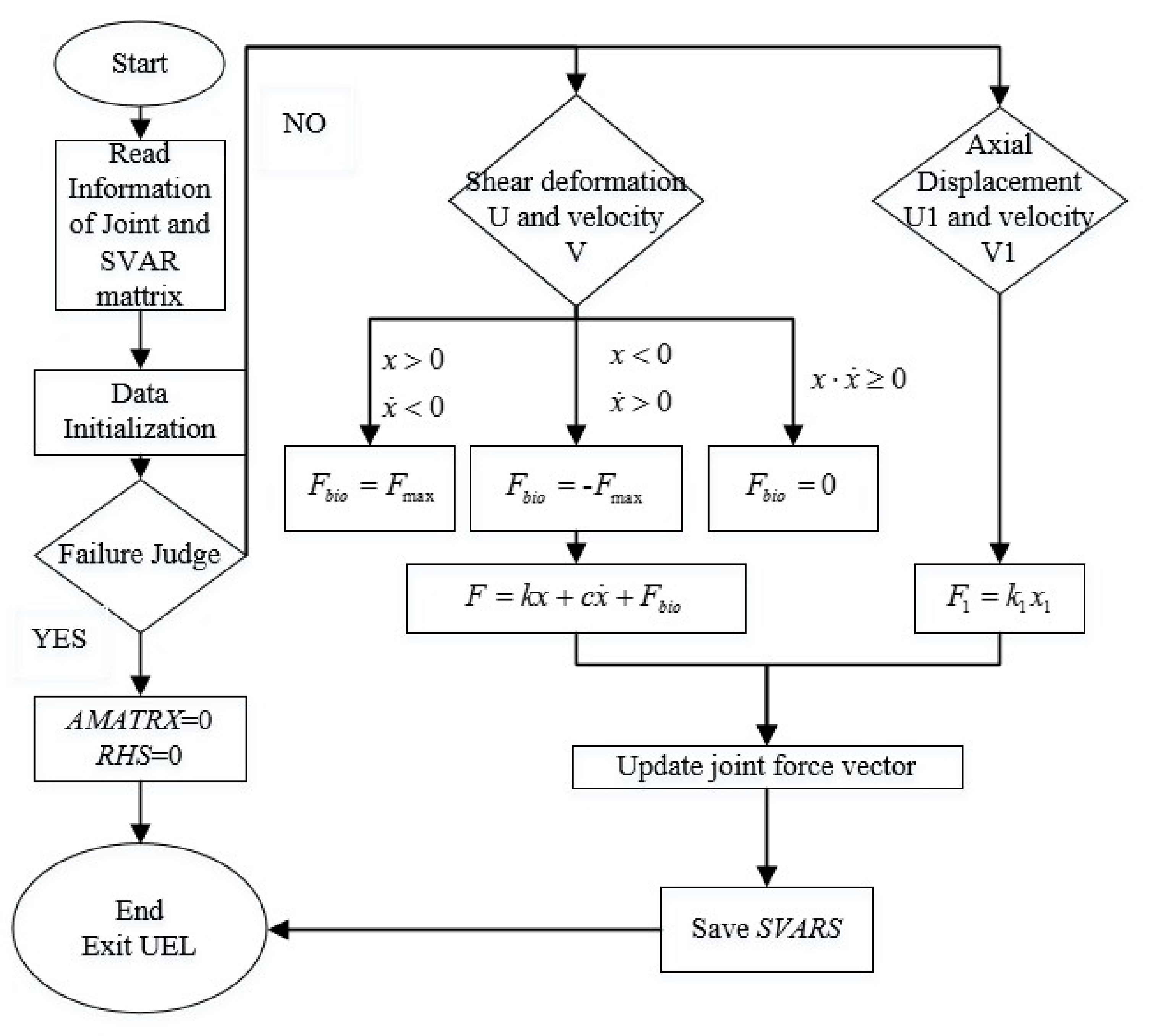

| UEL Parameters | Variable Name | Meaning | Units |
|---|---|---|---|
| props (1) | Kh | Horizontal shear stiffness | N/m |
| props (2) | Kv | Vertical pression stiffness | N/m |
| props (3) | Ch | Horizontal damping coefficient | N/(m/s) |
| props (4) | M | Mass of isolator | kg |
| props (5) | FBIO | Horizontal BIO force | N |
| Evaluation Index | Unit | Abaqus | Simulink (Error) | SAP2000 (Error) |
|---|---|---|---|---|
| dbmax | m | 0.0209 | 0.0213 (−1.9%) | 0.0216 (−3.2%) |
| asmax | m/s2 | 0.1848 | 0.1751 (5.5%) | 0.1883 (−1.9%) |
| Fmax | N | 5632 | 5683 (−0.9%) | 5742 (−1.9%) |
| Fbiomax | N | 3097 | 3096 (0%) | 3097 (0%) |
| Femax | N | 5648 | 5683 (−0.6%) | 5742 (−1.6%) |
| Parameter | Unit | Value |
|---|---|---|
| Material | C30 | |
| Section of Beam | mm | 250 × 600 |
| Section of Column | mm | 200 × 200 |
| Span | m | 6 |
| Height | m | 3 |
| Evaluation Index | Units | Abaqus | SAP2000 | Relative Error/% |
|---|---|---|---|---|
| dbmax | m | 0.1393 | 0.1395 | −0.1 |
| asmax | m/s2 | 1.4870 | 1.5097 | −1.5 |
| Fmax | N | 3744 | 3779 | −0.9 |
| Fbiomax | N | 401.02 | 400 | −0.3 |
| Femax | N | 3770 | 3779 | −0.2 |
| NGA# | Wave | Year | Type | R_jb [km] | R_rup [km] |
|---|---|---|---|---|---|
| 181 | H-E06140 | 1979 | Strike-Slip | 0 | 1.4 |
| 181 | H-E06230 | 1979 | Strike-Slip | 0 | 1.4 |
| 182 | H-E07140 | 1979 | Strike-Slip | 0.6 | 0.6 |
| 182 | H-E07230 | 1979 | Strike-Slip | 0.6 | 0.6 |
| 292 | A-STU000 | 1980 | Normal | 6.8 | 10.8 |
| 292 | A-STU270 | 1980 | Normal | 6.8 | 10.8 |
| 723 | B-PTS225 | 1987 | Strike-Slip | 0.9 | 0.9 |
| 723 | B-PTS315 | 1987 | Strike-Slip | 0.9 | 0.9 |
| 802 | STG000 | 1989 | Reverse-Oblique | 7.6 | 8.5 |
| 802 | STG090 | 1989 | Reverse-Oblique | 7.6 | 8.5 |
| 821 | ERZ-EW | 1992 | Strike-Slip | 0 | 4.4 |
| 821 | ERZ-NS | 1992 | Strike-Slip | 0 | 4.4 |
| 828 | PET000 | 1992 | Reverse | 0 | 8.2 |
| 828 | PET090 | 1992 | Reverse | 0 | 8.2 |
| 879 | LCN260 | 1992 | Strike-Slip | 2.2 | 2.2 |
| 879 | LCN345 | 1992 | Strike-Slip | 2.2 | 2.2 |
| 1063 | RRS228 | 1994 | Reverse | 0 | 6.5 |
| 1063 | RRS318 | 1994 | Reverse | 0 | 6.5 |
| 1086 | SYL090 | 1994 | Reverse | 1.7 | 5.3 |
| 1086 | SYL360 | 1994 | Reverse | 1.7 | 5.3 |
| 1165 | IZT090 | 1999 | Strike-Slip | 3.6 | 7.2 |
| 1165 | IZT180 | 1999 | Strike-Slip | 3.6 | 7.2 |
| 1503 | TCU065-E | 1999 | Reverse-Oblique | 0.6 | 0.6 |
| 1503 | TCU065-N | 1999 | Reverse-Oblique | 0.6 | 0.6 |
| 1529 | TCU102-E | 1999 | Reverse-Oblique | 1.5 | 1.5 |
| 1529 | TCU102-N | 1999 | Reverse-Oblique | 1.5 | 1.5 |
| 1605 | DZC180 | 1999 | Strike-Slip | 0 | 6.6 |
| 1605 | DZC270 | 1999 | Strike-Slip | 0 | 6.6 |
| Parameters | Unit | LRB700 (NSB700) | LNR600 |
|---|---|---|---|
| External diameter | mm | 700 | 600 |
| Vertical stiffness | kN/mm | 1858 | 1526 |
| Equivalent stiffness (γ = 1) | kN/mm | 2.208 | 1.103 |
| Equivalent damping index (γ = 1) | -- | 0.12 | 0 |
| Equivalent damping coefficient | kN/(m/s) | 125 | 0 |
| Number | -- | 27 | 20 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Shi, Z.; Shan, J.; Shi, W. Secondary Development and Application of Bio-Inspired Isolation System. Sustainability 2019, 11, 278. https://doi.org/10.3390/su11010278
Zhang Q, Shi Z, Shan J, Shi W. Secondary Development and Application of Bio-Inspired Isolation System. Sustainability. 2019; 11(1):278. https://doi.org/10.3390/su11010278
Chicago/Turabian StyleZhang, Quanwu, Zhiguo Shi, Jiazeng Shan, and Weixing Shi. 2019. "Secondary Development and Application of Bio-Inspired Isolation System" Sustainability 11, no. 1: 278. https://doi.org/10.3390/su11010278
APA StyleZhang, Q., Shi, Z., Shan, J., & Shi, W. (2019). Secondary Development and Application of Bio-Inspired Isolation System. Sustainability, 11(1), 278. https://doi.org/10.3390/su11010278





