Risk Transmission between Chinese and U.S. Agricultural Commodity Futures Markets—A CoVaR Approach
Abstract
1. Introduction
2. Methods and Data
2.1. Methods
2.1.1. Estimation of CoVaR
2.1.2. Estimation of Risk Transmission
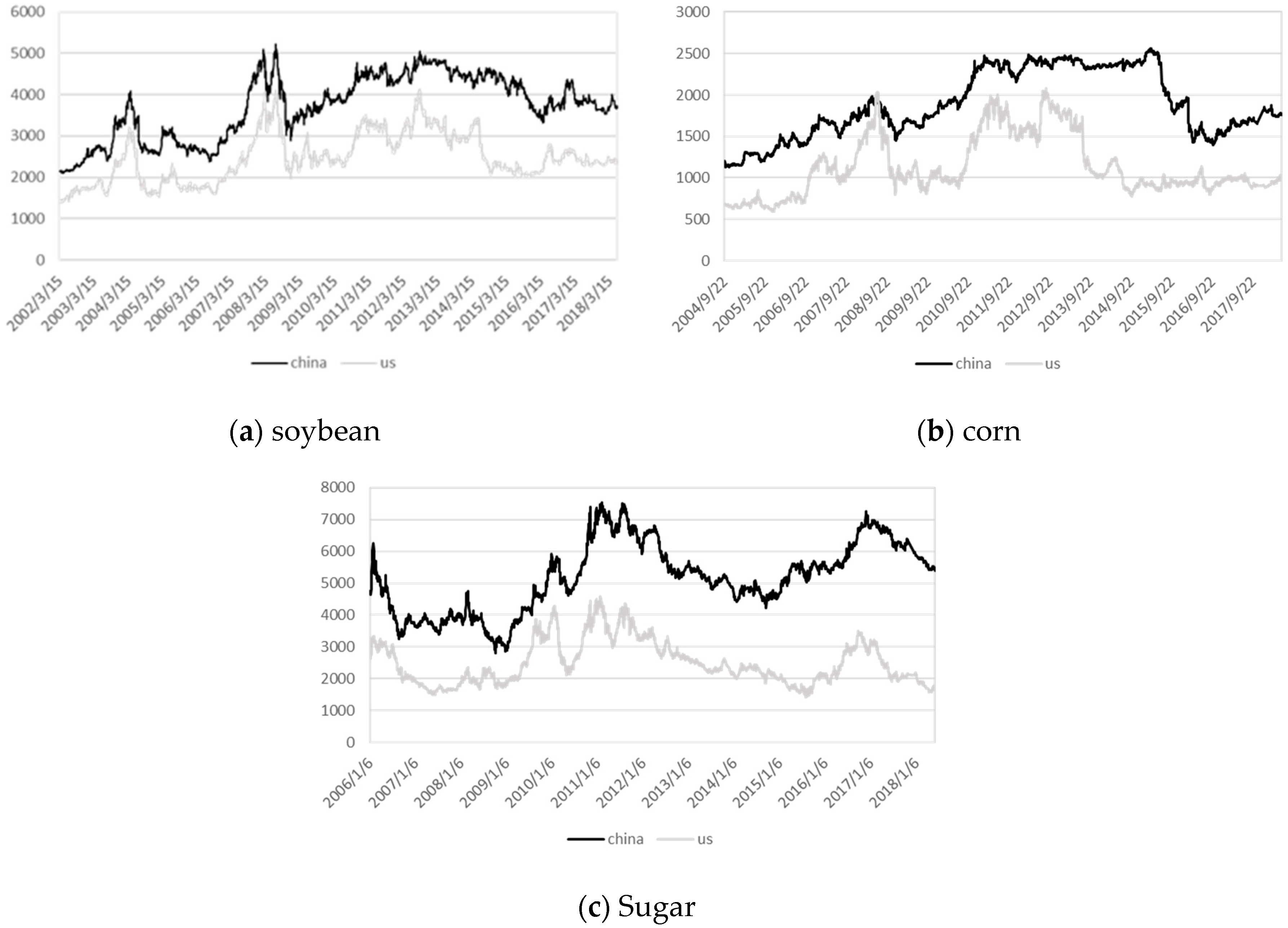
2.2. Data
3. Empirical Results
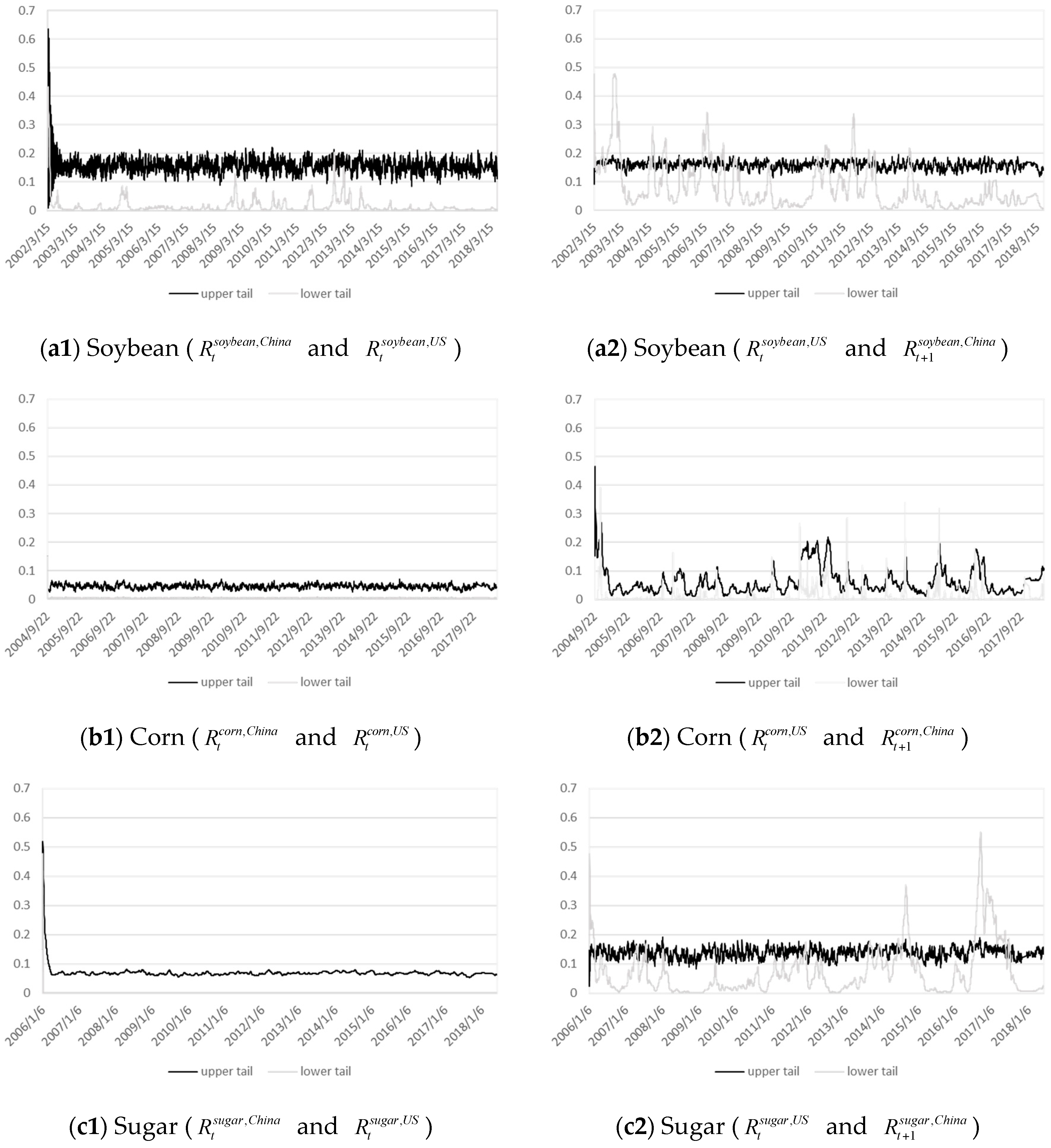
3.1. Copula and Tail Dependence
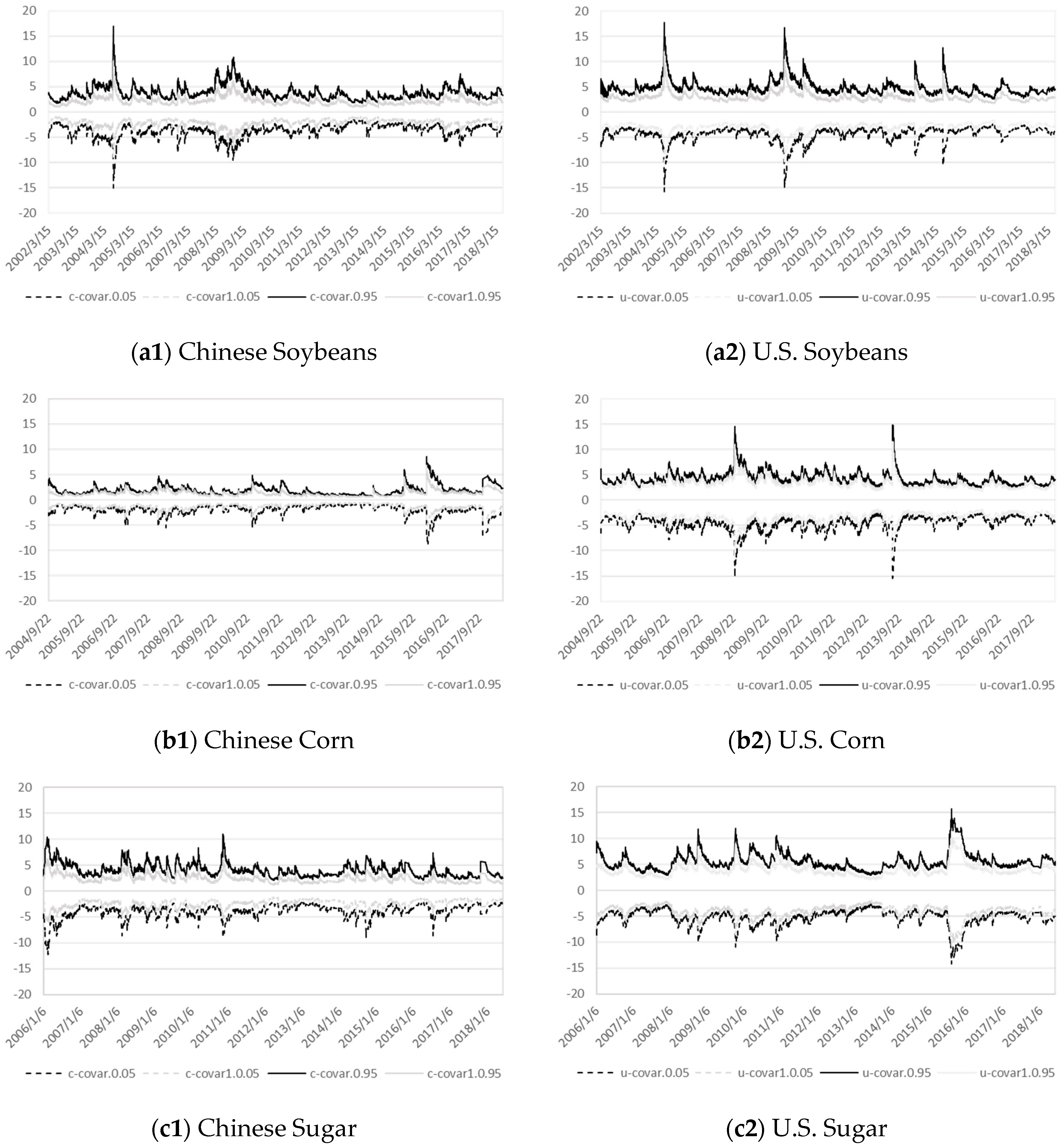
3.2. CoVaR and Risk Transmission
3.2.1. Estimation of Risk Transmission
3.2.2. Quantifying Risk Transmission
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- FIA. Available online: https://fimag.fia.org/ (accessed on 26 December 2018).
- Christofoletti, M.; Silva, R.; Mattos, F. The increasing participation of China in the world soybean market and its impact on price linkages in futures markets. In Proceedings of the NCCC-134 Conference on Applied Commodity Price Analysis, Forecasting, and Market Risk Management, St. Louis, MO, USA, 16–17 April 2012. [Google Scholar]
- Hernandez, M.A.; Ibarra, R.; Trupkin, D.R. How far do shocks move across borders? Examining volatility transmission in major agricultural futures markets. Eur. Rev. Agric. Econ. 2013, 41, 301–325. [Google Scholar] [CrossRef]
- Jiang, H.; Todorova, N.; Roca, E.; Su, J.-J. Dynamics of volatility transmission between the US and the Chinese agricultural futures markets. Appl. Econ. 2017, 49, 3435–3452. [Google Scholar] [CrossRef]
- FAO. Available online: http://www.fao.org/faostat/en/#rankings/commodities_by_country (accessed on 26 December 2018).
- BRIC. Available online: http://www.agdata.cn/ (accessed on 26 December 2018).
- Fung, H.-G.; Leung, W.K.; Xu, X.E. Information flows between the US and China commodity futures trading. Rev. Quant. Financ. Account. 2003, 21, 267–285. [Google Scholar] [CrossRef]
- Hua, R.; Chen, B. International linkages of the Chinese futures markets. Appl. Financ. Econ. 2007, 17, 1275–1287. [Google Scholar] [CrossRef]
- Du, W. International market integration under WTO: Evidence in the price behaviors of Chinese and US wheat futures. Selected Paper. In Proceedings of the American Agricultural Economics Association Annual Meeting, Denver, CO, USA, 1–4 August 2004. [Google Scholar]
- Zhang, Y.; Tong, X. Causality Diagrams for Zhengzhou Futures Sugar Prices. Math. Pract. Theor. 2012, 42, 33–40. [Google Scholar]
- Liu, C.-C. An Empirical Study on the Corn Futures Price Relevance between dec and cbot. J. Anhui Agric. Sci. 2009, 37, 899–903. [Google Scholar]
- Jiang, H.; Su, J.J.; Todorova, N.; Roca, E. Spillovers and Directional Predictability with a Cross-Quantilogram Analysis: The Case of US and Chinese Agricultural Futures. J. Futures Mark. 2016, 36, 1231–1255. [Google Scholar] [CrossRef]
- Liu, Q.; An, Y. Information transmission in informationally linked markets: Evidence from US and Chinese commodity futures markets. J. Int. Money Financ. 2011, 30, 778–795. [Google Scholar] [CrossRef]
- Adrian, T.; Brunnermeier, M. CoVar; Federal Reserve Bank of New York Staff Report, no. 348; Federal Reserve Bank of New York: New York, NY, USA, 2011. [Google Scholar]
- Girardi, G.; Ergün, A.T. Systemic risk measurement: Multivariate GARCH estimation of CoVaR. J. Bank Financ. 2013, 37, 3169–3180. [Google Scholar] [CrossRef]
- Bernal, O.; Gnabo, J.-Y.; Guilmin, G. Assessing the contribution of banks, insurance and other financial services to systemic risk. J. Bank Financ. 2014, 47, 270–287. [Google Scholar] [CrossRef]
- Abadie, A. Bootstrap tests for distributional treatment effects in instrumental variable models. J. Am. Stat. Assoc. 2002, 97, 284–292. [Google Scholar] [CrossRef]
- Karimalis, E.N.; Nomikos, N.K. Measuring systemic risk in the European banking sector: A Copula CoVaR approach. Eur. J. Financ. 2018, 24, 944–975. [Google Scholar] [CrossRef]
- Sklar, M. Fonctions de repartition an dimensions et leurs marges. Publ. Inst. Statist. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Patton, A.J. Modelling asymmetric exchange rate dependence. Int. Econ. Rev. 2006, 47, 527–556. [Google Scholar] [CrossRef]
- Reboredo, J.C.; Ugolini, A. Systemic risk in European sovereign debt markets: A CoVaR-copula approach. J. Int. Money Financ. 2015, 51, 214–244. [Google Scholar] [CrossRef]
- Reboredo, J.C.; Rivera-Castro, M.A.; Ugolini, A. Downside and upside risk spillovers between exchange rates and stock prices. J. Bank Financ. 2016, 62, 76–96. [Google Scholar] [CrossRef]
- Brorsen, B.W.; Ji, D. A relaxed lattice option pricing model: implied skewness and kurtosis. Agric. Financ. Rev. 2009, 69, 268–283. [Google Scholar]
- Mondovisione. Available online: http://www.mondovisione.com/media-and-resources/news/fia-releases-summary-statistics-for-2017-futures-and-options-volume-and-open-int/ (accessed on 26 December 2018).
- Janzen, J.P.; Adjemian, M.K. Estimating the location of world wheat price discovery. Am. J. Agric. Econ. 2017, 99, 1188–1207. [Google Scholar] [CrossRef]

| Commodity | CON | IMP | IMPUS | IMP/CON | IMPUS/CON |
|---|---|---|---|---|---|
| Chinese Soybean | 88,230 | 75,613 | 28,811 | 85.30 | 32.69 |
| Chinese Corn | 199,450 | 3631 | 1758 | 1.85 | 0.91 |
| Chinese Sugar | 14,480 | 3603 | 0.328 | 24.89 | 0.002 |
| Copula | Distribution Function | Tail Dependence |
|---|---|---|
| Clayton | ||
| Gumbel | ||
| BB1 |
| Commodity | Country | Futures Contract | Exchange | Rank |
|---|---|---|---|---|
| Soybean (15th March 2002 to 6th June 2018) | China | No. 1 Soybean Futures | DCE | 15 |
| U.S. | Soybean Futures | CBOT | 9 | |
| Corn (22nd September 2004 to 6th June 2018) | China | Corn Futures | DCE | 2 |
| U.S. | Corn Futures | CBOT | 3 | |
| Sugar (6th January 2006 to 6th June 2018) | China | White Sugar (SR) Futures | ZCE | 7 |
| U.S. | Sugar #11 Futures | ICE | 13 |
| Statistics | Soybean | Corn | Sugar | |||
|---|---|---|---|---|---|---|
| China | U.S. | China | U.S. | China | U.S. | |
| mean | 0.015 | 0.014 | 0.013 | 0.011 | 0.005 | −0.016 |
| s.d. | 1.253 | 1.799 | 0.938 | 2.089 | 1.353 | 2.447 |
| max | 7.517 | 6.819 | 9.094 | 12.763 | 8.454 | 15.182 |
| min | −19.382 | −28.054 | −16.101 | −26.810 | −7.779 | −19.876 |
| skewness | −1.036 *** | −2.415 *** | −0.861 *** | −1.067 *** | 0.272 *** | −0.284 *** |
| kurtosis | 22.404 *** | 33.877 *** | 51.068 *** | 19.892 *** | 7.070 *** | 9.992 *** |
| J.B.test | 57182 *** | 146670 *** | 292370 *** | 36635 *** | 1856 *** | 5419 *** |
| cor-a | 0.248 *** | 0.135 *** | 0.139 *** | |||
| cor-b | 0.273 *** | 0.129 *** | 0.261 *** | |||
| Parameters or Test | Soybean | Corn | Sugar | |||
|---|---|---|---|---|---|---|
| China | U.S. | China | U.S. | China | U.S. | |
| (g,h) | 4,2 | 3,2 | 4,3 | 2,4 | 4,2 | 3,2 |
| α | 0.064 | 0.044 | 0.0.055 | 0.061 | 0.088 | 0.044 |
| β | 0.935 | 0.941 | 0.944 | 0.924 | 0.907 | 0.947 |
| skew | 1.004 | 0.968 | 1.022 | 1.035 | 1.024 | 1.028 |
| shape | 3.307 | 4.613 | 2.716 | 4.617 | 3.520 | 4.369 |
| LB1(1) | 9.771 (0.002) | 0.927 [0.336] | 1.935 [0.164] | 0.0001 [0.991] | 5.133 [0.023] | 0.477 [0.450] |
| LB2(1) | 0.001 [0.979] | 0.336 [0.562] | 0.073 [0.967] | 0.074 [0.785] | 0.953 [0.329] | 1.296 [0.255] |
| KS test | 0.0028 [0.822] | 0.026 [0.659] | 0.0179 [0.6359] | 0.0024 [0.786] | 0.025 [0.913] | 0.031 [0.502] |
| Panel A: Copula Result forand | |||||||
| Soybean | |||||||
| Copula | AIC | ||||||
| Clayton | −2.819 *** (0.264) | −0.383 (0.264) | −0.890 *** (0.091) | −207.464 | |||
| Gumbel | −2.398 *** (0.196) | −0.381 * (0.193) | −0.907 *** (0.055) | −264.018 | |||
| Copula | AIC | ||||||
| BB1 | −1.594 ** (0.650) | −3.884 (2.109) | −0.965 *** (0.095) | 0.338 (0.491) | −2.075 (2.364) | 0.955 *** (0.021) | −287.379 |
| Corn | |||||||
| Copula | AIC | ||||||
| Clayton | −2.563 ** (0.693) | 0.329 (0.867) | −0.118 (0.211) | −60.641 | |||
| Gumbel | −3.378 *** (0.814) | 0.676 (0.945) | −0.398 (0.277) | −42.624 | |||
| Copula | AIC | ||||||
| BB1 | −2.827 ** (0.985) | −3.247 (4.000) | −0.365 (0.322) | −4.250 (4.539) | −3.286 (7.001) | −0.023 (0.323) | −63.407 |
| Sugar | |||||||
| Copula | AIC | ||||||
| Clayton | −2.624 ** (0.911) | 0.598 (0.500) | −0.121 (0.380) | −49.198 | |||
| Gumbel | −0.079 (0.162) | −0.030 (0.315) | 0.959 *** (0.041) | −55.533 | |||
| Copula | AIC | ||||||
| BB1 | −0.114 (0.318) | −0.134 (0.564) | 0.934 *** (0.089) | −9.064 (9.384) | −1.819 (92.431) | 9.911 (7.395) | −62.841 |
| Panel B: Copula Result forand | |||||||
| Soybean | |||||||
| Copula | AIC | ||||||
| Clayton | −2.346 *** (0.152) | −0.204 (0.072) | −0.995 *** (0.003) | −342.903 | |||
| Gumbel | −2.092 *** (0.148) | −0.145 (0.087) | −0.996 *** (0.004) | −375.327 | |||
| Copula | AIC | ||||||
| BB1 | −0.937 (0.502) | −1.627 (1.693) | −0.035 (0.033) | 0.214 * (0.101) | −1.035 * (0.509) | 0.977 *** (0.014) | −438.842 |
| Corn | |||||||
| Copula | AIC | ||||||
| Clayton | −3.348 *** (0.578) | −0.193 (0.410) | −0.657 ** (0.248) | −75.361 | |||
| Gumbel | 0.093 * (0.044) | −0.521 ** (0.194) | 0.971 *** (0.010) | −78.738 | |||
| Copula | AIC | ||||||
| BB1 | 0.143 (0.577) | −0.833 (2.073) | 0.959 *** (0.032) | 1.483 (10.837) | −10 (102.288) | 0.765 *** (2.426) | −101.683 |
| Sugar | |||||||
| Copula | AIC | ||||||
| Clayton | 0.047 * (0.020) | −0.313 ** (0.091) | 0.973 *** (0.008) | −213.927 | |||
| Gumbel | 0.021 (0.017) | −0.172 * (0.080) | 0.979 *** (0.012) | −212.239 | |||
| Copula | AIC | ||||||
| BB1 | −1.329 (1.178) | −3.089 (2.573) | −0.447 (0.685) | 0.251 * (0.11) | −1.231 * (0.523) | 0.974 *** (0.011) | −251.488 |
| Data | Commodity | Null Hypothesis | p-Value | |
|---|---|---|---|---|
| and | Soybean | lower tail > upper tail | 41.449 | 0 |
| Corn | lower tail > upper tail | 38.929 | 0 | |
| Sugar | lower tail > upper tail | 36.325 | 0 | |
| and | Soybean | lower tail > upper tail | 32.290 | 0 |
| Corn | lower tail > upper tail | 31.564 | 0 | |
| Sugar | lower tail > upper tail | 27.445 | 0 |
| Country | Confidence Level | Soybean | Corn | Sugar | |||
|---|---|---|---|---|---|---|---|
| p-Value | p-Value | p-Value | |||||
| China | 0.05 (downside) | 26.482 | 0 | 14.434 | 0 | 21.474 | 0 |
| U.S. | 0.05 (downside) | 25.512 | 0 | 16.910 | 0 | 15.817 | 0 |
| China | 0.95 (upside) | 27.495 | 0 | 12.585 | 0 | 22.795 | 0 |
| U.S. | 0.95 (upside) | 31.048 | 0 | 13.764 | 0 | 19.517 | 0 |
| Commodity | Risk Transmissions | Downside or Upside | Average | Standard Deviation |
|---|---|---|---|---|
| Soybean | China to U.S. | downside | 44.447 | 8.631 |
| China to U.S. | upside | 61.167 | 5.754 | |
| U.S. to China | downside | 75.549 | 16.894 | |
| U.S. to China | upside | 79.668 | 5.450 | |
| Corn | China to U.S. | downside | 34.598 | 2.087 |
| China to U.S. | upside | 26.981 | 4.088 | |
| U.S. to China | downside | 50.876 | 18.194 | |
| U.S. to China | upside | 44.578 | 26.007 | |
| Sugar | China to U.S. | downside | 29.814 | 2.200 |
| China to U.S. | upside | 40.351 | 4.855 | |
| U.S. to China | downside | 65.834 | 17.163 | |
| U.S. to China | upside | 71.711 | 5.882 |
| Panel A Risk Transmission from U.S. to China | |||
| Risk transmission | Null hypothesis | p-value | |
| Downside | corn > soybean | 27.112 | 0 |
| corn > sugar | 17.916 | 0 | |
| sugar > soybean | 23.098 | 0 | |
| Upside | corn > soybean | 32.831 | 0 |
| corn > sugar | 27.856 | 0 | |
| sugar > soybean | 20.489 | 0 | |
| Panel B risk transmission from China to U.S. | |||
| Risk transmission | Null hypothesis | p-value | |
| Downside | corn > soybean | 29.955 | 0 |
| corn > sugar | 0.103 | 0.963 | |
| sugar > soybean | 38.292 | 0 | |
| Upside | corn > soybean | 40.340 | 0 |
| corn > sugar | 36.076 | 0 | |
| sugar > soybean | 38.007 | 0 | |
| Commodity | Risk Transmission | Null Hypothesis | p-Value | |
|---|---|---|---|---|
| Soybean | U.S. to China | downside > upside | 17.856 | 0 |
| China to U.S. | downside > upside | 33.816 | 0 | |
| Corn | U.S. to China | downside > upside | 1.541 | 0.003 |
| China to U.S. | downside > upside | 0 | 1 | |
| Sugar | U.S. to China | downside > upside | 14.868 | 0 |
| China to U.S. | downside > upside | 35.899 | 0 |
| Commodity | Risk Transmission | Null Hypothesis | p-Value | |
|---|---|---|---|---|
| Soybean | Downside | China to U.S. > U.S. to China | 33.698 | 0 |
| Upside | China to U.S. > U.S. to China | 39.576 | 0 | |
| Corn | Downside | China to U.S. > U.S. to China | 31.418 | 0 |
| Upside | China to U.S. > U.S. to China | 19.991 | 0 | |
| Sugar | Downside | China to U.S. > U.S. to China | 36.091 | 0 |
| Upside | China to U.S. > U.S. to China | 35.857 | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ke, Y.; Li, C.; McKenzie, A.M.; Liu, P. Risk Transmission between Chinese and U.S. Agricultural Commodity Futures Markets—A CoVaR Approach. Sustainability 2019, 11, 239. https://doi.org/10.3390/su11010239
Ke Y, Li C, McKenzie AM, Liu P. Risk Transmission between Chinese and U.S. Agricultural Commodity Futures Markets—A CoVaR Approach. Sustainability. 2019; 11(1):239. https://doi.org/10.3390/su11010239
Chicago/Turabian StyleKe, Yangmin, Chongguang Li, Andrew M. McKenzie, and Ping Liu. 2019. "Risk Transmission between Chinese and U.S. Agricultural Commodity Futures Markets—A CoVaR Approach" Sustainability 11, no. 1: 239. https://doi.org/10.3390/su11010239
APA StyleKe, Y., Li, C., McKenzie, A. M., & Liu, P. (2019). Risk Transmission between Chinese and U.S. Agricultural Commodity Futures Markets—A CoVaR Approach. Sustainability, 11(1), 239. https://doi.org/10.3390/su11010239




