Development of Large-Scale and Quasi Multi-Physics Model for Whole Structure of the Typical Solid Oxide Fuel Cell Stacks
Abstract
1. Introduction
2. Materials and Methods
2.1. 3D Model Structure and Parameters
2.2. Multi-Physics Models and the Boundary Conditions
2.3. Mesh and Calculation
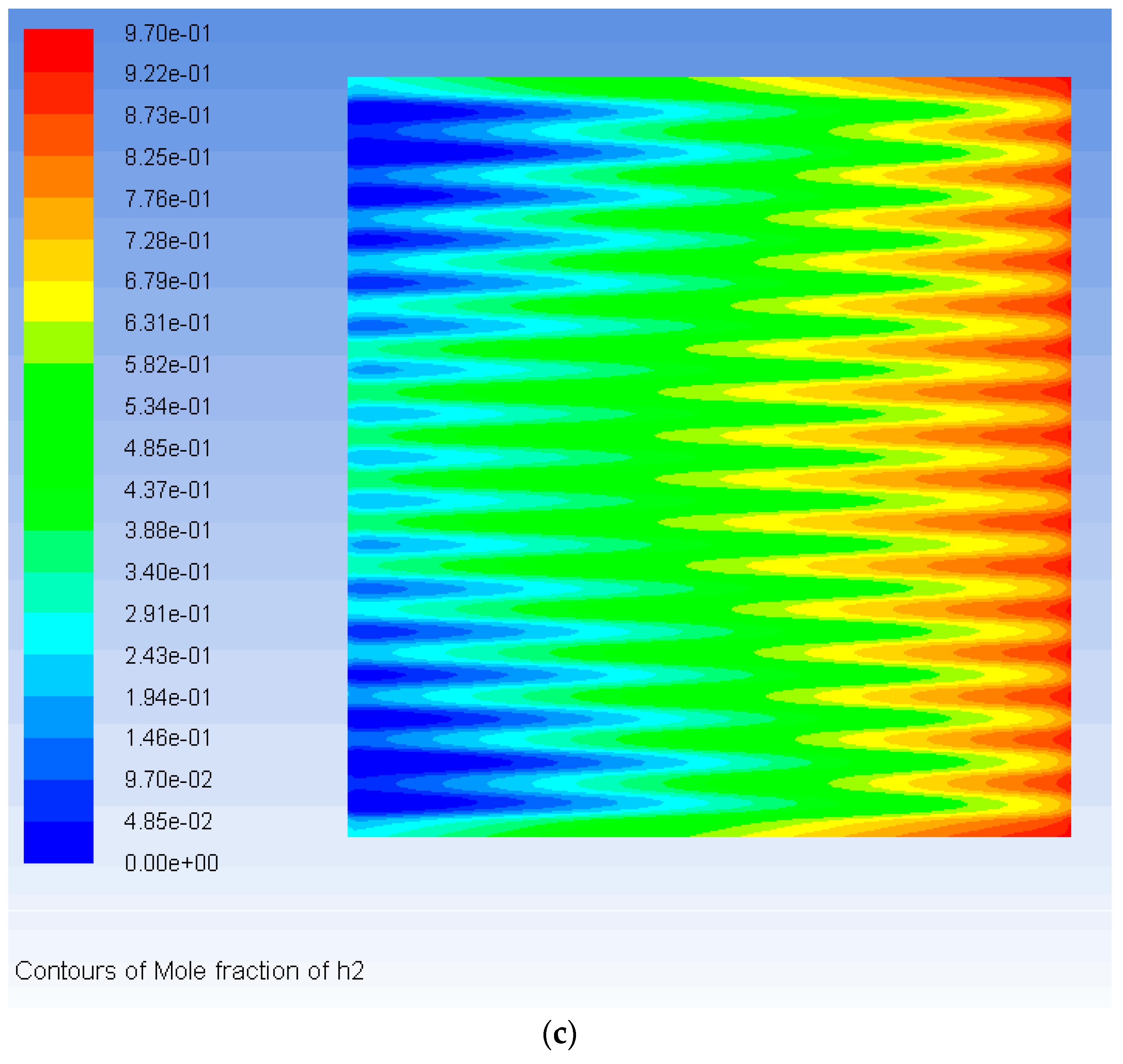
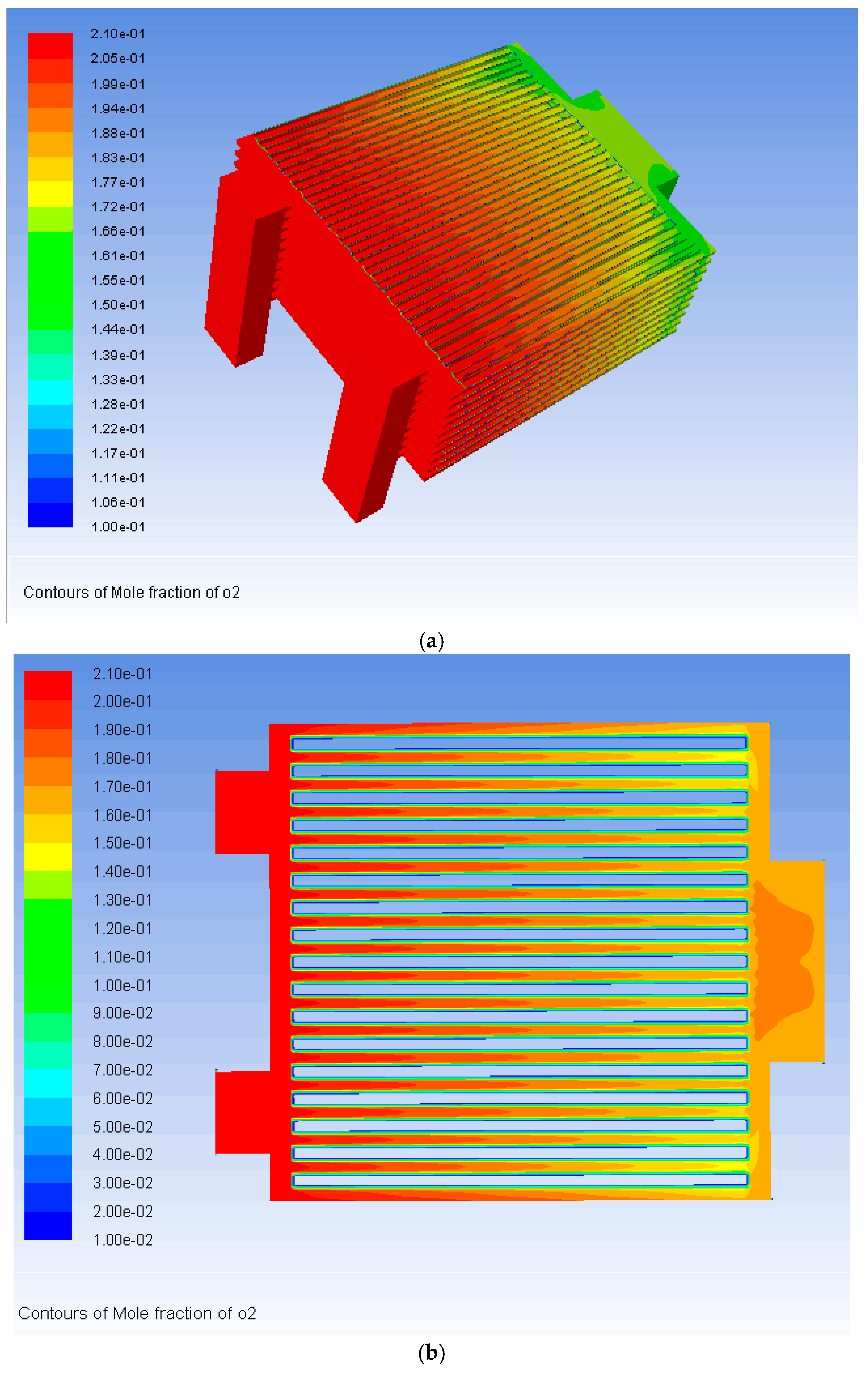
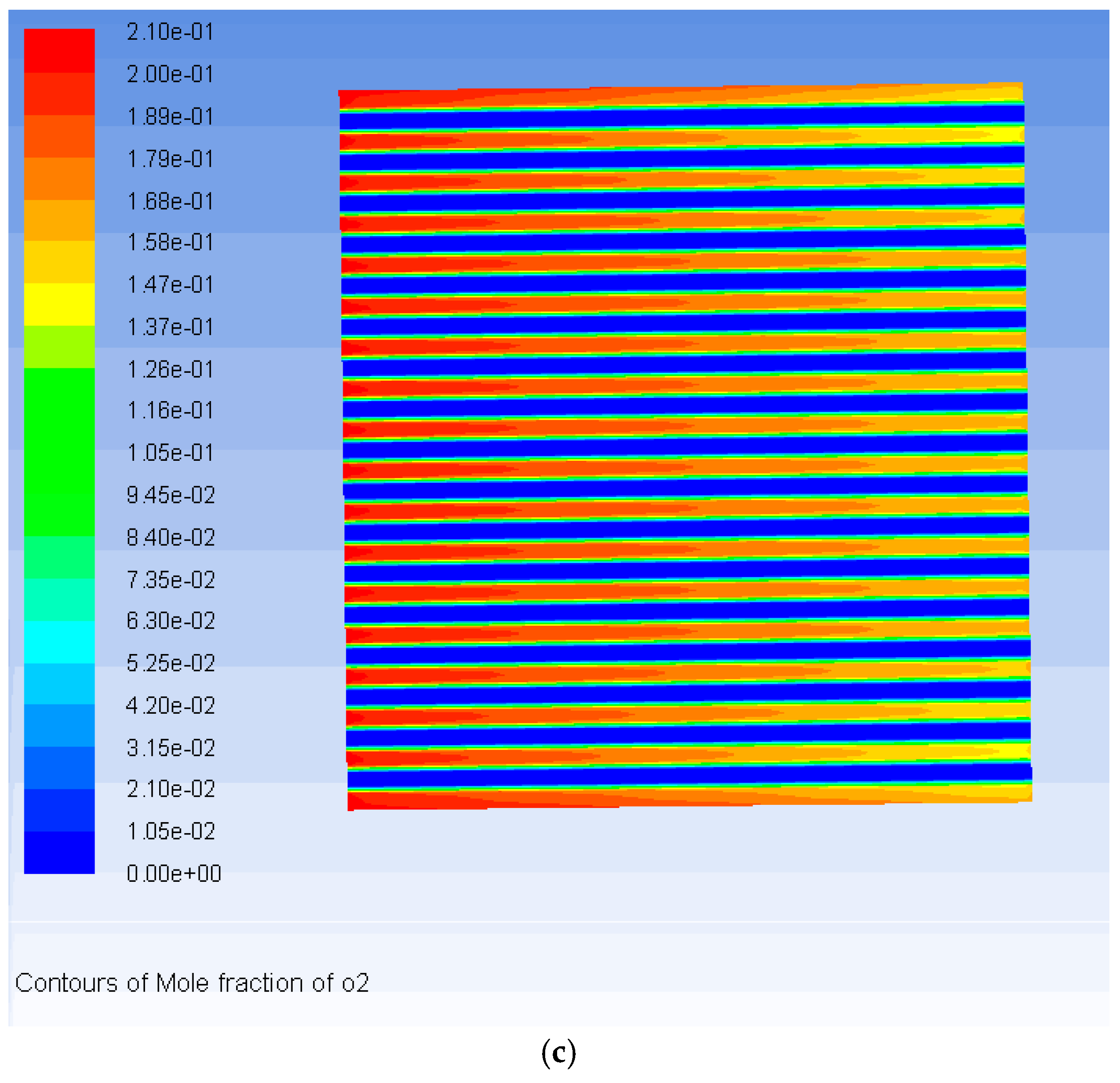
3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, Q.; Wei, H.-H.; Xu, Q. A Solid Oxide Fuel Cell (SOFC)-Based Biogas-from-Waste Generation System for Residential Buildings in China: A Feasibility Study. Sustainability 2018, 10, 2395. [Google Scholar] [CrossRef]
- Wu, L.; Sun, L.; Shen, J.; Hua, Q. Multiple Model Predictive Hybrid Feedforward Control of Fuel Cell Power Generation System. Sustainability 2018, 10, 437. [Google Scholar] [CrossRef]
- Shao, Z.P.; Haile, S.M. A high-performance cathode for the next generation of solid-oxide fuel cells. Nature 2004, 431, 170–173. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Akhtar, Z.; Li, P.; Wang, K. Mathematical Modeling Analysis and Optimization of Key Design Parameters of Proton-Conductive Solid Oxide Fuel Cells. Energies 2014, 7, 173–190. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, Q.; Lu, L.; Periasamy, V.; Tade, M.O.; Shao, Z. Multi scale and physics models for intermediate and low temperatures H+-solid oxide fuel cells with H+/e(−)/O2− mixed conducting properties: Part A, generalized percolation theory for LSCF-SDC-BZCY 3-component cathodes. J. Power Sources 2016, 303, 305–316. [Google Scholar] [CrossRef]
- Kong, W.; Gao, X.; Liu, S.; Su, S.; Chen, D. Optimization of the Interconnect Ribs for a Cathode-Supported Solid Oxide Fuel Cell. Energies 2014, 7, 295–313. [Google Scholar] [CrossRef]
- Enrico, A.; Cannarozzo, M.; Costamagna, P. Modeling Analysis of Bi-Layer Ni-(ZrO2)x(Y2O3)1−x Anodes for Anode-Supported Intermediate Temperature-Solid Oxide Fuel Cells. Energies 2014, 7, 5647–5674. [Google Scholar] [CrossRef]
- Chen, D.; Wang, H.; Zhang, S.; Tade, M.O.; Shao, Z.; Chen, H. Multiscale model for solid oxide fuel cell with electrode containing mixed conducting material. AlChE J. 2015, 61, 3786–3803. [Google Scholar] [CrossRef]
- Chen, D.; Hu, B.; Ding, K.; Yan, C.; Lu, L. The Geometry Effect of Cathode/Anode Areas Ratio on Electrochemical Performance of Button Fuel Cell Using Mixed Conducting Materials. Energies 2018, 11, 1–16. [Google Scholar] [CrossRef]
- Ni, M.; Shao, Z.; Chan, K. Modeling of Proton-Conducting Solid Oxide Fuel Cells Fueled with Syngas. Energies 2014, 7, 4381–4396. [Google Scholar] [CrossRef]
- Sun, L.; Hua, Q.; Shen, J.; Xue, Y.; Li, D.; Lee, K. A Combined Voltage Control Strategy for Fuel Cell. Sustainability 2017, 9, 1517. [Google Scholar] [CrossRef]
- Hirata, H.; Nakagaki, T.; Hori, M. Effect of gas channel height on gas flow and gas diffusion in a molten carbonate fuel cell stack. J. Power Sources 1999, 83, 41–49. [Google Scholar] [CrossRef]
- Huang, C.M.; Shy, S.S.; Leeb, C.H. On flow uniformity in various interconnects and its influence to cell performance of planar SOFC. J. Power Sources 2008, 183, 205–213. [Google Scholar] [CrossRef]
- Koh, J.-H.; Seo, H.-K.; Lee, C.G.; Yoo, Y.-S.; Lim, H.C. Pressure and flow distribution in internal gas manifolds of a fuel-cell stack. J. Power Sources 2003, 115, 54–65. [Google Scholar] [CrossRef]
- Cruz Rojas, A.; Lopez Lopez, G.; Gomez-Aguilar, J.; Alvarado, V.; Sandoval Torres, C. Control of the Air Supply Subsystem in a PEMFC with Balance of Plant Simulation. Sustainability 2017, 9, 73. [Google Scholar] [CrossRef]
- Qin, Y.; Sun, L.; Hua, Q.; Liu, P. A Fuzzy Adaptive PID Controller Design for Fuel Cell Power Plant. Sustainability 2018, 10, 2438. [Google Scholar] [CrossRef]
- Chen, D.; Zeng, Q.; Su, S.; Bi, W.; Ren, Z. Geometric optimization of a 10-cell modular planar solid oxide fuel cell stack manifold. Appl. Energy 2013, 112, 1100–1107. [Google Scholar] [CrossRef]
- Peksen, M. 3D transient multiphysics modelling of a complete high temperature fuel cell system using coupled CFD and FEM. Int. J. Hydrog. Energy 2014, 39, 5137–5147. [Google Scholar] [CrossRef]
- Chen, D.; Xu, Y.; Tade, M.O.; Shao, Z. General Regulation of Air Flow Distribution Characteristics within Planar Solid Oxide Fuel Cell Stacks. ACS Energy Lett. 2017, 2, 319–326. [Google Scholar] [CrossRef]
- Su, S.; He, H.; Chen, D.; Zhu, W.; Wu, Y.; Kong, W.; Wang, B.; Lu, L. Flow distribution analyzing for the solid oxide fuel cell short stacks with rectangular and discrete cylindrical rib configurations. Int. J. Hydrog. Energy 2015, 40, 577–592. [Google Scholar] [CrossRef]
- Chen, D.; Xu, Y.; Hu, B.; Yan, C.; Lu, L. Investigation of proper external air flow path for tubular fuel cell stacks with an anode support feature. Energy Convers. Manag. 2018, 171, 807–814. [Google Scholar] [CrossRef]
- Blum, L.; Groß, S.M.; Malzbender, J.; Pabst, U.; Peksen, M.; Peters, R.; Vinke, I.C. Investigation of solid oxide fuel cell sealing behavior under stack relevant conditions at Forschungszentrum Jülich. J. Power Sources 2011, 196, 7175–7181. [Google Scholar] [CrossRef]
- Yan, D.; Liang, L.J.; Yang, J.J.; Zhang, T.; Pu, J.; Chi, B.; Li, J. Performance degradation and analysis of 10-cell anode-supported SOFC stack with external manifold structure. Energy 2017, 125, 663–670. [Google Scholar] [CrossRef]
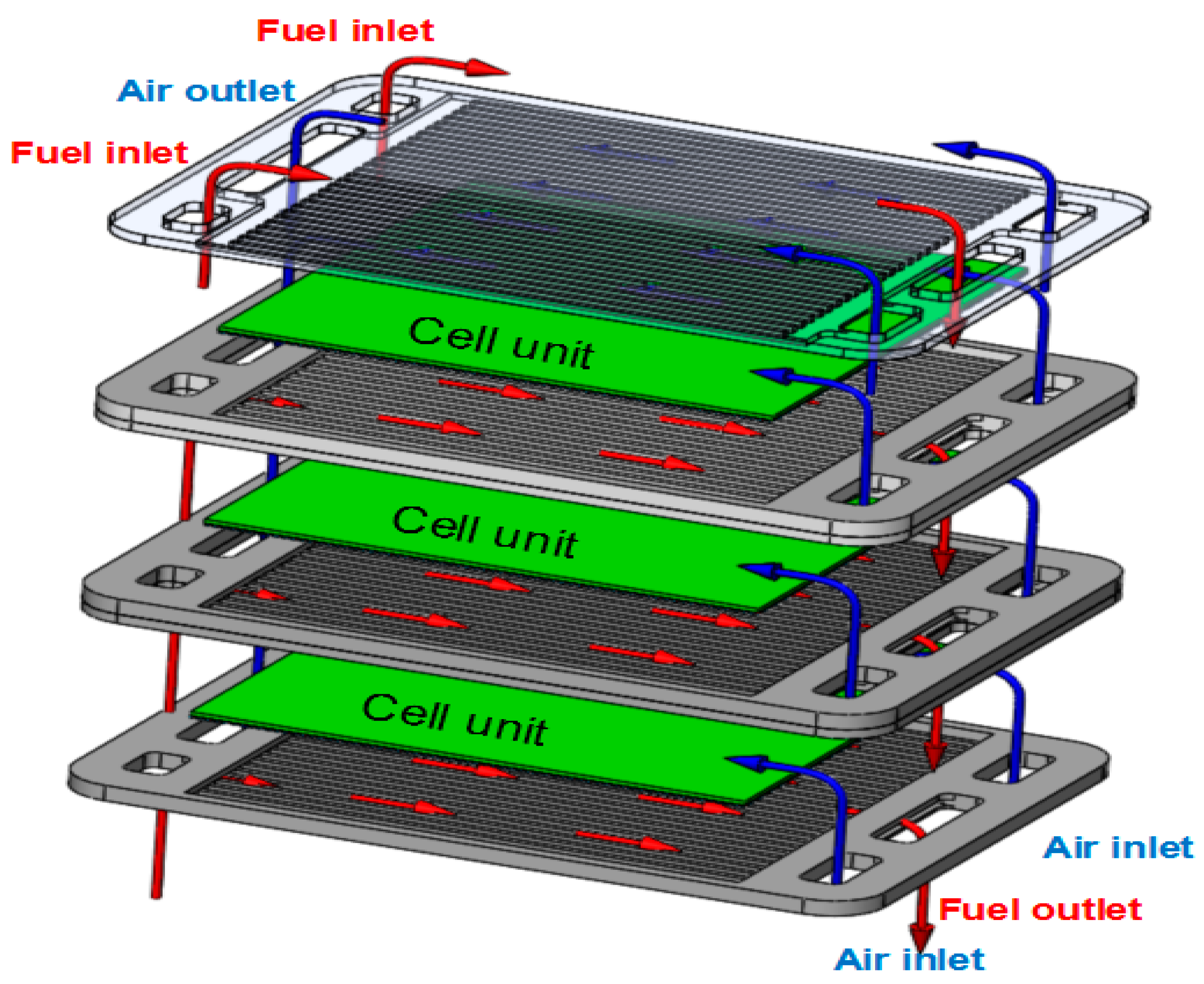

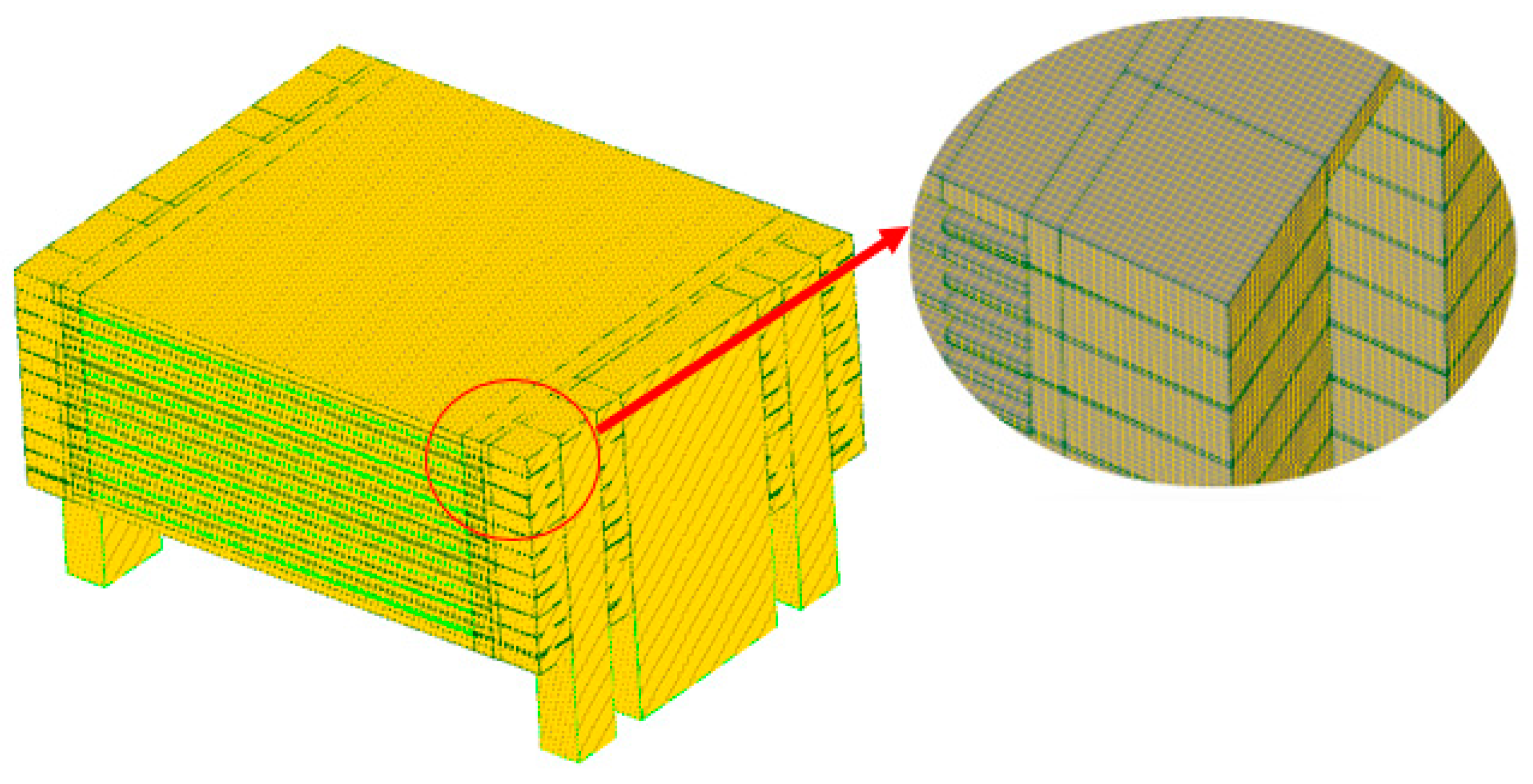


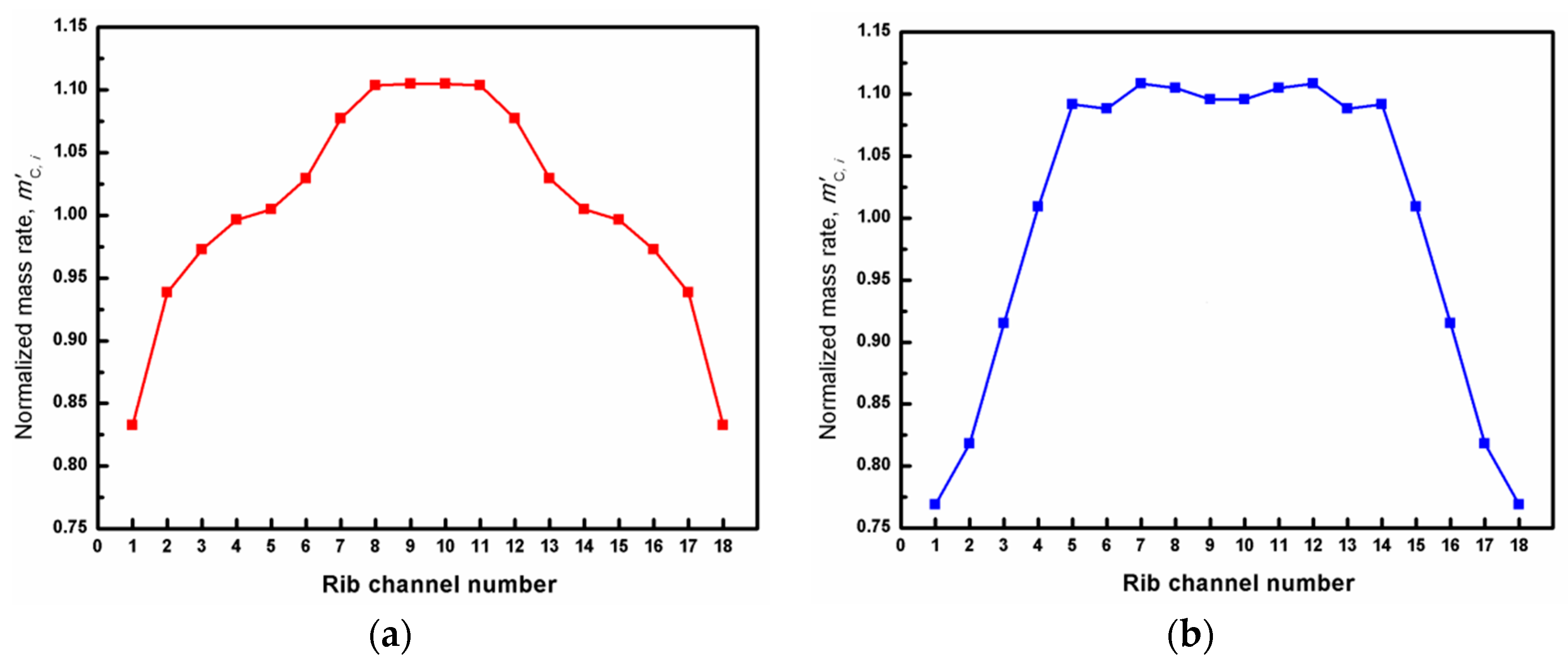
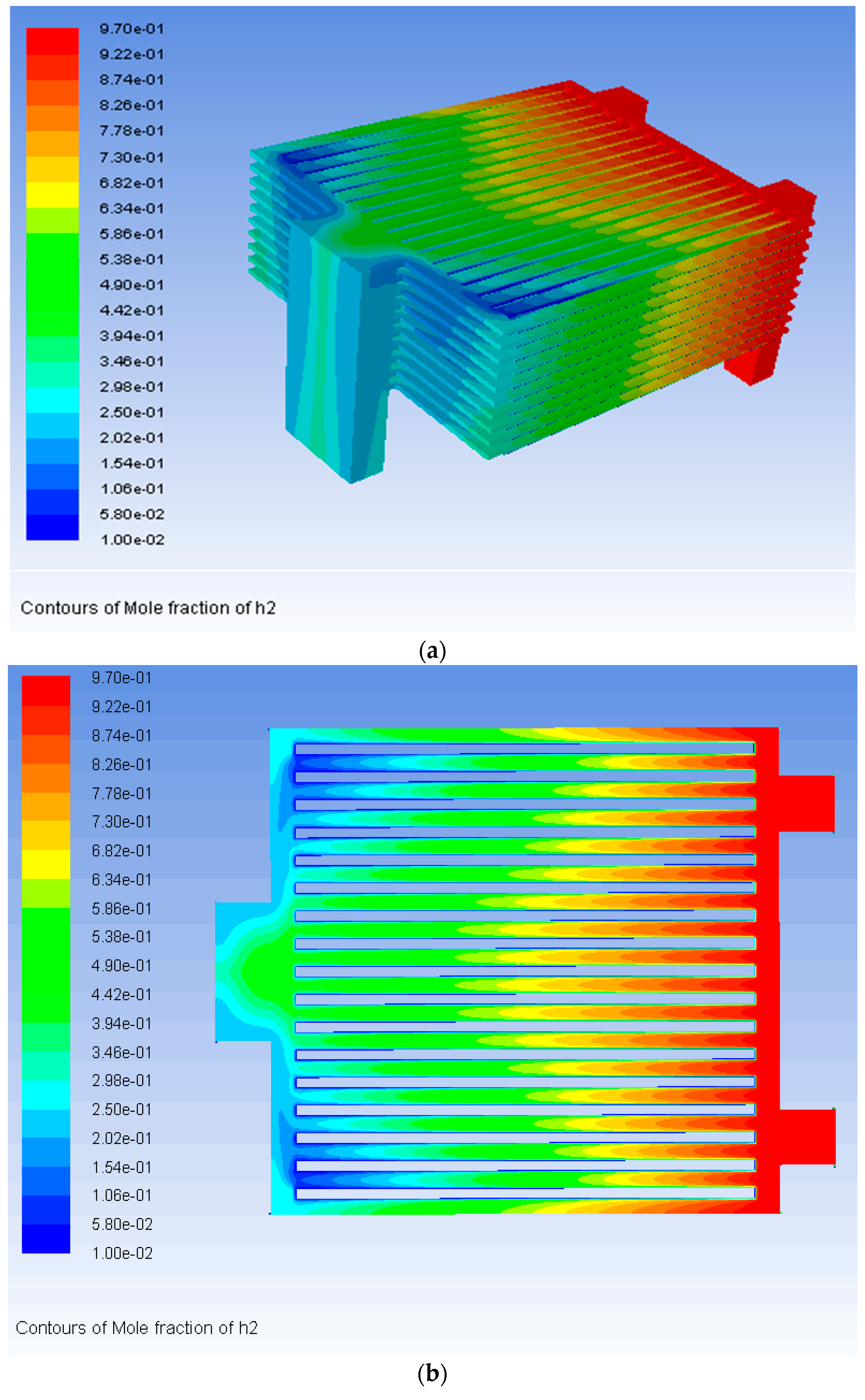

| Component and Operation Parameters | Fuel | Air |
|---|---|---|
| SOFC unit active area (mm × mm) | 100 × 105 | 100 × 105 |
| Inlet manifold (mm × mm) | 10 × 12 | 10 × 18 |
| Outlet manifold (mm × mm) | 10 × 30 | 10 × 44 |
| Height of each SOFC unit (mm) | 4.5 | 4.5 |
| Feeding header (mm × mm) | 5 × 105 | 5 × 105 |
| Exhaust header (mm × mm) | 5 × 105 | 5 × 105 |
| Solid rib (mm × mm) | 3 × 1.5 | 3 × 1.5 |
| Rib channel (mm × mm) | 3 × 1.5 | 3 × 1.5 |
| Operation temperature, T (K) | 1073.15 | |
| Operational current density, iop (A m−2) | 7000 | |
| Utilization, | 0.7 | 0.3 |
| Material Characteristics | Porous Anode | Electrolyte | Porous Cathode | Bipolar Plates |
|---|---|---|---|---|
| Density [kg·m−3] | 6870 | 5900 | 6570 | 8900 |
| Specific heat [J·kg−1·K−1] | 595 | 606 | 573 | 518 |
| Thermal conductivity [W·m−1·K−1] | 6 | 2.7 | 11 | 45 |
| Inlet Manifolds Entrances | Rib Channel-Anode | Anode-Electrolyte | Electrolyte-Cathode | Cathode-Rib Channel | Outlet Manifolds Exits | |
|---|---|---|---|---|---|---|
| Momentum conservation | Continuity | Insulation | Insulation | Continuity | 0 | |
| Fuel mass conservation | Continuity | Insulation | / | / | ||
| Air mass conservation | / | / | Insulation | Continuity | ||
| Energy conservation | T0 = 973 K | Continuity | Continuity | Continuity | Continuity |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Ma, S.; Zhang, X.; Chen, D.; He, J. Development of Large-Scale and Quasi Multi-Physics Model for Whole Structure of the Typical Solid Oxide Fuel Cell Stacks. Sustainability 2018, 10, 3094. https://doi.org/10.3390/su10093094
Ma J, Ma S, Zhang X, Chen D, He J. Development of Large-Scale and Quasi Multi-Physics Model for Whole Structure of the Typical Solid Oxide Fuel Cell Stacks. Sustainability. 2018; 10(9):3094. https://doi.org/10.3390/su10093094
Chicago/Turabian StyleMa, Jie, Suning Ma, Xinyi Zhang, Daifen Chen, and Juan He. 2018. "Development of Large-Scale and Quasi Multi-Physics Model for Whole Structure of the Typical Solid Oxide Fuel Cell Stacks" Sustainability 10, no. 9: 3094. https://doi.org/10.3390/su10093094
APA StyleMa, J., Ma, S., Zhang, X., Chen, D., & He, J. (2018). Development of Large-Scale and Quasi Multi-Physics Model for Whole Structure of the Typical Solid Oxide Fuel Cell Stacks. Sustainability, 10(9), 3094. https://doi.org/10.3390/su10093094




