A Model for the Optimal Recovery of Multiple Substances from Waste Water with a Focus on Phosphate
Abstract
1. Introduction
2. Phosphate in a Global Context
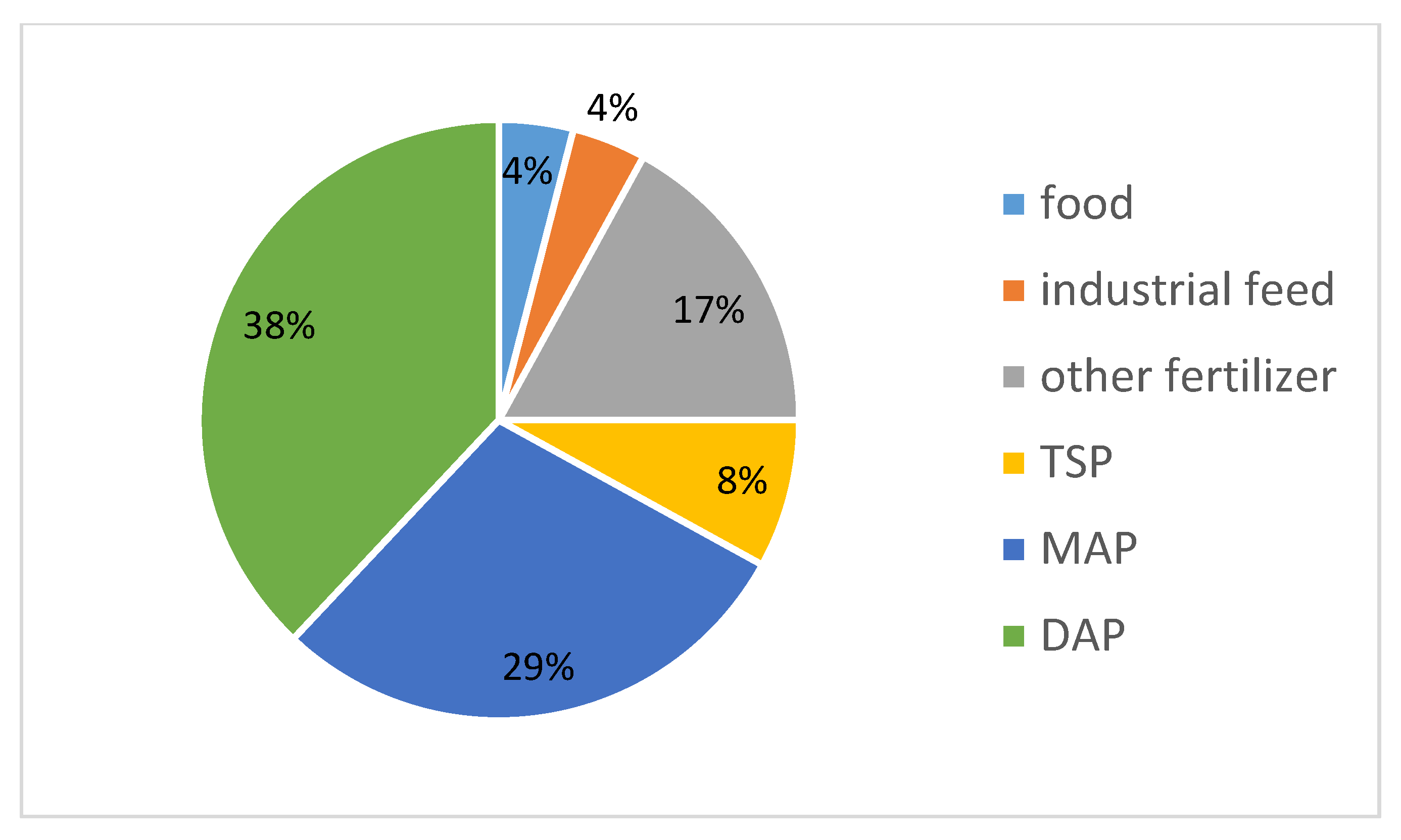
3. Why Phosphate Is Needed and Whether We Are Running Out of Phosphate Rock
4. Waste Water in a Waste Water Treatment Plant as a “Secondary Liquid Mine”
5. Modelling Conditions of Optimality for the Extraction of Phosphate from Waste Water
5.1. Optimal Control Theory
5.2. Assumptions
- for every x, qi we assume a specific cost function Ci (xi, qi)
- for every ri, sj we assume a specific cost function Cj (rj, sj)
- with the usual properties of smooth and continuous derivatives and cross-derivatives.
5.3. The Model
- the sum of revenues from sales of extractable elements
- the sum of revenues from elements to be removed and corrected for the respective reward/penalty fee,
- III.
- common overhead costs
- IV.
- the sum of costs of extraction of all respective elements
- V.
- the sum of costs of removal of all respective elements
- changes in the stock to be equal to the quantities of extracted and removed elements, respectively
- the pairwise proportionalities of elements to be extracted and removed,
- the limitation that quantities of extracted and removed elements cannot be larger than corresponding quantities entering the waste water at any time.
5.4. Interpretations
6. Conclusions and Suggestions for Further Research
- (i)
- Obviously, a computational case study, based on a scenario analysis, showing the relevance of the model would be useful.
- (ii)
- Focusing explicitly on other substances present in waste water, which merit an extraction, also adds to a better understanding of the applicability of the model.
- (iii)
- More complicated modelling of the presence of several substances without the assumption of fixed relative proportions, or—at least—changing relative proportions, may lead to a more general approach to the problem of simultaneous optimal extraction.
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Phosphate Production
| Country | 2008 | 2009 | 2010 | 2011 | 2012 |
|---|---|---|---|---|---|
| Algeria | 1800 | 1500 | 1500 | ||
| Australia | 2800 | 2500 | 1800 | 2650 | 2600 |
| Brazil | 6200 | 6000 | 5700 | 6200 | 6300 |
| Canada | 950 | 900 | 700 | 1000 | 900 |
| China | 50,700 | 55,000 | 68,000 | 81,000 | 89,000 |
| Egypt | 3000 | 3300 | 6000 | 6000 | 3000 |
| Israel | 3090 | 3000 | 3000 | ||
| India | 1240 | 1250 | 1260 | ||
| Iraq | 30 | 150 | |||
| Jordan | 6270 | 6000 | 6000 | 6000 | 6500 |
| Kazakhstan | |||||
| Mexico | 1510 | 1620 | 1700 | ||
| Morocco + W Sahara | 25,000 | 24,000 | 25,800 | 27,000 | 28,000 |
| Peru | 791 | 2540 | 2560 | ||
| Russia | 10,400 | 9000 | 11,000 | 11,200 | 11,300 |
| Saudi Arabia | 1000 | 1700 | |||
| Senegal | 700 | 700 | 950 | 980 | 980 |
| South Africa | 2290 | 2300 | 2500 | 2500 | 2500 |
| Syria | 2290 | 2300 | 3000 | 3100 | 2500 |
| Togo | 3220 | 3000 | 850 | 730 | 865 |
| Tunisia | 800 | 800 | 7600 | 5000 | 6000 |
| United States | 30,200 | 27,200 | 25,800 | 28,100 | 29,200 |
| Vietnam | |||||
| Other countries | 7440 | 7000 | 6400 | 6790 | 6000 |
| WORLD | 161,000 | 158,000 | 181,000 | 198,000 | 210,000 |
| Country | 2013 | 2014 | 2015 | 2016 | RESERVES 2016 |
| Algeria | 1500 | 1500 | 1400 | 1500 | 2200,000 |
| Australia | 2600 | 2600 | 2500 | 2500 | 1100.000 |
| Brazil | 6000 | 6750 | 6100 | 6500 | 320,000 |
| Canada | 400 | 76,000 | |||
| China | 108,000 | 100,000 | 120,000 | 138,000 | 3,100,000 |
| Egypt | 6500 | 6000 | 5500 | 5500 | 1,200,000 |
| Israel | 3500 | 3600 | 3540 | 3500 | 130,000 |
| India | 1270 | 2100 | 1500 | 1500 | 65,000 |
| Iraq | 250 | 250 | 430,000 | ||
| Jordan | 5400 | 6000 | 8340 | 8300 | 1,200,000 |
| Kazakhstan | 1600 | 1600 | 1840 | 1800 | 260,000 |
| Mexico | 1760 | 1700 | 1680 | 1700 | 30,000 |
| Morocco + W Sahara | 26,400 | 30,000 | 29,000 | 30,000 | 50,000,000 |
| Peru | 2580 | 2600 | 3880 | 4000 | 820,000 |
| Russia | 10,000 | 10,000 | 11,650 | 11,600 | 680,000 |
| Saudi Arabia | 3000 | 3000 | 4000 | 4000 | 680,000 |
| Senegal | 800 | 700 | 1240 | 1250 | 50,000 |
| South Africa | 2300 | 2200 | 1980 | 1700 | 1,500,000 |
| Syria | 500 | 1000 | 750 | 1,800,000 | |
| Togo | 1110 | 1200 | 1100 | 900 | 30,000 |
| Tunisia | 3500 | 5000 | 2800 | 3500 | 100,000 |
| United States | 31,200 | 27,100 | 27,400 | 27,800 | 1,100,000 |
| Vietnam | 2370 | 2400 | 2500 | 2800 | 30,000 |
| Other countries | 2580 | 2600 | 2470 | 2410 | 810,000 |
| WORLD | 225,000 | 220,000 | 241,000 | 261,000 | 68,000,000 |
References
- U.S. Geological Survey. Mineral Commodity Summaries 2018. Available online: https://minerals.usgs.gov/minerals/pubs/mcs/ (accessed on 25 February 2018).
- Harraz, H. Phosphate Deposits. 2015. Available online: https://www.slideshare.net/hzharraz/phosphite-ore-deposits (accessed on 15 January 2018).
- European Commission. Commission Staff Working Document—Report on Critical Raw Materials and the Circular Economy; European Commission: Brussels, Belgium, 2018. [Google Scholar]
- FAO. World Fertilizer Trends and Outlook to 2020. 2017. Available online: http://www.fao.org/3/a-i6895e.pdf (accessed on 7 August 2018).
- Grand View Research. Global Phosphate Fertilizers Market Outlook by Product (Monoammonium Phosphate, Diammonium Phosphate, Superphosphate), By Application (Cereals & Grains), Oilseeds, Fruits & Vegetables), and Segment Forecasts, 2018–2025, January 2018. Available online: https://www.grandviewresearch.com/press-release/global-phosphates-market (accessed on 15 March 2018).
- Centre set to roll out big fertilizer reform from June, 2017. India Times. 24 March 2017. Available online: http://timesofindia.indiatimes.com/india/centre-set-to-roll-out-big-fertilizer-reform-from-june/articleshow/57801760.cms (accessed on 22 December 2017).
- N-P-K World. Phosphate Snapshot—Fertilizers, Industrial Phosphates, Phosphate Fertilizers. 2013. Available online: https://npk101.wordpress.com/2013/05/27/phosphate-snapshot/ (accessed on 4 August 2018).
- Asimov, I. Asimov on Chemistry; Doubleday: New York, NY, USA, 1974. [Google Scholar]
- Phosphate in Agriculture. Available online: http://www.potashcorp.com/overview/nutrients/phosphate/overview/world-phosphate-acid-uses (accessed on 15 October 2017).
- Soil Use and Management, Special Issu on Phosphorous in Soils and Its Transfer to Waters. Available online: https://onlinelibrary.wiley.com/action/doSearch?field1=AllField&text1=phosphorous+in+soils&publication%5B%5D=14752743&Ppub=&AfterMonth=01&AfterYear=2013&BeforeMonth=12&BeforeYear=2013 (accessed on 2 August 2018).
- Amery, F.; Schoumans, O.F. Agricultural Phosphorus Legislation in Europe; ILVO: Merelbeke, Belgium, 2014. [Google Scholar]
- Phosphorus Famine: The Threat to Our Food Supply. Available online: https://www.scientificamerican.com/article/phosphorus-a-looming-crisis/ (accessed on 6 August 2018).
- Romm, J. Jeremy Grantham Must-Read, “Time to Wake Up: Days of Abundant Resources and Falling Prices Are Over Forever”. 2011. Available online: https://thinkprogress.org/jeremy-grantham-must-read-time-to-wake-up-days-of-abundant-resources-and-falling-prices-are-over-4332e8898c76/ (accessed on 15 March 2018).
- Faradji, C.; de Boer, M. How the Great Phosphorus Shortage Could Leave Us Short of Food. Available online: http://theconversation.com/how-the-great-phosphorus-shortage-could-leave-us-all-hungry-54432 (accessed on 15 March 2018).
- Cordell, D.; Drangert, J.-O.; White, S. The story of phosphorus: Global food security and food for thought. Glob. Environ. Chang. 2009, 19, 292–305. [Google Scholar] [CrossRef]
- Cordell, D.; White, S. Peak Phosphorus: Clarifying the Key Issues of a Vigorous Debate about Long-Term Phosphorus Security. Sustainability 2011, 3, 2027–2049. [Google Scholar] [CrossRef]
- Scholz, R.W.; Wellmer, F.W. Approaching a dynamic view on the availability of mineral resources: What we may learn from the case of phosphorous? Glob. Environ. Chang. 2013, 23, 11–27. [Google Scholar] [CrossRef]
- Scholz, R.W.; Wellmer, F.W. Comment on: “Recent revisions of phosphate rock reserves and resources: A critique” by Edixhoven et al. (2014)—Claridying comnents and thoughts on key conceptions, conclusions and interpretation to allow for sustainable action. Earth Syst. Dyn. 2016, 7, 1–15. [Google Scholar] [CrossRef]
- Liholt Sørensen, B.; Leinikka Dall, O.; Habib, K. Environmental and resource implications of phosphorus recovery from waste activated sludge. Waste Manag. 2015, 45, 391–399. [Google Scholar] [CrossRef] [PubMed]
- Xie, M.; Nghiem, L.D.; Price, W.E.; Elimelech, M. Toward Resource Recovery from Wastewater: Extraction of Phosphorus from Digested Sludge Using a Hybrid Forward Osmosis–Membrane Distillation Process. Environ. Sci. Technol. Lett. 2014, 1, 191–195. [Google Scholar] [CrossRef]
- Mayer, B.K.; Baker, L.A.; Boyer, T.H.; Drechsel, P.; Gifford, M.; Hanjra, M.A.; Parameswaran, P.; Stoltzfus, J.; Westerhoff, P.; Rittmann, B.E. Total Value of Phosphorus Recovery. Environ. Sci. Technol. 2016, 50, 6606–6620. [Google Scholar] [CrossRef] [PubMed]
- Phosphorous Removal from Wastewater. Available online: https://www.lenntech.com/phosphorous-removal.htm (accessed on 15 June 2018).
- Historical Phosphate Rock Prices and Price Chart. Available online: http://www.infomine.com/investment/metal-prices/phosphate-rock/all/ (accessed on 25 July 2018).
- Rock Phosphate monthly price. Available online: https://www.indexmundi.com/commodities/?commodity=rock-phosphate (accessed on 25 July 2018).
- Ellen Macarthur Foundation. Available online: www.ellenmacarthurfoundation.org (accessed on 15 July 2018).
- Caputo, M.R. Foundations of Dynamic Economic Analysis: Optimal Control Theory and Applications; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- USGS (Ed.) Mineral Resource of the Month: Phosphate Rock. December 2013. Available online: https://www.earthmagazine.org/article/mineral-resource-month-phosphate-rock (accessed on 30 October 2017).
- U.S. Geological Survey. Mineral Commodity Summaries 2015. Available online: https://minerals.usgs.gov/minerals/pubs/mcs/2015/mcs2015.pdf (accessed on 30 October 2017).
| 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | CAGR | |
|---|---|---|---|---|---|---|---|
| WORLD | 41,151 | 41,945 | 43,195 | 44,120 | 45,013 | 45,858 | 2.19 |
| AFRICA | 1448 | 1489 | 1529 | 1571 | 1614 | 1659 | 2.8 |
| North Africa | 633 | 642 | 653 | 664 | 675 | 686 | 1.6 |
| Sub-Saharan Africa | 815 | 847 | 876 | 907 | 939 | 973 | 3.6 |
| AMERICAS | 11,454 | 44,690 | 12,060 | 12,380 | 12,700 | 13,009 | 2.6 |
| North America | 5035 | 5070 | 5085 | 5123 | 5160 | 5187 | 0.6 |
| Latin America & Caribbean | 3420 | 3320 | 3975 | 7257 | 7539 | 7822 | 0.0 |
| ASIA | 22,918 | 23,312 | 24,056 | 24,544 | 25,005 | 25,432 | 2.1 |
| West Asia | 351 | 367 | 383 | 400 | 417 | 436 | 4.4 |
| South Asia | 8165 | 8435 | 9025 | 9383 | 9760 | 10107 | 4.4 |
| East Asia | 14,401 | 14,510 | 14,648 | 14,761 | 14,827 | 14,889 | 0.7 |
| EUROPE | 4026 | 4135 | 4217 | 4269 | 4319 | 4368 | 1.6 |
| Central Europe | 756 | 780 | 807 | 835 | 864 | 889 | 3.3 |
| West Europe | 1855 | 1863 | 1878 | 1861 | 1839 | 1818 | 0.4 |
| East Europe & Central Asia | 1415 | 1492 | 1532 | 1573 | 1616 | 1661 | 3.3 |
| OCEANIA | 1305 | 1319 | 1332 | 1356 | 1376 | 1390 | 1.3 |
| 1970 | 1980 | 1990 | 2000 | 2010 | 2020 | |
|---|---|---|---|---|---|---|
| World | 21,117 | 31,700 | 35,901 | 31,472 | 45,442 | 57,000 |
| China | 949 | 2744 | 5853 | 8610 | 16,943 | 22,400 |
| India | 541 | 1231 | 3259 | 4215 | 8017 | 16,600 |
| USA | 4346 | 4930 | 3811 | 3862 | 3883 | 3000 |
| Brazil | 417 | 1988 | 1202 | 2338 | 3385 | 4300 |
| Australia | 757 | 797 | 579 | 946 | 946 | 600 |
| Pakistan | 30 | 226 | 389 | 757 | 757 | 650 |
| Canada | 326 | 635 | 578 | 571 | 620 | 500 |
| Turkey | 176 | 619 | 625 | 629 | 515 | 450 |
| Japan | 656 | 690 | 690 | 583 | 424 | 400 |
| France | 1809 | 1773 | 1349 | 795 | 295 | 300 |
| Others | 11,108 | 16,066 | 17,568 | 9088 | 9658 | 9800 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bongaerts, J.C. A Model for the Optimal Recovery of Multiple Substances from Waste Water with a Focus on Phosphate. Sustainability 2018, 10, 2867. https://doi.org/10.3390/su10082867
Bongaerts JC. A Model for the Optimal Recovery of Multiple Substances from Waste Water with a Focus on Phosphate. Sustainability. 2018; 10(8):2867. https://doi.org/10.3390/su10082867
Chicago/Turabian StyleBongaerts, Jan C. 2018. "A Model for the Optimal Recovery of Multiple Substances from Waste Water with a Focus on Phosphate" Sustainability 10, no. 8: 2867. https://doi.org/10.3390/su10082867
APA StyleBongaerts, J. C. (2018). A Model for the Optimal Recovery of Multiple Substances from Waste Water with a Focus on Phosphate. Sustainability, 10(8), 2867. https://doi.org/10.3390/su10082867





