Does the Complexity of Evapotranspiration and Hydrological Models Enhance Robustness?
Abstract
1. Introduction
2. Materials and Methods
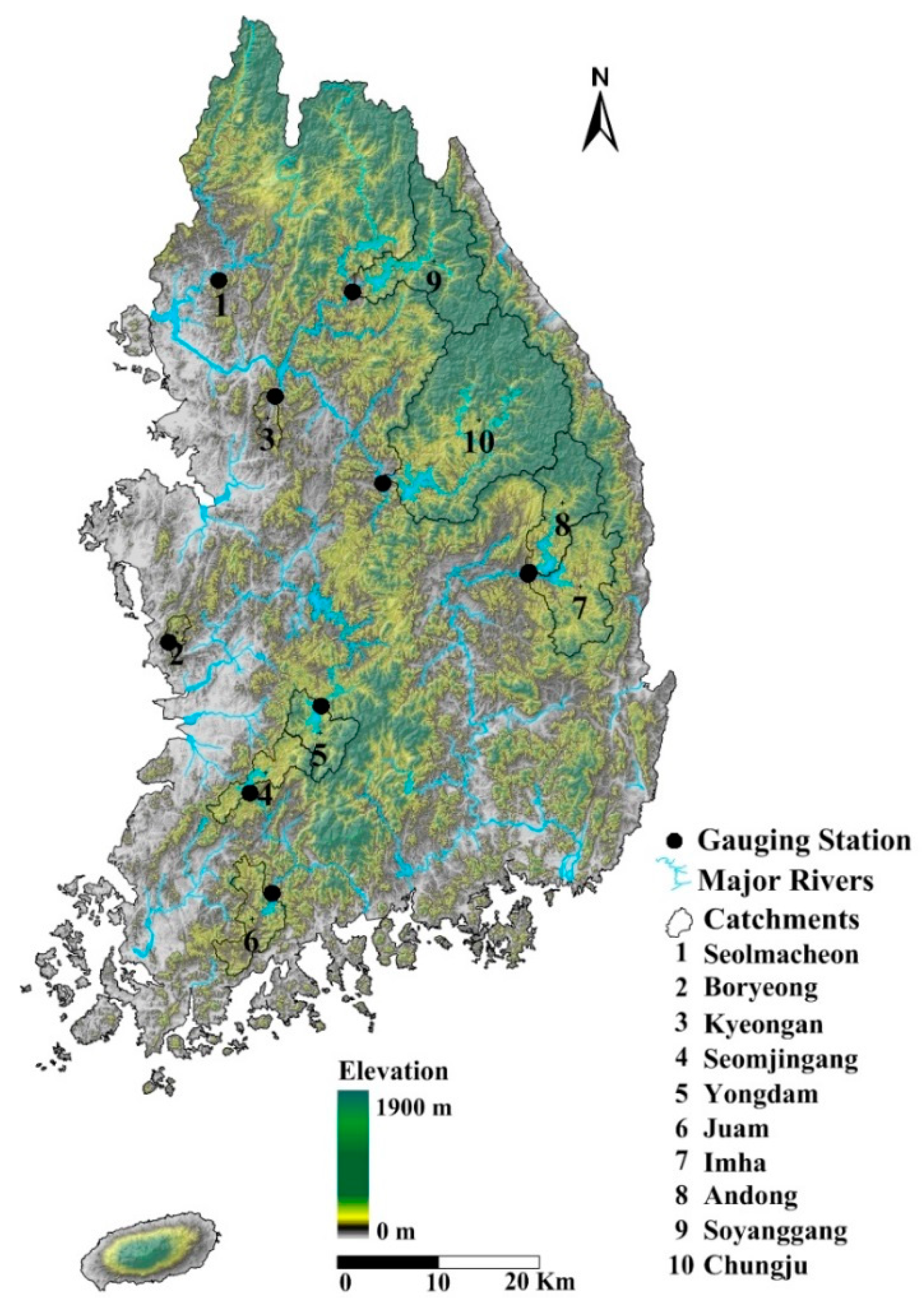
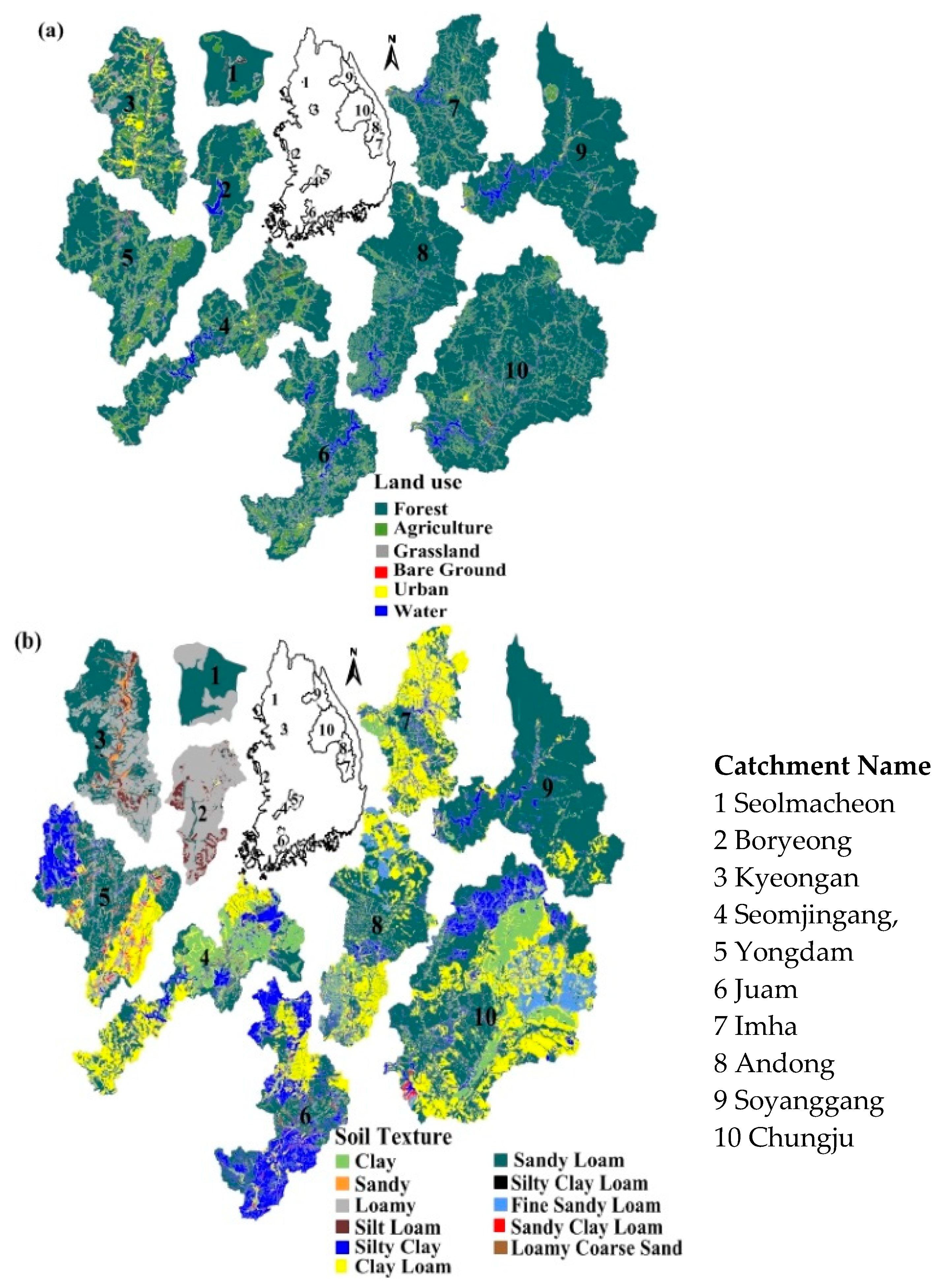
2.1. Study Area
2.2. Data
2.3. PET Estimation Methods
2.4. Overview of Hydrological Model Structure
2.4.1. GR4J
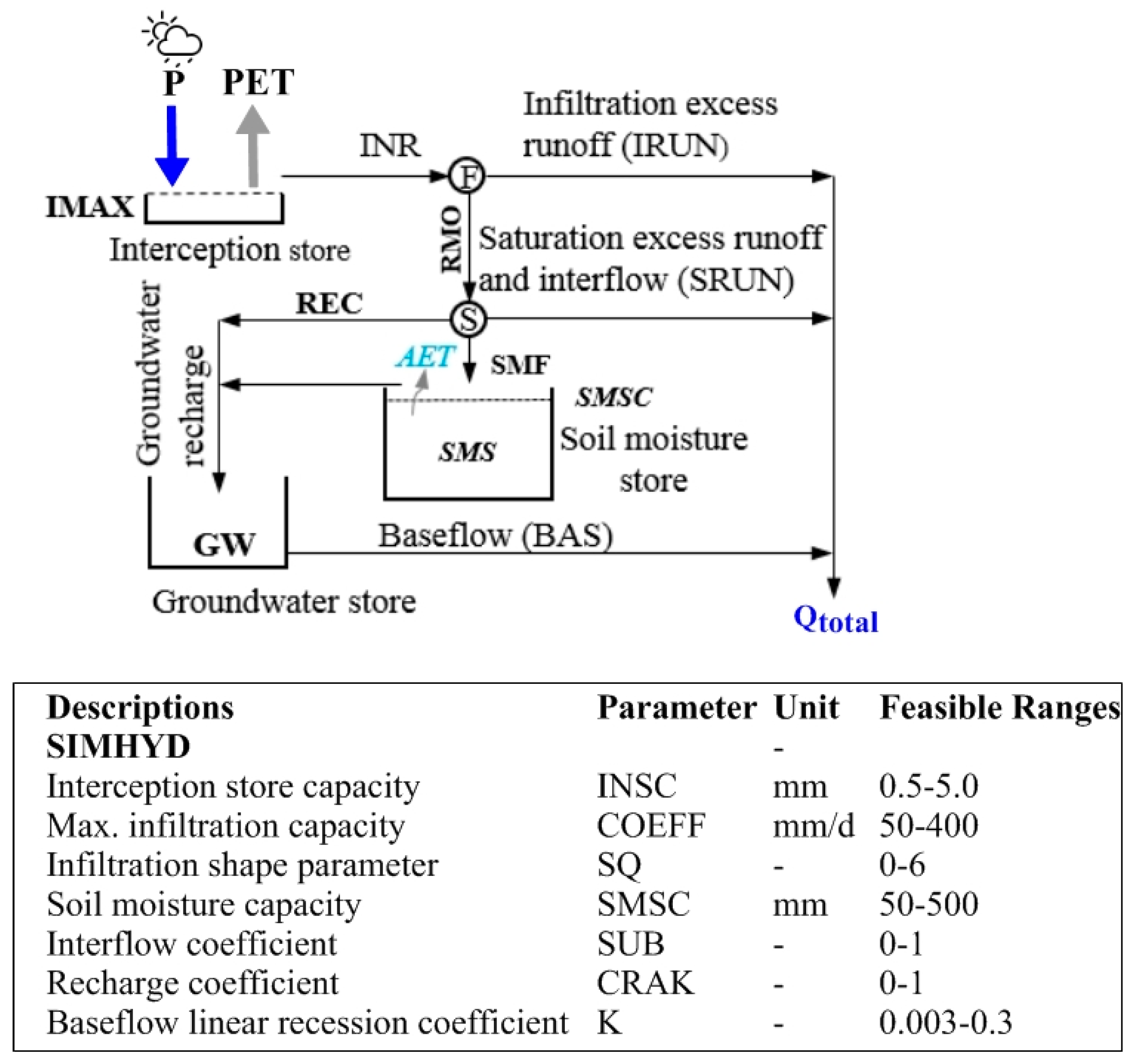
2.4.2. SIMHYD
2.4.3. CAT
2.4.4. TANK
2.4.5. SAC-SMA
2.5. Model Calibration and Validation
2.6. Model Complexity Comparison Criteria and Robustness
2.6.1. Model Complexity Comparison Criteria
2.6.2. Model Robustness
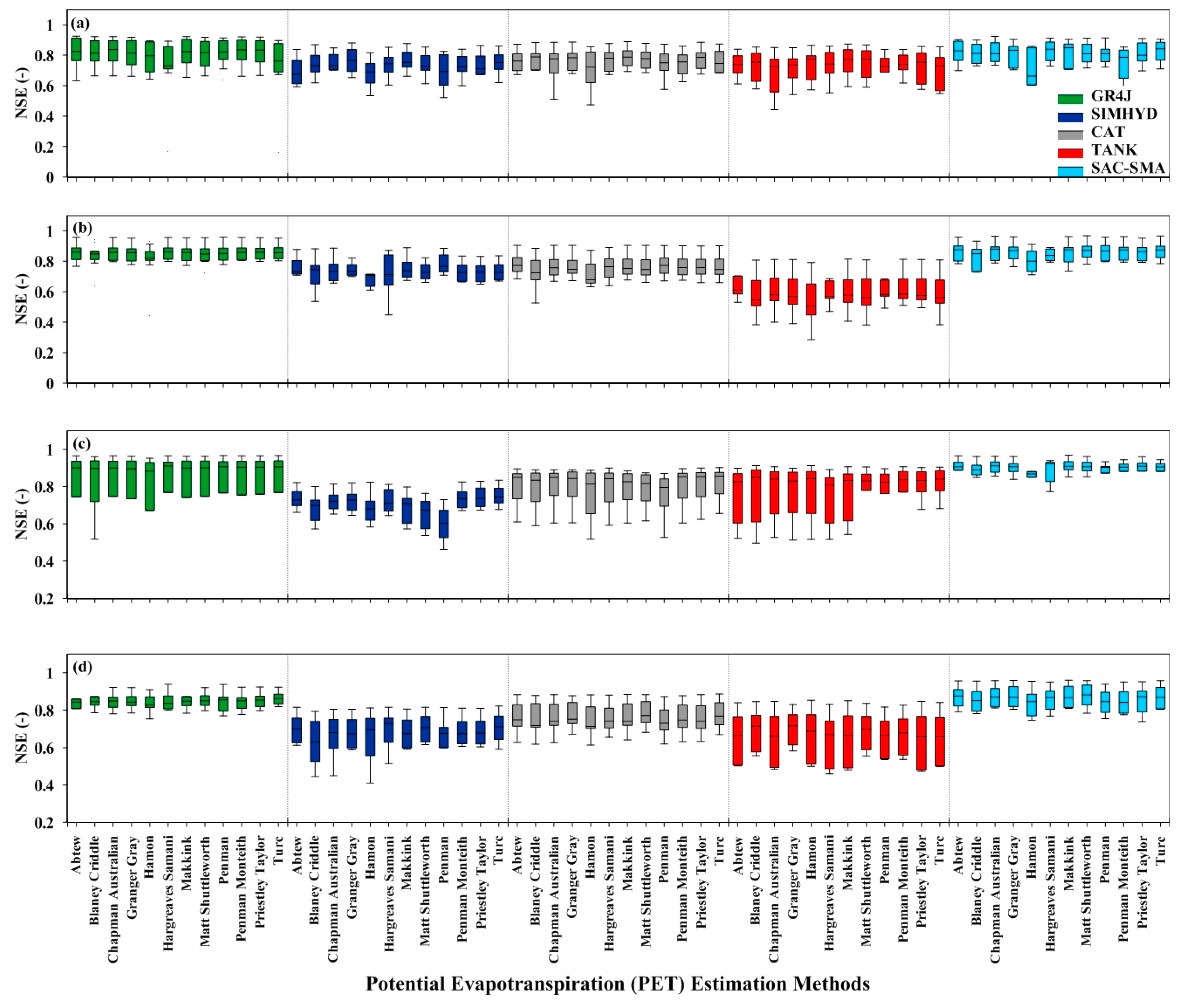
3. Results
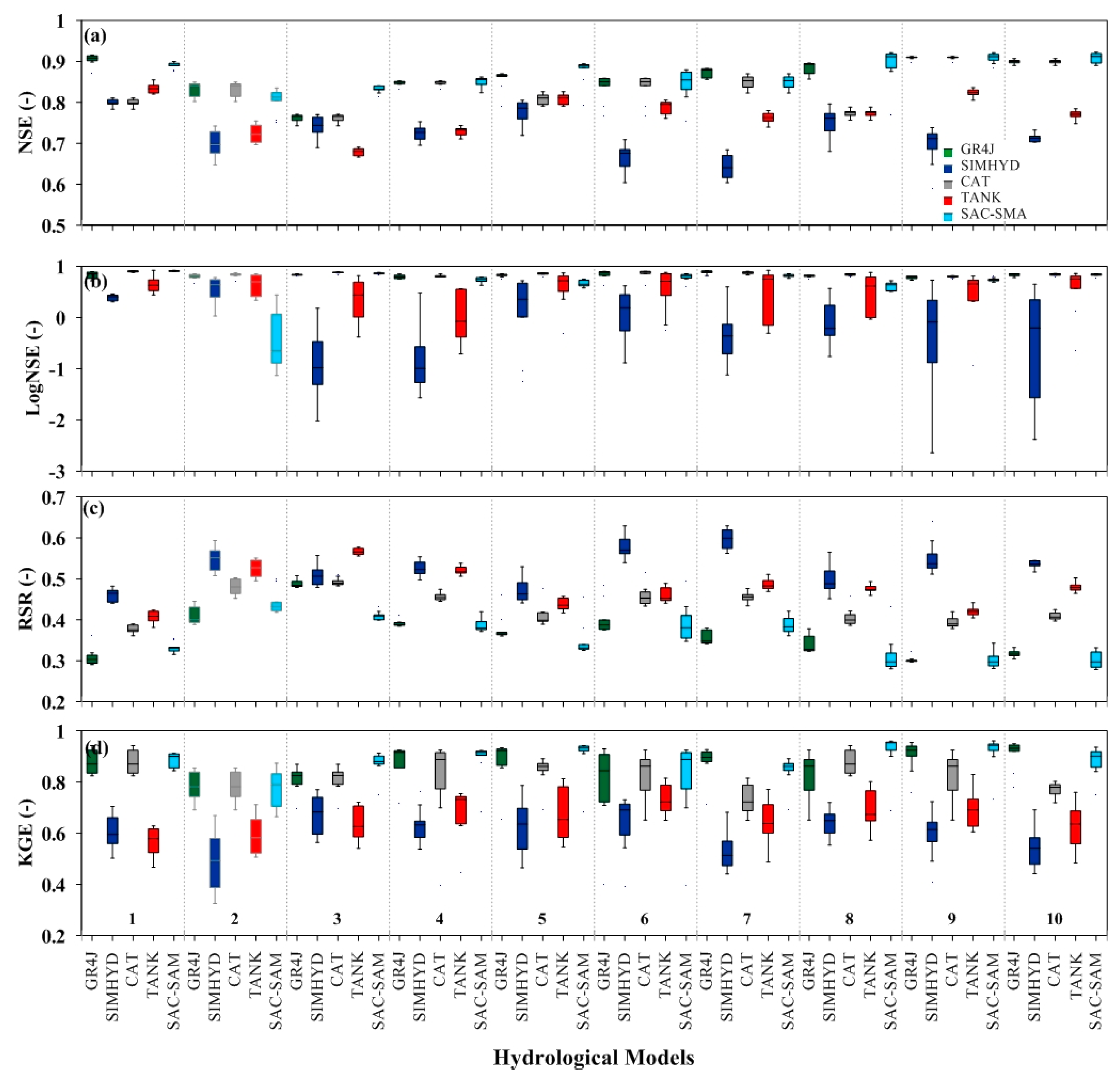
3.1. Calibration and Validation
3.2. Effect of Model Structure Complexity on Model Performance
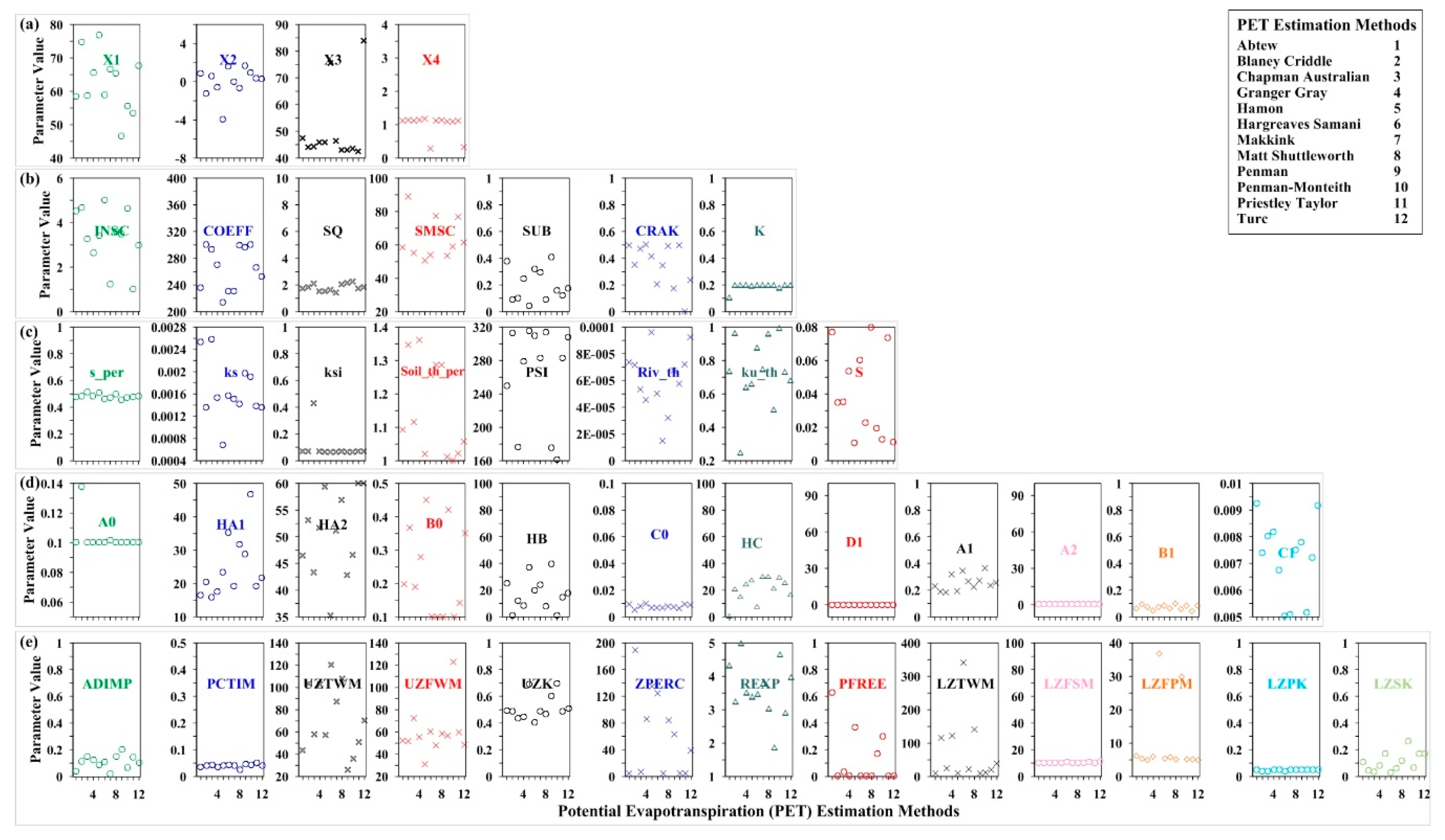
3.3. Effect of PET Complexity on Model Parameters
3.4. Effect of PET and Model Structure Complexity on Model Robustness
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| PET Estimation Methods | Formula | Required Data | Reference |
|---|---|---|---|
| Abtew | T, Rs | [112] | |
| Blaney Criddle | T, RH, n | [113] | |
| Chapman Australian | T, RH, Rs | [114] | |
| Granger Gray | T, RH, Rs | [115] | |
| Hamon | T, n | [116] | |
| Hargreaves Samani | T | [117] | |
| Makkink | T, Rs | [118] | |
| Matt Shuttleworth | T, RH, Rs, u | [119] | |
| Penman | T, RH, Rs | [120] | |
| Penman-Monteith | T, RH, Rs, n, u | [121] | |
| Priestley Taylor | T, RH, Rs | [122] | |
| Turc | , for RH > 50% | T, RH, Rs | [123] |
| , for RH < 50% |
| Seolmacheon | NSE | LogNSE | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PET Methods | GR4J | SIMHYD | CAT | TANK | SAC-SAM | GR4J | SIMHYD | CAT | TANK | SAC-SAM |
| Abtew | 0.85 | 0.87 | 0.80 | 0.89 | 0.87 | 0.71 | 0.18 | 0.85 | 0.91 | 0.87 |
| Blaney Criddle | 0.87 | 0.87 | 0.79 | 0.89 | 0.87 | 0.87 | 0.29 | 0.88 | 0.62 | 0.87 |
| Chapman Australian | 0.86 | 0.87 | 0.78 | 0.90 | 0.87 | 0.83 | 0.38 | 0.89 | 0.57 | 0.89 |
| Granger Gray | 0.90 | 0.84 | 0.80 | 0.89 | 0.84 | 0.87 | 0.31 | 0.88 | 0.47 | 0.89 |
| Hamon | 0.87 | 0.86 | 0.80 | 0.89 | 0.86 | 0.88 | 0.37 | 0.89 | 0.62 | 0.89 |
| Hargreaves Samani | 0.87 | 0.86 | 0.77 | 0.88 | 0.86 | 0.88 | 0.03 | 0.90 | 0.49 | 0.89 |
| Makkink | 0.85 | 0.85 | 0.80 | 0.90 | 0.85 | 0.81 | 0.34 | 0.88 | 0.32 | 0.88 |
| Matt Shuttleworth | 0.87 | 0.86 | 0.78 | 0.90 | 0.86 | 0.89 | 0.39 | 0.90 | 0.63 | 0.89 |
| Penman | 0.87 | 0.88 | 0.79 | 0.88 | 0.88 | 0.83 | 0.35 | 0.88 | 0.55 | 0.88 |
| Penman-Monteith | 0.86 | 0.87 | 0.79 | 0.89 | 0.87 | 0.84 | 0.38 | 0.89 | 0.45 | 0.88 |
| Priestley Taylor | 0.85 | 0.86 | 0.78 | 0.87 | 0.86 | 0.73 | 0.25 | 0.85 | 0.76 | 0.87 |
| Turc | 0.88 | 0.86 | 0.80 | 0.89 | 0.86 | 0.90 | 0.39 | 0.90 | 0.65 | 0.88 |
| Boryeong | ||||||||||
| Abtew | 0.85 | 0.66 | 0.79 | 0.77 | 0.79 | 0.82 | 0.46 | 0.81 | 0.24 | 0.15 |
| Blaney Criddle | 0.85 | 0.72 | 0.79 | 0.77 | 0.79 | 0.80 | 0.75 | 0.83 | 0.72 | −1.33 |
| Chapman Australian | 0.86 | 0.76 | 0.76 | 0.82 | 0.76 | 0.84 | 0.46 | 0.84 | 0.25 | −0.71 |
| Granger Gray | 0.85 | 0.74 | 0.79 | 0.77 | 0.79 | 0.81 | 0.72 | 0.83 | 0.62 | −1.00 |
| Hamon | 0.83 | 0.64 | 0.79 | 0.70 | 0.79 | 0.68 | 0.65 | 0.73 | 0.42 | 0.29 |
| Hargreaves Samani | 0.74 | 0.74 | 0.79 | 0.79 | 0.79 | 0.82 | 0.23 | 0.84 | 0.31 | 0.34 |
| Makkink | 0.85 | 0.72 | 0.81 | 0.76 | 0.81 | 0.84 | 0.63 | 0.85 | 0.66 | −0.82 |
| Matt Shuttleworth | 0.85 | 0.70 | 0.81 | 0.79 | 0.81 | 0.80 | 0.74 | 0.82 | 0.83 | −1.03 |
| Penman | 0.85 | 0.75 | 0.78 | 0.72 | 0.78 | 0.83 | −0.09 | 0.82 | 0.59 | 0.27 |
| Penman-Monteith | 0.86 | 0.74 | 0.80 | 0.80 | 0.80 | 0.84 | 0.40 | 0.82 | 0.74 | −0.40 |
| Priestley Taylor | 0.85 | 0.73 | 0.79 | 0.79 | 0.79 | 0.83 | 0.38 | 0.84 | 0.77 | −1.07 |
| Turc | 0.73 | 0.71 | 0.77 | 0.77 | 0.77 | 0.80 | 0.57 | 0.85 | 0.75 | −0.87 |
| Kyeongan | ||||||||||
| Abtew | 0.85 | 0.79 | 0.78 | 0.87 | 0.85 | 0.65 | −2.15 | 0.73 | 0.77 | 0.70 |
| Blaney Criddle | 0.86 | 0.75 | 0.82 | 0.87 | 0.86 | 0.76 | 0.16 | 0.77 | 0.49 | 0.70 |
| Chapman Australian | 0.86 | 0.72 | 0.80 | 0.87 | 0.86 | 0.70 | −2.09 | 0.74 | 0.66 | 0.68 |
| Granger Gray | 0.87 | 0.72 | 0.80 | 0.88 | 0.87 | 0.75 | −0.43 | 0.75 | 0.55 | 0.68 |
| Hamon | 0.86 | 0.70 | 0.82 | 0.82 | 0.86 | 0.77 | 0.15 | 0.79 | 0.60 | 0.75 |
| Hargreaves Samani | 0.86 | 0.72 | 0.78 | 0.86 | 0.86 | 0.68 | −1.54 | 0.74 | −0.45 | 0.71 |
| Makkink | 0.86 | 0.71 | 0.80 | 0.87 | 0.86 | 0.72 | −1.00 | 0.74 | −0.03 | 0.67 |
| Matt Shuttleworth | 0.87 | 0.76 | 0.80 | 0.88 | 0.87 | 0.76 | −0.52 | 0.78 | 0.42 | 0.72 |
| Penman | 0.83 | 0.69 | 0.78 | 0.86 | 0.83 | 0.53 | −1.64 | 0.69 | −0.14 | 0.72 |
| Penman-Monteith | 0.86 | 0.71 | 0.79 | 0.87 | 0.86 | 0.68 | −2.97 | 0.75 | 0.05 | 0.72 |
| Priestley Taylor | 0.86 | 0.67 | 0.81 | 0.87 | 0.86 | 0.72 | −1.11 | 0.76 | 0.27 | 0.72 |
| Turc | 0.87 | 0.68 | 0.81 | 0.87 | 0.87 | 0.76 | −0.50 | 0.79 | −0.18 | 0.73 |
| Seomjingang | ||||||||||
| Abtew | 0.91 | 0.81 | 0.80 | 0.90 | 0.81 | 0.83 | −0.72 | 0.83 | −0.32 | 0.79 |
| Blaney Criddle | 0.90 | 0.79 | 0.79 | 0.86 | 0.79 | 0.79 | 0.66 | 0.80 | 0.57 | 0.68 |
| Chapman Australian | 0.91 | 0.79 | 0.79 | 0.90 | 0.79 | 0.84 | −0.02 | 0.84 | 0.37 | 0.78 |
| Granger Gray | 0.91 | 0.80 | 0.79 | 0.90 | 0.80 | 0.83 | 0.05 | 0.83 | 0.51 | 0.76 |
| Hamon | 0.88 | 0.76 | 0.77 | 0.83 | 0.76 | 0.73 | 0.64 | 0.73 | 0.42 | 0.70 |
| Hargreaves Samani | 0.92 | 0.79 | 0.78 | 0.89 | 0.79 | 0.84 | −0.50 | 0.83 | −0.16 | 0.76 |
| Makkink | 0.91 | 0.81 | 0.79 | 0.90 | 0.81 | 0.84 | 0.20 | 0.84 | 0.44 | 0.79 |
| Matt Shuttleworth | 0.91 | 0.80 | 0.79 | 0.91 | 0.80 | 0.80 | −0.13 | 0.83 | 0.57 | 0.80 |
| Penman | 0.92 | 0.82 | 0.79 | 0.90 | 0.82 | 0.84 | −1.25 | 0.84 | −0.42 | 0.78 |
| Penman-Monteith | 0.91 | 0.79 | 0.79 | 0.90 | 0.79 | 0.84 | −0.93 | 0.84 | 0.10 | 0.77 |
| Priestley Taylor | 0.91 | 0.79 | 0.79 | 0.89 | 0.79 | 0.84 | −0.55 | 0.83 | 0.29 | 0.75 |
| Turc | 0.91 | 0.80 | 0.79 | 0.90 | 0.80 | 0.82 | −0.36 | 0.82 | 0.47 | 0.76 |
| Yongdam | ||||||||||
| Abtew | 0.91 | 0.79 | 0.89 | 0.89 | 0.89 | 0.85 | −2.80 | 0.86 | 0.49 | 0.46 |
| Blaney Criddle | 0.90 | 0.73 | 0.87 | 0.82 | 0.87 | 0.81 | 0.47 | 0.86 | 0.55 | 0.32 |
| Chapman Australian | 0.91 | 0.78 | 0.89 | 0.89 | 0.89 | 0.85 | −0.87 | 0.86 | 0.19 | 0.18 |
| Granger Gray | 0.90 | 0.78 | 0.88 | 0.89 | 0.88 | 0.84 | −0.09 | 0.84 | 0.64 | 0.46 |
| Hamon | 0.84 | 0.68 | 0.85 | 0.78 | 0.85 | 0.75 | 0.59 | 0.77 | 0.29 | 0.33 |
| Hargreaves Samani | 0.91 | 0.75 | 0.86 | 0.88 | 0.86 | 0.86 | −0.76 | 0.86 | −0.57 | 0.55 |
| Makkink | 0.90 | 0.77 | 0.88 | 0.89 | 0.88 | 0.85 | 0.23 | 0.86 | 0.63 | 0.33 |
| Matt Shuttleworth | 0.90 | 0.76 | 0.88 | 0.88 | 0.88 | 0.84 | 0.17 | 0.85 | 0.67 | 0.33 |
| Penman | 0.91 | 0.78 | 0.86 | 0.88 | 0.86 | 0.86 | −2.34 | 0.85 | 0.73 | 0.64 |
| Penman-Monteith | 0.91 | 0.77 | 0.88 | 0.88 | 0.88 | 0.86 | −0.67 | 0.86 | 0.46 | 0.56 |
| Priestley Taylor | 0.91 | 0.81 | 0.87 | 0.88 | 0.87 | 0.85 | −0.88 | 0.85 | 0.68 | 0.52 |
| Turc | 0.87 | 0.79 | 0.87 | 0.89 | 0.87 | 0.83 | 0.10 | 0.84 | 0.34 | 0.46 |
| Juam | ||||||||||
| Abtew | 0.90 | 0.66 | 0.84 | 0.88 | 0.84 | 0.88 | −0.46 | 0.90 | 0.85 | 0.86 |
| Blaney Criddle | 0.90 | 0.57 | 0.83 | 0.81 | 0.83 | 0.82 | 0.72 | 0.87 | 0.67 | 0.70 |
| Chapman Australian | 0.91 | 0.67 | 0.81 | 0.88 | 0.81 | 0.89 | 0.37 | 0.90 | 0.79 | 0.80 |
| Granger Gray | 0.90 | 0.70 | 0.81 | 0.84 | 0.81 | 0.81 | 0.41 | 0.86 | 0.56 | 0.84 |
| Hamon | 0.84 | 0.57 | 0.82 | 0.78 | 0.82 | 0.61 | 0.20 | 0.60 | 0.73 | 0.52 |
| Hargreaves Samani | 0.89 | 0.74 | 0.83 | 0.90 | 0.83 | 0.89 | −0.07 | 0.90 | 0.03 | 0.75 |
| Makkink | 0.91 | 0.60 | 0.85 | 0.84 | 0.85 | 0.86 | 0.54 | 0.90 | 0.87 | 0.85 |
| Matt Shuttleworth | 0.90 | 0.60 | 0.85 | 0.82 | 0.85 | 0.80 | 0.56 | 0.86 | 0.85 | 0.77 |
| Penman | 0.90 | 0.72 | 0.84 | 0.89 | 0.84 | 0.86 | 0.00 | 0.87 | 0.67 | 0.80 |
| Penman-Monteith | 0.91 | 0.69 | 0.84 | 0.88 | 0.84 | 0.90 | 0.15 | 0.89 | 0.08 | 0.85 |
| Priestley Taylor | 0.91 | 0.63 | 0.84 | 0.88 | 0.84 | 0.88 | 0.40 | 0.89 | 0.34 | 0.82 |
| Turc | 0.83 | 0.66 | 0.83 | 0.88 | 0.83 | 0.85 | 0.35 | 0.87 | 0.81 | 0.81 |
| Imha | ||||||||||
| Abtew | 0.69 | 0.61 | 0.64 | 0.67 | 0.69 | 0.70 | −1.53 | 0.73 | 0.89 | 0.70 |
| Blaney Criddle | 0.65 | 0.58 | 0.67 | 0.71 | 0.65 | 0.83 | 0.41 | 0.83 | 0.74 | 0.70 |
| Chapman Australian | 0.72 | 0.65 | 0.65 | 0.71 | 0.72 | 0.78 | −1.35 | 0.80 | −1.00 | 0.78 |
| Granger Gray | 0.67 | 0.62 | 0.60 | 0.66 | 0.67 | 0.82 | −0.44 | 0.80 | −0.03 | 0.71 |
| Hamon | 0.61 | 0.55 | 0.58 | 0.55 | 0.61 | 0.67 | 0.37 | 0.70 | 0.61 | 0.67 |
| Hargreaves Samani | 0.65 | 0.63 | 0.62 | 0.67 | 0.65 | 0.80 | −1.11 | 0.79 | 0.76 | 0.71 |
| Makkink | 0.70 | 0.62 | 0.64 | 0.72 | 0.70 | 0.80 | −0.63 | 0.78 | −0.61 | 0.65 |
| Matt Shuttleworth | 0.69 | 0.65 | 0.69 | 0.75 | 0.69 | 0.84 | −1.76 | 0.81 | 0.59 | 0.50 |
| Penman | 0.65 | 0.65 | 0.61 | 0.65 | 0.65 | 0.79 | −0.77 | 0.78 | 0.59 | 0.71 |
| Penman-Monteith | 0.72 | 0.65 | 0.68 | 0.67 | 0.72 | 0.76 | −2.05 | 0.75 | 0.86 | 0.60 |
| Priestley Taylor | 0.70 | 0.63 | 0.62 | 0.72 | 0.70 | 0.82 | −1.03 | 0.80 | −0.42 | 0.56 |
| Turc | 0.72 | 0.63 | 0.67 | 0.72 | 0.72 | 0.86 | −0.76 | 0.84 | −0.30 | 0.71 |
| Andong | ||||||||||
| Abtew | 0.83 | 0.69 | 0.74 | 0.84 | 0.83 | 0.79 | −1.63 | 0.80 | 0.78 | 0.51 |
| Blaney Criddle | 0.70 | 0.68 | 0.73 | 0.86 | 0.70 | 0.76 | 0.46 | 0.80 | 0.61 | 0.57 |
| Chapman Australian | 0.84 | 0.69 | 0.75 | 0.88 | 0.84 | 0.80 | −0.88 | 0.81 | −0.38 | 0.35 |
| Granger Gray | 0.82 | 0.69 | 0.73 | 0.86 | 0.82 | 0.76 | −0.18 | 0.79 | 0.30 | 0.29 |
| Hamon | 0.75 | 0.52 | 0.75 | 0.71 | 0.75 | 0.67 | 0.43 | 0.71 | 0.72 | 0.39 |
| Hargreaves Samani | 0.85 | 0.69 | 0.71 | 0.81 | 0.85 | 0.80 | −0.88 | 0.79 | −0.74 | 0.40 |
| Makkink | 0.83 | 0.71 | 0.73 | 0.89 | 0.83 | 0.78 | −0.45 | 0.81 | −0.42 | 0.33 |
| Matt Shuttleworth | 0.83 | 0.70 | 0.77 | 0.89 | 0.83 | 0.76 | 0.14 | 0.79 | 0.68 | 0.03 |
| Penman | 0.84 | 0.67 | 0.75 | 0.84 | 0.84 | 0.80 | −0.93 | 0.80 | 0.11 | 0.51 |
| Penman-Monteith | 0.84 | 0.69 | 0.74 | 0.88 | 0.84 | 0.80 | −0.81 | 0.81 | −0.57 | 0.48 |
| Priestley Taylor | 0.83 | 0.70 | 0.74 | 0.86 | 0.83 | 0.78 | −0.61 | 0.80 | 0.73 | 0.52 |
| Turc | 0.76 | 0.68 | 0.76 | 0.80 | 0.76 | 0.76 | −0.08 | 0.79 | 0.66 | 0.45 |
| Soyanggang | ||||||||||
| Abtew | 0.91 | 0.77 | 0.86 | 0.92 | 0.86 | 0.84 | −1.47 | 0.82 | −1.66 | 0.71 |
| Blaney Criddle | 0.91 | 0.75 | 0.88 | 0.92 | 0.88 | 0.80 | 0.55 | 0.84 | 0.69 | 0.79 |
| Chapman Australian | 0.91 | 0.76 | 0.87 | 0.93 | 0.87 | 0.84 | −0.52 | 0.84 | 0.66 | 0.73 |
| Granger Gray | 0.91 | 0.76 | 0.86 | 0.92 | 0.86 | 0.83 | −0.15 | 0.83 | 0.65 | 0.63 |
| Hamon | 0.90 | 0.77 | 0.88 | 0.90 | 0.88 | 0.79 | 0.66 | 0.80 | 0.77 | 0.72 |
| Hargreaves Samani | 0.91 | 0.75 | 0.84 | 0.92 | 0.84 | 0.84 | −1.68 | 0.83 | 0.03 | 0.66 |
| Makkink | 0.91 | 0.73 | 0.86 | 0.92 | 0.86 | 0.84 | −1.78 | 0.84 | 0.68 | 0.71 |
| Matt Shuttleworth | 0.91 | 0.69 | 0.86 | 0.92 | 0.86 | 0.83 | −0.80 | 0.83 | 0.68 | 0.67 |
| Penman | 0.92 | 0.62 | 0.87 | 0.91 | 0.87 | 0.84 | −4.15 | 0.82 | −0.04 | 0.71 |
| Penman-Monteith | 0.91 | 0.76 | 0.87 | 0.92 | 0.87 | 0.84 | −1.06 | 0.83 | 0.46 | 0.71 |
| Priestley Taylor | 0.91 | 0.78 | 0.87 | 0.92 | 0.87 | 0.83 | −0.45 | 0.82 | 0.62 | 0.68 |
| Turc | 0.92 | 0.78 | 0.87 | 0.92 | 0.87 | 0.82 | 0.13 | 0.82 | 0.47 | 0.73 |
| Chungju | ||||||||||
| Abtew | 0.79 | 0.66 | 0.60 | 0.84 | 0.79 | 0.86 | −1.67 | 0.86 | 0.80 | 0.83 |
| Blaney Criddle | 0.82 | 0.64 | 0.65 | 0.85 | 0.82 | 0.79 | 0.65 | 0.85 | 0.73 | 0.86 |
| Chapman Australian | 0.80 | 0.65 | 0.59 | 0.86 | 0.80 | 0.86 | −0.87 | 0.87 | −0.09 | 0.86 |
| Granger Gray | 0.81 | 0.66 | 0.66 | 0.85 | 0.85 | 0.85 | 0.33 | 0.86 | 0.44 | 0.86 |
| Hamon | 0.80 | 0.68 | 0.62 | 0.81 | 0.80 | 0.77 | 0.65 | 0.78 | 0.80 | 0.78 |
| Hargreaves Samani | 0.80 | 0.68 | 0.56 | 0.82 | 0.80 | 0.86 | −1.56 | 0.86 | 0.70 | 0.85 |
| Makkink | 0.81 | 0.66 | 0.59 | 0.85 | 0.81 | 0.86 | −0.23 | 0.87 | 0.68 | 0.87 |
| Matt Shuttleworth | 0.81 | 0.68 | 0.64 | 0.85 | 0.81 | 0.84 | 0.32 | 0.86 | 0.58 | 0.86 |
| Penman | 0.79 | 0.64 | 0.61 | 0.84 | 0.79 | 0.86 | −2.55 | 0.86 | 0.79 | 0.85 |
| Penman-Monteith | 0.80 | 0.64 | 0.62 | 0.82 | 0.80 | 0.86 | −1.09 | 0.86 | −0.92 | 0.84 |
| Priestley Taylor | 0.81 | 0.64 | 0.58 | 0.81 | 0.81 | 0.85 | −0.28 | 0.86 | 0.64 | 0.82 |
| Turc | 0.83 | 0.68 | 0.60 | 0.85 | 0.83 | 0.83 | 0.14 | 0.85 | 0.51 | 0.86 |
Appendix B





References
- Hrachowitz, M.; Clark, M.P. HESS Opinions: The complementary merits of competing modelling philosophies in hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 3953–3973. [Google Scholar] [CrossRef]
- Brown, C.M.; Lund, J.R.; Cai, X.; Reed, P.M.; Zagona, E.A.; Ostfeld, A.; Hall, J.; Characklis, G.W.; Yu, W.; Brekke, L. The future of water resources systems analysis: Toward a scientific framework for sustainable water management. Water Resour. Res. 2015, 51, 6110–6124. [Google Scholar] [CrossRef]
- Casadei, S.; Pierleoni, A.; Bellezza, M. Sustainability of Water Withdrawals in the Tiber River Basin (Central Italy). Sustainability 2018, 10, 485. [Google Scholar] [CrossRef]
- Park, D.; Kim, Y.; Um, M.-J.; Choi, S.-U. Robust Priority for Strategic Environmental Assessment with Incomplete Information Using Multi-Criteria Decision Making Analysis. Sustainability 2015, 7, 10233–10249. [Google Scholar] [CrossRef]
- Horne, J. Water Information as a Tool to Enhance Sustainable Water Management—The Australian Experience. Water 2015, 7, 2161–2183. [Google Scholar] [CrossRef]
- Chung, E.-S.; Abdulai, P.J.; Park, H.; Kim, Y.; Ahn, S.R.; Kim, S.J. Multi-Criteria Assessment of Spatial Robust Water Resource Vulnerability Using the TOPSIS Method Coupled with Objective and Subjective Weights in the Han River Basin. Sustainability 2016, 9, 29. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Does a large number of parameters enhance model performance? Comparative assessment of common catchment model structures on 429 catchments. J. Hydrol. 2001, 242, 275–301. [Google Scholar] [CrossRef]
- Beck, H.E.; van Dijk, A.I.; de Roo, A.; Dutra, E.; Fink, G.; Orth, R.; Schellekens, J. Global evaluation of runoff from 10 state-of-the-art hydrological models. Hydrol. Earth Syst. Sci. 2017, 21, 2881–2903. [Google Scholar] [CrossRef]
- Beven, K.J. Rainfall-Runoff Modelling: The Primer, 2nd ed.; Wiley-Blackwell: Chichester, UK; Hoboken, NJ, USA, 2012; ISBN 978-0-47-071459-1. [Google Scholar]
- Beven, K. How far can we go in distributed hydrological modelling? Hydrol. Earth Syst. Sci. Discuss. 2001, 5, 1–12. [Google Scholar] [CrossRef]
- Goderniaux, P.; Brouyère, S.; Fowler, H.J.; Blenkinsop, S.; Therrien, R.; Orban, P.; Dassargues, A. Large scale surface–subsurface hydrological model to assess climate change impacts on groundwater reserves. J. Hydrol. 2009, 373, 122–138. [Google Scholar] [CrossRef]
- Kim, N.W.; Chung, I.M.; Won, Y.S.; Arnold, J.G. Development and application of the integrated SWAT–MODFLOW model. J. Hydrol. 2008, 356, 1–16. [Google Scholar] [CrossRef]
- Butts, M.B.; Payne, J.T.; Kristensen, M.; Madsen, H. An evaluation of the impact of model structure on hydrological modelling uncertainty for streamflow simulation. J. Hydrol. 2004, 298, 242–266. [Google Scholar] [CrossRef]
- Bennett, J.C.; Robertson, D.E.; Ward, P.G.D.; Hapuarachchi, H.A.P.; Wang, Q.J. Calibrating hourly rainfall-runoff models with daily forcings for streamflow forecasting applications in meso-scale catchments. Environ. Model. Softw. 2016, 76, 20–36. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Jung, D.; Choi, Y.H.; Kim, J.H. Multiobjective Automatic Parameter Calibration of a Hydrological Model. Water 2017, 9, 187. [Google Scholar] [CrossRef]
- Andréassian, V.; Perrin, C.; Michel, C. Impact of imperfect potential evapotranspiration knowledge on the efficiency and parameters of watershed models. J. Hydrol. 2004, 286, 19–35. [Google Scholar] [CrossRef]
- Ficchì, A.; Perrin, C.; Andréassian, V. Impact of temporal resolution of inputs on hydrological model performance: An analysis based on 2400 flood events. J. Hydrol. 2016, 538, 454–470. [Google Scholar] [CrossRef]
- Oudin, L.; Michel, C.; Anctil, F. Which potential evapotranspiration input for a lumped rainfall-runoff model? Part 1—Can rainfall-runoff models effectively handle detailed potential evapotranspiration inputs? J. Hydrol. 2005, 303, 275–289. [Google Scholar] [CrossRef]
- Oudin, L.; Hervieu, F.; Michel, C.; Perrin, C.; Andréassian, V.; Anctil, F.; Loumagne, C. Which potential evapotranspiration input for a lumped rainfall-runoff model? Part 2—Towards a simple and efficient potential evapotranspiration model for rainfall–runoff modelling. J. Hydrol. 2005, 303, 290–306. [Google Scholar] [CrossRef]
- Knipper, K.; Hogue, T.; Scott, R.; Franz, K. Evapotranspiration Estimates Derived Using Multi-Platform Remote Sensing in a Semiarid Region. Remote Sens. 2017, 9, 184. [Google Scholar] [CrossRef]
- Harrigan, S.; Berghuijs, W. The Mystery of Evaporation. Streams of Thought. Young Hydrol. Soc. 2016, 10. [Google Scholar] [CrossRef]
- Guo, D.; Westra, S.; Maier, H.R. An R package for modelling actual, potential and reference evapotranspiration. Environ. Model. Softw. 2016, 78, 216–224. [Google Scholar] [CrossRef]
- Parmele, L.H. Errors in output of hydrologic models due to errors in input potential evapotranspiration. Water Resour. Res. 1972, 8, 348–359. [Google Scholar] [CrossRef]
- Nandakumar, N.; Mein, R.G. Uncertainty in rainfall-runoff model simulations and the implications for predicting the hydrologic effects of land-use change. J. Hydrol. 1997, 192, 211–232. [Google Scholar] [CrossRef]
- Paturel, J.E.; Servat, E.; Vassiliadis, A. Sensitivity of conceptual rainfall-runoff algorithms to errors in input data—Case of the GR2M model. J. Hydrol. 1995, 168, 111–125. [Google Scholar] [CrossRef]
- Xu, C.-Y.; Vandewiele, G.L. Sensitivity of monthly rainfall-runoff models to input errors and data length. Hydrol. Sci. J. 1994, 39, 157–176. [Google Scholar] [CrossRef]
- Xu, C.; Tunemar, L.; Chen, Y.D.; Singh, V.P. Evaluation of seasonal and spatial variations of lumped water balance model sensitivity to precipitation data errors. J. Hydrol. 2006, 324, 80–93. [Google Scholar] [CrossRef]
- Barella-Ortiz, A.; Polcher, J.; Tuzet, A.; Laval, K. Potential evaporation estimation through an unstressed surface-energy balance and its sensitivity to climate change. Hydrol. Earth Syst. Sci. 2013, 17, 4625–4639. [Google Scholar] [CrossRef]
- McVicar, T.R.; Roderick, M.L.; Donohue, R.J.; Li, L.T.; Van Niel, T.G.; Thomas, A.; Grieser, J.; Jhajharia, D.; Himri, Y.; Mahowald, N.M.; et al. Global review and synthesis of trends in observed terrestrial near-surface wind speeds: Implications for evaporation. J. Hydrol. 2012, 416–417, 182–205. [Google Scholar] [CrossRef]
- Andersson, L. Improvements of runoff models what way to go? Hydrol. Res. 1992, 23, 315–332. [Google Scholar] [CrossRef]
- Lindroth, A. Potential Evaporation—A Matter of Definition: A Comment on ‘Improvements of Runoff Models—What Way to Go’? Hydrol. Res. 1993, 24, 359–364. [Google Scholar] [CrossRef]
- Morton, F.I. Evaporation research—A critical review and its lessons for the environmental sciences. Crit. Rev. Environ. Sci. Technol. 1994, 24, 237–280. [Google Scholar] [CrossRef]
- Evans, J.P. Improving the characteristics of streamflow modeled by regional climate models. J. Hydrol. 2003, 284, 211–227. [Google Scholar] [CrossRef]
- Oudin, L.; Andréassian, V.; Perrin, C.; Anctil, F. Locating the sources of low-pass behavior within rainfall-runoff models: Low-pass behavior of rainfall-runoff models. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Oudin, L.; Perrin, C.; Mathevet, T.; Andréassian, V.; Michel, C. Impact of biased and randomly corrupted inputs on the efficiency and the parameters of watershed models. J. Hydrol. 2006, 320, 62–83. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models. Part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. GLUE: 20 years on. Hydrol. Process. 2014, 28, 5897–5918. [Google Scholar] [CrossRef]
- Moussa, R.; Chahinian, N. Comparison of different multi-objective calibration criteria using a conceptual rainfall-runoff model of flood events. Hydrol. Earth Syst. Sci. 2009, 13, 519–535. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Clark, M.P.; Slater, A.G.; Rupp, D.E.; Woods, R.A.; Vrugt, J.A.; Gupta, H.V.; Wagener, T.; Hay, L.E. Framework for Understanding Structural Errors (FUSE): A modular framework to diagnose differences between hydrological models. Water Resour. Res. 2008, 44, W00B02. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Qi, M.; Zhang, G.P. An investigation of model selection criteria for neural network time series forecasting. Eur. J. Oper. Res. 2001, 132, 666–680. [Google Scholar] [CrossRef]
- Laio, F.; Di Baldassarre, G.; Montanari, A. Model selection techniques for the frequency analysis of hydrological extremes. Water Resour. Res. 2009, 45, W07416. [Google Scholar] [CrossRef]
- Merz, R.; Parajka, J.; Blöschl, G. Time stability of catchment model parameters: Implications for climate impact analyses. Water Resour. Res. 2011, 47, W02531. [Google Scholar] [CrossRef]
- Coron, L.; Andréassian, V.; Perrin, C.; Bourqui, M.; Hendrickx, F. On the lack of robustness of hydrologic models regarding water balance simulation: A diagnostic approach applied to three models of increasing complexity on 20 mountainous catchments. Hydrol. Earth Syst. Sci. 2014, 18, 727–746. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V.K. Optimal use of the SCE-UA global optimization method for calibrating watershed models. J. Hydrol. 1994, 158, 265–284. [Google Scholar] [CrossRef]
- Ajami, N.K.; Gupta, H.; Wagener, T.; Sorooshian, S. Calibration of a semi-distributed hydrologic model for streamflow estimation along a river system. J. Hydrol. 2004, 298, 112–135. [Google Scholar] [CrossRef]
- Madsen, H. Automatic calibration of a conceptual rainfall–runoff model using multiple objectives. J. Hydrol. 2000, 235, 276–288. [Google Scholar] [CrossRef]
- Roy, T.; Gupta, H.V.; Serrat-Capdevila, A.; Valdes, J.B. Using satellite-based evapotranspiration estimates to improve the structure of a simple conceptual rainfall–runoff model. Hydrol. Earth Syst. Sci. 2017, 21, 879–896. [Google Scholar] [CrossRef]
- McMahon, T.A.; Peel, M.C.; Lowe, L.; Srikanthan, R.; McVicar, T.R. Estimating actual, potential, reference crop and pan evaporation using standard meteorological data: A pragmatic synthesis. Hydrol. Earth Syst. Sci. 2013, 17, 1331–1363. [Google Scholar] [CrossRef]
- Xu, C.-Y.; Singh, V.P. Cross Comparison of Empirical Equations for Calculating Potential Evapotranspiration with Data from Switzerland. Water Resour. Manag. 2002, 16, 197–219. [Google Scholar] [CrossRef]
- Brutsaert, W. Evaporation into the Atmosphere: Theory, History and Applications; Springer: Dordrecht, The Netherlands, 1982; ISBN 978-9-40-171497-6. [Google Scholar]
- Zhao, L.; Xia, J.; Xu, C.; Wang, Z.; Sobkowiak, L.; Long, C. Evapotranspiration estimation methods in hydrological models. J. Geogr. Sci. 2013, 23, 359–369. [Google Scholar] [CrossRef]
- García Hernández, J.; Claude, A.; Paredes Arquiola, J.; Roquier, B.; Boillat, J.-L. Integrated flood forecasting and management system in a complex catchment area in the Alps—Implementation of the MINERVE project in the Canton of Valais. In Special Session on Swiss Competences in River Engineering and Restoration, Proceedings of the River Flow 2014, Lausanne, Switzerland, 3–5 September 2014; EPFL: Leiden, Switzerland, 2014; pp. 87–97. [Google Scholar]
- Demirel, M.C.; Booij, M.J.; Hoekstra, A.Y. The skill of seasonal ensemble low-flow forecasts in the Moselle River for three different hydrological models. Hydrol. Earth Syst. Sci. 2015, 19, 275–291. [Google Scholar] [CrossRef]
- Kim, D.; Jung, I.W.; Chun, J.A. A comparative assessment of rainfall–runoff modelling against regional flow duration curves for ungauged catchments. Hydrol. Earth Syst. Sci. 2017, 21, 5647–5661. [Google Scholar] [CrossRef]
- Nepal, S.; Chen, J.; Penton, D.J.; Neumann, L.E.; Zheng, H.; Wahid, S. Spatial GR4J conceptualization of the Tamor glaciated alpine catchment in Eastern Nepal: Evaluation of GR4JSG against streamflow and MODIS snow extent: Hydrological Modelling in Tamor Catchment. Hydrol. Process. 2017, 31, 51–68. [Google Scholar] [CrossRef]
- Velázquez, J.A.; Anctil, F.; Ramos, M.H.; Perrin, C. Can a multi-model approach improve hydrological ensemble forecasting? A study on 29 French catchments using 16 hydrological model structures. Adv. Geosci. 2011, 29, 33–42. [Google Scholar] [CrossRef]
- Ajmal, M.; Khan, T.A.; Kim, T.-W. A CN-Based Ensembled Hydrological Model for Enhanced Watershed Runoff Prediction. Water 2016, 8, 20. [Google Scholar] [CrossRef]
- Tian, Y.; Booij, M.J.; Xu, Y.-P. Uncertainty in high and low flows due to model structure and parameter errors. Stoch. Environ. Res. Risk Assess. 2014, 28, 319–332. [Google Scholar] [CrossRef]
- Porter, J.W.; McMahon, T.A. Application of a catchment model in southeastern Australia. J. Hydrol. 1975, 24, 121–134. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; Peel, M.C.; Western, A.W. Application and testing of the simple rainfall-runoff model SIMHYD. In Mathematical Models of Small Watershed Hydrology and Applications; Singh, V.P., Frevert, D.K., Eds.; Water Resources Publications: Littleton, CO, USA, 2002; pp. 335–367. [Google Scholar]
- Chiew, F.H.S.; Kirono, D.G.C.; Kent, D.M.; Frost, A.J.; Charles, S.P.; Timbal, B.; Nguyen, K.C.; Fu, G. Comparison of runoff modelled using rainfall from different downscaling methods for historical and future climates. J. Hydrol. 2010, 387, 10–23. [Google Scholar] [CrossRef]
- Li, C.Z.; Zhang, L.; Wang, H.; Zhang, Y.Q.; Yu, F.L.; Yan, D.H. The transferability of hydrological models under nonstationary climatic conditions. Hydrol. Earth Syst. Sci. 2012, 16, 1239–1254. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Y. Regionalising rainfall-runoff modelling for predicting daily runoff: Comparing gridded spatial proximity and gridded integrated similarity approaches against their lumped counterparts. J. Hydrol. 2017, 550, 279–293. [Google Scholar] [CrossRef]
- Vaze, J.; Post, D.A.; Chiew, F.H.S.; Perraud, J.-M.; Teng, J.; Viney, N.R. Conceptual Rainfall–Runoff Model Performance with Different Spatial Rainfall Inputs. J. Hydrometeorol. 2011, 12, 1100–1112. [Google Scholar] [CrossRef]
- Yu, B.; Zhu, Z. A comparative assessment of AWBM and SimHyd for forested watersheds. Hydrol. Sci. J. 2015, 60, 1200–1212. [Google Scholar] [CrossRef]
- Peel, M.C.; Chiew, F.H.; Western, A.W.; McMahon, T.A. Extension of Unimpaired Monthly Streamflow Data and Regionalisation of Parameter Values to Estimate Streamflow in Ungauged Catchments; Australian Natural Resources Atlas: Melbourne, Australia, 2000. [Google Scholar]
- Kim, H.-J.; Jang, C.-H. Catchment Hydrologic Cycle Assessment Tool—A User Guide; Korea Institute of Civil Engineering and Building Technology: Goyang, Korea, 2017. [Google Scholar]
- Miller, J.D.; Kim, H.; Kjeldsen, T.R.; Packman, J.; Grebby, S.; Dearden, R. Assessing the impact of urbanization on storm runoff in a peri-urban catchment using historical change in impervious cover. J. Hydrol. 2014, 515, 59–70. [Google Scholar] [CrossRef]
- Kim, H.-J.; Jang, C.-H.; Noh, S.-J. Development and application of the catchment hydrologic cycle assessment tool considering urbanization (I)-Model development. J. Korea Water Resour. Assoc. 2012, 45, 203–215. [Google Scholar] [CrossRef]
- Green, W.H.; Ampt, G.A. Studies on Soil Phyics. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar] [CrossRef]
- Jang, C.H.; Kim, H.J.; Ahn, S.R.; Kim, S.J. Assessment of hydrological changes in a river basin as affected by climate change and water management practices, by using the cat model. Irrig. Drain. 2016, 65, 26–35. [Google Scholar] [CrossRef]
- Jang, C.-H.; Kim, H.-J.; Kim, J.-T. Prediction of Reservoir Water Level using CAT. J. Korean Soc. Agric. Eng. 2012, 54, 27–38. [Google Scholar] [CrossRef]
- Choi, S.; Jang, C.; Kim, H. Analysis of Short-term Runoff Characteristics of CAT-PEST Connected Model using Different Infiltration Analysis Methods. J. Korea Acad. Ind. Coop. Soc. 2016, 17, 26–41. [Google Scholar] [CrossRef]
- Hwang, S.; Kang, M.-S. Evaluation of the CAT Model in hydrological simulation for a small watershed. In Proceedings of the 2012 ASABE Annual International Meeting, Dallas, TX, USA, 29 July–1 August 2012; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2012; p. 1. [Google Scholar]
- Sugawara, M. Automatic calibration of the tank model/L’étalonnage automatique d’un modèle à cisterne. Hydrol. Sci. Bull. 1979, 24, 375–388. [Google Scholar] [CrossRef]
- Chadalawada, J.; Havlicek, V.; Babovic, V. A Genetic Programming Approach to System Identification of Rainfall-Runoff Models. Water Resour. Manag. 2017, 31, 3975–3992. [Google Scholar] [CrossRef]
- Sugawara, M. Tank model. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Resources Publications: Littleton, CO, USA, 1995; ISBN 0-918334-91-8. [Google Scholar]
- Lee, Y.H.; Singh, V.P. Tank Model for Sediment Yield. Water Resour. Manag. 2005, 19, 349–362. [Google Scholar] [CrossRef]
- Sung, Y.-K.; Kim, S.-H.; Kim, H.-J.; Kim, N.-W. The Applicability Study of SYMHYD and TANK Model Using Different Type of Objective Functions and Optimization Methods. J. Korea Water Resour. Assoc. 2004, 37, 121–131. [Google Scholar] [CrossRef]
- Yokoo, Y.; Chiba, T.; Shikano, Y.; Leong, C. Identifying dominant runoff mechanisms and their lumped modeling: A data-based modeling approach. Hydrol. Res. Lett. 2017, 11, 128–133. [Google Scholar] [CrossRef]
- Song, J.-H.; Her, Y.; Park, J.; Lee, K.-D.; Kang, M.-S. Simulink Implementation of a Hydrologic Model: A Tank Model Case Study. Water 2017, 9, 639. [Google Scholar] [CrossRef]
- Chen, R.-S.; Pi, L.-C.; Hsieh, C.-C. Application of Parameter Optimization Method for Calibrating Tank Model1. J. Am. Water Resour. Assoc. 2005, 41, 389–402. [Google Scholar] [CrossRef]
- Burnash, R.J.C. The NWS river forecast system-catchment modeling. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Resources Publications: Littleton, CO, USA, 1995; ISBN 0-918334-91-8. [Google Scholar]
- Wright, A.J.; Walker, J.P.; Pauwels, V.R.N. Estimating rainfall time series and model parameter distributions using model data reduction and inversion techniques. Water Resour. Res. 2017, 53, 6407–6424. [Google Scholar] [CrossRef]
- Bowman, A.L.; Franz, K.J.; Hogue, T.S. Case Studies of a MODIS-Based Potential Evapotranspiration Input to the Sacramento Soil Moisture Accounting Model. J. Hydrometeorol. 2016, 18, 151–158. [Google Scholar] [CrossRef]
- Heřmanovský, M.; Havlíček, V.; Hanel, M.; Pech, P. Regionalization of runoff models derived by genetic programming. J. Hydrol. 2017, 547, 544–556. [Google Scholar] [CrossRef]
- Huang, C.; Newman, A.J.; Clark, M.P.; Wood, A.W.; Zheng, X. Evaluation of snow data assimilation using the ensemble Kalman filter for seasonal streamflow prediction in the western United States. Hydrol. Earth Syst. Sci. 2017, 21, 635–650. [Google Scholar] [CrossRef]
- Katsanou, K.; Lambrakis, N. Modeling the Hellenic karst catchments with the Sacramento Soil Moisture Accounting model. Hydrogeol. J. 2017, 25, 757–769. [Google Scholar] [CrossRef]
- Shin, M.-J.; Guillaume, J.H.A.; Croke, B.F.W.; Jakeman, A.J. Addressing ten questions about conceptual rainfall–runoff models with global sensitivity analyses in R. J. Hydrol. 2013, 503, 135–152. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Gupta, H.V.; Dekker, S.C.; Sorooshian, S.; Wagener, T.; Bouten, W. Application of stochastic parameter optimization to the Sacramento Soil Moisture Accounting model. J. Hydrol. 2006, 325, 288–307. [Google Scholar] [CrossRef]
- Anderson, R.M.; Koren, V.I.; Reed, S.M. Using SSURGO data to improve Sacramento Model a priori parameter estimates. J. Hydrol. 2006, 320, 103–116. [Google Scholar] [CrossRef]
- Khu, S.-T.; Werner, M.G. Reduction of Monte-Carlo simulation runs for uncertainty estimation in hydrological modelling. Hydrol. Earth Syst. Sci. Discuss. 2003, 7, 680–692. [Google Scholar] [CrossRef]
- Lee, S.; Kang, T. Analysis of Constrained Optimization Problems by the SCE-UA with an Adaptive Penalty Function. J. Comput. Civ. Eng. 2016, 30, 04015035. [Google Scholar] [CrossRef]
- Van Griensven, A.; Meixner, T.; Grunwald, S.; Bishop, T.; Diluzio, M.; Srinivasan, R. A global sensitivity analysis tool for the parameters of multi-variable catchment models. J. Hydrol. 2006, 324, 10–23. [Google Scholar] [CrossRef]
- Rosenbrock, H. An automatic method for finding the greatest or least value of a function. Comput. J. 1960, 3, 175–184. [Google Scholar] [CrossRef]
- Liu, X.; Yang, T.; Hsu, K.; Liu, C.; Sorooshian, S. Evaluating the streamflow simulation capability of PERSIANN-CDR daily rainfall products in two river basins on the Tibetan Plateau. Hydrol. Earth Syst. Sci. 2017, 21, 169–181. [Google Scholar] [CrossRef]
- Kim, H.; Kim, S.; Shin, H.; Heo, J.-H. Appropriate model selection methods for nonstationary generalized extreme value models. J. Hydrol. 2017, 547, 557–574. [Google Scholar] [CrossRef]
- Gaganis, P.; Smith, L. A Bayesian Approach to the quantification of the effect of model error on the predictions of groundwater models. Water Resour. Res. 2001, 37, 2309–2322. [Google Scholar] [CrossRef]
- Kamruzzaman, M.; Shahriar, M.S.; Beecham, S. Assessment of Short Term Rainfall and Stream Flows in South Australia. Water 2014, 6, 3528–3544. [Google Scholar] [CrossRef]
- Wilby, R.L.; Abrahart, R.J.; Dawson, C.W. Detection of conceptual model rainfall-runoff processes inside an artificial neural network. Hydrol. Sci. J. 2003, 48, 163–181. [Google Scholar] [CrossRef]
- Coron, L.; Andréassian, V.; Perrin, C.; Lerat, J.; Vaze, J.; Bourqui, M.; Hendrickx, F. Crash testing hydrological models in contrasted climate conditions: An experiment on 216 Australian catchments. Water Resour. Res. 2012, 48, W05552. [Google Scholar] [CrossRef]
- Hornberger, G.M.; Beven, K.J.; Cosby, B.J.; Sappington, D.E. Shenandoah Watershed Study: Calibration of a Topography-Based, Variable Contributing Area Hydrological Model to a Small Forested Catchment. Water Resour. Res. 1985, 21, 1841–1850. [Google Scholar] [CrossRef]
- Loague, K.M.; Freeze, R.A. A Comparison of Rainfall-Runoff Modeling Techniques on Small Upland Catchments. Water Resour. Res. 1985, 21, 229–248. [Google Scholar] [CrossRef]
- Beven, K. Changing ideas in hydrology -The case of physically-based models. J. Hydrol. 1989, 105, 157–172. [Google Scholar] [CrossRef]
- Orth, R.; Staudinger, M.; Seneviratne, S.I.; Seibert, J.; Zappa, M. Does model performance improve with complexity? A case study with three hydrological models. J. Hydrol. 2015, 523, 147–159. [Google Scholar] [CrossRef]
- Gan, T.Y.; Dlamini, E.M.; Biftu, G.F. Effects of model complexity and structure, data quality, and objective functions on hydrologic modeling. J. Hydrol. 1997, 192, 81–103. [Google Scholar] [CrossRef]
- Abtew, W. Evapotranspiration Measurements and Modeling for Three Wetland Systems in South Florida1. J. Am. Water Resour. Assoc. 1996, 32, 465–473. [Google Scholar] [CrossRef]
- Allen, R.G.; Pruitt, W.O. Rational Use of the FAO Blaney-Criddle Formula. J. Irrig. Drain. Eng. 1986, 112, 139–155. [Google Scholar] [CrossRef]
- Chapman, T.G. Estimation of evaporation in rainfall-runoff models. In Proceedings of the MODSIM 2003 International Congress on Modelling and Simulation, Townsville, Australia, 14–17 July 2003; Volume 1, pp. 148–153. [Google Scholar]
- Granger, R.J.; Gray, D.M. Evaporation from natural nonsaturated surfaces. J. Hydrol. 1989, 111, 21–29. [Google Scholar] [CrossRef]
- Hamon, W.R. Estimating Potential Evapotranspiration. J. Hydraul. Div. 1961, 87, 107–120. [Google Scholar]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- De Bruin, H.A.R.; Lablans, W.N. Reference crop evapotranspiration determined with a modified Makkink equation. Hydrol. Process. 1998, 12, 1053–1062. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Wallace, J.S. Calculating the water requirements of irrigated crops in Australia using the Matt-Shuttleworth approach. Trans. ASABE 2009, 52, 1895–1906. [Google Scholar] [CrossRef]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. A 1948, 193, 120–145. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. FAO Irrigation and Drainage Paper No. 56; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998; Volume 56, pp. 97–156. [Google Scholar]
- Priestley, C.H.B.; Taylor, R.J. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Turc, L. Estimation of irrigation water requirements, potential evapotranspiration: A simple climatic formula evolved up to date. Ann. Agron. 1961, 12, 13–49. [Google Scholar]





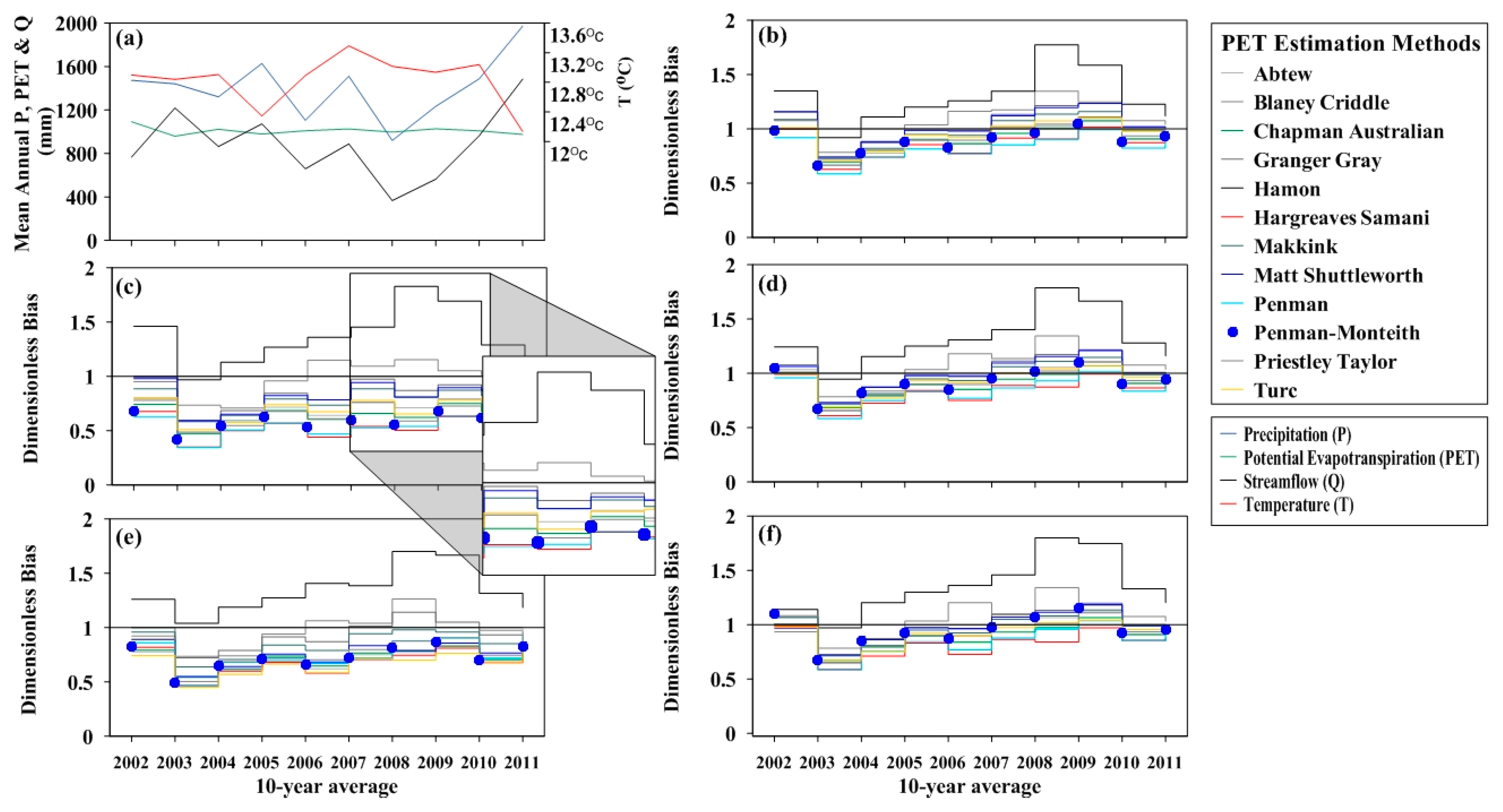
| No | 1 Catchment | Area (km2) | Mean Annual T (°C) | Mean Annual P (mm) | Mean Annual PET (mm) | Mean Annual Q (mm) | PET/P | Q/P |
|---|---|---|---|---|---|---|---|---|
| 1 | Seolmacheon | 8.50 | 11.19 | 1542.30 | 1226.65 | 1064.40 | 0.80 | 0.69 |
| 2 | Boryeong | 163.70 | 12.77 | 1425.43 | 1012.27 | 882.52 | 0.71 | 0.62 |
| 3 | Kyeongan | 262.40 | 12.76 | 1400.28 | 1326.09 | 937.12 | 0.95 | 0.67 |
| 4 | Seomjingang | 763 | 11.91 | 1466.98 | 815.19 | 883.34 | 0.56 | 0.60 |
| 5 | Yongdam | 930 | 11.11 | 1477.57 | 883.27 | 904.69 | 0.60 | 0.61 |
| 6 | Juam | 1010 | 14.61 | 1595.86 | 1017.39 | 776.18 | 0.64 | 0.49 |
| 7 | Imha | 1361 | 12.52 | 1073.55 | 940.98 | 575.06 | 0.88 | 0.54 |
| 8 | Andong | 1584 | 11.82 | 1302.23 | 1032.93 | 728.20 | 0.79 | 0.56 |
| 9 | Soyanggang | 2703 | 11.78 | 1394.90 | 840.89 | 915.85 | 0.60 | 0.66 |
| 10 | Chungju | 6648 | 12.10 | 1406.93 | 922.96 | 930.96 | 0.66 | 0.66 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Birhanu, D.; Kim, H.; Jang, C.; Park, S. Does the Complexity of Evapotranspiration and Hydrological Models Enhance Robustness? Sustainability 2018, 10, 2837. https://doi.org/10.3390/su10082837
Birhanu D, Kim H, Jang C, Park S. Does the Complexity of Evapotranspiration and Hydrological Models Enhance Robustness? Sustainability. 2018; 10(8):2837. https://doi.org/10.3390/su10082837
Chicago/Turabian StyleBirhanu, Dereje, Hyeonjun Kim, Cheolhee Jang, and Sanghyun Park. 2018. "Does the Complexity of Evapotranspiration and Hydrological Models Enhance Robustness?" Sustainability 10, no. 8: 2837. https://doi.org/10.3390/su10082837
APA StyleBirhanu, D., Kim, H., Jang, C., & Park, S. (2018). Does the Complexity of Evapotranspiration and Hydrological Models Enhance Robustness? Sustainability, 10(8), 2837. https://doi.org/10.3390/su10082837





