1. Introduction
Today, social network services (SNS) are an effective medium through which new information, such as opinions, news, and advertisements, is easily and quickly disseminated. The spread of these information starts when users create new posts. Subsequently, all subscribers and users who comment are notified of the new posts. To better understand the spread of these ideas, it is important to analyze how people propagate their thoughts based on their opinions and topics of interest, which are the underlying context and information flow.
Some applications for the proposed technique are viral marketing, where marketers quantify the impact of released products by applying sentiment analysis to understand unsatisfied consumers; influence analysis, determining how groups of users influence other groups; and trend detection, in which with the application of topic models, discussions, and opinions can be uncovered. In particular, in terms of social science, it is possible to understand the relationship among the users’ behaviors, the distinctions of communities and the information diffusion in social networks. Understanding users’ reactions are valuable since opinions can influence the news trend or purchase decisions. Therefore, the users’ opinions are vital to understanding the way information spreads and how communities interact among them.
There have been several studies on information flow modeling based on the structure of social network or the discovery of information diffusion processes without analyzing the structure of communication [
1,
2,
3,
4,
5,
6]. However, their studies have not shown the relation between context and information flow. A few studies have considered how to model information diffusion with a process structure. Kim et al. [
7] presented an information diffusion model using data of a blog to analyze the reposting behaviors of people. Although other studies have been carried out on information flows and SNS data [
8,
9,
10,
11], they can be used only to infer an information diffusion flow without considering the probability that communities will communicate or showing the contextual information. Kim et al. [
12] analyzed the behavioral patterns in SNS, News and Blog sites. However, the disadvantage in their study is the absence of opinions in the users’ comments. Opinions made by users in SNS can have a huge impact in society, therefore the analysis of these emotions are important to monitor the response of users to a specific news or product [
13]. There exist some studies in information diffusion based on sentiment [
14,
15,
16], but they do not consider the opinion flow between communities. Other researchers analyzed how to visualize topics and opinions in SNS [
17,
18,
19,
20,
21], but they lack in the information process flow. In this research, a new semantic hidden Markov model (HMM) for discovering information diffusion, named SentiFlow, is introduced to discover probabilistic information flow in consideration of topics and sentiment. It is an extension of HMM [
22] using text mining and process mining [
23]. The probabilities in the SentiFlow are computed based on maximum likelihood (ML) [
22]. In our previous studies [
24,
25], a method for probabilistic information flow of the communication between users and communities is presented. A method to underline the semantics and opinions in the interactions among user groups is suggested in this paper by applying community clustering algorithms to find user communities and by undertaking two different analyses, topic modeling and sentiment analysis, for the user comments. Finally, the traces of these communications are analyzed, and different information flow process models are generated. The goal is to answer the following important questions: (1) “What topics promote communication among user communities?” (2) “How are the positive, neutral, and negative opinions shared in the information diffusion process from a probabilistic point of view?”
The rest of the paper is organized as follows.
Section 2 describes the proposed methodology used in this work.
Section 3 describes the general algorithm used.
Section 4 provides the experimental results. Finally,
Section 5 concludes this work.
2. Framework
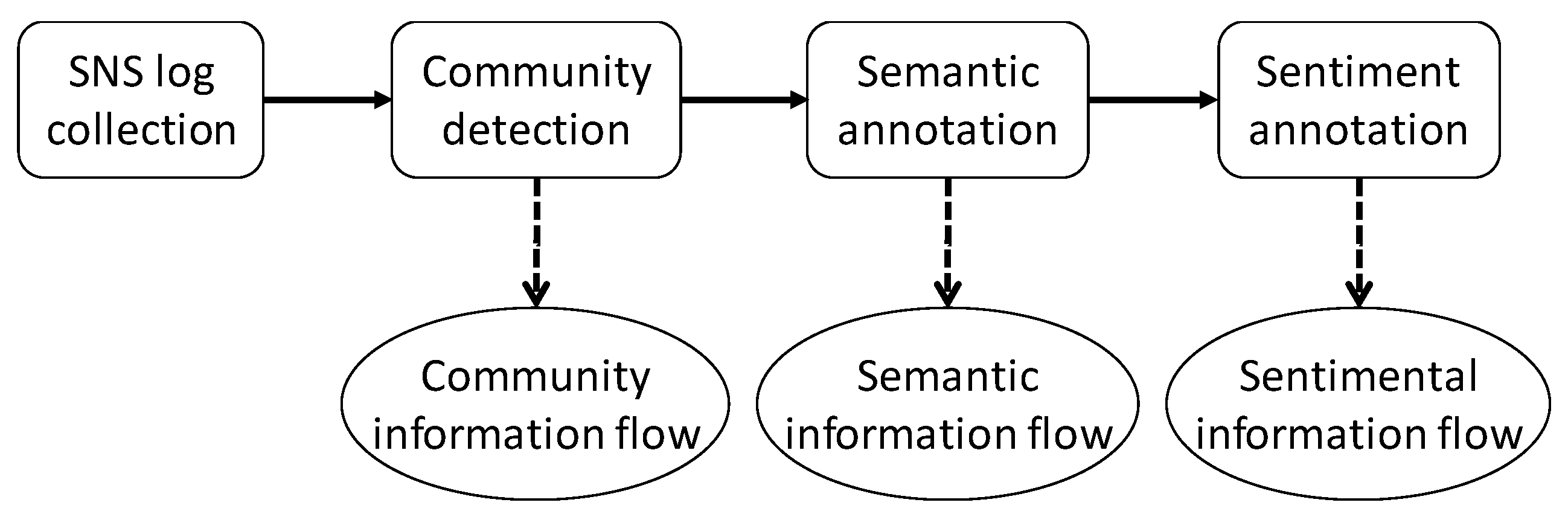
In this research, log data collected from SNS are used to discover information diffusion process. Generally, users in SNS wrote posts and their friends comment on the posts. Therefore, it can be assumed that, in a SNS log, each post of a specific user is characterized by many comments of his/her friends and the comments are ordered chronologically. From the SNS log, we first find the user communities based on their interaction and draw the information diffusion process. The topics of interest are found and annotated on the discovered process. Finally, the sentiment for the topics is analyzed for topics and users. The overall framework is depicted in
Figure 1.
2.1. SNS Log Collection
In SNS such as Facebook or Twitter, all posts are obtained along with the user’s name, user’s comments, and the timestamp indicating when it was posted to create an SNS log. In this research, it is assumed that users write comments to reply to other users and thus create or continue a discussion about a related post. Each post published by the fan page owner is characterized with a sequence of SNS events. An SNS event contains a user, the user comment, and the time when the comment was published. This sequence is ordered using the timestamp of the comment publication. An SNS log is defined below.
Definition 1. (SNS log) Letandbe the finite sets of all possible post identifiers and users, respectively. K and V are the numbers of posts and users, respectively. Posts are characterized by SNS events e, which in turn are characterized by various attributes. For any SNS event,is the value of attributein eventto have SNS event. Additionally, each post has an attribute action trace for a specific post, denoted by, and is defined as the sequence of SNS events in, i.e.,for 1 ≤ k ≤ K, where H is the number of events for p. An SNS log, denoted by, is a multi-set of action traces overandin the SNS.
To illustrate the operation of the proposed framework,
Table 1 presents an example SNS log with synthetic data. The example SNS log contains the post identification and the comment traces. The comment traces show the structure User
comment, where the user’s name is written and followed by the comment in subscript. Each user and comment are ordered by the timestamp for when the comment was published. The example SNS log contains six posts and 23 comments written by five users: Angela, George, John, Paul, and Ringo.
2.2. Information Flow among Communities
In this step, the communication of users and the interaction between them are analyzed. For this, users with similar behavior can be clustered into communities. The community detection analysis performs the next activities: identify the network structure inside the SNS log by applying community-detection algorithms, determine how the people across the comments are related, and help minimize the complexity of the discovered process model. The discovered communities represent the community states in the process model.
In the proposed framework, the Louvain modularity (LM) algorithm is used, which is often applied as a community detection method in social network analysis [
26]. LM detects and extracts communities in a network by providing the optimal number of communities and optimizing the value of modularity [
26], the results of which is used for the best grouping of users in this research. The user communities for this research also represent the information diffusion states for the process model. Moreover, the objective in this step is achieved by creating the information diffusion matrix. The information diffusion matrix represents the frequency of communication inside, outside, and among the communities. Thereby, the action traces in the posts can represent the sharing of information between user communities, which creates an information diffusion matrix to represent the information flow frequencies from one community to another. A process model is then obtained as output. The user community and the diffusion community matrix are defined as follows.
Definition 2. (User community) Letbe a finite set of users in SNS log L andfor 1 ≤ i ≤ N be a finite set of communities of users in L. A user communityis a subset of users grouped by the results of a community detection algorithm.
Definition 3. (Information diffusion matrix) Letbe user communities of SNS log L. The information diffusion matrix contains the information flow frequencies between two communities in C, which is denoted by, whererepresents the sum of the frequencies of information diffusion fromtoand, whereis the probability of being inat time 1 in every action trace.
The information diffusion process model indicates the beginning of the information diffusion and how the information spreads among the communities. The model mines the initial probability that describes the probability of which user community starts the information diffusion in each action trace. The calculation of the parameter values using A for the process model is shown in Equation (1). is obtained from the information flow frequency of the community , which follows community , divided by the total information flow frequency of all communities that follow .
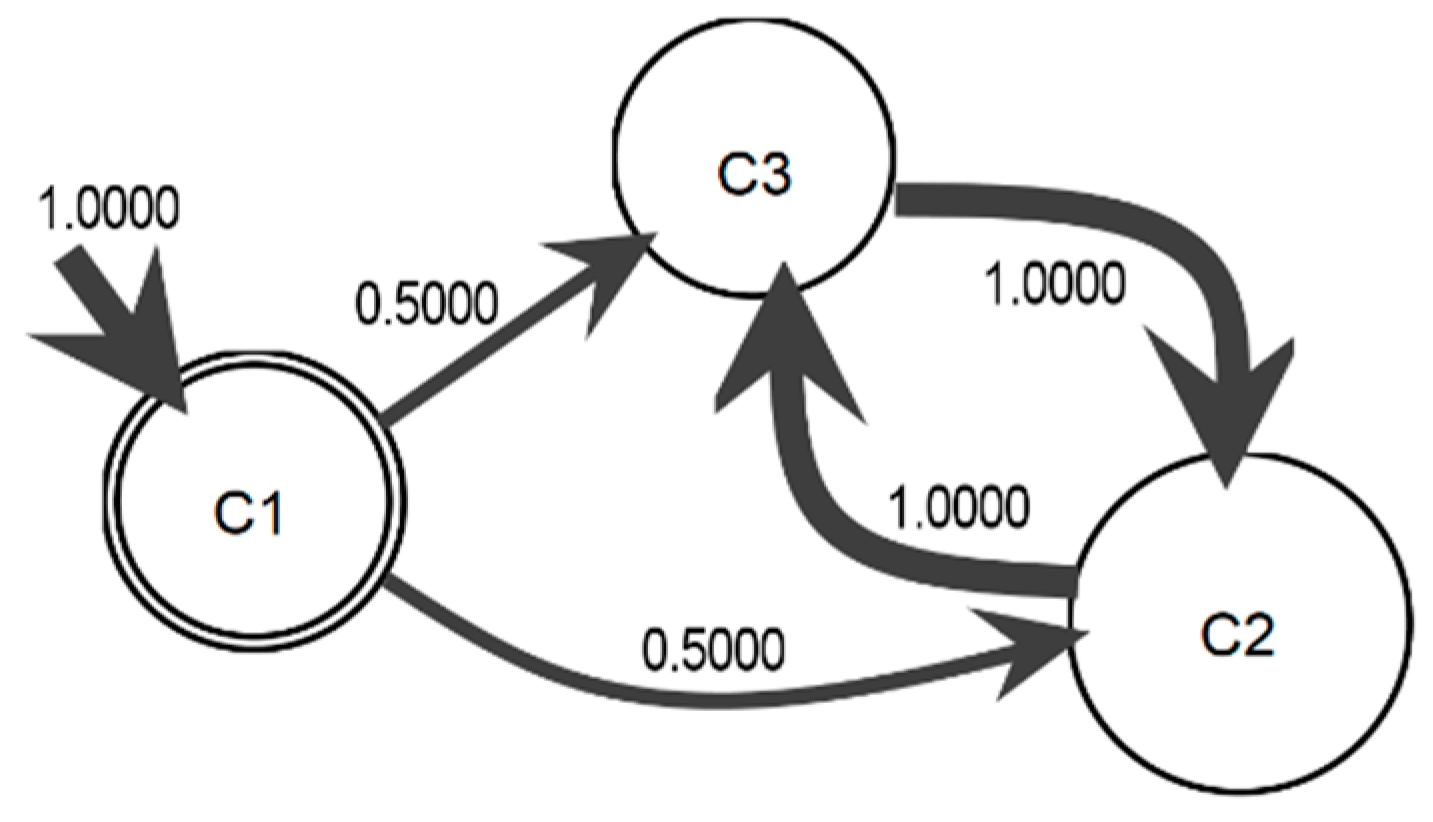
From the example introduced in
Table 1, it is seen that the communities with LM, for this example the resolution parameter value = 0.02, is used to show a better structure of the information diffusion from smaller clusters. The results of the LM algorithm are
c1 = {John, Angela},
c2 = {George, Ringo}, and
c3 = {Paul}.
Table 2 presents the first findings for the process model obtaining the matrix diffusion community
A and the probability of state transition
A′. In addition, the transition probability distribution is
π = (1, 0, 0) where
c1 always initiates the information diffusion.
The information diffusion process model can be drawn in
Figure 2. It is clear that the thickness of
c2 is greater because it has more incoming information diffusion than do the other communities. Moreover, the information diffusion between communities
c2 and
c3 is notable.
The information flow in this research is based on the detected communities as shown in
Figure 2. However, the communities may be changing over time. To obtain more reliable structure of the information flow, data in enough long period is needed for community detection.
2.3. Semantic Information Flow
The third step is the discovery of underlying topics where the meaning and sense of data are analyzed by extracting the principal keywords from comments to understand what people’s interests are and how the topics relate to them. As input, the user comments are collected, and tokenization of the words is conducted by breaking the comments into sentences and then into tokens to remove the English non-words, punctuation, and stop words. In this study, the probabilistic topic model technique called the latent Dirichlet allocation (LDA) is used to properly assign and discover the hidden context from the data. LDA can represent documents, signified by the comments of users as mixtures of topics, and then assigns the words with certain probabilities [
27]. Furthermore, in the semantic information diffusion process model, the frequent topics inside a community and the probability of those topics are analyzed.
To construct this semantic process model, analysis of the comments needs to be completed as described above. The first goal of this step is to find a small number of topics from the observations of user comments. Hence, the LDA algorithm is used to discover these topics. Thus, each topic found is assigned to each comment to finally obtain the topic matrix as a second goal. The topic matrix represents the frequency with which each user from a community publishes a comment for a specific topic. Therefore, the topic matrix can be defined.
Definition 4. (Topic matrix) Letbe information diffusion states of the information diffusion process of SNS logand, with 1 ≤ m ≤ M being a finite set of topics discovered from the LDA algorithm. The topic matrix is denoted by, where each elementcontains the sum of the frequencies in which a topicexists in the user comments of a communityin every action trace.
The calculation of the parameter values using B for the information diffusion process model is shown in Equation (2). is obtained from the frequency of community , which is paired with a topic , divided by the total frequency of all topics paired with .
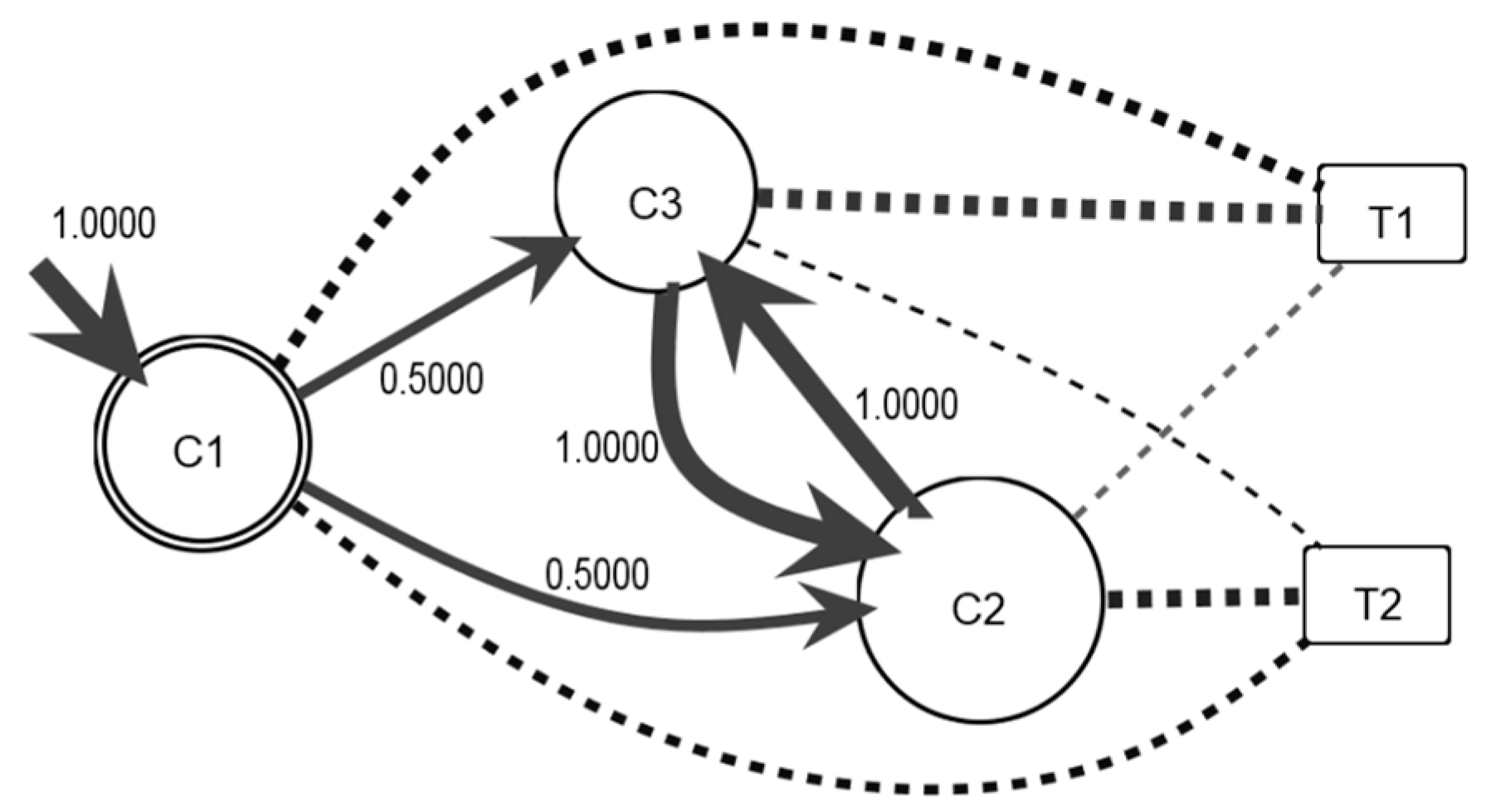
This step uses the community states, topic observations, and SNS log as inputs and generates a semantic process model as output. Moreover, a topic matrix is constructed and shows the frequency between the observed context and each community. The topics are determined from the user’s comments. To discover the topics, the LDA algorithm is used, and two topics are obtained from the comments of L1. The top eight keywords of the two topics are t1 = {need, nice, demand, happy, need demand, need persistent, ok, everything fine} and t2 = {think, wow perfect, pitiful, better, better reform, cool, everything, excellent}.
Table 3 presents the first findings for the semantic process model obtaining the topic matrix
B and the observation symbol probability matrix
B’.
Figure 3 shows the semantic information flow drawn from
B’. In the graphical representation, the dashed arcs created from the community state of the topic represent the interest of the community in the specific topic, and the thickness of the arc represents the probability between them.
2.4. Sentimental Information Flow
In this step, sentiment analysis, which is classification of the user comments based on sentiment, is performed to gain a better understanding of the user. The analysis is performed using the naïve Bayes sentiment classifier described in [
28] because this method shows good performance in many applications [
29]. In this research, the polarity of the comment is classified as a positive, neutral, or negative impression of the topics on which the users have commented.
The last output is the sentimental information flow. The model uses the previous matrices and creates a sentiment matrix that represents the probabilities of the sentiments of each community for a specific topic. The sentiment matrix is described below.
Definition 5. (Sentiment matrix) For SNS log, letbe a set of user communities in L,be a finite set of topics in L, andbe a tuple of positive, neutral, and negative sentiments discovered from naïve Bayes sentiment classifier. The sentiment matrix is a three-dimensional matrix), whereis the sum of the frequencies in which a sentimentexists in the user comments of a communityfor a topicin every action trace.
The calculation of the parameter values using D for the sentimental information flow model is shown in Equation (3). is obtained from the frequency of community and topic , that is paired with a sentiment , divided by the total frequency of all sentiments paired with and . After the construction of the diffusion community matrix, topic matrix, and sentiment matrix, the last step is the modeling of the sentimental information flow, called SentiFlow. A SentiFlow model can be defined as follows.
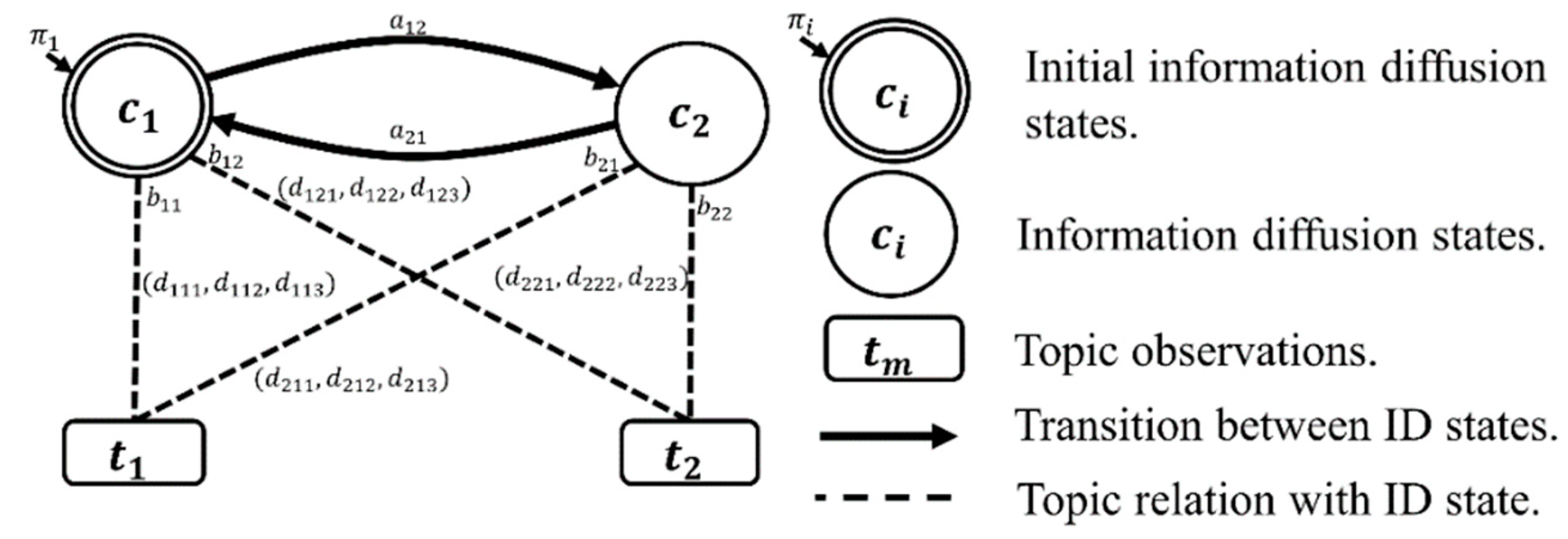
Definition 6. (SentiFlow) A SentiFlow model of SNS logis an extension of HMM for representing semantic and sentimental information diffusion. A SentiFlow model is denoted by, whereis the transition probability distribution of initial states,is a set of user communities,is a set of discovered topics,is the matrix of state transition probability distribution from information diffusion matrix,is the matrix of observation symbol probability distribution from topic matrixandis the three-dimensional matrix of sentiment probability distribution from sentiment matrix. Note thatfor,for, andfor.
for 1 ≤ i ≤ N, where is the probability of being in at time 1.
for 1 ≤ i ≤ N, where are the information diffusion states of .
for 1 ≤ m ≤ M, where are the observed topics of .
for 1 ≤ i, j ≤ N, where is the probability of state transition from to .
for 1 ≤ i ≤ N, 1 ≤ m ≤ M, where is the probability of observing in state .
for 1 ≤ i ≤ N, 1 ≤ m ≤ M, 1 ≤ r ≤ 3, where is the probability of observing a sentiment from a topic in a state .
Figure 4 provides the representational model with the notation used in this research. It should be noted that the probabilities of
B′ are shown, but simply indicate the thickness of the arc from a community to the respective topic.
The sentimental analysis step in our framework is for understanding the user opinions written in the comments and obtaining a sentiment matrix that has the frequencies from three types of sentiments (positive, negative, and neutral) from the discovered topics in the semantic annotation step. For the sentiment analysis, the naïve Bayes sentiment classifier is used to classify 12 positive, 10 negative, and 1 neutral commentaries.
Table 4 presents the findings for the sentimental annotation by obtaining a sentiment matrix
D and a sentiment probability matrix
D′.
Figure 5 presents the graphical representation of the SentiFlow model constructed from log
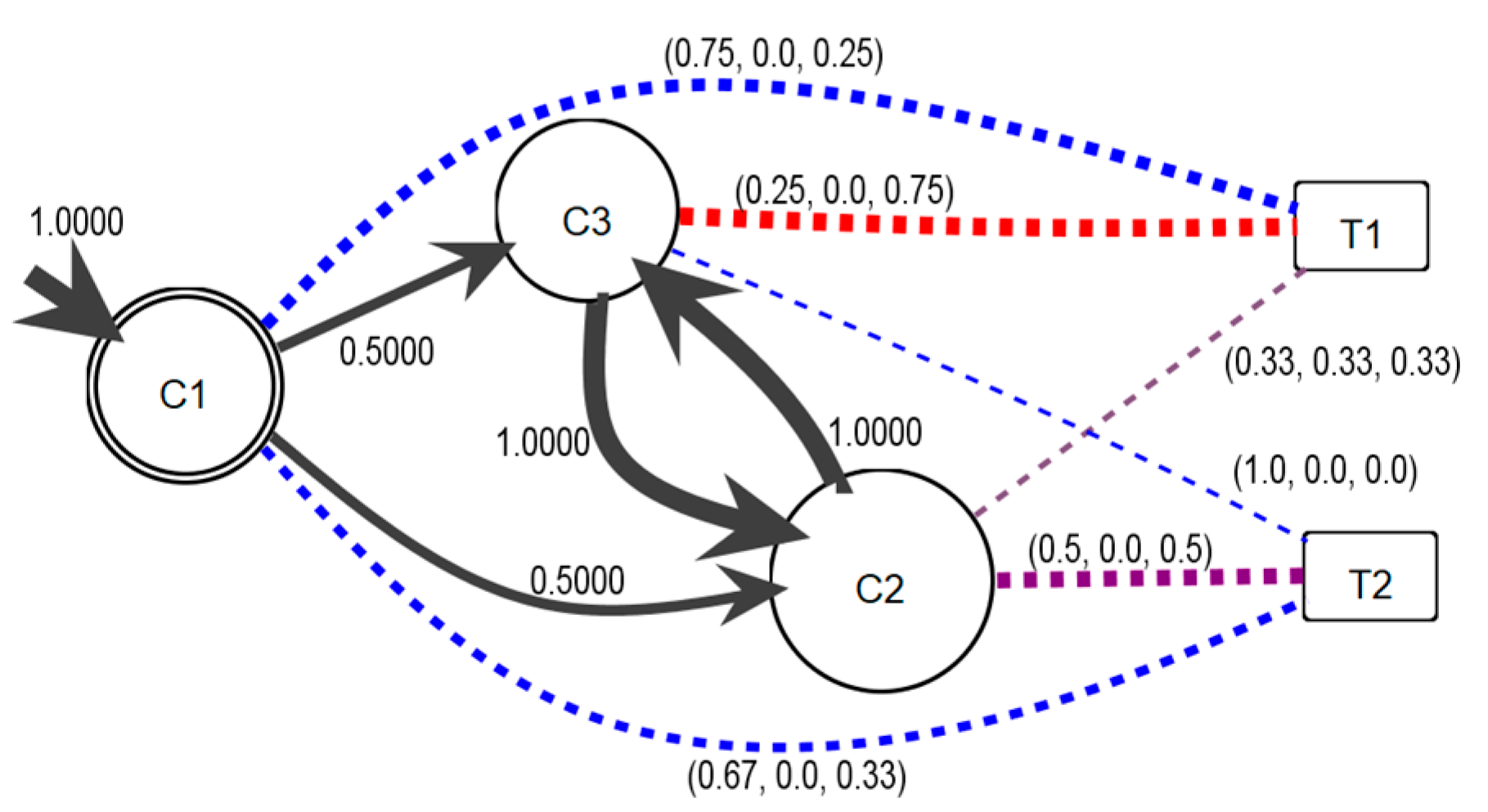
L1. The difference of color between the communities and topics is shown. For example,
c1 to
t1 shows a bluish color representing predominant positive commentaries (0.75) compared to negative commentaries (0.25). However,
c3 to
t1 presents predominantly negative commentaries for
t1 (0.75), with 0.25 positive commentaries. Additionally, community
c2 to topic
t2 has a mixture of sentiments in the comments, with 0.5 for both. The mapping color of the arc from a community to a topic represents the type of sentiment; the arc is red if the sentiment is negative, lime if neutral, and blue if positive.
A SentiFlow model provides the required information to answer the two questions presented at the end of
Section 1. The first question is about the topics that promote communication between communities. In this example, the communication between communities
c2 and
c3 was about topics
t1 and
t2, although
c2 mainly focused on
t2 and
c3 mainly focused on
t1. The second question is about how the sentiment is shared in the information diffusion process from a probabilistic perspective. As an example, the information diffusion from communities
c1 to
c2 for topic
t2 is used. Considering the sequence, <positive, positive>, the result can be analyzed using the forward algorithm [
22], and the probability of the sequence is
P (<positive, positive>|
Λ) = 1.0 × 0.67 × 0.5 × 0.5 = 0.1675. In the case of the sequence <neutral, neutral>, the probability is 0, and the sequence <negative, negative> is
P(<negative, negative>|
Λ) = 1.0 × 0.33 × 0.5 × 0.5 = 0.0825. Therefore, the probability that community
c2 responds positively to a positive comment of community
c1 is higher because community
c1 has a higher probability of posting a positive comment.
3. Algorithm
In this section, the overall procedure that was introduced in the proposed framework is described as an algorithm. The SentiFlow algorithm creates the structure Λ(L) = (π, C, T, A′, B′, D′) from an SNS log L = [σ] similar to an HMM structure λ(L) = (π, States, Observations, A′, B′), as shown in Algorithm 1. In the algorithm, LM is adopted for community algorithm detection, and it starts with the clustering of users U in the log (Lines 2–3). Next, for all traces in the log, the algorithm discovers from the user comments, first, the topics T as a result of the LDA algorithm and, second, the classification of the sentiments S from the naïve Bayes sentiment classifier for each user comment (Lines 4–6). Then, for each trace in the log, the algorithm finds initial communities , diffusion community matrix , topic matrix and sentiment matrix dimr (Lines 8–25). In particular, if two adjacent users belong to the same community, the algorithm skips the count in the diffusion community matrix, and the last SNS event is counted for its topic and sentiment. Afterwards, the state transition probability matrix A′, the observation symbol probability B’, and the opinion probability matrix D’ are calculated from A, B, and D using ML. Finally, the algorithm returns a SentiFlow model, Λ(L) = (π, C, T, A′, B′, D′).
| Algorithm 1. SentiFlow |
| 1: | Input: SNS log L = [σ], which is a multi-set of action traces σ in the SNS. |
| 2: | Output: A SentiFlow model, |
| 3: | Insert all users in L into a user set U. |
| 4: | Detect communities C from users U, and prepare function . |
| 5: | For each trace in L Do
Discover topics T from user comment, and prepare a function |
| 6: | . |
| 7: | Discover sentiments S, and prepare a function . |
| 8: | End For |
| 9: | For each trace in L Do |
| 10: | If e1 Then |
| 11: | Increase in . |
| 12: | End If |
| 13: | For each adjacent SNS event (eh, eh+1) in σ for 1 ≤ h ≤ H − 1 Do |
| 14: | ci = community(#u(eh)) and cj = community(#u(eh+1)). |
| 15: | tm = lda(#user_comment(eh)) and sr = nbsc(#user_comment(eh)). |
| 16: | If ci ≠ cj Then |
| 17: | Increase aij in A by 1. |
| 18: | End If |
| 19: | Increase bim in B by 1. |
| 20: | Increase dimr in D by 1. |
| 21: | If eh+2 = null Then |
| 22: | Increase bjm in B by m and tm = lda(#user_comment(eh+1)). |
| 23: | Increase djmr in D by m,r and sr = nbsc(#user_comment(eh+1)). |
| 24: | End If |
| 25: | End For |
| 26: | End For |
| 27: | Calculate the state transition probability matrix A′ = (a′ij) based on A = (aij). |
| 28: | Calculate the observation symbol probability matrix B′ = () based on topic matrix B = (). |
| 29: | Calculate the sentiment probability matrix D′ = () based on the sentiment matrix D = (). |
| 30: | Return a SentiFlow model, |
4. Experiments
In this research, the SentiFlow algorithm was implemented as a plug-in of the ProM platform to verify the proposed framework. ProM is the open source platform that provides practical applications for process mining and supports many kinds of process discovery algorithms [
23].
To illustrate the proposed algorithm, the posts of the CNN Facebook page from 1–5 April 2017 were used. The data contain 208 posts with a total of 67,831 users participating with 143,876 comments from 1 April to 6 June 2017.
To obtain information flow among communities, the community detection was analyzed by applying the LM algorithm. Then, the data were filtered to reduce the noise generated by the infrequent users; as a result, six communities were detected using a resolution parameter of 0.8 [
26]. The six detected communities,
c1 to
c6, contain 203, 1048, 13, 9, 25, and 121 users, respectively, among a total of 1419 users.
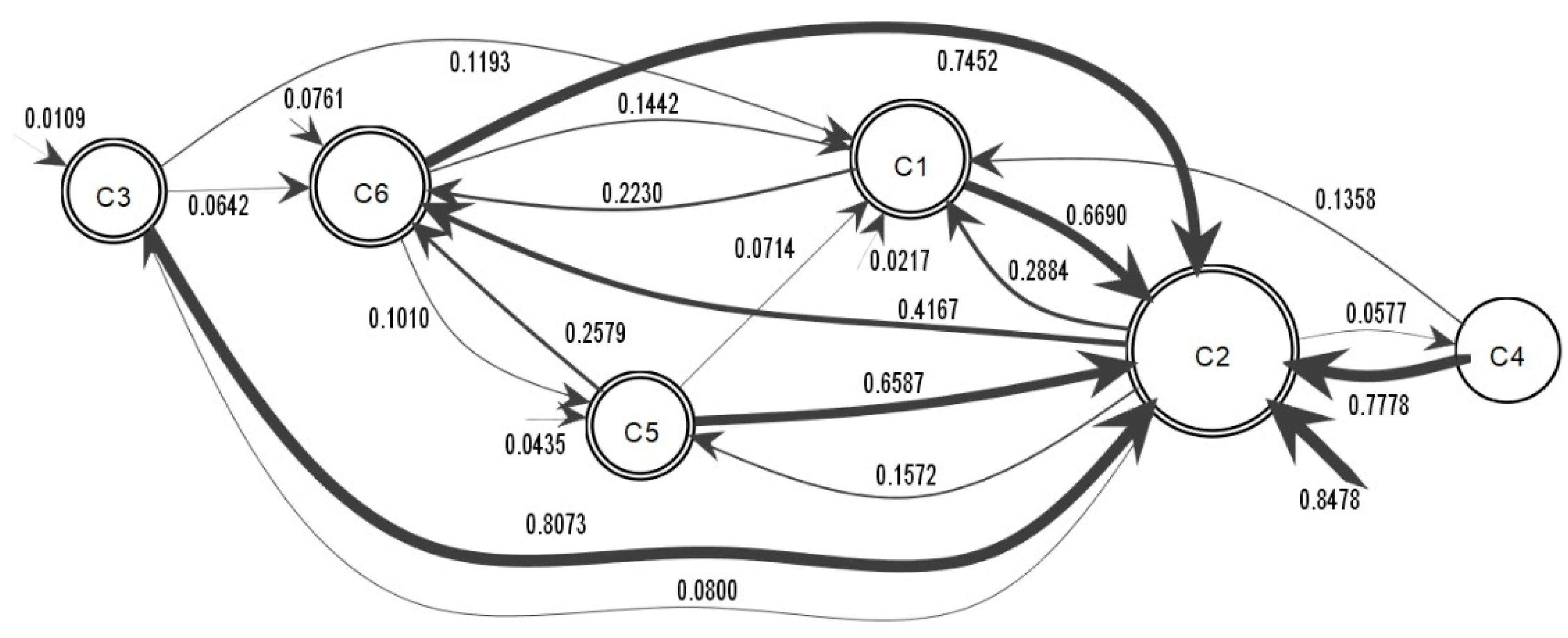
The result of the information diffusion process discovery based on detected communities is shown in
Figure 6; the number of comments in a community is represented by the size of the corresponding node in the figure, and the thickness of an arrow denotes the probability of information diffusion from one community to another. Community
c2 concentrates most of the information flows from
c1,
c3,
c4,
c5, and
c6, revealing a larger size from the higher incoming information flow from smaller communities and the number of user comments. Moreover, the information flow received from
c3 to
c2 shows the highest information diffusion probability among all communities. The threshold of information diffusion probability used for the process model visualization in
Figure 6 is 0.04. The threshold is used to present a readable process model removing the arcs with lower probability.
The topic annotation step started with analysis of the comments. First, the stop words, English non-words, and punctuation were removed. Second, duplicate and empty comments were removed. As a result, 13,706 comments and 92 posts were evaluated. To find the different topics of the comments, each word was tokenized as an input for the LDA algorithm.
Figure 7 presents a cloud word visualization of the token results for user comments.
Table 5 presents the five topics discovered from the LDA algorithm with their top eight keywords from the discovered comment topics. As shown, topics
t2 and
t3 share two keywords. The word “Trump” is repeated in
t1,
t2,
t3, and
t4 with notable importance in a mixture of topics, but relays in categorize individually each topic.
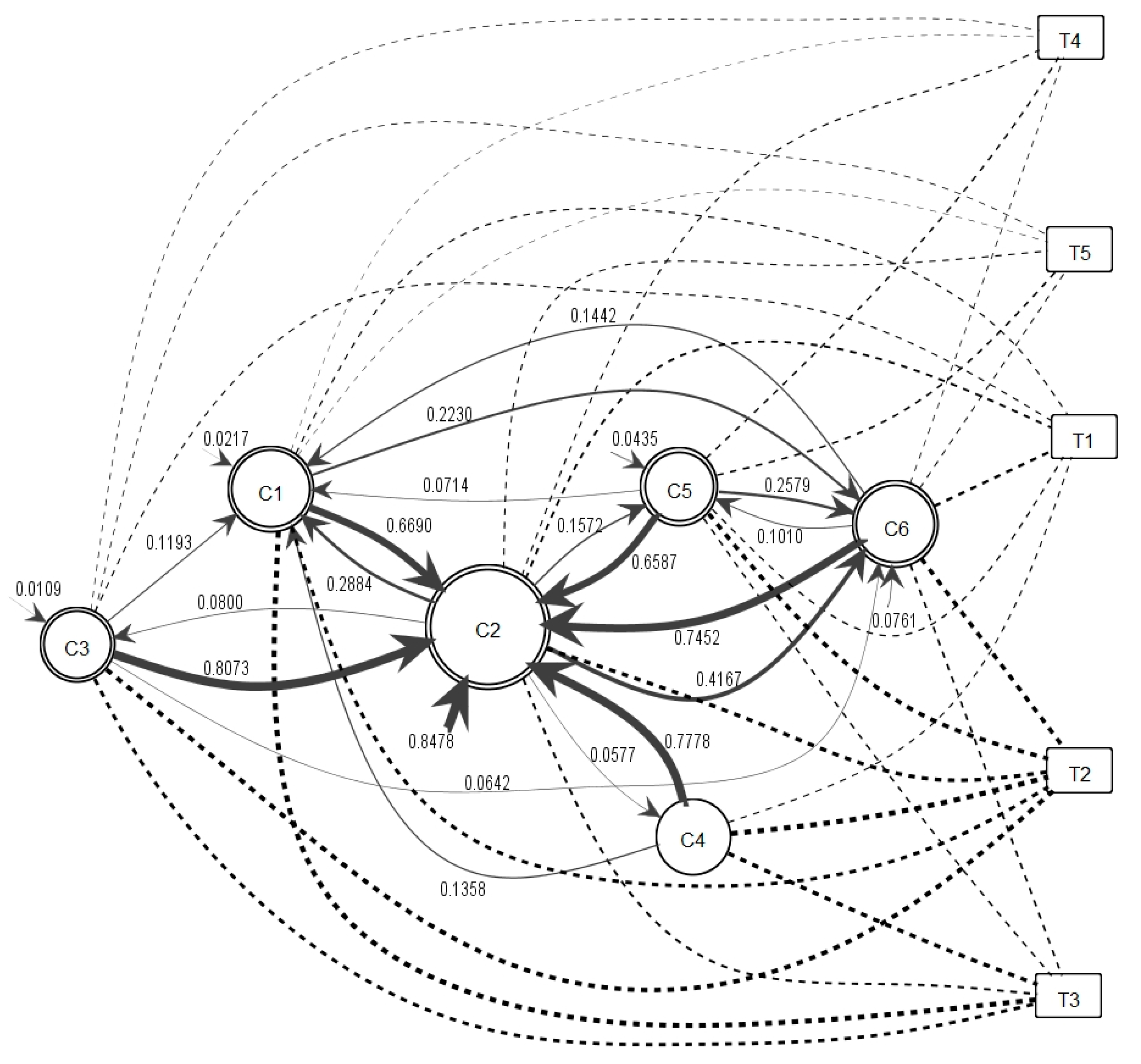
Figure 8 describes illustrates the semantic information flow between user communities. Here, the discovered topics from the LDA algorithm are shown as rectangles along with their identification name. The dashed arcs indicate the use of the topics from the communities. The topic
t2 has greater importance because it has many thicker arcs connecting communities than do other topics. Communities
c1,
c3, and
c4 present frequent use of keywords for topics
t2 and
t3. As in the previous step, the threshold used to present the information flow is 0.04.
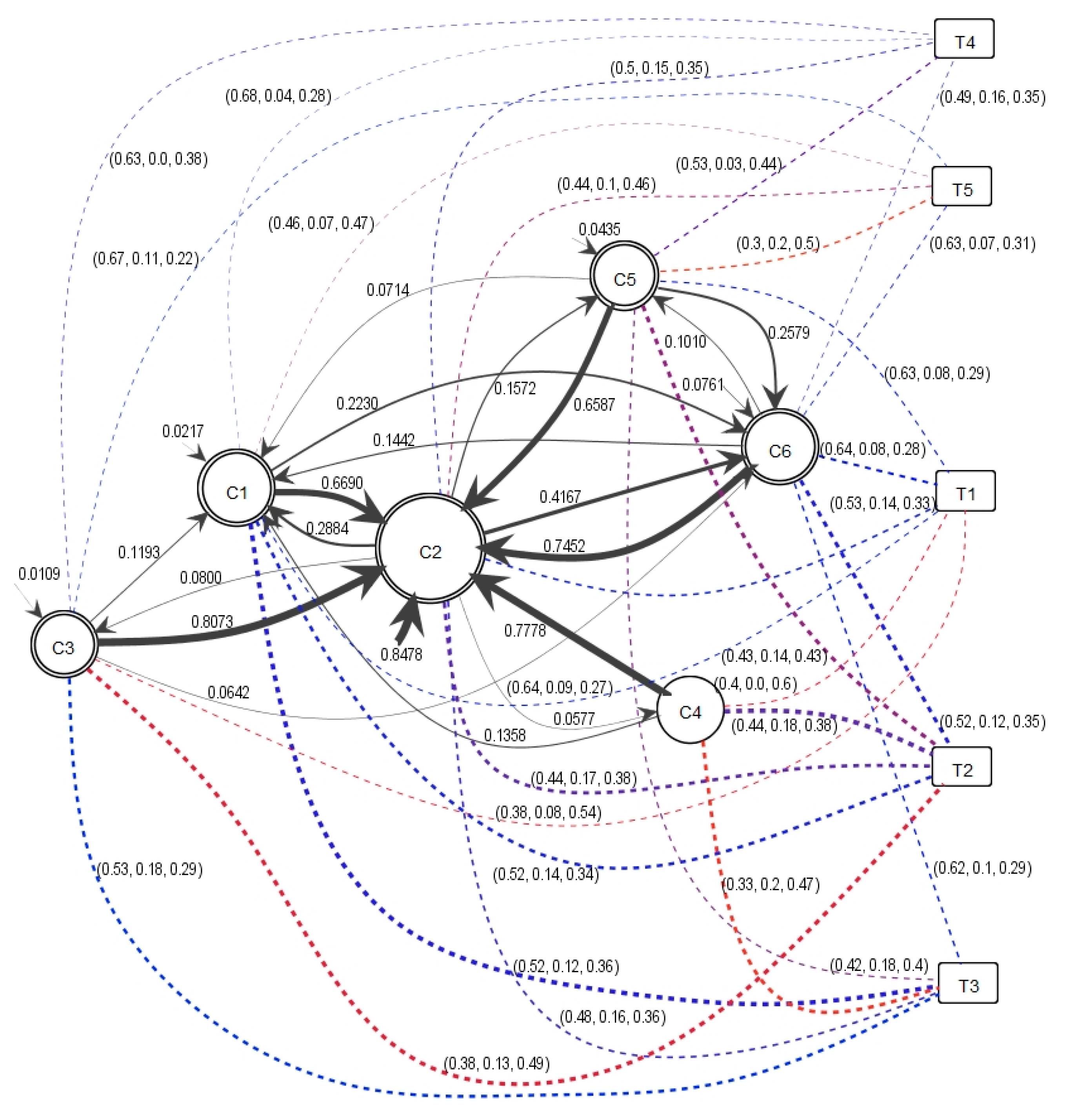
The last step is the generation of the sentimental information flow shown in
Figure 9. The model describes the probability of opinions by drawing the arc to a positive community in blue, neutral in green, and negative in red. In more detail, a label with three probabilities of positive, neutral, and negative comments is added on the corresponding arc in order. An example of a negative opinion is shown by a reddish dashed arc representing
c3 over
t2. Conversely, a positive probability opinion can be observed from
c3 toward
t3 with a bluish color. The figure shows that
c5 toward
t2 shows a mixture of opinions and has relative balance between positive and negative opinions. In general, neutral opinions show a lower probability than positive and negative opinions.
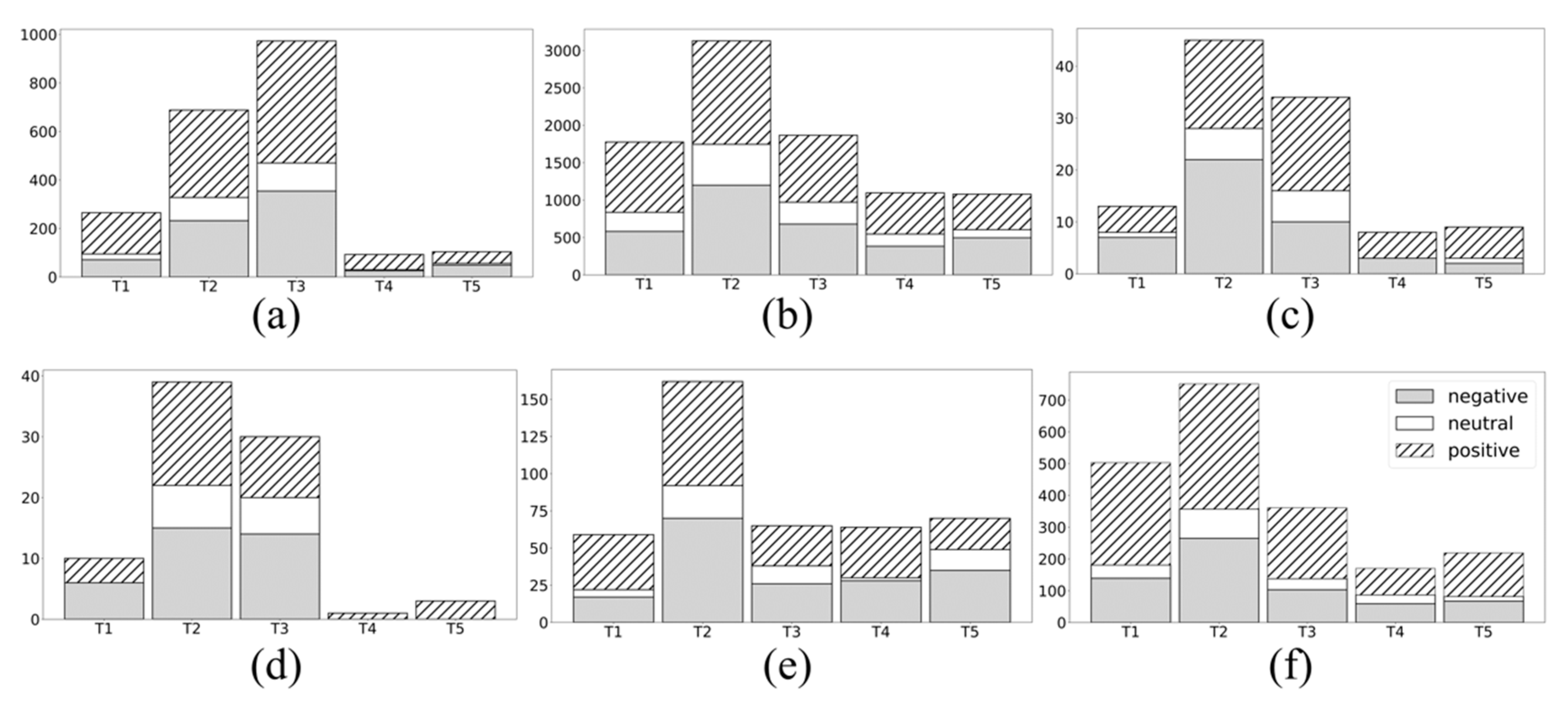
Figure 10 illustrates the relationship between the five discovered topics and the opinions with a total of 6820 positive, 4957 negative, and 1910 neutral comments, separated into the six communities. There are two trend topics,
t2 and
t3, followed by
t1 and
t4 and finally
t5 as the least discussed. In addition, community
c5 has a similar amount of interest between topics
t1,
t3,
t4, and
t5. Furthermore, topic
t2 is the most commented upon among all the communities with the exception of community
c1, which focuses on topic
t3.
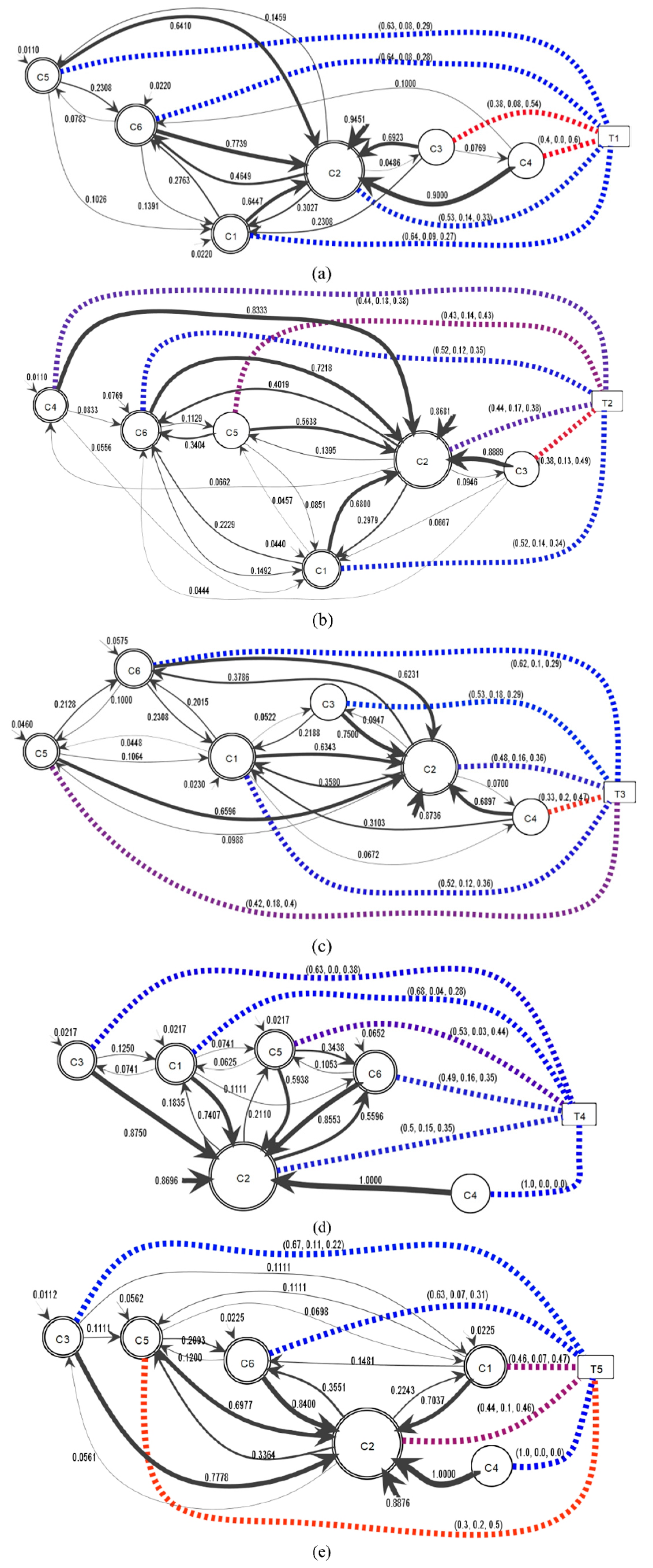
The individual information flows for each topic are shown in
Figure 11 using the threshold of 0.04. In the different information flows, community
c2 is continuously the largest community and concentrates most of the information flows from
c1,
c3,
c4,
c5, and
c6 from the different topics.
Figure 11a shows a SentiFlow model from topic
t1 with a different flow from
Figure 9, where community
c3 does not provide an initial probability and indicates an information diffusion to
c4 with probability 0.0769. Additionally,
c3 and
c4 have a predominant negative opinion in contrast to
c1,
c2,
c5, and
c6 with a positive opinion. In
Figure 11b, the initial information diffusion
changed for community
c4 not presented in other SentiFlow models with probability of 0.0110. In addition,
c4,
c5, and
c2 have a purple color to note they have an opinion divided between negative and positive. However,
c6 shows a greater positive opinion, whereas
c3 presents a greater negative opinion. In
Figure 10a, community
c1 has the most comments for topic
t3, but, in
Figure 11c,
c1 is smaller than
c2 because there are more user comments than in
c1. Positive opinions are expressed in
c1,
c2,
c3, and
c6, whereas while negative opinions are expressed in
c4, and mixed opinions are expressed by users from
c5. In
Figure 11d,e, good information flow is observed between all communities with the exception of
c4. In this case, the community does not show an incoming information flow because the probabilities are below 0.04. For
Figure 11d, a general predominant positive opinion can be seen for almost all communities, even though
c5 has a combination of positive and negative opinions. In the sentiment information diffusion for topic
t5,
c3,
c4, and
c6, have a positive opinion, in contrast to
c5 with negative comments and
c1 and
c2 with a balanced opinion between positive and negative, as shown in
Figure 11e.
Figure 11 shows how the topics promote communication between the communities. This answers the first question in this study. For example,
Figure 11c presents a description of the information diffusion for topic
t3, with the communication between community
c4 and community
c1 with a probability of 0.3103 and with a response communication probability of 0.0672, which is not observed in the other information diffusion flows. As a response for the second question about how the sentiments are shared from a probabilistic view, the example of information diffusion from community
c2 to community
c4 for topic
t1 shown in
Figure 11a is analyzed. Taking the sequence of communities <
c2,
c3,
c4> and the sequence of sentiments <positive, positive, positive>, the probability of the sequence is
P (<positive, positive, positive>|
Λ) = 0.9451 × 0.53 × 0.0486 × 0.38 × 0.0769 × 0.4 = 2.8455 × 10
−4. Moreover, if the communication from community
c2 to community
c6 and the sequence of sentiments <positive, positive> are analyzed, the probability is
P (<positive, positive>|
Λ) = 0.9451 × 0.53 × 0.4649 × 0.64 = 0.1490 because the only way that
c2 can communicate with
c4 is through
c3, decreasing the probability of the positive sentiment, instead of from
c2 to
c6, where the information diffusion does not need an intermediary community.
5. Conclusions
In this work, an information diffusion process discovery method for SNS was proposed to understand information flow among users better. A SentiFlow model is developed by extending the HMM technique to include process mining by adapting the information from SNS. To understand how the context of user groups is connected with the information flow, different techniques such as an LM for community detection, LDA for natural language preprocessing, and the naïve Bayes classifier for sentiment analysis were used. The proposed method suggested the use of these algorithms, but, in the future, new algorithms can easily be adapted for more accurate and helpful analysis.
The proposed framework has the advantage of allowing users to understand the information flows by displaying the different paths and possible sequences of information delivery obtained from the different users’ comments with corresponding probabilities. Analysis of the community of users who plays significant roles in the discovered process shows their sentiment for a related topic.
Three types of information flow diagrams provide the following information. The community information flow describes how the user communities spread their ideas among each other. Moreover, the semantic information flow shown demonstrates how the topics are related with the communities, distinguishing the importance of the topics in each community. Finally, the sentimental information flow presents the potential information to find the focus groups with positive, neutral, or negative opinions and how they influence other user groups according to topic. Additionally, different information diffusion models can be separated and analyzed for each topic.
However, this research still has some limitations. This research focused on understanding the information flow inside a single SNS page, although it can be extended to analyze multiple sites or the whole SNS service. The user profiles of gender, age, and region were not considered in this research, although they may be useful to understand the interactions among users in more detail. In addition, a broader range of human emotions such as anger, joy, and sadness could be used to study the effects of emotions on public opinion. Another limitation is that this research is based on community detection, but the communities may not be stable over time. The study of the reliable community detection can be conducted. In addition, this study focused on the architecture of information diffusion with topic and sentiment, while the analysis methods such as information diffusion process discovery and topic and sentiment analysis were not evaluated. To show the reliability of the analysis result, the detailed methods may be able to be evaluated with evaluation measures such as precision, recall, and F-score.
In future work, a hierarchical model of information flow can be induced to provide different views according to level of abstraction. An integrated approach to capture major interactions among user can be developed without separating the community detection stage and the information flow mining step since the two steps are closely dependent with each other. The dynamics of information flow can also be analyzed to detect the changes of information diffusion in SNS over time.