5.1. Regression Results
To apply spatial econometrics models with statistical validity, a spatial autocorrelation test should be carried out beforehand. We chose to use Moran’s I statistic for our spatial data [
64]. The results of Moran’s I indicated that there is spatial dependency in our data at a 99% or higher level, as shown in
Table 3. Based on the results of the Moran’s I analysis, regression analyses for the three spatial econometric models explained in Equations (1)–(3) were conducted, the results of which are presented in
Appendix B.
Table A5 and
Table A6 in
Appendix B list the results of the regression analysis of the three econometrics models for the policy implemented areas and the non-implemented areas, respectively. The results show that both the hypothesis of no spatially lagged dependent variable and the hypothesis of no spatially autocorrelated error term should be rejected at the highest significance level at
p < 0.01. The results of a spatially lagged dependent variable and a spatially autocorrelated disturbance prove to be statistically significant effects in all three econometrics models for both areas. SAR and SEM show statistically significant effects for the spatially lagged dependent variable (
rho) and the spatially autocorrelated disturbance (
lambda) and both spatial dependency variables are statistically significant in the SAC model. The explanatory power is slightly higher in the models of the policy implemented area (55–66%) than those of the non-implemented area (36–46%). Among the three spatial econometrics models, SAC displays the highest explanatory power (
2 = adjusted
R2) (cf.
Appendix B). Therefore, we decide to use the SAC model in the application of the decomposition method for evaluating the CRVDP.
Table 4 presents the estimation results of the SAC model for both areas. The explanatory powers of two areas represented by the adjusted R-squares are 0.46 for the implemented-areas and 0.66 for the non-implemented areas. Considering the cross-sectional characteristics of our data with eight degrees of freedom, the explanatory power of both areas is acceptable for the investigation of individual parameters. The application of the SAC model reveals some interesting results with regard to the determinants of the standard of living in an area, not all of which were expected a priori.
If other factors are held constant, the proportion of population (POP) was found to be positively associated with the standard of living in 1995 (p < 0.01) for both areas. The elasticity of living standard in an area with respect to population is 0.11–0.12, implying that a 1% increase in population is expected to increase the average living standard in an area by 0.11–0.12%. This suggests that rural areas that are more susceptible to urbanization encroachment may offer a better living environment. As expected, the presence of a large elderly population (OLD) in a given rural area is negatively correlated with the level of living standards in both areas. A 1% increase in the number of elderly results in a 0.3% decrease in living standard in the policy non-implemented areas at p < 0.1. However, the effect is much weaker (0.02%) for the policy implemented area with no statistical significance. We suspect that, during the past few decades, aging structure has changed dramatically due to out-migration of younger age groups in the policy implemented areas. This results in the prevailing abundance of elderly people in the policy implemented area. Proportion of farmers (FARM) markedly differs between the two areas. The independent variable is negatively associated with the living standard in the policy implemented area, although this relationship is not significantly different from zero. The reverse is true for the policy non-implemented area, with the highest significance level at p < 0.01. This implies that individual farmers’ contributions to enhancing living standard in an area is much greater in the policy non-implemented area than in the policy implemented area.
Agricultural sales (AGSALE), which represent agricultural productivity in rural area, are positively associated with living standard in the policy non-implemented area, but this effect is not significant in the policy implemented area. Rate of return of agricultural sales to the living standard is twice as large in the implemented area (4.1%) than in the non-implemented area (2.1%). This implies that agriculture is a major economic driver in most rural areas, although agricultural activity is not an enduring emblem for the poorer rural areas in Korea. As expected, the larger is the proportion of farmland (AGLAND) in rural areas, the better is the living standard of the area. This may suggest that agricultural land is functioning as an economic asset in both areas and the elasticity value suggests that a 1% increase in the farmland will enhance the living standard of an area by 0.24% for the policy implemented area and 0.17% for the non-implemented area.
The rate of return by crop to our dependent variable, standard of living in an area, showed the expected effects. The greater the cultivation of such crops as vegetables or upland crops (TYPE1) and fruit, special crops or flower (TYPE 2), the bigger the rate of return for the crops. A 1% increase with respect to the vegetables and upland crops results in a 0.05% increase of the living standard in the policy non-implemented area. The rate of return for the crop in the policy implemented area is slightly higher (0.07%) than in the non-implemented area. The estimates for both independent variables are statistically significant for the policy non-implemented area at p < 0.05 or higher. However, the effect is significantly different from zero for only the vegetables and upland crops in the policy implemented area at a marginal level, p < 0.10.
While some independent variables show similar patterns with respect to our dependent variable, other variables display significant differences between the two areas. To identify differences in the effects of each independent variable on the living standard between areas, we carried out the Wald test, assuming no covariance between the independent variables as shown below:
We identified two independent variables (proportion of elderly people and proportion of farmers) that were significantly different between the two areas. The effect of an aging population on living standard in the policy implemented area was negative and statistically significant, whereas no significant difference was detected in the non-implemented area. As mentioned previously, farmers’ contribution to enhancing living standards in an area was much higher in the policy non-implemented area than in the policy implemented area; that is, the relative availability of human capital was also a determining factor for the difference in living standards between the two areas. This finding is consistent with those reported by Agarwal et al. [
55], who detected a strong relationship between economic performance and human capital in rural areas. We suspect that it was the impacts of these two independent variables that influenced the differential living standards between the two areas.
As mentioned before, the direct effect measures how a change in an independent variable in rural area
i affects the dependent variable in the area, including feedback effects. The feedback effects occur as a result of impacts rippling through neighboring rural areas and then returning back to the original area. Indirect effects—also called spillover effects—compute the average impact of a change in an independent variable in area
i on the dependent variable in all other different locations
j. Direct effects are used to test whether a particular variable has a significant effect on the dependent variable within its own geographic area, while indirect effects are used to test whether spillovers into neighboring areas occur [
65].
Table 5 presents the results of the direct and indirect effects of independent variables on living standards in rural areas in Korea.
We found that the direct effect estimates have the same signs and similar magnitudes as the point estimates of the independent variables in both areas, as shown in
Table 4. Moreover, significance levels for individual parameters in both areas parallel those presented in
Table 4, so explanations regarding the independent variables here would be redundant. The feedback effects of the independent variables on living standards in rural areas show a wide range of impacts and are not negligible. For example, the direct effect and the coefficient estimate of the population in the policy implemented area were 0.1409 and 0.1116, respectively, thus the feedback effect is approximately 21%. Other feedback effects range 20–50% in policy implemented areas and 0–17% in the non-implemented areas.
We found that the magnitude of the indirect effects is much larger than their associated direct effects. This may seem counterintuitive, as spillover effects would seem more similar to second-order effects that should be smaller in magnitude than would direct effects. Because the scalar summary measures of the indirect effects provided by [
66] combine spatial spillovers in all other areas to produce a single numerical value for the indirect effect estimate, this is not unusual in diverse empirical applications (cf. [
26]) particularly if spatial observations are large, as in the present study (1098 + 290 − 1 = 1387).
5.2. Decomposition Results
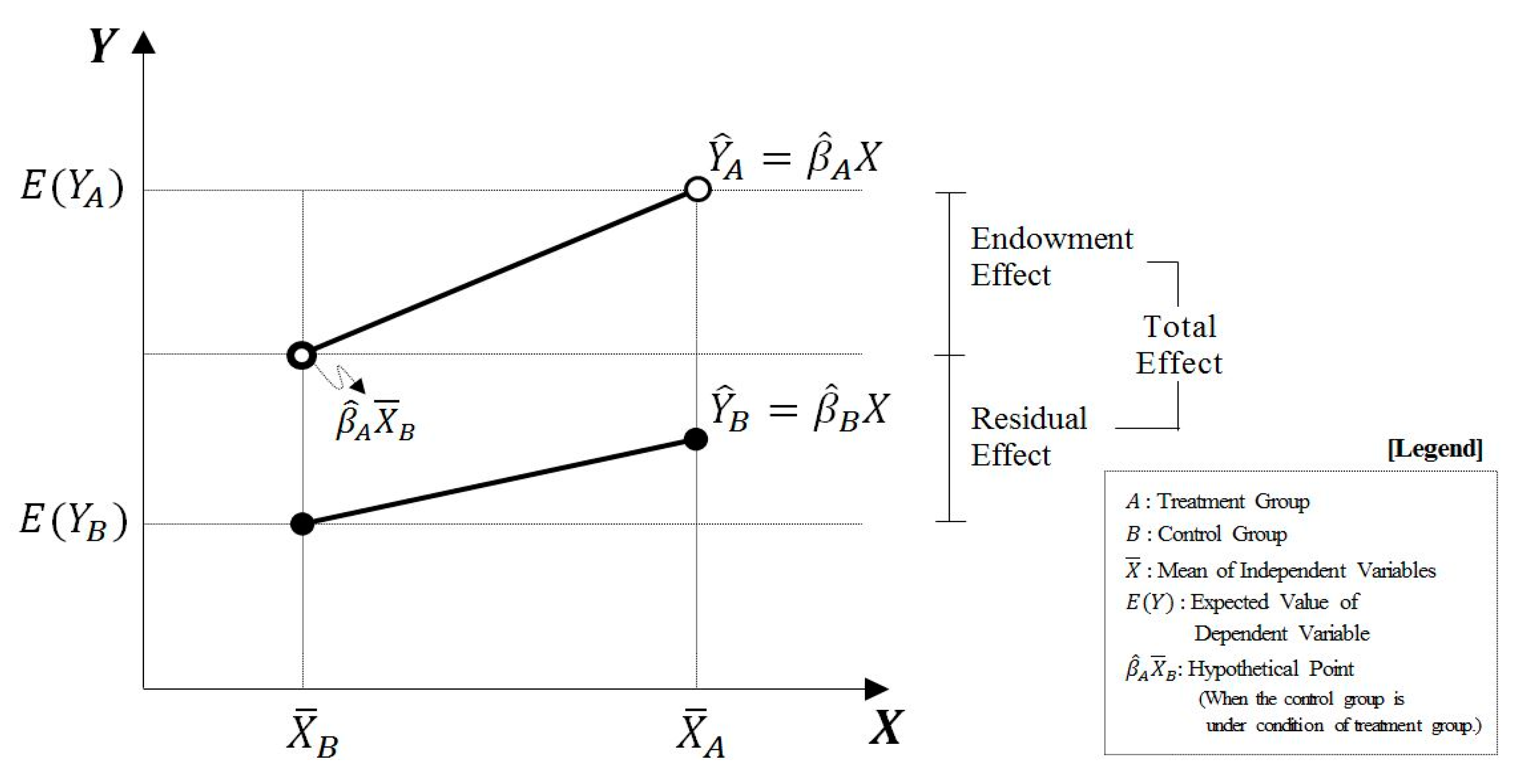
To determine the quantitative implications of the above estimates, the regression results must be simulated to calculate the mean differences of policy implemented and non-implemented areas of the CRVDP, while controlling for spatial characteristics of other independent variables. What is the net effect of mean differences of the policy on the program implemented areas compared with non-implemented areas? What areas where the program had not implemented before would be affected if this program had been enforced? To address these sequential questions, a treatment group should be composed of the areas where the program had been implemented, and a control group should be composed of the areas where the program had not implemented.
We utilize the regression results in
Table 4 to conduct a decomposition method applying Equations (10) and (11), with results presented in
Table 6. The results show that the difference between the two areas (0.6320) is composed of the negative endowment effect (−0.0264) and the positive residual effect (0.6584). This implies that the net policy impact calculated after ruling out the endowment effect (which can be explained by the difference of independent variables between the two areas) is 1.04 times as high as the observed impact. That is, the contribution of controlled independent variables in making a better living environment is negative (−4.19%). However, largely due to the uncontrolled policy effect in the residual effect, we can say that the standard of living of the policy impacted areas was enhanced following program implementation; in other words, while the changes in demographics, spatial and agricultural factors in the policy impacted areas are less favorable in producing a better living environment, diverse government policies (such as the CRVDP) intended to enhance living conditions in rural areas have offset the negative changes in the countryside.
The decomposition of residual effects also confirms that the CRVDP has been effective. A constant effect of 0.7987 (126.38%), an average effect contributing to living standards in an area, offset the negative coefficient effect of −0.1403 (−22.19%) to reach the positive residual effect, which implies that the impact of the policy can also be detected indirectly. These positive findings are much clearer when we look more deeply into the composition of individual coefficient effects decomposed from the net effect (refer to
Table A7 in
Appendix C). In explaining the total endowment effect (−0.0264), demographic variables contributed approximately 92% of total variation, approximately 12.5 times higher explanatory power than that of spatial/agricultural variables. Proportions of population and farmers in an area contributed approximately 89% of total variation of the endowment effect, implying that the major depreciation of the policy implemented area can be explained by these two variables. However, the explanatory power of the spatial/agricultural variables that the CRVDP mainly targets for improvement is approximately 10 times higher (−19.42%) than that of demographic variables (−1.88%). Therefore, the CRVDP can be said to have moderately helped to enhance living conditions in the policy implemented rural areas.