1. Introduction
In order to satisfy the power demands that have been increasing since 2002, the Korean government establishes 15-year Generation System Expansion Plans biannually, of which there are seven to date. These plans are based on the National Energy Master Plan, which is the governing document for the Basic Plan for Electricity Demand and Supply. As its name indicates, the Generation System Expansion Plan minimizes the aspects of the operation of the power generation system, focusing more on the expansion plan for the generation system.
In establishing the Basic Plan for Electricity Demand and Supply, which contains construction plans for power generators, the dynamic optimal energy mix planning model WASP (Wein Automatic System Planning) is used, but it only utilizes reliability criteria determined by the reserve rate, which causes it to provide only the most limited index to secure a stable power supply. However, as the Basic Plan for Electricity Demand and Supply is completed after consideration of a comprehensive set of data regarding the intent to construct and further modification measures are taken, the results of the energy mix calculated by the basic plan is adequate. If such background conditions are ignored and only WASP is used to calculate the energy mix, the model will produce high ratios of nuclear power, which has an absolute superiority over other power sources in terms of cost, making it difficult to find a truly adequate energy mix enabling a stable power supply.
As such, the current paper seeks to find a method for calculating the optimal energy mix that minimizes the total cost (including fixed cost determined by whether power generators are constructed, fuel costs related to power output, and environmental cost) while making it possible to operate a stable power generation system responsive to changes to load. In order to achieve this end, this paper formalizes the question of optimal energy mix and selects an optimization tool that can linearize the non-linear characteristics of the question to suggest the results of the analysis. Therefore, this study presents the algorithm of the process from the methodology for analyzing the demand data of the future to the establishment of the generation system expansion and the operation planning of the power generation facility, and the composition of an integrated model for deriving an optimal solution. The following are important elements to be presented through this study.
- (1)
Establishment of a methodology for power generation extension at the planning level
- (2)
Development of a model for calculating the realized operation and maintenance costs including the operating conditions of power utilities.
- (3)
Development of an integrated model for connecting planning and operation levels
- (4)
Estimation of the verification of the proposed model based on the domestic electricity demand supply program
This research focuses on model development for the extension of power plans in the domestic electricity supply and demand program. The electricity that is the object of this research has a particular characteristic in that all kinds of power plants generate identical goods, with the same quality but in different ways.
The product costs per utilities are different and the price predominance among those is determined in advance. Electricity is a volatile product that has no conception of stock and becomes extinct just after generation. If supply is lacking, it can cause a national crisis, thus it is necessary to retain a margin of power, even though it is not efficient. The criteria for the extension of power utilities include not just average demand but peak demand, in order to prevent the worst outcome.
To establish the extension planning of a generation system, the next issue of concern is to have a margin of power. This research designs the model with two types of reserved margin, such as a utility reserved margin and an instant reserved margin. The utility reserved margin is to prevent an uncertain situation by retaining a utility capacity that is greater than the expected demand of the peak times of year based on the concept of safe stock. The instant margin is additional reserved electricity that enables a stable supply at the operational level, even if the demand of electricity increases suddenly.
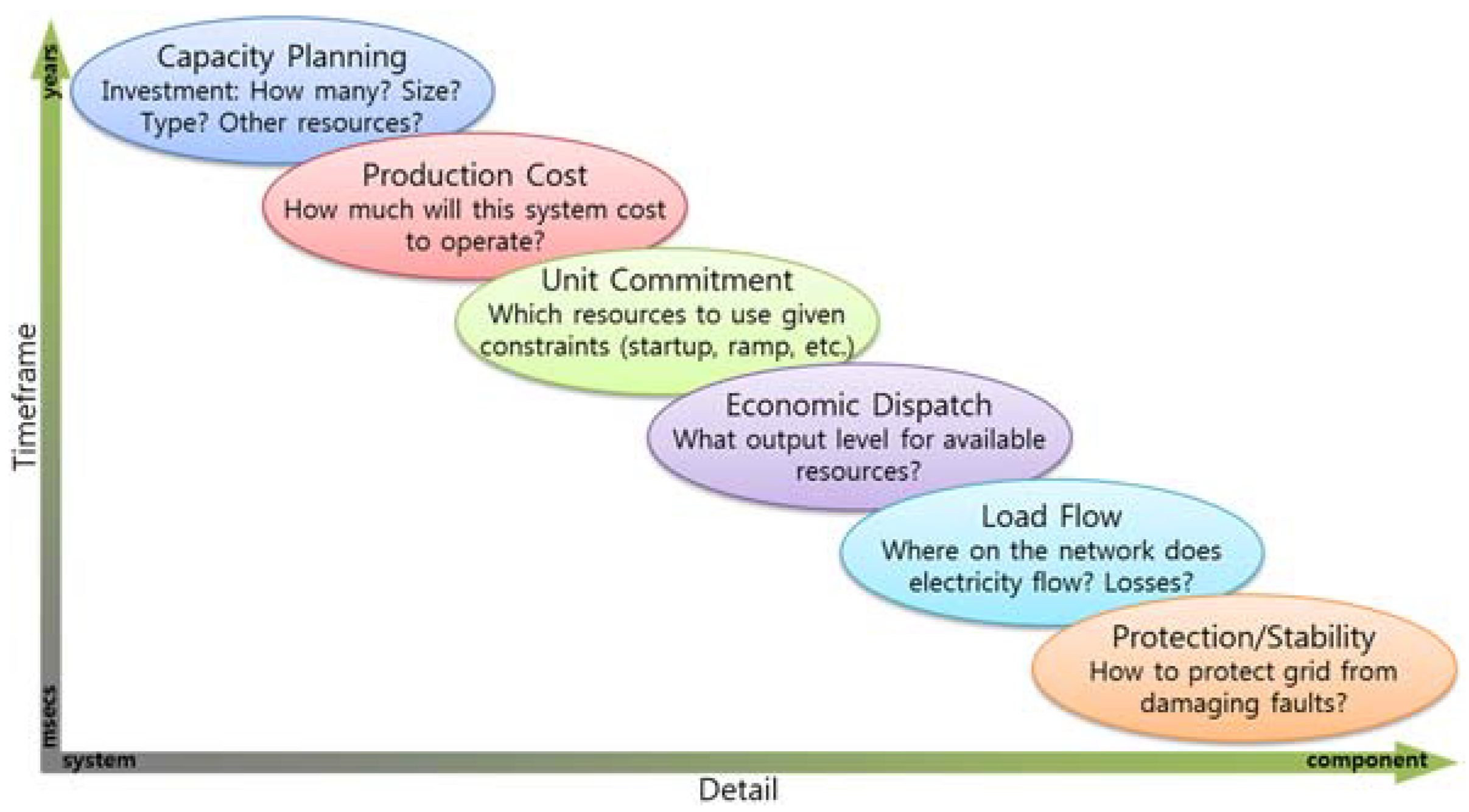
In reality, the model of the electricity system can be classified into six stages.
Figure 1 shows a cascading chain of these models working across a range of timescales from milliseconds to years with an associated trade-off in the level of engineering detail captured [
1].
Among the six stages, this research proposes an integration model considering four stages such as capacity planning, production cost, unit commitment and economic dispatching. At the stage of capacity planning, feasible solutions are generated through the setting of a utility reserved ratio. Next, the unit commitment stage establishes the optimization model, reflecting the operational constraints that should be considered in the activation of a realistic generation system. In the economic dispatch stage, we derive the power generation amount per utilities and other expenses that satisfy time-based demand based on the optimization model in the unit commitment stage. Lastly, the production cost stage generates the construction, operation and maintenance costs through cost-minimizing.
We finally design the optimal extension planning of power generation utilities to maintain both the operational constraints and supply stabilization, as well as to satisfy the future increasing electricity demand, based on the concept of such electricity systems.
In this respect, this study has academic implications for the establishment of optimal power plant expansion plans to meet future increasing power demand while maintaining operational considerations and supply stability.
The structure of the current thesis is as follows:
Section 2 summarizes previous studies on Generation System Expansion Plan, and how the current study differs from them.
Section 3 explains the research model and experiment environment for the optimal Generation System Expansion Planning presented in this study. In
Section 4, we first generate future electricity demand data to be used in the statistical experiments, and defines detailed data related to the operation of power plants. We propose a generation system scheduling model that determines which system will be turned on and off when, in order to satisfy hourly electricity demands.
Section 5 discusses an Integrated Generation System Expansion Planning methodology that can cater to operational elements and maintain supply stability while satisfying increasing electricity demands. Lastly,
Section 6 makes conclusions based on the experiment results and discusses implications of the current research as well as recommendations for future studies in the area.
2. Literature Review
2.1. Generation System Expansion Planning
Recently, research on trading in the electric power market has been actively conducted. Bahrami and Amini [
2] proposed an energy trading algorithm that can optimize the cost of load aggregators and profit of the generators in a power market environment where a distributed power source is expanding such as a smart grid. The future smart grid aims to empower utility companies and users to make more informed energy management decisions [
3]. In addition, Demand Response is becoming more important as the smart grid is spread and spread. In this regard, much research has been conducted to manage the load on the consumer side and to minimize the electricity cost [
4,
5]. Although these studies are important, as mentioned above, we have studied the construction of power generation sources that focus on the demand and supply of electricity considering the scale of the research model.
In general, the power generation system plan refers to the Generation System Expansion Plans that power companies set to predict and satisfy the future electricity demand of their jurisdiction. Investment costs are returned through electricity fees, and in case the electricity market is competitive, the power generation operator forecasts future market conditions to review collecting the investment and make decisions on the construction of power generators [
6].
The Generation System Expansion Plan is an act of determining the construction of various types of power generators to adequately satisfy electricity demands. Construction of power plants requires immense financial and time investment, and the generators operate for long terms of more than thirty years in general. Because power generators have varied construction costs, construction periods, plant capacities, variable costs, operational characteristics, and operational periods, various studies have been conducted to determine how to select power generators for construction.
Several methods have been developed to solve the problem, such as stochastic dynamic programming [
7], non-linear programming (NLP) [
8], mixed-integer linear programming (MILP) [
9], multi-objective programming [
10], evolutionary programming (e.g., GAs) [
11,
12,
13,
14,
15,
16,
17,
18], and other heuristics and mathematical approaches [
19,
20,
21]. The formulation of the problem objective and constraints varies in each implementation, incorporating emissions costs and other environmental constraints (NOx, SOx), transmission constraints, reliability criteria, demand-side management programs, reserve margins, location and financial constraints.
The following are papers that use optimization methodology: Majumdar and Chattopadhyay [
9] generated solutions using mixed-integer linear programming (MILP) methodology, and executed sensitivity analysis based on the application of financial planning and changes to various options. Meza et al. [
10] reflected construction costs, operation and maintenance costs, transmission costs, environmental effects, and changes in the fuel process, as limiting factors to solve the problems via multi-objective linear programming. Tekiner et al. [
21] utilized Monte-Carlo simulation to calculate the power plant operation rate and power generation output, and proposed a multi-objective optimization model that considers environmental effects in addition to limitations already applied to the previous Generation System Expansion Plans. Ahmed et al. [
22] generated solutions using a mixed-integer linear programming (MILP) model that applies a levelized cost, but was only able to calculate the capacity ratio structure of various power generation system types in the final year, rather than a yearly construction plan. Cheng et al. [
23] developed the Chinese Generation System Expansion Plan methodology, which considers geographical conditions in China to propose a model that takes into account geographical structures and inter-regional transmission conditions. Flores et al. [
24] mathematically suggested a typical Generation System Expansion Plan model that takes into account power generation conditions in Argentina, but it cannot calculate short-term operation because of characteristics of the long-term expansion plan model.
The following are representative studies using the stochastic methodology. Mo et al. [
7], Botterud and Ilic [
25] proposed solutions to the Generation System Expansion Plan problem through a stochastic dynamic programming model that takes into account the uncertainties in demand and fuel prices. In addition, most expansion plan research using the stochastic methodology apply probability values through the Markov chain process in order to define uncertainty factors as yearly variability of demand and fuel prices and reflect them in a probabilistic manner.
In addition, there are multiple studies that use heuristic methodologies. Park et al. [
12], Kannan et al. [
16], Firmo and Legey [
13], Sirikum et al. [
14], Sepasian et al. [
20] are examples of this. Most heuristics-related studies solve the problem through GA (Genetic Algorithm), hybrid GA and develop customized models that fit the situations of each nation, and deduce a cost function based on the models.
Integrated software packages have also been developed for the solution of the centralized Generation System Expansion Planning (GSEP). WASP, which is the most general method for modifying the dynamic planning method, began to be developed in 1973 by TVA (Tennessee Valley Authority) and ORNL (Oak Ridge National Laboratory). Afterwards, in order to use WASP more effectively, International Atomic Energy Agency (IAEA) set out to complement Model for Analysis of Energy Demand (MAND) and hydro-thermal power system, developing further versions up to WASP-IV. WASP-IV is a computing model to establish long-term energy-mix development plan, which aims to minimize the system cost by generating the optimal construction plan for each year, from the beginning to the end of the plan period. The model uses a probabilistic simulation and dynamic planning method to select candidate plans that minimize total power generation costs, taking into account investment costs, operation costs, fuel costs, and remaining values. The WASP model was used widely in Korea as the mathematical planning model for selecting the minimum cost alternative for an electricity supply and demand plan [
26].
2.2. Generation System Operation Planning
A power generation system operation plan is a scheduling problem to determine which power plant to start-up and shut-down at what times in order to satisfy hourly electricity demands. Through this plan, an hourly power generation plan by plant and realistic operation and maintenance costs are calculated. Many previous unit commitment studies solve highly complex problems that consider various limiting factors, but because of this, a power generation schedule that can be calculated through the models are limited to the short-term, such as daily. Depending on their purpose, unit commitments do not have to be long-term. However, due to the strength in which unit commitment shows similar results to actual power generation conditions, the model can have much meaning if the problem is expanded to long-term scheduling. In such terms, the following shows the categorization of previous unit commitment studies into short-term and long-term scheduling problems. First, Delarue et al. [
27] conducted a study on short-term unit commitment, analyzed the Belgian electricity system through a typical model that takes into account the operational state of power plants, such as start-up and shut-down. Delarue et al. [
28] studied the daily operation costs of introducing wind power generation and the resulting environmental influences. Andrianesis et al. [
29] suggested a power generation system operation plan model for the Greek electricity system, which reflected a condition in which a monopoly was transitioning to a competitive market system. Simoglou et al. [
30] generated the optimal operation scheduling for the stable operation of a power plant based on the previous day’s electricity demand data. Li and Shahidehpour [
31] proposed an operation planning model aiming to maximize the revenue of power generation companies, rather than establishing a plan from the perspective of supply stability that previous models took.
For long-term SCUC, various methods have also been proposed [
32,
33,
34]. In Vemuri and Lemonidis [
32], the Lagrangian relaxation (LR) method is used to decompose the fuel-constrained unit commitment problem into a linear fuel dispatch problem and a unit commitment problem. LR is also employed in Fu et al. [
34] to divide the long-term SCUC into tractable short-term subproblems without fuel or emission constraints. In addition, studies such as Thorin et al. [
35] and Seki et al. [
36] apply the Lagrangian relaxation (LR) method. Handschin and Slomsmi [
33] use a two-stage method to solve the unit commitment problem with long-term energy constraints. The optimal daily energy for each unit is calculated in the first stage, and then the unit commitment problem is solved in the second stage. Wang et al. [
37] presents a fast bounding technique to improve the traditional branch-and-cut algorithm. Based on the work in Wang et al. [
37], an inducing-objective-function-based method is proposed in Bai et al. [
38]. In addition, a study by Chen et al. [
39] based on the stochastic method was proposed, and Voorspools and D’haeseleer [
40] generated operation plan patterns for each power generation system, designated priority for the patterns, and conducted probabilistic scenario analysis on them.
3. Research Methodology
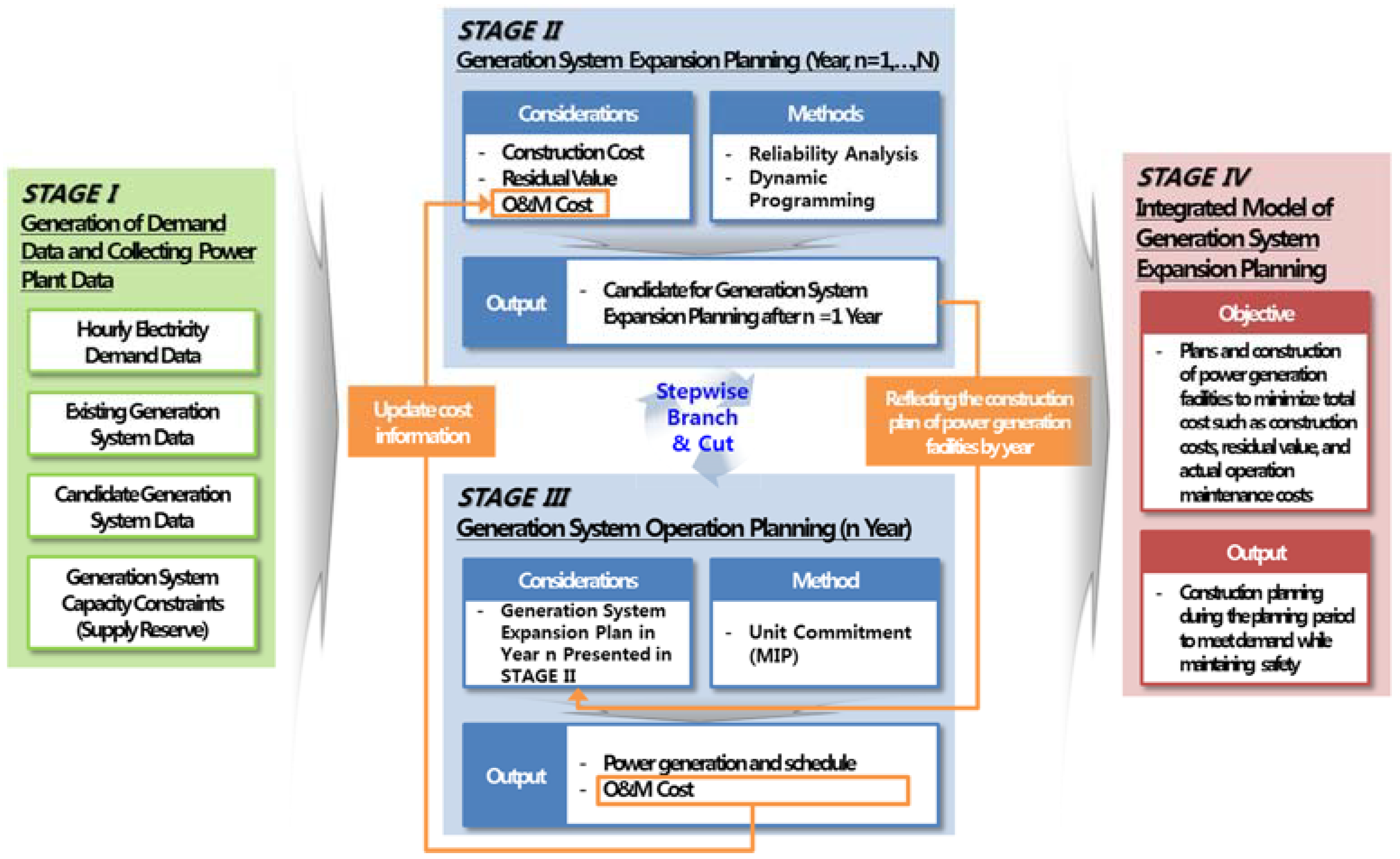
The current study proposes architecture and a methodology for an Integrated Generation System Expansion Planning Model as shown in
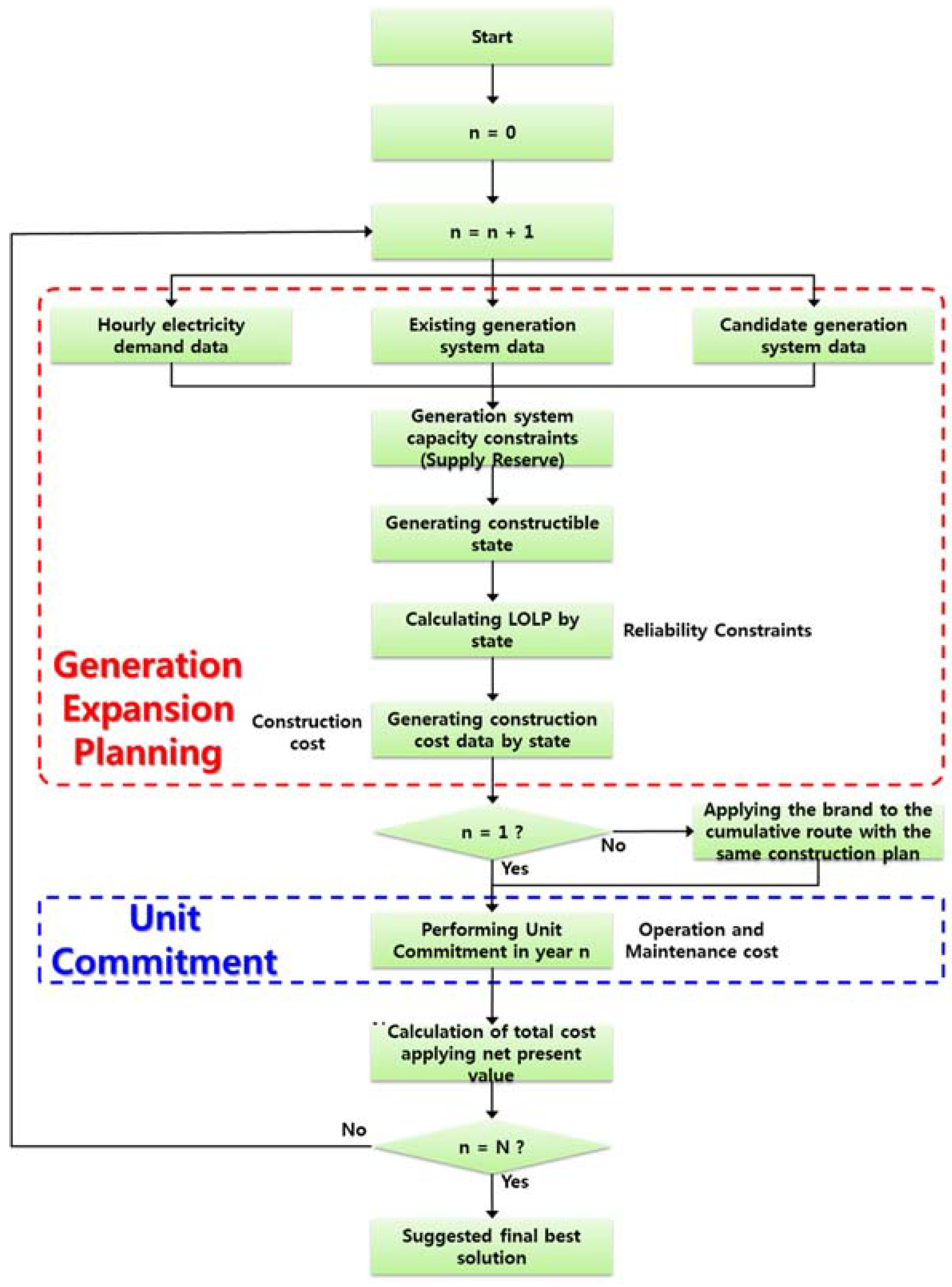
Figure 2. The architecture is composed of a plan-level model that satisfies both electricity demands that will increase in the future as well as the reserve rate, and an operation-level model to consider operational elements and maintain the stability of the electricity supply. The methodology consists of Stages I–IV. In Stage I, future electricity demand data is generated and power plant data is collected. In Stage II, the previous Generation System Expansion Plan methodology is used to deduce a feasible solution and construction costs that satisfy the reserve rate. In Stage III, mixed integer programming (MIP)-based power generation system operation plan methodology is used to deduce numbers on the operation of power generation system, such as year-round operation and maintenance costs, power generation output, and a maintenance plan. In Stage IV, a feasible solution for the duration of the plan (deduced in Stage II) and operation and maintenance cost information are combined to produce the optimal solution that minimizes the total cost.
Evaluation in Stage IV is executed in order to simultaneously satisfy the yearly maximum electricity demands in the long term and electricity supply stability in the short term. It is noted that the hybrid integrated models cannot be directly used in stability analysis or optimization due to (1) the varied and often conflicting objectives for the different levels (planning and scheduling); (2) computational complexity of the optimization model, especially the operation planning (unit commitment) model that should consider all power plants and the time horizon.
Prior to configuring the model, the data on future electricity demands were generated to establish an expansion plan. The hourly electricity demand pattern shows that the demands have seasonal characteristics by week or year. In order to utilize such characteristics, dual-seasonality Holt-Winters time series model [
41] was used to generate future electricity demand data. The details of the models can be found in
Section 3. In addition, data for power plants used in the current study and other related data were defined and collected.
A model similar to the Generation System Expansion Plan model used in Korea was optimized and reconfigured based on a probability model as part of activities in Stage II (refer to
Section 4). Through this, the current study deduced the significance and limitations of the current Korean Generation System Expansion Plan model, and the model was verified using its results and the results of the (Sixth) Basic Plan for Electricity Demand and Supply [
42].
In Stage III, a power generation system operation plan model is an optimized model expressing the schedules of each power plant that can satisfy the electricity demands. The general methodology of unit commitment is a question of deducing a schedule that can minimize the costs by reflecting detailed elements related to the operation and outage of power plants as limitations. In fact, because different nations and power generation companies have different types and number of power plants, questions adequate for individual situations are defined so that solutions can be deduced when dealing with unit commitment problems. One issue that may arise is that the complexity of calculations may increase. Because of this, most unit commitment problems have a goal of establishing a short-term power plant schedule. The current study, however, sets out to propose a long-term power plant schedule model based on MIP, which can be applied to the new Generation System Expansion Plan methodology to compute the power generation output and operation and maintenance cost of power plant.
Previously in Stage II, we were able to compute the power plant construction plan and construction cost by year through the Expansion Plan, and Stage II enabled the calculation of power generation output and the operation and maintenance cost of each power plant, through the operation plan. In particular, the schedule optimization (Stage III) is described by presenting the decision variable, objective functions and the optimization methodology. The specifications for interactions of the expansion and operation models for use in Stage IV of the proposed architecture are detailed. In order to eliminate the infinitely many feasible solutions that are generated by the Expansion Plan in Stage II, branch-and-cut method for the total cost is applied in a forward direction.
Section 6 details other connections of models and their integration.
Statistical experiments were configured with IBM ILOG OPL-CPLEX 6.3, the optimal commercial package used in the industry. The software was executed on a PC (Core(TM) i5-2500 CPU 3.3 GHz).
4. Data Generation and Model Composition
4.1. Generation of Demand Data
Unlike regular time series, electricity demand data take the multiple pattern (classified by time, day of the week, and season), which makes it important to consider such multiple patterns in order to improve the predictability of the model. According to the recent very-short-term power demand forecast research, the predictability of a model can be improved by applying patterns by the day or by the hour, rather than applying the same daily pattern throughout, when considering the seasonal differences in electricity demand. For example, Gould et al. [
43] compared the electricity demand curves for each day of the week to categorize data into four patterns (Mondays to Thursdays, Fridays, Saturdays, and Sundays), and applied appropriate patterns for each instance of estimation to increase the predictive power of the model. In addition, Taylor and Snyder [
44] segmented the pattern further, by the hour (Monday until 8:30 a.m., Tuesdays to Thursdays, Friday after 11:00, weekends) to construct a general model with even better predictive power. The application of the latest electricity demand forecast model must be preceded by the analysis of electricity demand by the hour and day of the week.
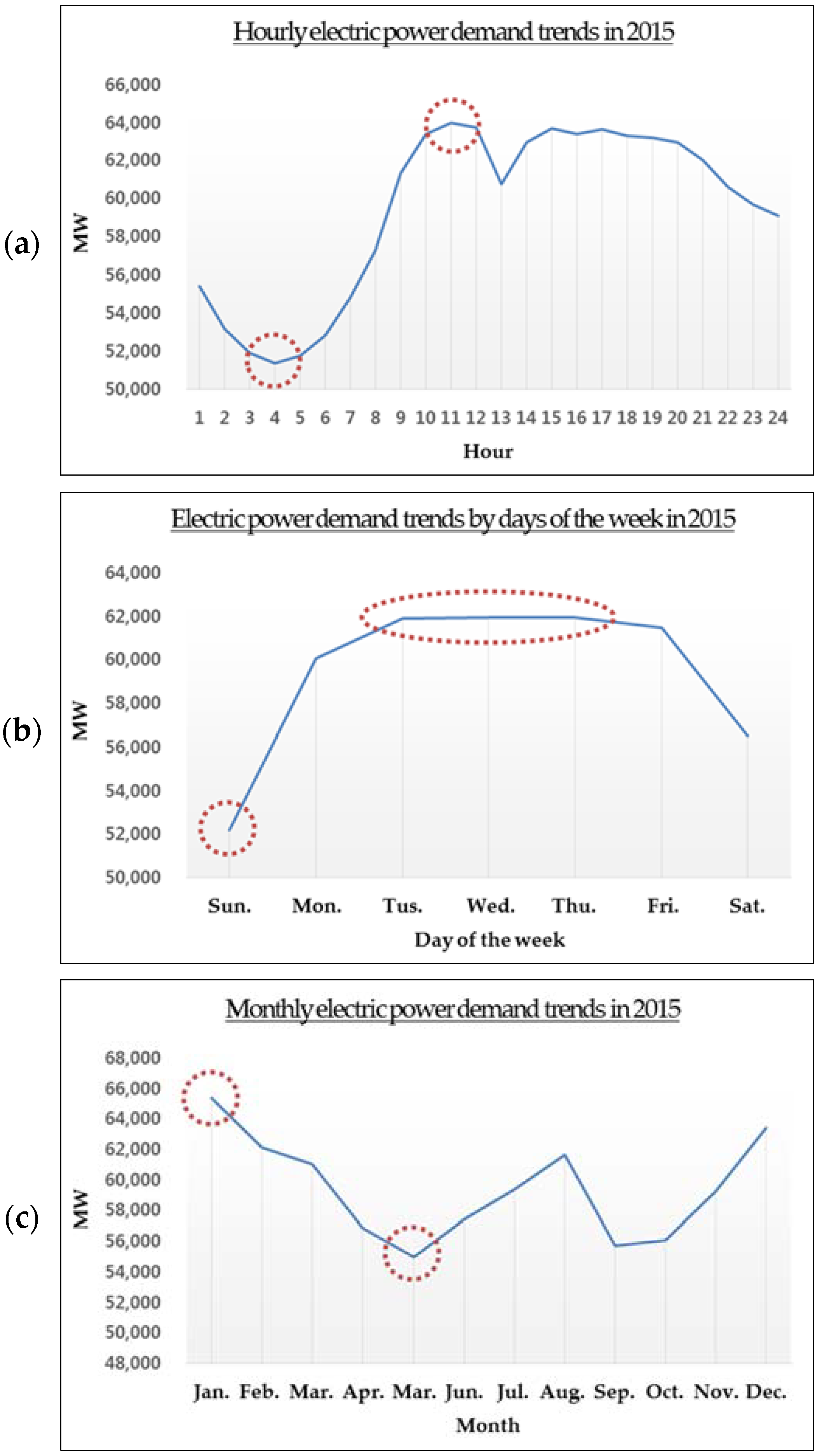
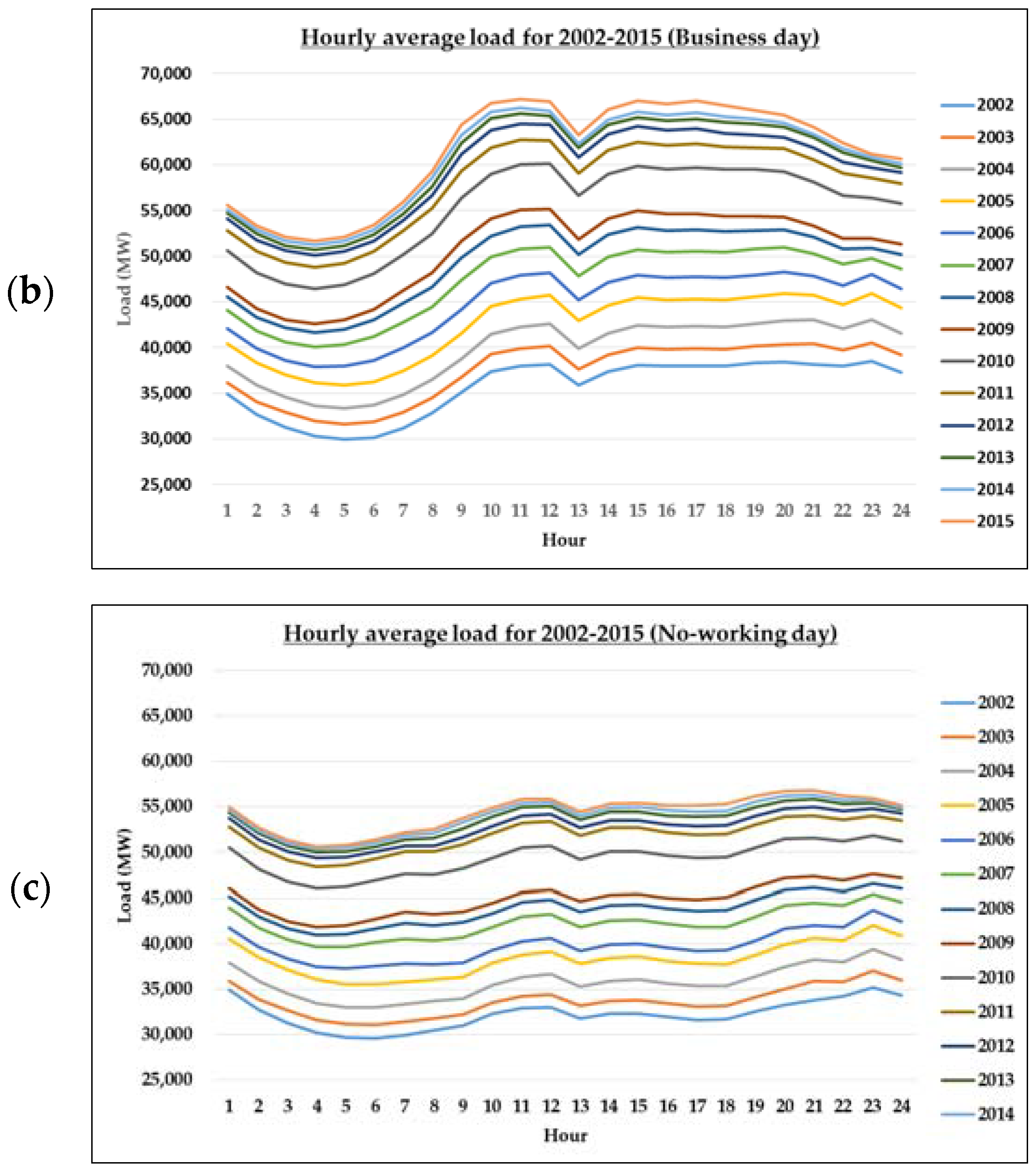
The business day pattern displayed in
Figure 3 shows a very similar pattern to the yearly average pattern. Lowest load is reached at around 04:00 in the morning, after which the load continues to increase to surpass daily average at around 09:00, reaching the daily peak at around 12:00. At around 13:00, which is lunchtime, the load decreases to match the daily average, and increases again at around 15:00 to a point near the daily peak.
The non-working day (weekends and holidays) load pattern in
Figure 4 shows a large difference from the business day load pattern. From 02:00 to 10:00, the load is lower than the respective daily average, but it increases beginning at 19:00 due to lighting demands, forming daily average at around 23:00.
The time series model considered for the electricity demand forecast model in the current study is the Holt-Winters seasonal method.
Generally, the power demand data does not follow the basic premise of the model in which the same pattern is repeated every cycle. In order to minimize the variation of these unstable patterns, we used the sliding window method in this study. The sliding window method is a method for estimating the coefficient of the model newly at each time point while sequentially moving the starting point while keeping the size of the sample period in the sample fixed. The size of the sliding window is fixed at 1820 (7 days × 52 weeks × 5 years of daily data) days, which can be considered both daytime and year-to-day, and the daily load on the next day of each sliding window is predicted Based on the model coefficients estimated in each of the sliding windows, the next day’s forecast was derived over 364 days from 1 January 2015 to 30 December 2015.
The daily power demand data has a periodicity by every week (7 days) and year (364 days), so we consider a double seasonal Holt-Winters.
Table 1 shows the results of the parameter estimation. The comparison of the prediction performance of the model is based on the root mean square error (RMSE) and the mean absolute percentage error (MAPE), as shown in Equations (1) and (2). In addition, comparisons were done by month as shown in
Table 2.
Figure 5 shows the results comparing actual demands and forecasting demand derived from the model based on 2015, through a time series analysis. Data with a deviation greater than the reference value are excluded from the analysis as outliers.
In the same way, forecasting demand data from 2016 to 2030 was generated, reflecting the annual growth rate of electricity consumption and peak demand in the national power supply and demand plan. For generating realistic data, the power consumption pattern of past holidays and the pattern of unexpected increase in power consumption due to weather characteristics were utilized in the model.
4.2. Data Collection of Power Plants
Key input variables relating to the generation system include economic variables such as predicted electricity demand, construction unit price, fuel cost, discount rate, inflation, as well as technical variables and reliability indices (LOLP: loss of load probability) such as power generator capacity, forced outage rate, days of preventive maintenance, operating and maintenance costs, and heat consumption of power generators. Such input data are variables that affect the optimization process, whose changes can cause large differences in the yearly power generator mix calculated by the model. As such, in order to generate a reasonable plan, the input variables demanded by the model must be correctly interpreted and the data must undergo sensitivity analyses. For example, the construction unit price for each candidate power generator indicates direct investment cost; the Generation System Expansion Plan uses the yearly investment cost, expressed as “Fixed Prices from Initial Year of the Plan,” is converted to the cost at the time of construction completion using the real discount rate, ultimately using the sum of the latter cost as the total construction cost. This method is used to utilize the dynamic planning method and expresses the yearly construction cost in terms of the price at the time of construction completion.
Table 3 is a summary of major input variables related to the generation system.
4.3. Generation System Expansion Planning Model Composition
The basic goal of the Generation System Expansion Plan is to find the energy mix that minimizes the objective function, which is the sum of current-value yearly investment cost and operating cost, under the restriction of satisfying the supply of reliability. Because generation systems are operated for two to five decades once constructed, and the generation mix of a year impacts the future generation mix, the optimal system mix for one year cannot be deemed optimal for the entire planning period. As such, the issue of power supply development planning takes on dynamic features, in which the generation mix among years are interrelated.
In order to maintain consistency with the ongoing energy policy of South Korea, we refer to the 7th Electricity Supply and Demand Plan to estimate the baseline of the GHG emission of the year 2030 for the generation sector, the major features of which focus on the low carbon energy mix; firstly, the four pre-arranged coal-fired power plants are excluded due to their high GHG emissions, the result of which eventually decreases the ratio of the coal-fired power plants. Policy planners reached an agreement that these excluded plants will be replaced with two new 1500 MW nuclear power plants. Secondly, the facility capacities of renewable energy are expected to be up to 33,890 MW and its portion will be 11% in 2035. Finally, the active demand management plan is fortified in connection with the energy efficiency and information technology.
For the purpose of establishing the baseline of the 2030 GHG emission volume, we make use of the WASP model which the IAEA has distributed to estimate electricity generation quantities. We anticipate the emission volume using the standard emission coefficient issued by the IAEA in
Table 4.
4.4. Generation System Operation Planning
4.4.1. Model Description
In the 1960s and 70s, mixed integer programming (MIP) was suggested to solve the unit commitment plan problem in earnest [
45], and in the 70s and 80s, dynamic programming, as an algorithm for unit commitment plan for energy management system (EMS), was developed [
46,
47]. Dynamic programming, because it searches for all possible power generator combinations, can come up with the optimal solution, but if the number of power generators is too large, it takes too much time for calculation, effectively disabling the search for the optimal solution. In order to solve these problems, variations of DP, such as DP-sequential combination (DP-SC) and DP-truncated combination (DP-TC) were developed. In recent years, new variations of DP, such as Fuzzy-DP [
48,
49] were created as well. Since then, from the early 1980s to today, methods such as Lagrange’s Method of Undetermined Coefficients, expert system, purge theory, neural network, genetic algorithm, and evolution programming appeared in the field. Lagrange’s Method of Undetermined Coefficients, however, is adequate for optimizing large-scale systems, while the duality of the algorithm itself prevents it from reflecting the feasibility of the solution and the limiting conditions on power generators [
50,
51]. Most recently, a deterministic unit commitment (DUC) algorithm was developed [
52], which is able to rapidly obtain solutions that are overwhelmingly economical compared to those yielded by other methods, but the performance of this new algorithm cannot be guaranteed for a multiplicity of limiting conditions. As such, no algorithm currently in existence can find the optimal solution in a short amount of time, in the face of all limiting conditions.
The problem of basic unit commitment planning is to find the optimal power generator outage/operation combination that satisfies multiple limiting conditions while minimizing the total power generation cost. The types of power generating system include steam power (anthracite coal, bituminous coal, heavy oil, LNG), combined thermal power (combined cycle: general, thermal cogeneration), hydroelectric power, internal combustion power, and nuclear power. In the case of nuclear power, the power generation output is almost fixed, because of which it is generally excluded from the unit commitment planning or is a part of a special unit commitment plan, as in the case of France. Hydroelectric power is excluded from the unit commitment plan due to rainfall and social and environmental limitations, or as in the case of Canada and Scandinavian countries, hydroelectric power plants are constructed in mass to operate a separate hydrothermal unit commitment plan [
53]. As such, most of the power generators used in the unit commitment plan are thermal ones, which can be started in a matter of hours, making normal unit commitment plans to determine the combination of power generators by the hour.
The combination of operation/outage states during a time period is called the state during time period, and the number of possible states is shown in Equation (3), where the total number of input power generators is [
54].
where,
That is, the number of possible operation/outage combinations possible during the time period is
, which makes it that the number of possible operation/outage combinations for ten power generators for 24 h in a day is
. Furthermore, the limiting conditions, system limiting conditions, and power generator limiting conditions generated from the relationship with previous time periods must be satisfied for every state of every hour, the curse of dimensionality frequently occurs, in which the dimensions are too large to calculate the solution to the optimal unit commitment problem. In other words, the problem of unit commitment planning is an optimization problem in the form of large-scale combined non-convex, which includes numerous equation/inequation limiting conditions and integer/real number variables [
52,
55].
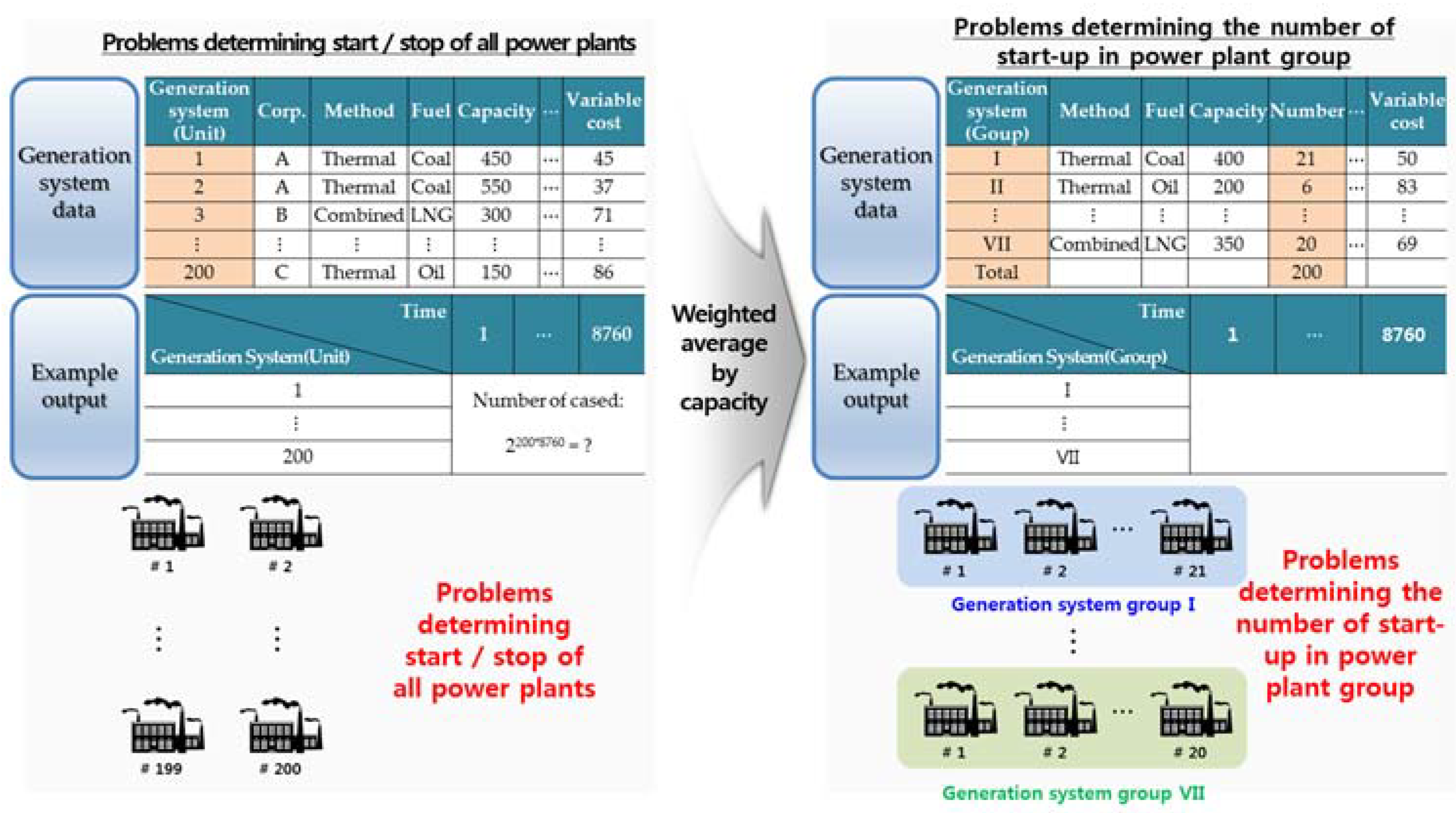
In solving the unit commitment problem for each power plant, as suggested in previous sections, a high number of cases amounting to NP-hard exist to solve a long-term problem of calculating actual operating and maintenance costs over a year. That is, while it would be possible to solve the problem for a small number of power generation systems, the number of variables and cases will radically increase when there are more power generation systems under consideration. Such a problem can be solved by grouping power generation systems with similar characteristics.
Table 5 displays information on unit commitment for major power plants in Korea. There are 140 power plants of three types (eight types if categorized by capacity), and the number goes up to 200 if various other power plants are considered. In this case, there are many equations to solve the unit commitment problem, as shown in
Figure 6, and because a total of 8760 h must be considered in order to calculate a year’s worth of total operating and maintenance costs, the number of equations exponentially increase as shown in
Figure 6. In order to solve this problem, the power plants are grouped by their characteristics to create less than ten types, thereby simplifying power plant data. Power generation systems cannot be randomly built by power generation companies; rather, there are established sizes and types of power plants that can be constructed, and power generation systems within the same category share many constraints, which makes it acceptable to group seemingly similar generators. A significance test is conducted in the next Section, by comparing with other grouping problems at the demand level, with which the basic problem can deduce results. The process by which a decision variable is deduced in the unit commitment problem shows that the previous problem of determining the on/off status of all power plants in the group is simplified into an integer programming problem in which the number of power plants participating in the operation among the group of power plants. For example, if the calculations determined that there are twelve power plants being operated during a certain period in power plant group 1, in which there are twenty members, the number of stopped power plants in the said group would automatically be eight.
The grouping of power generation systems necessitates partial changes to the previous equation. First, weights were given for the capacity of each group when calculating its characteristic values. Next, since piecewise linear approximation is impossible for heat consumption rate, it was changed to linear expression. This is possible because most of the power plants have a secondary coefficient of fuel usage function that is under , which has a similar form to the linear form. Lastly, as the major decision variables have been changed to integer, not binary, form, it became impossible to distinguish the three starting conditions for each power plant in the group (hot/warm/cold). As such, these were unified into a single starting condition for application. For this, the frequency of starting conditions in normal situations were considered to apply the average as the weight of the characteristic.
4.4.2. Model Formulation
The GSOP model objective function to be minimized is formulated as follows:
As shown in Equation (4), objective function includes the maintenance and repair costs, operating costs including fuel cost, and costs for turning the power generation system on and off. The maintenance and repair cost of the system is determined by variable
, which determines the time of maintenance and repair for power generation system in each year, as shown in Equation (5). Equation (6) is on the operating cost, and includes the fuel use volume, fuel cost, and variable operating costs. Costs for turning the system on consider the costs, and are elaborated in Equation (7).
Formula (8) expresses the fuel use for power generation volume; fuel use volume function generally takes the form of quadratic expression, that is, a nonlinear form. Nonlinear quadratic expression, however, must be converted to linear function form for MILP solution.
The model constraints are as follows:
- ◆
- ◆
- ◆
Inter-Period Ramping Limits:
- ◆
Minimum Up and Down Times:
- ◆
Unit Minimum and Maximum Output
- ◆
frequency regulation Reserve Requirements:
- ◆
Contingency (Non-spinning), Supplementary (on-demand) Reserve Requirements:
- ◆
Reserve Upper Bound Vector Constraints:
- ◆
- ◆
Peak Period (Winter/Summer) Reserve Rate Lower-bound Constraints:
- ◆
- ◆
Simultaneity Constraints:
Equation (9) refers to the range of power plants in which the unit commitment can be performed, excluding the power plants under maintenance in the group. Equation (10) is the balance equation for power generation volume by each power plant. Equations (11) and (12) are equations for deducing the actual power generation output in consideration of operating status and primary and secondary reserve power. In addition, when the actual demand shows a large difference from forecasted demand, power plants may need to radically increase or decrease output in a short amount of time. In such cases, Equations such as (13) and (14) may be required, which are related to the ramping up and down of power generation which also takes into account the characteristics of each power plant. Furthermore, Equations (15) and (16) are about the minimal time required to maintain the respective statuses when the power plants are started or shut down. Equation (17) is the boundary of power generation considering unit commitment. Equations related to reserve power are categorized into primary reserve power, shown in Equations (18)–(20), and secondary reserve power, expressed through Equations (21)–(24). The current study defines primary reserve power as being used to satisfy the power shortage caused by rapid changes in demands, while secondary reserve power is used to respond to electricity shortage caused by output decline from force power plant outages. Primary reserve power was calculated for LNG, petroleum, pumped storage, and hydroelectric power plants, which are more rapidly responsive, and secondary reserve power was calculated for coal power plants that are in states of operation or outage. Equations (25)–(28) are interaction equations that show the possible maximum output of primary and secondary reserve powers, taking the operating statuses and inherent characteristics of each power plant into account. Equation (29) is a balance equation for the change in the number of power plants in operation during this period compared to the previous period. Equations (30) and (31) express the minimum reserve power that must be maintained as per policy during winter and summer times with high electricity demands.
Next, Equations (32)–(35) are related to the maintenance and repair of power plants. They are interaction equations that express the satisfaction of minimum maintenance and repair days required for each power plant, calculation of timing for maintenance and repairs, and minimum maintenance period. Equation (36) is a constraint on the minimum value of maintenance required in a group.
4.5. Results of the Experiment: National Plan for Electricity Supply and Demand
Using the mathematical model of unit commitment for grouped power generation systems that verified statistical significance, this section generated
Table 6, which contains unit commitment plans for all Korean power plants, as well as their detailed operation and maintenance costs and power generation outputs in January 2013. For the experiment, major Korean power plants were grouped into five types and ten types. The total number of power plants is 168, which excludes new and renewable energy and collective energy power generation systems.
From the operation and maintenance costs perspective, the price of fossil fuel is causing the fuel to take large amounts of operation and maintenance costs. In contrast, nuclear power plants, which have lower fuel prices and generate much base power, have a high rate of variable costs, which rise and fall depending on the power generation output. Furthermore, the fact that operation/shutdown costs take up 20% of all operation and maintenance costs indicates that precise calculation of operation/shutdown cost is important for computing operation and maintenance costs.
In addition, in order to compare the detailed operation and maintenance costs deduced by the operation plan in this section with operation and maintenance cost deduced from Stage II (Generation System Expansion Plan),
Table 7 was set up to comparatively view fuel costs, detailed operation and maintenance costs, capacities, power generation outputs, operation rate, and average days in operation for January 2013.
Because the results are deduced for the same period, they show similar values for most items, but a comparison of operation and maintenance costs reveals that those calculated in Stage II (Power Generation System Expansion Plan) and Stage III (Power Generation System Operation Plan) differ to a degree. Because the experiment was conducted for a macro-model of a long-term expansion plan, operation and maintenance costs calculated in Stage II were used as a parameter after simplifying operation and maintenance cost history collected in advance. In contrast, operation and maintenance costs calculated in Stage III are a result of the unit commitment plan of all power plants responding to actual hourly demands, which also provides all detailed operation and maintenance cost items. Comparing the two operation and maintenance costs yields similar results, with a slightly higher value to that deduced by the unit commitment plan. This is thought to be the result of a difference in unit commitment cost. The major factor is thought to be the increase in operation and shutdown frequency of fossil fuel generators using coal, oil, and LNG. Excluding these, the operation and maintenance costs for Stage II, 3 during the same experiment time is the same.
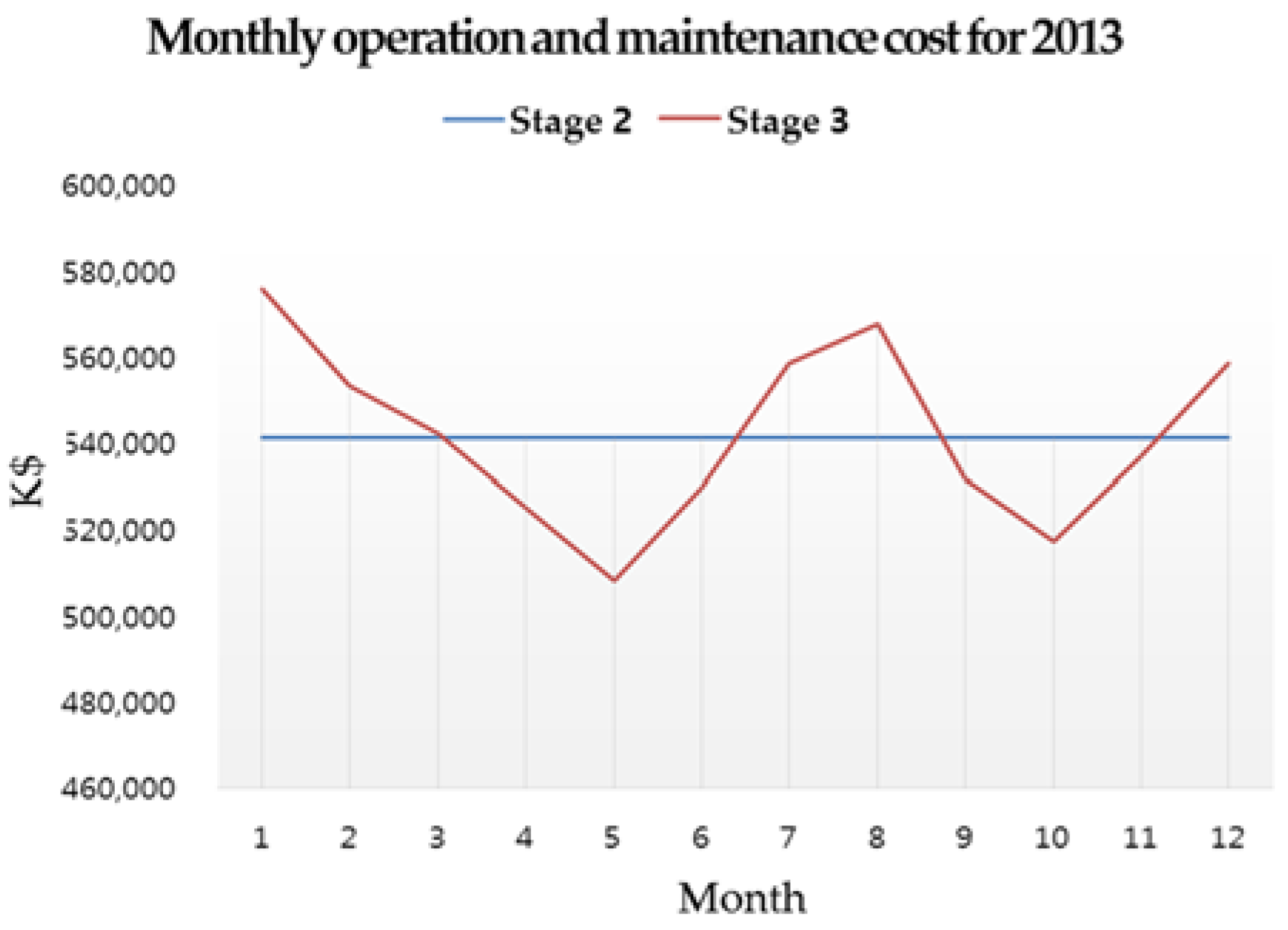
The following
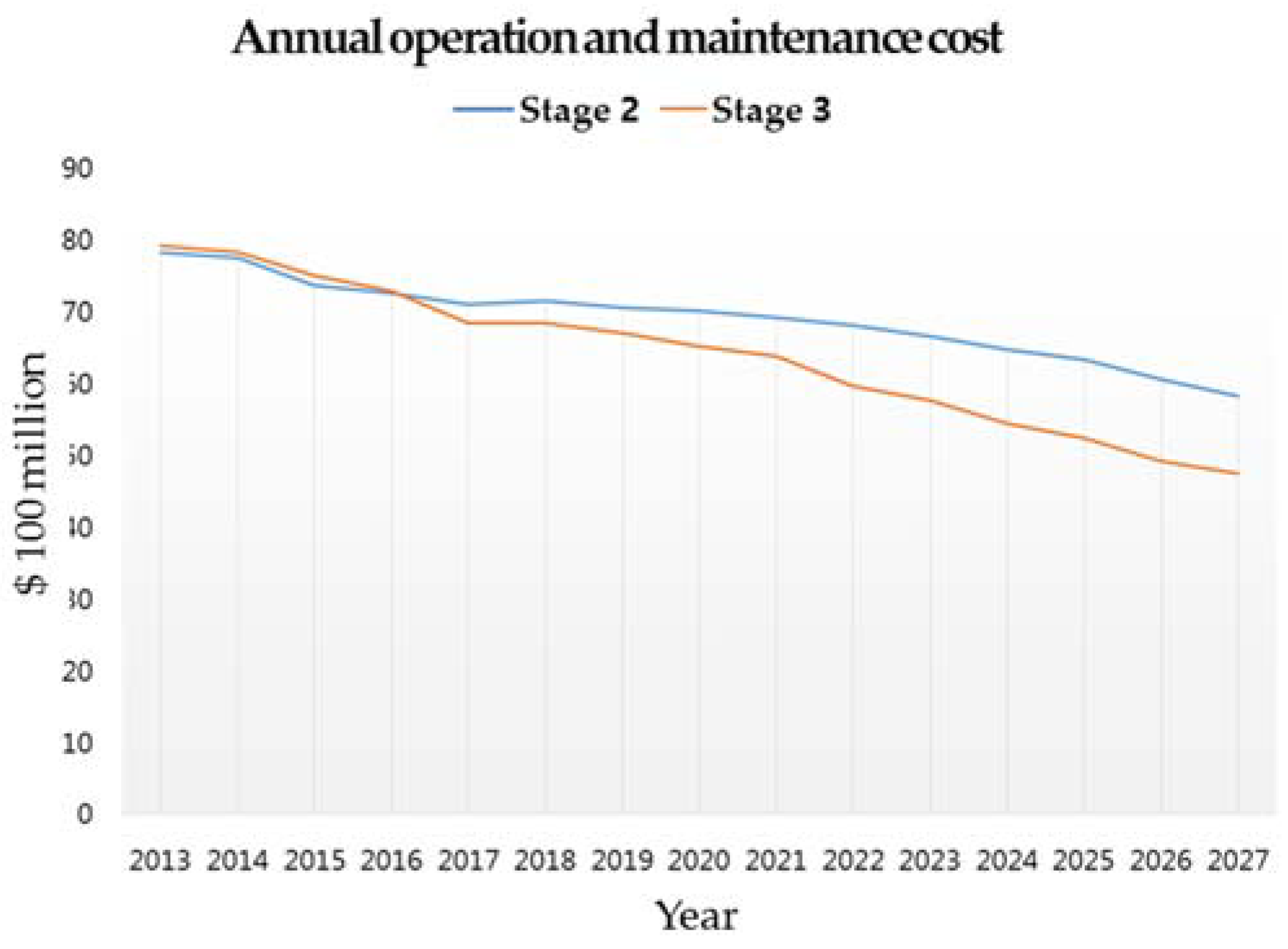
Figure 7 and
Figure 8 compare the monthly operation and maintenance costs (minus fuel cost) in 2013 and yearly operation and maintenance costs. For the monthly operation and maintenance costs, the same in Stage II is used as a parameter-fixing value as mentioned before, but that in Stage III is variable depending on seasonal features, similar to actual power plant operation conditions. Because of this, operation and maintenance costs calculated in Stage II and Stage III become more different towards the end of the planned period, which indicates that the operation and maintenance costs of Stage II may be distorted.
5. Integrated Model Composition and Case Study
A long-term plan is established using the Generation System Expansion Planning methodology suggested in Stage II. The most problematic thing in this is the algorithm for calculating operating costs. The previous Generation System Expansion Plan used a probability simulation to compute the operating costs, and the precision of the simulation differed depending on whether the results were to be used for long-term or short-term planning. In the short-term plan, such as a power generation plan or a fuel supply plan, the evaluation of operating costs utilizes hourly load data, considering the maintenance plan and power generator unit commitment, in the process of precision simulation. However, the evaluation for long-term plans such as the Generation System Expansion Plan does not take into account a more detailed unit commitment plan, and only simplified versions of repair plans as well as the load duration curve—as opposed to hourly load—are used. This is because the calculation time increases exponentially if mathematical planning techniques such as dynamic programming are used to find the Generation System Expansion Plan that minimizes investment and operating costs, as they consider thousands of simulations for each state in each year. As such, the current study used a probability simulation for a MILP-based and operating cost-based Generation System Expansion Plan despite lower reliability. However, the less-precise operating cost-based Generation System Expansion Plan will yield errors as years advance.
The operating cost evaluation in short-term plans utilizes unit commitment analysis to establish an operating schedule for short periods of one day or one week. The process was discussed in the previous section. The current study proposed a methodology for analyzing unit commitment via grouping power plants, in order to enable the consideration of operating cost evaluation in long-term plans. Under the assumption that this methodology guarantees the precision of demand data, the current study executed statistical verification that it has a similar result to the previous unit commitment methodology. Through this, the current study assesses that it would be possible to realistically and precisely evaluate the operating costs by applying a long-term unit commitment analysis method via grouping of power plants, which can replace the previous system that has the limitation of lower precision.
As such, the current section looks to propose a related model and algorithm that utilize the advantages of generation system expansion planning suggested in Stage II, and unit commitment analysis suggested in Stage III.
5.1. Algorithm of Integrated Model
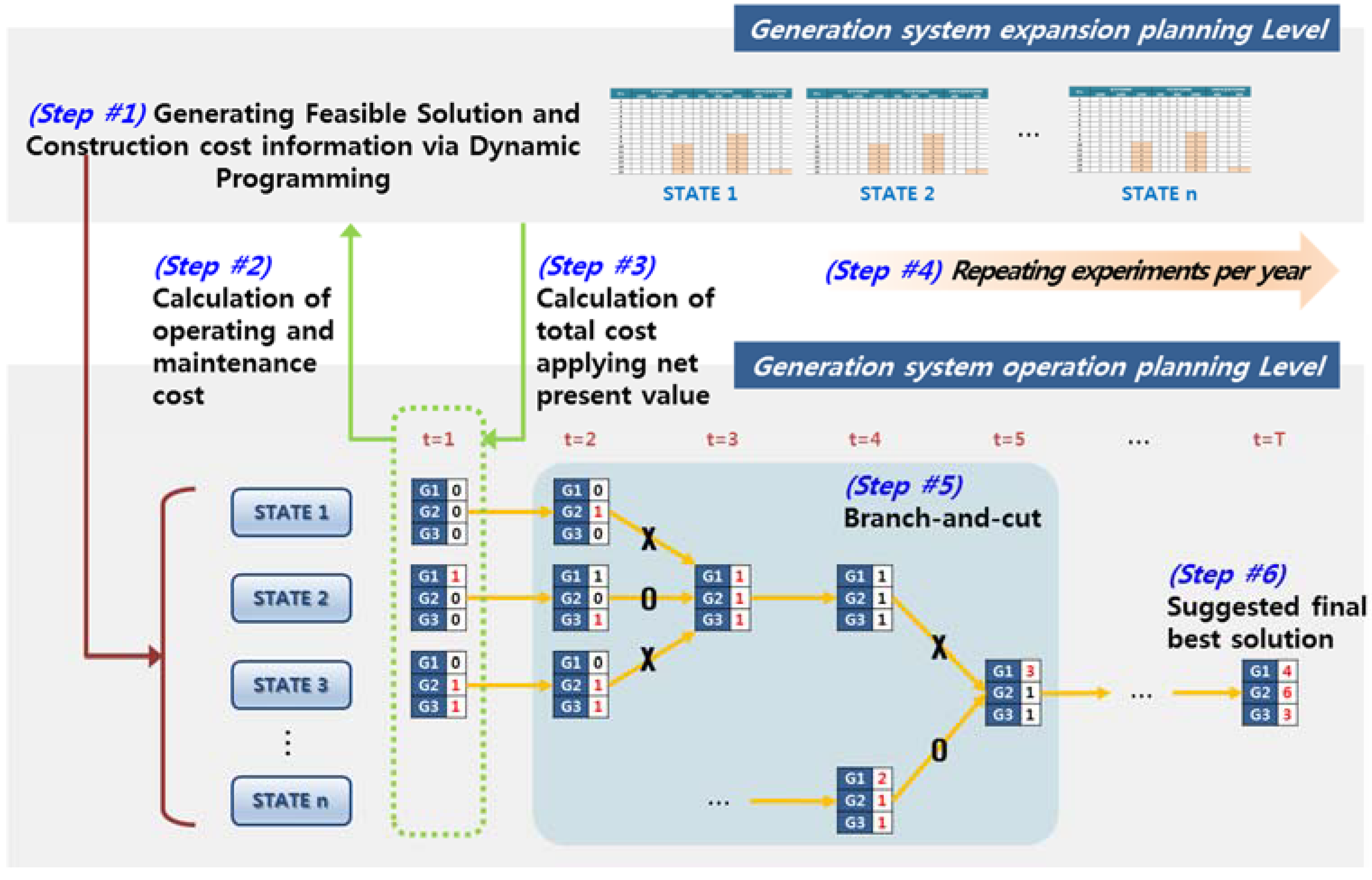
As show in
Figure 9 and
Figure 10, using the Generation System Expansion Plan utilizing the DP concept, step 1 generates a feasible solution for the aggregate paths including the number of power generation system constructed in each year. Step 2 deduces the total operating and maintenance costs that reflects the initial years’ construction plan for all routes, using a generation system operating plan. Step three deduces the construction costs for each year and the remaining value for all routes in the Generation System Expansion Plan, and calculates the total cost, adding the operating and maintenance cost (converted to the current value) resulting from step 2. In step 4, the second and third steps are repeated in order for each year. In addition, because there are too many cases to deduce all total operating and maintenance cost for each year, we cut the routes that do not require calculation. In step 5, a branch-and-cut method is applied; if the aggregate paths for multiple same construction plans overlap in the same year, the path with the minimum total cost until the previous year is selected and the remaining paths are cut. Here, after the branches are unified into one, one optimal path will be selected for further procedure; the path may not be optimal if the total cost until the previous year is not the minimum among many options. Step 6 is a repetition of step 2 to step 5 until the end of the planned year. At the end, the total cost of paths that are not cut until the completion of the algorithm are compared to select one most optimal path.
5.2. Results of Integrated Model Experiment and Comparative Analysis
5.2.1. Results of Integrated Model Experiment
Table 8 shows the results of the integrated model algorithm discussed in the previous section. First, the results showed that two nuclear, six coal, and five LNG power plants will be constructed by the final year of 2027 during the plan. In terms of costs, construction cost was
$12.81 billion, the remaining value was
$10.08 billion, and operation and maintenance costs were
$96.95 billion, with the total cost being analyzed as
$99.18 billion.
Considering that the operation and maintenance costs are more than twenty times that of the realistic construction cost (construction cost—remaining value), it would be most effective to propose a construction plan that can reduce operation and maintenance costs, in order to cut total costs.
5.2.2. Comparison with Generation System Expansion Plan (Stage II) Results
As shown in
Table 9, a comparison of the experiment results from the integrated model and the previous expansion plan deduced from Stage II showed that new nuclear power plants were −2 and LNG was +3. Construction cost of the two plans were similar, and in terms of cost, a comparison with the previous expansion plan model (Stage II) shows that the operation and maintenance costs deduced through Stage IV (integrated model) are lower by
$7.8 billion. This is analyzed to be an effect of the lower operation rate of nuclear power plants and the higher utility rate of LNG power plants. In fact, the cost difference of
$7.8 billion between the two plans is large enough to construct an additional four nuclear power plants and five coal plants, which makes it important to remove the distortion effect of operation and maintenance costs in the previous expansion model. In addition, when establishing a long-term development plan, the effect of applying a power generation system operation plan (unit commitment plan) in Stage III to calculate operation and maintenance costs will be very large.
5.2.3. Comparison with National Electricity Demand and Supply Plan
Lastly,
Table 10 shows the comparison between the experiment results deduced through the integrated model (Stage IV) and the construction plan suggested in the national electricity demand and supply plan. Compared to the national electricity demand and supply plan, the results of the integrated model had −2 new nuclear plants, −3 coal plants, and +5 LNG plants. The proportion of LNG power plants increased in the experiment results of the integrated model because of the following reasons: First, the model is analyzed to select LNG combined thermal power plants as being more optimal when a high operation reserve rate is required when the rise and fall of demand is high, because they can turn on instantaneously in ramping up and down or stopped state. Next, the fuel cost of LNG is analyzed to be lower due to the introduction of shale gas, which increased the competitiveness of LNG combined thermal power plants.
6. Conclusions
The current study aims to establish the optimal Generation System Expansion Plan that can satisfy the increasing electricity demand while maintaining operational elements and the stability of the energy supply. Detailed goals following this objective are suggesting the optimal Generation System Expansion Plan methodology that integrates the planning level and operational level and verifying the validity of the model based on actual data in the national electricity demand and supply plan. Architecture meeting these objectives is divided into four stages. Stage I estimates the seasonal Holt-Winters time series function to generate future demand data to be used in establishing the Generation System Expansion Plan and executed statistical significant verification. In addition, power plant data to be used in the actual Generation System Expansion Plan were defined and verified data were collected.
Stage II involved the previous Generation System Expansion Plan model. In other words, based on the WASP-IV model, Korea’s power supply and demand plan results were derived. The Korea Power Exchange has been using the WASP-IV model to derive the electricity supply plan from the first plan to the present 7th plan. Therefore, we used the results of the power development plan as a basic case to compare the results of the integrated model and power plants with similar characteristics were grouped to reduce the calculation complexity of unit commitment in Stage III.
Stage II served to generate a feasible solution considering the maximum demand and capacity reserve rate and produced construction costs excluding the remaining value of new power plants. In Stage III, a unit commitment model that can calculate power generation output and operation and maintenance cost was established, formalizing the problem of grouping power plants with similar characteristics to reduce the calculation complexity in a long-term expansion plan. Considering the limitations of the previous Generation System Expansion Plan, Stage IV proposed an integrated model in which the models proposed in Stage II and III interact. That is, this integrated model provides the optimal solution that minimizes the total cost among the results from multiple expansion plan candidates, by connecting the expansion plan candidates and construction cost information provided in Stage II and realistic operation and maintenance cost information. Through this model, the current study provided a quick method for finding the solution using a branch-and-cut technique on many possible combinations of feasible solutions. By establishing the same environment as the process of setting up a national electricity demand and supply plan, the current study proposed a result through the integrated model. In addition, the previous methodology provided in Stage II was used to provide comparison/analysis of the results of the national electricity demand and supply plan.
Based on the limitations of the long-term electricity demand and supply plan established by the government, the current study produced a power generation system operation plan model that can calculate realistic operation and maintenance costs. In addition, the study is meaningful in that it provided a methodology that can connect the Generation System Expansion plan and an operation plan. However, there is still a great deal of work to be done. Extensions are possible in the methodological aspects, technological aspects and the applications described in this research.
First, uncertainties must be considered when establishing plans for the future. Among the parameters used in the current study, ones with the highest uncertainty are demand data and fuel prices. The Generation System Expansion Plan produces solutions with a plan period of more than fifteen years. In such a case, it is impossible to precisely forecast long-term electricity demands and fuel prices based on the current point of time. As such, the research must expand into a stochastic optimization model or a robust optimization model that can solve such problems in this respect.
Next, the Korean government announced to the international community that it will cut national greenhouse gas emissions by 37% of business-as-usual (BAU) by 2030. Under such circumstances, greenhouse gas emissions in the Korean power generation industry accounted for 36.7% of national greenhouse gas emissions in 2011, which indicates that the industry must reduce its emissions to meet the government goal by 2030. As such, there is a need to transition to a model that can calculate the industry’s yearly greenhouse gas emissions for the Korean government to meet its emissions goal. In addition, the industry must expand the model to consider fuel sources, such as new and renewable energy and CCS that can further reduce greenhouse gas emissions.
Finally, when the smart grid policy becomes commonplace, it will be necessary to consider a model of the power generation market that reflects the introduction of small scale distributed power sources and an integrated model that is linked to the power trading market.