1. Introduction
The forthcoming fifth-generation (5G) wireless networks are expected to provide high-speed seamless multimedia services with low latency and excellent reliability [
1]. The scope of 5G services is not limited to personal wireless communications but extends to the services associated with mobile gadgets, wearable devices, sensors, actuators, machines, robots, vehicles, and other applications [
2]. 5G technology is expected to be a combination of cooperative heterogeneous networks of multi-tier communication systems and different radio access technologies [
3,
4]. The heterogeneous feature in 5G technology will provide orders-of-magnitude improvement, including 1000 times higher data volume per area, 10–100 times more connected devices, 10–100 times higher user data rates, one-tenth the energy consumption, and sub-millisecond end-to-end latency. However, the challenges faced by 5G systems are manifold because of the heterogeneity in terms of services, classification of devices, deployment scenarios, environments, and mobility [
4,
5]. In addition to its heterogeneous nature, another major challenge surrounding 5G is the random and diverse high-volume user data [
5,
6]. A large number of users, i.e., active connections, having different quality of service (QoS) requirements, is also a challenging task for 5G networks [
6]. Hence, to provide the services promised by 5G, innovative changes in both wireless technologies and core networks are required [
2,
6].
Aspects such as mobility, latency, widespread coverage, Internet of Things (IoT) services [
7], peak data rates, area traffic capacity, energy efficiency, spectrum efficiency, and spectrum utilization are the key performance indicators that can be regarded as technical requirements for 5G networks [
2,
8]. Hence, 5G technology requires new radio frequencies with wider spectrum bands to deliver the promised performance improvements. The ITU-R IMT-2020 (5G) vision includes three usage scenarios; enhanced mobile broadband (eMBB), massive machine type communication (mMTC), and ultra-reliable and low latency communications (URLLC) [
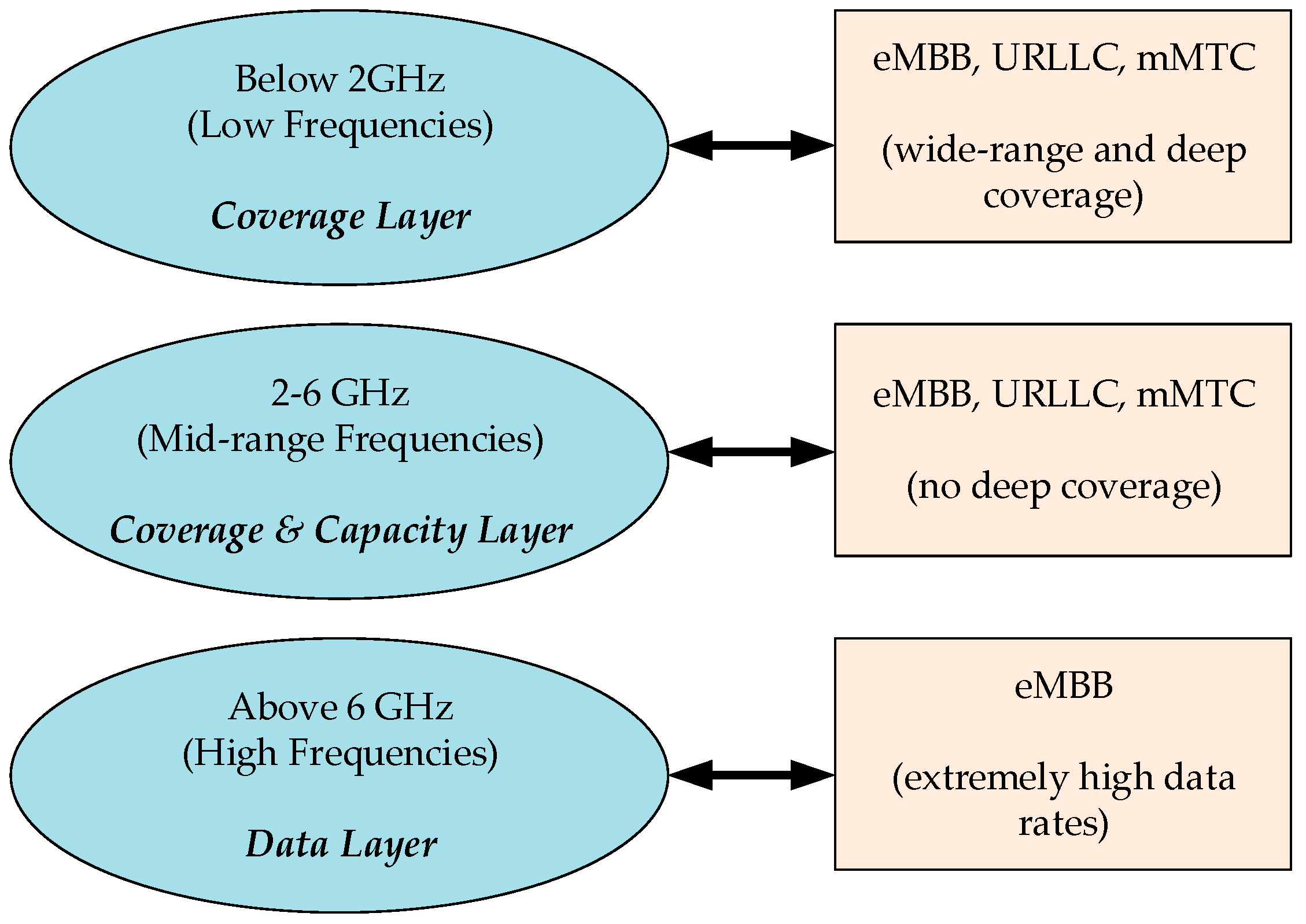
8]. In this regard, a multi-layer spectrum approach, as shown in
Figure 1, is proposed for a wide range of proposed scenarios, use cases, and requirements associated with 5G. The spectrum distribution includes the 2–6 GHz range (C-band), the above-6-GHz range, and the below-2-GHz range. Each band-range has specific characteristics to make it suitable for certain deployment scenarios. The low range has good propagation aspects to make it suitable for the coverage, though it is limited in capacity. The mid-range offers a reasonable mixture of coverage and capacity for 5G services, because it is suitable for the coverage for urban deployment, along with the increased capacity. The high range is needed for 5G services such as ultra-high-speed mobile broadband, but has limited coverage. Recently, the highly uncongested 60-GHz band, known as the millimeter radio (mmWave) band, has become the next major frequency band for wireless communication services, because of its short-range and wider-area applications. Researchers have started investigating mmWave communication in various scenarios. The band is capable of delivering high-speed services, though with less range, and can be ideal for small-cell networks [
9].
1.1. Background and Motivation
The key requirements for 5G technology include near-zero delay, high reliability, device support for heterogeneous networks, spectrum flexibility, and energy efficiency. Spectrum allocation is considered one of the major problems among the mentioned requirements [
1,
9]. The static spectrum allocation policies are inefficient for meeting the ever-growing demand of spectrum resources, which are needed for high-speed wireless access in 5G cellular networks [
10]. Radio resources have become increasingly scarce because of the static spectrum allocation approaches. The unlicensed users cannot access the licensed bands, making the bands under-utilized [
6,
10]. Spectrum allocation flexibility and spectrum utilization efficiency can be achieved with different proposed technologies, such as LTE-WiFi aggregation (LWA) [
11], operations in millimeter-wave band [
12], LTE over the unlicensed band (LTE-U) [
13], multicasting [
14,
15], layer-division multiplexing [
14,
16], ultra-dense small cells in 5G architecture [
17], non-orthogonal multiple access (NOMA) [
18,
19,
20], and software-defined cognitive radio network (SD-CRN) [
21,
22,
23,
24,
25].
LTE-U has emerged as an effective way to improve the spectral efficiency and capacity of wireless networks. Using LTE-U along with superior techniques such as carrier aggregation (CA), the performance of wireless networks can be improved significantly. However, an effective coexistence mechanism between LTE-U and Wi-Fi systems is necessary. Millimeter wave communications leverage the large-bandwidth potentially available at mmWave frequency band to provide the high data rates, and is considered to be a promising technology for the next-generation cellular networks. However, the performance evaluation of mmWave mobile communication systems, such as quantitative analysis of system-level propagation performance, and architecture evaluation need to be explored. Multicasting is a popular technique to simultaneously convey data to a group of terminals through point-to-multipoint communications, with positive impact on capacity and spectrum efficiency of the cellular systems. However, multicast traffic over 5G networks does not involve the end-user devices only, but also machine-type communications for IoT. In future broadcasting systems, layer-division multiplexing has been proposed to enable mobile TV on top of conventional terrestrial digital TV services, increasing the efficiency of the spectrum. In 5G systems, vehicular-to-everything (V2X) communications will also gain higher interest considering the ultra-dense and high-load scenarios. NOMA is one of the promising radio access techniques for performance enhancement and greater spectrum efficiency in 5G systems. In NOMA, multiple users are served at the same time and frequency, but are multiplexed based on the power or code domains. The integration of NOMA protocols with CR systems improves the spectral efficiency significantly. However, the performance analysis of a cooperative CR-NOMA schemes requires high computational complexity. Furthermore, in a possible radio-band assignment for 5G networks, different frequency bands will be used for macro cells and ultra-dense small cells. Such a 5G architecture will require intelligent spectrum sensing using CR technology to aggregate the spectrum bandwidths for small and large cells.
The software-defined cognitive radio network (SD-CRN) is a promising technology to mitigate the spectrum scarcity and spectrum under-utilization issues in wireless systems. Enabling CR features in dense 5G networks can maximize the spectrum utilization. The users are generally categorized into a multi-tiered hierarchy in CR systems; primary users (PUs) have priority of spectrum access over the secondary users (SUs) [
24]. Dynamic spectrum access techniques enable time-division multiple access (TDMA)-based spectrum sharing between the PUs and SUs, without requiring any major modifications in the primary systems [
22,
23,
24]. The three possible paradigms of spectrum access in CRNs include overlay, underlay, and interweave [
25,
26]. In underlay schemes, SU and PU may transmit simultaneously under the constraint of SUs’ interference to the PU. On the contrary, in overlay schemes, SU not only transmits its own signal, but also assists the primary transmissions through some relaying techniques. In interweave-based schemes, SU is capable of exploiting the spectrum opportunities via spectrum sensing, hence enhancing the utilization efficiency of spectrum. In interweave CR (I-CR) systems, SUs are allowed to opportunistically exploit the primary network, without interrupting the primary transmissions significantly. The successful integration of the PU with SUs is subject to the condition that a certain QoS level for a PU must be guaranteed, and can be accomplished through spectrum sensing. Hence, reliable spectrum sensing, using software-defined radio technology and an advanced cognition engine, is the most crucial part of CRNs [
25,
26,
27,
28]. Spectrum sensing is performed either independently or in a cooperative manner. If a SU detects PU transmission, it needs to release the channel and switch to another idle channel if one is available, or wait if no vacant channel is available. Energy detection (ED), spectral detection, and waveform detection are the common spectrum sensing techniques in I-CRN [
27]. The ED scheme is one of the conventional channel sensing approaches. It provides relatively low computational complexity because it relies on PU signal power detection. In addition, a priori knowledge of the PU signal is not required. However, a major drawback for the ED scheme is that it has poor sensing performance in low-SNR conditions. Cooperative spectrum sensing (CSS) is one of the efficient approaches used to combat the hidden terminal problems, deep fading, and shadowing effects. CSS approaches exploit the spatial diversity by deploying multiple distributed SUs [
28]. In such a case, a central node, i.e., a fusion center (FC), makes a final decision on the availability of considered channel by combining the local sensing information of multiple SUs. The FC applies data fusion techniques, such as equal gain combining, maximal ratio combination, and Bayesian fusion, or decision fusion techniques such as the
AND,
OR, and
K-OUT-N rules [
27,
28]. When multiple SUs exist, better sensing performance can be achieved while allocating less time to the sensing operations [
19,
29].
1.2. Related Work
The performance of the opportunistic spectrum access (OSA)-based I-CRNs has been lavishly published. A substantial amount of research has been dedicated to the CR architecture, to its operating principle, mobility, and spectrum sensing performance both in perfect and realistic imperfect sensing scenarios [
28,
29,
30,
31,
32,
33,
34,
35,
36,
37]. Nevertheless, analytical modelling of the spectrum utilization due to dynamic nature of the PU is a challenging task [
30,
31,
32,
33,
34,
35,
36,
37]. In our own prior contribution [
19], we studied the improvement of the sum rate by optimizing the sensing operating point, e.g., the sensing threshold, in conventional orthogonal CR networks, because sensing errors, i.e., missed-detection events and false alarms, cannot be avoided in real-time spectrum sensing. We also investigated the optimal sensing operating points, adaptive to different sensing parameters, to maximize the achievable sum rates of the considered networks. Bradonjic et al. [
30] discussed the operation of the CR networks over a dynamic bandwidth in both time and space. The integration of users in CRN requires SUs to be capable of efficient sensing and keeping precise track of the primary transmissions. The unique characteristic of SUs co-existing with PUs is the dynamic nature of the spectrum availability. The CRN operates over a dynamic bandwidth (i.e., both in time and space) that inherently forms clusters. Hence, it is important to consider both the spatial and temporal dimensions of spectrum opportunities on the basis of PU activities. The network topologies, based on the interaction between the integrated users, depend on the physical proximity and availability of the spectrum holes. Specifically, Ozger et al. [
34], and Sun et al. [
37] discussed the utilization of spectrum for different network topologies. For the communicating SU nodes, the packet must be transmitted to the corresponding receiver without any significant error, along with the correct detection of spatial-temporal spectral opportunity. However, the transmitted packet may be severely damaged by the poor channel conditions, thus degrading the transmission reliability. Moreover, Mehrnoush et al. [
31] analyzed the impact of spectrum handoff on the performance of considered CRN. Spectrum handoff occurs when a channel is being utilized by a SU and a PU appears. Thus, the SU needs to vacate the channel and migrate to another channel in order to transmit a packet successfully. In a nutshell, spectrum-aware communication in CRNs requires timely and accurate detection of the spatial-temporal spectrum access opportunities, efficient spectrum mobility (spectrum handoff) when required, and successful transmission of the SU and PU packets.
1.3. Contribution of the Paper
This paper further develops our research on the utilization of spectrum [
32,
33]. In Ref. [
32,
33], we formulated and analyzed the utilization of spectrum for the SUs and PU, i.e., sum utilization of spectrum. In Ref. [
33], we considered different SU and PU co-existing scenarios, and investigated the sum utilization of spectrum, with retransmission capability for the SU, to ensure the reliable packet delivery. We characterized the gain in the sum utilization of spectrum with the SU retransmission capability, as SU was allowed to retransmit its packet during the PU mean inactive duration, and SU packet length, in order to improve the link reliability. In our previous studies, sum utilization of spectrum was characterized while considering the single channel. By contrast, in this study, we formulate and analyze the utilization of spectrum policy for multi-channel scenarios, with the aid of sensing and handoff capabilities. We investigate the utilization of spectrum for PU and SU, with SU opportunistically operating on various PU channels. We derive closed-form expressions for sum utilization of spectrum, evaluating the impact of spectrum handoff under different network topologies. Our performance results show that the spectrum handoff approach, based on sensing outcomes and PU interruptions, enhances the sum utilization of spectrum.
2. System Model
In this section, we present the system model, assumptions, and spectrum sensing design. We assume a decentralized interweave TDMA hierarchical CR network, with nodes self-organizing into a network [
19,
29,
33]. In the study, we consider a CRN with
N narrowband channels, with each narrowband channel licensed to a PU. It is assumed that a SU employs an ED scheme. The performance metric in term of detection probability and false-alarm probability measures the performance of the ED scheme. On the basis of the probability density function (PDF) of the test statistic, complex-valued phase-shift keying signaling, and circularly symmetric complex Gaussian noise [
32,
33,
34], the closed-form expressions of sensing probabilities are considered. The SU is assumed to be equipped with a single narrowband antenna to sense the considered channel. This assumption would be applied to real-world hardware-constrained CRNs. A SU performs sensing procedure in a sequential order, with a fixed sampling frequency and constant transmit power, to locate the spectrum holes. The considered channels are assumed to be idle or busy depending on the sensing outcomes. We assume that the SU transmitter is always ready to transmit the packet, provided that considered channel is available [
36]. The secondary network cannot guarantee on-time services, i.e., QoS is not guaranteed. The suitable traffic pattern for the secondary network can be best-effort data. Therefore, we assume that the secondary traffic is back-logged, i.e., the secondary queue always has a data to be transmitted. It is also assumed that the SU has the switching capability to drive multiple spectrum handoffs. We assume that the spectrum sensing procedure is executed until handoff operation is initiated. In this study, spectrum handoff delay is not considered, and is assumed that the handoff is executed immediately when necessary. In addition, the sensing duration is assumed to be identical at each channel. We consider a single set of communicating SU nodes for the system, and that the sensing procedure is performed at each channel.
For ease of reference, we summarize our commonly used notations in
Table 1.
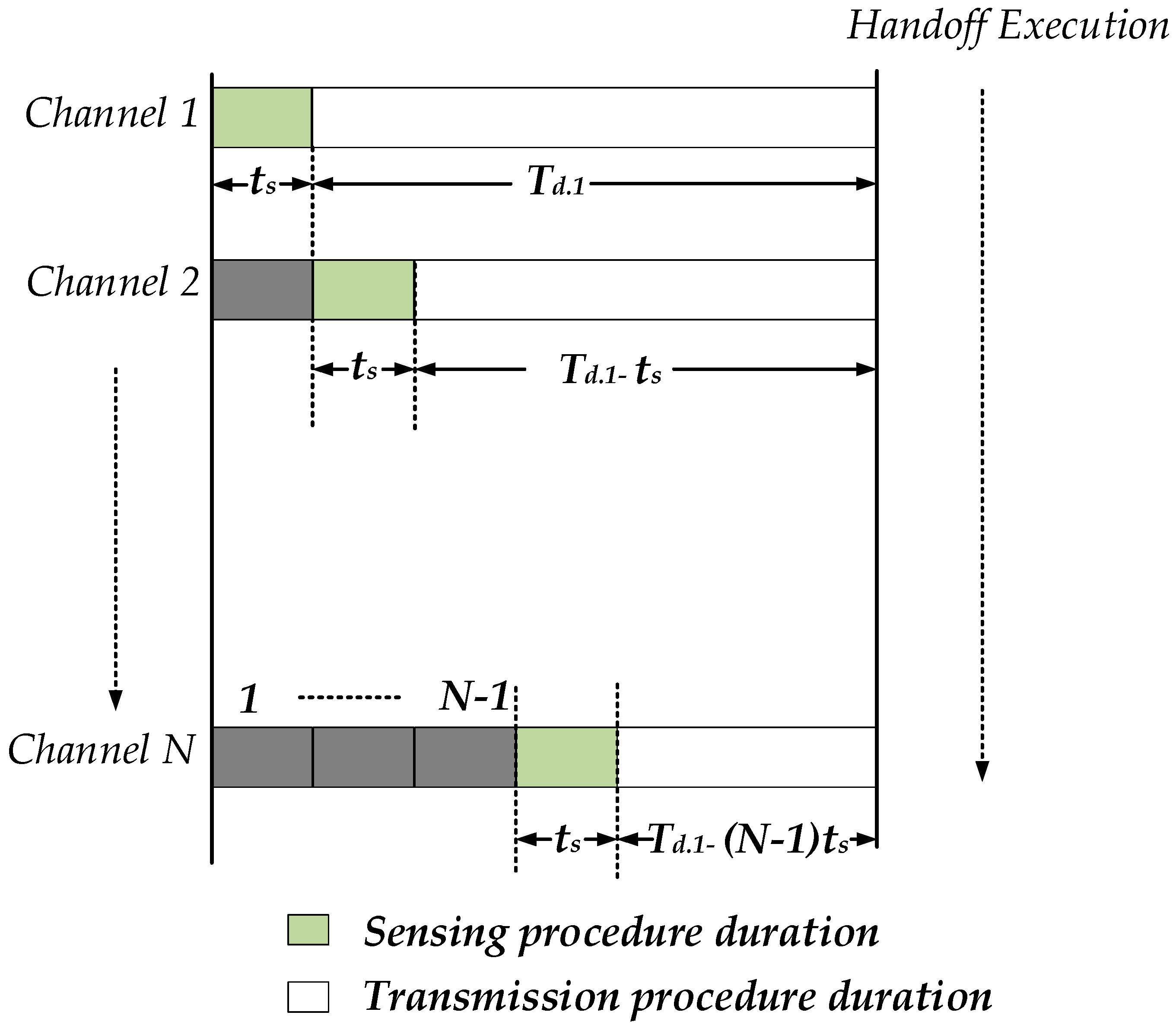
The time slots in OSA-based frame structure of SU over different channels is shown in
Figure 2. The frame structure consists of sensing time and transmission time over the given set of channels. After the sensing procedure is complete, the SU transmits in the unoccupied channel for the transmission time. The available transmission time in the
channel, i.e., after the
handoff, is
. It is assumed that if the
jth channel is found free, the SU will be able to transmit the corresponding packet in the available transmission duration, and will not sense the next channel, i.e., (
j + 1)th channel. In this study, we assume the upper limit for the allowable number of handoffs, i.e.,
N, and also, that the transmission duration over the considered channel is enough to transmit the corresponding packet. If the
Nth channel is found busy, the SU waits for the next time-slot to sense the first channel again. For a given detection threshold, an inherent tradeoff [
19] exists in the frame structure between the sensing time and transmission time over the considered channel. It is assumed that the packet transmissions of SU and PU are synchronized at each slot.
We assume that the PU is authorized to use a fixed spectrum, which is divided into a set of narrowband channels
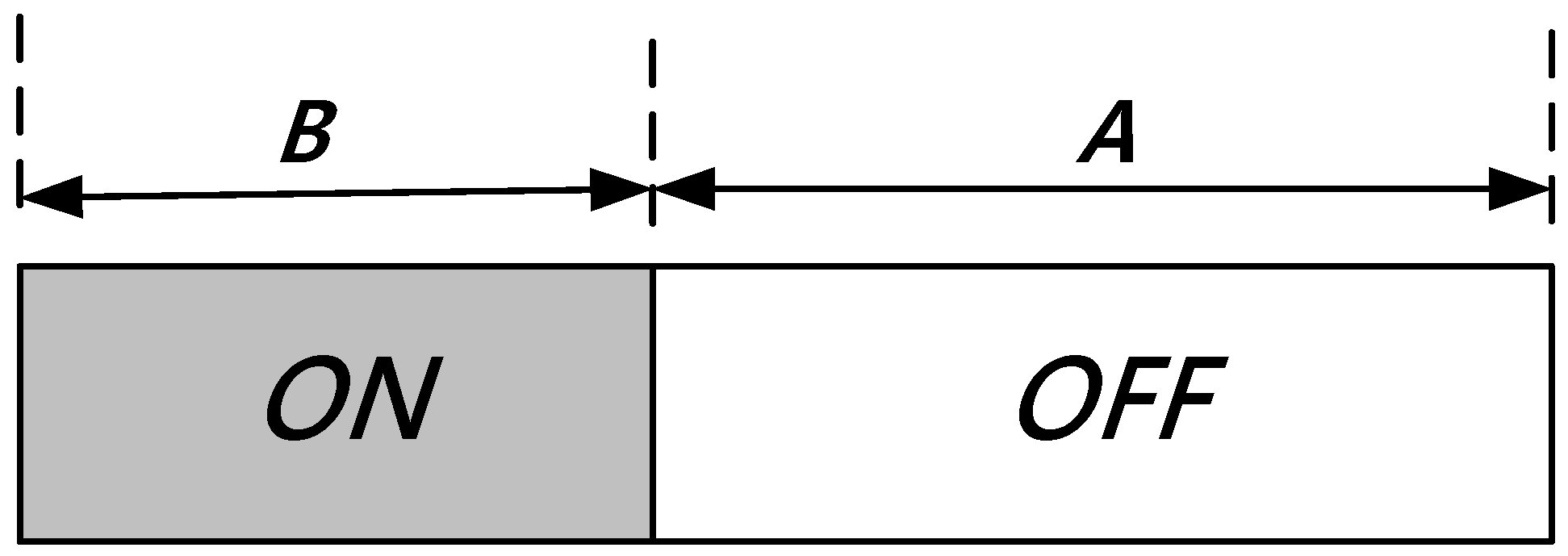
. We assume that PU traffic across all the primary channels is independent and identically distributed. Therefore, the utility performance in a case that the handoff channel is randomly selected is the same as that in a case that the handoff channel is sequentially selected. Hence, activity of a PU over the channels is sensed in a sequential order, starting from the first channel. If the current channel is idle, a packet is transmitted to the corresponding receiver. If the channel is busy, the SU switches to the next channel with the aid of spectrum handoff, and senses the PU activity in the next channel. The activity of PU on a channel is modeled by discrete-time semi-Markov (two-state) process [
36,
37,
38,
39,
40], as shown in
Figure 3. The states alternate between the
OFF and
ON states. The
ON state represents that channel is occupied by the PU, and the
OFF state represents that channel is not occupied by the PU. Without the loss of generality, we assume that the length of
OFF and
ON durations is represented by the random variables
A and
B, respectively, and follows exponential distribution with means
R and
S, respectively. At any time, the probabilities that the PU is in
ON, and
OFF states are given by
PON =
S/(
S +
R), and
POFF =
R/(
S +
R), respectively. Furthermore, it is assumed that the states of the considered channel are independent of those of the other channels.
To model the imperfections of the channel sensing by incorporating sensing errors [
33,
34,
35,
36], the states of the considered channel are represented by missed-detections and false-alarm probabilities, and are calculated by the activity of PU and estimated sensing outcomes. A detection event occurs when a SU successfully senses an occupied channel, and a false alarm indicates a busy status for an idle channel (i.e., the transmission opportunity is wasted). As shown in our previous work [
19], a higher detection probability results in better protection for the PU, and a higher false alarm probability means less chance for the SU to utilize the channel. The utilization of the spectrum can be improved with the selection of the optimal sensing operating point depending on the sensing parameters (e.g., SNR) and sensing duration [
33]. In the considered ED scheme, the detected signal is squared and integrated over the observation interval, and then the output is compared to a fixed threshold to make a local decision. In this study, the sum utilization of spectrum, i.e., joint utilization of spectrum by the SU and PU, is considered. Thus, the sensing performance under the QoS constraints for PU or SU can be formulated [
37]. We consider the sensing performance subject to a QoS constraint for the PU, i.e., the probability of detection is set at a desired value (to give a desired level of protection to the PU), and the probability of false alarm is obtained at a given SNR or sensing duration.
The receiver operating characteristic with given assumptions is expressed as
where
is the channel index,
(detection probability) and
(false alarm probability) are the sensing pair on the
jth channel,
is the SNR of the PU signal at the SU on the
jth channel,
is the number of sensing samples of the SU on the
jth channel, and
Q(·) and
Q−1(·) denote the complementary distribution function of the standard Gaussian and its inverse, respectively.
The four possible cases of sensing outcomes and PU activities, i.e., PONPD, PONPMD, POFFPFA, and POFF(1 − PFA), are considered for the proposed analysis, and are assumed to be identical for all channels. In detail, PONPD refers to a scenario where the activity of a PU on a channel is represented by the ON state, and the state is correctly detected by a SU. PONPMD refers to the case where the PU is in the ON state, but the state is incorrectly detected by the SU, and a missed detection occurs. POFFPFA refers to the case where the PU is in the OFF state, but the state is incorrectly detected by the SU, and a false alarm occurs. Similarly, POFF(1 − PFA) refers to the scenario where the PU is in the OFF state, and the state is correctly detected by the SU. A CR transmitter, i.e., SU, switches to the next channel for the two cases, i.e., PONPMD and POFFPFA. In our work, we assume that the sum utilization of spectrum is contributed only when a SU detects the state of the considered channel correctly, i.e., POFF(1 − PFA) and PONPD. The access contention for the SUs is not considered.
3. Sum Utilization of Spectrum
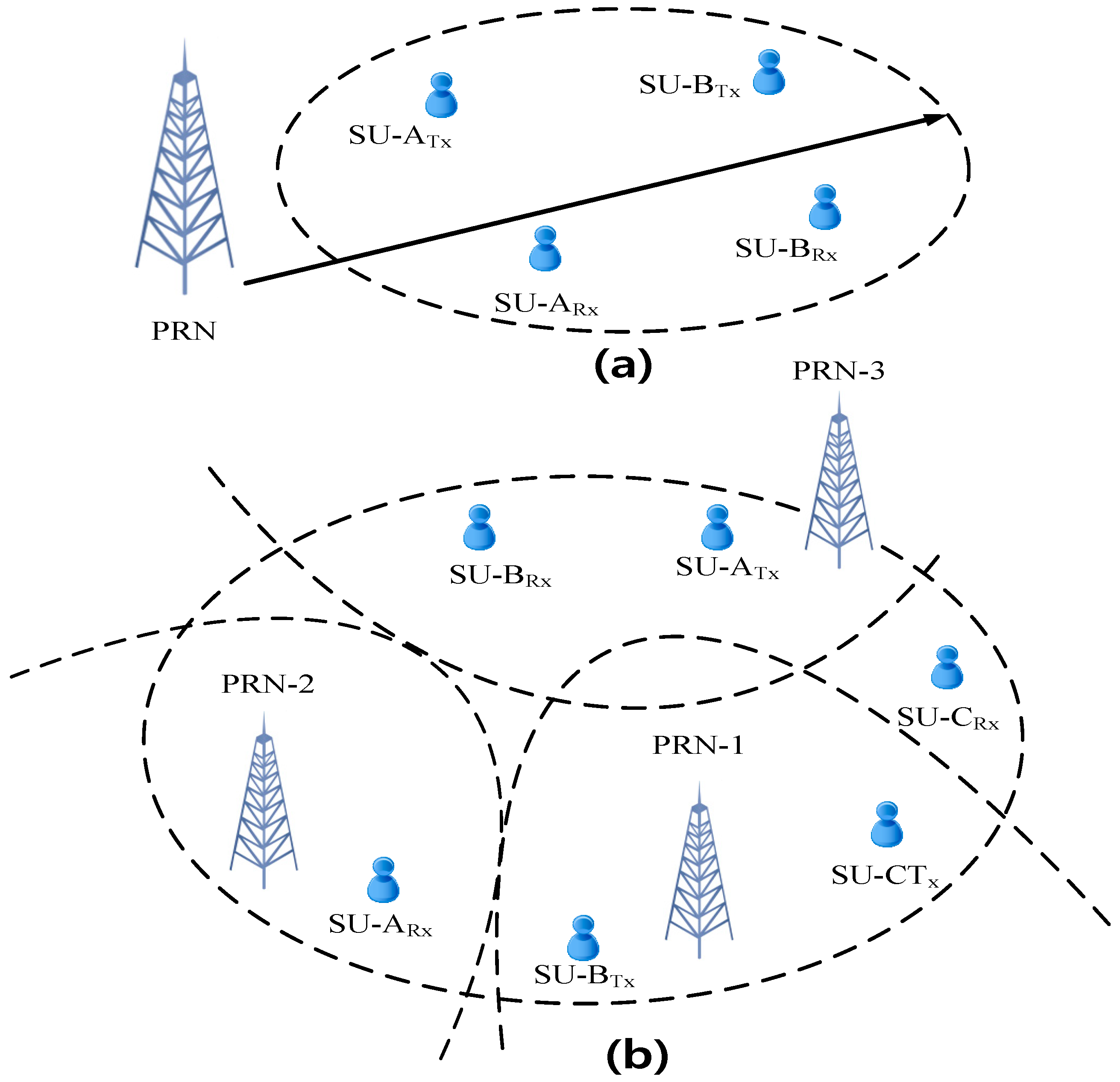
In this section, we consider different PU and SU co-existing network topologies and describe the formulation and analysis of sum utilization of spectrum for different sets of channels. We consider two topological models, i.e., topology-1, and topology-2, as shown in
Figure 4, to investigate both the spatial and temporal variation conditions on the set of idle channels between the communicating SUs [
30]. The sum utilization of spectrum is evaluated for both topological models separately. Topology-1 considers the identical sets of idle channels for the communicating SUs, because both SUs are within the coverage range of the same PU. As shown in
Figure 4, the communicating SUs, i.e.,
SU-ATx and
SU-ARx, or the
SU-BTx and
SU-BRx, lie within the communication range of the same primary network (PRN). Hence, the variation conditions on the set of idle channels is temporal only. For topology-2, communicating SUs are subjected to activity from a possibly different set of PUs. The PU coverage range is comparable to that of the SUs. As shown in
Figure 4, the communicating SUs, i.e.,
SU-ATx and
SU-ARx, are within the communication range of different PRNs, i.e., PRN-3 and PRN-2, respectively. Hence, the variations of the idle channels are both spatial and temporal.
The considered channel
j can be found busy under two scenarios: the PU state is
ON and the state is correctly detected, and the PU state is
OFF and a false alarm occurs. The probability that the channel
j is found busy is expressed as
Furthermore, the channel
j can be found idle under two scenarios: the PU state is
OFF and the state is correctly detected, and the PU state is
ON and is not detected. The probability that channel
j is found idle is expressed as
Under the two-state model,
H0 and
H1 denote the events to consider the
OFF and
ON states, respectively, of the PU in the current channel. Given Equation (3), channel
j in a given time-slot can also be regarded as idle because of a missed detection. The actual free channel
j, without a false alarm, is estimated. Thus, the probability of detecting the spectrum opportunity, for the current channel
j, is expressed as
After detecting the spectral opportunity correctly, the communicating SUs require a successful transmission condition. The successful transmission of a packet depends on the activity of PU, i.e., the PU must not access the licensed spectrum band during the transmission of SU packet. Hence, the probability of no activity during the sensing and transmission periods for a single-channel scenario is defined as
Similarly, the probability of no activity during the sensing and transmission periods, for the
channel among a set of
N channels, is defined as
where
, and
, denote the packet size (in bits) in the first, and the
jth channels, respectively.
In this study, we assume that the number of bits
are transmitted in the available transmission time
of the first channel. After the first handover,
(i.e.,
) bits are transmitted in the available transmission time
of the second channel. Moreover,
(i.e.,
) bits are transmitted on the
channel, after the
handover, in the available transmission time
. If the transmission duration is reduced after handoff, the number of transmitted bits is also reduced with the ratio of transmission duration. A channel error [
40] occurs when the SNR of a received packet is low because of path loss or a deep fading. The probability of obtaining an error-free packet over the
channel, because of channel errors only for the cognitive transmission, can be expressed as
where
is the SNR of the secondary transmission (i.e., transmitted power), and
BER is the bit error rate for BPSK in the Rayleigh fading channel and can be expressed as [
40]
We assume that the probability of an error-free transmission of packets that are transmitted in the case of a missed detection is one because the primary and secondary packets collide. In this study, we use the probability for the PU utilization over the given channel set. The probability of sum utilization of spectrum for topology-1 depends on the probability of detecting the spectrum opportunity at the transmitting and receiving SU nodes, probability of no activity during transmission, probability of error-free transmission, and the PU’s own utilization probability.
From Equations (4), (6), and (8), and PU utilization probability, the probability of sum utilization of spectrum for a single-channel scenario under topology-1 can be expressed as
For the multi-channel scenario, the number of bits in a packet is reduced in each try after handoff; hence, the weighting factor is introduced to consider the utilization as per the transmitted number of bits in each channel. The weighting factor is considered for the second channel because bits are transmitted in the available transmission time. Moreover, the weighting factor is considered for the jth channel, after the handoff, because bits are transmitted in the available transmission time.
Hence, the probability of sum utilization of spectrum, with the set of
N channels under topology-1, can be expressed as
Next, we investigate the sum utilization of spectrum under topology-2. Let
T be the union region of all those PRNs having coverage areas of the communicating SUs. In such a case, the probability of sum utilization of spectrum for topology-2 must be characterized for the two scenarios
S1 and
S2.
S1 refers to a scenario in which no PU is present within region
T.
S2 refers to a scenario in which there are
k PUs present within region
T. We assume that PUs are deployed with a uniform distribution with density Ω. Thus, the probability that no PU is present within region
T can be expressed as [
34]
For the S1 case, the probability of detecting the spectrum opportunity at both SU communicating nodes, and the probability that no PU is present within region T, are considered for the sum utilization of spectrum for the SU.
From Equations (4), (8) and (12), the probability of sum utilization of spectrum for the SU, for a single-channel scenario under
S1 of topology-2, is expressed by
For the
S2 scenario, assume that
k.PUs, and
PUs.OFF, are the required events that represent the
k PUs present within region
T, and those PUs have an
OFF state during SU transmission. The probability that there are
k PUs in the region
T is expressed in [
34] as
Hence, the probability that
k PUs are present within region
T, and are in the idle state during SU transmission over the first channel, can be expressed as [
34]
which can be simplified as
For the S2 case, the probability of detecting the spectrum opportunity at both SU communicating nodes, and the probability that k PUs present within region T have an idle state, are considered for the sum utilization of spectrum for the SU.
From Equations (4), (8) and (18), the probability of sum utilization of spectrum for the SU, for a single-channel scenario under
S2 of topology-2 is expressed by
Thus, from Equations (13) and (19), and PU utilization probability, the probability of sum utilization of spectrum for a single-channel scenario under topology-2 can be expressed as
The probability of sum utilization of spectrum for the SU with the set of
N channels under
S1 of topology-2 is expressed by
Similarly, the probability of sum utilization of spectrum for the SU with the set of
N channels under
S2 of topology-2 is expressed by
From Equations (21) and (22) and PU utilization probability, the probability of sum utilization of spectrum with the set of
N channels under topology-2 can be expressed as
4. Numerical Results and Discussion
In this section, numerical results are provided to evaluate the performance of sum utilization of spectrum under different network topologies, PU activities, sensing parameters, and sets of channels. In our simulation setup, we consider a CRN co-existing with a PRN that is licensed to use a set of
N = 5 frequency bands. The communication range of PU and SU is varied to allow different values of probabilities and sensing parameters. The licensed bands are occupied by a PU according to the PU model as shown in
Figure 3. To obtain the numerical results examined in this section, the key parameters are chosen as follows:
= 1000 bits,
= 100 kbps,
R = 20 ms to 100 ms,
= 1 ms to 10 ms, and Ω = 0.0001 m
−2. The sensing SNR at the SU is considered to be −15 dB. The SNR for the secondary transmissions over each channel is set to 30 dB, and hence, the
BER value is set to 0.00025. Unless otherwise stated, we consider the fair model of the PU for the channel status, i.e., P
ON = P
OFF = 0.5. The targeted detection probability
is set to 90%, to restrict the interference probability to the PU to 10% or less. The values of these parameters are considered accordingly to validate the characteristics of the considered set of channels and network behavior. In the simulation runs, the maximum of five channels, each occupied by a single PU, are considered. The observation period commences from the first narrowband accessible channel to the last one.
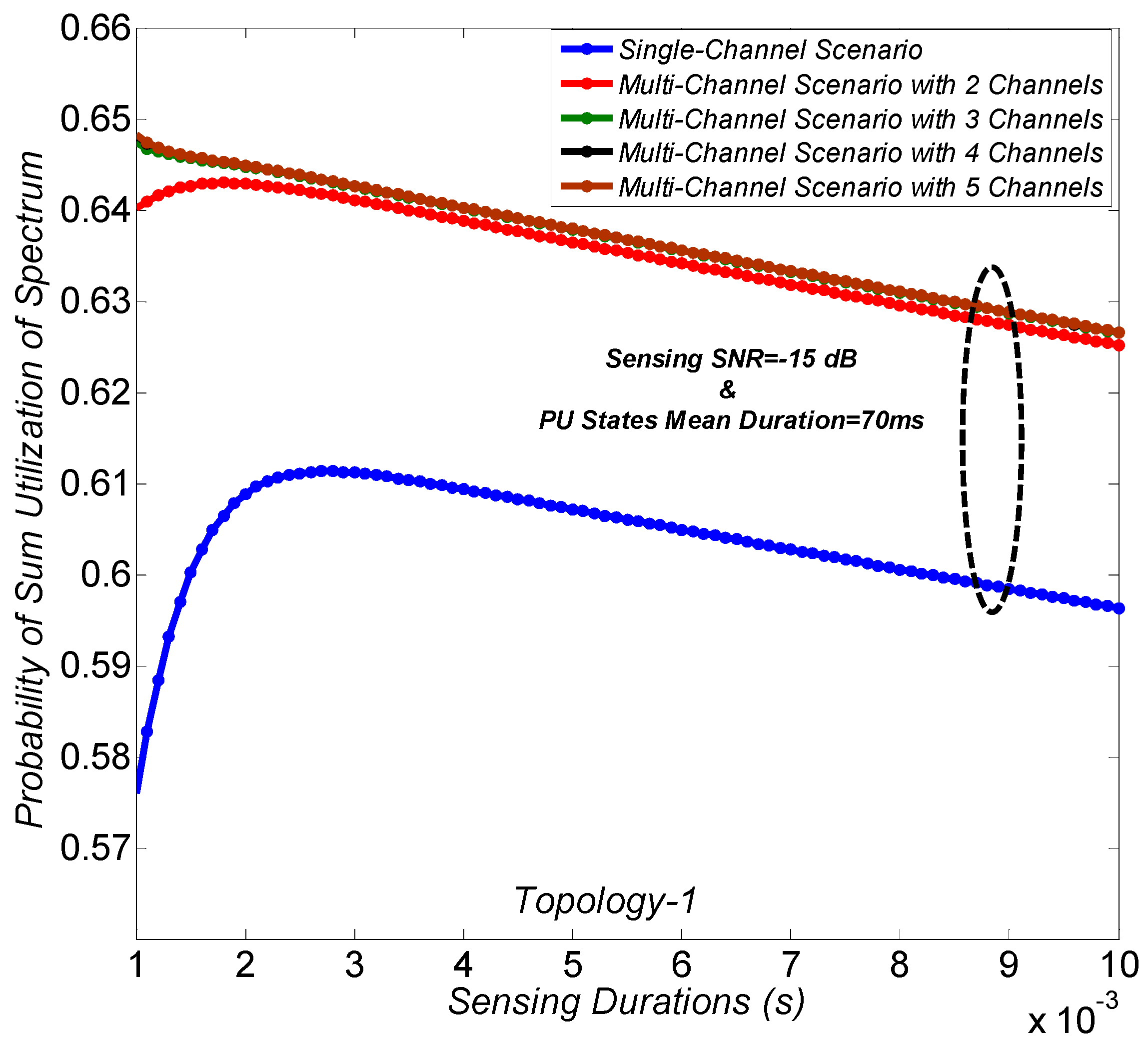
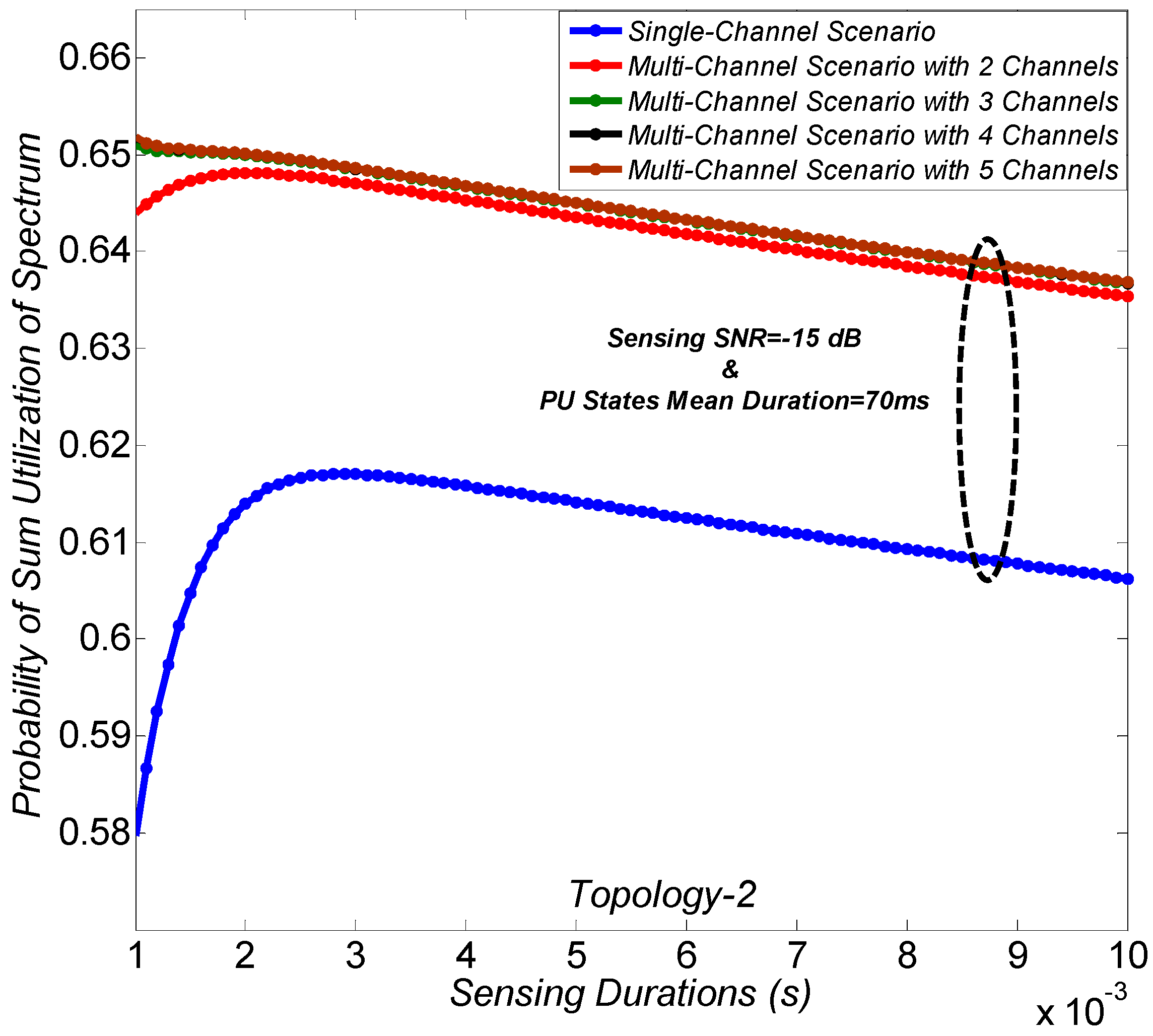
Figure 5 and
Figure 6 illustrate the probability of sum utilization of spectrum with different sensing durations and sets of channels, under the topology-1 model and topology-2 model, respectively. “Multi-channel” refers to a scenario in which different numbers of narrowband channels are considered, and the sum utilization probability over different numbers of narrowband channels is summed. The number of transmitted bits in a packet in the multi-channel scenario is adjusted as per the available transmission duration over that channel, and the weighting factor is added to consider the utilization as per the transmitted number of bits.
Figure 5 and
Figure 6 validate the inherent tradeoff in the utilization of spectrum of the SU for single-channel scenario over different sensing durations. With the targeted detection probability, the spectrum utilization performance for the PU is considered to be the same. The tradeoff exists for any value of PU states mean durations considering the fair model of the PU for its channel status, i.e., the same PU states probabilities. The tradeoff exists between the two probabilities, i.e., the probability of “no activity during transmission” and the probability of “detecting the spectrum opportunity”. In detail, the increase in probability of “detecting the spectrum opportunity” over the shorter sensing durations is dominant over the decrease in probability of “no activity during transmission.” Similarly, the decrease in probability of “no activity during transmission” over the longer sensing durations is dominant over the increase in probability of “detecting the spectrum opportunity”. Hence, our results validate that an optimal sensing duration exists for single-channel scenario. However, the optimal sensing duration depends on the handoff probability and considered sensing parameters. It can be seen that the performance of the sum utilization of spectrum improves with the number of channels. The reason is that the multiple-channel scenario considers the transmission of a packet in the next channel for each PU interruption, and hence, enhances the reliability of the transmitted packet. However, the performance improvement is not significant when a large number of channels is considered. The reason is that in such a case, the handoff probability is not significant. Importantly, the result validates that it is necessary to consider the optimal number of channels subject to the considered network and sensing parameters in order to achieve the optimal sum utilization performance.
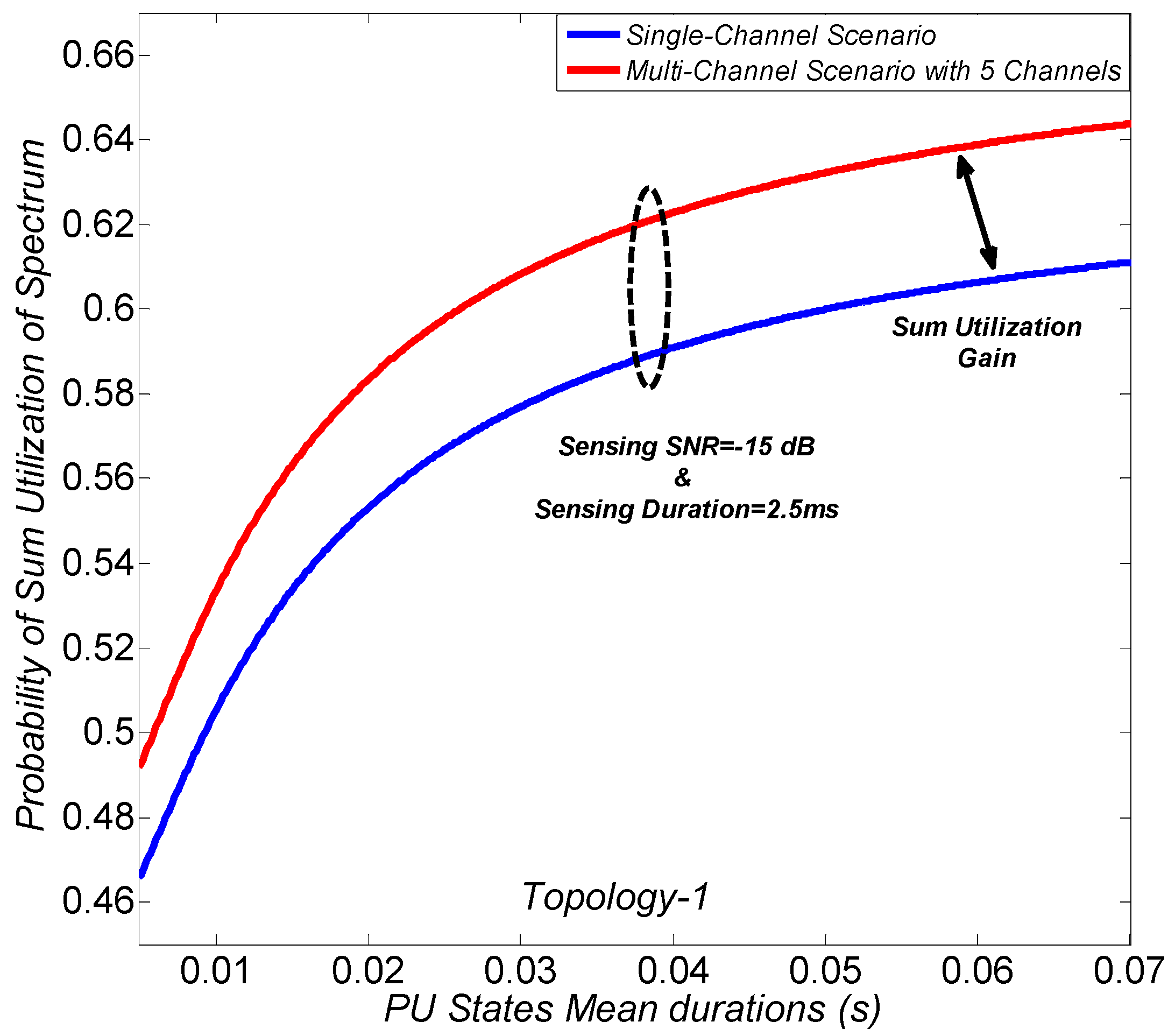
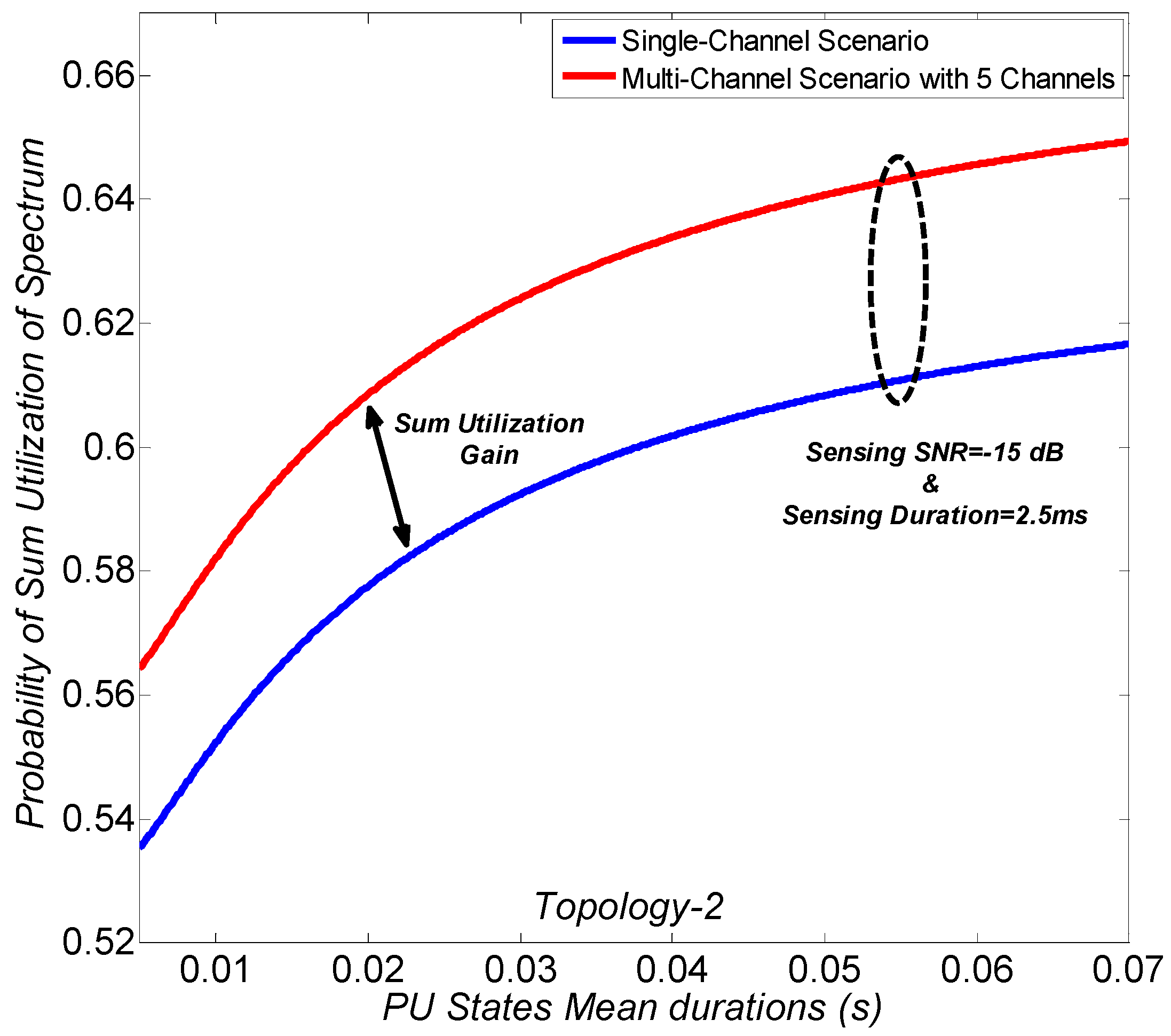
Figure 7 and
Figure 8 show the probability of sum utilization of spectrum with different PU states mean durations, for single- and multi-channel scenarios, under the topology-1 and topology-2 models, respectively. In the legend, “multi-channel” refers to a scenario in which five narrowband channels are considered, and the sum utilization for all the possible cases over five channels is considered. As previously explained, the fair model of the PU for channel status, i.e., same PU states probabilities, is considered. The number of transmitted bits is adjusted as per the available transmission duration in each channel, and the weighting factor is added accordingly. Again, the result shows that the performance of the sum utilization of spectrum improves with the number of channels. The sum utilization gain is shown for both topology models. In this study, the sum utilization gain refers to the performance improvement of the multi-channel scenario, as compared to the single-channel scenario. The sum utilization gain is achieved because of the handoff capability of SU, and considering the transmission of a packet in the next channel for each PU interruption. It can also be seen that the sum utilization of spectrum increases with the increase in the PU states mean durations. The PU states mean durations includes both the PU mean active and mean inactive durations. By considering the same PU states probabilities and targeted detection probability, the spectrum utilization performance for the PU is considered to be the same. However, a longer PU states mean duration indicates a longer PU mean inactive duration, and hence more spectrum utilization opportunities for the SU. In detail, the probability of “no activity during transmission” increases with the increase in the PU states mean duration, thereby increasing the probability of sum utilization of spectrum. This result illustrates the need to identify the optimal range of PU states mean durations subject to the considered sensing parameters to obtain the maximum sum utilization gain with the multi-channel scenario.
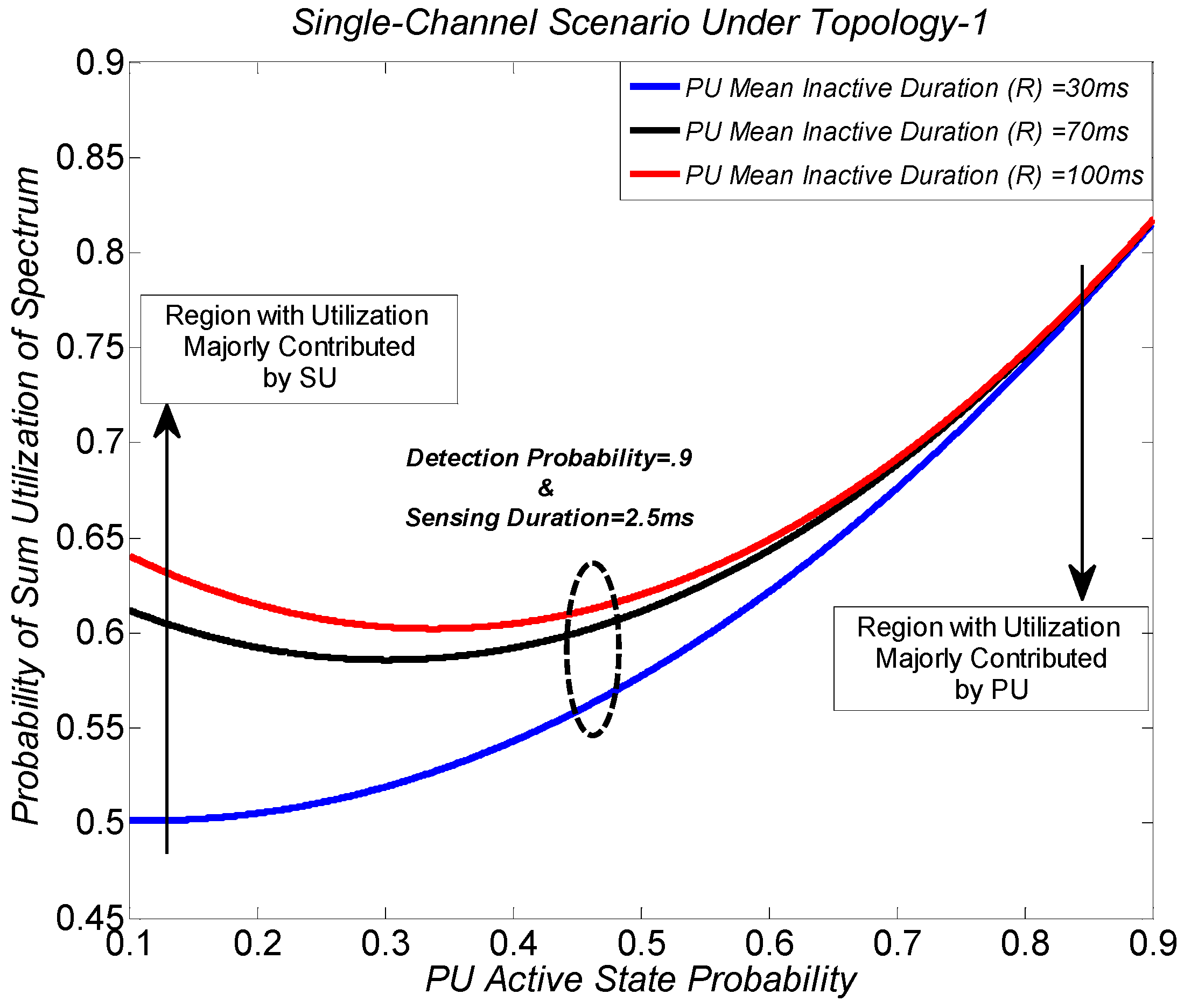
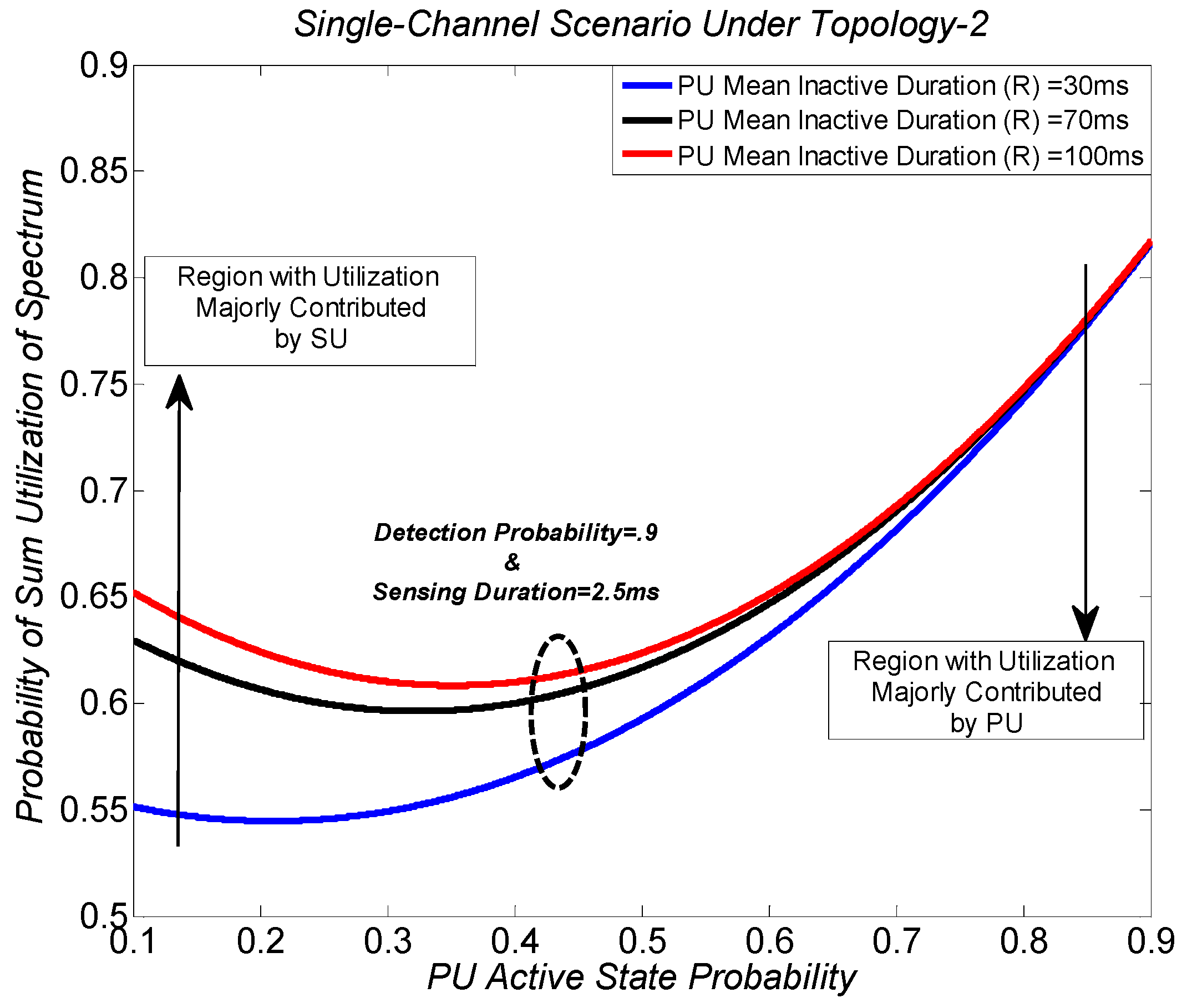
Figure 9 and
Figure 10 show the probability of sum utilization of spectrum with different PU active state probabilities and PU mean inactive durations for the single-channel scenario under topology-1 and topology-2, respectively. At the PU active state probability P
ON = 0.1, the utilization of spectrum is dominantly contributed by the SU. At the PU active state probability P
ON = 0.9, the utilization of spectrum is dominantly contributed by the PU. The sum utilization of spectrum increases when the PU uses the channel more actively. In addition, the overall utilization of spectrum when dominantly contributed by the PU is higher than when dominantly contributed by the SU, because the PU contributes more to the overall sum utilization of spectrum when the targeted detection probability is set to be 0.9. Furthermore, it can be seen in
Figure 9 and
Figure 10 that the sum utilization of spectrum increases with the increase in PU mean inactive durations. As explained previously, the spectrum utilization performance for the PU is considered to be the same because of the fixed targeted detection probability. However, longer PU mean inactive durations cause more spectrum utilization opportunities for the SU, and hence the probability of sum utilization of spectrum increases. It can also be observed that the increase in the sum utilization of spectrum with the PU mean inactive durations is dominant when the SU uses the channel more actively. However, the performance of the sum utilization of spectrum converges when the PU uses the channel more actively. The reason is that the SU’s utilization of spectrum is at a minimum when PU uses the channel more actively, and the PU mean inactive durations only affect the utilization performance of the SU. The results validated that it is important to identify the range of PU states probabilities subject to the targeted detection probability and PU states mean durations to achieve the required sum utilization performance.
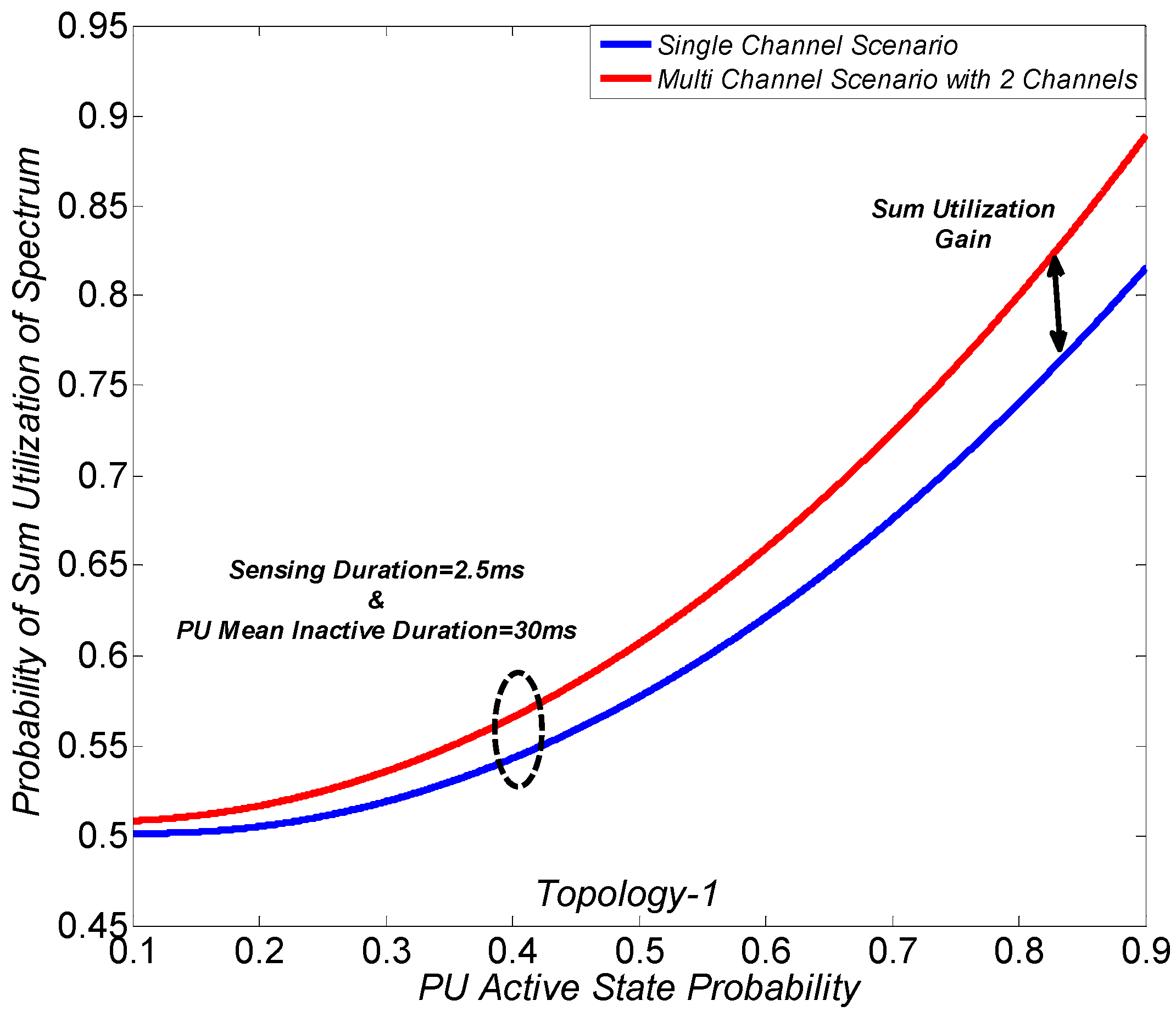
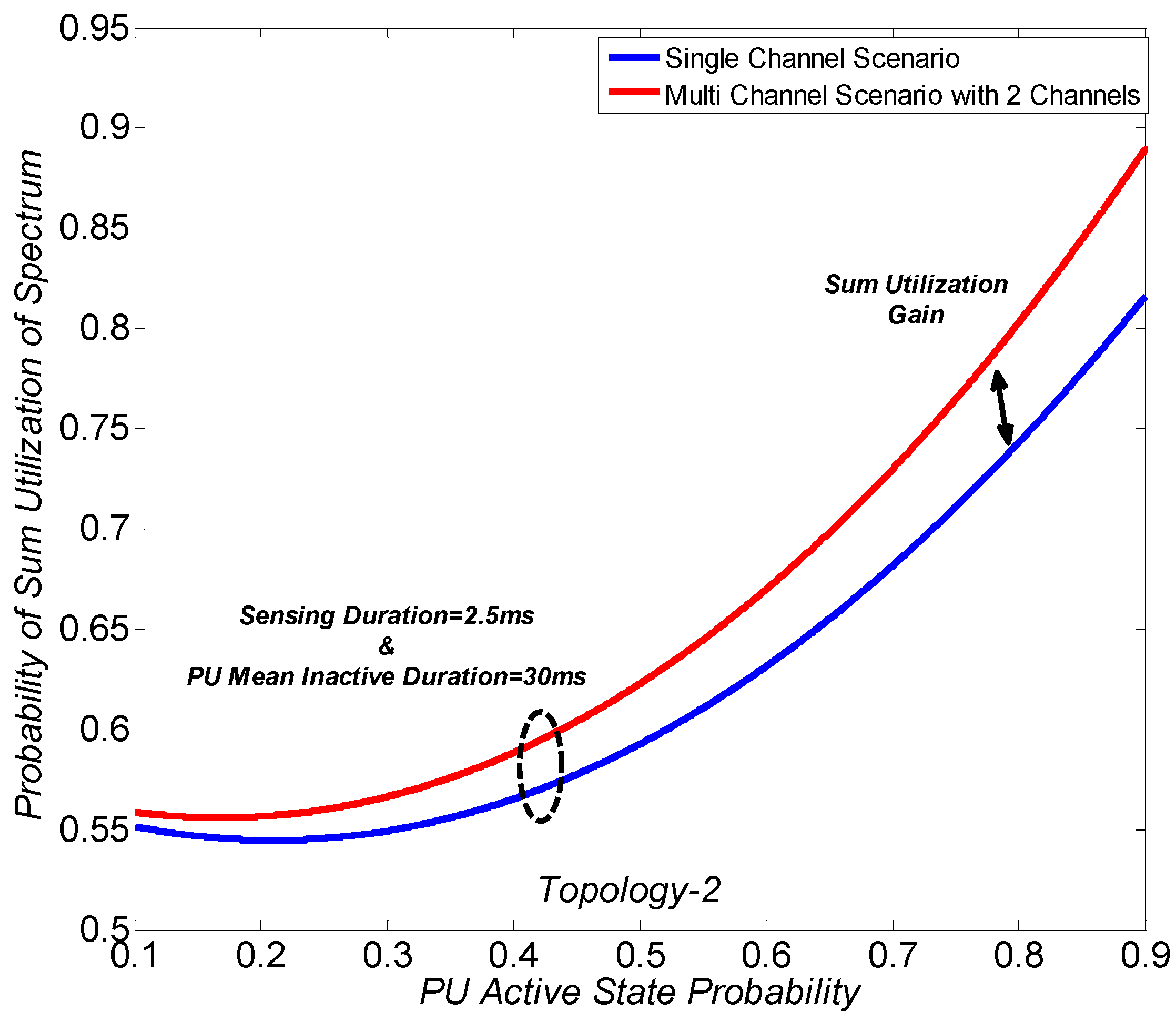
Figure 11 and
Figure 12 show the probability of sum utilization of spectrum with different PU active state probabilities for single- and multiple-channel scenarios under topology-1 and topology-2, respectively. In the multi-channel scenario, two narrowband channels are considered, and the utilization probability over the two channels is summed. As explained previously, the number of transmitted bits are fixed for the first channel. Moreover, the number of transmitted bits in the second channel is adjusted as per the available transmission duration, and the weighting factor is added to consider the utilization as per the transmitted number of bits. It can be seen in
Figure 11 and
Figure 12 that for a given PU mean inactive duration, the sum utilization of spectrum for the multi-channel scenario also increases when the PU uses the channel more actively. The reason is the same, as the PU contributes more to the overall sum utilization of spectrum because of the targeted detection probability. The performance improvement for the multi-channel scenario is achieved for any model of channel status, i.e., different PU states probabilities. The reason is that the handoff probability is considered to be the same for any PU channel status. Hence, the transmission of a packet in the next channel for each PU interruption is considered, and the sum utilization gain is achieved.