Parameter Uncertainty Analysis of the Life Cycle Inventory Database: Application to Greenhouse Gas Emissions from Brown Rice Production in IDEA
Abstract
:1. Introduction
- assess the applicability of the semi-quantitative DQI approach and the stochastic modeling approach to the parameter uncertainty analysis of the brown rice production and compare the uncertainty analysis results from both approaches;
- develop a method for the parameter uncertainty analysis of the agricultural DB in the IDEA.
2. Materials and Methods
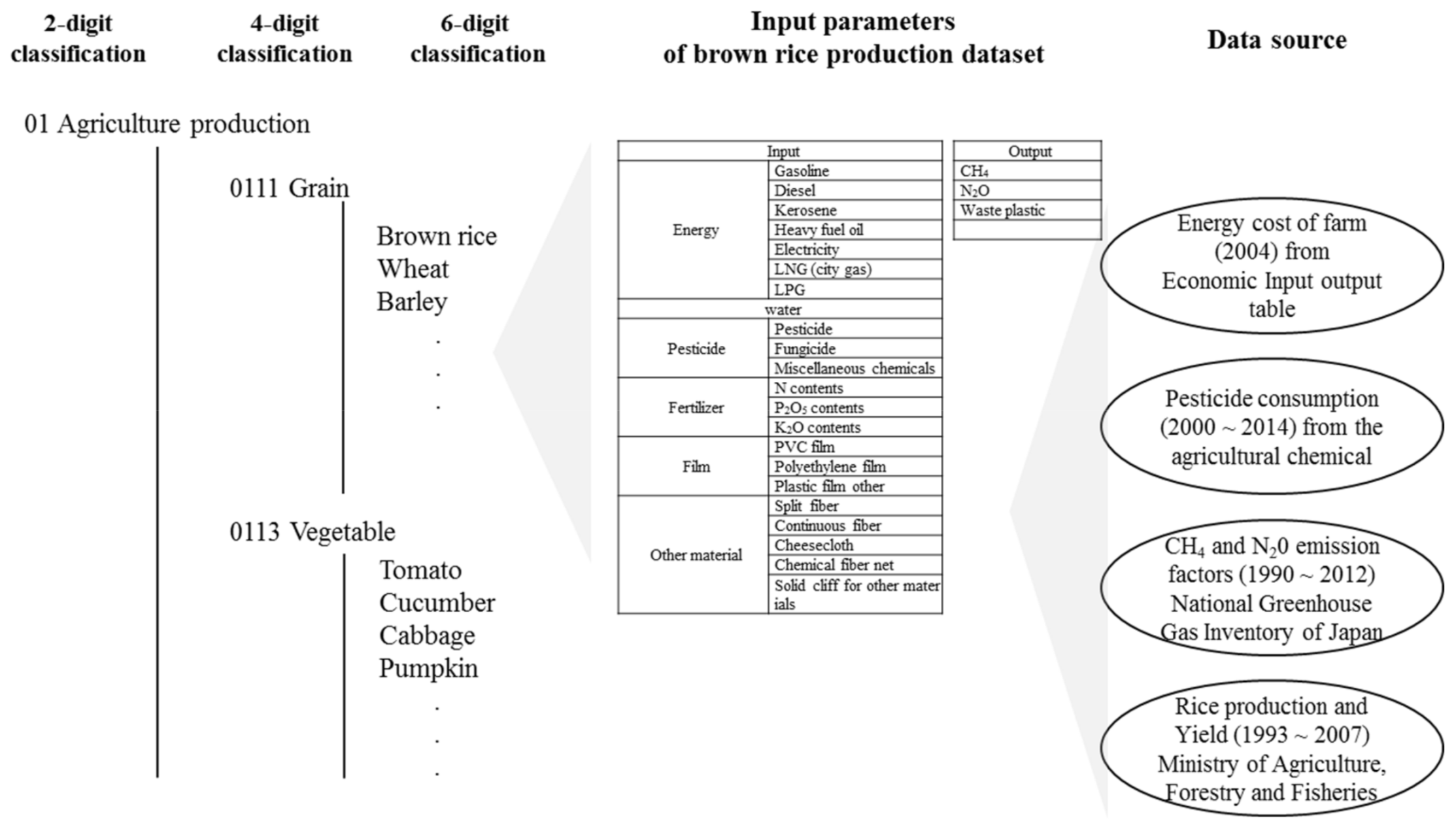
2.1. Brown Rice Production in the IDEA
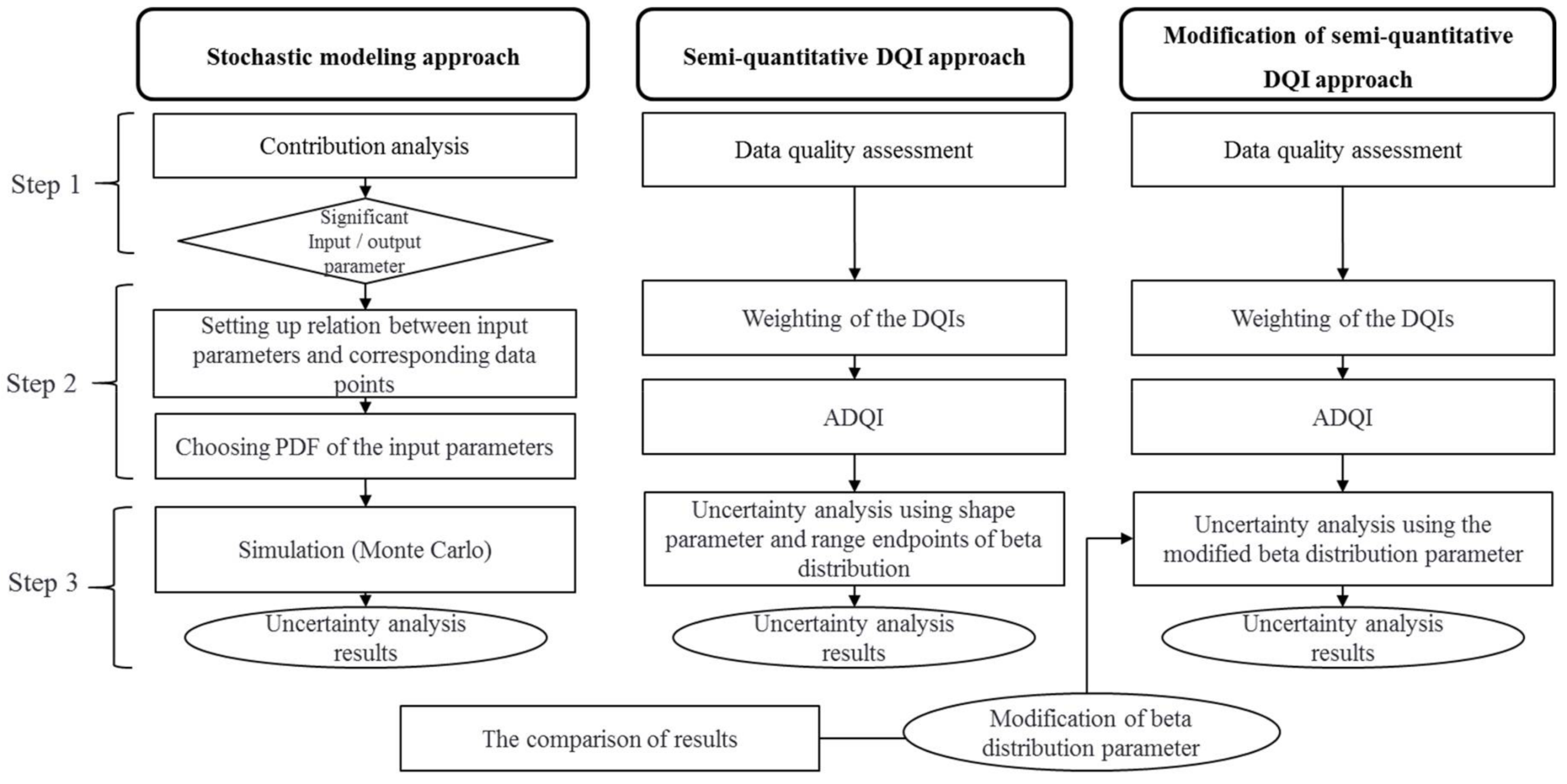
2.2. Overview of the Parameter Uncertainty Analysis
2.3. Stochastic Modeling Approach
2.3.1. Step 1. Contribution Analysis
2.3.2. Step 2. Choosing Probability Density Function
2.3.3. Step 3. Monte Carlo Simulation
2.4. Semi-Quantitative DQI Approach
2.4.1. Step 1. Data Quality Assessment (DQA)
2.4.2. Step 2. Aggregated DQI (ADQI)
2.4.3. Step 3. Uncertainty Analysis Using the Transformation Matrix
2.5. Modification of the Semi-Quantitative DQI Approach for IDEA
3. Results
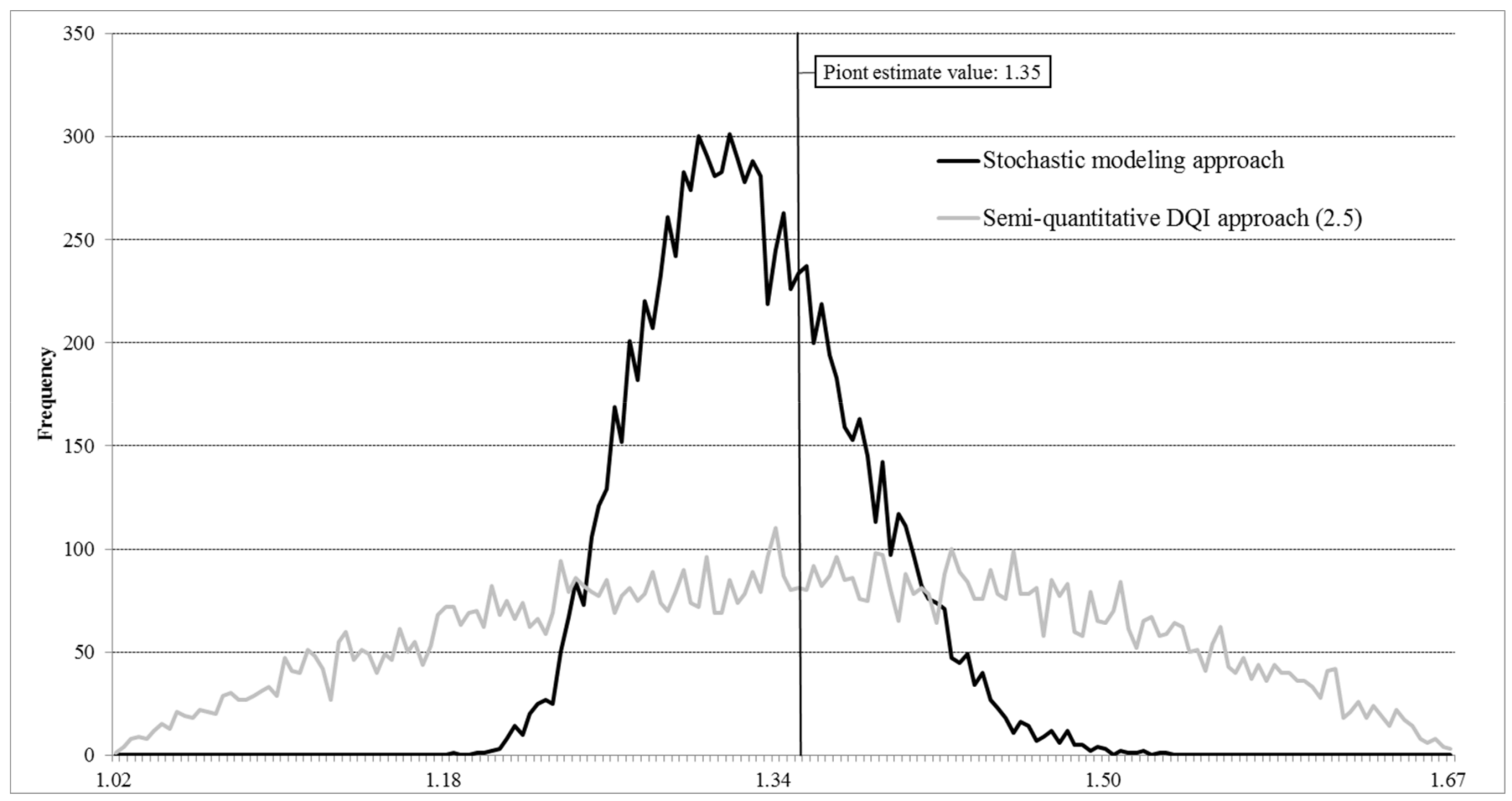
3.1. Stochastic Modeling Approach
3.2. Semi-Quantitative DQI Approach
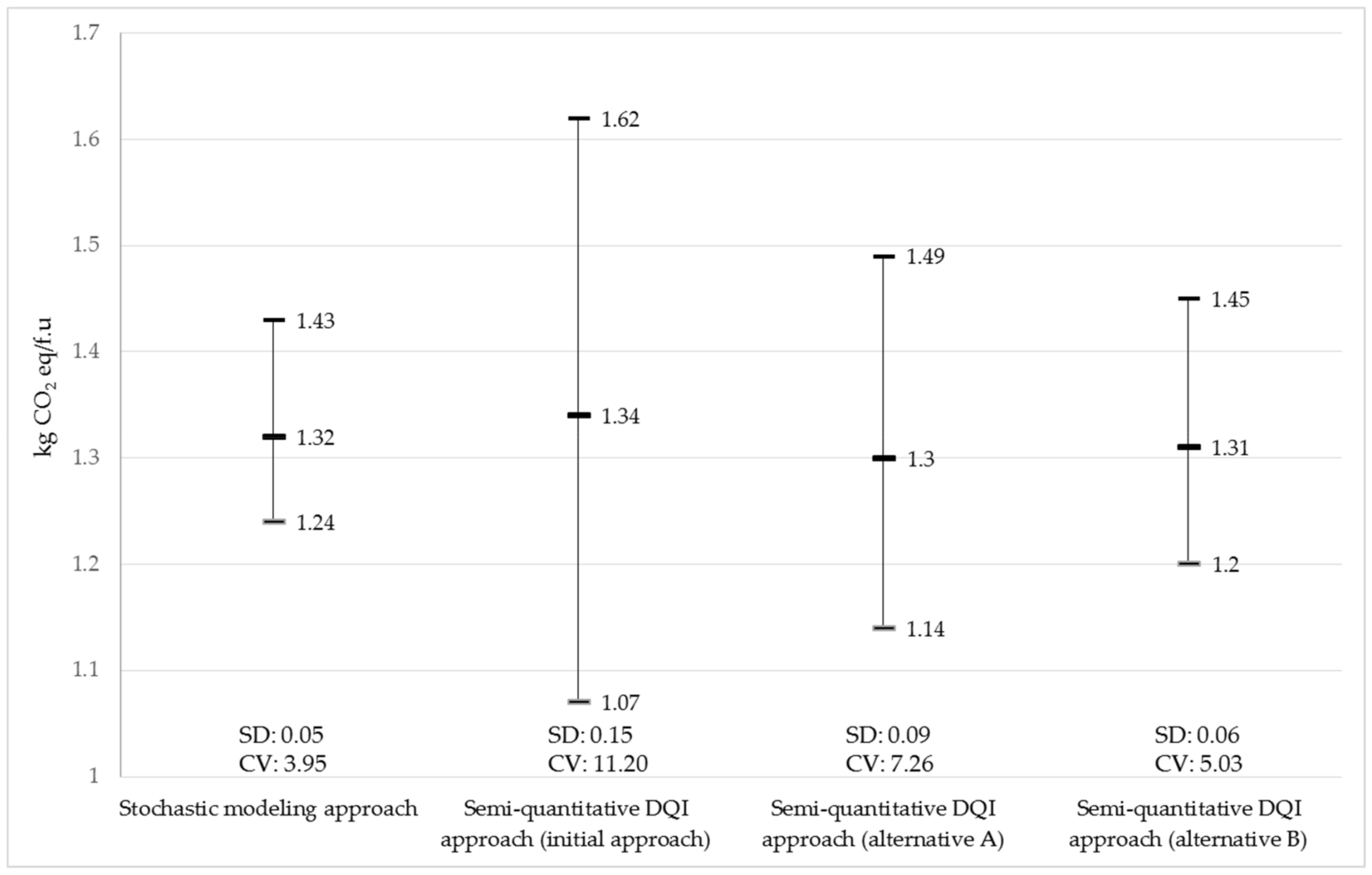
3.3. Modification of the Semi-Quantitative DQI Approach for the Agriculture Dataset in the IDEA
4. Discussion
5. Conclusions
- A simple method for the parameter uncertainty analysis of the agriculture industry dataset was proposed by modifying the beta distribution parameters (transformation matrix including the endpoint range, shape parameter, and aggregated DQI (ADQI) scales) in the semi-quantitative DQI approach based on the stochastic modeling result.
- The stochastic modeling approach provides the best estimate of the true mean of the sample space; however, because of the excessive requirements for the number of data points, its use in uncertainty analyses is not practical.
Author Contributions
Conflicts of Interest
References
- Huijbregts, M.A. Application of uncertainty and variability in LCA. Int. J. Life Cycle Assess. 1998, 3, 273–280. [Google Scholar] [CrossRef]
- Heijungs, R.; Huijbregts, M.A. A review of approaches to treat uncertainty in LCA. In Proceedings of the International Environmental Modelling and Software Society (IEMSS) Conference, Osnabruck, Germany, 14–17 June 2004. [Google Scholar]
- Funtowicz, S.O.; Ravetz, J.R. Uncertainty and Quality in Science for Policy; Springer Science & Business Media: Berlin, Germany, 1990; Volume 15. [Google Scholar]
- Firestone, M.; Fenner-Crisp, P.; Barry, T.; Bennett, D.; Chang, S.; Callahan, M.; Barnes, D. Guiding Principles for Monte Carlo Analysis; US Environmental Protection Agency: Washington, DC, USA, 1997.
- Huijbregts, M.A.; Gilijamse, W.; Ragas, A.M.; Reijnders, L. Evaluating uncertainty in environmental life-cycle assessment. A case study comparing two insulation options for a Dutch one-family dwelling. Environ. Sci. Technol. 2003, 37, 2600–2608. [Google Scholar] [CrossRef] [PubMed]
- Lloyd, S.M.; Ries, R. Characterizing, propagating, and analyzing uncertainty in life-cycle assessment: A survey of quantitative approaches. J. Ind. Ecol. 2007, 11, 161–179. [Google Scholar] [CrossRef]
- Linkov, I.; Burmistrov, D. Model uncertainty and choices made by modelers: Lessons learned from the international atomic energy agency model intercomparisons. Risk Anal. 2003, 23, 1297–1308. [Google Scholar] [CrossRef] [PubMed]
- Huijbregts, M.A.; Geelen, L.M.; Hertwich, E.G.; McKone, T.E.; Van De Meent, D. A comparison between the multimedia fate and exposure models caltox and uniform system for evaluation of substances adapted for life-cycle assessment based on the population intake fraction of toxic pollutants. Environ. Toxicol. Chem. 2005, 24, 486–493. [Google Scholar] [CrossRef] [PubMed]
- JLCA. LCA Japan Forum; Trend of LCA Database in Japan. 2013. Available online: http://lca-forum.org/researchdb/pdf/h24_jlca_db.pdf (accessed on 1 February 2018). (In Japanese).
- Japan Environmental Management Association for Industry (JEMI). MiLCA Guidebook, Japan Environmental Management Association for Industry (JEMAI). 2014. Available online: http://milca-milca.net/download-files/MiLCAguidebook_En.pdf (accessed on 1 February 2018).
- Sonnemann, G.; Vigon, B. Global Guidance Principles for Life Cycle Assessment Databases. A Basis for Greener Processes and Products; UNEP/SETAC Life Cycle Initiative, United Nations Environment Programme (UNEP): Paris, France, 2011. [Google Scholar]
- Tahara, K.; Onoye, T.; Kobayashi, K.; Yamagishi, K.; Tsuruta, S.; Nakano, K. Development of Inventory Database for Environmental Analysis (IDEA). In Proceedings of the 9th International Conference on EcoBalance, Tokyo, Japan, 9–12 November 2010. [Google Scholar]
- Heijungs, R. Identification of key issues for further investigation in improving the reliability of life-cycle assessments. J. Clean. Prod. 1996, 4, 159–166. [Google Scholar] [CrossRef]
- Heijungs, R. Sensitivity coefficients for matrix-based LCA. Int. J. Life Cycle Assess. 2010, 15, 511–520. [Google Scholar] [CrossRef]
- Maurice, B.; Frischknecht, R.; Coelho-Schwirtz, V.; Hungerbühler, K. Uncertainty analysis in life cycle inventory. Application to the production of electricity with French coal power plants. J. Clean. Prod. 2000, 8, 95–108. [Google Scholar] [CrossRef]
- Heijungs, R.; Frischknecht, R. Representing statistical distributions for uncertain parameters in LCA. Relationships between mathematical forms, their representation in ecospold, and their representation in CMLCA (7p). Int. J. Life Cycle Assess. 2005, 10, 248–254. [Google Scholar] [CrossRef]
- Sonnemann, G.W.; Schuhmacher, M.; Castells, F. Uncertainty assessment by a Monte Carlo simulation in a life cycle inventory of electricity produced by a waste incinerator. J. Clean. Prod. 2003, 11, 279–292. [Google Scholar] [CrossRef]
- Kennedy, D.J.; Montgomery, D.C.; Quay, B.H. Data Quality—Stochastic environmental life cycle assessment modeling. Int. J. Life Cycle Assess. 1996, 1, 199–207. [Google Scholar] [CrossRef]
- Canter, K.G.; Kennedy, D.J.; Montgomery, D.C.; Keats, J.B.; Carlyle, W.M. Screening stochastic life cycle assessment inventory models. Int. J. Life Cycle Assess. 2002, 7, 18–26. [Google Scholar] [CrossRef]
- Wang, E.; Shen, Z.; Neal, J.; Shi, J.; Berryman, C.; Schwer, A. An AHP-weighted aggregated data quality indicator (AWADQI) approach for estimating embodied energy of building materials. Int. J. Life Cycle Assess. 2012, 17, 764–773. [Google Scholar] [CrossRef]
- Frischknecht, R.; Jungbluth, N.; Althaus, H.J.; Doka, G.; Dones, R.; Heck, T.; Spielmann, M. The ecoinvent database: Overview and methodological framework (7p). Int. J. Life Cycle Assess. 2005, 10, 3–9. [Google Scholar] [CrossRef]
- Muller, S.; Lesage, P.; Ciroth, A.; Mutel, C.; Weidema, B.P.; Samson, R. The application of the pedigree approach to the distributions foreseen in ecoinvent v3. Int. J. Life Cycle Assess. 2016, 21, 1327–1337. [Google Scholar] [CrossRef]
- Ciroth, A.; Fleischer, G.; Steinbach, J. Uncertainty calculation in life cycle assessments. Int. J. Life Cycle Assess. 2004, 9, 216–226. [Google Scholar] [CrossRef]
- Weidema, B.P.; Bauer, C.; Hischier, R.; Mutel, C.; Nemecek, T.; Reinhard, J.; Wernet, G. Overview and Methodology: Data Quality Guideline for the Ecoinvent Database Version 3. 2013. Available online: http://vbn.aau.dk/ws/files/176769045/Overview_and_methodology.pdf (accessed on 22 March 2018).
- Ciroth, A.; Muller, S.; Weidema, B.; Lesage, P. Empirically based uncertainty factors for the pedigree matrix in ecoinvent. Int. J. Life Cycle Assess. 2016, 21, 1338–1348. [Google Scholar] [CrossRef]
- Kennedy, D.J.; Montgomery, D.C.; Keats, B.J. Data Quality—Assessing input data uncertainty in life cycle assessment inventory models. Int. J. Life Cycle Assess. 1997, 2, 229–239. [Google Scholar] [CrossRef]
- Weidema, B.P.; Wesnæs, M.S. Data quality management for life cycle inventories—An example of using data quality indicators. J. Clean. Prod. 1996, 4, 167–174. [Google Scholar] [CrossRef]
- Weidema, B.P. Multi-user test of the data quality matrix for product life cycle inventory data. Int. J. Life Cycle Assess. 1998, 3, 259–265. [Google Scholar] [CrossRef]
- Wang, E.; Shen, Z. A hybrid data quality indicator and statistical method for improving uncertainty analysis in LCA of complex system-application to the whole-building embodied energy analysis. J. Clean. Prod. 2013, 43, 166–173. [Google Scholar] [CrossRef]
- Baek, C.Y.; Park, K.H.; Tahara, K.; Chun, Y.Y. Data Quality Assessment of the Uncertainty Analysis Applied to the Greenhouse Gas Emissions of a Dairy Cow System. Sustainability 2017, 9, 1676. [Google Scholar] [CrossRef]
- Bolin, B. A History of the Science and Politics of Climate Change; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). IPCC Climate Change Fourth Assessment Report: Climate Change; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2007. [Google Scholar]
- Baek, C.Y.; Lee, K.M.; Park, K.H. Quantification and control of the greenhouse gas emissions from a dairy cow system. J. Clean. Prod. 2014, 70, 50–60. [Google Scholar] [CrossRef]
- International Organization for Standardization (ISO). 14044: Environmental Management—Life Cycle Assessment—Requirements and Guidelines; International Organization for Standardization: Geneva, Switzerland, 2006. [Google Scholar]
- The statistical yearbook of Ministry of Agriculture, Forestry and Fisheries (MAFF). 2017. Available online: http://www.maff.go.jp/e/data/stat/index.html (accessed on 1 February 2018).
- Ministry of Internal Affairs and Communications (MIAC). The Japanese Economy and 2000 Input-Output Tables; Ministry of Internal Affairs and Communications (MIAC): Tokyo, Japan, 2004. Available online: http://www.soumu.go.jp/english/dgpp_ss/data/io/index.htm (accessed on 1 August 2017).
- Japan Crop Protection Association (JCPA). The Statistical Data for Agricultural Chemical; Japan Crop Protection Association (JCPA): Tokyo, Japan, 2000–2014; Available online: http://www.jcpa.or.jp/labo/data.html (accessed on 1 February 2018). (In Japanese)
- Ministry of Environment (ME). National Greenhouse Gas Inventory Report of Japan; Ministry of Environment (ME), National Institute for Environmental Studies: Tokyo, Japan, 2012. Available online: http://www-gio.nies.go.jp/aboutghg/nir/2012/NIR-JPN-2012-v3.0E.pdf (accessed on 1 February 2018).
- Bevington, P.R.; Robinson, D.K. Data Reduction and Error Analysis; McGraw–Hill: New York, NY, USA, 2003. [Google Scholar]
- Pham, H. (Ed.) Springer Handbook of Engineering Statistics; Springer Science & Business Media: Berlin, Germany, 2006. [Google Scholar]
- Ross, T.J. Fuzzy Logic with Engineering Applications; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Massey, F.J., Jr. The Kolmogorov-Smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Griffin, D.; Shaw, P.; Stacey, R. Knowing and acting in conditions of uncertainty: A complexity perspective. Syst. Pract. Act. Res. 1999, 12, 295–309. [Google Scholar] [CrossRef]
- Oracle. Crystal Ball 11.1.2 User’s Guide; Oracle: Redwood, CA, USA, 2012; Volume 43. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Saaty, T.L. How to make a decision: The analytic hierarchy process. Interfaces 1994, 24, 19–43. [Google Scholar] [CrossRef]
- Hahn, G.J.; Shapiro, S.S. Statistical Models in Engineering. In Statistical Models in Engineering; John Wiley & Sons: Hoboken, NJ, USA, 1968. [Google Scholar]
- Tan, R.R.; Culaba, A.B.; Purvis, M.R. Application of possibility theory in the life-cycle inventory assessment of biofuels. Int. J. Energy Res. 2002, 26, 737–745. [Google Scholar] [CrossRef]
- Venkatesh, A.; Jaramillo, P.; Griffin, W.M.; Matthews, H.S. Uncertainty analysis of life cycle greenhouse gas emissions from petroleum-based fuels and impacts on low carbon fuel policies. Environ. Sci. Technol. 2010, 45, 125–131. [Google Scholar] [CrossRef] [PubMed]
- Finnveden, G.; Lindfors, L.G. Data quality of life cycle inventory data—Rules of thumb. Int. J. Life Cycle Assess. 1998, 3, 65–66. [Google Scholar] [CrossRef]
- Hedbrant, J.; Sörme, L. Data vagueness and uncertainties in urban heavy-metal data collection. Water Air Soil Pollut. Focus 2001, 1, 43–53. [Google Scholar] [CrossRef]
- Meier, M.A. Eco-efficiency Evaluation of Waste Gas Purification Systems in the Chemical Industry. Doctor’s Thesis, ETH Zürich, Zürich, Switzerland, 1997. [Google Scholar]
- Saur, K.; Finkbeiner, M.; Hoffmann, R.; Eyerer, P.; Schöch, H.; Beddies, H. How to Handle Uncertainties and Assumptions in Interpreting LCA Results? In 1998 Total Life Cycle Conference Proceedings; Society of Automotive Engineers: Warrendale, PA, USA, 1998; pp. 373–382. [Google Scholar]
| Aggregated DQI Scores | Beta Distribution Parameter | |
|---|---|---|
| Shape Parameters (α, β) | Range Endpoints (%) | |
| 1 | 5, 5 | 10 |
| 1.5 | 4, 4 | 15 |
| 2 | 3, 3 | 20 |
| 2.5 | 2, 2 | 25 |
| 3 | 1, 1 | 30 |
| 3.5 | 1, 1 | 35 |
| 4 | 1, 1 | 40 |
| 4.5 | 1, 1 | 45 |
| 5 | 1, 1 | 50 |
| Parameters in Equations (1)–(3) | Number of Data Points | Range of Value | Reference | ||
|---|---|---|---|---|---|
| Energy | 15 | 5.57–7.75 yen/kg | [35,36] | ||
| Diesel | 15 | 19.09–81.11 yen/L | [35,36] | ||
| Kerosene | 15 | 15.15–88.43 yen/L | [35,36] | ||
| Electricity | 15 | 14.01–16.30 yen/kwh | [35,36] | ||
| LPG | 15 | 39.06–72.85 yen/kg | [35,36] | ||
| Pesticides | Miscellaneous chemicals | 15 | 13,344–37,000 ton/year | [37] | |
| Pesticides | 15 | 47,459–75,000 ton/year | [37] | ||
| Rice production | Amount of brown rice production | 18 | 7,791,500–11,980,700 ton/year | [35] | |
| Methane (land) | 9 | 15.85–16.17 g CH4/m2·year | [38] | ||
| Parameter | Input | Stochastic Parameter | |
|---|---|---|---|
| Methane (land) | 0.03100 (kg/f.u.) | Beta | Minimum = 0.02793, Maximum = 0.03414, Alpha = 2.0, Beta = 3.0 |
| Miscellaneous chemicals (insect-fungicide) | 0.01060 (kg/f.u.) | Beta | Minimum = 0.00645, Maximum = 0.015900, Alpha = 2.09, Beta = 4.28 |
| Diesel | 0.04850 (L/f.u.) | Beta | Minimum = 0.03200, Maximum = 0.09100, Alpha = 0.64, Beta = 1.72 |
| Kerosene | 0.02290 (L/f.u.) | Beta | Minimum = 0.02061, Maximum = 0.02520, Alpha = 2.0, Beta = 3.0 |
| Pesticides | 0.00483 (kg/f.u.) | Lognormal | Mean = 0.00388, Std. Dev. = 0.00124, Location = 0.000270 |
| Electricity | 0.07227 (kwh/f.u.) | Pareto | Location = 0.06456 Shape = 9.44472 |
| Liquefied petroleum gas | 0.00008 (kg/f.u.) | Lognormal | Mean = 0.00008, Std. Dev. = 0.00001, Location = 0.00007 |
| DQI | DQA | Weighting Factor | ADQI | Beta Distribution Parameter |
|---|---|---|---|---|
| Reliability | 3 | 0.473 | 2.615 (assume 2.5 to apply to the beta distribution) | Shape parameters (α, β; 2, 2); range endpoint, ±25%) |
| Completeness | 2 | 0.241 | ||
| Temporal correlation | 3 | 0.147 | ||
| Geographical correlation | 1 | 0.072 | ||
| Technological correlation | 3 | 0.067 |
| Beta Distribution Parameter | ||||
|---|---|---|---|---|
| ADQI | Shape Parameters (α, β) | Initial Endpoint Range (%) | Alternative A (%) | Alternative B (%) |
| 1 | 4, 5 | 10.00 | 5.00 | 2.50 |
| 1.5 | 4, 5 | 15.00 | 7.50 | 3.75 |
| 2 | 3, 4 | 20.00 | 10.00 | 5.00 |
| 2.25 | 3, 4 | - | 12.50 | 7.50 |
| 2.5 | 3, 4 | 25.00 | 15.00 | 10.00 |
| 2.75 | 2, 3 | - | 17.50 | 12.50 |
| 3 | 2, 3 | 30.00 | 20.00 | 15.00 |
| 3.25 | 2, 3 | - | 22.50 | 17.50 |
| 3.5 | 1, 2 | 35.00 | 25.00 | 20.00 |
| 3.75 | 1, 2 | - | 27.50 | 22.50 |
| 4 | 1, 2 | 40.00 | 30.00 | 25.00 |
| 4.5 | 0, 1 | 45.00 | 35.00 | 30.00 |
| 5 | 0, 1 | 50.00 | 40.00 | 35.00 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baek, C.-Y.; Tahara, K.; Park, K.-H. Parameter Uncertainty Analysis of the Life Cycle Inventory Database: Application to Greenhouse Gas Emissions from Brown Rice Production in IDEA. Sustainability 2018, 10, 922. https://doi.org/10.3390/su10040922
Baek C-Y, Tahara K, Park K-H. Parameter Uncertainty Analysis of the Life Cycle Inventory Database: Application to Greenhouse Gas Emissions from Brown Rice Production in IDEA. Sustainability. 2018; 10(4):922. https://doi.org/10.3390/su10040922
Chicago/Turabian StyleBaek, Chun-Youl, Kiyotaka Tahara, and Kyu-Hyun Park. 2018. "Parameter Uncertainty Analysis of the Life Cycle Inventory Database: Application to Greenhouse Gas Emissions from Brown Rice Production in IDEA" Sustainability 10, no. 4: 922. https://doi.org/10.3390/su10040922
APA StyleBaek, C.-Y., Tahara, K., & Park, K.-H. (2018). Parameter Uncertainty Analysis of the Life Cycle Inventory Database: Application to Greenhouse Gas Emissions from Brown Rice Production in IDEA. Sustainability, 10(4), 922. https://doi.org/10.3390/su10040922




