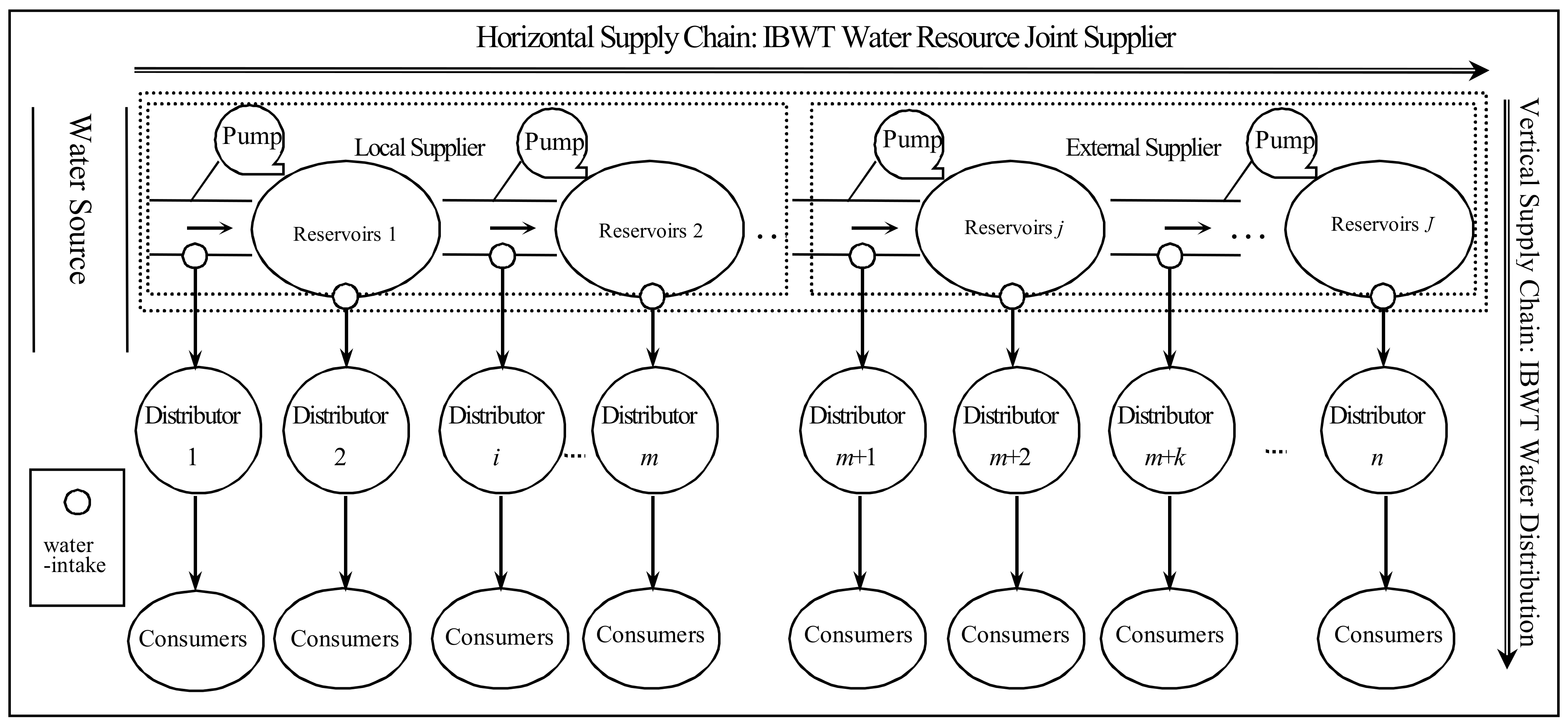
Based on the actual characteristics of real IBWT projects in the world (for example, the South-to-North Water Diversion project in China), an IBWT green supply chain for the numerical analysis is developed. We assume there are six water-intakes and six water distributors in the IBWT green supply chain, i.e., n = 6. Three water distributors are supplied by the local supplier (i.e., m = 3), and three water distributors are supplied by the external supplier (i.e., n − m = 3).
The numerical analysis assesses and compares the pricing, WGL improvement, and quantity decisions, as well as the resulting social welfare, consumers’ surplus, and net profits of the IBWT supplier, distributors, and supply chain for the IBWT green supply chain equilibrium and coordination models, considering whether the social welfare is maximized or not.
8.3. Results Comparison of Numerical Analysis
This section provides a comparison analysis between the numerical analysis results of
Section 8.1 and those of
Section 8.2, with focus on the pricing decisions, quantity decisions, WGL improvement, economic benefits, and social welfare benefits.
(1) Comparing the numerical results between IBWT green supply chain equilibrium with the SWM (
Table 6) and IBWT supply chain equilibrium without the SWM (
Table 8), we can find that (i) The equilibrium retail prices with the SWM scenario (0.30, 0.61, 0.97, 1.38, 1.84, and 2.35) are less than those without the SWM scenario (0.45, 0.90, 1.37, 1.85, 2.34, and 2.84), respectively; (ii) The equilibrium usage prices with the SWM scenario (0.05, 0.16, 0.37, 0.68, 1.09, and 1.60) are less than those without the SWM scenario (0.35, 0.75, 1.17, 1.61, 2.08, and 2.58), respectively; (iii) The equilibrium ordering quantities with the SWM scenario (20,100,503; 39,195,980; 53,266,332; 62,311,558; 66,331,658; and 65,326,633) are higher than those without the SWM scenario (5,000,000; 9,750,000; 13,250,000; 15,500,000; 16,500,000; and 16,250,000), respectively; (iv) The wholesale price with the SWM scenario (0.58) is higher than that without the SWM scenario (0.14); (v) The equilibrium profits of the distributors with the SWM scenario (3,940,302; 15,263,248; 28,273,021; 38,727,302; 43,898,889; and 42,575,690) are higher than those without the SWM scenario (150,000; 850,625; 1,655,625; 2,302,500; 2,622,500; and 2,540,625), respectively. The equilibrium profits of the IBWT local supplier and external supplier with the SWM scenario (207,914,225; 138,609,484) are higher than those without the SWM scenario (13,106,250; 8,737,500), respectively, and the equilibrium profit of the IBWT green supply chain with the SWM scenario (519,202,162) is higher than that without the SWM scenario (31,965,625), respectively; (vi) The social welfare with the SWM scenario (86,006,030) is higher than that without the SWM scenario (37,326,563); (vii) The consumers’ surplus with the SWM scenario (86,639,226) is higher than that without the SWM scenario (5,360,938).
(2) Comparing the numerical results between IBWT green supply chain coordination with the SWM (
Table 7) and IBWT supply chain coordination without the SWM (
Table 9), we can find that: (i) The optimal retail prices with the SWM scenario (0.30, 0.61, 0.97, 1.38, 1.84, and 2.35) are less than those without the SWM scenario (0.40, 0.81, 1.24, 1.69, 2.17, and 2.68), respectively; (ii) The coordinated usage prices with the SWM scenario (0.02, 0.08, 0.18, 0.34, 0.54, and 0.80) are less than those without the SWM scenario (0.13, 0.28, 0.45, 0.65, 0.88, and 1.13), respectively; (iii) The optimal ordering quantities with the SWM scenario (20,100,503; 39,195,980; 53,266,332; 62,311,558; 66,331,658; and 65,326,633) are higher than those without the SWM scenario (10,000,000; 19,500,000; 26,500,000; 31,000,000; 33,000,000; and 32,500,000), respectively; (iv) The wholesale price with the SWM scenario (0.15) is higher than that without the SWM scenario (0.07); (v) The coordinated profits of the distributors with the SWM scenario (1,915,101; 7,562,420; 14,051,044; 19,265,117; 21,844,446; and 21,184,500) are higher than those without the SWM scenario (400,000; 1,801,250; 3,411,250; 4,705,000; 5,345,000; and 5,181,250), respectively, the coordinated profits of the IBWT local supplier and external supplier with the SWM scenario (52,093,577; 34,729,051) are higher than those without the SWM scenario (13,106,250; 8,737,500), respectively, and the coordinated profit of the IBWT green supply chain with the SWM scenario (172,645,256) is higher than that without the SWM scenario (42,687,500), respectively; (vi) The social welfare with the SWM scenario (86,006,030) is higher than that without the SWM scenario (64,131,250); and (vii) The consumers’ surplus with the SWM scenario (86,639,and 226) is higher than that without the SWM scenario (21,443, and 750).
(3) Comparing the numerical results between IBWT green supply chain equilibrium with the SWM (
Table 6) and IBWT green supply chain coordination with the SWM (
Table 7), we can find that (i) The proportions of the total subsidy factor allocated to the
ith water-intake under the equilibrium decision (0.07, 0.13, 0.17, 0.20, 0.22, and 0.21) are equal to those under the coordination decision, respectively; (ii) The retail prices under the equilibrium decision (0.30, 0.61, 0.97, 1.38, 1.84, and 2.35) are equal to those under the coordination decision, respectively; (iii) The usage prices under the equilibrium decision (0.05, 0.16, 0.37, 0.68, 1.09, and 1.60) are higher than those under the coordination decision (0.02, 0.08, 0.18, 0.34, 0.54, and 0.80); (iv) The ordering quantities under the equilibrium decision (20,100,503; 39,195,980; 53,266,332; 62,311,558; 66,331,658; and 65,326,633) are equal to those under the coordination decision; (v) The WGL improvement under the equilibrium decision (100.50, 195.98, 266.33, 311.56, 331.66, and 326.63) is equal to that under the coordination decision; (vi) The wholesale price under the equilibrium decision (0.58) is higher than that under the coordination decision (0.15); (vii) The profits of the distributors under the equilibrium decision (3,940,302; 15,263,248; 28,273,021; 38,727,302; 43,898,889; and 42,575,690) are higher than those under the coordination decision (1,915,101; 7,562,420; 14,051,044; 19,265,117; 21,844,446; and 21,184,500), respectively, the profits of the IBWT local supplier and external supplier under the equilibrium decision (207,914,225; 138,609,484) are higher than those under the coordination decision (52,093,577; 34,729,051), respectively, and the profit of the IBWT green supply chain under the equilibrium decision (519,202,162) is higher than that under the coordination decision (172,645,256), respectively; (viii) The social welfare under the equilibrium decision (86,006,030) is equal to that under the coordination decision; (ix) the consumers’ surplus under the equilibrium decision (86,639,226) is equal to that under the coordination decision; (x) The government’s subsidy under the equilibrium decision (519,835,358) is higher than that under the coordination decision (173,278,453).
(4) Comparing the numerical results between IBWT supply chain equilibrium without the SWM (
Table 8) and IBWT supply chain coordination without the SWM (
Table 9), we can find that (i) The retail prices under the equilibrium decision (0.45, 0.90, 1.37, 1.85, 2.34, and 2.84) are higher those under the coordination decision (0.40, 0.81, 1.24, 1.69, 2.17, and 2.68); (ii) The usage prices under the equilibrium decision (0.35, 0.75, 1.17, 1.61, 2.08, and 2.58) are higher than those under the coordination decision (0.13, 0.28, 0.45, 0.65, 0.88, and 1.13); (iii) The ordering quantities under the equilibrium decision (5,000,000; 9,750,000; 13,250,000; 15,500,000; 16,500,000; and 16,250,000) are less than those under the coordination decision (10,000,000; 19,500,000; 26,500,000; 31,000,000; 33,000,000; and 32,500,000); (iv) The wholesale price under the equilibrium decision (0.14) is higher than that under the coordination decision (0.07); (v) The profits of the distributors under the equilibrium decision (150,000; 850,625; 1,655,625; 2,302,500; 2,622,500; and 2,540,625) are lower than those under the coordination decision (400,000; 1,801,250; 3,411,250; 4,705,000; 5,345,000; and 5,181,250), respectively, the profits of the IBWT local supplier and external supplier under the equilibrium decision (13,106,250; 8,737,500) are lower than those under the coordination decision (13,106,250; 8,737,500), respectively, and the profits of the IBWT supply chain under the equilibrium decision (31,965,625) is less than that under the coordination decision (42,687,500), respectively; (vi) The social welfare under the equilibrium decision (37,326,563) is less than that under the coordination decision (64,131,250); (vii) The consumers’ surplus under the equilibrium decision (5,360,938) is less than that under the coordination decision (21,443,750).