1. Introduction
Air pollution is hazardous chemicals released into the atmosphere by a number of natural and/or anthropogenic activities. The change of atmospheric composition is attributed to the combustion of fossil fuels [
1]. Air pollutants, such as carbon monoxide (CO), respirable particulate matter (PM
2.5 and PM
10), nitrogen oxides (NO
x), ozone (O
3), sulphur dioxide (SO
2), nitrogen dioxide (NO
2), and nitric oxide (NO), differ in their reaction properties, chemical composition, time of disintegration, emission, and diffuse ability over short or long distances. Air pollution has both acute and chronic impacts on human health, and causes or aggravates numerous organic and systemic diseases, such as heart disease, respiratory irritation, lung cancer, chronic bronchitis, and acute respiratory infections, which will bring about premature mortality and reduce life expectancy [
2,
3,
4]. Therefore, air pollution is a fundamental issue of global concern. Atmospheric pollution in China is very serious. The “Environmental Performance Index: 2016 Report” released by Yale University showed that as the world’s second largest economy, the air quality in China was the second-lowest in the world, only slightly better than in Bangladesh, and even India was still ahead of China [
5]. China has become a disaster area of air pollution in the world, and air pollution has largely covered the vast majority of the country. Especially in recent years, foggy and hazy weather has frequently attacked Northern and Eastern China, making air pollution control the most prominent and urgent environmental problem at present.
The AQI is a simple and generalized scale or indicator to assess air quality status. The AQI in China is developed based on GB3095-2012, introduced by the ministry of environmental protection of the People’s Republic of China, which covers six pollutants, including PM
10, PM
2.5, SO
2, CO, NO
2, and O
3 [
6]. According to air quality standards (GB3095-2012), the AQI could be divided into six levels: excellent (0~50), good (51~100), mild pollution (101~150), moderate pollution (151~200), heavy pollution (201~300), and serious pollution (>300). As the AQI increases, the pollution level increases. For the government, the AQI is a powerful tool for formulating policies related to air quality management and pollution mitigation measures; meanwhile it is also an important index for the general public to rapidly estimate the air quality condition. Thus, the reliable and effective forecasting of the AQI is significantly important, because it can be used to enforce appropriate suggestions and regulations for preventing and evading air pollution damage.
The empirical methods to forecast various air quality indexes generally fall into four categories: the autoregressive integrated moving average method (ARIMA), multiple linear method (MLR), artificial neural networks (ANNs), and hybrid methods [
7]. The ARIMA is a traditional forecasting technique, widely used for analyzing nonlinear time series data [
8,
9]. However, it is constrained by the assumptions of stationarity and linearity, and only suitable for the linear form of time series data [
10]. The MLR method is a classical statistical techniques compared to other approaches. Due to its accuracy of interpretation, the MLR also remains useful and widely used in the prediction field [
11,
12]. However, the MLR can’t capture the non-linear relationships between input and output variables and is not suitable for complex systems [
13].
The ANNs is characterized by self-learning, self-organization, strong mapping ability, and generalization, which can implement approximating nonlinear functions with arbitrary accuracy; thus, the ANNs can perform better than traditional statistical models for forecasting AQI [
14,
15,
16,
17,
18]. However, an ANN is unable to present a clear formula for the forecasting model [
19,
20,
21]. Almost as remarkably, many studies successfully and widely employed the hybrid model in pollution index forecasting and proved that the hybrid model generally had more precise forecasts than the monomial forecast model [
7,
8,
10,
22,
23,
24].
The analysis of the AQI time series is difficult because of the irregularity, randomness, and non-stationarity. The existing research methods, such as ARIMA, MLR, ANNs, and hybrid model, are just a forecast of time series data, and cannot capture the pattern information and change law hidden behind AQI fluctuation. This make it difficult to answer the following questions: What patterns exist in the AQI change? Which patterns are the most vital and play a leading role? Is there a huge gap in the influence of AQI patterns? Which patterns are closer to others and easily change? Which patterns are the hub of AQI pattern transformation and essential to control the air pollution diffusion? Are there disparate subgroups or clusters in the AQI network? What are the characteristics of each subgroup or cluster? Is there a hierarchy or ranking in the AQI network? Which vertices have higher ranking? Are there small-world phenomena or scale-free properties in the AQI network? Obviously, the answers to these questions are crucial for revealing the AQI fluctuation law and internal mechanisms, and can also provide evidence for formulating the measures about preventing and controlling air pollution. Our study will construct an AQI directed-weighted network by transforming time series data into a symbol sequence, apply complex network theory to analyze the topological properties, and give answers to the above questions. Meanwhile, our study also provides a methodological perspective and ideas for time series forecast, contributing to existing studies.
On the other hand, although complex network theory has been used across many science fields in recent years, only a few studies have conducted complex network theory on the time series forecasting. For instance, Gao, An, Liu, and Ding (2011) used a complex network to analyze the linkage between crude oil future prices and spot price from 25 November 2002 to 24 September 2010 [
25]. Wan, Shu, and Guo (2012) presented a method to model frequent patterns and their interaction relationship in sequences based on a complex network [
26]. Zhou, Gong, Zhi, and Feng (2008) collected data of the surface temperature from 160 Chinese weather observations and investigated the topology of Chinese climate networks by using a complex network [
27]. Until now, few scholars have established an AQI network and used complex network theory to study the AQI change law. Therefore, this study is undertaken to analyze the AQI time series data with complex network theory, to fill the research gap.
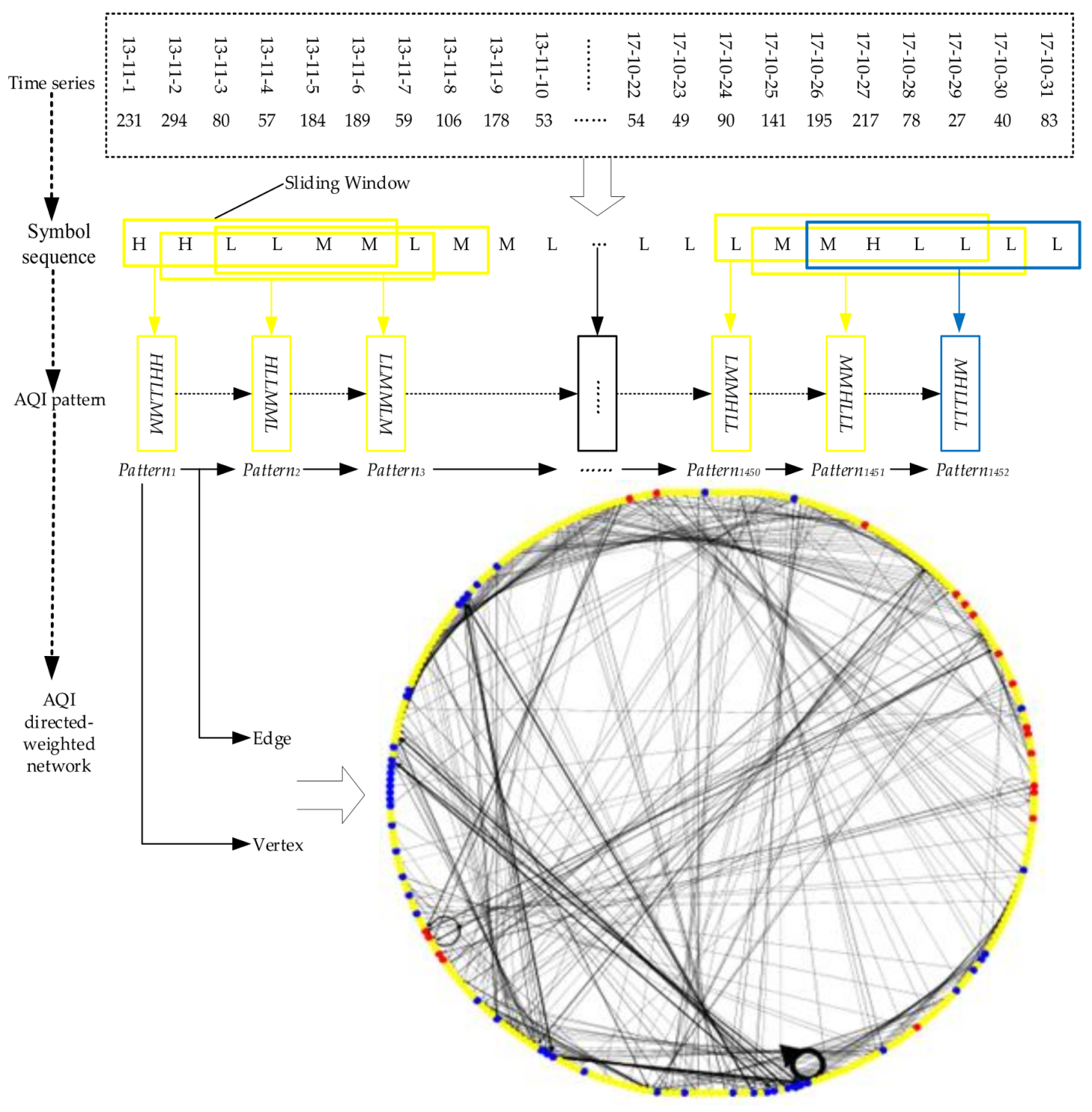
This study selected the time serial data of the AQI in Beijing from 1 November 2013 to 31 October 2017; transformed it into a symbol sequence consisting of three characters {H, M, L} through the coarse graining process; then defined 272 AQI patterns as vertices to create one directed-weighted network of the AQI via sliding sequence; and finally analyzed the topological properties of vertex strength, strength distribution, weighted clustering coefficient, betweenness centralization, islands, distance, proximity prestige, ranking and triadic.
The rest of this article is organized as follows. The data and complex network theory are introduced, and the AQI complex network is constructed in
Section 2. The topological properties of the AQI complex network are analyzed in
Section 3. At last, conclusions are summarized and future research is suggested in
Section 4.
4. Conclusions and Discussion
This study converted time series data into a symbol sequence through the coarse graining process; established the directed-weighted network of the AQI; then analyzed the centrality, clusterability, and ranking of the AQI network. The main results and conclusions are summarized as follows.
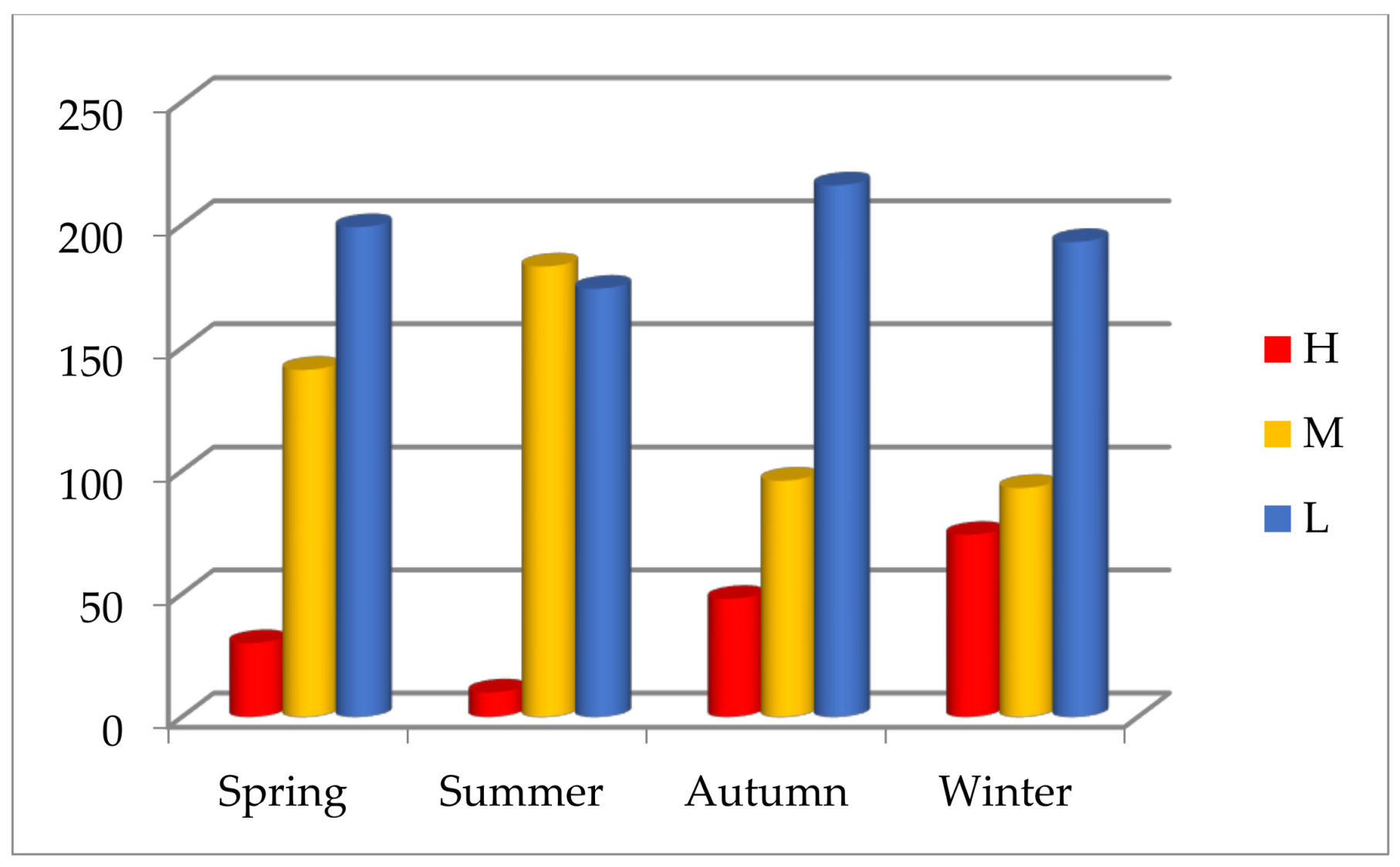
The statistics show that air pollution in Beijing is serious, but air quality improves gradually. The AQI in Beijing has seasonal variations; heavy or serious air pollution mostly recurs in winter, and the excellent or good air quality often appears in autumn. The statistical results are consistent with the subjective experience, perhaps because the meteorological conditions of autumn in Beijing are better and favorable for the diffusion of air pollutants.
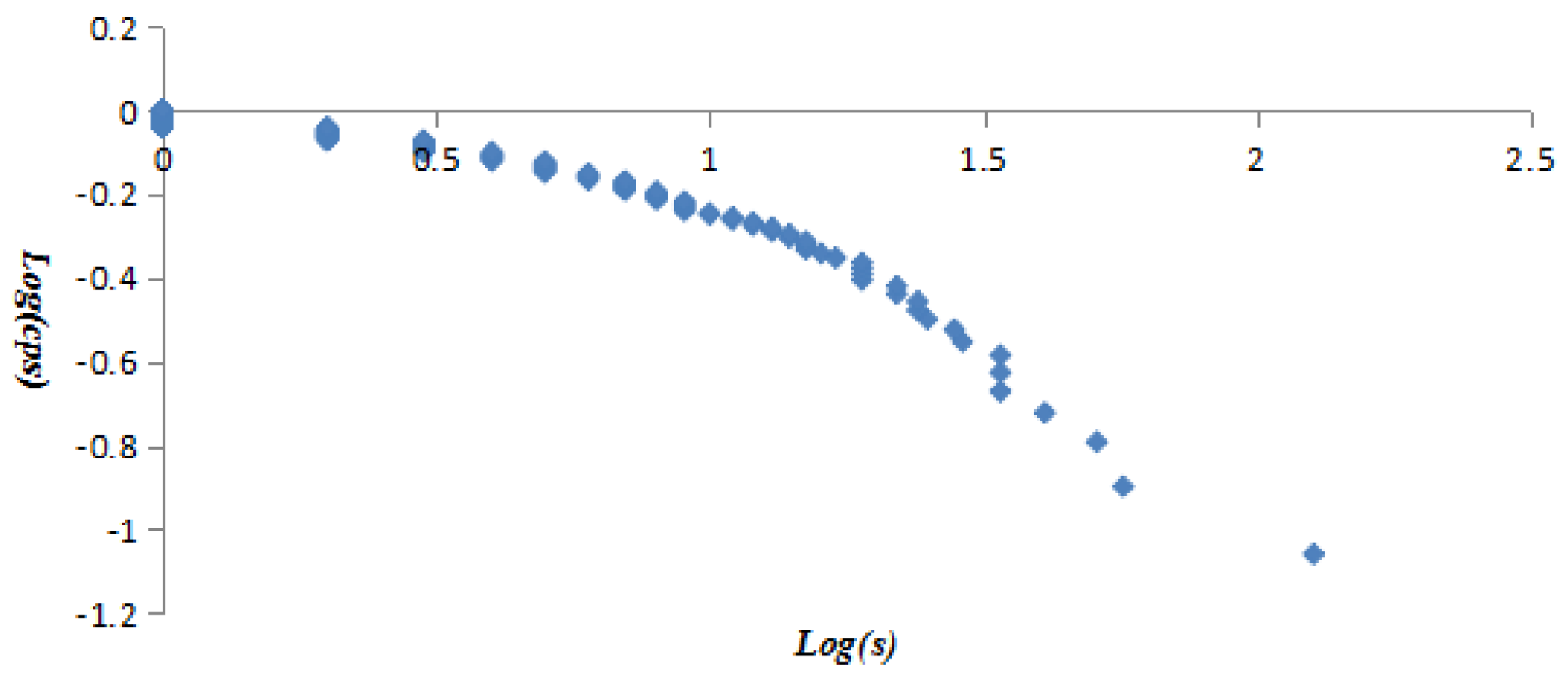
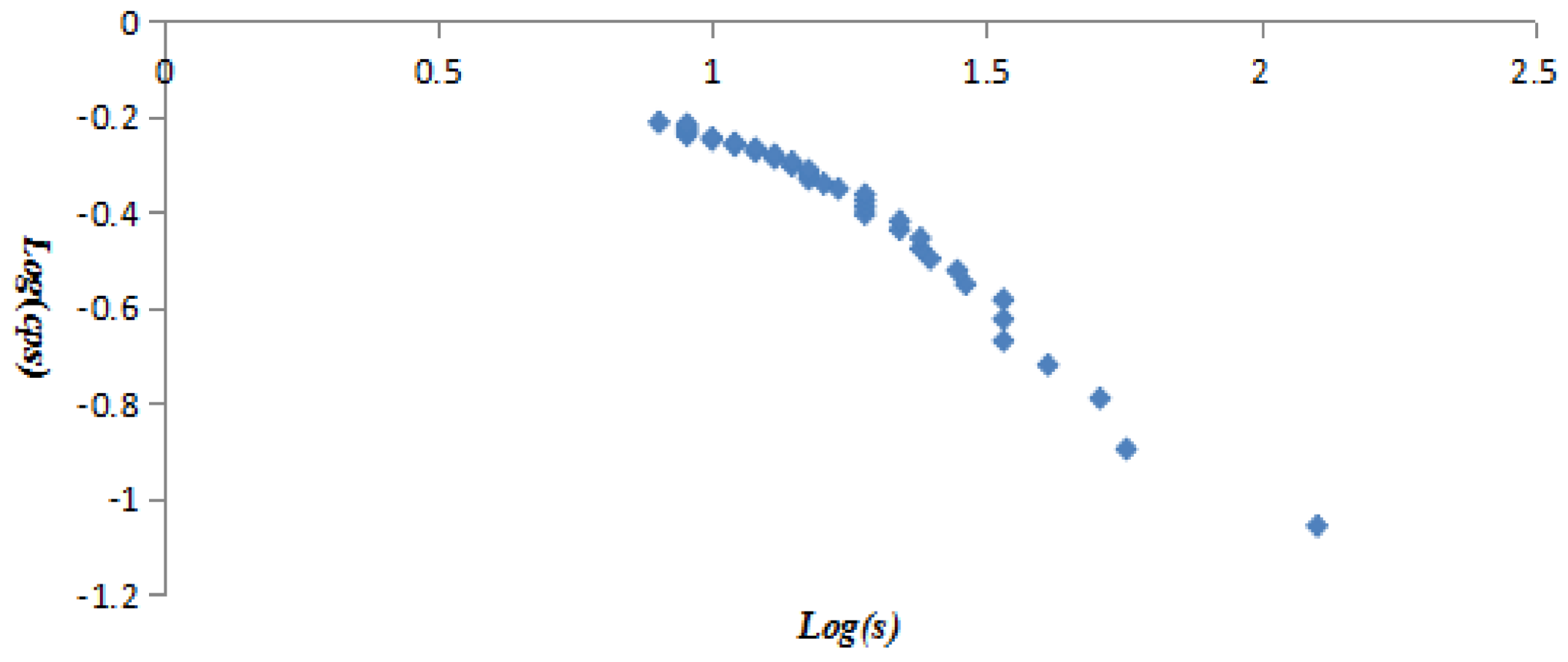
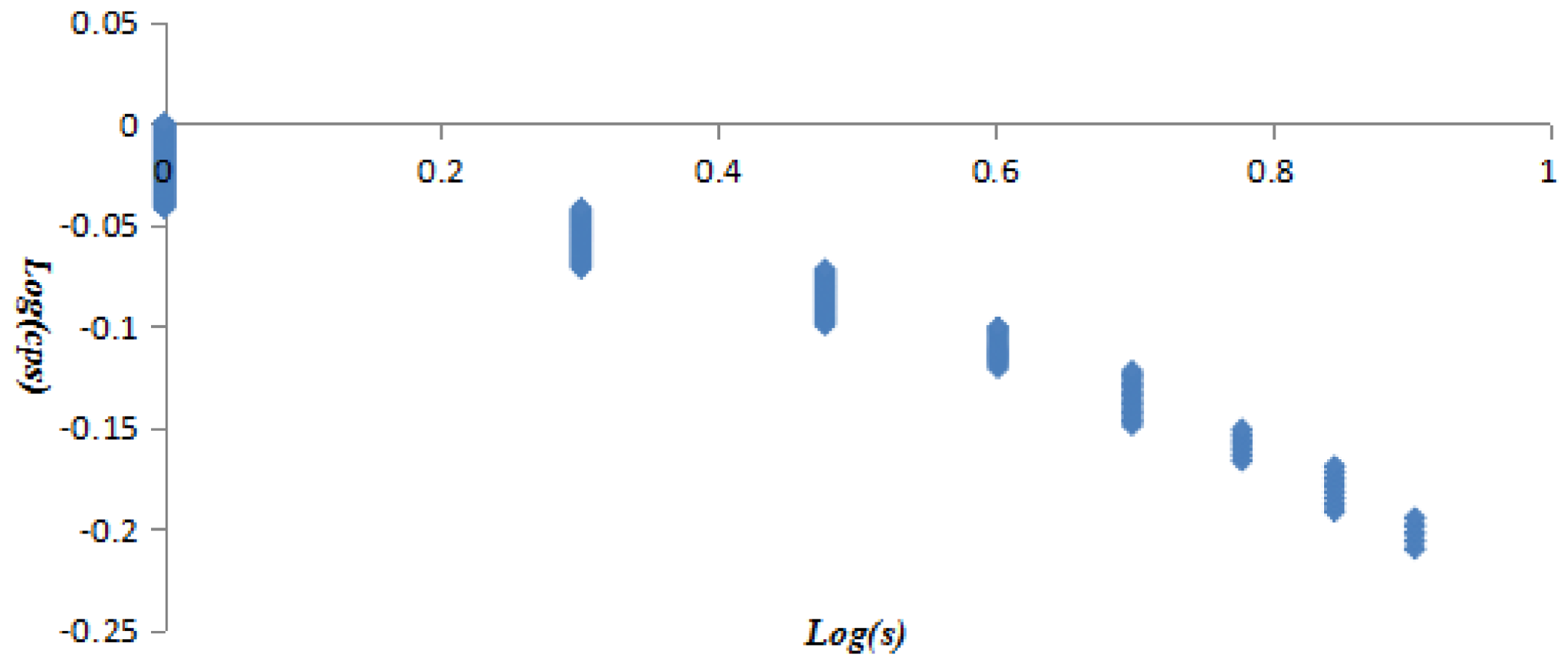
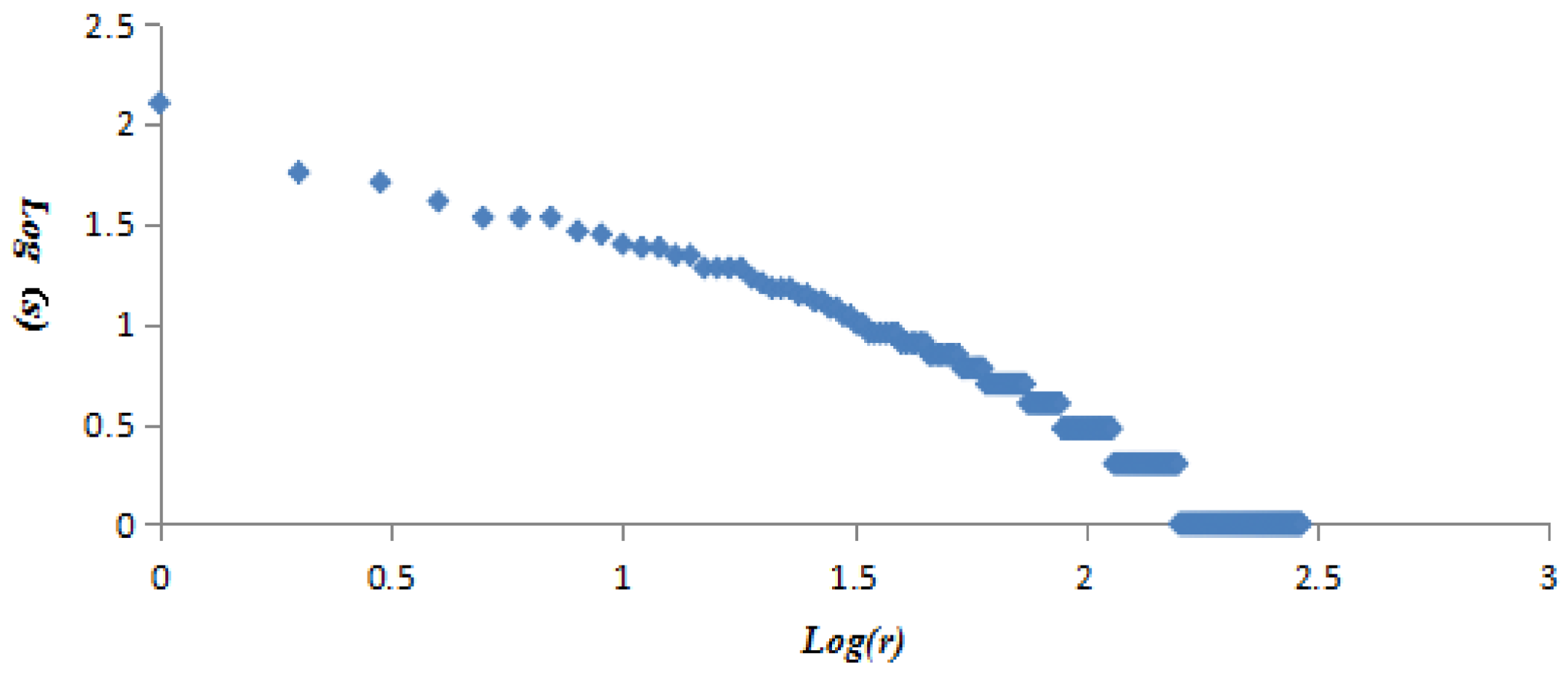
The vertex strength and cumulative strength distribution, and vertex strength and ranking follow “power-law” distribution; the AQI network is a scale-free network, which means only a few AQI patterns—represented by so-called super vertices which play a leading role in the AQI network—appear frequently. The best or worst air quality in Beijing is rare; mild or moderate air pollution often occurs. The probability of heavy or serious air pollution lasting for 4 or 5 days is very low, close to 0.
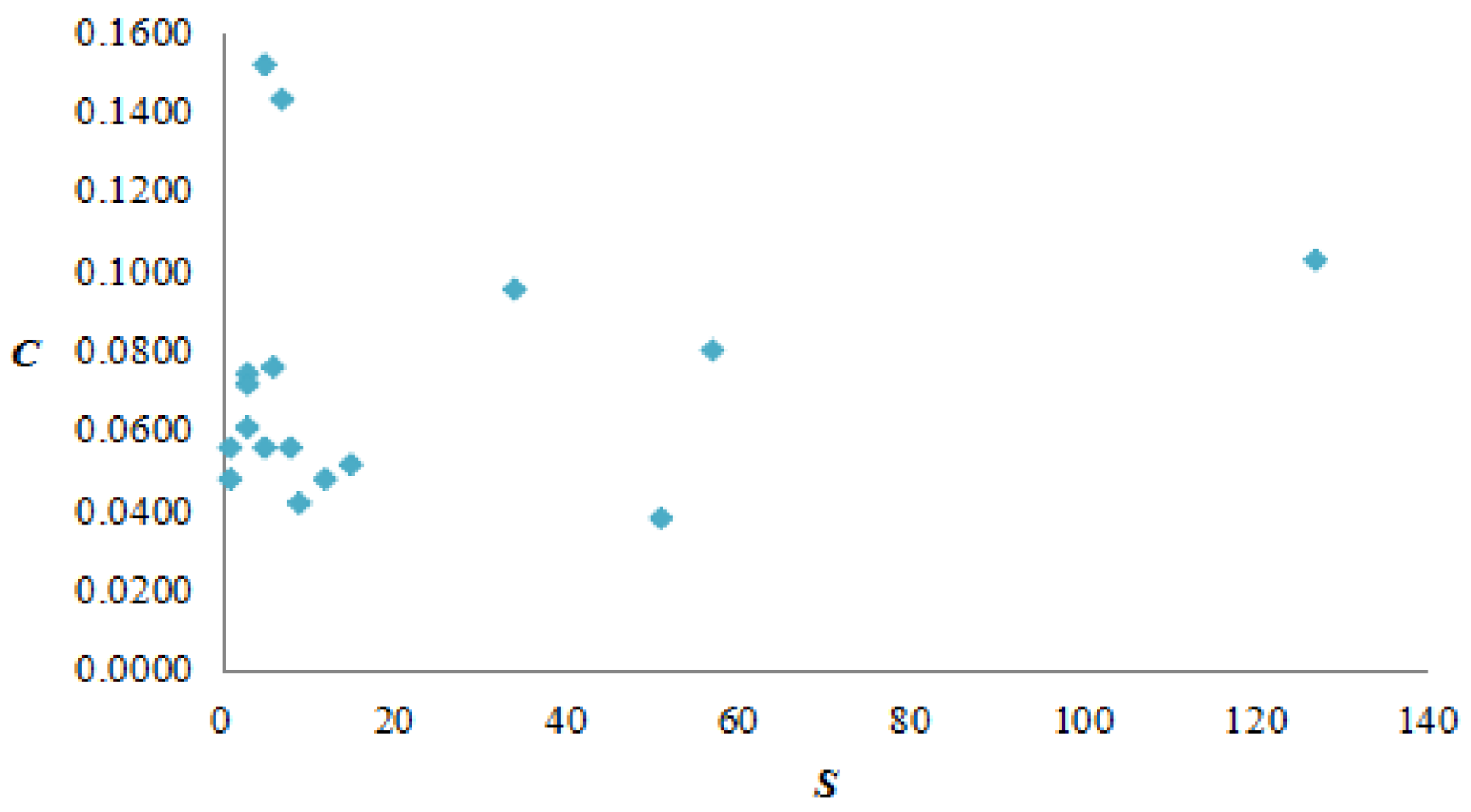
17 vertices have a weighted clustering coefficient greater than 0. The vertex MMMMM has both larger vertex strength and weighted clustering coefficient, holding an important position in the AQI network. The correlation between vertex strength and weighted clustering coefficient is not strong and the AQI network presented complicated polymorphism.
The AQI network does not have an obvious central tendency towards intermediaries, but the varieties in the intermediation of the vertices still exist; 20.55% of vertices account for nearly ½ of the intermediaries in the AQI network. It is difficult to restrain the diffusion of air pollution by controlling the intermediate vertex, but it is also possible.
The vertices of the AQI network fall into six islands; the largest island represented by HHHHHH contains 132 vertices, which means the AQI pattern of heavy or serious air pollution lasting six days is very cohesive, always lingering for a long time.
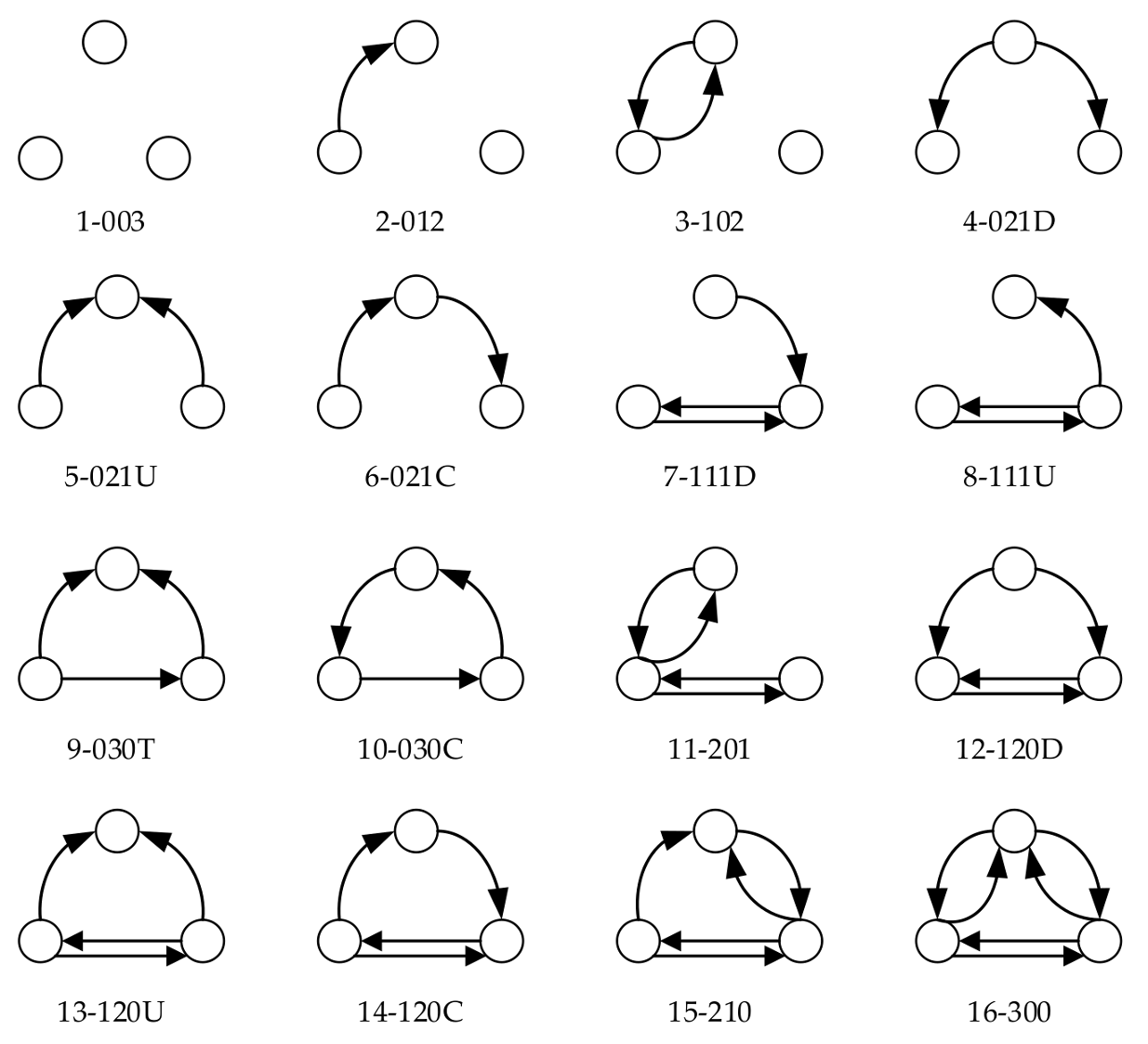
The AQI network is a fully connected network, which does not have obvious small-world phenomena; the mean distance of 68.4932% vertices is 6.120–9.973, and the conversion of AQI patterns presents the characteristics of periodicity and regularity. The 64 vertices had high proximity prestige and dominated the AQI network. They are often the endpoints or residential locations in the air pollution diffusion process, dominating the diffusion of air pollution. The number of triads 2-012 is the largest, and the AQI network seems to follow the transitivity model, however, many other triads appear less than expected by chance, which casts some doubt on the reliability of the chi-square measure.
Air pollution is one essential environmental problem. Our study firstly applies complex network theory to analyze the AQI, and reveals the AQI fluctuation law and internal mechanism, which can provide evidence for formulating the countermeasures about preventing and controlling air pollution. Meanwhile, our study also presents a new approach for time series prediction, contributing to existing studies. In different areas and times, air quality is affected by different factors, such as atmospheric conditions, fossil fuel emissions, landform features, and measures for prevention and control of pollution. Although revealing the topological properties hidden behind the AQI time series, this study does not analyze the factors that lead to the change of air quality. Constructing an influence factors model to reveal the causes of AQI pattern variety in different times is the research direction and content for the future.