Investigation on Performance of a Modified Breakwater-Integrated OWC Wave Energy Converter
Abstract
:1. Introduction
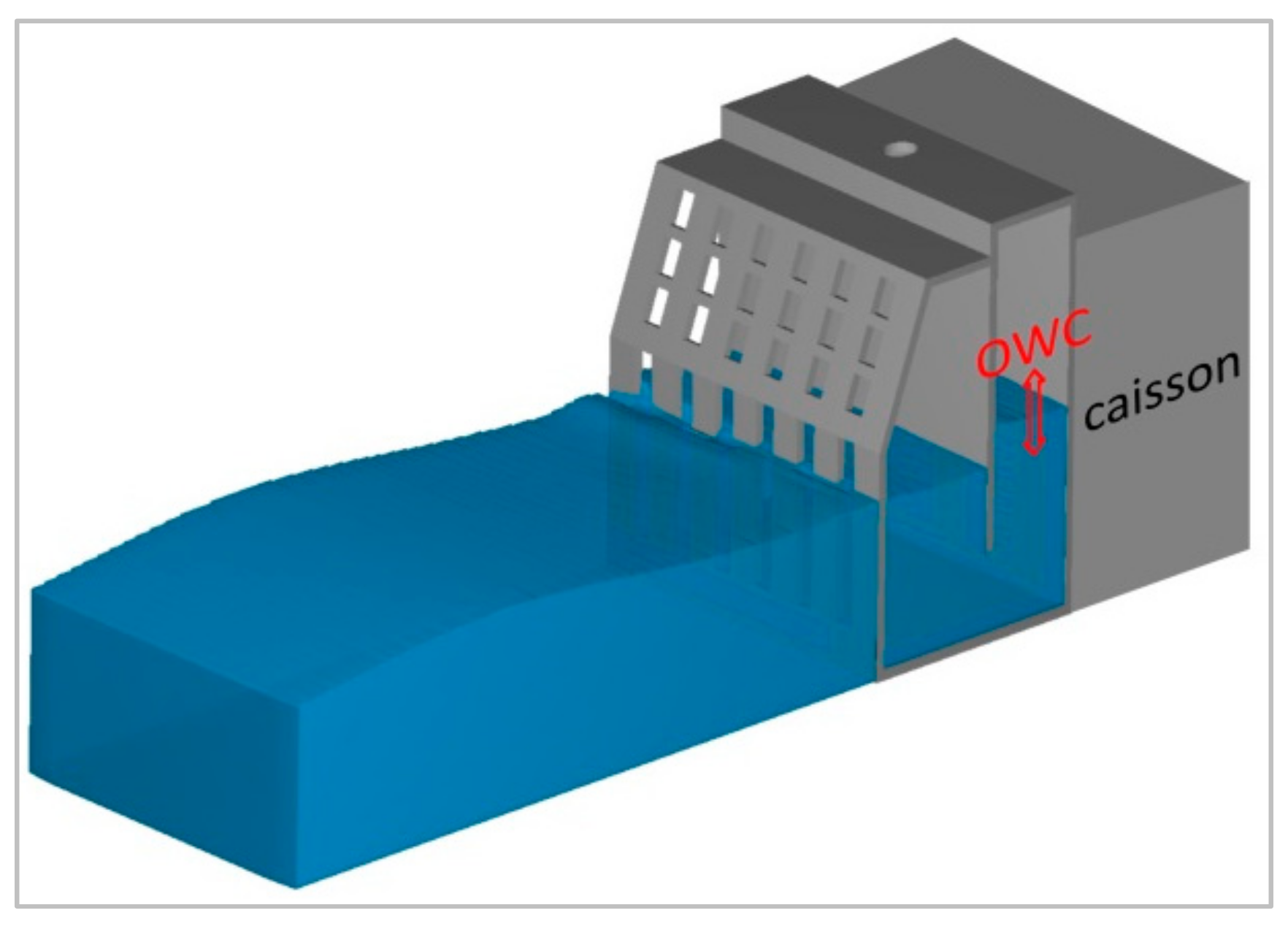
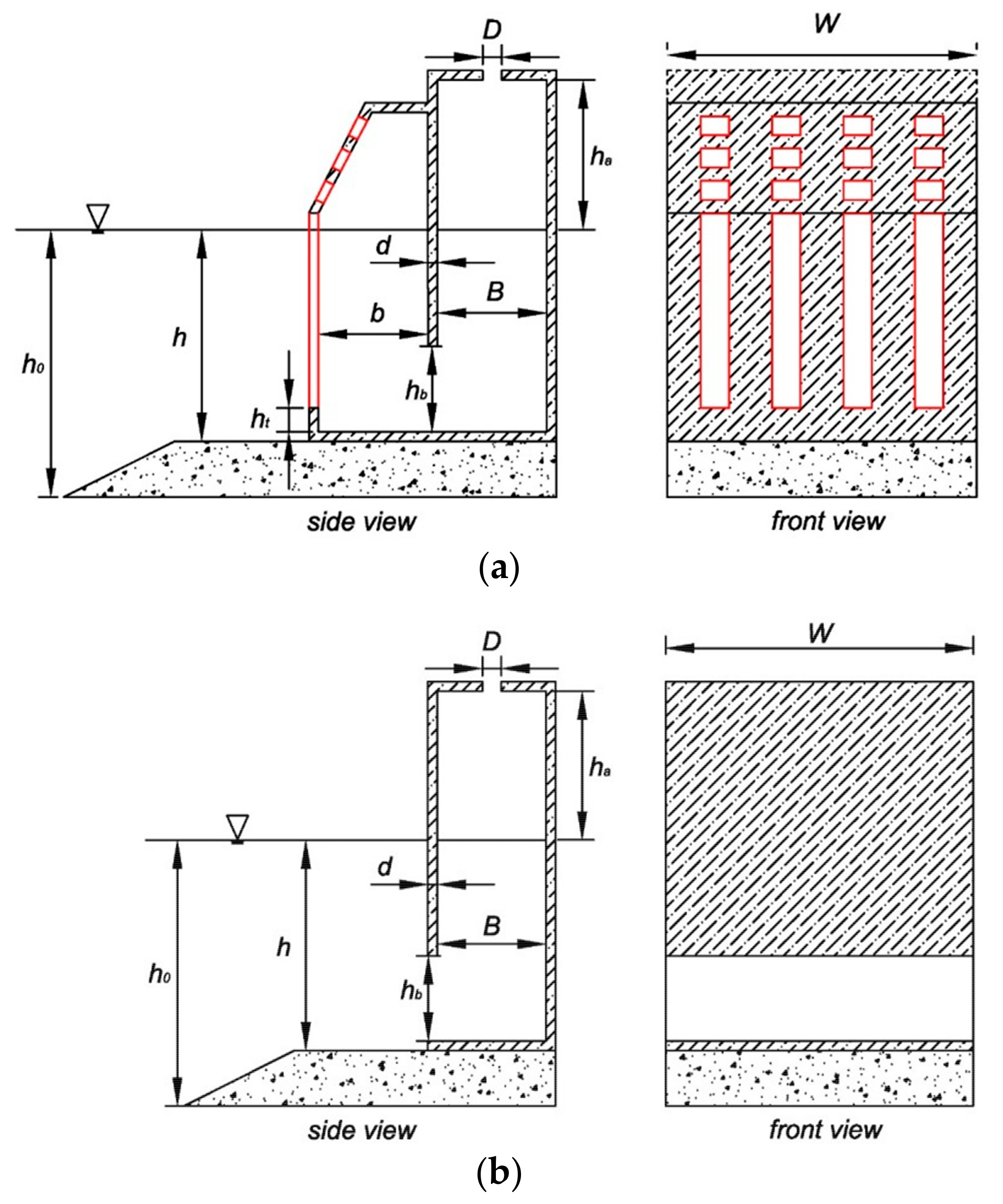
2. Configuration of the Modified OWC
3. 3D CFD Modelling
4. OWC Hydrodynamic Efficiency
5. Experiments and Validations
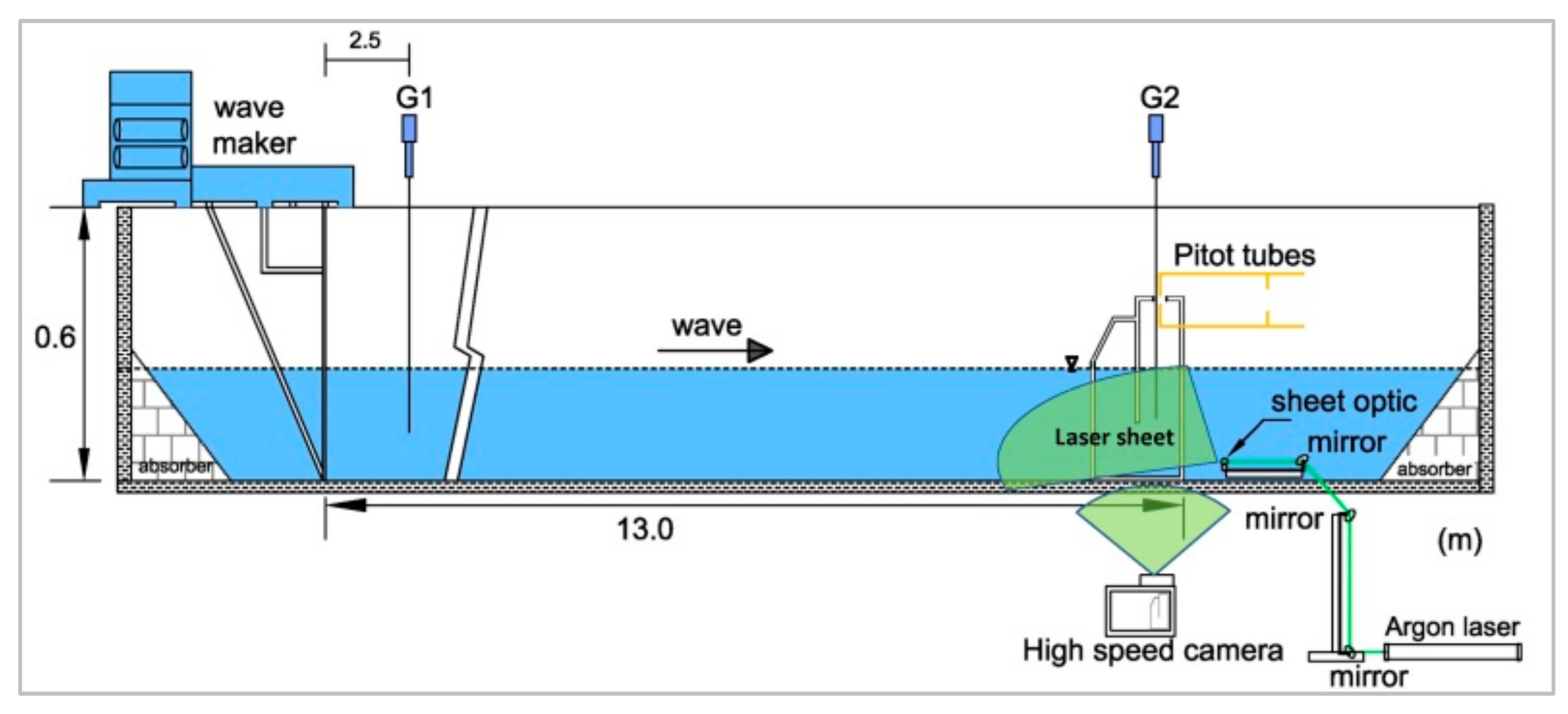
5.1. Experiments
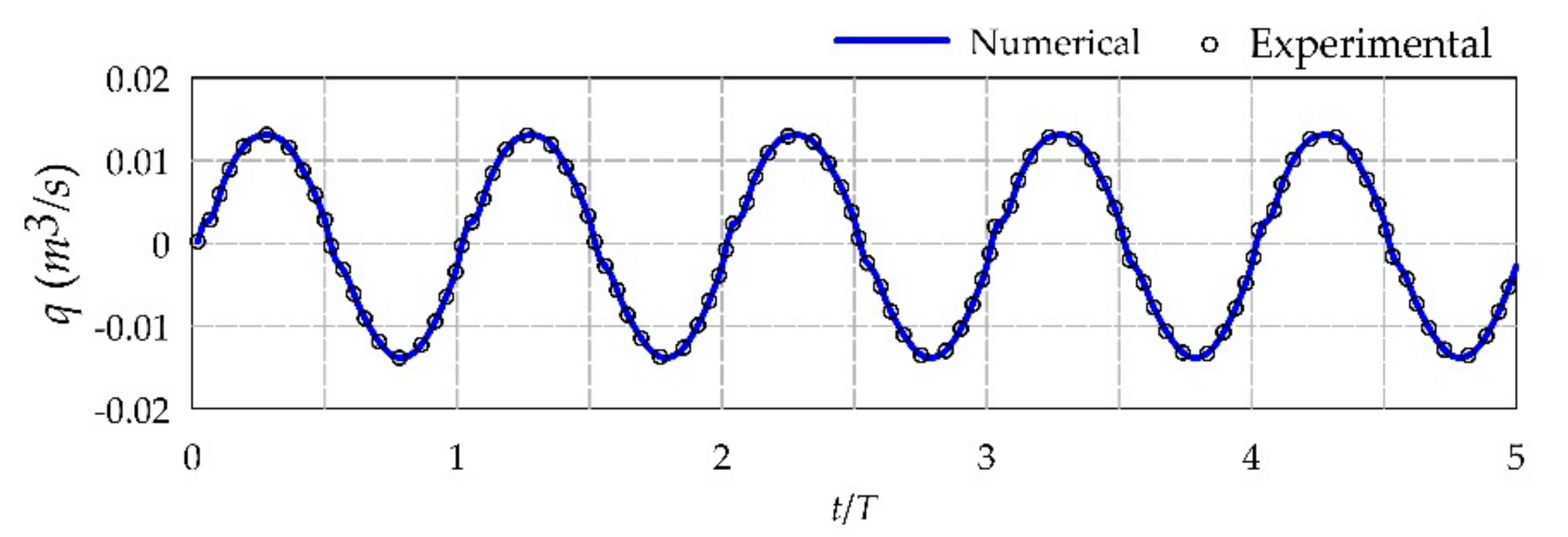
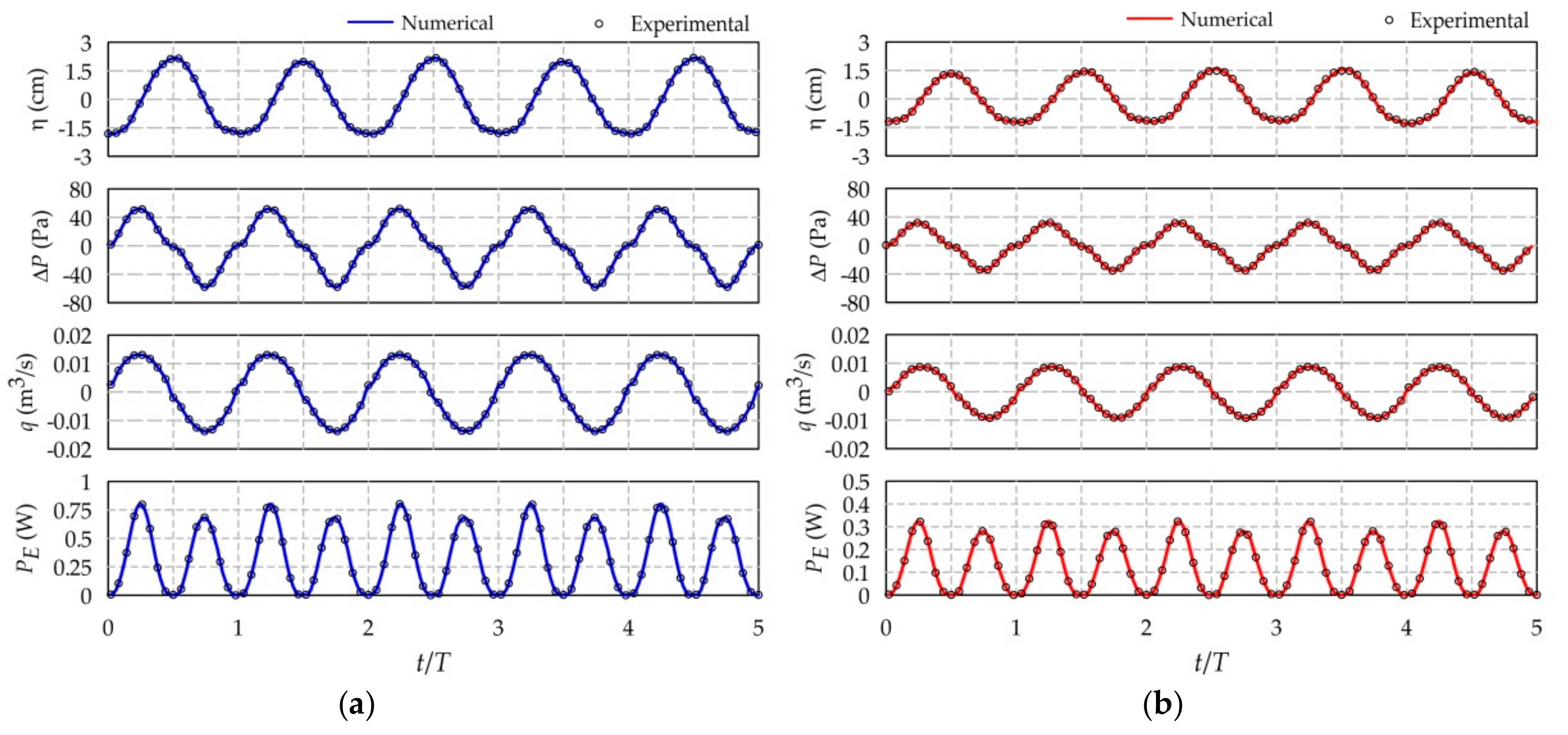
5.2. Validations
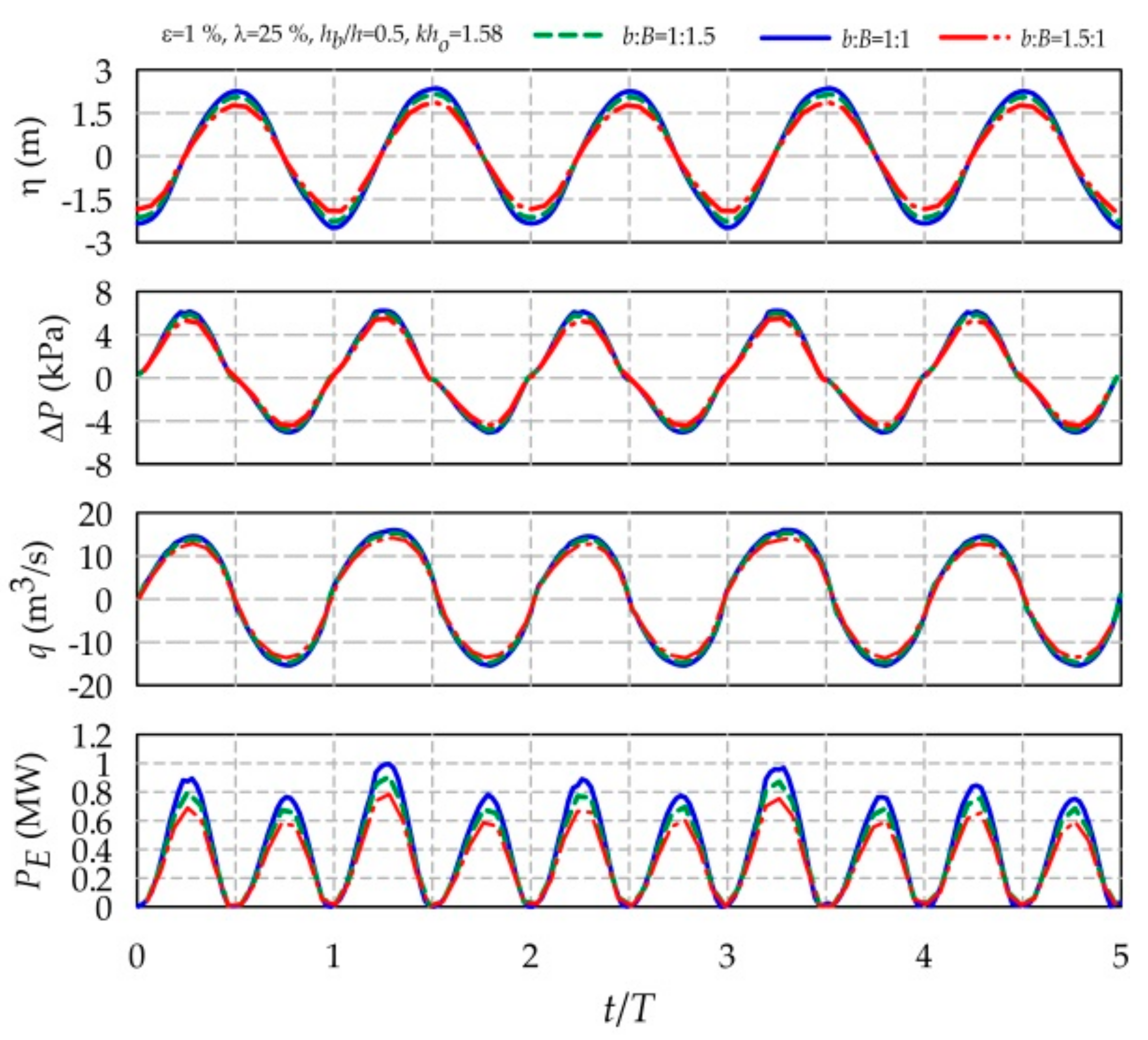
5.2.1. Hydrodynamic Performance Parameters
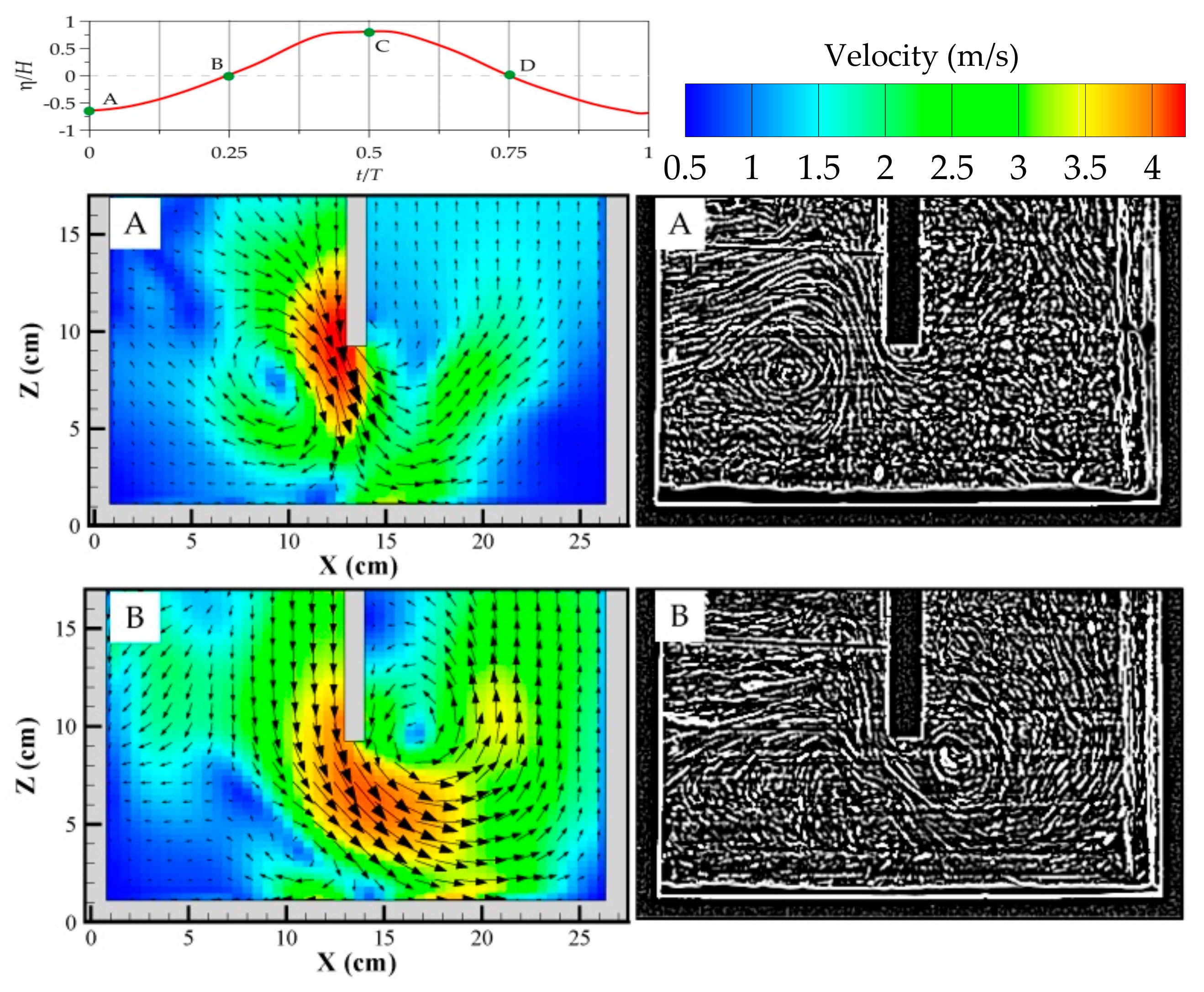
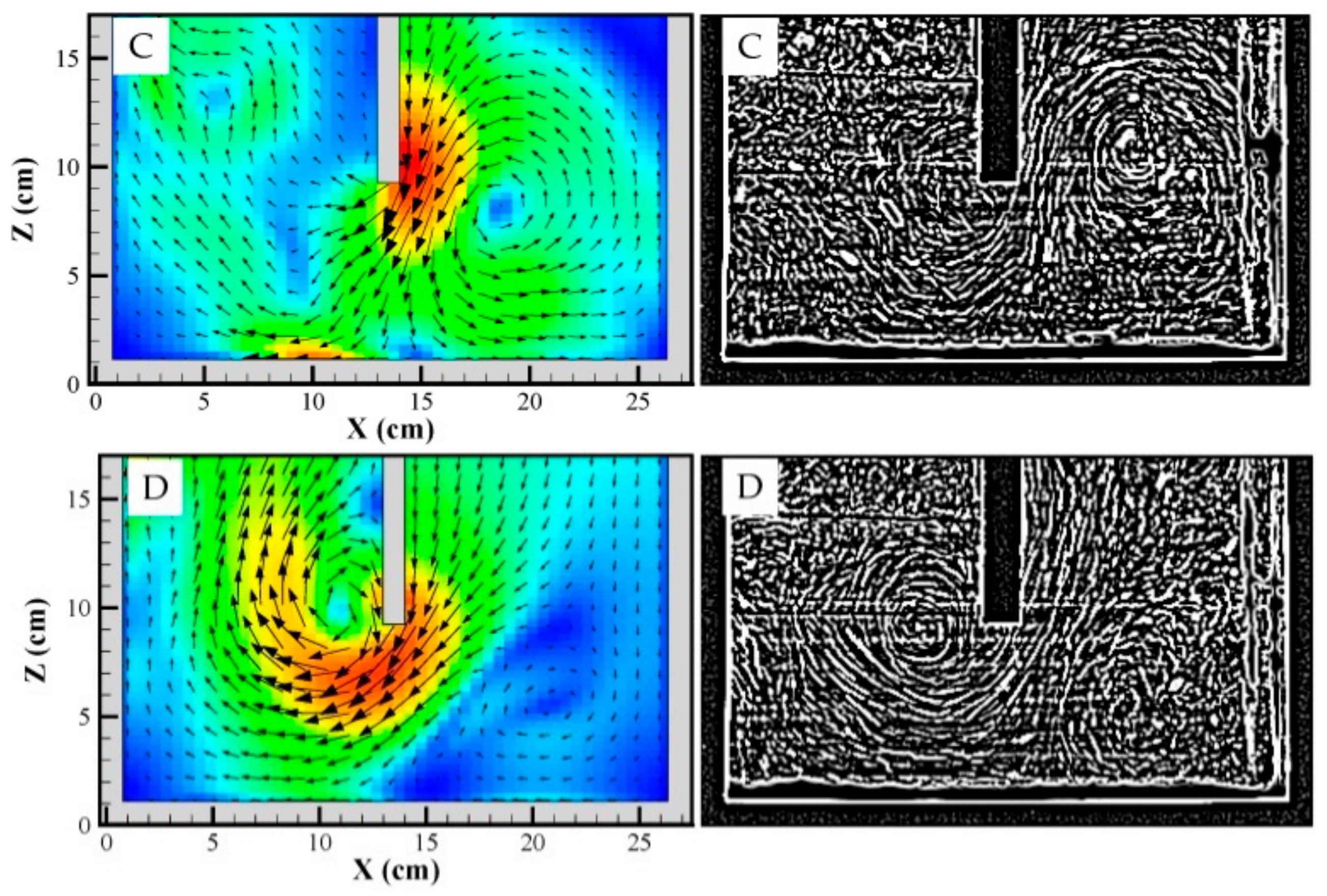
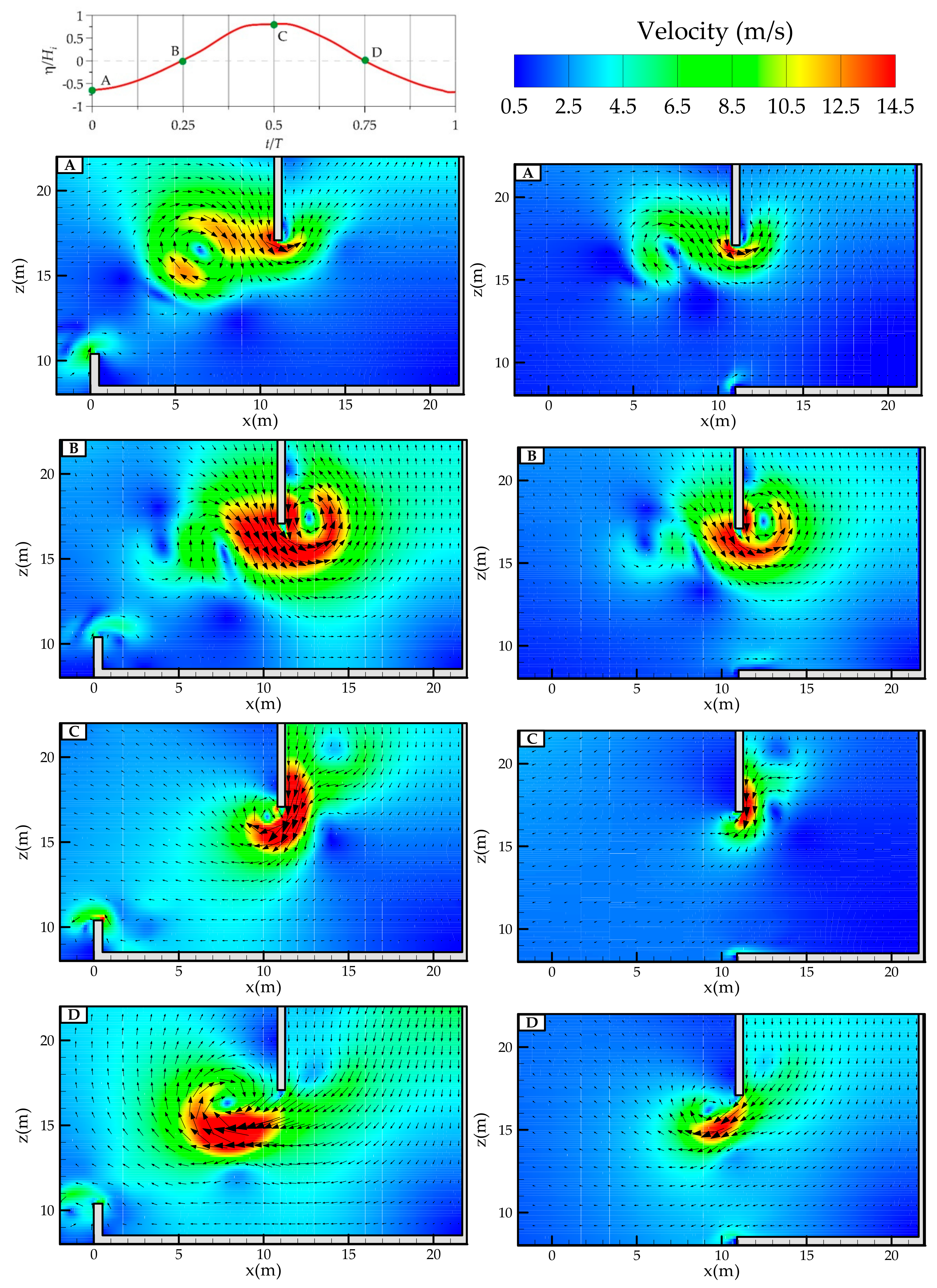
5.2.2. Flow Patterns
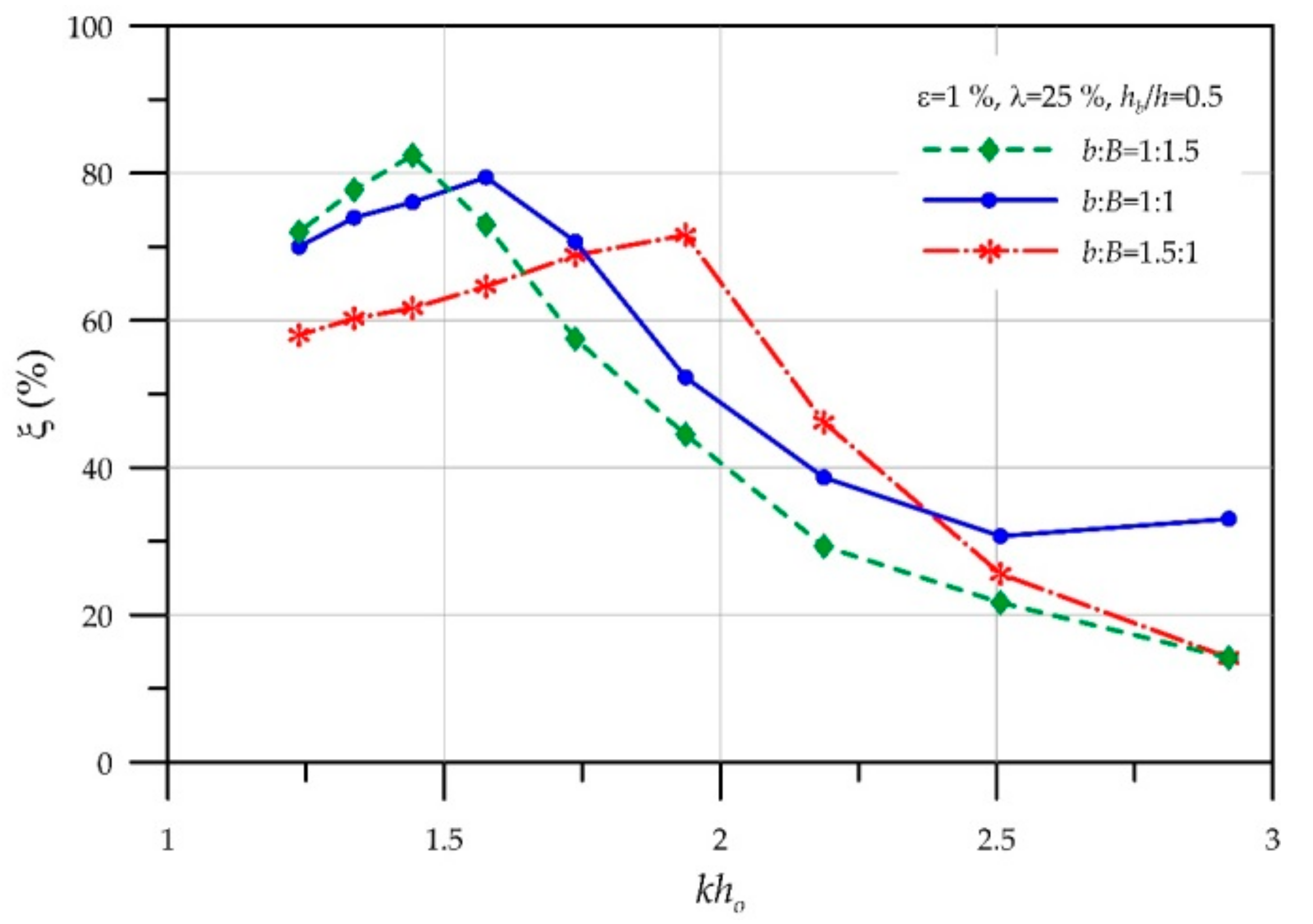
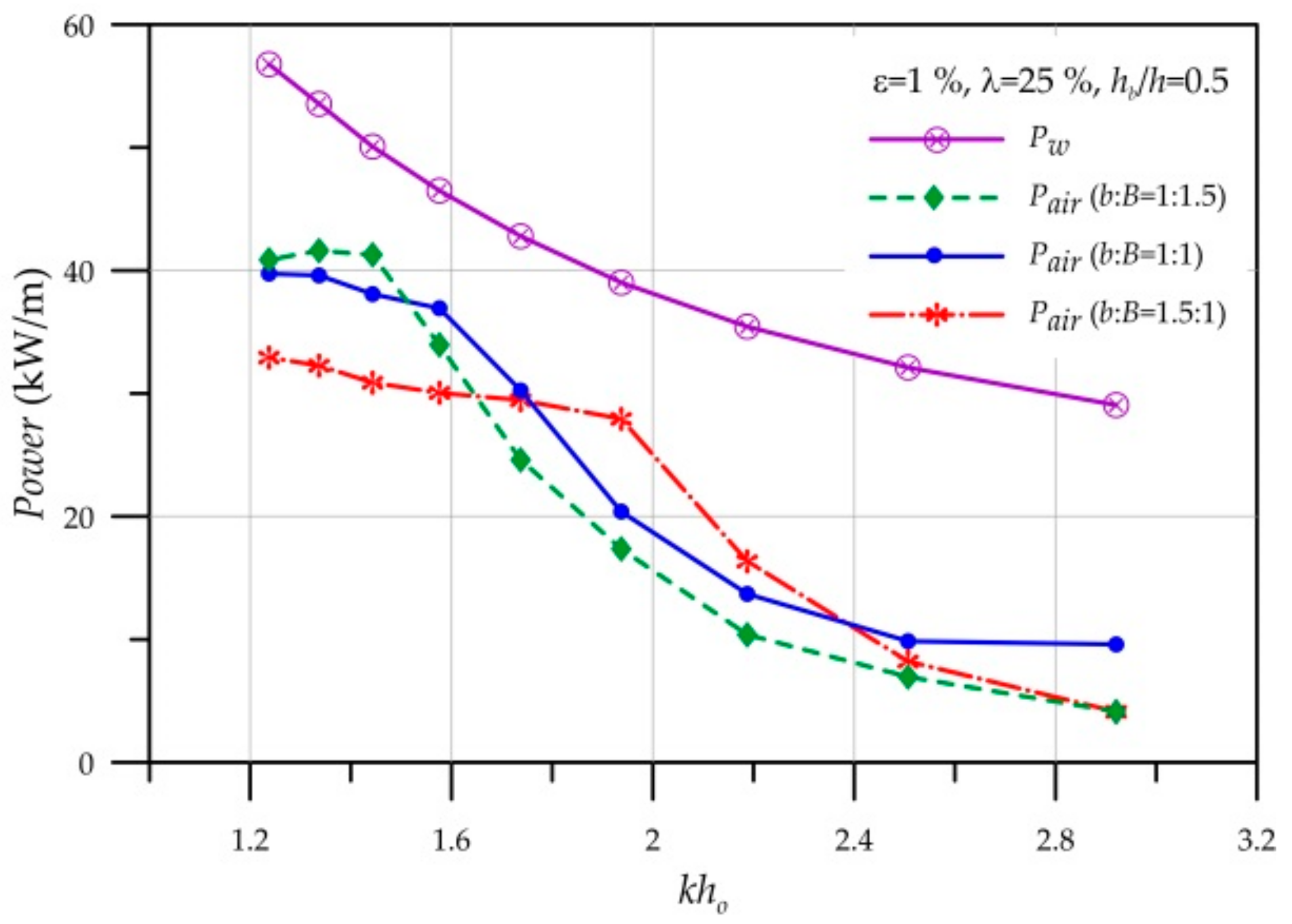
6. Effects of Chamber Geometry on Hydrodynamic Efficiency
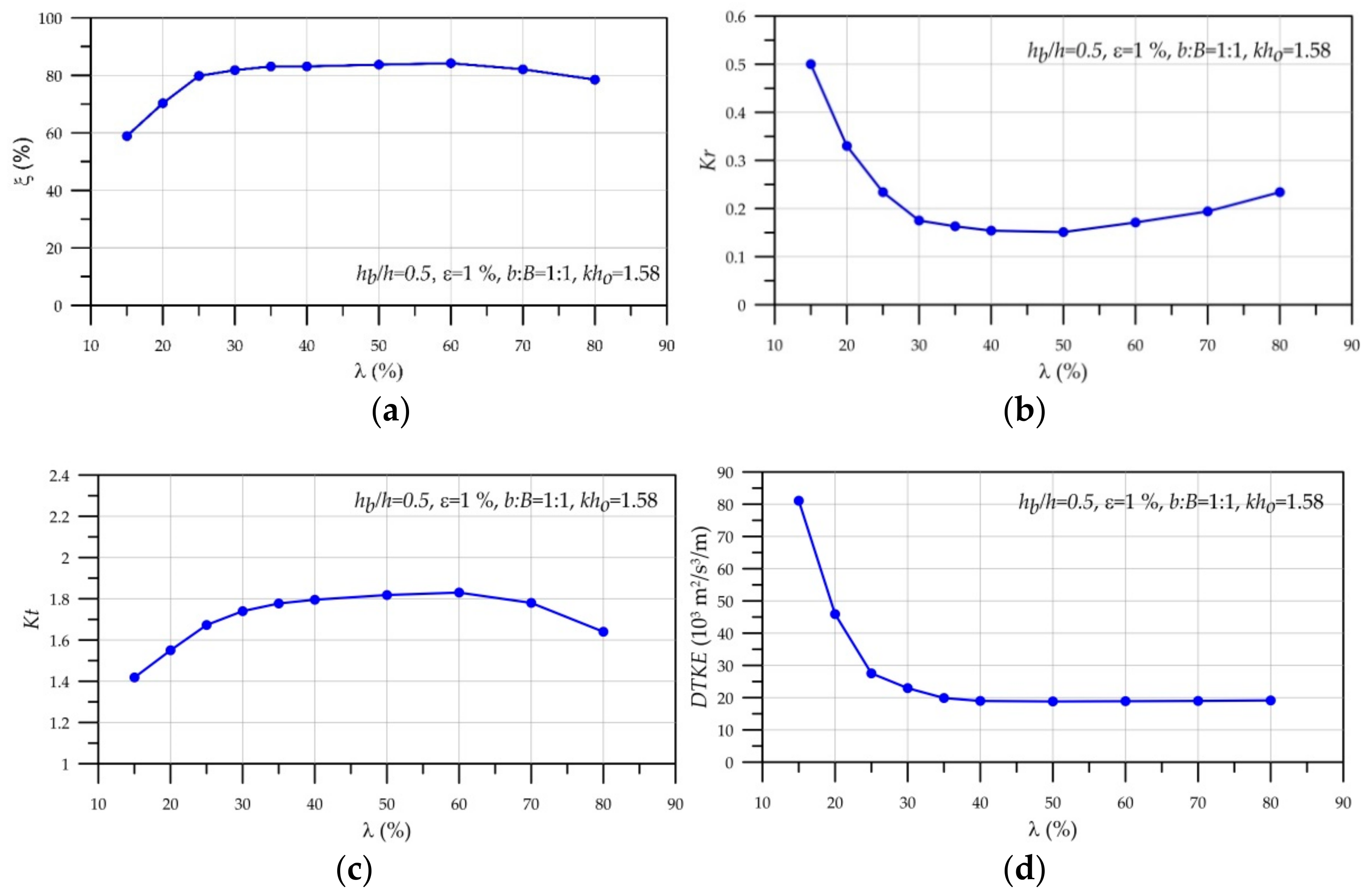
6.1. Effect of the Chamber Breadth
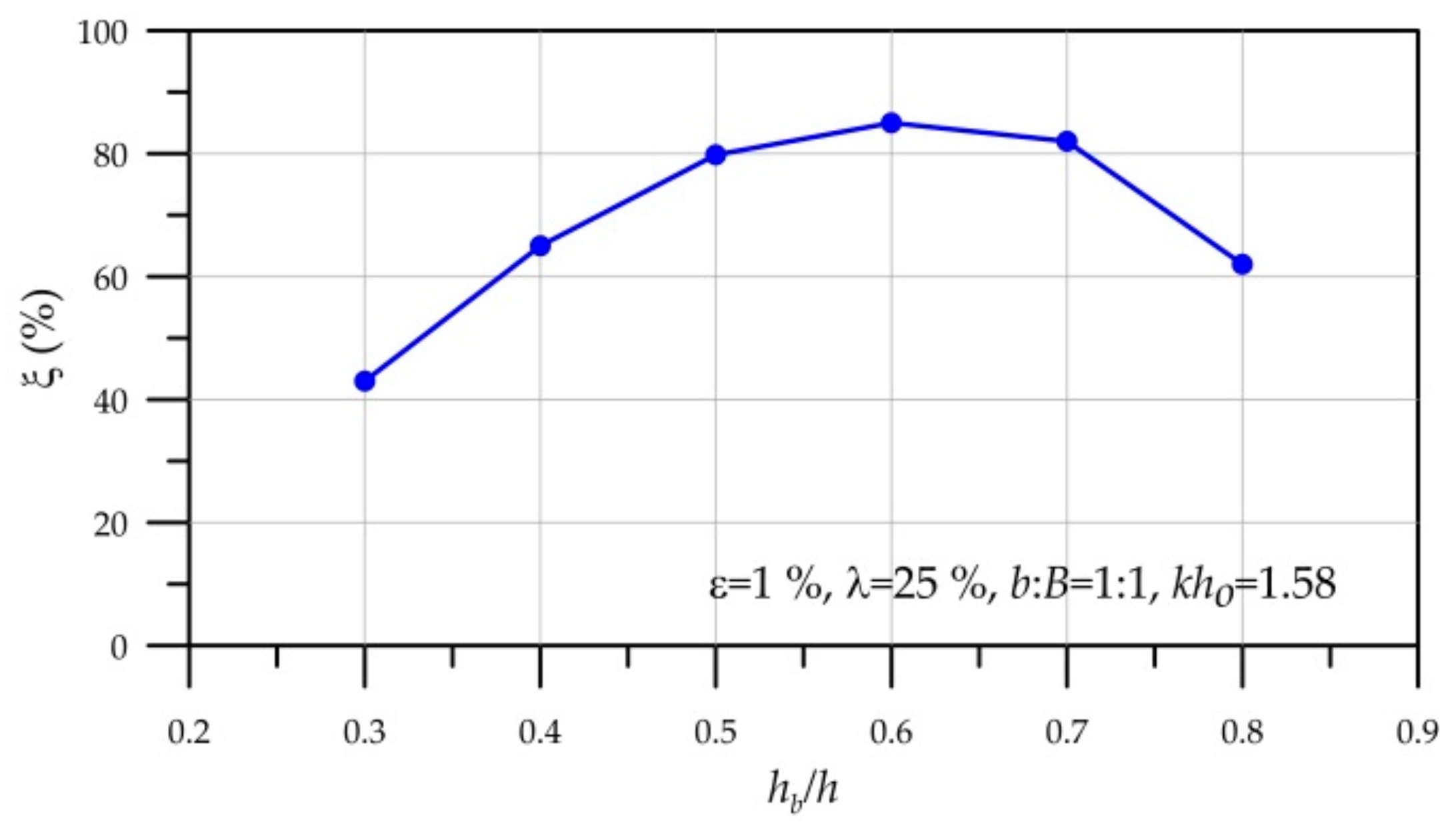
6.2. Effect of Opening Height of Submerged Wall
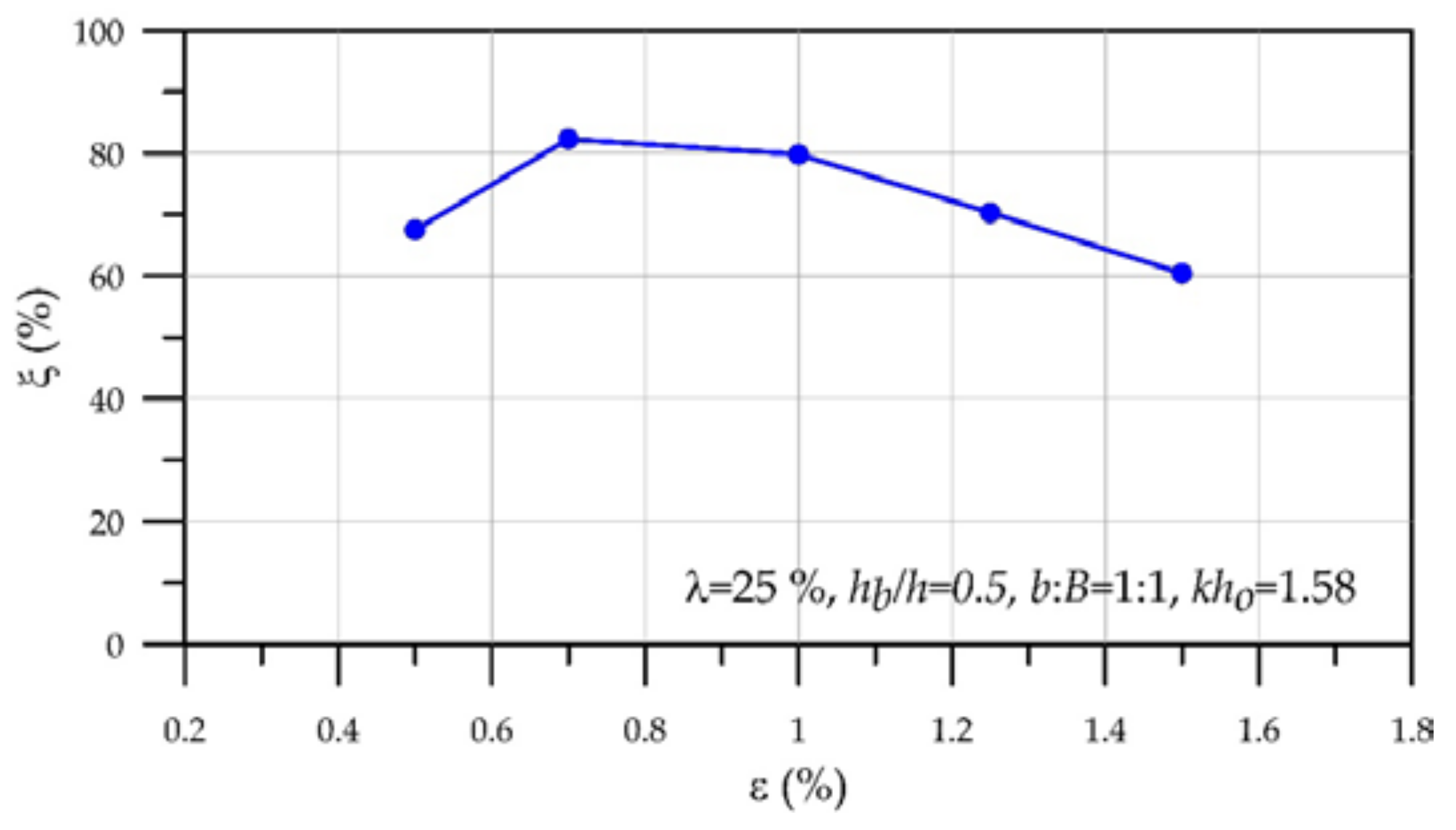
6.3. Effect of Orifice Scale
6.4. Effect of Porosity of Perforated Front Wall
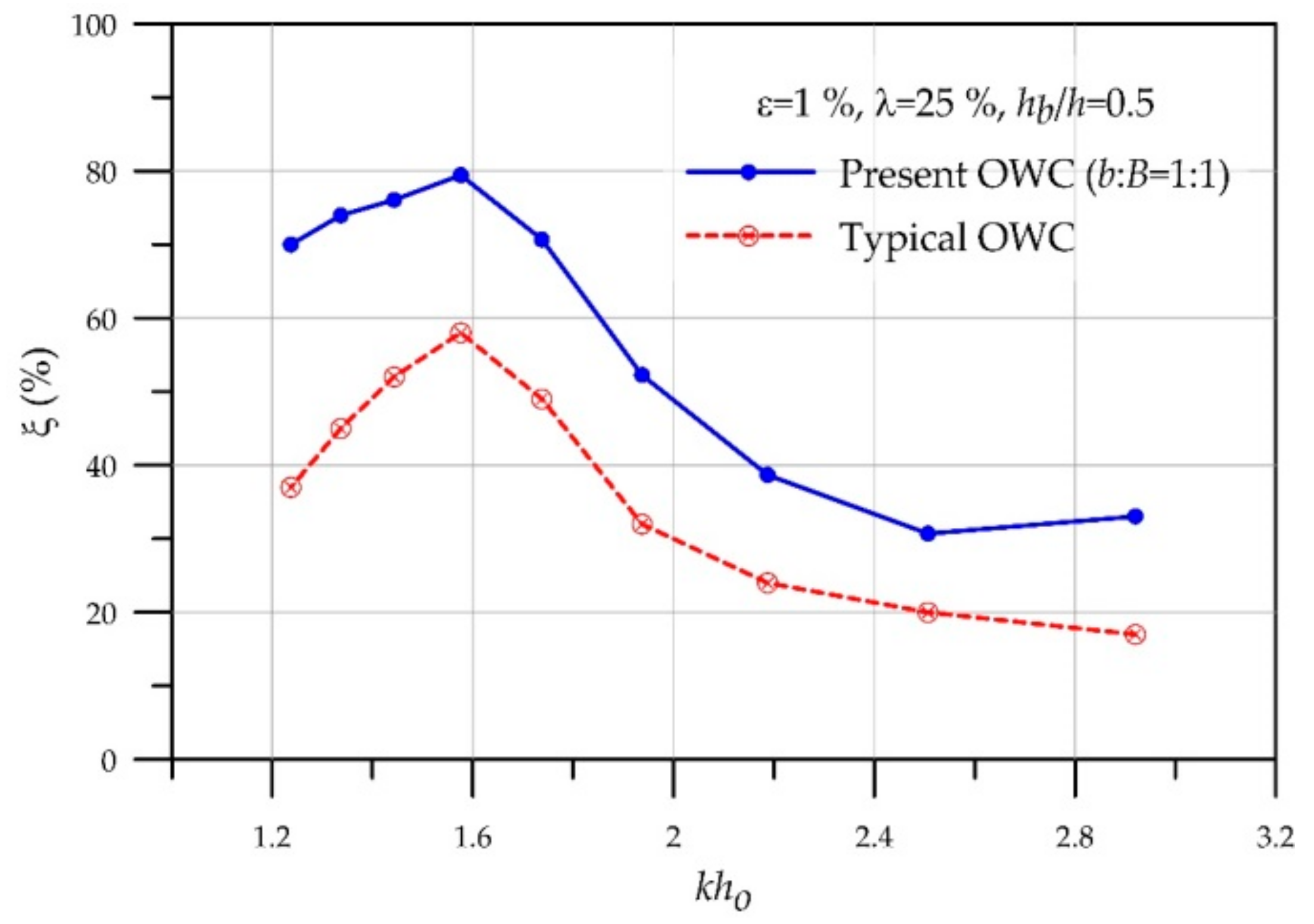
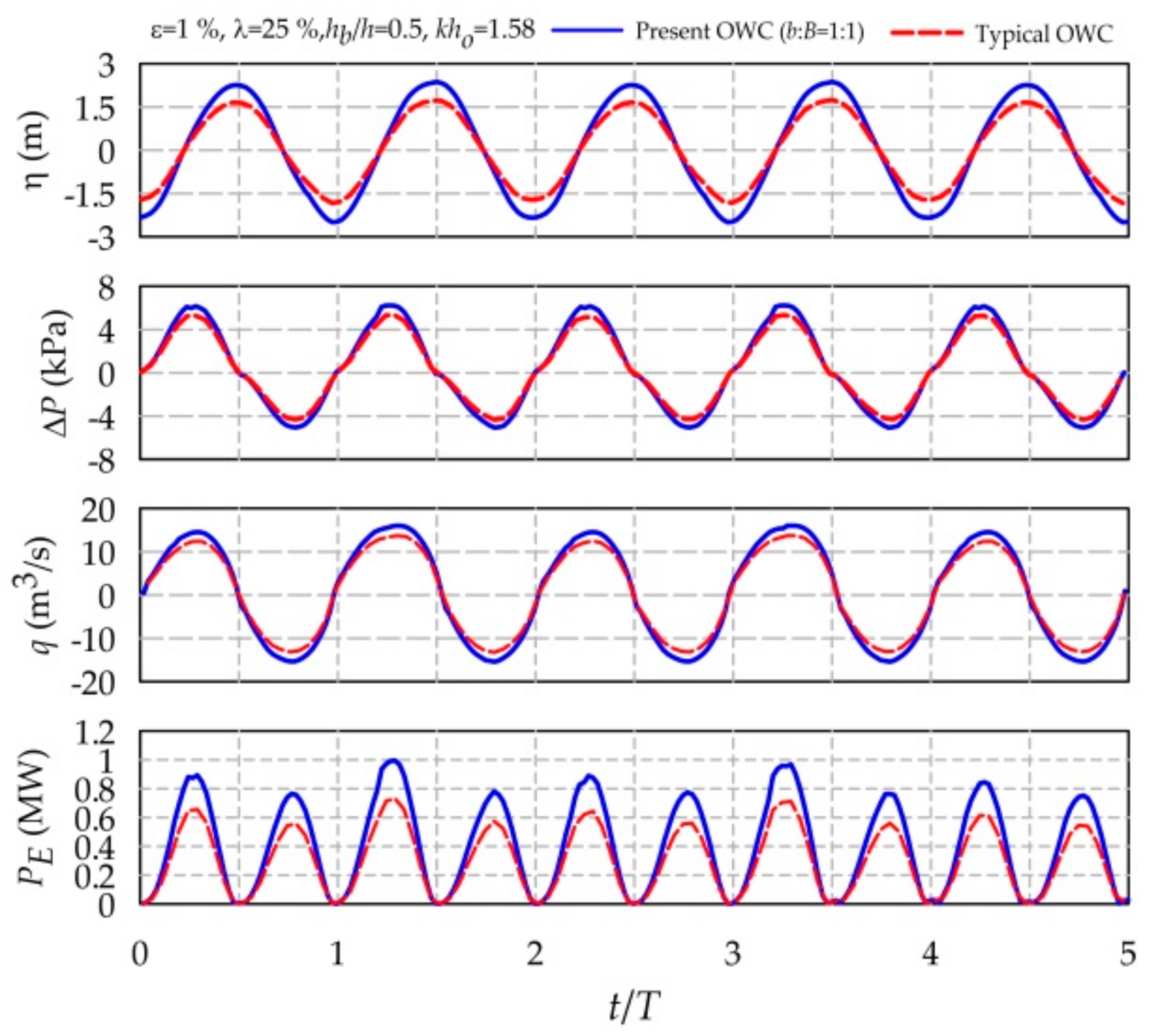
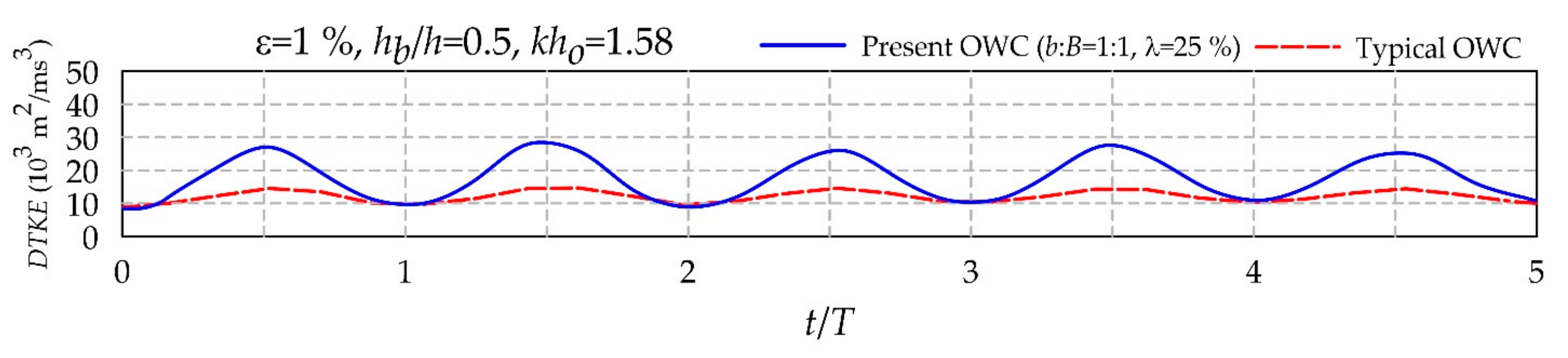
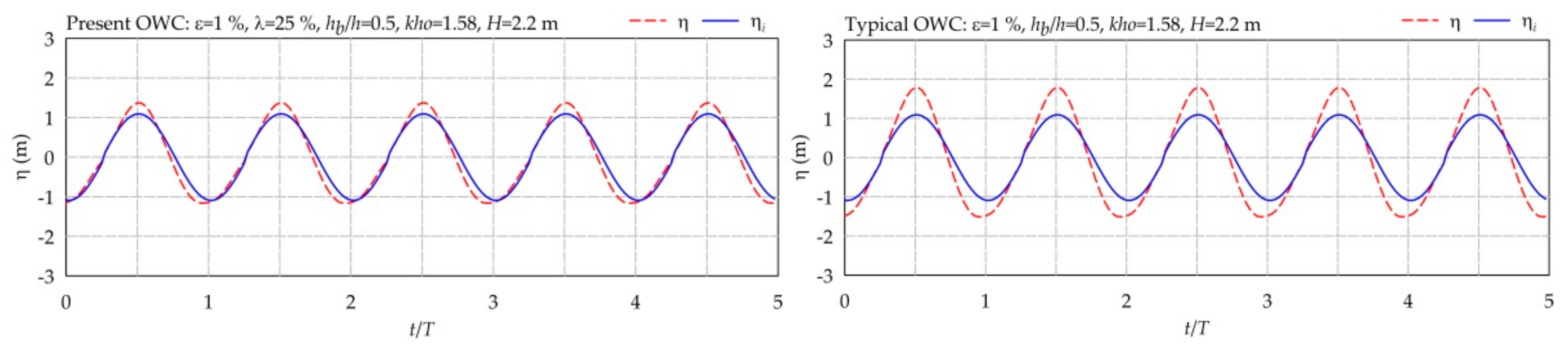
7. Comparisons of Present and Typical OWC Devices
8. Conclusions
9. Patents
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Falcão, A.F.O.; Henriques, J.C.C. Oscillating-water-column wave energy converters and air turbines: A review. Renew. Energy 2015, 85, 1391–1424. [Google Scholar] [CrossRef]
- Ohneda, H.; Igarashi, S.; Shinbo, O.; Sekihara, S.; Suzuki, K.; Kubota, H. Construction procedure of a wave power extracting caisson breakwater. In Proceedings of the 3rd Symposium on Ocean Wave Energy Utilization, Tokyo, Japan, 22–23 January 1991. [Google Scholar]
- Suzuki, M.; Arakawa, C.; Takahashi, S. Performance of wave power generating system installed in breakwater at Sakata port in Japan. In Proceedings of the 14th International Offshore and Polar Engineering Conference, Toulon, France, 23–28 May 2004. [Google Scholar]
- Torre-Enciso, Y.; Ortubia, I.; de Aguileta Lopez, L.I.; Marques, J. Mutriku wave power plant: From the thinking out to the reality. In Proceedings of the 8th European Wave Tidal Energy Conference, Uppsala, Sweden, 7–10 September 2009. [Google Scholar]
- Arena, F.; Romolo, A.; Malara, G.; Ascanelli, A. On design and building of a UOWC wave energy converter in the Mediterranean sea. In Proceedings of the 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013. [Google Scholar]
- Viviano, A.; Naty, S.; Foti, E.; Bruce, T.; Allsop, W.; Vicinanza, D. Large-scale experiments on the behaviour of a generalised Oscillating Water Column under random waves. Renew. Energy 2016, 99, 875–887. [Google Scholar] [CrossRef]
- Naty, S.; Viviano, A.; Foti, E. Wave energy exploitation system integrated in the coastal structure of a mediterranean port. Sustainability 2016, 8, 1342. [Google Scholar] [CrossRef]
- Vicinanza, D.; Margheritini, L.; Kofoed, J.P.; Buccino, M. The SSG wave energy converter: Performance, status and recent developments. Energies 2012, 5, 193–226. [Google Scholar] [CrossRef]
- Iuppa, C.; Contestabile, P.; Cavallaro, L.; Foti, E.; Vicinanza, D. Hydraulic performance of an innovative breakwater for overtopping wave energy conversion. Sustainability 2016, 8, 1226. [Google Scholar] [CrossRef]
- Contestabile, P.; Iuppa, C.; Di Lauro, E.; Cavallaro, L.; Andersen, T.L.; Vicinanza, D. Wave loadings acting on innovative rubble mound breakwater for overtopping wave energy conversion. Coast. Eng. 2017, 122, 60–74. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.C.; Teng, B.; Jiang, J.J.; Ma, B.L. Total horizontal and vertical forces of irregular waves on partially perforated caisson breakwaters. Coast. Eng. 2008, 55, 537–552. [Google Scholar] [CrossRef]
- Huang, J.; Li, Y.; Liu, Y. Hydraulic performance and wave loadings of perforated/slotted coastal structures: A review. Ocean Eng. 2011, 38, 1031–1053. [Google Scholar] [CrossRef]
- Chandrasekaran, S.; Madhavi, N.; Sampath, S. Force reduction on ocean structures with perforated members. Adv. Struct. Eng. 2015, 647–661. [Google Scholar] [CrossRef]
- Evans, D.V. The oscillating water column wave energy device. J. Inst. Math. Appl. 1978, 22, 423–433. [Google Scholar] [CrossRef]
- Evans, D.V.; Porter, R. Hydrodynamic characteristics of an oscillating water column device. Appl. Ocean Res. 1955, 17, 155–164. [Google Scholar] [CrossRef]
- Martin-Rivas, H.; Mei, C.C. Wave power extraction from an oscillating water column at the tip of a breakwater. J. Fluid Mech. 2008, 626, 395–414. [Google Scholar] [CrossRef]
- Martin-Rivas, H.; Mei, C.C. Wave power extraction from an oscillating water column along a straight coast. Ocean Eng. 2009, 36, 426–433. [Google Scholar] [CrossRef]
- Lovas, S.; Mei, C.C.; Liu, Y. Oscillating water column at a coastal corner for wave power extraction. Appl. Ocean Res. 2010, 32, 267–283. [Google Scholar] [CrossRef]
- Zhang, Y.; Zou, Q.P.; Greaves, D. Air-water two phase flow modeling of hydrodynamic performance of an oscillating water column device. Renew. Energy 2012, 41, 159–170. [Google Scholar] [CrossRef]
- Liu, Z.; Hyun, B.S.; Hong, K.Y. Application of numerical wave tank to OWC air chamber for wave energy conversion. In Proceedings of the 18th International Offshore and Polar Engineering Conference, Vancouver, BC, Canada, 6–11 July 2008. [Google Scholar]
- EI Marhani, A.; Castro Ruiz, F.; Rodriguez, M.A.; Parra Santos, M.T. Numerical modeling in wave energy conversion systems. Energy 2008, 33, 1246–1253. [Google Scholar]
- Iturrioz, A.; Guanche, R.; Armesto, J.A.; Alves, M.A.; Vidal, C.; Losada, I.J. Time-domain modeling of a fixed detached oscillating water column towards a floating multi-chamber device. Ocean Eng. 2014, 76, 65–74. [Google Scholar] [CrossRef]
- López, I.; Pereiras, B.; Castro, F.; Iglesias, G. Optimisation of turbine-induced damping for an OWC wave energy converter using a RANS-VOF numerical model. Appl. Energy 2014, 127, 105–114. [Google Scholar] [CrossRef]
- Ning, D.Z.; Shi, J.; Zou, Q.P.; Teng, B. Investigation of hydrodynamic performance of an OWC wave energy device using a fully nonlinear HOBEM. Energy 2015, 83, 177–188. [Google Scholar] [CrossRef]
- Ning, D.Z.; Wang, R.Q.; Chang, C.W. Numerical simulation of a dual-chamber oscillating water column wave energy converter. Sustainability 2017, 9, 1599. [Google Scholar] [CrossRef]
- Iturrioz, A.; Guanche, R.; Lara, J.L.; Vidal, C.; Losada, I.J. Validation of OpenFOAM® for oscillating water column three-dimensional modeling. Ocean Eng. 2015, 107, 222–236. [Google Scholar] [CrossRef]
- Torres, F.R.; Teixeira, P.R.F.; Didier, E. Study of the turbine power output of an oscillating water column device by using a hydrodynamic-aerodynamic coupled model. Ocean Eng. 2016, 125, 147–154. [Google Scholar] [CrossRef]
- Elhanafi, A.; Macfarlane, G.; Fleming, A.; Leong, Z. Scaling and air compressibility effects on a three-dimensional offshore stationary OWC wave energy converter. Appl. Energy 2017, 189, 1–20. [Google Scholar] [CrossRef]
- Kuo, Y.S.; Chung, C.Y.; Hsiao, S.C.; Wang, Y.K. Hydrodynamic characteristics of oscillating water column caisson breakwaters. Renew. Energy 2017, 103, 439–447. [Google Scholar] [CrossRef]
- Crespo, A.J.C.; Altomare, C.; Domínguez, J.M.; González-Cao, J.; Moncho Gómez-Gesteira, M. Towards simulating floating offshore oscillating water column converters with smoothed particle hydrodynamics. Coast. Eng. 2017, 126, 11–16. [Google Scholar] [CrossRef]
- Sarmento, A.J.N.A. Wave flume experiments on two dimensional oscillating water column wave energy devices. Exp. Fluids 1992, 12, 286–292. [Google Scholar] [CrossRef]
- Sarmento, A.J.N.A.; Falcão, A.F.O. Wave generation by an oscillating surface-pressure and its application in wave-energy extraction. J. Fluid Mech. 1985, 150, 467–485. [Google Scholar] [CrossRef]
- Tseng, R.S.; Wu, R.H.; Huang, C.C. Model study of a shoreline wave-power system. Ocean Eng. 2000, 27, 801–821. [Google Scholar] [CrossRef]
- Boccotti, P.; Filianoti, P.; Fiamma, V.; Arena, F. Caisson breakwaters embodying an OWC with a small opening-part II: A small-scale field experiment. Ocean Eng. 2007, 34, 820–841. [Google Scholar] [CrossRef]
- Morris-Thomas, T.M.; Irvin, R.J.; Thiagarajan, K.P. An investigation into the hydrodynamic efficiency of an oscillating water column. J. Offshore Mech. Arct. Eng. 2007, 129, 273–278. [Google Scholar] [CrossRef]
- He, F.; Huang, Z.; Law, A.W.K. An experimental study of a floating breakwater with asymmetric pneumatic chambers for wave energy extraction. Appl. Energy 2013, 106, 222–231. [Google Scholar] [CrossRef]
- López, I.; Castro, A.; Iglesias, G. Hydrodynamic performance of an oscillating water column wave energy converter by means of particle imaging velocimetry. Energy 2015, 83, 89–103. [Google Scholar] [CrossRef]
- Delauré, Y.M.C.; Lewis, A. 3D hydrodynamic modelling of fixed oscillating water column wave power plant by a boundary element methods. Ocean Eng. 2003, 30, 309–330. [Google Scholar] [CrossRef]
- Ning, D.Z.; Wang, R.Q.; Zou, Q.P.; Teng, B. An experimental investigation of hydrodynamics of a fixed OWC wave energy converter. Appl. Energy 2016, 168, 636–648. [Google Scholar] [CrossRef]
- Chiu, Y.F.; Su, C.H.; Tseng, H.M. Oceanographically Observation Data—Annual Report 2013 (Taichung Harbor); Report No. MOTC-IOT-103-H2DA001e-H3; Institute of Transportation, Ministry of Transportation and Communications: Taipei, Taiwan, 2013. [Google Scholar]
- Taiwan International Ports Corporation, Ltd. The Forty-Year Master Planning of Taichung Harbor; Ministry of Transportation and Communications: Taipei, Taiwan, 2017. [Google Scholar]
- Flow Science, Inc. FLOW-3D User Manual; Flow Science, Inc.: Sante Fe, NM, USA, 2012. [Google Scholar]
- Hirt, C.W. Volume-fraction techniques: Powerful tools for wind engineering. J. Wind Eng. Indust. Aero. 1993, 46–47, 327–338. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for dynamics of free boundaries. J. Comp. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A. Renormalization group analysis of turbulence. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A.; Thangam, S.; Gatski, T.B.; Speziale, C.G. Development of turbulence models for shear flows by a double expansion technique. Phys. Fluids A 1992, 4, 1510–1520. [Google Scholar] [CrossRef]
- Speziale, C.G.; Thangam, S. Analysis of an RNG based turbulence model for separated flows. Int. J. Eng. Sci. 1992, 30, 1379–1388. [Google Scholar] [CrossRef]
- Choi, B.H.; Kim, D.C.; Pelinovsky, E.; Woo, S.B. Three-dimensional simulation of tsunami run-up around conical island. Coast. Eng. 2007, 54, 618–629. [Google Scholar] [CrossRef]
- Tsai, C.P.; Chen, Y.C.; Sihombing, T.O.; Lin, C. Simulations of moving effect of coastal vegetation on tsunami damping. Nat. Hazards Earth Syst. Sci. 2017, 17, 693–702. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Fenton, J.D. A Fourier approximation method for steady water waves. J. Fluid Mech. 1981, 104, 119–137. [Google Scholar] [CrossRef]
- Munson, B.R.; Okiishi, T.H.; Huebsh, W.W.; Rothmayer, A.P. Fluid Mechanics, 7th ed.; John Wiley & Sons Singapore Pte Ltd.: Singapore, 2013. [Google Scholar]
- Goda, Y.; Suzuki, Y. Estimation of incident and reflection waves in random wave experiments. In Proceedings of the 15th International Conference Coastal Engineering, Honolulu, HI, USA, 11–17 July 1976. [Google Scholar]
- Elhanafi, A.; Fleming, A.; Macfarlane, G.; Leong, Z. Numerical energy balance analysis for an onshore oscillating water column wave energy converter. Energy 2016, 116, 539–557. [Google Scholar] [CrossRef]

| ΔX | ΔY | ΔZ | ΔZ (Water Surface Region) | |
|---|---|---|---|---|
| zone A | L/56~L/186 | W/10 | H/22 | H/44 |
| zone B | L/112~L/372 | W/20 | H/44 | H/88 |
| zone C | L/112~L/372 | W/20 | H/66 | H/132 |
| zone D | D/10~D/18 | D/10~D/18 | d/5 | - |
| zone S | L/168~L/558 | W/20 | H/66 | H/132 |
| Parameters | Present OWC Device | Typical OWC Device | |
|---|---|---|---|
| incident wave | H | 3.45 cm | 3.45 cm |
| T | 0.875 s | 0.875 s | |
| h | 21.0 cm | 21.0 cm | |
| ho | 21.0 cm | 21.0 cm | |
| kho | 1.285 | 1.285 | |
| geometry of OWC device | B | 11.5 cm | 11.5 cm |
| b | 11.5 cm | - | |
| hb | 9.0 cm | 9.0 cm | |
| ht | 2.0 cm | - | |
| D | 4.0 cm | 4.0 cm | |
| d | 1.0 cm | 1.0 cm | |
| ha | 9.0 cm | 9.0 cm | |
| λ | 25% | - | |
| W | 48.0 cm | 48.0 cm | |
| Parameters | Present OWC Device | Typical OWC Device | |
|---|---|---|---|
| incident wave | H | 2.2 m | 2.2 m |
| T | 6.0–10.0 s | 6.0–10.0 s | |
| h | 18.0 m | 18.0 m | |
| ho | 26.0 m | 26.0 m | |
| kho | 1.25–2.92 | 1.25–2.92 | |
| geometry of OWC device | b + B | 21.0 m | - |
| B | 8.4, 10.5, 12.6 m | 10.5 m | |
| b | 8.4, 10.5, 12.6 m | - | |
| hb | 5.4–14.4 m | 9.0 m | |
| ht | 1.5 m | - | |
| D | 0.82–1.41m | 1.15 m | |
| d | 0.5 m | 0.5 m | |
| ha | 8.0 m | 8.0 m | |
| λ | 15%–60% | - | |
| W | 10.0 m | 10.0 m | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, C.-P.; Ko, C.-H.; Chen, Y.-C. Investigation on Performance of a Modified Breakwater-Integrated OWC Wave Energy Converter. Sustainability 2018, 10, 643. https://doi.org/10.3390/su10030643
Tsai C-P, Ko C-H, Chen Y-C. Investigation on Performance of a Modified Breakwater-Integrated OWC Wave Energy Converter. Sustainability. 2018; 10(3):643. https://doi.org/10.3390/su10030643
Chicago/Turabian StyleTsai, Ching-Piao, Chun-Han Ko, and Ying-Chi Chen. 2018. "Investigation on Performance of a Modified Breakwater-Integrated OWC Wave Energy Converter" Sustainability 10, no. 3: 643. https://doi.org/10.3390/su10030643
APA StyleTsai, C.-P., Ko, C.-H., & Chen, Y.-C. (2018). Investigation on Performance of a Modified Breakwater-Integrated OWC Wave Energy Converter. Sustainability, 10(3), 643. https://doi.org/10.3390/su10030643





