1. Introduction
Financial statements are the basic documents that reflect the financial status of a company [
1,
2,
3,
4,
5,
6]. Financial statements are also the main basis of decision-making for the investing public, creditors, stakeholders, and other users of accounting information. They are also statements of listed companies about their operating performance, financial status, and social responsibilities. However, financial statement fraud seems to be occurring at an increasing pace and with a growing magnitude [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14]. Financial statements fraud seriously damages the sustainable development of enterprises and financial markets [
5,
6,
11,
14].
Over the past decade, numerous cases of financial reporting fraud have occurred in both the U.S. and Taiwan. Examples in the U.S. are Enron in 2001, Xerox and K-Mart in 2002, WorldCom in 2003, AIG in 2005, and IBM in 2008. Examples in Taiwan include Procomp Informatics, Summit Technology, Infodisc Technology, and ABIT Computer in 2004, Rebar in 2007, and XPEC Entertainment in 2016. It is, therefore, essential to develop methods to detect fraudulent activities early on.
The U.S. Congress passed the Sarbanes-Oxley Act in 2002, aiming to impose greater responsibilities on management and auditors in order to prevent corporate fraud. The highlight of the Sarbanes-Oxley Act includes the strengthening of regulatory oversight and corporate governance, and the independence of auditors. Meanwhile, the Public Company Accounting Oversight Board (PCAOB) was established, along with new stipulations regarding auditors’ independence and internal control. For example, accounting firms are no longer allowed to provide both auditing and non-auditing services to the same client. Meanwhile, there is enhanced monitoring of internal auditors within corporations. According to the principles and regulations in the Sarbanes-Oxley Act, accountants and auditors shall collate sufficient and appropriate evidence during the auditing process in order to determine the conclusion of their opinions on the audited firms as an ongoing concern. It is required that accountants and auditors avoid any deliberate or major negligence that could directly or indirectly assist management in fraudulent financing reporting. These are greatly correlated to corporate governance. Corporate governance includes an enterprise’s perfect internal control system, internal auditing system, independent director system, audit committee, external accountant auditing, checking of tax personnel, management and standard of financial and corporate regulations, and checking of financial competent authority personnel, etc.
A series of corporate fraud cases have led to various measures to protect the investing public and capital markets. The year 2002 saw the U.S. Congress pass the Sarbanes-Oxley Act, while the American Institute for Certified Public Accountants (AICPA) published the Statement on Auditing Standards (SAS) No. 99, Consideration of Fraud in Financial Statements. The purpose is to enhance the accuracy and reliability of financial reporting and disclosure by companies. Accountants and auditors shall collate sufficient and appropriate evidence during the auditing process in order to determine the conclusion of their opinions on the audited firms as an ongoing concern. Meanwhile, accountants and auditors must avoid any deliberate or major negligence that could directly or indirectly assist management in fraudulent financing reporting. Company boards are required to establish an effective management system and fraud prevention mechanism to mitigate the possibility of corporate shenanigans. In Taiwan, the Statement on Auditing Standards (SAS) No. 43, Consideration of Fraud in Financial Statements, took effect in 2006. These standards can effectively urge auditors to spot errors in financial reports and mitigate any material or false representations caused by fraudulent activities. As management may seek to manipulate earnings, auditors should also establish a task force (according to Articles 27 to 31) to discuss whether there are signs indicating the possibility of earnings manipulation and decide the corresponding auditing procedures (Article 10, Article 15, and Article 29). The Statement on Auditing Standards (SAS) No. 45, which became effective in 2016, also require auditors to reach a conclusion on whether they can be reasonably sure that there are no material or false representations in the financial statements as a result of fraud or errors. To reach this conclusion, auditors shall consider whether they have acquired sufficient and appropriate evidence and whether the to-be-corrected misrepresentations (in terms of amounts or aggregated numbers) are material (Article 7).
Companies are confronted with increasing challenges and risk management issues amid fierce market competition and the uncertainties of the global economy. Given the changes in politics, economies, and business environments in the Asia Pacific region, companies in Taiwan should continue to develop opportunities in China and Southeast Asia by identifying new investments and possibilities. In the process of seeking steady growth and overcoming difficulties, companies should comply with laws and meet global changes. The business challenges associated with investing in emerging markets enhance the incentives for manipulating financial statements in order to evade taxes in the home country or to move capital overseas. The number of cases of financial reporting fraud continues to increase. Each occurrence is a heavy blow to investors, creditors, and stakeholders, and it costs society dearly. Therefore, the establishment of an effective model to detect financial reporting fraud is an important issue.
Basely [
15] finds a correlation between accounting fraud and non-financial information, such as corporate governance. When a company has a good financial status, and has a good corporate governance mechanism in place, it is likely to report financial statements fraud. Therefore, it is necessary to take into account non-financial information in the assessment of accounting fraud. The establishment of pre-warning models to detect fraudulent activities in financial reporting has been a focal point of academic discussions. In the early days, the prediction of financial distress or bankruptcy often used financial ratios as the tool [
1,
16,
17,
18]. Later, cash flow was also incorporated [
19,
20,
21]. In recent years, corporate governance has been included as part of the equation for the prediction of financial crises or accounting fraud [
3,
4,
5,
6,
10,
11,
13,
14,
15,
22,
23]. In sum, the discriminatory models must add or delete variables over time to effectively identify the companies likely to report accounting fraud.
Financial statements fraud is a typical classification problem [
10]. The calculations for a classification problem are based on the variable attribute values of the known classified data. The derived classification rules are then applied to the unclassified data in order to reach the final classification conclusion. Most of the literatures on accounting fraud detection apply traditional regression analysis. In recent years, a number of experts and researchers have attempted to use data mining to reduce detection errors. Data mining techniques have two basic functions: (1) Top-down hypothesis testing. People can try to prove or take counter examples in order to verify presupposed ideas; (2) Bottom-up knowledge discovery. The existing data tell us something that is not known. Compared with the traditional regression analysis method, data mining techniques are more suitable for conducting classification and prediction in a very precise way, which is the target of this research. The current scientific and academic literature is seeking rules or classifications from previous data to further achieve the purpose of prediction or detection. Simply speaking, for instance, data mining techniques can be used for classification to distinguish what kind of movies respondents will see according to their age, sex, and social and economic status. Data mining techniques are employed to predict or detect who its audience is when a new film is released. In other words, the above-mentioned classification result is further analyzed to find the target audience when a new film is released. Machine learning and data mining with an extensive amount of data yields more accurate prediction and classification outcomes, compared to the traditional approach of regression analysis. Artificial neural networks (ANN), decision trees (DT), support vector machines (SVM), and Bayesian belief networks (BBN) are all popular tools for the detection of accounting fraud [
3,
4,
5,
6,
11,
14].
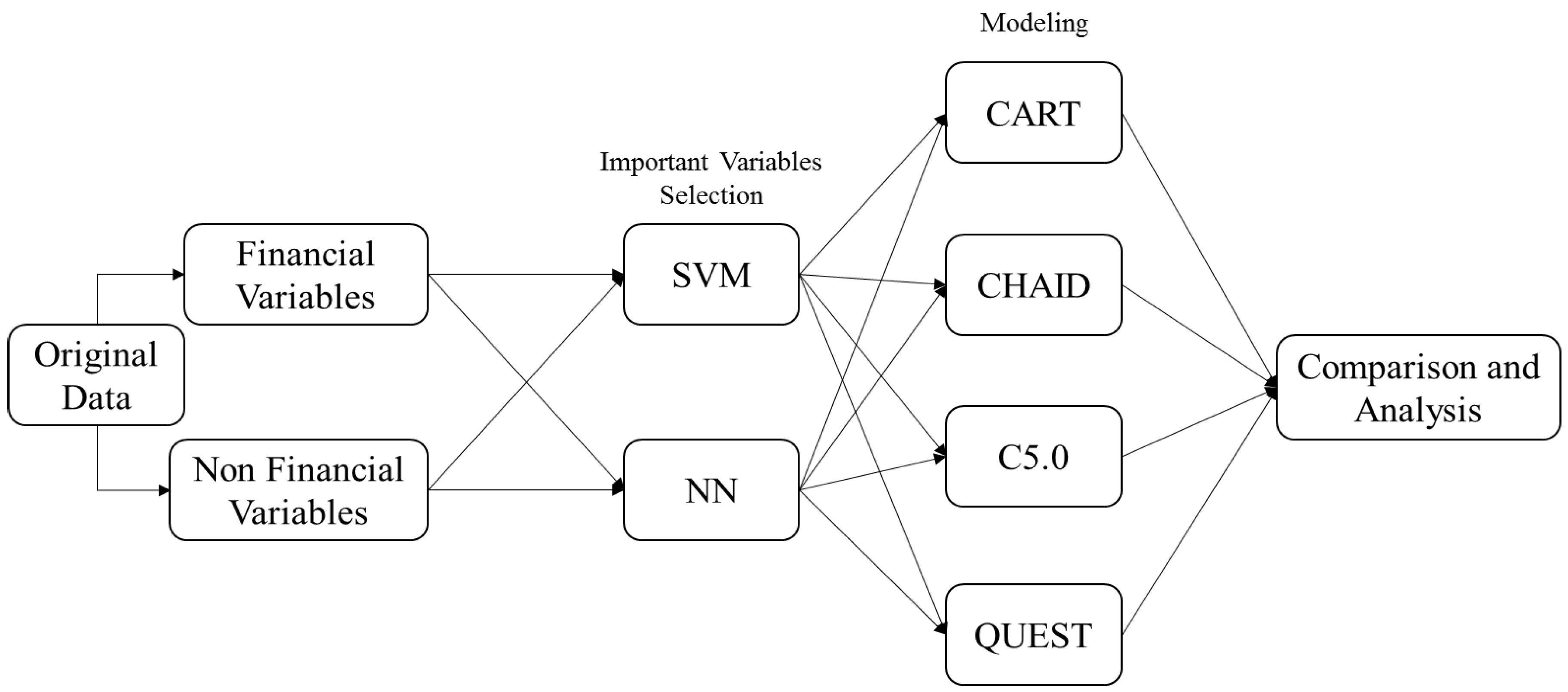
This study aims to establish a superior model to detect enterprises’ financial statements fraud by spotting the early signs, in order to mitigate the losses to investors, auditors, and all stakeholders in the financial market. In the first stage, this study deploys an artificial neural network (ANN) and a support vector machine (SVM) to screen important variables. In the second stage, four decision-tree techniques are applied (classification and regression tree (CART), chi-square automatic interaction detector (CHAID), C5.0, and quick unbiased efficient statistical tree (QUEST)) to construct classification models and make comparisons. Both financial and non-financial variables are adopted in order to enhance the prediction accuracy for detecting financial statements fraud.
2. Materials and Methods
ANN and SVM are suitable for selecting important variables, while CART, CHAID, C5.0, and QUEST are suitable for classifying, predicting, and detecting variables [
3,
4,
5,
6]. In the first stage, the artificial neural network (ANN) and support vector machine (SVM) techniques are used to screen important variables. In the second stage, four decision-tree techniques are applied (CART, CHAID, C5.0 and QUEST) to construct classification models and make comparisons.
2.1. Artificial Neural Network
An artificial neural network (ANN) is a structure similar to the neurons in a human brain. It is an information processing system that mimics biological nerves and that can receive and combine multiple inputs to make predictions. The artificial neural network is a kind of artificial intelligence machine where the mathematical method is used to make the computer have the ability to deduce the outcome through the computer’s rapid calculation ability. It must go through a learning process (i.e., machine learning) so that it can have the deduction ability—that is, someone tells it what kind of situation will result in what kind of outcome. If you tell it the correct examples, then it will answer you correctly. It can even analogize the possible outcome for the examples not learned before.
The units that are processed by an ANN are neurons. They serve two purposes: (1) pass-through, in which incomplete data points for node inputs do not result in a significant influence on the network; and (2) adaptive learning, which refers to adjustments to the weight of connections between nodes. The basic structure of an ANN consists of an input layer, a hidden layer, and an output layer. The output value of each processing element is transmitted to another processing unit and becomes the input value of that unit.
The back propagation neural network (BPNN) is the most widely used model, with key parameters in hidden layers, error correction functions, and learning ratios.
Refenes et al. [
24] suggest the use of the following equation to determine the number of hidden layers on the basis of the principles for convergence and generalization:
The number of the next hidden layers is the natural logarithm of the neurons in the previous layer.
Error correction functions use the gradient steepest descent method to minimize the error function. The input of each training value is accompanied with an adjustment to the connection weight by the network. The adjustment extent and the error function change in the same direction as the sensitivity to the value. The calculations are as follows:
The symbol
σ denotes the learning ratio, which measures the adjustment extent for each weight. The error function serves to evaluate the learning quality. The greater the
e value, the larger the error and the poorer the learning quality. The calculation of the error function is as follows:
where
Ob is the target output value of the
b-th output neuron in the output layer of the training value, and
yb is estimated output value of the
b-th output neuron in the output layer of the training example.
The connecting weight
ωab between the
a-th neuron and the
b-th neuron in the hidden layer of the error function can be expressed with the following equation of the chain rule:
The error of the
b-th output neuron of the output layer is denoted as ∀
b:
The weighted correction value between the output layer and the hidden layer is expressed as follows:
The threshold correction for the output neuron can be then expressed as follows:
Equations (5)–(7) repeat the simulations and calculations to gradually narrow down the difference between the target value and the estimated value as intended by the neural network.
2.2. Support Vector Machine (SVM)
The support vector machine (SVM), developed by Vapnik [
25], is an artificial intelligence learning method. It is a machine learning technique based on statistical learning theory and structural risk minimization. The purpose is to identify the optimal separating hyperplane to divide two or more classes of data with the learning mechanism by training the input data. It is a type of supervised learning to predict and classify items in the field of data mining.
Assume that there are n number of data points existing in the eigenspace,
, the symbol
indicates the classification for data point
. These data points serve as the training data for the identification of the optimal separating hyperplane as follows:
The symbol
denotes the separating margin, and
is a constant. There could be multiple solutions to
, but the optimal
is the one with the maximum margin. The following equation is the solution to the optimization problem:
After the network learning obtains the
with the maximum margin, it is then possible to establish the classification
by using Equation (10) on the test data that has yet to be classified:
2.3. Decision Tree
Decision trees are one of the simplest methods for inductive learning [
26]. They can process both continuous and discrete variables. A tree structure is established with known facts and classifications in order to generalize relevant judgment rules. The decision trees used in this paper are CART, CHAID, C5.0, and QUEST, which are explained below.
CART (classification and regression tree) is a binary decision-tree technique developed by Breiman et al. in 1984. It is used for continuous data or non-parametric data for classification. The decision of dividing conditions is based on the quantity and attributes of the data, as well as the Gini index. Each division separates the data into two sub-sets, and the process is repeated for each sub-set to identify the next dividing conditions. Data continues to be divided into two sub-sets in order to construct a tree structure. The process is finished when data is no longer divisible.
The Gini index aims to separate the largest category (measured by the number of observations) from others in the node. Assume Data S contains N categories,
C1, C2, …, CN. Based on the splitting condition
v for Attribute
A,
S is divided into {
SL,
SR}. The symbols
li and
ri denote the number of observations belonging to and not belonging to Category
Ci in sub-sets
SL and
SR, respectively (I = 1,2,…,N). If Cn is the largest category in
S, the calculation of the Gini value is as expressed in Equation (11):
CHAID (chi-square automatic interaction detector) is a branch of the decision tree algorithm. Developed by Kass in 1980, the CHAID algorithm mainly relies on chi-square tests in the process of constructing decision trees, and the optimal splitting branch is identified by repeating the process of combinations and divisions. The CHAID algorithm boasts certain advantages in the development of decision trees, as it confirms the eigenvariable and the splitting value on the basis of statistical significance. This is beneficial to the optimization of the branching process.
C5.0 was developed by Quinlan [
27] as an improvement of ID3. The ID3 methodology refers to information gain as the criteria of constructing decision trees, and this typically results in over-learning due to an excessively large number of input variables. C5.0 uses the gains ratio to replace the previous criteria. However, the fundamental concept remains the same. The development of a decision tree is based on entropy, no matter how the tree structure is grown. The calculations are expressed in Equations (12) and (13). Assume a set of data contains two categories,
A and
B, with
a being the number of observations for Category
A and
b being the number of observations for Category
B. The expected value of this data set can be expressed with
I (
A,
B):
The entropy value of each attribute is estimated accordingly. The symbol
ai denotes the number of sub-sets for Attribute
C in Category
A. The symbol
bi denotes the number of sub-sets for Attribute
C in Category
B. The entropy value of Attribute
C based on the sub-sets for Attribute
C can be estimated as follows:
Equation (14) is used to calculate the Gain Index for Attribute
C and other attributes. The tree structure is grown starting with the attributes with high Gain Index values:
To resolve the problems associated with having too many splitting branches due to the failure to process continuous rows of data, C5.0 normalizes the gains ratio, as expressed in Equations (15) and (16):
In Equation (16), the symbol Si denotes the number of sub-sets after the categorization of Attribute A, and S is the total number of datasets. The C5.0 methodology ranks the values of continuous rows of data, and calculates again the gains ratio of individual categories. The value with the largest gain is used as the splitting point for the tree structure.
QUEST (quick unbiased efficient statistical tree) assumes the target variable is continuous for the creation of splitting rules. This algorithm can quickly perform calculations and can avoid the bias possibly seen in other methods. It is also suitable for explanatory variables with multiple categories. However, the QUEST methodology can only handle binary categories. If the target variable is continuous for the classification rule, the ANOVA-F test is used. If the target variable is categorical, the chi-square test is used. The branching criterion is the minimum p value. The attribute variable smaller than the significance level α is used as the optimal branching variable. If there is no variable smaller than α, Levene’s test is used to select the variable with the most inconsistency in terms of homogeneity. Otherwise, it will not be possible to divide further.
2.4. Sampling and Variable Selection
2.4.1. Data Sources
The sampling period is 2004–2014 and the sampling pool is companies listed on either the Taiwan Stock Exchange or the Taipei Exchange that have reported financial statement fraud. This study refers to the Major Securities Crimes, Prosecutions, and Sentences published by the Securities and Futures Investors Protection Center and the Securities and Futures Bureau for the misrepresentation of financial statements. These companies were prosecuted pursuant to Article 155 and Article 157 of the Securities and Exchange Act and Taiwan SAS No. 43. A total of 40 fraudulent companies are chosen, including one department store, two steel manufacturers, five textile producers, two biotech companies, two construction firms, and 28 electronics companies (as shown in
Table 1). In order to control external environment factors, such as time periods, industries, and firm sizes, this study matches the sampled companies for comparisons. By referring to the sample matching principles developed by Kotsiantis et al. [
28], a fraudulent company is matched with three regular companies in the same year and same industry (FSF:Non-FSF = 1:3). The matches are regular companies with similar asset values during the year before the surfacing of financial statement fraud. Therefore, this study samples a total of 160 companies, i.e., 40 fraudulent companies and 120 regular companies.
2.4.2. Variable Definitions
(1) Dependent variable: The dependent variable is a dummy variable: 0 for regular companies and 1 for fraudulent companies.
(2) Independent variables: This study selects a total of 22 research variables, comprised of 19 financial variables and three non-financial variables. The definitions of individual variables are summarized in
Table 2.
2.5. Research Process
Before the construction of the models, this study selects a total of 22 variables that may affect the probability of financial statement fraud. As mentioned before, ANN and SVM are suitable for selecting important variables, while CART, CHAID, C5.0, and QUEST are suitable for classifying, predicting, and detecting variables. Twenty-two variables must be screened by machine learning, and those variables having the greater effect are chosen; then, the detecting work in the second stage is started. In this case, the accuracy can be improved significantly. The research procedures are shown below. In the first stage of the modeling, the SVM and ANN are used to screen the input variables with a significant influence. The second stage of the research process applies four different decision tree techniques (CART, CHAID, C5.0, and QUEST) to establish the classification models. A comparison and analysis are then made on the predictive outcomes and accuracy for accounting fraud. The research procedures are illustrated in
Figure 1.
3. Empirical Results
This study establishes FSF detection models in two stages. In Stage I, the ANN and SVM are used as variable selection methods by IBM SPSS Modeler 14.1. The selection results are described below.
3.1. ANN Algorithm Selection
This study uses a total of 160 companies (40 fraudulent companies and 120 regular companies), 22 research variables, and 11 years of data (2004–2014), with a total of 38,720 data items (160 × 22 × 11 = 38,720) to operate the ANN execution variable selection through IBM SPSS Modeler 14.1. A total of 10 variables are selected (variable importance value ≥ 0.05), as shown in
Table 3. The order of importance of the variables is: X20: audited by BIG4 or not; X21: restatement of financial statements or not; X13: quick ratio; X19: ROA; X03: net income/total assets; X16: pre-tax profit ratio; X11: debt ratio; X10: operating income/Sales revenue; X12: current ratio; and X22: type of audit report.
3.2. SVM Algorithm Selection
Similar to the ANN algorithm selection, this study also uses 38,720 data items to execute SVM variable selection through IBM SPSS Modeler 14.1. A total of three variables are selected (variable importance value ≥ 0.05), as shown in
Table 4. The order of importance of the variables is: X08: operating expense/sales revenue; X20: audited by BIG4 or not; and X01: inventory/current assets.
3.3. Construction of the Models and Cross-Validation
After the significant variables are selected in Stage I, CART, CHAID, C5.0, and QUEST are used for modeling in Stage II. After normalization of the selected variables, random non-repeated sampling is conducted. This study adopts IBM SPSS Modeler 14.1 to conduct the ten-fold cross-validation, which is recognized by academic circles as a more rigorous method to increase the detection accuracy rate [
5,
6,
14], the Type I error rate, and the Type II error rate. The dataset is divided into ten parts: nine parts are used as a training group in turn, and one part is used as the test group to be experimented with one by one. The average of the detection accuracy rate is thus increased.
3.3.1. ANN Models
As shown in
Table 5, after the ANN models go through the ten-fold cross-validation, the ANN + CART model has the highest detection accuracy of FSF (90.21%). Regarding the overall accuracy, ANN + CART also has the highest detection accuracy (90.83%). As shown in
Table 6, ANN + CART presents the lowest Type I error rate (9.79%) and Type II error rate (8.55%).
3.3.2. SVM Models
As shown in
Table 7, after the SVM models go through the ten-fold cross-validation, the SVM + CART model has the highest detection accuracy of FSF (86.18%). Regarding the overall accuracy, SVM + CART also has the highest detection accuracy (85.98%). As shown in
Table 8, SVM + CART presents the lowest Type I error rate (13.82%) and Type II error rate (14.22%).
4. Discussion
Based on the above empirical results, the ANN + CART model reports the highest detection accuracy of FSF (90.21%) and the overall accuracy (90.83%) among the eight models built by this study to detect financial statements fraud. ANN + CART also has the lowest Type I error rate (9.79%) and Type II error rate (8.55%). Therefore, it is the best detection model constructed in this study for detecting financial statements fraud.
This study is greatly different from previous studies using data mining techniques to detect the fraud of enterprises’ financial statements. In the first stage, this study deploys an ANN and SVM to screen important variables. In the second stage, four decision-tree techniques are applied (CART, CHAID, C5.0, and QUEST) to construct detection models. For data mining techniques used in this study, the ANN and SVM are suitable for selecting important variables; CART, CHAID, C5.0, and QUEST are suitable for classifying, predicting, and detecting variables. A total of 22 variables that may affect financial statements fraud are selected (including financial and non-financial variables; see
Table 2), in order to improve the detection accuracy of models. The 22 variables are screened by the ANN or SVM, and those having a greater effect are chosen (variable importance value ≥ 0.05). If the variables are not filtered in Stage I (ANN or SVM), the 22 variables are directly modeled via CART, CHAID, C5.0, and QUEST, or other data mining techniques. In other words, the model is built in only one stage. Then, based on the basic concepts of statistics, the accuracy of the model is greatly reduced and it becomes less rigorous. Therefore, this study builds the model in two stages. The empirical results of this study indicate that the first stage filters the following important variables through the artificial neural network (ANN) (including financial and non-financial variables): audited by BIG4 or not; restatement of financial statements or not; quick ratio; ROA; net income/total assets; pre-tax profit ratio; debt ratio; operating income/sales revenue; current ratio; and type of audit report, which is a very important reference for the detection and checking of financial statements fraud.
This study also adopts the ten-fold cross-validation, which is recognized in academic circles as a more rigorous method to increase the detection accuracy. Among the eight financial statements fraud detection models established by this study, two of them have an accuracy of more than 90%, and another two of them have an accuracy of more than 85%. The detection accuracy of the models is good in the fields of social sciences research (all of the models’ detection accuracy is over 75%). As for the ANN + CART model (90.83%, ranked the first in overall accuracy), and the ANN + CHAID model (90.37%, ranked the second in overall accuracy), CART (classification and regression tree), and CHAID (chi-square automatic interaction detector) are two important techniques of the decision tree algorithm. The empirical research also finds that the classifying, predicting, and detecting abilities of both techniques (CART and CHAID) are very good. On the other hand, as for the empirical results of this study, it cannot be arbitrarily argued that the ability or effect of using the ANN to filter important variables is necessarily better than that of the support vector machine (SVM), which depends on the overall situation of the model construction. For example, among the models created by this study, Stage I uses the ANN and Stage II uses the four techniques of the decision tree algorithm, with the overall accuracy: ANN + CART (90.83%), ANN + CHAID (90.37%), and ANN + C5.0 (88.02%), which have higher detection accuracy than SVM + CART (85.98%). The detection accuracy of ANN + QUEST is 84.14%, which is lower than that of SVM + CART (85.98%).
However, this study also finds that, among the 8 models, the classifying, predicting, and detecting ability rank of CART, CHAID, C5.0, and QUEST in Stage II is: CART > CHAID > C5.0 > QUEST. Based on the discussion above, this study provides rigorous and effective financial statements fraud detection models. This is also instructive for other researchers or practitioners. It can also be considered for future studies using other data mining techniques to detect the fraud of enterprises’ financial statements.
5. Conclusions and Suggestions
Financial reports provide all stakeholders in the financial market with useful information on the current situation and prospect of companies. Financial statements fraud is the deliberate falsification of statements or omissions in the figures or footnotes for the purpose of misleading users. The board may force management to achieve earnings targets, or management may choose to manipulate earnings in order to ensure their bonuses, if their bonuses are linked with reported earnings. Fraudulent conduct in the preparation of financial statements may help management to obtain personal gain, such as promotions, salary raises, or a higher value of company shares. Occasionally companies will present false financial statements in order to access long-term debt financing or prop up share prices. Each case of corporate fraud is a heavy blow to investors, creditors, and stakeholders. It disrupts financial markets and costs society dearly. Financial statements fraud seriously damages the sustainable development of enterprises and financial markets. Therefore, the establishment of an effective model to detect enterprises’ financial statement fraud is an important and urgent issue.
Enterprises’ financial statements fraud, especially listed companies, not only cheats stakeholders, such as shareholders, investors, potential investors, suppliers, clients, and customers, but also damages enterprises’ survival and sustainable operations, as well as the health of financial markets and sustainable development. For instance, in 2001 Enron caused great harm to the American economy and significantly affected the sustainable development of the American financial market. Even if accountants and auditors inspect financial statements by adhering to relevant laws and regulations to detect fraudulent misconduct by management, there will always be omissions. The establishment of a rigorous and effective model to detect enterprises’ financial statements fraud that can be applied by CPAs and auditors could greatly reduce enterprises’ financial statements fraud and audit risks to produce an impeding effect on enterprises’ management and help enterprises and financial markets maintain sustainable development. This study’s rigorous and effective two-stage model to detect financial statements fraud can be used as a reference for accountants, auditors, securities analysts, financial analysts, academic professionals, and enterprises and financial markets supervisors. Such is the practical and academic contribution of this study.
This study conducts an empirical study by sampling financial and non-financial data over a research period of eleven years. A total of 22 variables that may affect financial statements fraud are selected on the basis of a literature review (see
Table 2). In order to improve the accuracy of financial statements fraud detection significantly, the 22 variables must be screened through machine learning, and the variables having the greater effect are chosen; then, the detecting work in the second stage is started. In the first stage of modeling, SVM and ANN are used to screen the input variables with significant influence. In the second stage, four typical decision-tree techniques (QUEST, C5.0, CART, and CHAID) are deployed to construct classification models, in order to compare and analyze the accuracy of financial statements fraud detection. Based on the empirical results, the ANN + CART model reports the highest detection accuracy of FSF (90.21%) and the overall accuracy (90.83%) among the eight models built by this study to detect financial statements fraud. ANN + CART also has the lowest Type I error rate (9.79%) and Type II error rate (8.55%). Therefore, it is the best detection model constructed by this study for the detection of financial statements fraud. The lower Type I and Type II error rate can also reduce relevant costs significantly [
14].
This study also makes a number of suggestions to deter or prevent financial statements fraud. First, legal requirements from regulators concerning the establishment of robust internal control and audit systems by corporations and assistance to accountants and auditors in implementation must be put in place. Second, there must be transparency of financial information by listed companies, as required by laws and regulations, so that the public can serve as a monitoring mechanism. Third, CPAs and auditors should act as gatekeepers and investigators of accounting information and financial reporting. Fourth, auditors should show willingness to issue qualified opinions or adverse opinions, as required by the duties, if they have concerns over the integrity of financial information and the customer fails to make improvements after communication. Fifth, there should be enhancement of corporate governance with a sufficient number of independent directors and the establishment of an audit committee comprised of independent directors, shareholder representatives, and external experts. Finally, the legal liability for financial statements fraud should be extended to business owners, CEOs, CFOs, accounting managers (or controllers), internal auditors and accountants, external auditors, and CPAs.
As mentioned in previous studies, compared to the traditional approach of regression analysis, data mining techniques are more rigorous and accurate in detecting financial statements fraud [
3,
4,
5,
6,
11,
14]. In terms of contributions to academic research and theoretical implications, this study conducts a new successful research for using hybrid data mining techniques to detect the fraud of enterprises’ financial statements and provides several rigorous and effective financial statements fraud detection models different from previous studies in the literature. There are also existing limitations in this study. First, the financial market in Taiwan is small in size and scope, compared to the U.S., European Union, the U.K, China, or Japan. The number of listed companies in Taiwan is also relatively small in scale. Second, the competent authority of Taiwan strictly supervises the financial market and listed companies. As a result, not many listed companies are fraudulent in their financial reporting. The application of the models constructed by this study to detect financial statements fraud to other countries or economies requires modification of the relevant metrics or variables depending on the economic systems, fraud-related laws and regulations, and financial markets practice of different countries or regions.