Thermal Environmental Design in Outdoor Space Focusing on Radiation Environment Influenced by Ground Cover Material and Solar Shading, through the Examination on the Redevelopment Buildings in Front of Central Osaka Station
Abstract
1. Introduction
2. Outline of Study Site Characteristics and Calculation Method
2.1. Study Site
2.2. Calculation Method
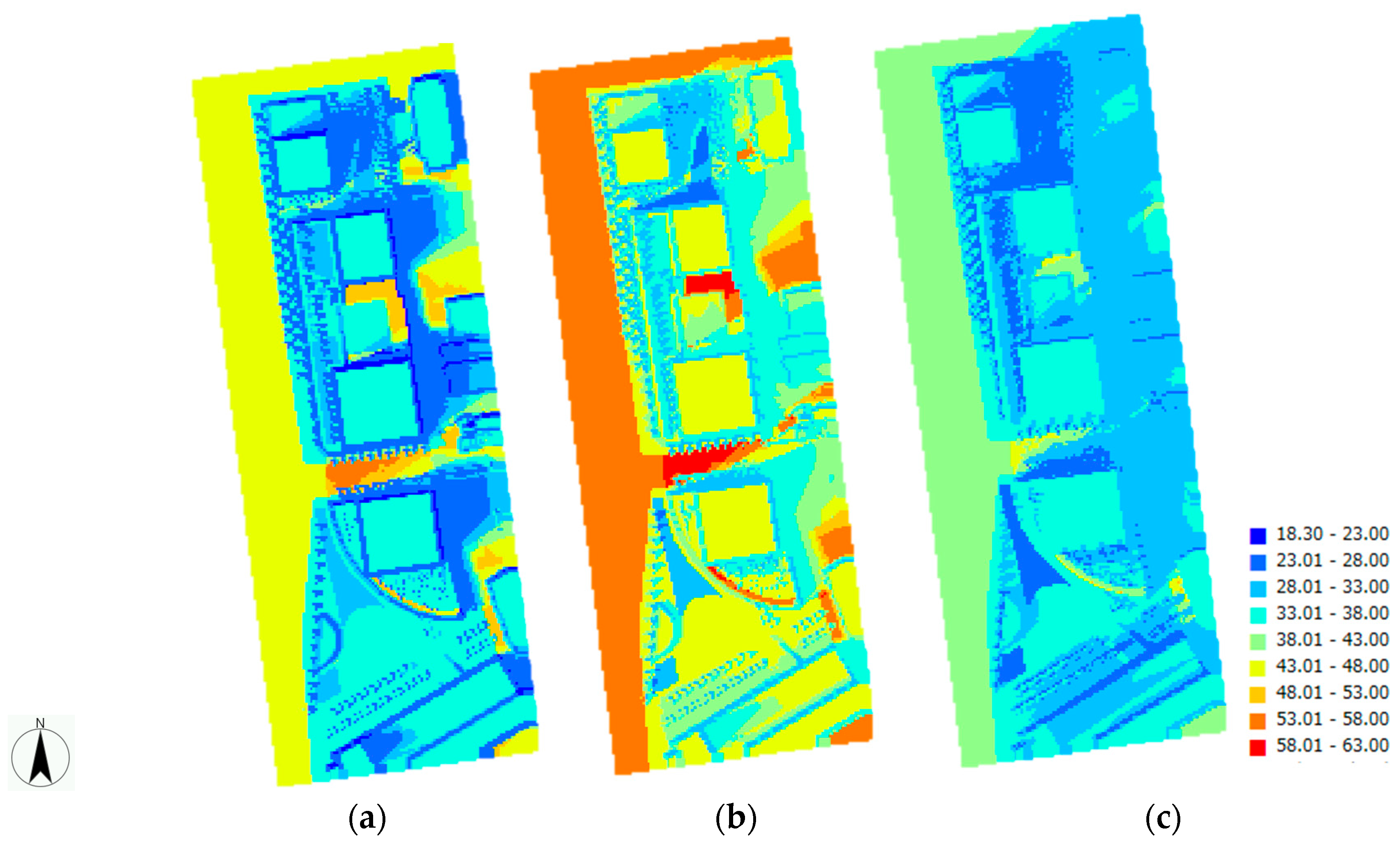
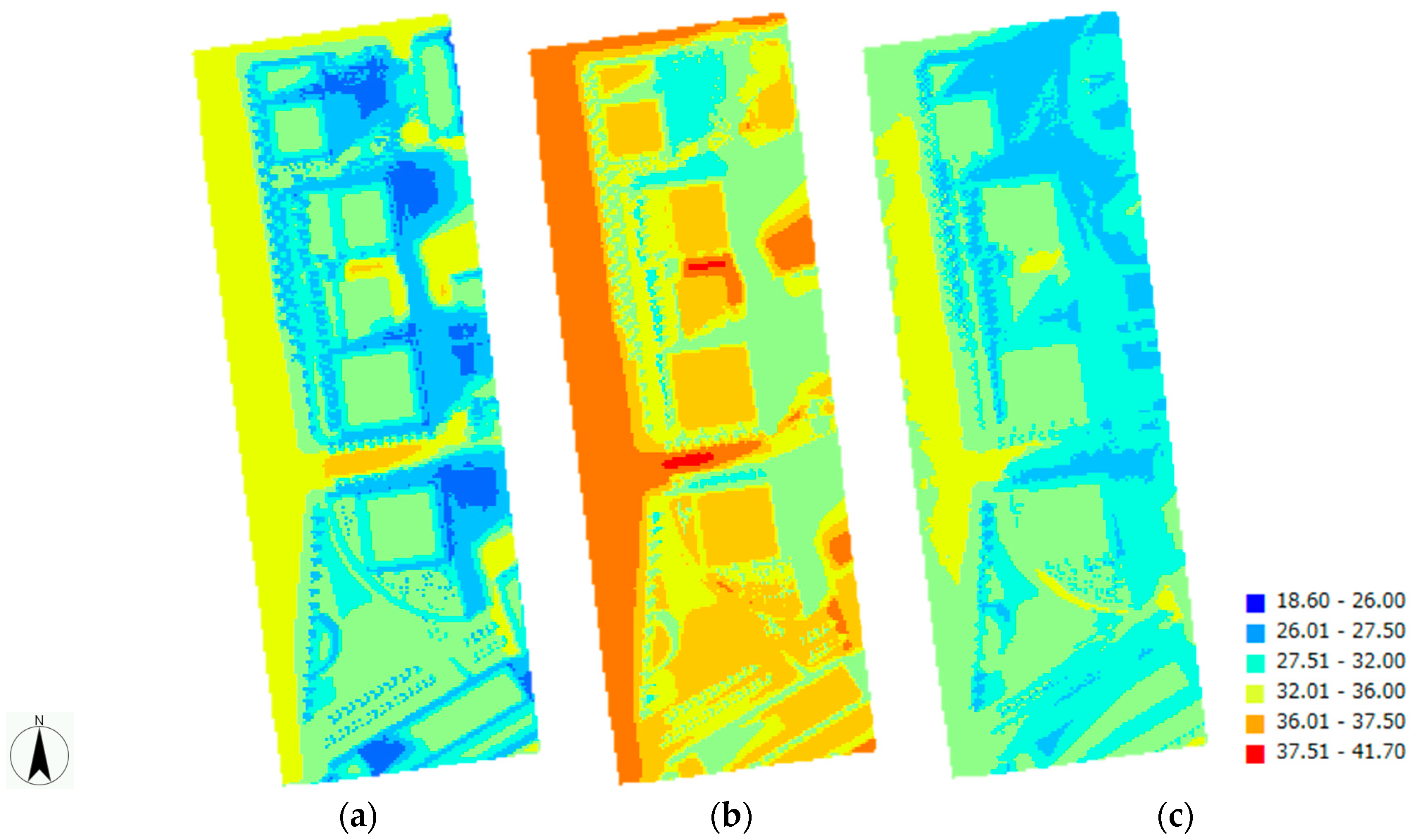
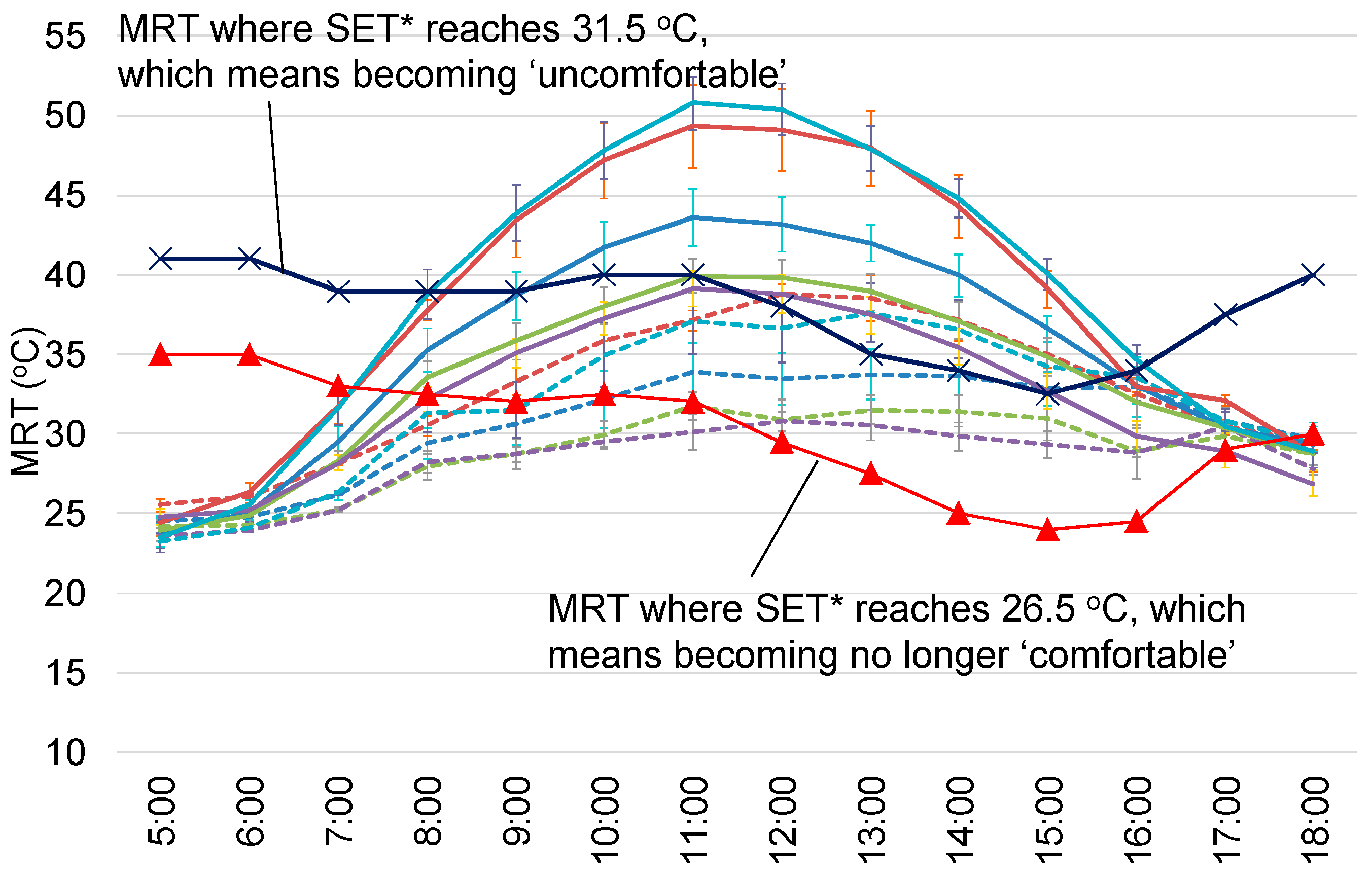
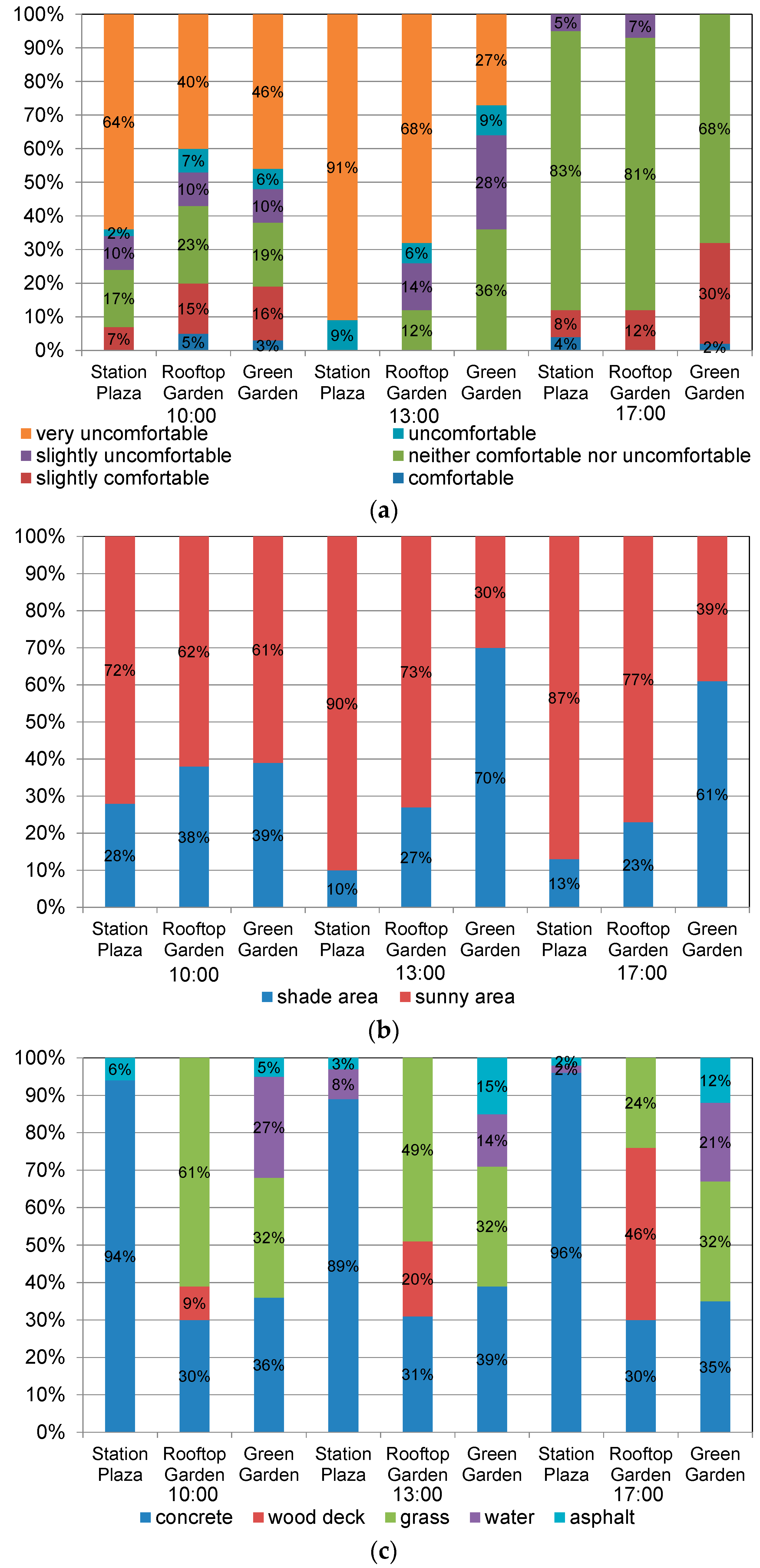
3. Calculation Results
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Oke, T.R. Street design and urban canopy layer climate. Energy Build. 1988, 11, 103–113. [Google Scholar] [CrossRef]
- Arnfield, A.J. Street design and urban canyon solar access. Energy Build. 1990, 14, 117–131. [Google Scholar] [CrossRef]
- Olgyay, V. Design with Climate: Bioclimatic Approach to Architectural Regionalism; Princeton University Press: Princeton, NJ, USA, 1963. [Google Scholar]
- Santamouris, M.; Asimakopoulos, D. Passive Cooling of Buildings; James and James: London, UK, 1996. [Google Scholar]
- Grosso, M.; Chiesa, G. Environmental indicators for evaluating properties. 2015; pp. 59–70. Available online: http://www.agenziaentrate.gov.it/wps/file/Nsilib/Nsi/Archivio/Agenzia+comunica/Prodotti+editoriali/Territorio+Italia/Archivio+Territorio+Italia+-+English+version/Territorio+Italia+2+2015+EN/Environmental+indicators+en/OKIndicatori+ambientali+EN.pdf (accessed on 28 January 2018). [CrossRef]
- Beckers, B. Solar Energy at Urban Scale; Wiley and Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Eliasson, I. Urban Geometry, surface temperature and air temperature. Energy Build. 1990, 15, 141–145. [Google Scholar] [CrossRef]
- Ali-Toudert, F.; Mayer, H. Numerical study on the effects of aspect ratio and orientation of an urban street canyon on outdoor thermal comfort in hot and dry climate. Build. Environ. 2006, 41, 94–108. [Google Scholar] [CrossRef]
- Ali-Toudert, F.; Mayer, H. Effects of asymmetry, galleries, overhanging façades and vegetation on thermal comfort in urban street canyons. Sol. Energy 2007, 81, 742–754. [Google Scholar] [CrossRef]
- Martinelli, L.; Lin, T.P.; Matzarakis, A. Assessment of the influence of daily shadings pattern on human thermal comfort and attendance in Rome during summer period. Build. Environ. 2015, 92, 30–38. [Google Scholar] [CrossRef]
- Abreu-Harbich, L.V.; Labaki, L.C.; Matzarakis, A. Effect of tree planting design and tree species on human thermal comfort in the tropics. Landsc. Urban Plan. 2015, 138, 99–109. [Google Scholar] [CrossRef]
- Algeciras, J.A.R.; Consuegra, L.G.; Matzarakis, A. Spatial-temporal study on the effects of urban street configurations on human thermal comfort in the world heritage city of Camagüey-Cuba. Build. Environ. 2016, 101, 85–101. [Google Scholar] [CrossRef]
- Lee, H.; Mayer, H.; Chen, L. Contribution of trees and grasslands to the mitigation of human heat stress in a residential district of Freiburg, Southwest Germany. Landsc. Urban Plan. 2016, 148, 37–50. [Google Scholar] [CrossRef]
- Zheng, S.; Zhao, L.; Li, Q. Numerical simulation of the impact of different vegetation species on the outdoor thermal environment. Urban For. Urban Green. 2016, 18, 138–150. [Google Scholar] [CrossRef]
- Blazejczyk, K.; Epstein, Y.; Jendritzky, G.; Staiger, H.; Tinz, B. Comparison of UTCI to selected thermal indices. Int. J. Biometeorol. 2012, 56, 515–535. [Google Scholar] [CrossRef] [PubMed]
- Jendritzky, G.; de Dear, R.; Havenith, G. UTCI—Why another thermal index? Int. J. Biometeorol. 2012, 56, 421–428. [Google Scholar] [CrossRef] [PubMed]
- Takebayashi, H.; Kasahara, M.; Tanabe, S.; Kouyama, M. Analysis of Solar Radiation Shading Effects by Trees in the Open Space around Buildings. Sustainability 2017, 9, 1398. [Google Scholar] [CrossRef]
- Perini, K.; Magliocco, A. Effects of vegetation, urban density, building height, and atmospheric conditions on local temperatures and thermal comfort. Urban For. Urban Green. 2014, 13, 495–506. [Google Scholar] [CrossRef]
- Perini, K.; Sabbion, P. Urban Sustainability and River Restoration: Green and Blue Infrastructure; Wiley-Blackwell: Hoboken, NJ, USA, 2017. [Google Scholar]
- Chiesa, G.; Grosso, M. Early-design method to localize outdoor activities on microclimate criteria. In Proceedings of the International Conference on Urban Comfort and Environmental Quality, URBAN-CEQ, Genoa, Italy, 28–29 September 2017; pp. 25–29. [Google Scholar]
- Chen, L.; Yu, B.; Yang, F.; Mayer, H. Intra-urban differences of mean radiant temperature in different urban settings in Shanghai and implications for heat stress under heat waves: AGIS-based approach. Energy Build. 2016, 130, 829–842. [Google Scholar] [CrossRef]
- Grand Front Osaka. Available online: http://umeda-connect.jp/special/vol10/part01.html (accessed on 24 October 2017).
- Takebayashi, H.; Ishii, E.; Moriyama, M.; Sakaki, A.; Nakajima, S.; Ueda, H. Study to examine the potential for solar energy utilization based on the relationship between urban morphology and solar radiation gain on building rooftops and wall surfaces. Sol. Energy 2015, 119, 362–369. [Google Scholar] [CrossRef]
- Gagge, A.P.; Stolwik, J.A.J.; Nishi, Y. A standard predictive index of human responses to the thermal environment. ASHRAE Trans. 1986, 92, 709–731. [Google Scholar]
- Gagge, A.P.; Stolwik, J.A.J.; Nishi, Y. An effective temperature scale based on a simple model of human physiological regulatory response. ASHRAE Trans. 1971, 77, 247–257. [Google Scholar]
- Ishii, A.; Katayama, T.; Shiotsuki, Y.; Yoshimizu, H.; Abe, Y. Experimental study on comfort sensation of people in the outdoor environment. J. Archit. Plan. 1988, 386, 28–37. [Google Scholar] [CrossRef]
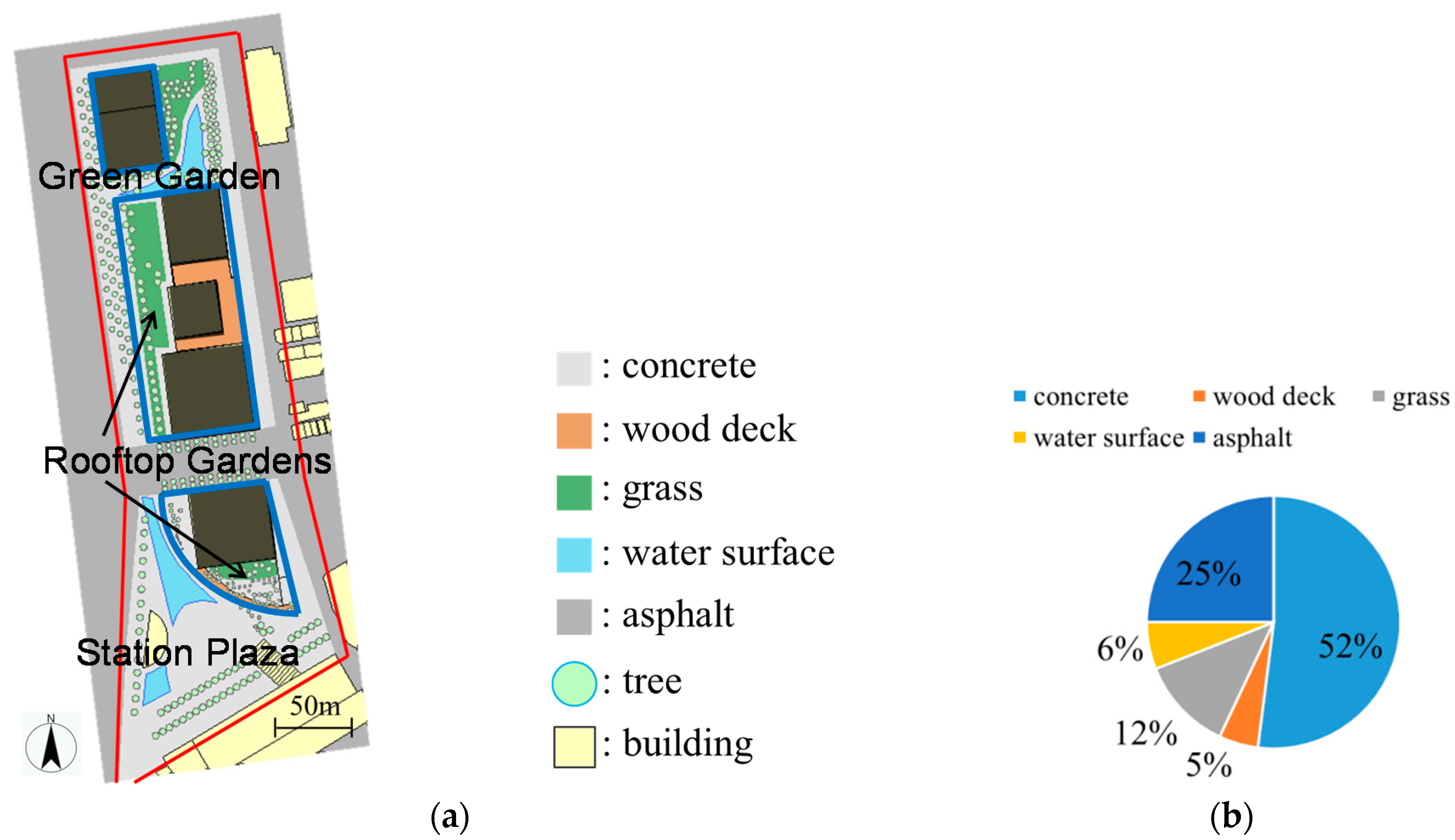
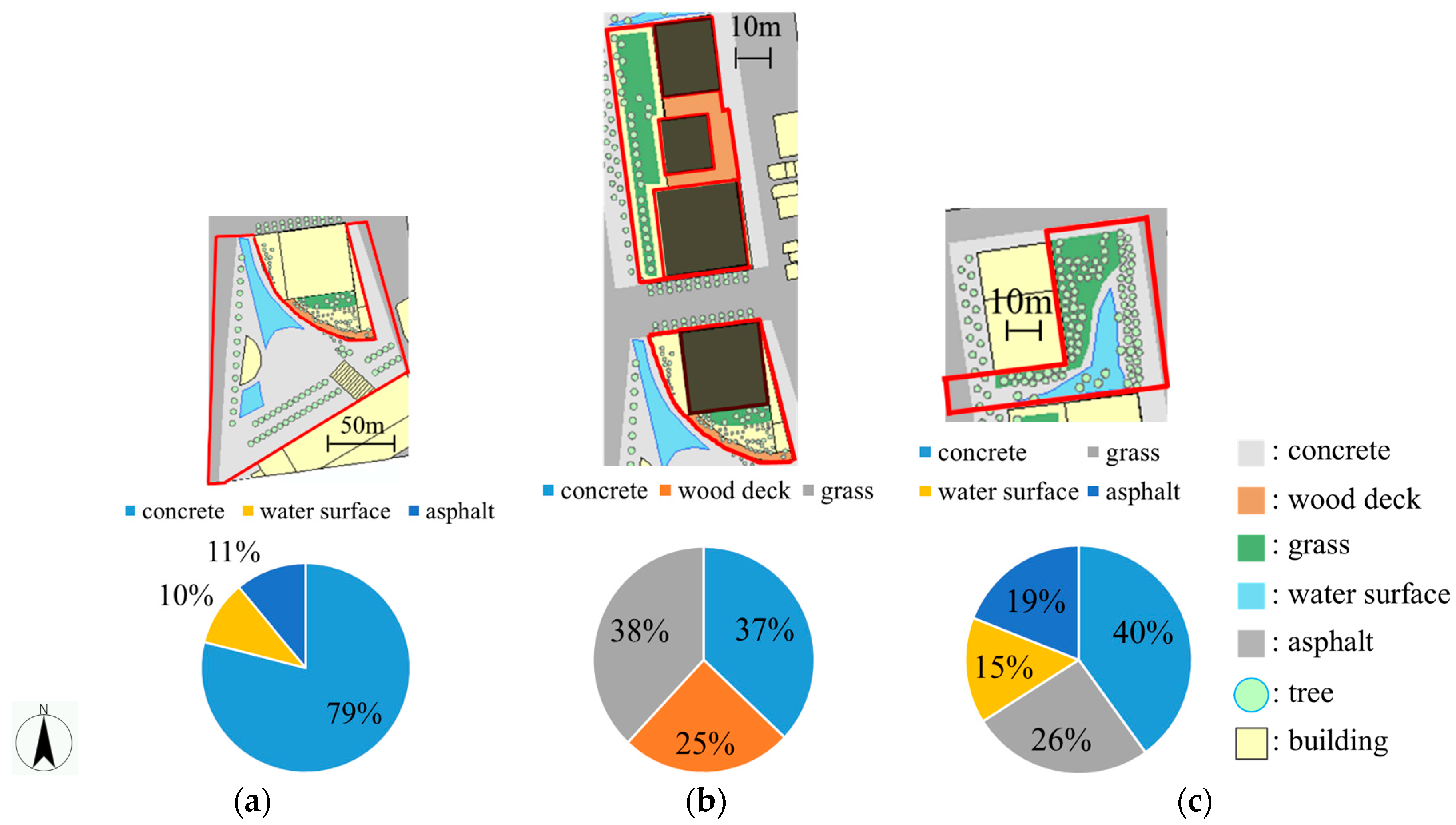

| Solar Reflectance [-] | Evaporative Efficiency [-] | Heat Conductivity [W/(mK)] | Emissivity [-] | Thermal Capacity [kJ/(m3·K)] | |
|---|---|---|---|---|---|
| Concrete | 0.35 | 0.0 | 1.70 | 0.95 | 1934 |
| Wood deck | 0.15 | 0.0 | 0.50 | 1.00 | 1130 |
| Grass | 0.30 | 0.3 | 3.00 | 0.90 | 3000 |
| Water | depends on incident angle | 1.0 | 7.00 | 1.00 | 9000 |
| Asphalt | 0.15 | 0.0 | 0.74 | 1.00 | 2056 |
| Soil | - | 0.0 | 0.62 | - | 1583 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takebayashi, H.; Kyogoku, S. Thermal Environmental Design in Outdoor Space Focusing on Radiation Environment Influenced by Ground Cover Material and Solar Shading, through the Examination on the Redevelopment Buildings in Front of Central Osaka Station. Sustainability 2018, 10, 337. https://doi.org/10.3390/su10020337
Takebayashi H, Kyogoku S. Thermal Environmental Design in Outdoor Space Focusing on Radiation Environment Influenced by Ground Cover Material and Solar Shading, through the Examination on the Redevelopment Buildings in Front of Central Osaka Station. Sustainability. 2018; 10(2):337. https://doi.org/10.3390/su10020337
Chicago/Turabian StyleTakebayashi, Hideki, and Sae Kyogoku. 2018. "Thermal Environmental Design in Outdoor Space Focusing on Radiation Environment Influenced by Ground Cover Material and Solar Shading, through the Examination on the Redevelopment Buildings in Front of Central Osaka Station" Sustainability 10, no. 2: 337. https://doi.org/10.3390/su10020337
APA StyleTakebayashi, H., & Kyogoku, S. (2018). Thermal Environmental Design in Outdoor Space Focusing on Radiation Environment Influenced by Ground Cover Material and Solar Shading, through the Examination on the Redevelopment Buildings in Front of Central Osaka Station. Sustainability, 10(2), 337. https://doi.org/10.3390/su10020337






