1. Introduction
The energy consumption in building sector accounts for about one third of the primary energy consumption in the world [
1]. About 40% of the total energy in the U.S. was consumed by buildings [
2]. The building energy consumption in China is second only to the USA [
1] and is increasing with the great demand for thermal comfort. Therefore, it is very important to design energy efficient buildings to minimize building energy consumption while maintaining or improving the indoor thermal comfort level.
The building energy demand can be alleviated through improved/optimized building design to reduce the thermal load of the buildings [
3,
4,
5]. Thermal load and thermal comfort of buildings are affected by a number of factors, among which thermal mass (in particular the thickness of the concrete slab), insulation level, absorptance of solar radiation of the exterior walls/roof, and glazing ratio (also known as the window-to-wall ratio) are four factors that have important impacts [
6]: (1) thermal mass can affect the fluctuation of the daily temperature inside the house; (2) insulation can affect the conduction heat gain/loss through the opaque envelope; and (3) the absorptance of solar radiation of the opaque envelope and the location and size of the windows can affect the solar heat gain.
Various approaches have been applied to improve building design through the consideration of thermal mass, insulation level, absorptance of solar radiation, and glazing ratio, and they have been studied at different levels of detail, e.g., uniform solar absorptance for all exterior walls [
7,
8,
9], different solar absorptance for each external wall [
10], one solar absorptance variable for the roof [
8,
11], uniform window size for all façades [
5,
7,
9,
12,
13,
14,
15,
16,
17], different window sizes for each façade [
18,
19,
20,
21,
22,
23,
24,
25,
26,
27], uniform insulation level for exterior walls and roof [
13,
28], uniform external wall insulation level [
17,
22,
29], one variable for external wall insulation and one variable for roof insulation [
5,
11,
12,
21,
30,
31,
32,
33], different insulation levels for each wall [
34], and uniform thermal mass for all external walls [
20,
21,
28,
29]. By taking into account the building design variables and using optimization algorithms, the reduction on building energy consumption can be as much as 50% with thermal comfort improved by 1.5% [
23].
So far, no literature has been found that has proposed a design optimization considering thermal mass, insulation level, absorbance of solar radiation for each exterior wall/roof, and glazing ratio for each façade at the same time. However, to achieve full potential of energy savings with improved thermal comfort in building design, all those variables deserve to be fully explored. Optimization on each of the parameters can result in improvement for the building performance (reduction of thermal load and discomfort degree hours). When one more parameter is added for optimization, further improvement can be achieved, which results in a greater reduction on thermal load and discomfort degree hours. As the number of design variables increases, the level of complexity to obtain optimal design solutions also increases. One way to solve this problem is to use parallel computing technology, e.g., the optimization time was reduced from almost 12 days to 4.4 h for the cases with 108 and 1016 possibilities when coupled optimization approach with simulation software [
9], and from 118 h to 3 h with 48 processors using parallel computing for the case with six discrete variables [
35]. The other way is to use an energy prediction model to characterize building behavior and then combine this with genetic algorithm, where most of the time was used to generate the sample data, e.g., it took three weeks to generate the results of thermal load and comfort level of 450 cases for two residential houses in Canada, and it took around 7 min to complete the optimization process which may take 10 years when using simulation software coupled with a genetic algorithm directly [
20]. As parallel computing resources are not always available, the latter approach is adopted in this paper by developing prediction models to couple with genetic algorithms to find the optimal design solutions.
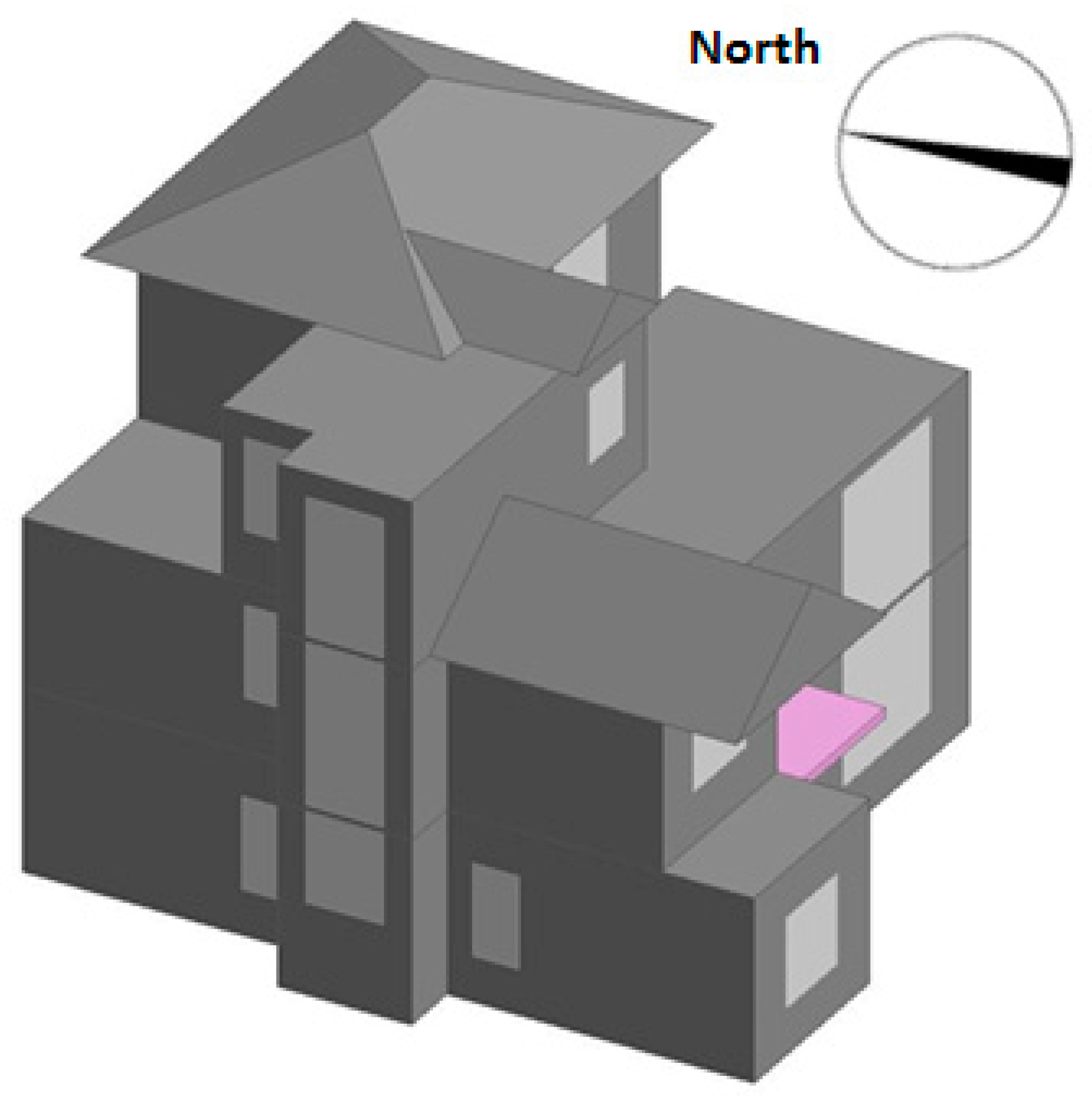
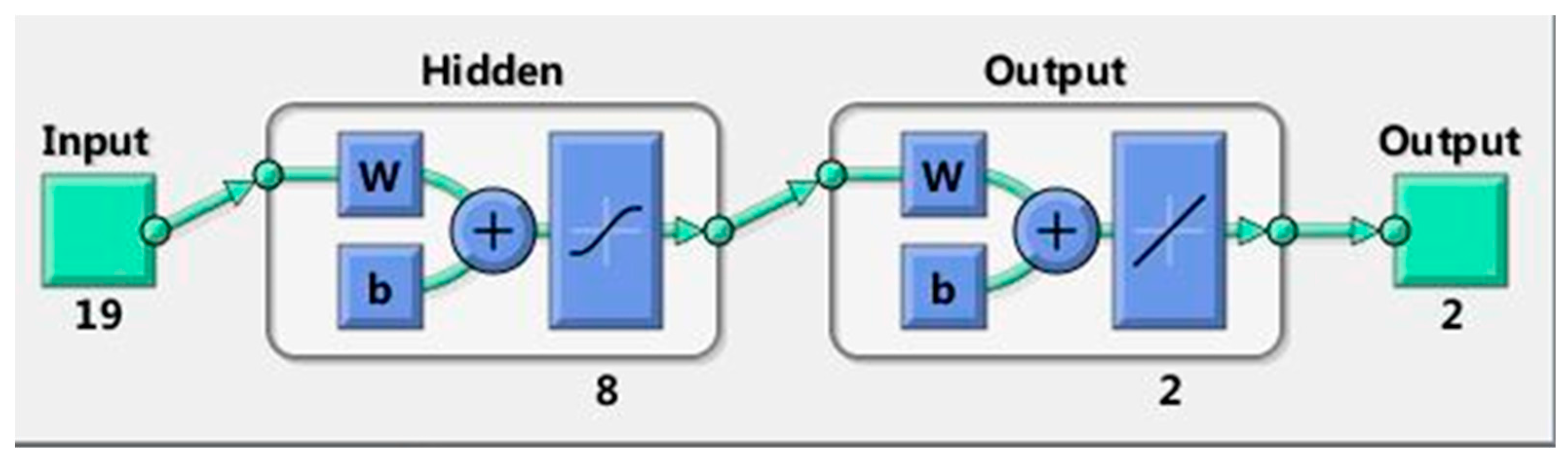
In this paper, different variables of thermal mass, insulation, absorbance of solar radiation are assigned for each exterior wall/roof, and the glazing ratios for each façade are considered separately. A total of 19 variables are considered, including five variables for concrete thickness, five variables for insulation thickness, five variables for the absorptance of solar radiation for each exterior walls/roof, and four variables for the window-to-wall ratio of each façade. In order to reduce the computation time, the Latin Hypercube Sampling Method is used to create the samples required to generate prediction models, and the commercial software, DesignBuilder (DesignBuilder Software Ltd, Stroud, Gloucestershire, UK) [
36], is used to calculate the sub-hourly heating load, cooling load, and indoor air temperature to evaluate the thermal comfort condition. Two typical prediction models, multi-linear regression (MLR) model and an artificial neural network (ANN) model, are developed based on the sample data and coupled with a multi-objective genetic algorithm to find the optimal design solutions. The results from the two objective functions, namely, thermal load and annual discomfort degree hours, are also compared with the outcomes using the cooling load, heating load, summer discomfort degree hours, and winter discomfort degree hours as the objective functions for optimization.
The advantage of using the described method is that each component of the building envelope can be customized and the values of the building design parameters do not have to be the same if their orientations are different. The optimal model can be achieved by performing optimization with as many measures as possible, so that the least amount of materials can be determined to construct a building with a high indoor thermal comfort level and low thermal load. The accurate modeling can ensure utilizing the least amount of materials to achieve optimal building performance. Optimal usage of material for different building components can be selected to achieve a minimum thermal load and discomfort degree hours, which is different from traditional design, and can improve the quality of construction project. This is coincidence with 3D printing technology where the material for each component can be tailored. It is expected that advancement of 3D house printing technology will make it possible for wide application in design practice in the future.
4. Results and Discussion
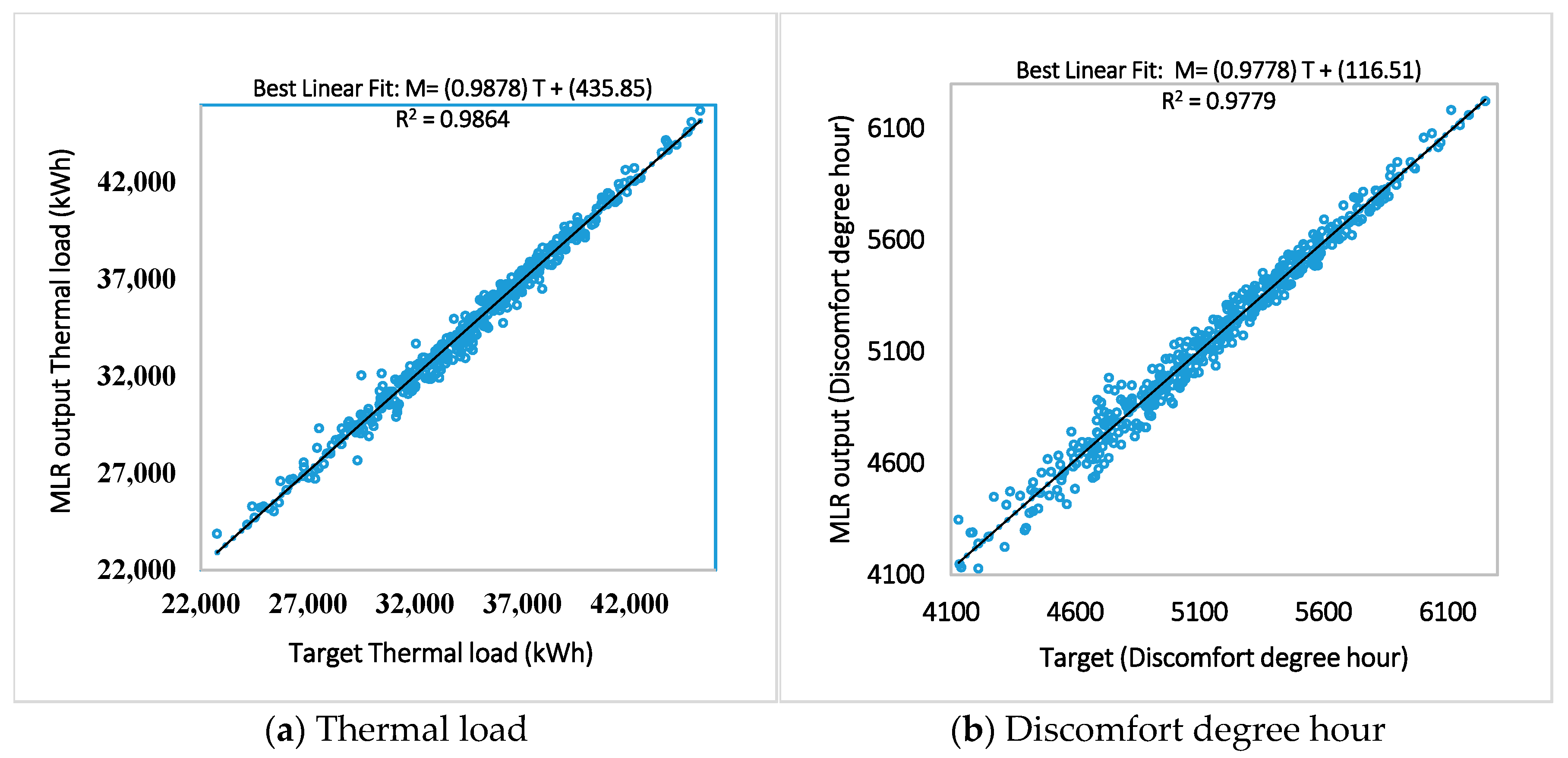
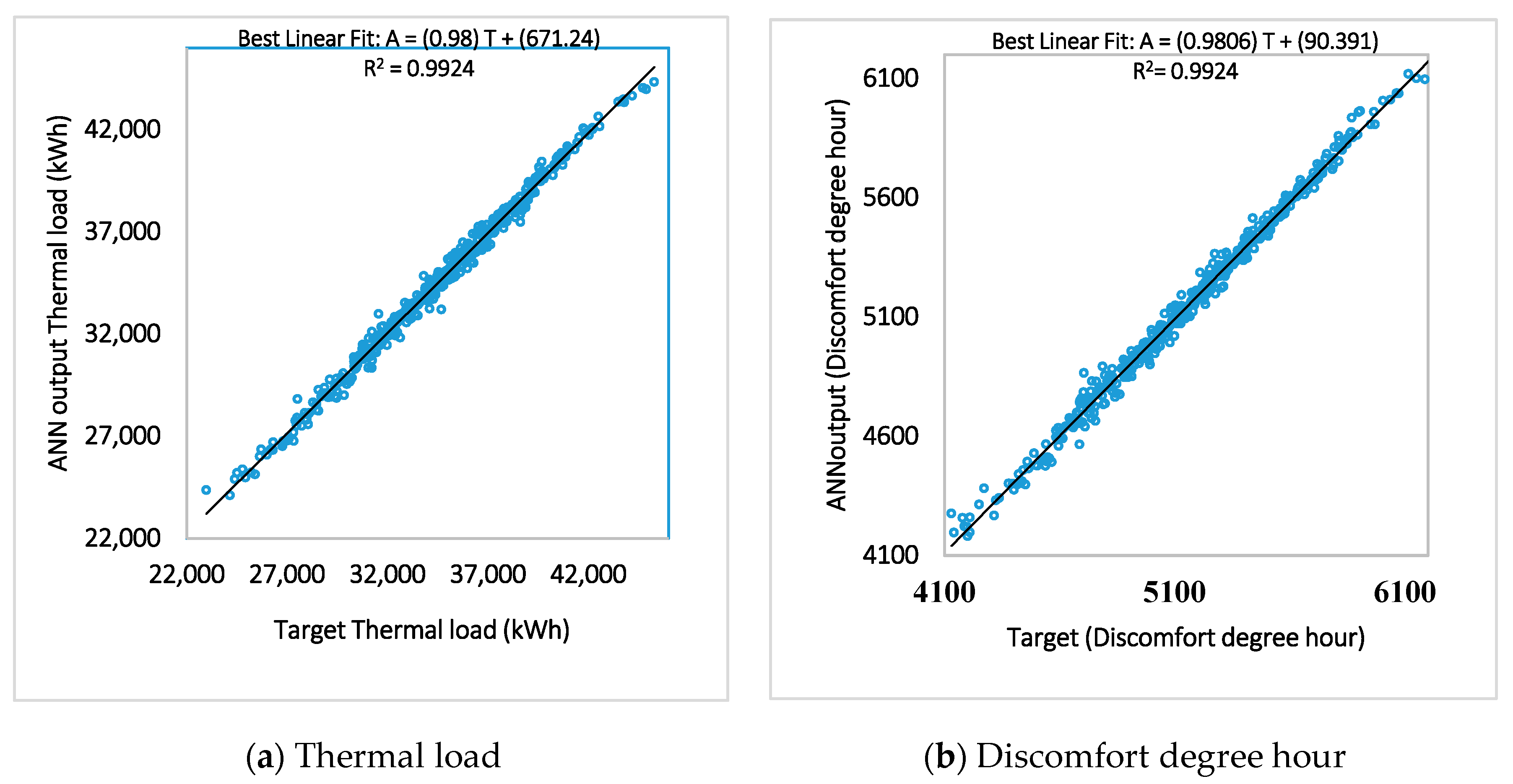
Since the prediction results from all models are in good agreement with simulation results, the ANN models and MLR models are coupled with a multi-objective genetic algorithm to find the optimal design solutions.
4.1. MLR with GA
The regression models (Equations (7) and (8)) are used as the fitness functions for a multi-objective optimization program using genetic algorithm developed in MATLAB. The constraints of the variables are presented as follows:
The program ran a number of times and each time came out with 1–4 Pareto front solutions when converged. A total of 45 solutions are obtained after 29 runs, after which the ranges of the outcomes for each design parameter stays unchanged. The maximum, minimum, median, average values, and standard deviations for the outcomes of the thermal load, number of discomfort degree hours, and each variable are summarized in
Table 5.
It is observed that the medians for the thickness of the concrete layer are higher than 0.24 m; for the insulation layer, are 52.9–63.9 mm; for the absorptance of solar radiation, are 0.167–0.424; and for the window-to-wall ratio, are 11.1–12.2%. There are differences on the values of design variables at different orientations, meaning the building can be adaptively designed to minimize the impact of outside weather conditions on the indoor environment.
The thermal load and number of discomfort degree hours for the best solution are 19,568.9 kWh and 3721.2 °C·h (19,000.4 kWh and 3755.4 °C·h from DesignBuilder (DesignBuilder Software Ltd., Stroud, Gloucestershire, UK)), while the ones for the base building are 23,233.0 kWh and 4840.0 °C·h. The reduction on the thermal load and number of discomfort degree hours are 18.2% and 22.4%, respectively. The relative errors on the predictions of the thermal load and discomfort degree hours are 2.99% and −0.91%, respectively.
4.2. ANN with GA
The ANN models developed in
Section 3.3 are used as the fitness functions for the multi-objective optimization program, and the same constraints of the variables as in
Section 4.1 are applied.
The program ran for a number of times and each time came out with 1–12 Pareto front solutions. A total of 44 solutions are obtained after 14 runs. The maximum, minimum, median, average values, and standard deviation for the outcomes of the thermal load, number of discomfort hours, and each variable are summarized in
Table 6.
It is observed that the medians for the thickness of the concrete layer are higher than 0.21 m, for the insulation layer are 58.5–75.2 mm, for the absorbance of solar radiation are 0.194–0.5406, and for the window-to-wall ratio are 12.1–15.4%.
The thermal load and number of discomfort degree hours for the best solution are 18,938.4kWh and 3592.8 °C·h (19,276.63 kWh and 3773.5 °C·h from DesignBuilder (DesignBuilder Software Ltd., Stroud, Gloucestershire, UK)). The reduction on the thermal load and number of discomfort degree hours are 17.0% and 22.2%, respectively. The relative errors on the predictions of the thermal load and discomfort degree hours are 1.75% and 4.76%, respectively.
4.3. Optimization with Different Combinations of Parameters
The ANNGA approach is applied for optimization on different combinations of parameters. The results on the optimization are presented in
Table 7, where “1” refers to the concrete thickness; “2” refers to the insulation thickness; “3” refers to the absorptance of solar radiation; and “4” refers to the window-to-wall ratio. The results clearly show that when one more group of parameters is added, there is a further improvement on the building performance.
4.4. Optimization with Four Objective Functions
The ANN models for the total hourly cooling load (Q
C), heating load (Q
H), discomfort heating degree hours (I
W), and cooling degree hours (I
S) are developed and used as fitness functions for the multi-objective optimization program. A total of 70 Pareto front solutions are generated and summarized as in
Table 8.
It can be found that although a few solutions can achieve total thermal load and number of discomfort degree hours as low as the ones presented in
Section 4.1 and
Section 4.2, the average values of which are much higher, indicating lower optimization performance. Therefore, two objective functions are sufficient for optimization purpose.