Day-Ahead Forecasting of Hourly Photovoltaic Power Based on Robust Multilayer Perception
Abstract
1. Introduction
2. Methodology
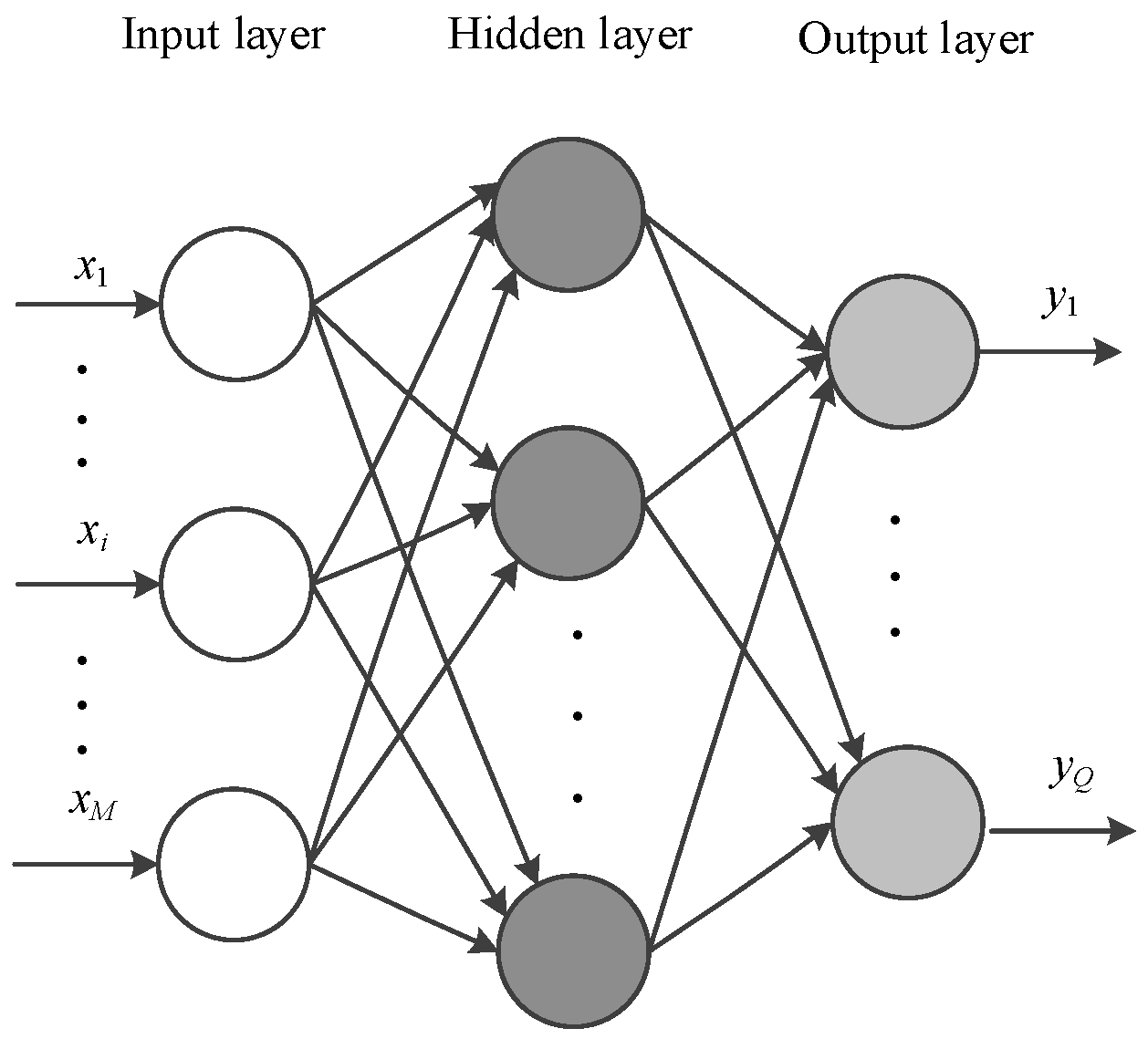
2.1. Multilayer Perception Network
2.2. Pseudo-Huber Loss
3. Case Study
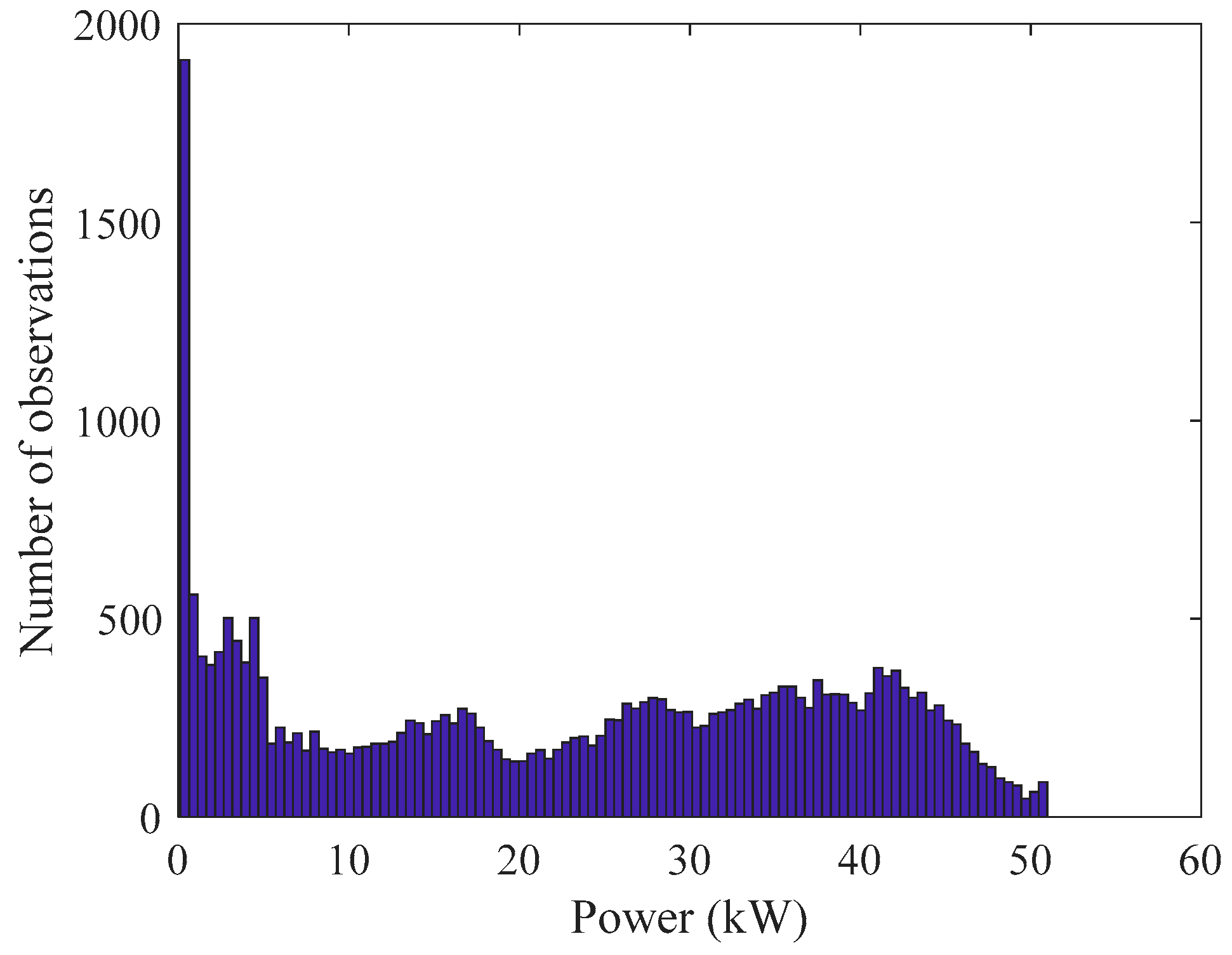
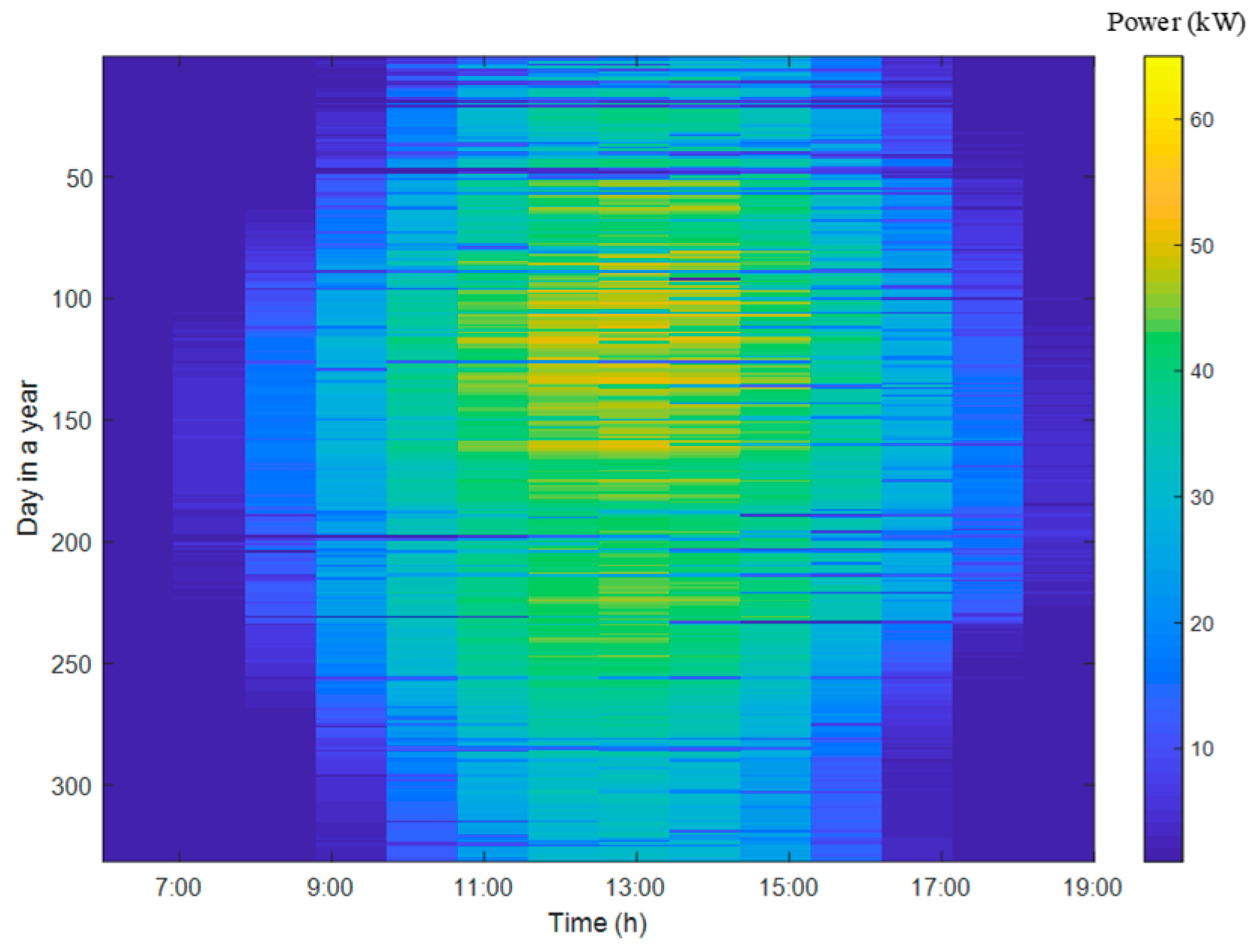
3.1. Data Description
3.2. Performance Metrics
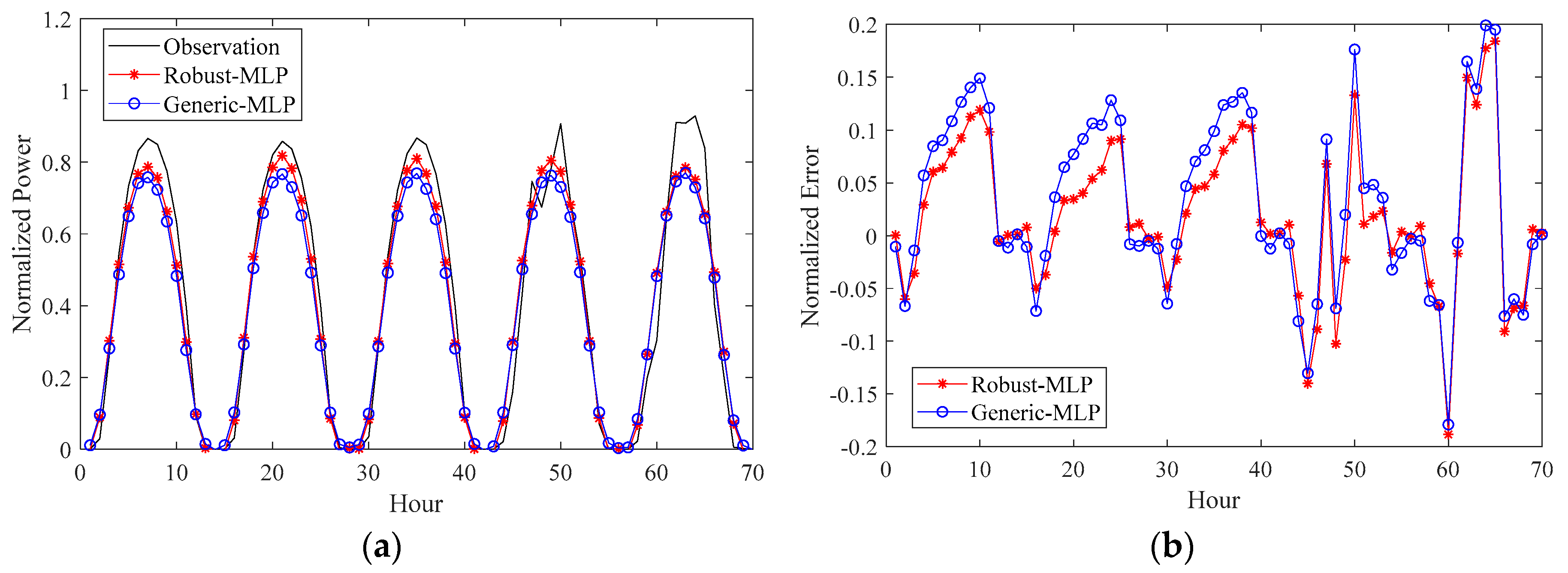
3.3. Numerical Results and Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Huang, C.; Wang, L.; Lai, L. Data-driven short-term solar irradiance forecasting based on information of neighboring sites. IEEE Trans. Ind. Electron. 2018. [Google Scholar] [CrossRef]
- Sobri, S.; Koohi-Kamali, S.; Rahim, N.A. Solar photovoltaic generation forecasting methods: A review. Energy Convers. Manag. 2018, 156, 459–497. [Google Scholar] [CrossRef]
- Zhang, Y.; Gatsis, N.; Giannakis, G.B. Robust Energy Management for Microgrids With High-Penetration Renewables. IEEE Trans. Sustain. Energy 2013, 4, 944–953. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Salmasi, F.R. Robust Optimal Power Management System for a Hybrid AC/DC Micro-Grid. IEEE Trans. Sustain. Energy 2015, 6, 675–687. [Google Scholar] [CrossRef]
- Sardou, I.G.; Zare, M.; Azad-Farsani, E. Robust energy management of a microgrid with photovoltaic inverters in VAR compensation mode. Int. J. Electr. Power Energy Syst. 2018, 98, 118–132. [Google Scholar] [CrossRef]
- Wang, L.; Huang, C. A novel Elite Opposition-based Jaya algorithm for parameter estimation of photovoltaic cell models. Optik 2018, 155, 351–356. [Google Scholar] [CrossRef]
- Huang, C.; Wang, L. Simulation study on the degradation process of photovoltaic modules. Energy Convers. Manag. 2018, 165, 236–243. [Google Scholar] [CrossRef]
- Andrade, J.R.; Bessa, R.J. Improving Renewable Energy Forecasting With a Grid of Numerical Weather Predictions. IEEE Trans. Sustain. Energy 2017, 8, 1571–1580. [Google Scholar] [CrossRef]
- Wu, J.; Chan, C.K. Prediction of hourly solar radiation using a novel hybrid model of ARMA and TDNN. Sol. Energy 2011, 85, 808–817. [Google Scholar]
- Li, Y.T.; Su, Y.; Shu, L.J. An ARMAX model for forecasting the power output of a grid connected photovoltaic system. Renew. Energy 2014, 66, 78–89. [Google Scholar] [CrossRef]
- Leva, S.; Dolara, A.; Grimaccia, F.; Mussetta, M.; Ogliari, E. Analysis and validation of 24 hours ahead neural network forecasting of photovoltaic output power. Math. Comput. Simul. 2017, 131, 88–100. [Google Scholar] [CrossRef]
- Capizzi, G.; Napoli, C.; Bonanno, F. Innovative Second-Generation Wavelets Construction With Recurrent Neural Networks for Solar Radiation Forecasting. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1805–1815. [Google Scholar] [CrossRef] [PubMed]
- Luo, X.; Sun, J.; Wang, L.; Wang, W.; Zhao, W.; Wu, J.; Wang, J.-H.; Zhang, Z. Short-Term Wind Speed Forecasting via Stacked Extreme Learning Machine With Generalized Correntropy. IEEE Trans. Ind. Inform. 2018, 14, 4963–4971. [Google Scholar] [CrossRef]
- Zendehboudi, A.; Baseer, M.A.; Saidur, R. Application of support vector machine models for forecasting solar and wind energy resources: A review. J. Clean. Prod. 2018, 199, 272–285. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, Z.J.; Bensoussan, A. Forecasting of daily global solar radiation using wavelet transform-coupled Gaussian process regression: Case study in Spain. In Proceedings of the 2016 IEEE Innovative Smart Grid Technologies-Asia (ISGT-Asia), Melbourne, Australia, 28 November–1 December 2016; pp. 799–804. [Google Scholar]
- Capizzi, G.; Sciuto, G.L.; Napoli, C.; Tramontana, E. Advanced and Adaptive Dispatch for Smart Grids by means of Predictive Models. IEEE Trans. Smart Grid 2017, 9, 6684–6691. [Google Scholar] [CrossRef]
- Mellit, A.; Pavan, A.M. A 24-h forecast of solar irradiance using artificial neural network: Application for performance prediction of a grid-connected PV plant at Trieste, Italy. Sol. Energy 2010, 84, 807–821. [Google Scholar] [CrossRef]
- Ehsan, R.M.; Simon, S.P.; Venkateswaran, P. Day-ahead forecasting of solar photovoltaic output power using multilayer perceptron. Neural Comput. Appl. 2017, 28, 3981–3992. [Google Scholar] [CrossRef]
- Gigoni, L.; Betti, A.; Crisostomi, E.; Franco, A.; Tucci, M.; Bizzarri, F.; Mucci, D. Day-Ahead Hourly Forecasting of Power Generation From Photovoltaic Plants. IEEE Trans. Sustain. Energy 2018, 9, 831–842. [Google Scholar] [CrossRef]
- Huang, C.; Bensoussan, A.; Edesess, M.; Tsui, K.L. Improvement in artificial neural network-based estimation of grid connected photovoltaic power output. Renew. Energy 2016, 97, 838–848. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv, 2014; arXiv:1412.6980. [Google Scholar]
- Barron, J.T. A more general robust loss function. arXiv, 2017; arXiv:1701.03077. [Google Scholar]
- Wang, L.; Zhang, Z.J.; Huang, C.; Tsui, K.L. A GPU-accelerated parallel Jaya algorithm for efficiently estimating Li-ion battery model parameters. Appl. Soft Comput. 2018, 65, 12–20. [Google Scholar] [CrossRef]
- Huang, C.; Wang, L.; Yeung, R.S.C.; Zhang, Z.J.; Chung, H.S.H.; Bensoussan, A. A Prediction Model-Guided Jaya Algorithm for the PV System Maximum Power Point Tracking. IEEE Trans. Sustain. Energy 2018, 9, 45–55. [Google Scholar] [CrossRef]
- Huang, C.; Wang, L.; Long, H.; Luo, X.; Wang, J.-H. A Hybrid Global Maximum Power Point Tracking Method for Photovoltaic Arrays under Partial Shading Conditions. Optik 2018, 180, 665–674. [Google Scholar] [CrossRef]
- Wang, L.; Huang, C.; Huang, L.M. Parameter estimation of the soil water retention curve model with Jaya algorithm. Comput. Electron. Agric. 2018, 151, 349–353. [Google Scholar] [CrossRef]
| Nominal DC power | 68.48 kW |
| PV module type | NU-U240F1 |
| PV module manufacturer | Sharp |
| Inverter type | 50 kW |
| Inverter manufacturer | SatCon Technology |
| Method | RMSE | MAE |
|---|---|---|
| Robust-MLP | 0.0775 | 0.0439 |
| Generic-MLP | 0.0788 | 0.0459 |
| Persistence | 0.0978 | 0.0474 |
| Hour | RMSE | MAE | ||||
|---|---|---|---|---|---|---|
| Robust-MLP | Generic-MLP | Persistence | Robust-MLP | Generic-MLP | Persistence | |
| 6:00 | 0.0089 | 0.0110 | 0.0086 | 0.0053 | 0.0071 | 0.0032 |
| 7:00 | 0.0277 | 0.0297 | 0.0319 | 0.0167 | 0.0191 | 0.0139 |
| 8:00 | 0.0566 | 0.0572 | 0.0630 | 0.0391 | 0.0398 | 0.0339 |
| 9:00 | 0.0790 | 0.0808 | 0.0961 | 0.0530 | 0.0551 | 0.0538 |
| 10:00 | 0.0995 | 0.1013 | 0.1221 | 0.0649 | 0.0670 | 0.0686 |
| 11:00 | 0.0990 | 0.1012 | 0.1245 | 0.0657 | 0.0687 | 0.0725 |
| 12:00 | 0.1072 | 0.1086 | 0.1407 | 0.0724 | 0.0754 | 0.0849 |
| 13:00 | 0.1178 | 0.1197 | 0.1546 | 0.0768 | 0.0793 | 0.0937 |
| 14:00 | 0.1112 | 0.1125 | 0.1446 | 0.0729 | 0.0753 | 0.0879 |
| 15:00 | 0.1020 | 0.1038 | 0.1245 | 0.0690 | 0.0719 | 0.0775 |
| 16:00 | 0.0703 | 0.0711 | 0.0881 | 0.0520 | 0.0539 | 0.0492 |
| 17:00 | 0.0289 | 0.0299 | 0.0351 | 0.0200 | 0.0207 | 0.0193 |
| 18:00 | 0.0099 | 0.0118 | 0.0093 | 0.0060 | 0.0074 | 0.0042 |
| 19:00 | 0.0025 | 0.0029 | 0.0019 | 0.0013 | 0.0016 | 0.0007 |
| Method | RMSE | MAE |
|---|---|---|
| Robust-MLP | 0.6508 | 0.4370 |
| Generic-MLP | 0.6635 | 0.4511 |
| Persistence | 0.7988 | 0.4990 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.; Cao, L.; Peng, N.; Li, S.; Zhang, J.; Wang, L.; Luo, X.; Wang, J.-H. Day-Ahead Forecasting of Hourly Photovoltaic Power Based on Robust Multilayer Perception. Sustainability 2018, 10, 4863. https://doi.org/10.3390/su10124863
Huang C, Cao L, Peng N, Li S, Zhang J, Wang L, Luo X, Wang J-H. Day-Ahead Forecasting of Hourly Photovoltaic Power Based on Robust Multilayer Perception. Sustainability. 2018; 10(12):4863. https://doi.org/10.3390/su10124863
Chicago/Turabian StyleHuang, Chao, Longpeng Cao, Nanxin Peng, Sijia Li, Jing Zhang, Long Wang, Xiong Luo, and Jenq-Haur Wang. 2018. "Day-Ahead Forecasting of Hourly Photovoltaic Power Based on Robust Multilayer Perception" Sustainability 10, no. 12: 4863. https://doi.org/10.3390/su10124863
APA StyleHuang, C., Cao, L., Peng, N., Li, S., Zhang, J., Wang, L., Luo, X., & Wang, J.-H. (2018). Day-Ahead Forecasting of Hourly Photovoltaic Power Based on Robust Multilayer Perception. Sustainability, 10(12), 4863. https://doi.org/10.3390/su10124863








