Sustainable Inventory Management for Environmental Impact through Partial Backordering and Multi-Trade-Credit-Period
Abstract
1. Introduction
2. Literature Review
3. Problem Definition, Notation, and Assumptions
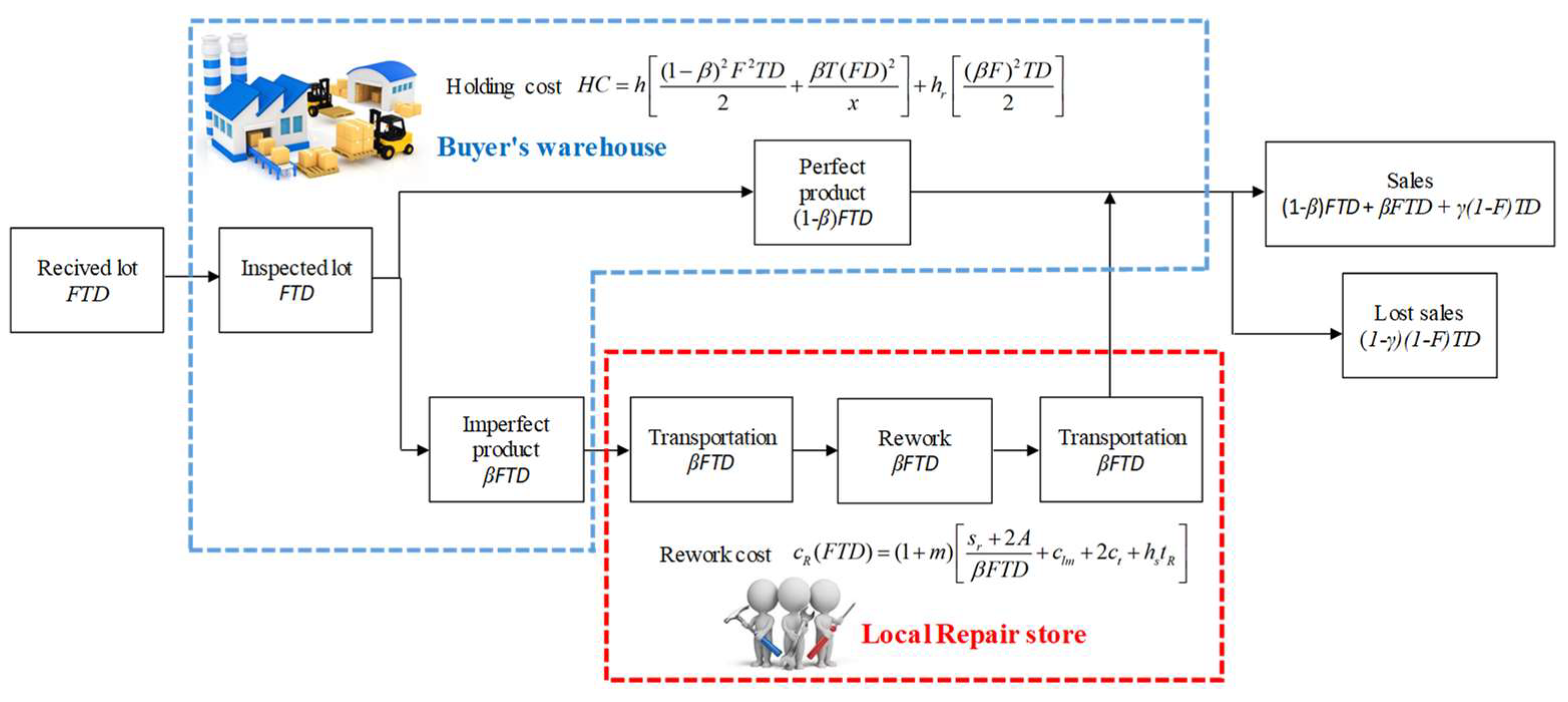
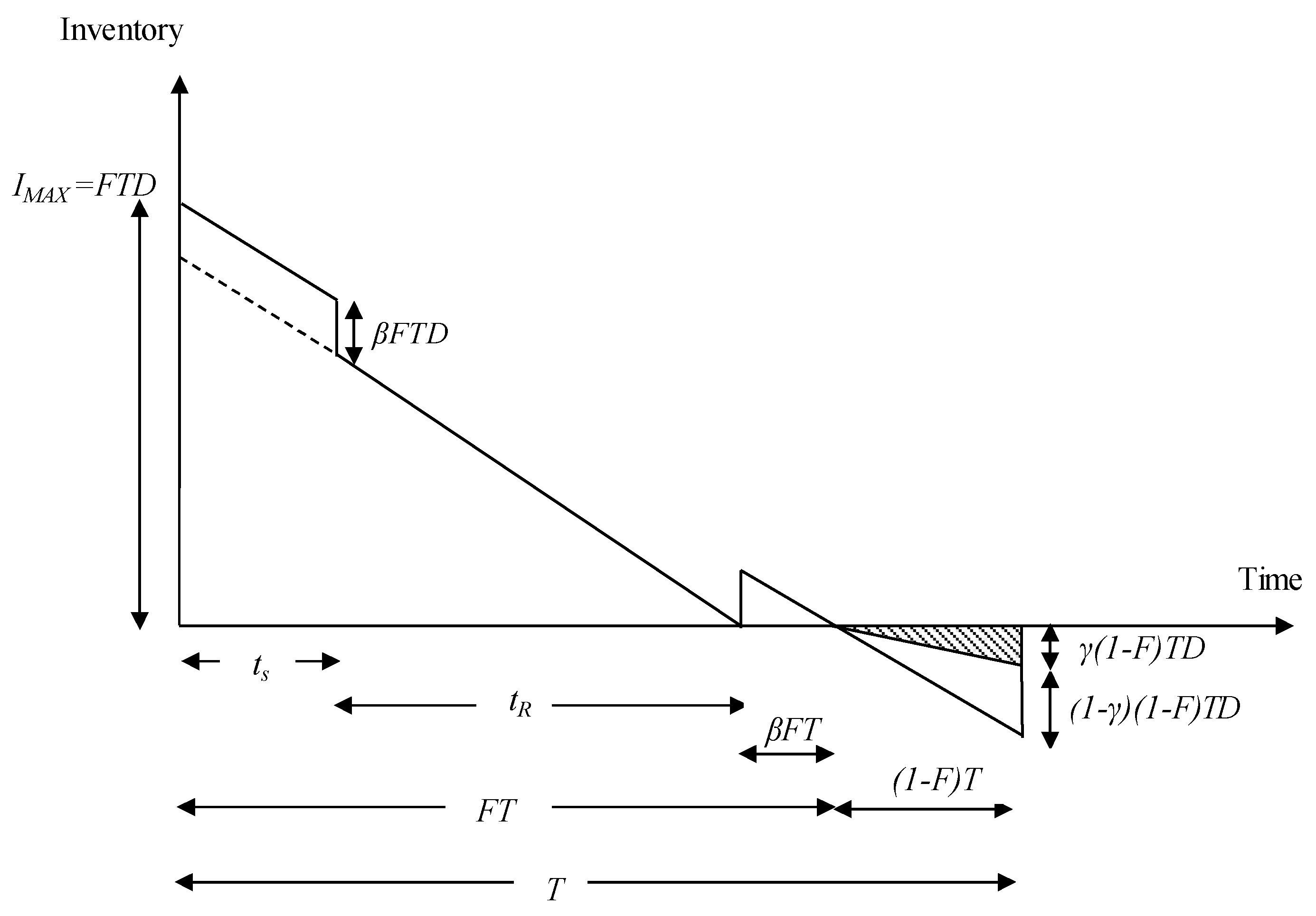
3.1. Problem Definition
3.2. Notation
- T
- cycle time (time unit)
- F
- fraction of time that has a positive inventory level (%)
- Q
- Order size per cycle (units)
- D
- demand rate per unit time (units/time unit)
- X
- screening rate (units/time unit)
- ts
- screening time of products (time unit)
- tR
- transportation, rework, and return time for imperfect products (time unit)
- tT
- total transportation time of imperfect products (time unit)
- R
- rework rate (units/time unit)
- A
- fixed cost of transportation ($/trip)
- β
- percentage of imperfect items (%)
- O
- ordering cost of buyer ($/order)
- sr
- setup cost of repair store ($/setup)
- h
- holding cost of perfect items ($/unit/time unit)
- h’
- carbon emission cost per item on holding perfect items ($/unit/time unit)
- hr
- holding cost of rework products ($/unit/time unit)
- hr’
- carbon emission cost per item on holding rework item ($/unit/time unit)
- hs
- holding cost at repair store ($/unit/time unit)
- hs’
- carbon emission cost per item on holding item at repair store ($/unit/time unit)
- Cs
- screening cost per unit ($/unit)
- Cu
- purchasing cost of one unit ($/unit)
- ct
- transportation cost of the imperfect item per unit ($/unit)
- clm
- labor and material cost required to repair a unit product ($/unit)
- l
- cost incurred due to a loss of sales ($/unit/time unit)
- g
- penalty cost incurred due to goodwill loss (S/unit)
- w
- percentage of imperfect items passed to customers (%)
- u
- unit return cost of the imperfect product (S/unit)
- π
- backordered cost ($/unit/time unit)
- P
- selling price of one unit (S/unit)
- γ
- percentage of backordered demand (%)
- m
- markup percentage by rework store (%)
- M
- first permissible delay period for payment (time unit)
- N
- second permissible delay period for payment (time unit)
- Ie
- interest earned (%)
- Ic1
- interest charged for period M (%)
- Ic2
- interest charged for period N (%)
3.3. Assumptions
- The inventory system has a single type of product.
- Warehouse carbon emission is due to the energy consumption per unit item. Thus, according to carbon tax policy, carbon emission cost per unit item h’, hr’, and hs’ is considered for holding perfect items, holding repair items, and holding items at the repair store, respectively.
- There is a chance to receive a lot with a fraction of defective items from a global supplier, which is from other country.
- Shortages are allowed and these are partially backordered.
- Demand and inspection rates are considered as constant and known.
- The screening process and demand occur at the same time, but the screening rate is faster than the demand rate (x > D).
- Imperfect products have minor damage and can be repairable in a controlled system and all imperfect products are reworked.
- The percentage of imperfect products are given and known.
- The relationship between the purchasing cost of buyer Cu and selling price of buyer P is P ≥ Cu.
- The holding cost of reworked products is higher than the initial holding cost of perfect items (hR > h).
- The reworked products are returned back when the inventory level of the system becomes zero.
- As the shipment lot is received, the backordered demand is fulfilled first.
- The supplier allows a multi-trade-credit-periods M and N to the buyer. During these periods, the buyer sells the product and utilizes its income to earn interest with rate of Ie.
- If the buyer fails to make the payment to the supplier during the first credit period M, then interest Ic1 is charged, and later if the buyer again fails to make the payment to the supplier during second allowable time N, then additional interest is also charged at a rate of Ic2.
- The percentage of defective items are sent to customers, which are returned back to the buyer in the next cycle. The buyer pays a cost per unit for these returned products and a cost per unit as a penalty cost incurred due to goodwill loss.
4. Mathematical Modeling
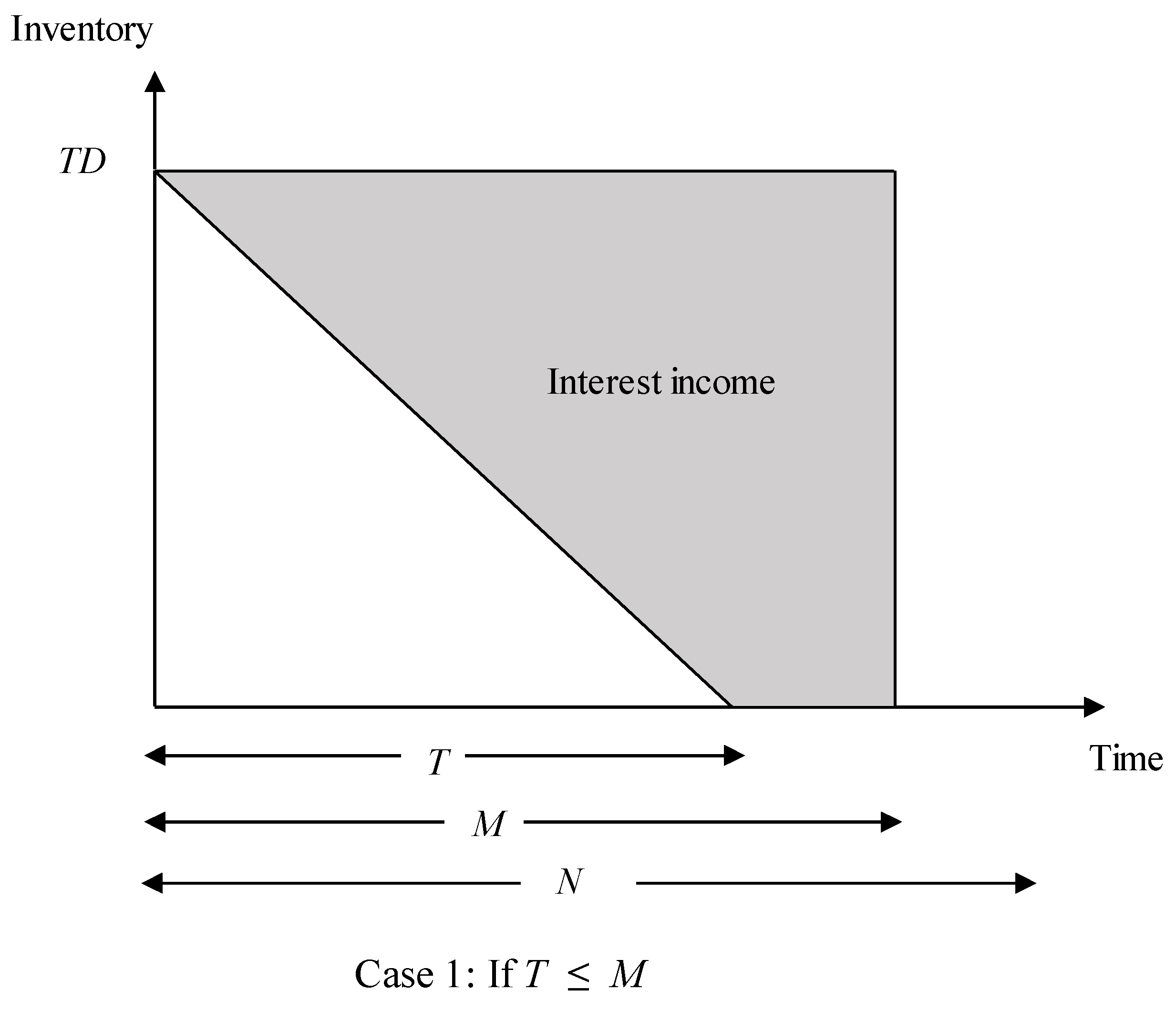
- Case 1.
- Total Profit (TP1) if T ≤ M:
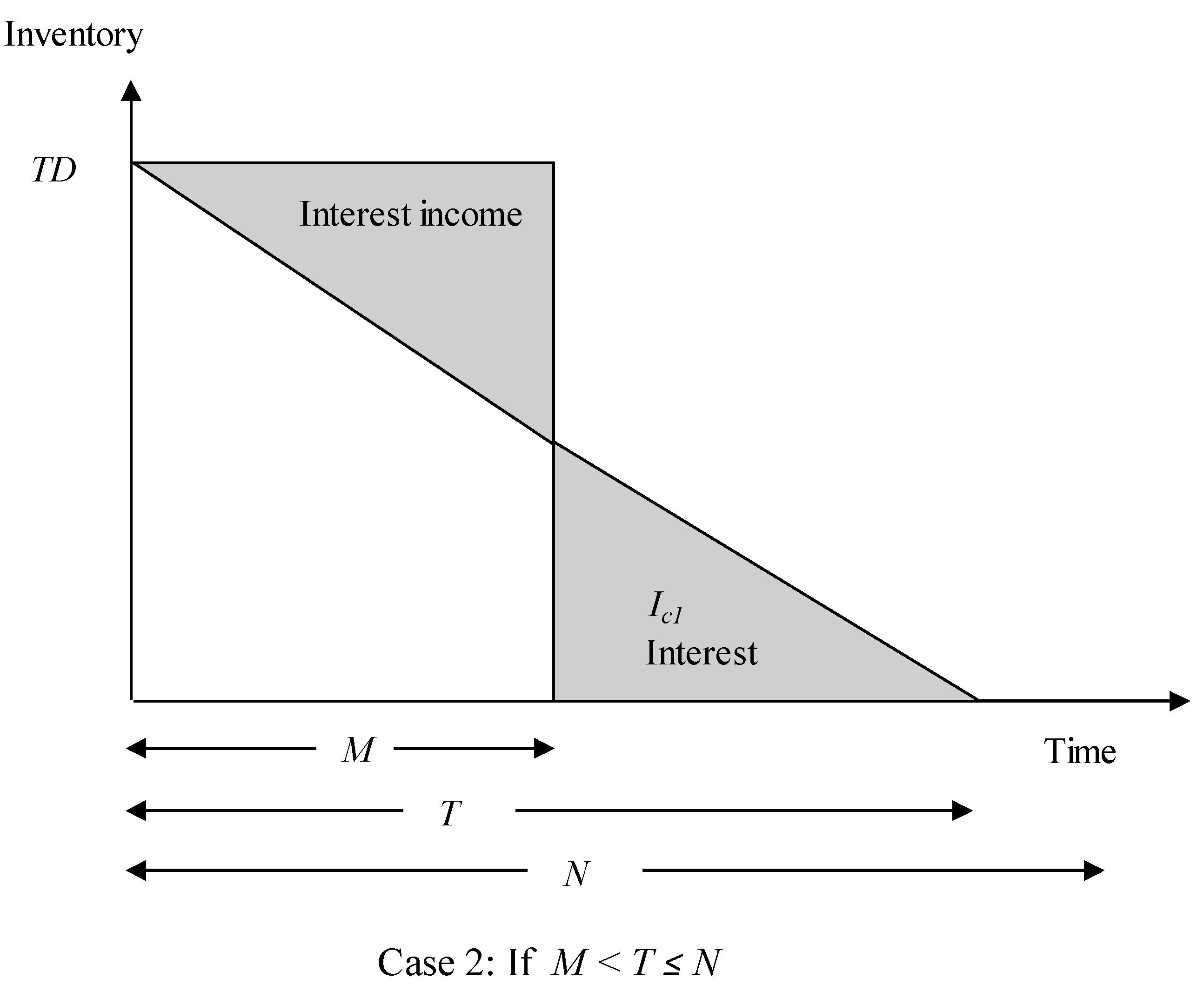
- Case 2.
- Total Profit (TP2) if M < T ≤ N:
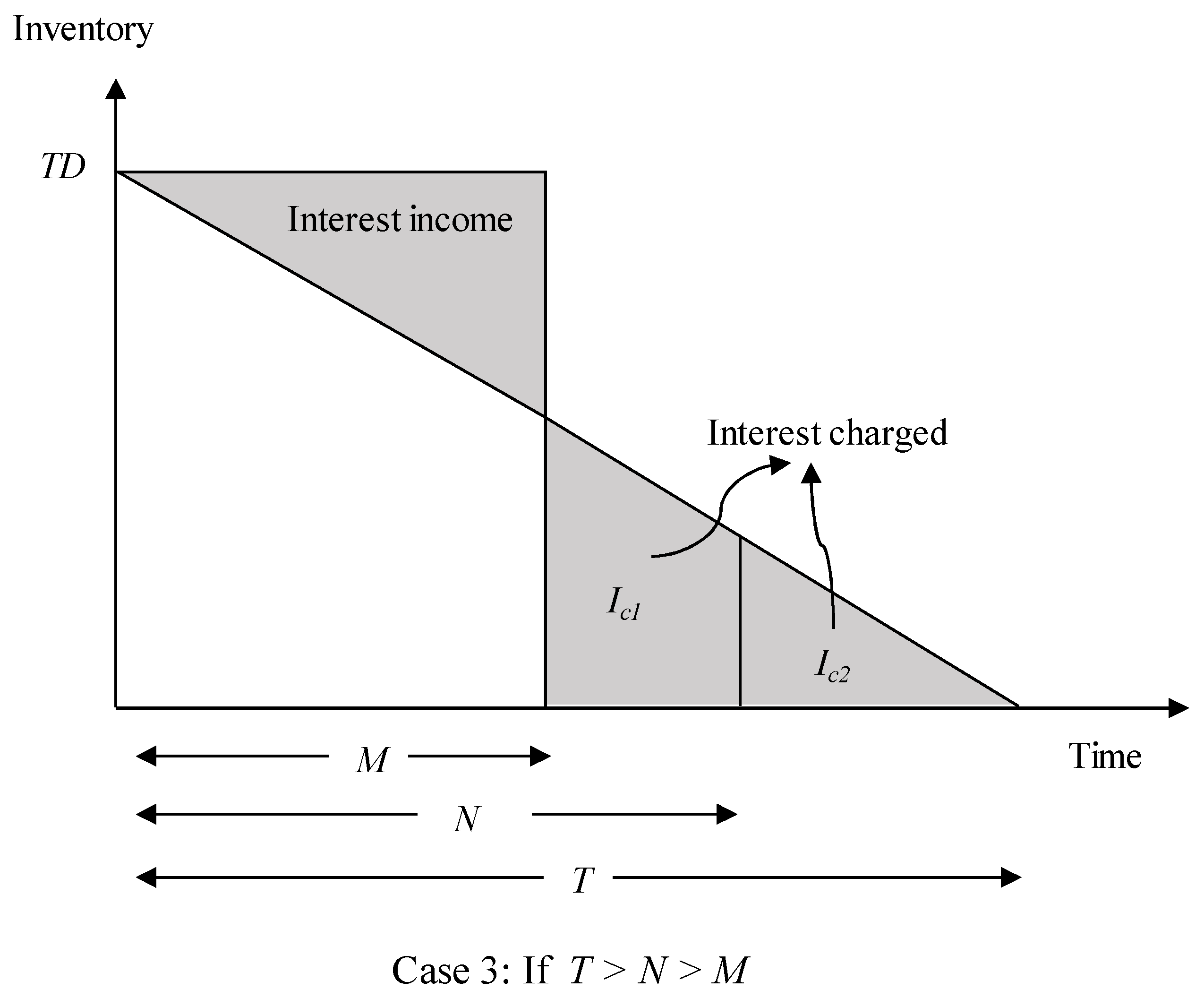
- Case 3.
- Total Profit (TP3) if T > N:where P is the selling price per unit, Cu is the product cost per unit, Ie is interest earned per unit, Ic1 is interest charged per unit for the permissible delay period M, and Ic2 is interest charged per unit for permissible delay period N.
4.1. Optimal Values of F and T for Case 1
4.2. Optimal Values of F and T for Case 2
4.3. Optimal Values of F and T for Case 3
5. Numerical Example
Results
6. Sensitivity Analysis
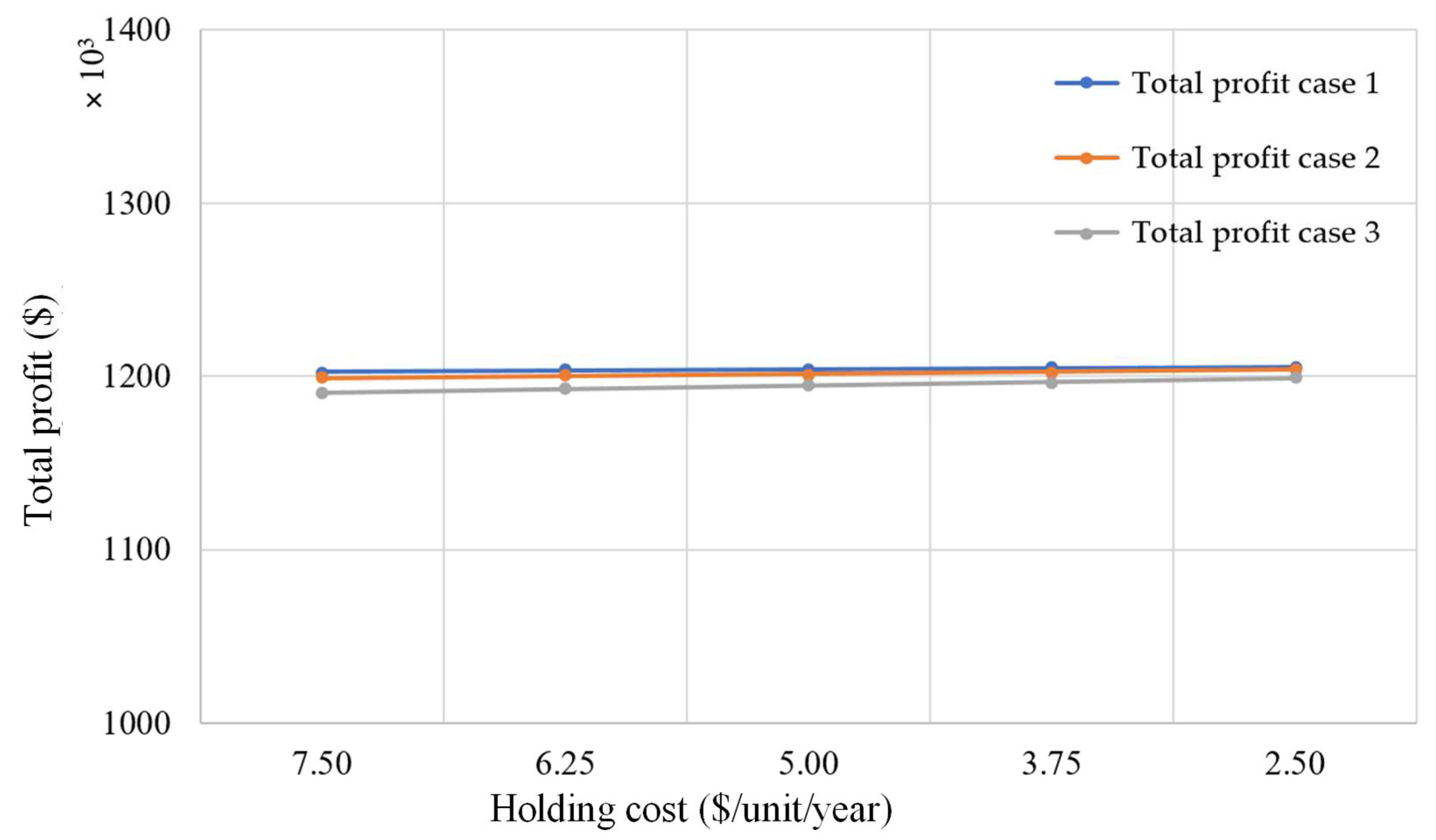
- Change in a parameter value of holding cost h causes a minor change in total profit for all scenarios. Furthermore, an increment in the value of h by 25% and 50% creates a decrease in TP of 0.11% and 0.06% for Case 1, decreases of 0.10% and 0.21% for Case 2, and decreases of 0.17% and 0.34% for Case 3, respectively. Similarly, a decrement in the value of h by 25% and 50% creates a total profit increase by 0.06% and 0.06% for Case 1, increases of by 0.10% and 0.21% for Case 2, and increases of 0.17% and 0.34% for Case 3, respectively. This shows that there an equilibrium point exists. Also, it illustrates that TP is equally sensitive to both negative and positive changes of parameter h.
- The outcome of a parameter change in the backorder cost π creates a minor change in total profit for all cases. Though, the increment in the value of π by 25% and 50% causes a decrease in each case. Similarly, for a decrement in the value of parameter π by both 25% and 50%, the total profit increases. It is valuable to state that it lies in an equilibrium state. Also, TP is equally sensitive to both negative and positive changes of parameter π.
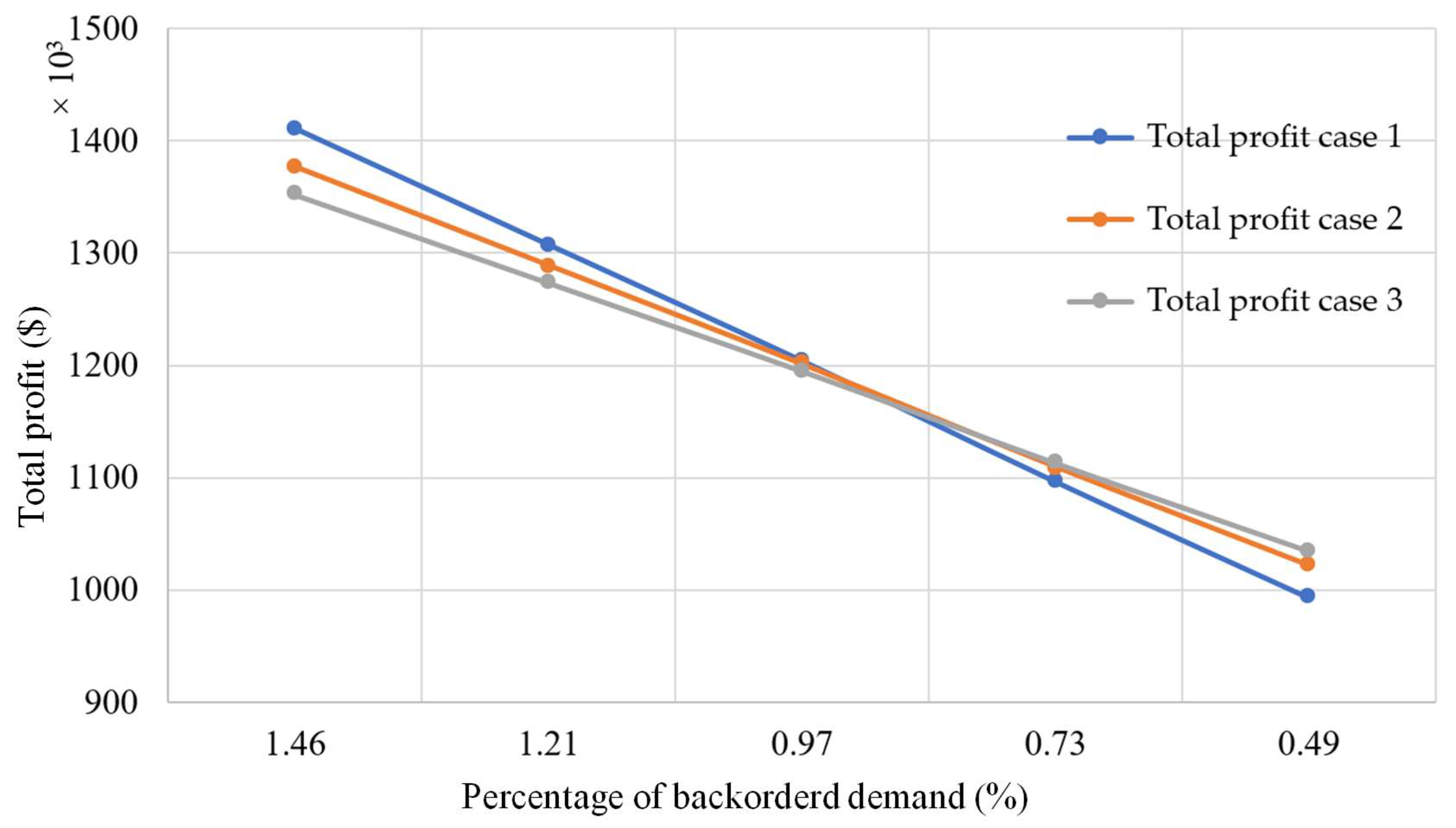
- The result of a parameter change in the fraction of backorder demand γ causes a major change in the total profit for different cases. Moreover, an increment in the value of γ by 25% and 50% causes an increase in TP by 8.58%, 7.31%, and 6.57%, and 17.16%, 14.63%, and 13.14% for Case 1, Case 2, and Case 3, respectively. Likewise, for a decrement in the value of parameter γ by 25% and 50%, the total profit decreases by 8.93%, 7.62%, and 6.84%, and 17.51%, 14.93%, and 13.42% for Case 1, Case 2, and Case 3, respectively. This does not lie in an equilibrium position. Also, it shows that TP is equally sensitive to both negative and positive change of the parameter γ.
- The fixed transportation cost of the imperfect item for repair shops cT causes a minor change in total profit for all cases. Furthermore, the increment in the value of cT by 25% and 50% causes a decrease in TP. Similarly, a decrement in the value of parameter cT by 25% and 50%, decreases the total profit. It is exists in an equilibrium position and also total profit is equally sensitive to both negative and positive change of the parameter cT.
- The labor and material cost for repair shops clm causes a minor change in total profit for all cases. The increment in the value of parameter cT by 25% and 50% causes a decrease in the total profit for each case. Similarly, a decrement in the value of cT by 25% and 50% causes a decrease in the total profit. It also exists in an equilibrium state.
- The percentage of the return of imperfect items w causes a small change in annual profit in all three cases. If the value of w is increased by 25% and 50%, then TP decreases for all cases. Similarly, if we decrease the said parameter by 25% and 50%, the annual total profit increases for each case. Therefore, the change in the parameter causes an inverse change in annual total profit but this lies in an equilibrium position.
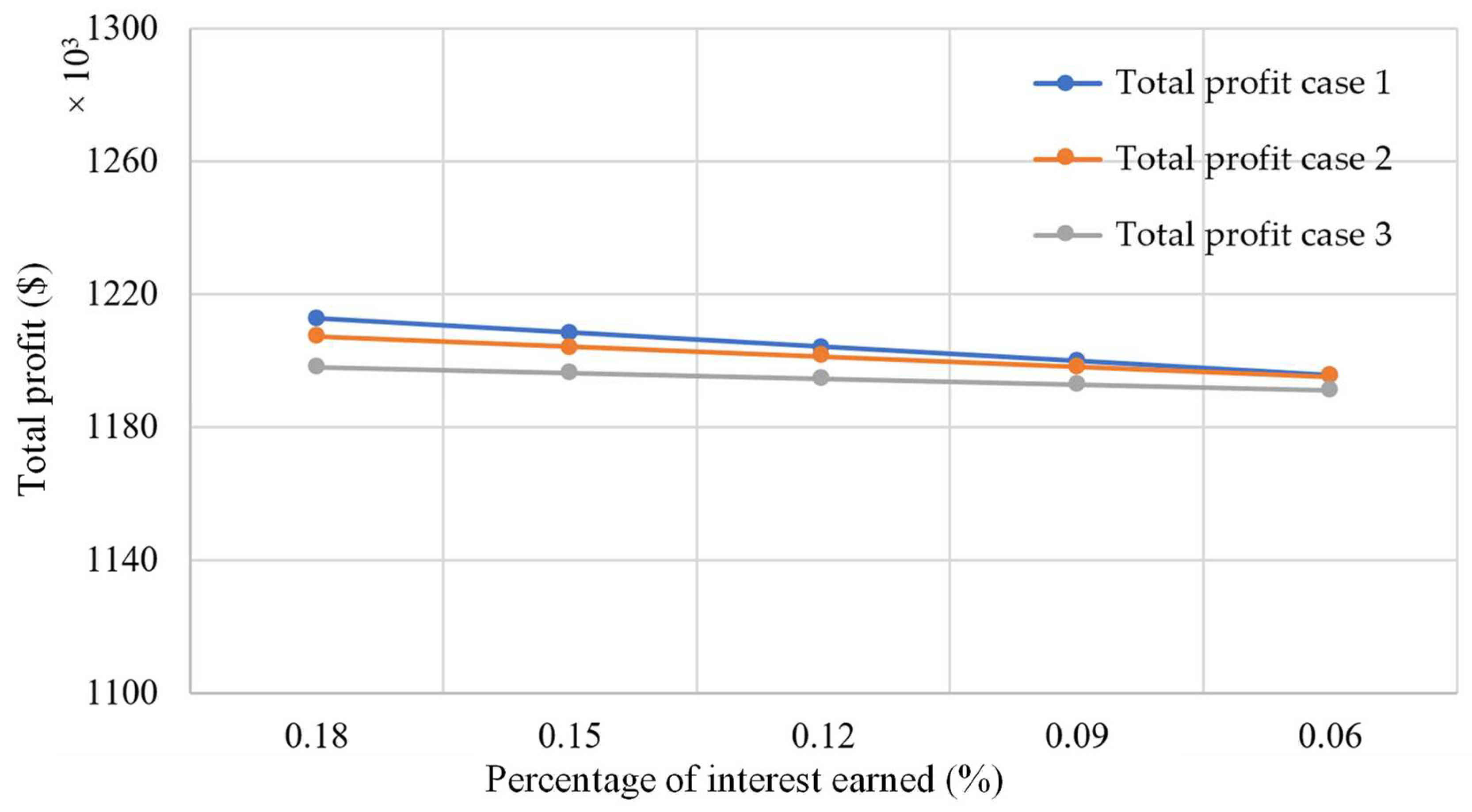
- The outcome of a parameter change in the interest earned per dollar per year Ie causes a minor change in total profit for each case. Additionally, if the value of Ie is increased by 25% and 50%, then total profit also increases for all cases. Similarly, a decrement in the value of parameter Ie by 25% and 50% causes a decrease in total profit. The result shows that total profit is closely related to interest earned and it also exists in an equilibrium state.
- The result of a parameter change in interest charged Ic1 and Ic2 are not applicable to Case 1, as no interest is charged for this case. Also, Ic2 is not applicable to Case 2, as no interest rate Ic2 is charged for this case. For Case 2 and Case 3, Ic1 causes a minor change in total profit. Additionally, if the value of Ic1 is increased by 25% and 50%, then total profit increases for both cases. Similarly, if we decrease the parameter Ic1 by 25% and 50%, the annual total profit decreases. A similar pattern is shown for parameter Ic2 in Case 3. An equilibrium position also exists in their patterns.
- The first permissible delay period M causes a marginal change in annual total profit for Case 1 and Case 2 only. The incremental change in this parameter by 25% and 50% causes an increase in total profit for Case 1, but in contrast for Case 2 with an increase in 50 % of this parameter, the total profit is decreased. For a 25% increment in the parameter, Case 2 shows a similar pattern as Case 1. On the other hand, a decrease in parameter M by 25% and 50% causes a decrease in total profit for both cases.
- The second permissible delay period N causes a change in total profit for Case 2 and Case 3 only. The Case 1 has no concern with it. The incremental change in this parameter by 25% causes an increase in total profit for both cases, but in contrast by increasing 50% and also by decreasing 25% and 50%, the total profit is decreased in both cases.
7. Managerial Insights
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
Appendix E
References
- Porteus, E.L. Optimal lot sizing, process quality improvement and setup cost reduction. Oper. Res. 1986, 34, 137–144. [Google Scholar] [CrossRef]
- Rosenblatt, M.J.; Lee, H.L. Economic production cycles with imperfect production processes. IIE Trans. 1986, 18, 48–55. [Google Scholar] [CrossRef]
- Salameh, M.; Jaber, M. Economic production quantity model for items with imperfect quality. Int. J. Prod. Econ. 2000, 64, 59–64. [Google Scholar] [CrossRef]
- Eroglu, A.; Ozdemir, G. An economic order quantity model with defective items and shortages. Int. J. Prod. Econ. 2007, 106, 544–549. [Google Scholar] [CrossRef]
- Roy, M.D.; Sana, S.S.; Chaudhuri, K. An economic order quantity model of imperfect quality items with partial backlogging. Int. J. Syst. Sci. 2011, 42, 1409–1419. [Google Scholar] [CrossRef]
- Vörös, J. Economic order and production quantity models without constraint on the percentage of defective items. Cent. Eur. J. Oper. Res. 2013, 21, 867–885. [Google Scholar] [CrossRef]
- Hsu, J.-T.; Hsu, L.-F. An EOQ model with imperfect quality items, inspection errors, shortage backordering, and sales returns. Int. J. Prod. Econ. 2013, 143, 162–170. [Google Scholar] [CrossRef]
- Rad, M.A.; Khoshalhan, F.; Glock, C.H. Optimizing inventory and sales decisions in a two-stage supply chain with imperfect production and backorders. Comput. Ind. Eng. 2014, 74, 219–227. [Google Scholar] [CrossRef]
- Kazemi, N.; Abdul-Rashid, S.H.; Ghazilla, R.A.R.; Shekarian, E.; Zanoni, S. Economic order quantity models for items with imperfect quality and emission considerations. Int. J. Syst. Sci. Oper. Logist. 2016, 99–115. [Google Scholar] [CrossRef]
- Marchi, B.; Zanoni, S.; Zavanella, L.; Jaber, M. Green supply chain with learning in production and environmental investments. IFAC-PapersOnLine 2018, 51, 1738–1743. [Google Scholar] [CrossRef]
- Bazan, E.; Jaber, M.Y.; El Saadany, A.M. Carbon emissions and energy effects on manufacturing–remanufacturing inventory models. Comput. Ind. Eng. 2015, 88, 307–316. [Google Scholar] [CrossRef]
- Wahab, M.; Mamun, S.; Ongkunaruk, P. EOQ models for a coordinated two-level international supply chain considering imperfect items and environmental impact. Int. J. Prod. Econ. 2011, 134, 151–158. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Soleymanfar, V.R.; Govindan, K. Sustainable economic production quantity models for inventory systems with shortage. J. Clean. Prod. 2018, 174, 1011–1020. [Google Scholar] [CrossRef]
- Manna, A.; Das, B.; Dey, J.; Mondal, S. Two layers green supply chain imperfect production inventory model under bi-level credit period. Tékhne 2017, 15, 124–142. [Google Scholar] [CrossRef]
- Sarkar, B.; Ahmed, W.; Kim, N. Joint effects of variable carbon emission cost and multi-delay-in-payments under single-setup-multiple-delivery policy in a global sustainable supply chain. J. Clean. Prod. 2018, 185, 421–445. [Google Scholar] [CrossRef]
- Kim, M.-S.; Sarkar, B. Multi-stage cleaner production process with quality improvement and lead time dependent ordering cost. J. Clean. Prod. 2017, 144, 572–590. [Google Scholar] [CrossRef]
- Moshtagh, M.S.; Taleizadeh, A.A. Stochastic integrated manufacturing and remanufacturing model with shortage, rework and quality based return rate in a closed loop supply chain. J. Clean. Prod. 2017, 141, 1548–1573. [Google Scholar] [CrossRef]
- Li, D.; Zhao, Y.; Zhang, L.; Chen, X.; Cao, C. Impact of quality management on green innovation. J. Clean. Prod. 2018, 170, 462–470. [Google Scholar] [CrossRef]
- Ahmed, W.; Sarkar, B. Impact of carbon emissions in a sustainable supply chain management for a second generation biofuel. J. Clean. Prod. 2018, 186, 807–820. [Google Scholar] [CrossRef]
- Younesi, M.; Roghanian, E. A framework for sustainable product design: A hybrid fuzzy approach based on Quality Function Deployment for Environment. J. Clean. Prod. 2015, 108, 385–394. [Google Scholar] [CrossRef]
- Skouri, K.; Konstantaras, I.; Lagodimos, A.; Papachristos, S. An EOQ model with backorders and rejection of defective supply batches. Int. J. Prod. Econ. 2014, 155, 148–154. [Google Scholar] [CrossRef]
- Chakraborty, T.; Giri, B. Lot sizing in a deteriorating production system under inspections, imperfect maintenance and reworks. Oper. Res. 2014, 14, 29–50. [Google Scholar] [CrossRef]
- Sarkar, B.; Cárdenas-Barrón, L.E.; Sarkar, M.; Singgih, M.L. An economic production quantity model with random defective rate, rework process and backorders for a single stage production system. J. Manuf. Syst. 2014, 33, 423–435. [Google Scholar] [CrossRef]
- Jaber, M.Y.; Zanoni, S.; Zavanella, L.E. Economic order quantity models for imperfect items with buy and repair options. Int. J. Prod. Econ. 2014, 155, 126–131. [Google Scholar] [CrossRef]
- Sharifi, E.; Sobhanallahi, M.A.; Mirzazadeh, A.; Shabani, S. An EOQ model for imperfect quality items with partial backordering under screening errors. Cogent Eng. 2015, 2, 994258. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Lashgari, M.; Akram, R.; Heydari, J. Imperfect economic production quantity model with upstream trade credit periods linked to raw material order quantity and downstream trade credit periods. Appl. Math. Model. 2016, 40, 8777–8793. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, C.; Li, C.; Zhong, Y. A synergic economic order quantity model with trade credit, shortages, imperfect quality and inspection errors. Appl. Math. Model. 2016, 40, 1012–1028. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Khanbaglo, M.P.S.; Cárdenas-Barrón, L.E. An EOQ inventory model with partial backordering and reparation of imperfect products. Int. J. Prod. Econ. 2016, 182, 418–434. [Google Scholar] [CrossRef]
- Sarkar, B.; Saren, S. Product inspection policy for an imperfect production system with inspection errors and warranty cost. Eur. J. Oper. Res. 2016, 248, 263–271. [Google Scholar] [CrossRef]
- Dey, O. A fuzzy random integrated inventory model with imperfect production under optimal vendor investment. Oper. Res. 2017, 1–15. [Google Scholar] [CrossRef]
- Kang, C.W.; Ullah, M.; Sarkar, B.; Hussain, I.; Akhtar, R. Impact of random defective rate on lot size focusing work-in-process inventory in manufacturing system. Int. J. Prod. Res. 2017, 55, 1748–1766. [Google Scholar] [CrossRef]
- Wuttke, D.A.; Blome, C.; Heese, H.S.; Protopappa-Sieke, M. Supply chain finance: Optimal introduction and adoption decisions. Int. J. Prod. Econ. 2016, 178, 72–81. [Google Scholar] [CrossRef]
- Pfohl, H.-C.; Gomm, M. Supply chain finance: Optimizing financial flows in supply chains. Logist. Res. 2009, 1, 149–161. [Google Scholar] [CrossRef]
- Goyal, S.K. Economic order quantity under conditions of permissible delay in payments. J. Oper. Res. Soc. 1985, 36, 335–338. [Google Scholar] [CrossRef]
- Chand, S.; Ward, J. A note on “Economic order quantity under conditions of permissible delay in payments”. J. Oper. Res. Soc. 1987, 38, 83–84. [Google Scholar]
- Shah, N.H. Probabilistic time-scheduling model for an exponentially decaying inventory when delays in payments are permissible. Int. J. Prod. Econ. 1993, 32, 77–82. [Google Scholar] [CrossRef]
- Huang, Y.-F. Optimal retailer’s ordering policies in the EOQ model under trade credit financing. J. Oper. Res. Soc. 2003, 54, 1011–1015. [Google Scholar] [CrossRef]
- Soni, H.; Shah, N.H. Optimal ordering policy for stock-dependent demand under progressive payment scheme. Eur. J. Oper. Res. 2008, 184, 91–100. [Google Scholar] [CrossRef]
- Tsao, Y.-C.; Chen, T.-H.; Zhang, Q.-H. Effects of maintenance policy on an imperfect production system under trade credit. Int. J. Prod. Res. 2013, 51, 1549–1562. [Google Scholar] [CrossRef]
- Sana, S.S.; Chedid, J.A.; Navarro, K.S. A three layer supply chain model with multiple suppliers, manufacturers and retailers for multiple items. Appl. Math. Comput. 2014, 229, 139–150. [Google Scholar] [CrossRef]
- Yang, M.; Tseng, W.-C. Three-echelon inventory model with permissible delay in payments under controllable lead time and backorder consideration. Math. Probl. Eng. 2014, 2014. [Google Scholar] [CrossRef]
- Jaggi, C.K.; Yadavalli, V.; Verma, M.; Sharma, A. An EOQ model with allowable shortage under trade credit in different scenario. Appl. Math. Comput. 2015, 252, 541–551. [Google Scholar] [CrossRef]
- Soni, H.N.; Patel, K.A. Optimal strategy for an integrated inventory system involving variable production and defective items under retailer partial trade credit policy. Decis. Support Syst. 2012, 54, 235–247. [Google Scholar] [CrossRef]
- Tsao, Y.-C.; Linh, V.T. Supply Chain Network Designs Developed for Deteriorating Items under Conditions of Trade Credit and Partial Backordering. Netw. Spat. Econ. 2016, 16, 933–956. [Google Scholar] [CrossRef]
- Giri, B.; Sharma, S. Optimal ordering policy for an inventory system with linearly increasing demand and allowable shortages under two levels trade credit financing. Oper. Res. 2016, 16, 25–50. [Google Scholar] [CrossRef]
- Tiwari, S.; Ahmed, W.; Sarkar, B. Multi-item sustainable green production system under trade-credit and partial backordering. J. Clean. Prod. 2018, 204, 82–95. [Google Scholar] [CrossRef]
- Tsao, Y.-C.; Zhang, Q.; Fang, H.-P.; Lee, P.-L. Two-tiered pricing and ordering for non-instantaneous deteriorating items under trade credit. Oper. Res. 2017, 1–20. [Google Scholar] [CrossRef]
- Banu, A.; Mondal, S.K. Analyzing an inventory model with two-level trade credit period including the effect of customers’ credit on the demand function using q-fuzzy number. Oper. Res. 2018, 1–29. [Google Scholar] [CrossRef]
| Author (s) | Inventory Model | Imperfect Products | Backordering | Trade Credit Policy | Rework | Sustainability | Multi Delay-in-Payment |
|---|---|---|---|---|---|---|---|
| Goyal (1985) [34] | √ | √ | |||||
| Porteus (1986) [1] | √ | √ | |||||
| Huang (2003) [37] | √ | √ | |||||
| Soni and Shah (2008) [38] | √ | ||||||
| Roy et al. (2011) [5] | √ | √ | √ | ||||
| Soni and Patel (2012) [43] | √ | √ | √ | ||||
| Sana et al. (2014) [40] | √ | √ | √ | ||||
| Yang and Tseng (2014) [41] | √ | √ | √ | √ | √ | ||
| Sarkar et al. (2014) [23] | √ | √ | √ | √ | |||
| Jaber et al. (2014) [24] | √ | √ | √ | ||||
| Sharifi et al. (2015) [25] | √ | √ | √ | ||||
| Taleizadeh et al. (2016) [26] | √ | √ | √ | √ | |||
| Sarkar and Saren (2016) [29] | √ | √ | |||||
| Taleizadeh et al. (2016) [28] | √ | √ | √ | √ | |||
| Tsao and Linh (2016) [44] | √ | √ | √ | ||||
| Kim and Sarkar (2017) [16] | √ | √ | √ | ||||
| Marchi et al. (2018) [10] | √ | √ | |||||
| Sarkar et al. (2018) [15] | √ | √ | √ | ||||
| Tiwari et al. (2018) [46] | √ | √ | √ | √ | √ | ||
| This Paper | √ | √ | √ | √ | √ | √ | √ |
| Parameter | Symbol | Value | Units |
|---|---|---|---|
| Demand rate | D | 50,000 | units/year |
| Screening rate | x | 175,200 | units/year |
| Repaired rate | R | 50,000 | units/year |
| Ordering cost | O | 100 | $/order |
| Purchase cost | Cu | 25 | $/unit |
| Selling price | P | 50 | $/unit |
| Holding cost of perfect product | h | 4 | $/unit/year |
| Holding cost at repair store | hs | 3 | $/unit/year |
| Holding cost of rework product | hr | 5 | $/unit/year |
| Carbon cost for holding perfect product | h’ | 1 | $/unit/year |
| Carbon cost at repair store for holding product | hs’ | 1 | $/unit/year |
| Carbon cost for holding rework product | hr’ | 1 | $/unit/year |
| Inspection cost | Cs | 0.5 | $/unit |
| Backorder cost | π | 20 | $/unit/year |
| Lost sales cost | l | 0.5 | $/unit/year |
| Fraction of backordered demand | γ | 97% | percent |
| Fixed setup cost of repair store | sr | 100 | $/setup |
| Fixed cost (transportation) | A | 200 | $/trip |
| Transportation cost per unit | ct | 2 | $/unit |
| Labor and material cost per unit | clm | 5 | $/unit |
| Transport time | tT | 2/220 | year |
| Markup percentage | m | 20% | percent |
| Percentage of imperfect items | β | 0.04% | percent |
| Penalty cost from goodwill loss | g | 15 | $/unit |
| Return cost | u | 3 | $/unit |
| Percentage of imperfect items returned | w | 0.02% | percent |
| First permissible delay period | M | 30 | days |
| Second permissible delay period | N | 45 | days |
| Interest earned | Ie | 12% | percent |
| Interest charged for period M | Ic1 | 13% | percent |
| Interest charged for period N | Ic2 | 20% | percent |
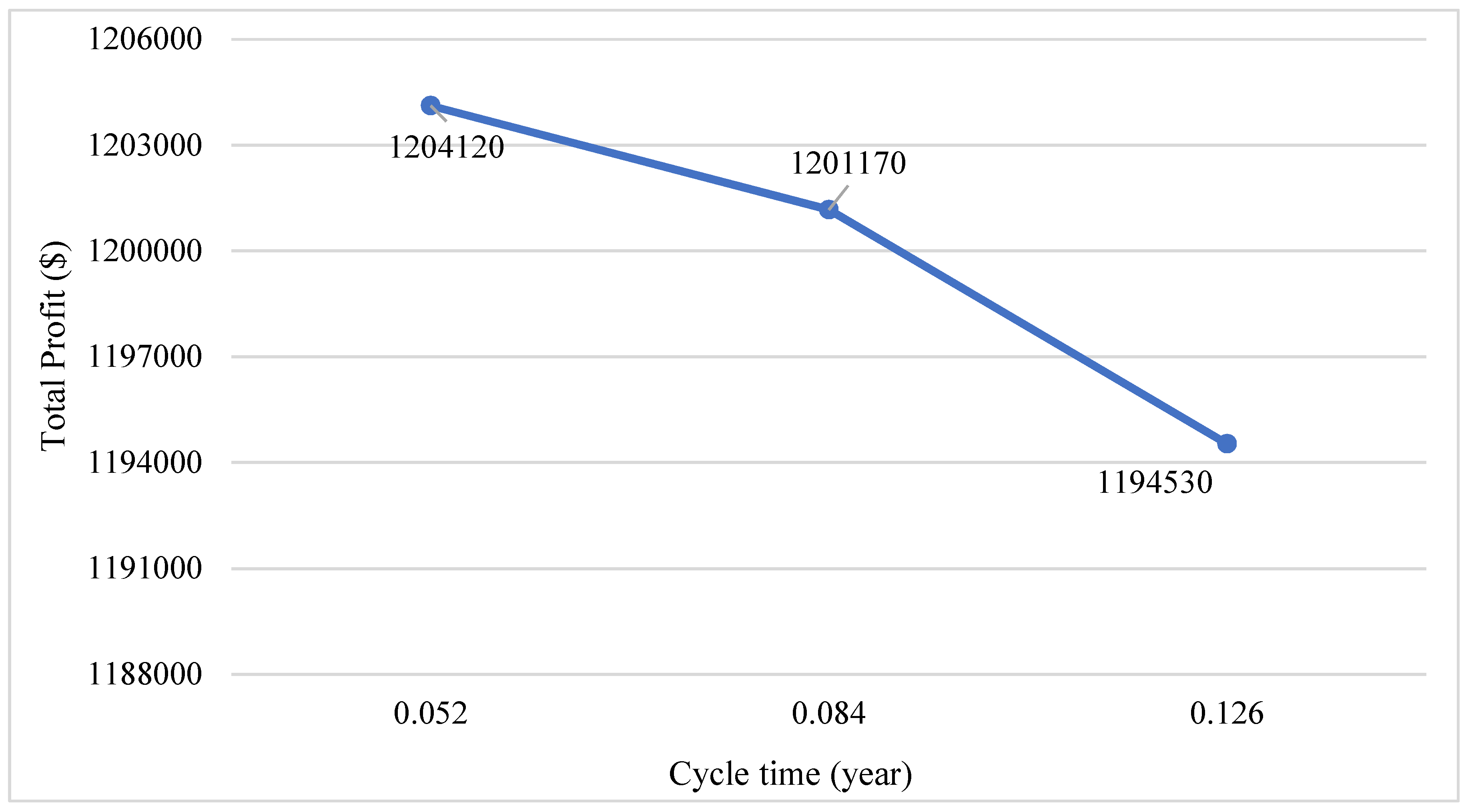
| Scenario | T (year) | F (%) | Q (units) | TP ($) |
|---|---|---|---|---|
| Case 1 | 0.052 | 0.66 | 2600 | 1,204,120 |
| Case 2 | 0.084 | 0.71 | 4200 | 1,201,170 |
| Case 3 | 0.126 | 0.74 | 6300 | 1,194,530 |
| Parameter | % Change | % Change TP (T,F) | ||
|---|---|---|---|---|
| Case 1 | Case 2 | Case 3 | ||
| h | +50 | −0.11 | −0.21 | −0.34 |
| +25 | −0.06 | −0.10 | −0.17 | |
| −25 | +0.06 | +0.10 | +0.17 | |
| −50 | +0.11 | +0.21 | +0.34 | |
| π | +50 | −0.12 | −0.14 | −0.17 |
| +25 | −0.06 | −0.07 | −0.09 | |
| −25 | +0.06 | +0.07 | +0.09 | |
| −50 | +0.12 | +0.14 | +0.17 | |
| γ | +50 | +17.16 | +14.63 | +13.14 |
| +25 | +8.58 | +7.31 | +6.57 | |
| −25 | −8.93 | −7.62 | −6.84 | |
| −50 | −17.51 | −14.93 | −13.42 | |
| ct | +50 | −0.26 | −0.28 | −0.29 |
| +25 | −0.13 | −0.14 | −0.15 | |
| −25 | +0.13 | +0.14 | +0.15 | |
| −50 | +0.26 | +0.28 | +0.29 | |
| clm | +50 | −0.33 | −0.35 | −0.37 |
| +25 | −0.16 | −0.18 | −0.18 | |
| −25 | +0.16 | +0.18 | +0.18 | |
| −50 | +0.33 | +0.35 | +0.37 | |
| w | +50 | −0.30 | −0.32 | −0.33 |
| +25 | −0.15 | −0.16 | −0.17 | |
| −25 | +0.15 | +0.16 | +0.17 | |
| −50 | +0.30 | +0.32 | +0.33 | |
| Ie | +50 | +0.71 | +0.51 | +0.29 |
| +25 | +0.36 | +0.26 | +0.15 | |
| −25 | −0.35 | −0.26 | −0.15 | |
| −50 | −0.71 | −0.51 | −0.29 | |
| Ic1 | +50 | N/A | +0.51 | +0.29 |
| +25 | N/A | +0.26 | +0.15 | |
| −25 | N/A | −0.26 | −0.15 | |
| −50 | N/A | −0.51 | −0.29 | |
| Ic2 | +50 | N/A | N/A | +0.29 |
| +25 | N/A | N/A | +0.15 | |
| −25 | N/A | N/A | −0.15 | |
| −50 | N/A | N/A | −0.29 | |
| M | +50 | +1.03 | −0.36 | N/A |
| +25 | +0.52 | +0.24 | N/A | |
| −25 | −0.52 | −0.31 | N/A | |
| −50 | −1.09 | −0.77 | N/A | |
| N | +50 | N/A | −0.36 | −0.04 |
| +25 | N/A | +0.24 | +0.003 | |
| −25 | N/A | −0.31 | −0.03 | |
| −50 | N/A | −0.77 | −0.23 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarkar, B.; Ahmed, W.; Choi, S.-B.; Tayyab, M. Sustainable Inventory Management for Environmental Impact through Partial Backordering and Multi-Trade-Credit-Period. Sustainability 2018, 10, 4761. https://doi.org/10.3390/su10124761
Sarkar B, Ahmed W, Choi S-B, Tayyab M. Sustainable Inventory Management for Environmental Impact through Partial Backordering and Multi-Trade-Credit-Period. Sustainability. 2018; 10(12):4761. https://doi.org/10.3390/su10124761
Chicago/Turabian StyleSarkar, Biswajit, Waqas Ahmed, Seok-Beom Choi, and Muhammad Tayyab. 2018. "Sustainable Inventory Management for Environmental Impact through Partial Backordering and Multi-Trade-Credit-Period" Sustainability 10, no. 12: 4761. https://doi.org/10.3390/su10124761
APA StyleSarkar, B., Ahmed, W., Choi, S.-B., & Tayyab, M. (2018). Sustainable Inventory Management for Environmental Impact through Partial Backordering and Multi-Trade-Credit-Period. Sustainability, 10(12), 4761. https://doi.org/10.3390/su10124761






