Credit Risk Diffusion in Supply Chain Finance: A Complex Networks Perspective
Abstract
1. Introduction
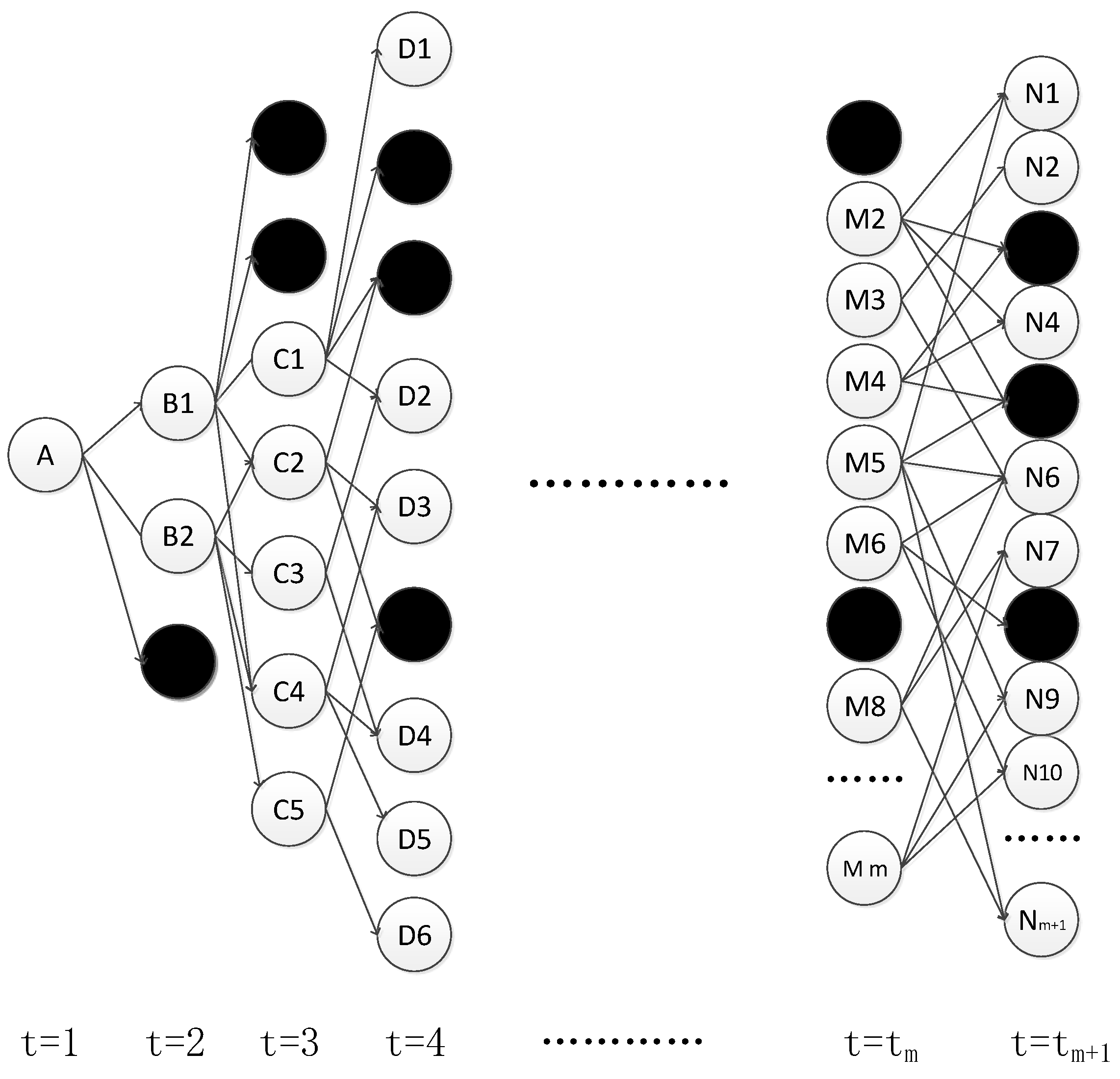
2. Construction of a Supply Chain Finance Network
- (1)
- Growth mechanism: starting from a network with nodes, each time a new node is introduced, it is connected to the existing nodes, and .
- (2)
- Priority connection mechanism: the probability that a new node is connected to an existing node is , which can be expressed as the relationship between the node with a node degree of and the sum of the node degrees is .
3. Modeling Supply Chain Finance Network Using Complex Networks
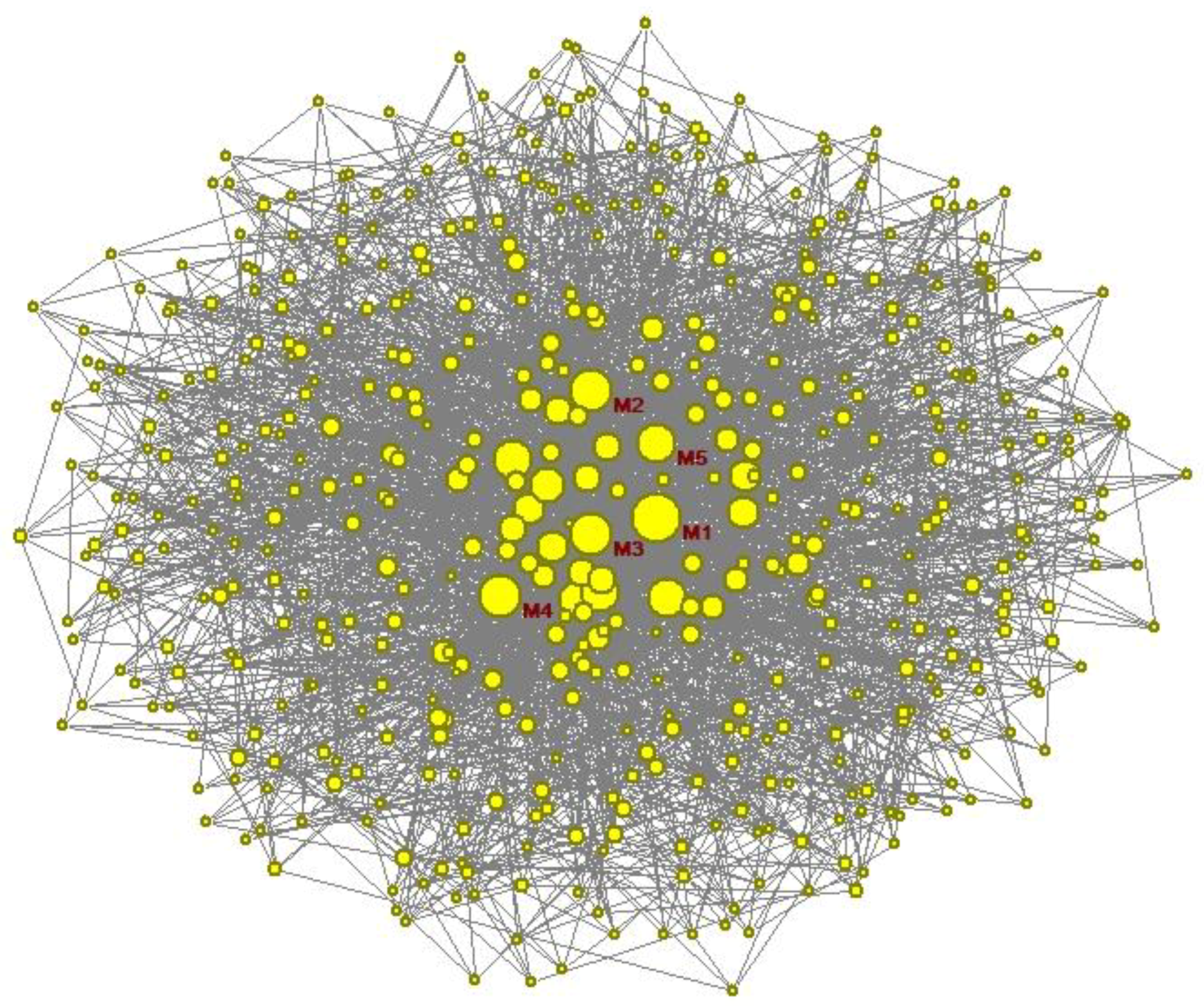
3.1. Analysis of Credit Risk Diffusion in Supply Chain Finance
3.2. Model Construction
4. Simulation Result and Discussion
4.1. Algorithm Design
- (1)
- Generating basic network model, = 1000, .
- (2)
- Random selection of a node as the initial infected node in the network.
- (3)
- Find out the suspicious nodes of infection connected to the infected nodes, determine the number of infected nodes in its neighbors and calculate the impact, compare with the risk threshold of the enterprise, and finally determine the new node at this moment. Suppose that the state of the node is represented by (0 or 1), where represents the node as a healthy node, and represents the node is an infected node. Referring to previous research literature, the impact on enterprise nodes can be expressed aswhere , represents the connecting edge between node and node , means that the nodes are directly connected, otherwise it is 0. αi represents the number of nodes that have been infected in the neighbor nodes of suspicious infected nodes. The larger the number, the greater the impact on the enterprise, which is similar to the situation of the credit risk diffusion in the network of supply chain finance in reality. This indicator is related to the degree of the node. Generally speaking, the greater the degree of the node, the larger the value of this indicator. βi describes the external impact of enterprises, which can be used to refer to the enterprise loss in supply chain financial networks caused by external credit risk contagion. The enterprise’s risk threshold reflects the ability of the company to resist credit risk. Combined with the analysis in the above model, the risk threshold of node can be set as :represents the assets under the financing project left behind after the company has suffered some normal or unpredictable losses in its normal production and business activities. Its existence describes the risks originating from the company itself. According to the setting above in which is a random value, is then also a random value. Here for ease of analysis, it is assumed that is referred to in the model as a randomly generated value.
- (4)
- The cure time of the enterprises in the network is and the initial setting is = 2.
- (5)
- When an infected enterprise appears in the network, it will be infused repeatedly according to the above procedure until the stable state of the network is reached and the time set in the simulation is 40-time steps.
4.2. Analysis of Simulation Result
- (6)
- The influence of influencing factors on the density of infected nodes in the network: Changes are made under the premise of the basic parameters of the network and . The simulation results obtained within the range of 40 time steps are shown in Figure 4.
4.3. Further Simulation Analysis
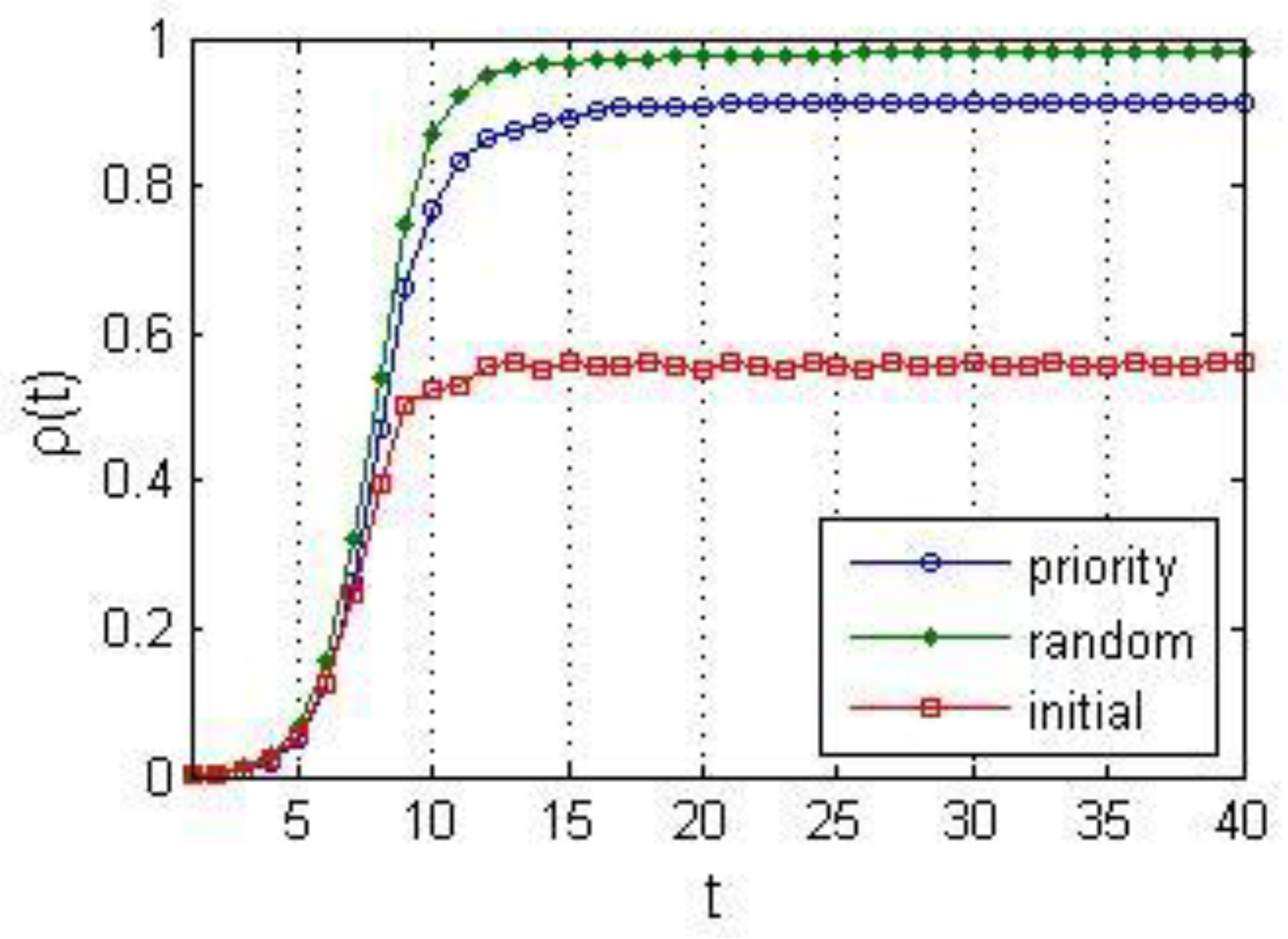
4.3.1. Selection of Initial Infection Nodes
4.3.2. Different Cure Strategies
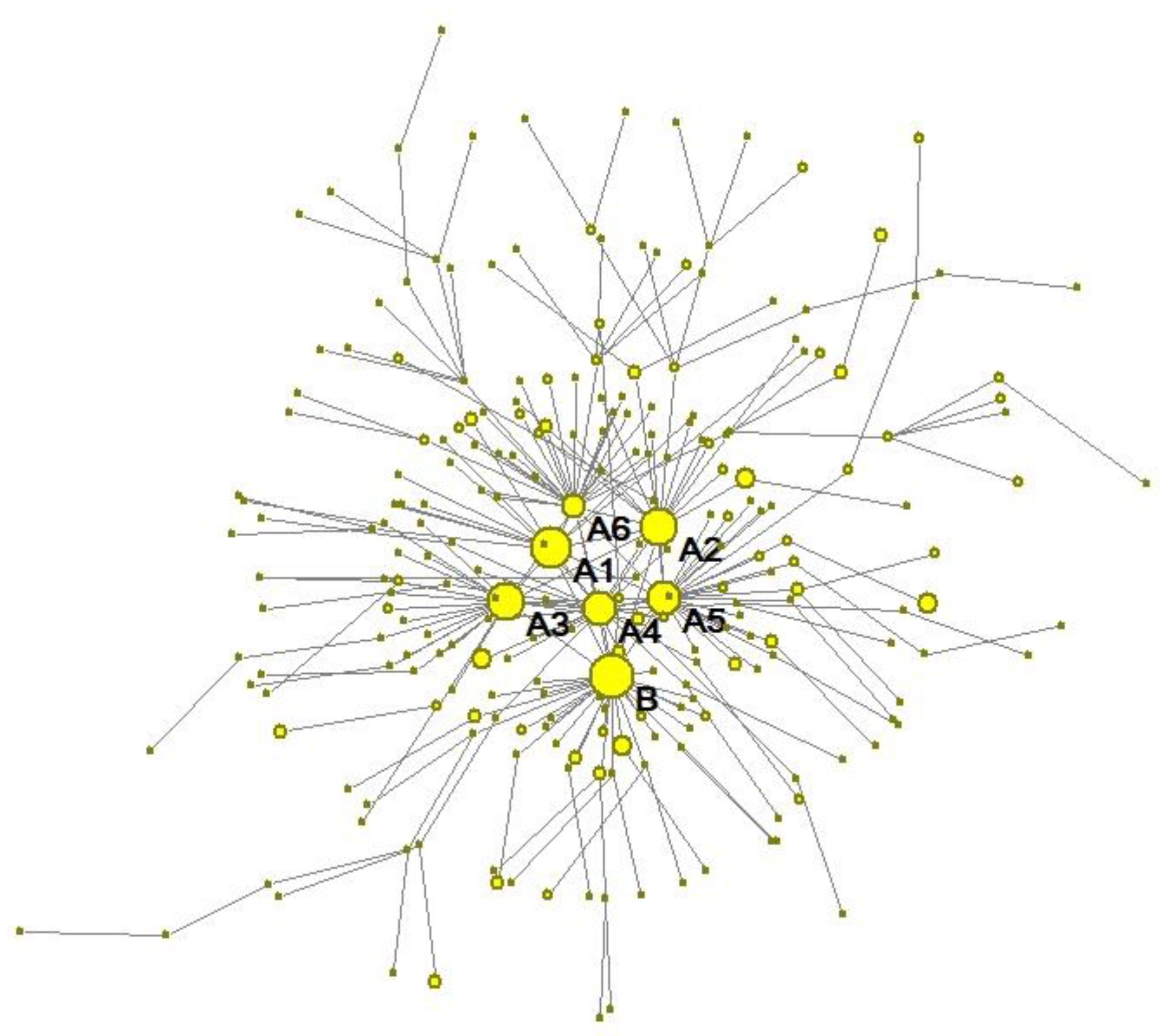
5. Case Analysis and Discussion
5.1. Case Description and Variable Assignment
5.2. Case Analysis
5.2.1. Construction of Supply Chain Finance Network
5.2.2. Selection of Initial Infection Nodes
5.2.3. Different Cure Strategies
5.2.4. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xiong, X.; Ma, J.; Zhao, W.J.; Wang, X.Y.; Zhang, J. Credit Risk Evaluation in Supply Chain Finance Model. Nankai Bus. Rev. 2009, 12, 92–98. [Google Scholar]
- Davis, M.; Lo, V. Infectious Defaults. Quant. Financ. 2001, 1, 382–387. [Google Scholar] [CrossRef]
- Jarrow, R.A.; Yu, F. Counterparty Risk and the Pricing of Defaultable Securities. J. Financ. 2001, 56, 1765–1799. [Google Scholar] [CrossRef]
- Giesecke, K.; Weber, S. Cyclical Correlations, Credit Contagion, and Portfolio Losses. J. Bank. Financ. 2004, 28, 3009–3036. [Google Scholar] [CrossRef]
- Jorion, P.; Zhang, G. Credit Contagion from Counterparty Risk. J. Financ. 2009, 64, 2053–2087. [Google Scholar] [CrossRef]
- Leung, K.S.; Yue, K.K. Counterparty Risk for Credit Default Swaps: Markov Chain Interacting Intensities Model with Stochastic Intensity. Asia-Pac. Financ. Mark. 2009, 16, 169. [Google Scholar] [CrossRef]
- Li, D.X.; Financial, A. The Valuation of Basket Credit Derivatives: A Copula Function Approach; AXA Financial: New York, NY, USA, 2000. [Google Scholar]
- Giesecke, K. A Simple Exponential Model for Dependent Defaults. Soc. Sci. Electron. Publ. 2002, 13, 74–83. [Google Scholar] [CrossRef]
- Nier, E.; Yang, J.; Yorulmazer, T.; Alentorn, A. Network Models and Financial Stability. Soc. Sci. Electron. Publ. 2007, 31, 2033–2060. [Google Scholar] [CrossRef]
- Steinbacher, M.; Steinbacher, M.; Steinbacher, M. Credit Contagion in Financial Markets: A Network-Based Approach. Muchich Personal RePEc Archive (MPRA) Paper 49616. 2013. Available online: https://mpra.ub.uni-muenchen.de/49616/1/MPRA_paper_49616.pdf (accessed on 30 October 2018).
- Anagnostou, I.; Sourabh, S.; Kandhai, D. Incorporating Contagion in Portfolio Credit Risk Models Using Network Theory. Complexity 2018, 2018, 6076173. [Google Scholar] [CrossRef]
- Petrone, D.; Latora, V. A Dynamic Approach Merging Network Theory and Credit Risk Techniques to Assess Systemic Risk in Financial Networks. Sci. Rep. 2018, 8, 5561. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, M. Complex Systems: Network Thinking. Artif. Intell. 2006, 170, 1194–1212. [Google Scholar] [CrossRef]
- Yang, K.; Zhang, Z.Y. SIS-RP Model and Simulation of Supply Chain Network Risk Propagation. J. Beijing Jiaotong Univ. 2013, 37, 122–126. [Google Scholar]
- Chen, T.Q.; He, J.M. Research on Credit Risk Contagion Model Based on Complex Network. Soft Sci. 2014, 22, 1–10. [Google Scholar]
- Zhong, S.; Zhao, Y. A Buisness System towards Supply Chain Finance Based on Complex Network. In Proceedings of the International Conference on Logistics, Informatics and Service Sciences, Barcelona, Spain, 27–29 July 2015. [Google Scholar]
- Pastor-Satorras, R.; Vespignani, A. Epidemic Dynamics and Endemic States in Complex Networks. Phys. Rev. E 2001, 63, 066117. [Google Scholar] [CrossRef]
- Chen, Q.; Du, F. Financial Innovation, Systematic Risk and Commercial Banks’ Stability in China: Theory and Evidence. Appl. Econ. 2016, 48, 3887–3898. [Google Scholar] [CrossRef]
- Hearnshaw, E.J.S.; Wilson, M.J. A Complex Network Approach to Supply Chain Network Theory. Int. J. Oper. Prod. Manag. 2013, 33, 442–469. [Google Scholar] [CrossRef]
- Hofmann, E. Supply Chain Finance: Some Conceptual Insights; Springer: Berlin, Germany, 2005. [Google Scholar]
- Wang, Q.; Hartmann-Wendels, T. Credit Default Risk Contagion Modeling. J. Financ. Res. 2008, 10, 162–173. [Google Scholar]
- Bellamy, M.A.; Basole, R.C. Network Analysis of Supply Chain Systems: A Systematic Review and Future Research. Syst. Eng. 2013, 16, 235–249. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collectivedynamics of ’small-World’ Networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Shang, Y. L Distinct Clusterings and Characteristic Path Lengths in Dynamic Small-world Networks with identical limit degree distribution. J. Stat. Phys. 2012, 149, 505–518. [Google Scholar] [CrossRef]
- Xin, Y.H.; Sun, Y.M. Analysis and Simulation Research of Supply Chain Robustness Considering the Risk Transmission. Sci. Technol. Manag. Res. 2017, 37, 245–253. [Google Scholar]
- Wang, W.; Fu, W.P. Review of Research on Modeling and Simulation for Dynamics and Complexity of Supply Chain Systems. J. Syst. Simul. 2010, 22, 71–279. [Google Scholar]
- Barabási, A.L.; Albert, R.; Jeong, H. Mean-Field Theory for Scale-Free Random Networks. Phys. A Stat. Mech. Its Appl. 1999, 272, 173–187. [Google Scholar] [CrossRef]
- Chakrabarty, B.; Zhang, G. Credit Contagion Channels: Market Microstructure Evidence from Lehman Brothers’ Bankruptcy. Financ. Manag. 2012, 41, 320–343. [Google Scholar] [CrossRef]
- Shang, Y. L Vulnerability of networks: Fractional percolation on random graphs. Phys. Rev. E 2014, 89, 012813. [Google Scholar] [CrossRef]
- Shang, Y. L Modeling epidemic spread with awareness and heterogeneous transmission rates in networks. J. Boil. Phys. 2013, 39, 489–500. [Google Scholar] [CrossRef]
- Shang, Y. L Discrete-time Epidemic Dynamics with Awareness in Random Networks. Int. J. Biomath. 2013, 6, 135007. [Google Scholar] [CrossRef]






| Influential Factors | Risk Diffusion Effect Index | |
|---|---|---|
| Critical Value of Risk Propagation Probability | Steady Infection Density | |
| general financing ratio | − | + |
| cure time | − | + |
| network structure | − | + |
| network scale | − | unknown |
| Influencing Factors | Risk Diffusion Effect Index | ||
|---|---|---|---|
| Critical Value of Risk Propagation Probability | Steady Infection Density | Risk Diffusion Speed | |
| general financing ratio | − | + | + |
| cure time | 0 | + | 0 |
| network structure | − | + | + |
| network scale | 0 | 0 | 0 |
| Name of Variable | Assignment | Explanation |
|---|---|---|
| network scale | 246 | sum of enterprise B and suppliers with financing needs |
| network structure | core enterprise B | |
| initial network | sum of enterprise B and A-level suppliers | |
| assets under financing program | funds of suppliers occupied by enterprise B | |
| assets available for debt repayment | assets available to suppliers for mortgage financing | |
| general financing ratio | the mortgage rate of ordinary residential buildings | |
| financing amount | non-mortgage financing | |
| mortgage financing | ||
| cure time | recovery time of infected enterprises | |
| probability of risk propagation | risk propagation probability among enterprises |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Chen, D.; Wang, L.; Han, C. Credit Risk Diffusion in Supply Chain Finance: A Complex Networks Perspective. Sustainability 2018, 10, 4608. https://doi.org/10.3390/su10124608
Zhao Z, Chen D, Wang L, Han C. Credit Risk Diffusion in Supply Chain Finance: A Complex Networks Perspective. Sustainability. 2018; 10(12):4608. https://doi.org/10.3390/su10124608
Chicago/Turabian StyleZhao, Zebin, Dongling Chen, Luqi Wang, and Chuqiao Han. 2018. "Credit Risk Diffusion in Supply Chain Finance: A Complex Networks Perspective" Sustainability 10, no. 12: 4608. https://doi.org/10.3390/su10124608
APA StyleZhao, Z., Chen, D., Wang, L., & Han, C. (2018). Credit Risk Diffusion in Supply Chain Finance: A Complex Networks Perspective. Sustainability, 10(12), 4608. https://doi.org/10.3390/su10124608




