Can Polyolefin Fibre Reinforced Concrete Improve the Sustainability of a Flyover Bridge?
Abstract
1. Introduction
2. Material Modelling
2.1. Reinforced Concrete
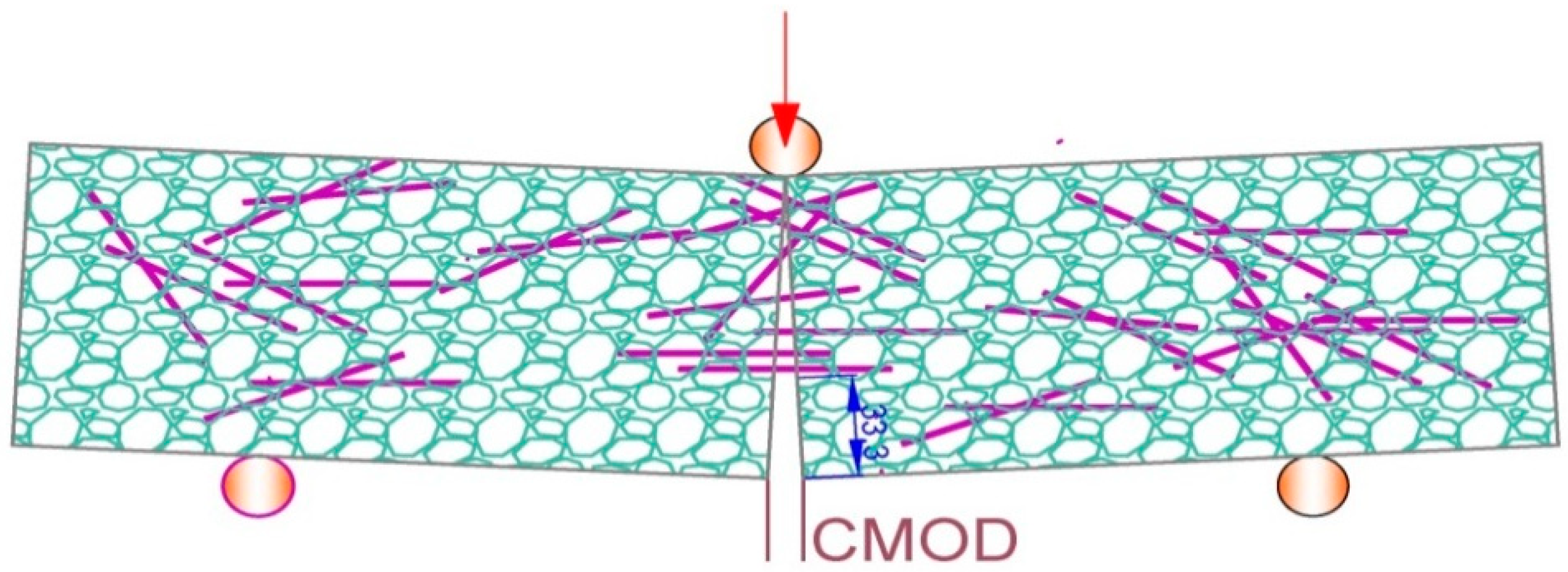
2.2. FRC
3. Structural Design Methodology
- The maximum compressive strain in concrete greater than compressive ultimate strain: εcmax > εcu = 0.35%.
- The tensile strain in main reinforcement greater than the ultimate strain of steel: εs > εsu = 1.00%.
- The crack width in concrete greater than the ultimate crack width: w > wu.
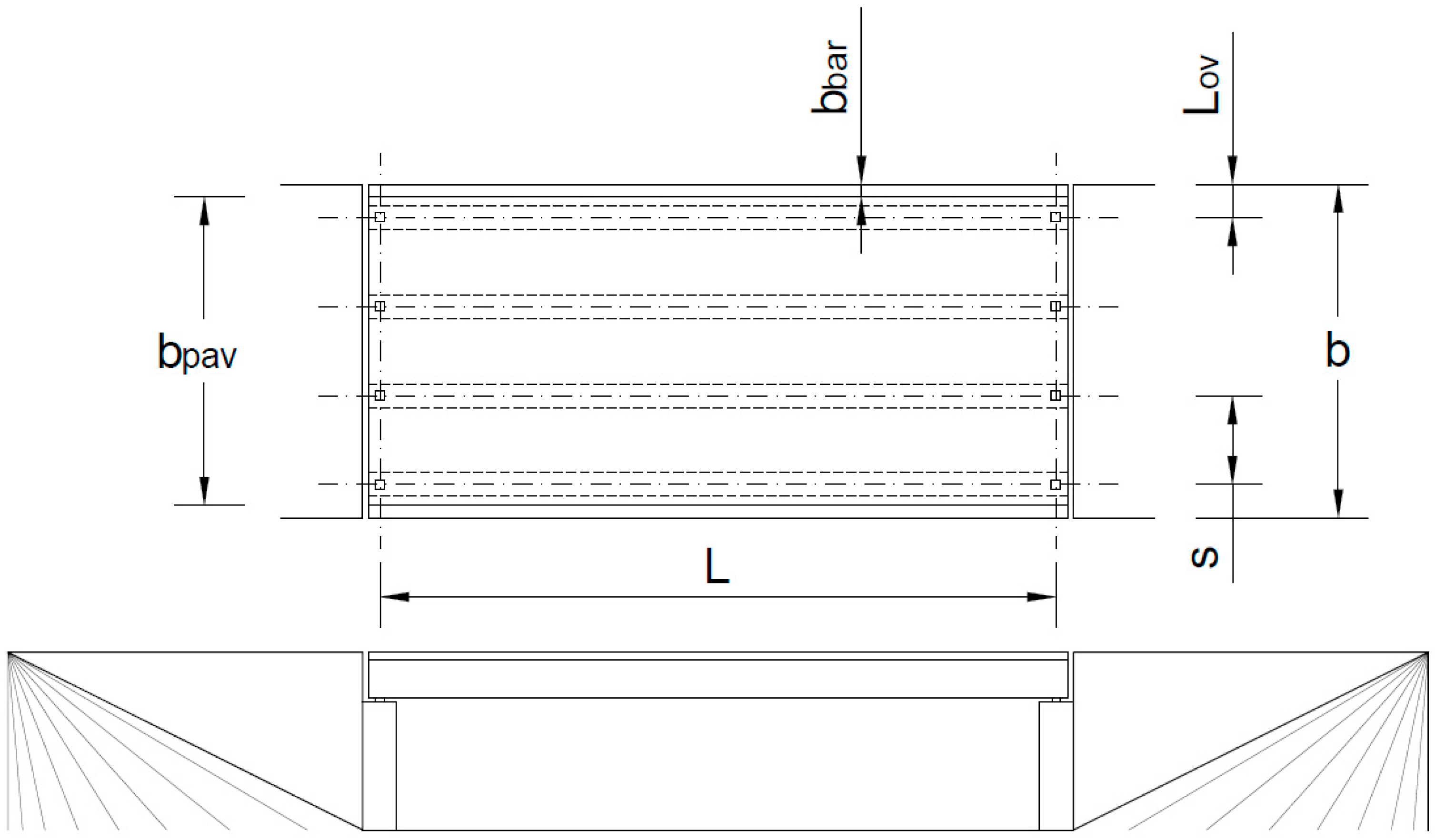
4. Application to a Bridge Typology
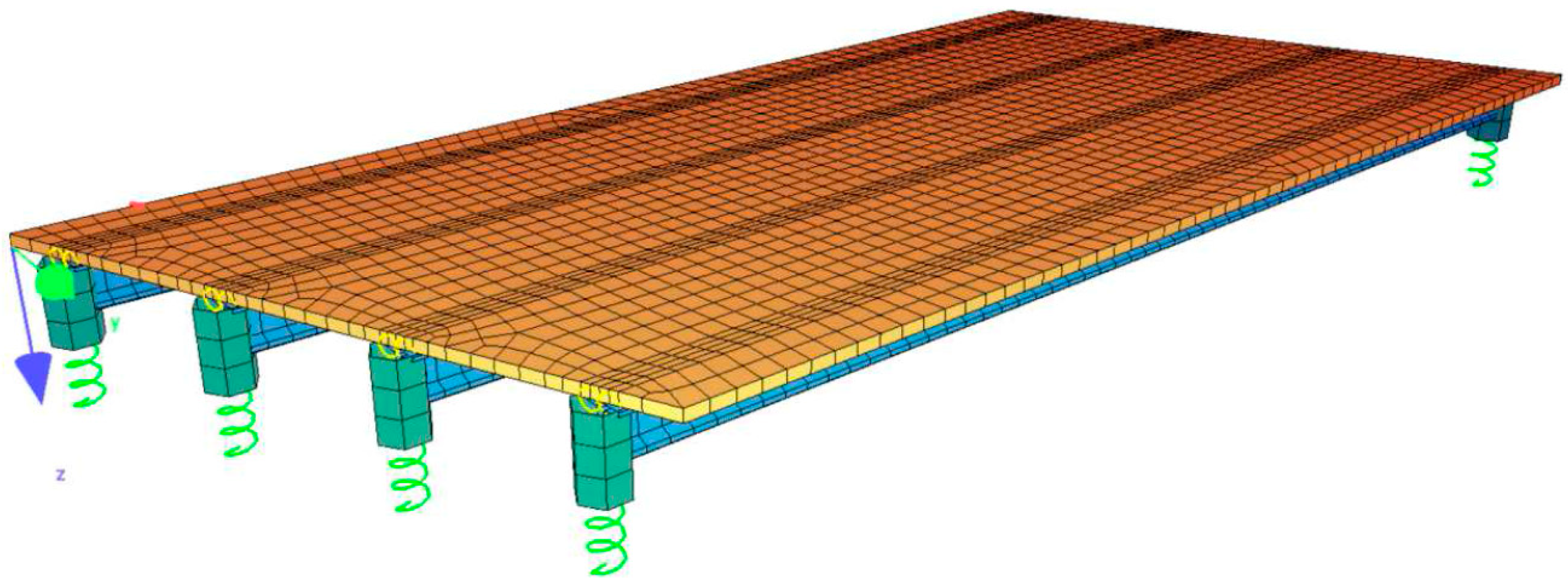
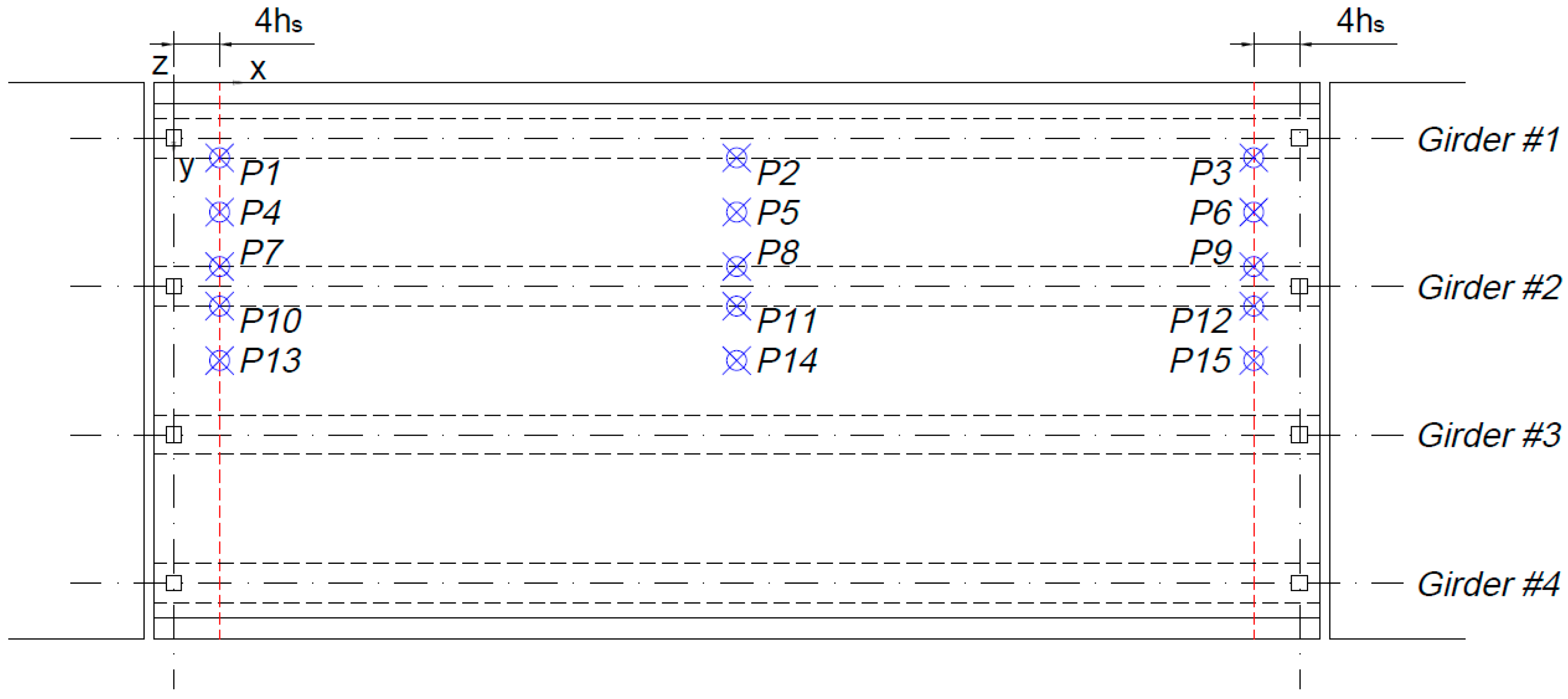
4.1. Description of the Numerical Model
4.2. Results Obtained and Calculation of the Reinforcement
5. MIVES Evaluation of the Proposed Bridges
5.1. Description of the MIVES Method
5.2. Discussion of the Case Study
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, C.; Habert, G.; Bouzidi, Y.; Jullien, A. Environmental impact of cement production: Detail of the different processes and cement plant variability evaluation. J. Clean. Prod. 2010, 18, 478–485. [Google Scholar] [CrossRef]
- Mikulčić, H.; Vujanović, M.; Duić, N. Reducing the CO2 emissions in Croatian cement industry. Appl. Energy 2013, 101, 41–48. [Google Scholar] [CrossRef]
- Benhelal, E.; Zahedi, G.; Shamsaei, E.; Bahadori, A. Global strategies and potentials to curb CO2 emissions in cement industry. J. Clean. Prod. 2013, 51, 142–161. [Google Scholar] [CrossRef]
- China Statistic Yearbook; National Bureau of Statistics of the People’s Republic of China: Beijing, China, 2012.
- He, F.; Zhang, Q.; Lei, J.; Fu, W.; Xu, X. Energy efficiency and productivity change of China’s iron and steel industry: Accounting for undesirable outputs. Energy Policy 2013, 54, 204–213. [Google Scholar] [CrossRef]
- El Fattah, A.A.; Al-Duais, I.; Riding, R.; Thomas, M. Field evaluation of corrosion mitigation on reinforced concrete in marine exposure conditions. Constr. Build. Mater. 2018, 165, 663–674. [Google Scholar] [CrossRef]
- Xu, F.; Xiao, Y.; Wang, S.; Li, W.; Liu, W.; Du, D. Numerical model for corrosion rate of steel reinforcement in cracked reinforced concrete structure. Constr. Build. Mater. 2018, 180, 55–67. [Google Scholar] [CrossRef]
- Thompson, N.; Yunovich, M.; Dunmire, D. Cost of corrosion and corrosion maintenance strategies. Corros. Rev. 2007, 25, 247–262. [Google Scholar] [CrossRef]
- Val, D.V.; Stewart, M.G. Life-cycle cost analysis of reinforced concrete structures in marine environments. Struct. Saf. 2003, 25, 343–362. [Google Scholar] [CrossRef]
- Angulo-Ramírez, D.; de Gutiérrez, R.M.; Puertas, F. Alkali-activated Portland blast-furnace slag cement: Mechanical properties and hydration. Constr. Build. Mater. 2017, 140, 119–128. [Google Scholar] [CrossRef]
- Li, G.; Zhang, A.; Song, A.; Liu, S.; Zhang, J. Ground granulated blast furnace slag effect on the durability of ternary cementitious system exposed to combined attack of chloride and sulfate. Constr. Build. Mater. 2018, 158, 640–648. [Google Scholar] [CrossRef]
- Dalton, J.; Gardner, K.; Seager, T.; Weimer, M.; Spear, J.; Magee, B. Properties of Portland cement made from contaminated sediments. Resour. Conserv. Recycl. 2004, 41, 227–241. [Google Scholar] [CrossRef]
- Aydin, E.; Arel, H.Ş. Characterization of high-volume fly-ash cement pastes for sustainable construction applications. Constr. Build. Mater. 2017, 157, 96–107. [Google Scholar] [CrossRef]
- De Vries, P. Concrete recycled: Crushed concrete aggregate. In Proceedings of the International Conference: Concrete in the Service of Mankind. I. Concrete for Environment Enhancement and Protection, Scotland, UK, 24–26 June 1996; pp. 121–130. [Google Scholar]
- EHE-08. Spanish Structural Concrete Code; Spanish Minister of Public Works: Madrid, Spain, 2008; 720p.
- Fiol, F.; Thomas, C.; Muñoz, C.; Ortega-López, V.; Manso, J. The influence of recycled aggregates from precast elements on the mechanical properties of structural self-compacting concrete. Constr. Build. Mater. 2018, 182, 309–323. [Google Scholar] [CrossRef]
- Hossein, M.; Tahir, M.M. Durability performance of concrete incorporating waste metalized plastic fibres and palm oil fuel ash. Constr. Build. Mater. 2018, 180, 92–102. [Google Scholar]
- Frazão, C.; Camões, A.; Barros, J.; Gonçalves, D. Durability of steel fiber reinforced self-compacting concrete. Constr. Build. Mater. 2015, 80, 155–166. [Google Scholar] [CrossRef]
- Alberti, M.G.; Enfedaque, A.; Gálvez, J.C. On the mechanical properties and fracture behavior of polyolefin fiber-reinforced self-compacting concrete. Constr. Build. Mater. 2014, 55, 274–288. [Google Scholar] [CrossRef]
- Alberti, M.G.; Enfedaque, A.; Gálvez, J.C. Comparison between polyolefin fibre reinforced vibrated conventional concrete and self-compacting concrete. Constr. Build. Mater. 2015, 85, 182–194. [Google Scholar] [CrossRef]
- Pons, O.; de la Fuente, A.; Aguado, A. The use of MIVES as a sustainability assessment MCDM method for architecture and civil engineering applications. Sustainability 2016, 8, 460. [Google Scholar] [CrossRef]
- Fib. Model Code 2010; Fédération Internationale du Béton fib/International Federation for Structural Concrete: Paris, France, October 2013; 434p. [Google Scholar]
- Reyes, E.; Gálvez, J.; Casati, M.; Cendón, D.; Sancho, J.; Planas, J. An embedded cohesive crack model for finite element analysis of brickwork masonry fracture. Eng. Fract. Mech. 2009, 76, 1930–1944. [Google Scholar] [CrossRef]
- Gálvez, J.; Planas, J.; Sancho, J.; Reyes, E.; Cendón, D.; Casati, M. An embedded cohesive crack model for finite element analysis of quasi-brittle materials. Eng. Fract. Mech. 2013, 109, 369–386. [Google Scholar] [CrossRef]
- Sancho, J.; Planas, J.; Cendón, D.; Reyes, E.; Gálvez, J. An embedded crack model for finite element analysis of concrete fracture. Eng. Fract. Mech. 2007, 74, 75–86. [Google Scholar] [CrossRef]
- Zollo, R. Fiber-reinforced concrete: An overview after 30 years of development. Cem. Concr. Compos. 1997, 19, 107–122. [Google Scholar] [CrossRef]
- DBV. Merkblatt Stahlfaserbeton Deutsche Beton Vereins; DBV: Berlin, Germany, 2001. [Google Scholar]
- Guide for the Design and Construction of Fiber-Reinforced Concrete Structures; CNR-DT 204; Consiglio Nazionale delle Riserche: Roma, Italy, 2006.
- Blanco, A.; Pujadas, P.; de la Fuente, A.; Cavalaro, S.; Aguado, A. Application of constitutive models in European codes to RC–FRC. Constr. Build. Mater. 2013, 40, 246–259. [Google Scholar] [CrossRef]
- Di Prisco, M.; Plizzari, G.; Vandewalle, L. Fibre reinforced concrete: New design perspectives. Mater. Struct. 2009, 42, 1261–1281. [Google Scholar] [CrossRef]
- Alberti, M.G.; Enfedaque, A.; Gálvez, J.C.; Reyes, E. Numerical modelling of the fracture of polyolefin fibre reinforced concrete by using a cohesive fracture approach. Compos. Part B Eng. 2017, 111, 200–210. [Google Scholar] [CrossRef]
- Enfedaque, A.; Alberti, M.; Gálvez, J.; Domingo, J. Numerical simulation of the fracture behaviour of glass fibre reinforced cement. Constr. Build. Mater. 2017, 136, 108–117. [Google Scholar] [CrossRef]
- Buyle, M.; Braet, J.; Audenaert, A. Life cycle assessment in the construction sector: A review. Renew. Sustain. Energy Rev. 2013, 26, 379–388. [Google Scholar] [CrossRef]
- Ortiz, O.; Castells, F.; Sonnemann, G. Sustainability in the construction industry: A review of recent developments based on LCA. Constr. Build. Mater. 2009, 23, 8–39. [Google Scholar] [CrossRef]
- ISO 14040. Environmental Management–Life Cycle Assessment–Principles and Framework; International Organization for Standardization ISO: London, UK, 2006; 20p. [Google Scholar]
- European Commission. International Reference Life Cycle Data System (ILCD) Handbook e General Guide for Life Cycle Assessment e Detailed Guidance; Institute for Environment and Sustainability: Ispra, Italy, 2010. [Google Scholar]
- Glass, J.; Dyer, T.; Georgopoulos, C.; Goodier, C.; Paine, K.; Parry, T.; Baumann, H.; Gluch, P. Future use of life-cycle assessment in civil engineering. ICE Construct. Mater 2013, 166, 204–212. [Google Scholar] [CrossRef]
- Asiedu, Y.; Gu, P. Product life cycle cost analysis: State of the art review. Ind. J. Prod. Res. 1998, 36, 883–908. [Google Scholar] [CrossRef]
- Cabeza, F.; Rincón, L.; Vilariño, V.; Castell, G. Life Cycle Assessment (LCA) and life Cycle Energy Analysis (LCEA) of buildings and the building sector: A review. Renew. Sustain. Energy Rev. 2014, 29, 394–416. [Google Scholar] [CrossRef]
- Allesch, A.; Brunner, P. Material flow analysis as a decision support tool for waste management: A literature review. J. Ind. Ecol. 2015, 19, 753–764. [Google Scholar] [CrossRef]
- Liu, L.; Issam, S.; Hermreck, C.; Chong, W. Integrating G2G, C2C and resource flow analysis into life cycle assessment framework: A case of construction steel’s resource loop. Resour. Conserv. Recycl. 2015, 102, 143–152. [Google Scholar]
- Marjaba, G.; Chidiac, S. Sustainability and resiliency metrics for buildings—Critical review. Build. Environ. 2016, 101, 116–125. [Google Scholar] [CrossRef]
- Quale, J.; Eckelman, M.; Williams, K.; Slodits, G. Construction matters: Comparing environmental impacts of building modular and conventional homes in the United States. J. Ind. Ecol. 2012, 16, 243–253. [Google Scholar] [CrossRef]
- Malin, N. Life cycle assessment for whole buildings: Seeking the holy grail. Build. Des. Constr. 2005, 46, 6–11. [Google Scholar]
- Kohler, N.; Moffatt, S. Life-cycle analysis of the built environment. Sustain. Build. Constr. 2003, 26, 17–21. [Google Scholar]
- San-Jose, J.; Garrucho, I. A system approach to the environmental analysis industry of buildings. Build. Environ. 2010, 45, 673–683. [Google Scholar] [CrossRef]
- San-Jose, J.; Cuadrado, J. Industrial building design stage based on a system approach to their environmental sustainability. Constr. Build. Mater. 2010, 24, 438–447. [Google Scholar] [CrossRef]
- Reyes, J.; San-Jose, J.; Cuadrado, J.; Sancibrian, R. Health & Safety criteria for determining the value of sustainable construction projects. Saf. Sci. 2014, 62, 221–232. [Google Scholar]
- San-José, J.T.; Losada, R.; Cuadrado, J.; Garrucho, I. Approach to the quantification of the sustainable value in industrial buildings. Build. Environ. 2007, 42, 3916–3923. [Google Scholar] [CrossRef]
- Pardo-Bosch, F.; Aguado, A. Investment priorities for the management of hydraulic structures. Struct. Infrastruct. Eng. 2015, 11, 1338–1351. [Google Scholar] [CrossRef]
- De la Fuente, A.; Armengou, J.; Pons, O.; Aguado, A. Multi-criteria decision-making model for assessing the sustainability index of wind-turbine support systems: Application to a new precast concrete alternative. J. Civ. Eng. Manag. 2017, 23, 194–203. [Google Scholar] [CrossRef]

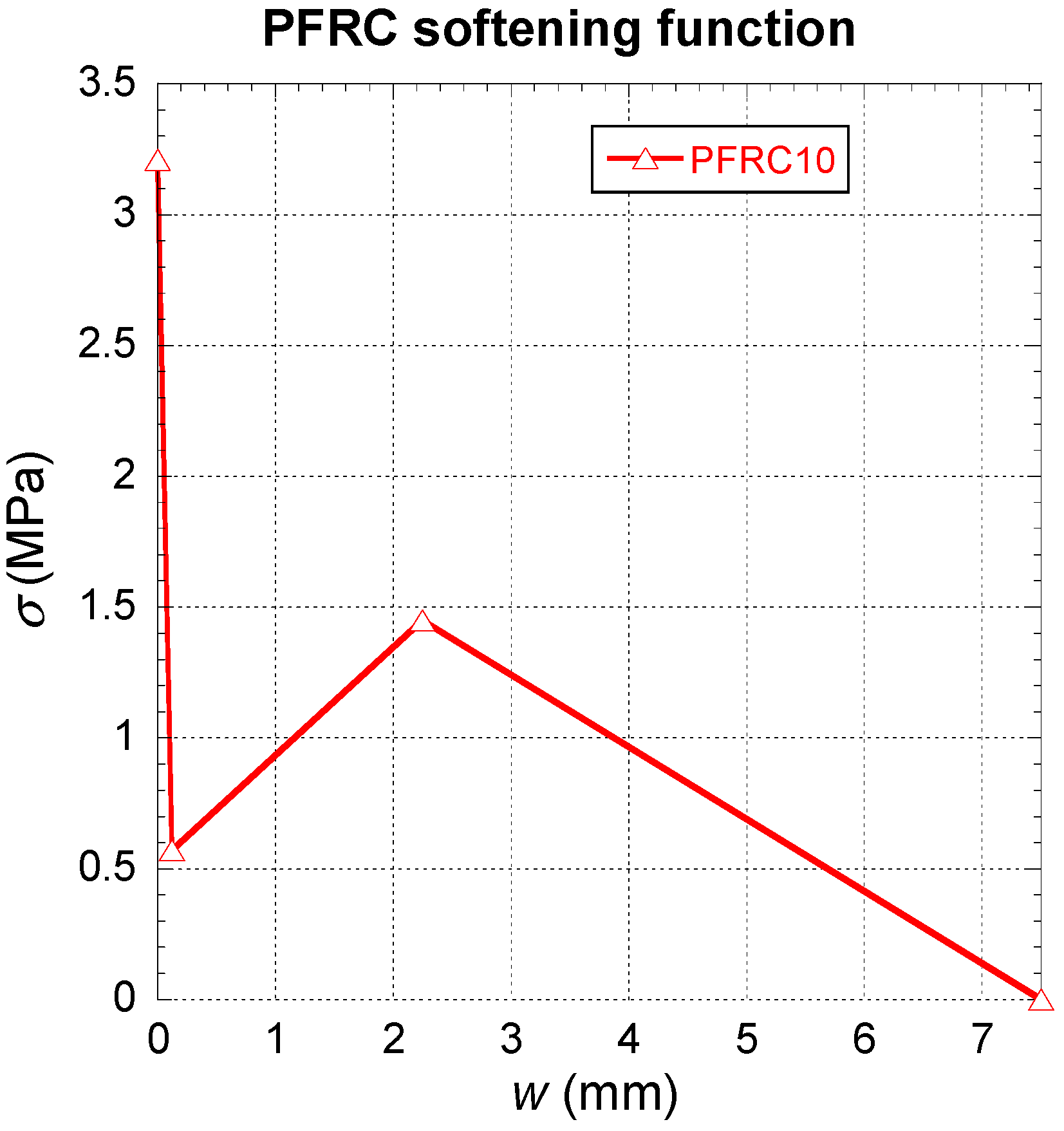

| Density (kg/m3) | Length (mm) | Equivalent Diameter (mm) | Tensile Strength (MPa) | Elastic Modulus (GPa) | Fibres Per kg | Ultimate Strain (%) |
|---|---|---|---|---|---|---|
| 910 | 60 | 0.903 | 400 | 9 | 27,000 | 20 |
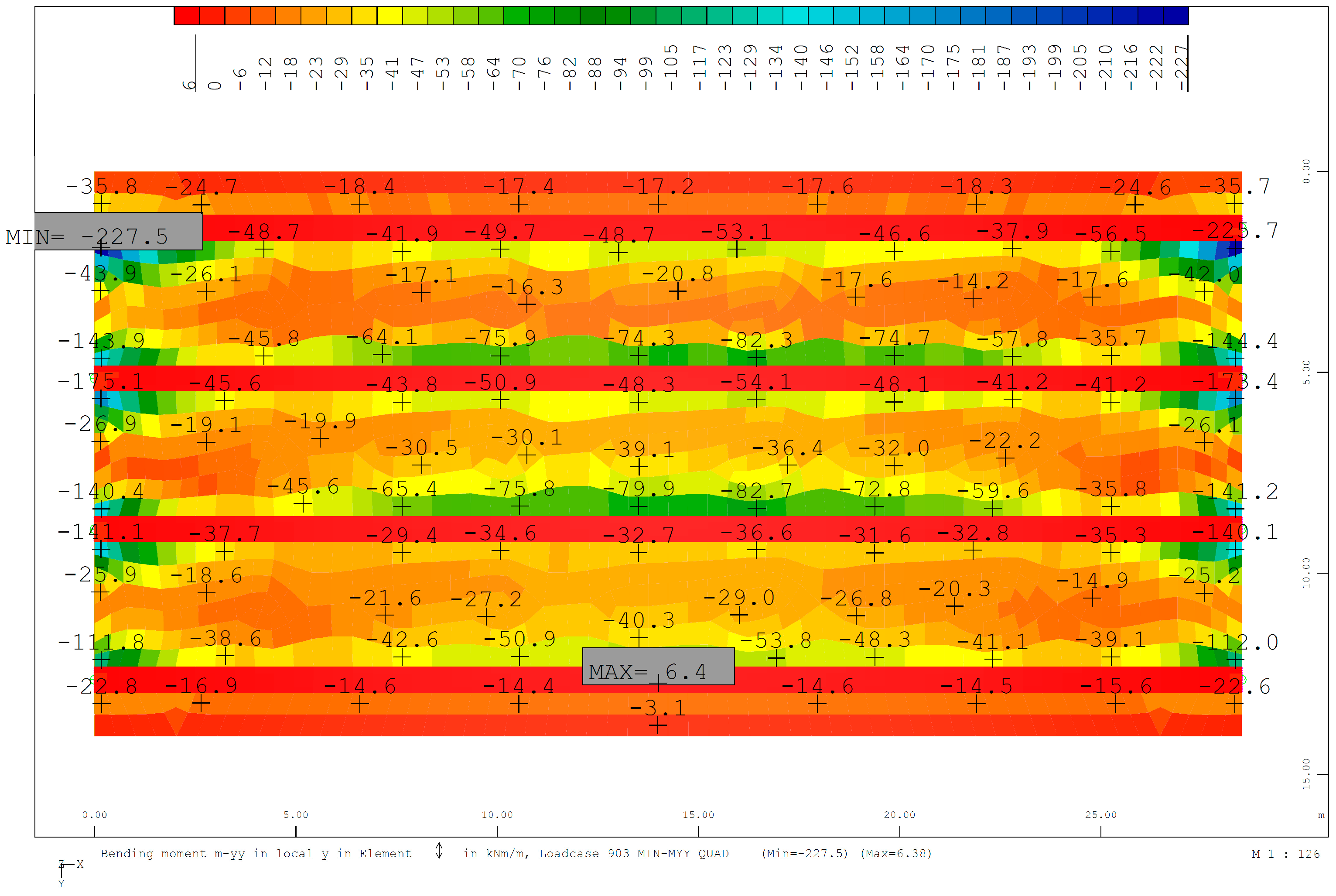
| Design Case: M+yy | Design Case: M−yy | |||||||
|---|---|---|---|---|---|---|---|---|
| Calc. Point | M+yy,max (mkN/m) | RC | PFRC 10 | M−yy,max (mkN/m) | RC | PFRC 10 | ||
| Reinforcement | Reduction Feasible? | Reinforcement | Reinforcement | Reduction Feasible? | Reinforcement | |||
| P1 | 80.5 | Ø16 @ 20 cm | - | - | −160.0 | Ø20 @ 15 cm | - | - |
| P2 | 57.8 | Ø16 @ 30 cm | - | - | −51.7 | Ø16 @ 30 cm | - | - |
| P3 | 83.0 | Ø16 @ 20 cm | - | - | −163.2 | Ø20 @ 15 cm | - | - |
| P4 | 86.2 | Ø16 @ 20 cm | - | - | −36.3 | Ø16 @ 30 cm | - | - |
| P5 | 90.4 | Ø16 @ 15 cm | Yes | Ø16 @ 20 cm | −20.8 | Ø16 @ 30 cm | - | - |
| P6 | 86.8 | Ø16 @ 20 cm | - | - | −42.0 | Ø16 @ 30 cm | - | - |
| P7 | 105.3 | Ø16 @ 15 cm | Yes | Ø16 @ 20 cm | −101.7 | Ø16 @ 15 cm | Yes | Ø16 @ 20 cm |
| P8 | 68.7 | Ø16 @ 20 cm | Yes | Ø16 @ 30 cm | −76.8 | Ø16 @ 20 cm | Yes | Ø16 @ 30 cm |
| P9 | 102.9 | Ø16 @ 15 cm | Yes | Ø16 @ 20 cm | −98.1 | Ø16 @ 15 cm | Yes | Ø16 @ 20 cm |
| P10 | 59.5 | Ø16 @ 30 cm | - | - | −114.3 | Ø16 @ 15 cm | - | - |
| P11 | 87.2 | Ø16 @ 20 cm | - | - | −51.5 | Ø16 @ 30 cm | - | - |
| P12 | 60.7 | Ø16 @ 20 cm | Yes | Ø16 @ 30 cm | −118.5 | Ø20 @ 20 cm | Yes | Ø16 @ 15 cm |
| P13 | 86.9 | Ø16 @ 20 cm | - | - | −22.9 | Ø16 @ 30 cm | - | - |
| P14 | 120.8 | Ø20 @ 20 cm | Yes | Ø16 @ 15 cm | −36.5 | Ø16 @ 30 cm | - | - |
| P15 | 87.1 | Ø16 @ 20 cm | - | - | −26.1 | Ø16 @ 30 cm | - | - |
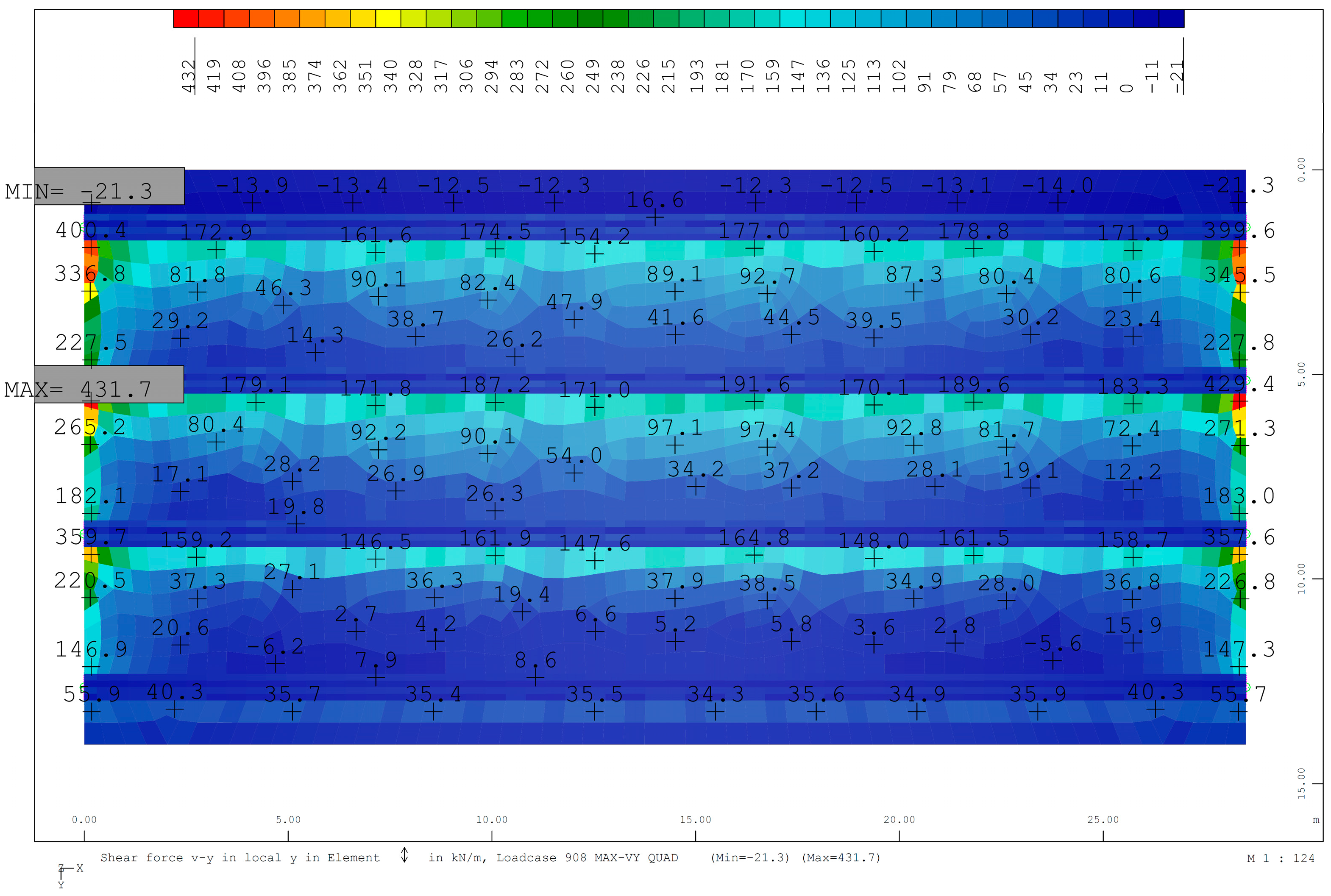
| Design Case: Vyy (PFRC) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Calc. Point | |Vyy,max| (kN/m) | Longitudinal Reinforcement | RC | PFRC 10 | |||||
| VRd,c (kN/m) | VRd,s (kN/m) | Reinforcement ([cm2/m]/mL) | fFtuk (MPa) | VRd,F (kN/m) | VRd,s (kN/m) | Reinforcement ([cm2/m]/mL) | |||
| P1 | 211.2 | Ø20 @ 15 cm | 162.7 | 48.4 | 2.4 | 0.355 | 211.2 | - | No reinforc. |
| P2 | 168.6 | Ø16 @ 30 cm | 111.7 | 56.8 | 2.7 | 0.728 | 168.6 | - | No reinforc. |
| P3 | 216.8 | Ø20 @ 15 cm | 162.7 | 54.1 | 2.6 | 0.409 | 216.8 | - | No reinforc. |
| P7 | 212.1 | Ø16 @ 20 cm | 140.8 | 71.3 | 3.4 | 1.104 | 214.1 | - | No reinforc. |
| P8 | 190.0 | Ø16 @ 30 cm | 127.9 | 62.1 | 3.0 | 1.147 | 188.9 | 1.1 | 0.1 |
| P9 | 208.6 | Ø16 @ 20 cm | 140.8 | 67.8 | 3.3 | 1.000 | 208.6 | - | No reinforc. |
| P10 | 224.3 | Ø16 @ 15 cm | 140.8 | 83.5 | 4.0 | 0.911 | 224.3 | - | No reinforc. |
| P11 | 181.8 | Ø16 @ 30 cm | 111.7 | 70.1 | 3.4 | 0.991 | 181.8 | - | No reinforc. |
| P12 | 228.7 | Ø16 @ 15 cm | 147.9 | 80.9 | 3.9 | 0.985 | 228.7 | - | No reinforc. |
| Reinforced Concrete | PFRC 10 | |||||||
|---|---|---|---|---|---|---|---|---|
| Bending | Stress | Shear | Stress | Bending | Stress | Shear | Stress | |
| Centre | 8.6 | M+ | 2.3 | Vyy | 7.5 | M+ | 0 | Vyy |
| Sides | 8.1 | M+ | 2.9 | Vyy | 7.2 | M+ | 0.2 | Vyy |
| Centre | 6.1 | M− | 2.3 | Vyy | 5.7 | M− | 0 | Vyy |
| Sides | 9.7 | M− | 2.9 | Vyy | 8.9 | M− | 0.2 | Vyy |
| Partial reinforcement | 15.6 | 5.0 | 14.1 | 0.1 | ||||
| Total reinforcement | ρ | 20.6 | ρ | 14.2 | ||||
| Requirement | (R. Weights) | Criteria | (C. Weights) | Indicators | (I. Weights) | |
|---|---|---|---|---|---|---|
| R1. Economic | 50% | C1 Total costs. Direct + Indirect | 40% | I1 Total costs including construction time | 100% | 100% |
| C2 Quality | 10% | I2 Non-quality costs | 100% | 100% | ||
| C3 Dismantling | 10% | I3 Dismantling costs | 100% | 100% | ||
| C4 Service-life | 40% | I4 Cost of service. Maintenance. Energy. Change of use. | 80% | 100% | ||
| I5 Resilience. Risk of disaster × cost of reconstruction + lack of use | 20% | |||||
| 100% | ||||||
| R2. Environmental | 30% | C5 Material consumption at construction time | 20% | I6 Cement | 25% | 100% |
| I7 Aggregates | 10% | |||||
| I8 Reinforcement (steel mesh, steel fibres and polyolefin fibres) | 15% | |||||
| I9 Water | 25% | |||||
| I10 Auxiliary Materials | 15% | |||||
| I11 Reused Material | 10% | |||||
| C5 Material consumption for maintenance | 20% | I6 Cement | 25% | 100% | ||
| I7 Aggregates | 10% | |||||
| I8 Reinforcement (steel mesh, steel fibres, polyolefin fibres) | 15% | |||||
| I9 Water | 25% | |||||
| I10 Auxiliary materials | 15% | |||||
| I11 Reused material | 10% | |||||
| C6 Emissions at construction time | 20% | I12 Global warming potential | 80% | 100% | ||
| I13 Total waste | 20% | |||||
| C6 Emissions for maintenance | 20% | I12 Global warming potential | 80% | 100% | ||
| I13 Total waste | 20% | |||||
| C7 Energy | 20% | I14 Embodied energy | 20% | 100% | ||
| I15 Construction energy | 40% | |||||
| I16 Service and maintenance energy | 40% | |||||
| 100% | ||||||
| R3. Social | 20% | C8 Third parties | 50% | I17 Comfort. Thermal, air and, among others, noise. | 10% | 100% |
| I18 Noise pollution. Construction | 15% | |||||
| I19 Particles pollution. Construction | 15% | |||||
| I20 Traffic disturbances. Construction | 15% | |||||
| I18 Noise pollution. Maintenance | 15% | |||||
| I19 Particles pollution. Maintenance | 15% | |||||
| I20 Traffic disturbances. Maintenance | 15% | |||||
| C9 Risks | 50% | I21 Health and safety during construction | 40% | 100% | ||
| I22 Health and safety during maintenance | 40% | |||||
| I23 Occupant safety. Risk of Disaster x cost of life disruption | 20% | |||||
| 100% | 100% |
| Steel Mesh | Polyolefin Fibres | |||||||
|---|---|---|---|---|---|---|---|---|
| REQUIREMENT | Score * Rweights | Score * Cweights | Score * Iweights | Score (0–100) | Score * Rweights | Score * Cweights | Score * Iweights | Score (0–100) |
| R1. Economic | 35.39 | 33.71 | 84.28 | 84 | 28.28 | 21.74 | 54.34 | 54 |
| 4.54 | 45.40 | 45 | 3.28 | 32.82 | 33 | |||
| 8.00 | 80.00 | 80 | 7.00 | 70.00 | 70 | |||
| 24.53 | 48.00 | 60 | 24.53 | 48.00 | 60 | |||
| 13.33 | 67 | 13.33 | 67 | |||||
| R2. Environmental | 21.15 | 17.55 | 10.20 | 41 | 15.87 | 13.71 | 10.20 | 41 |
| 5.67 | 57 | 5.67 | 57 | |||||
| 61.74 | 412 | 42.54 | 284 | |||||
| 7.34 | 29 | 7.34 | 29 | |||||
| 2.81 | 19 | 2.81 | 19 | |||||
| 0.00 | 0 | 0.00 | 0 | |||||
| 8.72 | 10.42 | 42 | 4.36 | 5.21 | 21 | |||
| 4.93 | 49 | 2.47 | 25 | |||||
| 12.35 | 82 | 6.17 | 41 | |||||
| 6.51 | 26 | 3.26 | 13 | |||||
| 9.38 | 63 | 4.69 | 31 | |||||
| 0.00 | 0 | 0.00 | 0 | |||||
| 15.12 | 57.60 | 72 | 10.42 | 39.69 | 50 | |||
| 18.00 | 90 | 12.40 | 62 | |||||
| 15.12 | 57.60 | 72 | 10.42 | 39.69 | 50 | |||
| 18.00 | 90 | 12.40 | 62 | |||||
| 14.00 | 20.00 | 100 | 14.00 | 20.00 | 100 | |||
| 40.00 | 100 | 40.00 | 100 | |||||
| 10.00 | 25 | 10.00 | 25 | |||||
| R3. Social | 14.90 | 36.50 | 10.00 | 100 | 14.22 | 34.70 | 10.00 | 100 |
| 15.00 | 100 | 15.00 | 100 | |||||
| 15.00 | 100 | 15.00 | 100 | |||||
| 15.00 | 100 | 15.00 | 100 | |||||
| 6.00 | 40 | 4.80 | 32 | |||||
| 6.00 | 40 | 4.80 | 32 | |||||
| 6.00 | 40 | 4.80 | 32 | |||||
| 38.00 | 40.00 | 100 | 36.40 | 40.00 | 100 | |||
| 16.00 | 40 | 12.80 | 32 | |||||
| 20.00 | 100 | 20.00 | 100 | |||||
| 71 | Total | 58 | Total | |||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Enfedaque, A.; Alberti, M.G.; Gálvez, J.C.; Rivera, M.; Simón-Talero, J.M. Can Polyolefin Fibre Reinforced Concrete Improve the Sustainability of a Flyover Bridge? Sustainability 2018, 10, 4583. https://doi.org/10.3390/su10124583
Enfedaque A, Alberti MG, Gálvez JC, Rivera M, Simón-Talero JM. Can Polyolefin Fibre Reinforced Concrete Improve the Sustainability of a Flyover Bridge? Sustainability. 2018; 10(12):4583. https://doi.org/10.3390/su10124583
Chicago/Turabian StyleEnfedaque, Alejandro, Marcos G. Alberti, Jaime C. Gálvez, Marino Rivera, and José M. Simón-Talero. 2018. "Can Polyolefin Fibre Reinforced Concrete Improve the Sustainability of a Flyover Bridge?" Sustainability 10, no. 12: 4583. https://doi.org/10.3390/su10124583
APA StyleEnfedaque, A., Alberti, M. G., Gálvez, J. C., Rivera, M., & Simón-Talero, J. M. (2018). Can Polyolefin Fibre Reinforced Concrete Improve the Sustainability of a Flyover Bridge? Sustainability, 10(12), 4583. https://doi.org/10.3390/su10124583







