Real Estate Soars and Financial Crises: Recent Stories
Abstract
1. Introduction
2. Data and Methodology
2.1. Data
2.2. Log-Periodic Power Law
2.3. Generalized Spillover Analysis
2.4. Granger Causality Test
3. Results and Discussion
3.1. Diagnosis of the Real Economy and the Real Estate Market
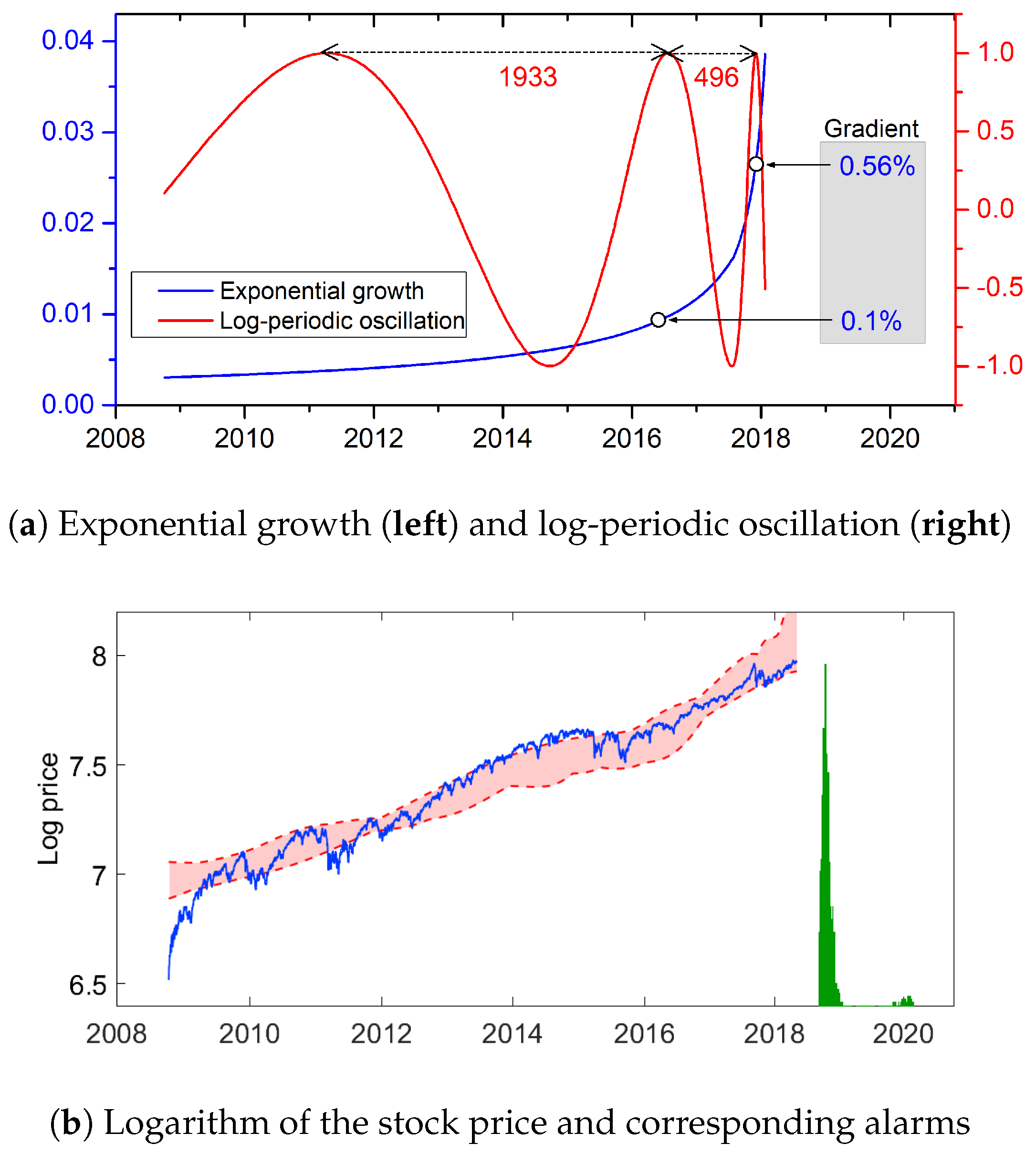
3.2. Risk of Financial Crash
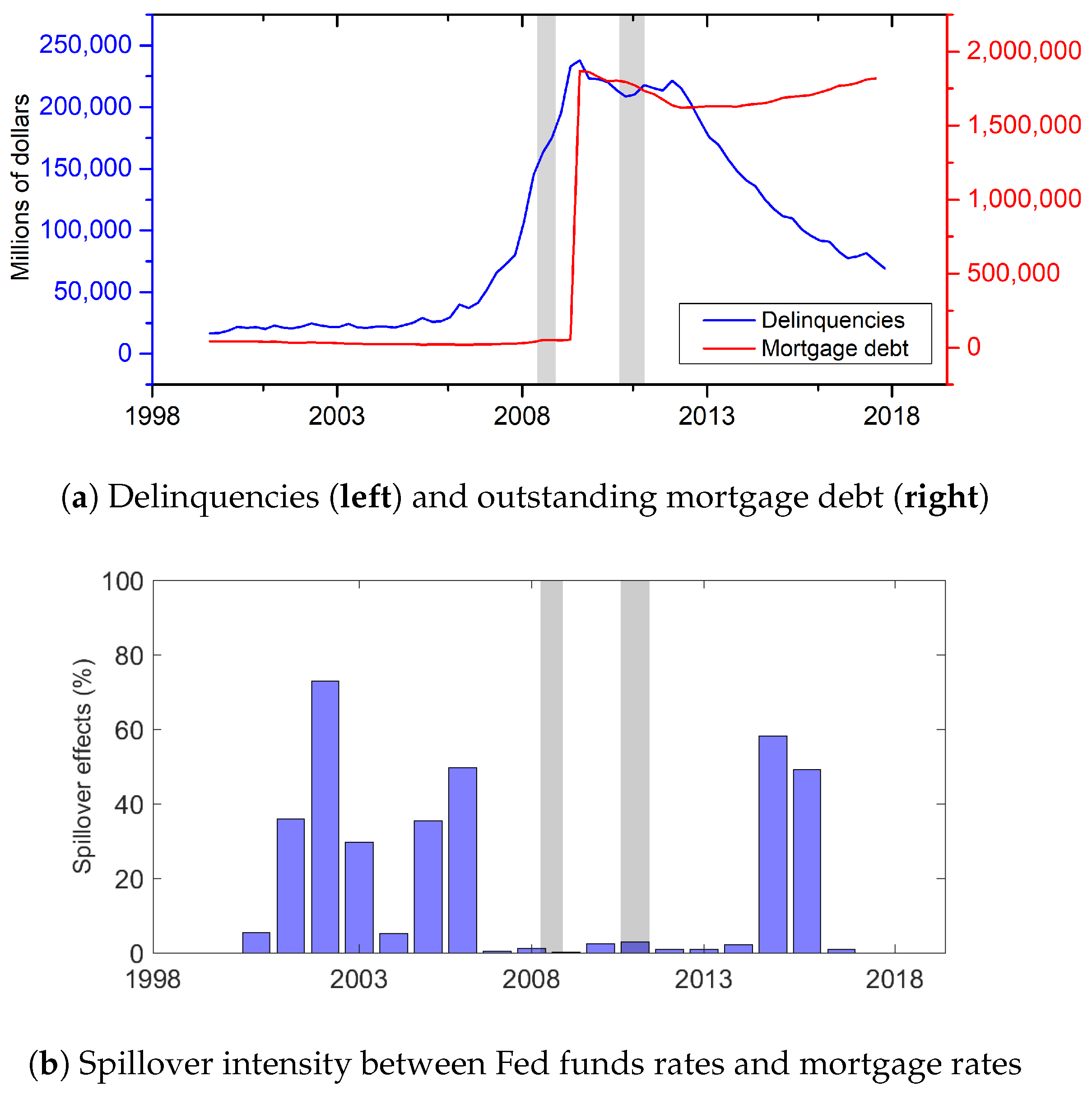
3.3. Impact of the Real Estate Market on a Financial Crash
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Farrell, C. Is the next recession on its way? Forbes, 3 August 2018. [Google Scholar]
- Bernstein, J. The question isn’t when is the next recession coming; It’s what are we going to do about it. Washington Post, 5 July 2018. [Google Scholar]
- Olick, D. Housing confidence hits record high as home prices skyrocket. Consumer News and Business Channel, 7 May 2018. [Google Scholar]
- Colvin, G. The end is near for the economic boom. Fortune, 19 July 2018. [Google Scholar]
- Gopal, P. This rare bear who called the crash warns housing is too hot again. Bloomberg, 23 January 2018. [Google Scholar]
- Herring, R.; Wachter, S. Bubbles in real estate markets. In Asset Price Bubbles: The Implications for Monetary, Regulatory, and International Policies; Hunter, W., Kaufman, G., Pomerleano, M., Eds.; MIT Press: Cambridge, MA, USA, 2003; pp. 217–230. [Google Scholar]
- Sornette, D.; Woodard, R. Financial bubbles, real estate bubbles, derivative bubbles, and the financial and economic crisis. In Econophysics Approaches to Large-Scale Business Data and Financial Crisis; Takayasu, M., Watanabe, T., Takayasu, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 101–148. [Google Scholar]
- Phillips, P.C.; Yu, J. Dating the timeline of financial bubbles during the subprime crisis. Quant. Econ. 2011, 2, 455–491. [Google Scholar] [CrossRef]
- Mishkin, F.S. Over the cliff: From the subprime to the global financial crisis. J. Econ. Perspect. 2011, 25, 49–70. [Google Scholar] [CrossRef]
- Shiller, R.J. The Subprime Solution: How Today’s Global Financial Crisis Happened, and What to Do About It; Princeton University Press: Princeton, NJ, USA, 2012; pp. 29–70. [Google Scholar]
- Campbell, J.Y.; Hentschel, L. No news is good news: An asymmetric model of changing volatility in stock returns. J. Financ. Econ. 1992, 31, 281–318. [Google Scholar] [CrossRef]
- Frankland, R.; Smith, A.; Wilkins, T.; Varnell, E.; Holtham, A.; Biffis, E.; Eshun, S.; Dullaway, D. Modelling extreme market events. A report of the benchmarking stochastic models working party. Br. Actuar. J. 2009, 15, 99–201. [Google Scholar] [CrossRef]
- Allen, F.; Morris, S.; Postlewaite, A. Finite bubbles with short sale constraints and asymmetric information. J. Econ. Theory 1993, 61, 206–229. [Google Scholar] [CrossRef]
- Brunnermeier, M.K. Bubbles. In Banking Crises; Springer: Berlin/Heidelberg, Germany, 2016; pp. 28–36. [Google Scholar]
- Johansen, A.; Ledoit, O.; Sornette, D. Crashes as critical points. Int. J. Theor. Appl. Financ. 2000, 3, 219–255. [Google Scholar] [CrossRef]
- Clark, A. Evidence of log-periodicity in corporate bond spreads. Phys. A 2004, 338, 585–595. [Google Scholar] [CrossRef]
- Filimonov, V.; Sornette, D. A stable and robust calibration scheme of the log-periodic power law model. Phys. A 2013, 392, 3698–3707. [Google Scholar] [CrossRef]
- Johansen, A.; Sornette, D. Critical crashes. Risk 1999, 12, 91–94. [Google Scholar]
- Johansen, A.; Sornette, D.; Ledoit, O. Predicting financial crashes using discrete scale invariance. J. Risk 1999, 1, 5–32. [Google Scholar] [CrossRef]
- Zhou, W.; Sornette, D. A case study of speculative financial bubbles in the South African stock market 2003–2006. Phys. A 2009, 388, 869–880. [Google Scholar] [CrossRef]
- Dai, B.; Zhang, F.; Targia, D.; Ahn, K. Forecasting financial crashes: Revisit to log-periodic power law. Complexity 2018, 4237471. [Google Scholar] [CrossRef]
- Geraskin, P.; Fantazzini, D. Everything you always wanted to know about log-periodic power laws for bubble modeling but were afraid to ask. Eur. J. Financ. 2013, 19, 366–391. [Google Scholar] [CrossRef]
- Sornette, D. Why Stock Markets Crash: Critical Events in Complex Financial Systems; Princeton University Press: Princeton, NJ, USA, 2017; Chapter 3; pp. 82–133. [Google Scholar]
- Zhou, W.; Sornette, D. Is there a real-estate bubble in the US? Phys. A 2006, 361, 297–308. [Google Scholar] [CrossRef]
- Jang, H.; Ahn, K.; Kim, D.; Song, Y. Detection and prediction of house price bubbles: Evidence from a new city. In Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018; Volume 10862, pp. 782–795. [Google Scholar]
- Zhou, W.; Sornette, D. 2000–2003 real estate bubble in the UK but not in the USA. Phys. A 2003, 329, 249–263. [Google Scholar] [CrossRef]
- Vandewalle, N.; Boveroux, P.; Minguet, A.; Ausloos, M. The crash of October 1987 seen as a phase transition: Amplitude and universality. Phys. A 1998, 255, 201–210. [Google Scholar] [CrossRef]
- Vandewalle, N.; Ausloos, M.; Boveroux, P.; Minguet, A. Visualizing the log-periodic pattern before crashes. Eur. Phys. J. B Condens. Matter Complex Syst. 1999, 9, 355–359. [Google Scholar] [CrossRef]
- Drozdz, S.; Ruf, F.; Speth, J.; Wójcik, M. Imprints of log-periodic self-similarity in the stock market. Eur. Phys. J. B Condens. Matter Complex Syst. 1999, 10, 589–593. [Google Scholar] [CrossRef]
- Feigenbaum, J.A. A statistical analysis of log-periodic precursors to financial crashes. Quant. Financ. 2001, 1, 346–360. [Google Scholar] [CrossRef]
- Feigenbaum, J.A.; Freund, P.G. Discrete Scale Invariance and the “Second Black Monday”. Mod. Phys. Lett. B 1998, 12, 57–60. [Google Scholar] [CrossRef]
- Drozdz, S.; Kwapien, J.; Oswiecimka, P. Criticality characteristics of current oil price dynamics. Acta Phys. Pol. A 2008, 114, 699–702. [Google Scholar] [CrossRef]
- Czarnecki, Ł; Grech, D.; Pamuła, G. Comparison study of global and local approaches describing critical phenomena on the Polish stock exchange market. Phys. A 2008, 387, 6801–6811. [Google Scholar] [CrossRef]
- Korzeniowski, P.; Kuropka, I. Forecasting the critical points of stock markets’ indices using log-periodic power law. Ekonometria 2013, 1, 100–110. [Google Scholar]
- Jacobsson, E. How to Predict Crashes in Financial Markets with the Log-Periodic Power Law. Master Dissertation, Department of Mathematical Statistics, Stockholm University, Stockholm, Sweden, 2009. [Google Scholar]
- Liberatore, V. Computational LPPL fit to financial bubbles. arXiv, 2010; arXiv:1003.2920. [Google Scholar]
- Cvijović, D.; Klinowski, J. Taboo search: An approach to the multiple minima problem. Science 1995, 267, 664–666. [Google Scholar] [CrossRef] [PubMed]
- Fantazzini, D. Modeling bubbles and anti-bubbles in bear markets. In The Handbook of Trading; McGRAW-HILL: New York, NY, USA, 2010; pp. 365–388. [Google Scholar]
- Filimonov, V.; Demos, G.; Sornette, D. Modified profile likelihood inference and interval forecast of the burst of financial bubbles. Quant. Financ. 2017, 17, 1167–1186. [Google Scholar] [CrossRef]
- Holt, J. A summary of the primary causes of the housing bubble and the resulting credit crisis: A non-technical paper. J. Bus. Inq. 2009, 8, 120–129. [Google Scholar]
- Wold, H. Causality and econometrics. Econometrica 1954, 22, 162–177. [Google Scholar] [CrossRef]
- Pesaran, H.H.; Shin, Y. Generalized impulse response analysis in linear multivariate models. Econ. Lett. 1998, 58, 17–29. [Google Scholar] [CrossRef]
- Diebold, F.X.; Yilmaz, K. Better to give than to receive: Predictive directional measurement of volatility spillovers. Int. J. Forecast. 2012, 28, 57–66. [Google Scholar] [CrossRef]
- Granger, C.W. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Chiou-Wei, S.Z.; Chen, C.F.; Zhu, Z. Economic growth and energy consumption revisited: Evidence from linear and nonlinear Granger causality. Energy Econ. 2008, 30, 3063–3076. [Google Scholar] [CrossRef]
- Sims, C.A. Macroeconomics and reality. Econometrica 1980, 48, 1–48. [Google Scholar] [CrossRef]
- Phillips, M. What’s the yield curve? ‘A powerful signal of recessions’ has wall street’s attention. New York Times, 5 June 2018. [Google Scholar]
- Ang, A.; Piazzesi, M.; Wei, M. What does the yield curve tell us about GDP growth? J. Econom. 2006, 131, 359–403. [Google Scholar] [CrossRef]
- Rudebusch, G.D.; Williams, J.C. Forecasting recessions: The puzzle of the enduring power of the yield curve. J. Bus. Econ. Stat. 2009, 27, 492–503. [Google Scholar] [CrossRef]
- Shiratsuka, S. The asset price bubble in Japan in the 1980s: Lessons for financial and macroeconomic stability. Bank Int. Settl. Pap. 2005, 21, 42–62. [Google Scholar]
- Kurz-Kim, J.R. Early warning indicator for financial crashes using the log periodic power law. Appl. Econ. Lett. 2012, 19, 1465–1469. [Google Scholar] [CrossRef]
- Johansen, A.; Sornette, D. Bubbles and anti-bubbles in Latin-American, Asian and Western stock markets: An empirical study. Int. J. Theor. Appl. Financ. 2001, 4, 853–920. [Google Scholar] [CrossRef]
- Brée, D.S.; Joseph, N.L. Testing for financial crashes using the log periodic power law model. Int. Rev. Financ. Anal. 2013, 30, 287–297. [Google Scholar] [CrossRef]
- Lin, L.; Ren, R.; Sornette, D. The volatility-confined LPPL model: A consistent model of ‘explosive’ financial bubbles with mean-reverting residuals. Int. Rev. Financ. Anal. 2014, 33, 210–225. [Google Scholar] [CrossRef]
- Johansen, A. Characterization of large price variations in financial markets. Phys. A 2003, 324, 157–166. [Google Scholar] [CrossRef]
- Christofi, A.; Christofi, P.; Malindretos, J. Lessons from the 2007–2008 financial crisis and action for the future. Int. J. Econ. Res. 2011, 8, 45–60. [Google Scholar]
- Jarocinski, M.; Smets, F. House Prices and the Stance of Monetary Policy; European Central Bank: Frankfurt, Germany, 2008. [Google Scholar]
- Taylor, J.B. Economic policy and the financial crisis: An empirical analysis of what went wrong. Crit. Rev. 2009, 21, 341–364. [Google Scholar] [CrossRef]
- Hagen, J.; Schuknecht, L.; Wolswijk, G. Government bond risk premiums in the EU revisited: The impact of the financial crisis. Eur. J. Political Econ. 2011, 27, 36–43. [Google Scholar] [CrossRef]
- Frutos, J.C.; Garcia-de Andoain, C.; Heider, F.; Papsdorf, P. Stressed Interbank Markets: Evidence From the European Financial and Sovereign Debt Crisis; European Central Bank: Frankfurt, Germany, 2016. [Google Scholar]
- Woo, S. STATA for Economic Analysis; Jiphil Media: Seoul, Korea, 2016; Chapter 15; pp. 255–264. [Google Scholar]

| Frequency | Mean | Std | Max | Min | Skewness | Kurtosis | |
|---|---|---|---|---|---|---|---|
| S&P500 (%) | Daily | 0.0146 | 1.2120 | 10.9572 | −9.4695 | −0.2083 | 11.6945 |
| Yield spread (%) | Daily | 1.4237 | 0.8897 | 2.9100 | −0.5200 | −0.4182 | 2.1092 |
| CSI (%) | Monthly | 0.3125 | 0.8094 | 2.0170 | −2.2844 | −0.6118 | 3.2687 |
| CPI (%) | Monthly | 0.1791 | 0.3035 | 1.3675 | −1.7864 | −1.3296 | 12.1315 |
| Fed funds rate (%) | Monthly | 1.7591 | 2.0121 | 6.5400 | 0.0700 | 1.0421 | 2.6726 |
| Mortgage rate (%) | Monthly | 5.2923 | 1.2998 | 8.5150 | 3.3450 | 0.3286 | 2.1742 |
| Delinquencies (m$) | Quarterly | 98,555 | 76,937 | 237,837 | 16,632 | 0.4733 | 1.6969 |
| Mortgage debt (m$) | Quarterly | 794,479 | 846,463 | 1,870,040 | 20,363 | 0.2039 | 1.0575 |
| A | B | C | ||||
|---|---|---|---|---|---|---|
| 8.22 | −0.001 | 2832.52 | 0.85 | −0.07 | 5.90 | 0.95 |
| Period | Causal Direction | Chi-Square | |
|---|---|---|---|
| Whole-period | 2000.01–2018.01 | S&P500 → CSI | 9.42 ** |
| CSI → S&P500 | 2.33 | ||
| Pre-crisis | 2003.03–2008.08 | S&P500 → CSI | 3.04 |
| CSI → S&P500 | 14.05 *** | ||
| 2003.03–2008.07 | S&P500 → CSI | 3.18 | |
| CSI → S&P500 | 13.68 *** | ||
| 2003.03–2008.06 | S&P500 → CSI | 0.48 | |
| CSI → S&P500 | 13.34 *** | ||
| 2003.03–2008.05 | S&P500 → CSI | 0.33 | |
| CSI → S&P500 | 13.80 *** | ||
| In-crisis | 2008.09–2009.05 | S&P500 → CSI | 0.71 |
| CSI → S&P500 | 1.03 | ||
| Post-crisis | 2009.06–2018.01 | S&P500 → CSI | 14.23 *** |
| CSI → S&P500 | 1.88 | ||
| 2009.07–2018.01 | S&P500 → CSI | 14.12 *** | |
| CSI → S&P500 | 1.48 | ||
| 2009.08–2018.01 | S&P500 → CSI | 14.92 *** | |
| CSI → S&P500 | 1.31 | ||
| 2009.09–2018.01 | S&P500 → CSI | 14.78 *** | |
| CSI → S&P500 | 1.31 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jang, H.; Song, Y.; Sohn, S.; Ahn, K. Real Estate Soars and Financial Crises: Recent Stories. Sustainability 2018, 10, 4559. https://doi.org/10.3390/su10124559
Jang H, Song Y, Sohn S, Ahn K. Real Estate Soars and Financial Crises: Recent Stories. Sustainability. 2018; 10(12):4559. https://doi.org/10.3390/su10124559
Chicago/Turabian StyleJang, Hanwool, Yena Song, Sungbin Sohn, and Kwangwon Ahn. 2018. "Real Estate Soars and Financial Crises: Recent Stories" Sustainability 10, no. 12: 4559. https://doi.org/10.3390/su10124559
APA StyleJang, H., Song, Y., Sohn, S., & Ahn, K. (2018). Real Estate Soars and Financial Crises: Recent Stories. Sustainability, 10(12), 4559. https://doi.org/10.3390/su10124559





