1. Introduction
The issue of global warming has become one of the grave challenges facing human beings in the 21st century. The emissions of green-house gases and the shortage of resources have already attracted attention from international organizations. Environmental protection and energy consumption reduction have become a critical means to promote sustainable development of the global economy, and countries are actively taking measures to deal with them [
1]. Currently, international organizations have introduced a series of conventions and policies for curbing emissions of greenhouse gases such as
United Nations’ Framework Convention on Climate Change,
Kyoto Protocol. The
Paris Agreement which came into force on 4 November, 2016, requires industrialized nations to cut the emission of greenhouse gases and aims to control the rise in global average temperature within 2 degrees Celsius [
2]. Restraints on carbon emissions can be a fundamental approach to curb greenhouse gases, so governments are actively controlling the carbon emissions produced by enterprises in the production process. For example,
European Union Emissions Trading System (EU-ETS) which was implemented in 2005, has set a cap on corporate carbon emissions [
3]; while Sweden, Finland, Denmark and other nations levy carbon tax to reduce carbon emissions from enterprises [
4,
5]. The Chinese government has also made commitments to reduce CO
2 emissions based on unit GDP by 40%–50% in 2020 as opposed to 2005. In order to fulfill this commitment, China launched the carbon market in 2017 [
6]. Enterprises attach great importance to the control of carbon emissions because the constraints of carbon emissions can tremendously affect commercial profits, competitive advantages and decisions on production and operations of enterprises [
7,
8]. To curb carbon emissions, enterprises should emphasize the operations decisions in production and management.
The growing salience of environmental problems prompts the manufacturers to make environment-friendly products and integrate remanufacturing into their production. In February, 2017, American Remanufacturing Industrial Association issued
Technical Specifications for Remanufacturing Processes, upgrading and categorizing some relevant remanufacturing concepts and definitions. It regulates that the quality of remanufactured products should not be inferior to that of new products (“like new” or “better than new”), and their performance and quality should be guaranteed. Actually, remanufacturing may improve customer services and enhance economic and competitive advantages of enterprises [
9]. Remanufacturing brings economic and environmental benefits to enterprises [
2]. Governments and enterprises now attach greater importance to remanufacturing. For instance, Waste Electrical and Electronic Equipment (WEEE) in Europe provided impetus to implementation of reverse logistics, requiring the manufacturer to focus on remanufacturing so as to reduce the demand for natural resources and to cut waste generation [
10]. Based on the statistics of
European Remanufacturing Network (ERN), European remanufacturing had covered such fields as aerospace, vehicles, electronics, mechanics and medical equipment till the end of 2015, with an approximate value of 30 billion Euros. The figure is estimated to reach 100 billion Euros by 2030. Remanufacturing has become a critical part of future manufacturing development in European Union. As an advocate of remanufacturing, China formulated and issued
High End Intelligent Remanufacturing Action Plan (2018–2020) on 31 October, 2017, aiming to achieve a value of 200 billion RMB in remanufacturing by 2020. A number of companies combine recycling used products with remanufacturing. For example, Dell, Apple and Hewlett Packard encourage their customers to cooperate in the recycling of second-hand electronics and have constructed a system of reverse logistics, and Samsung promoted remanufactured smart phones in 2016 [
11,
12]. A host of scholars have investigated closed-loop supply chains involved in recycling processes, such as recycling motivation, the choice of products for recycling, pricing and coordination, reverse logistic network design, and channel management [
13,
14,
15,
16,
17]. To follow the theme of global energy conservation and emissions reduction, some scholars focus on the issue of carbon emissions and incorporate the closed-loop supply chains with carbon quota, carbon trade and government subsidies in their research [
18,
19,
20]. Governments are the subjects who regulate carbon emissions and play a pivotal role in the overall supply chains.
In addition to governments, enterprises should also assume social responsibility of environmental protection. Corporate social responsibility (CSR) is inseparable from the environment, society, economy, and stakeholders. Amaeshi et al. [
21] showed that corporate social responsibility has become an increasingly prevalent operations philosophy in developed economies and moves towards globalization through capitalist practices represented by multinational corporations. An array of companies have implemented CSR in supply chains, such as Apple, Hewlett Packard, Adidas, Wal-Mart, Nike and many others [
22]. Actually, enterprises participate in events of corporate social responsibility in order to boost their reputations, address management risks and create customer loyalty [
23]. CSR may help companies to boost sales and raise capital and brand cognition, thus offering opportunities for enterprises to generate value. In close-loop supply chains, CSR increases the recycling rate of used products, leading corporations to achieve greater profits [
24]. Integrating CSR into the classic framework of managing closed-loop supply chains and considering its impacts on operations of supply chains are meaningful theoretically and empirically. Currently, studies of closed-loop supply chains associated with CSR focus on pricing strategies and coordination, whereas the environmental benefits from CSR have rarely been quantitatively examined. To bridge this gap, this article considers the optimal decisions of closed-loop supply chains with CSR under the backdrop of constraints of carbon emissions. To manifest impacts of carbon emissions on corporate economy, this article introduces government reward and punishment mechanisms to restrain carbon emissions from enterprises. This complements the existing literature on closed-loop supply chains and investigates impacts of CSR strength on carbon emissions from enterprises, thus further demonstrating environmental effects of CSR. Additionally, enterprises with social responsibility should show concern for social welfare, and thus, this article explores the roles of constraints of carbon emissions and CSR and analyses the associations among governments, enterprises, society and environment, thereby providing insights for governments and enterprises. This article attempts to address the following questions.
In closed-loop supply chains with social responsibility, how do the constraints of carbon emissions affect carbon emissions from enterprises? How do governments formulate the most rational policy on carbon emissions?
With the constraints of carbon emissions, how does CSR affect product pricing and recycling strategies? Can enterprises with CSR earn greater profits?
How is CSR associated with carbon emissions? How does CSR affect carbon emissions?
How do constraints of carbon emissions and CSR influence social welfare? How do recycling rates and carbon emissions change in the model of maximizing social welfare?
The organization of this article is as follows. Part 2 presents a literature review. Part 3 describes the model parameters setting and assumptions in three cases: the benchmark model; the model of CSR; and the model of maximizing social welfare. In Part 4, we solve the optimal decision of the three cases and the proposed three main propositions. In Part 5, impacts of main parameters for optimal decisions are analyzed. In Part 6, numerical examples and analyses are deployed to test the major propositions and findings. Part 7 draws conclusions and points out the limitations of this article and our future research orientations.
2. Literature Review
This article involves three strands of research, namely closed-loop supply chains, carbon emissions, social responsibility, and sustainable supply chain.
2.1. Closed-Loop Supply Chains
At present, there is plentiful literature on closed-loop supply chains. Many scholars have studied dual-channel closed-loop supply chains from different perspectives, such as production plans and inventory management, reverse logistics network design and channel management. In these studies, pricing and recycling strategies in closed-loop supply chains are a main research orientation for the majority of scholars, which can be one of the main contents in this article too. A multitude of scholars consider pricing and coordination in closed-loop supply chains under different channel strategies. To illustrate, Xie and Chen [
25] calculated optimal prices, sales and recycling rates when the dual-channel supply chain system is stable. Xie et al. [
26] examined the pricing decisions and contract coordination in dual-channel closed-loop supply chains and obtain the optimal online and offline prices, wholesale prices and advertising costs. Saha et al. [
27] adopted the reward-driven policy to obtain used products particularly for remanufacturing and consider the optimal pricing decisions in the supply chain structure consisting of manufacturers, third-party reclaimers and retailers. Giri et al. [
28] studied dual-channel closed-loop supply chains in which the manufacturer sells products to customers through the traditional retail and internet channels and analyzed pricing and profit decisions in supply chains from five distinct perspectives. Gan et al. [
29] discussed the features of closed-loop supply chains made up of manufacturers, retailers and collectors in the decentralized channel and determined the optimal pricing decisions of retailers, collectors and manufacturers in relation to products with short life cycles. Some research has been concerned with pricing and recycling strategies in closed-loop supply chains in the context of competition and cooperation. Jena and Sarmah [
30] examine closed-loop supply chains composed of two competitive manufacturers and construct mathematical models with optimal decisions in three different cases: non-cooperative system, channel cooperative system and global cooperative system, and the results show that the global cooperative system is optimal. Wu et al. [
31] looked at production and coordination strategies of the closed-loop supply chain consisting of one manufacturer and two competing retailers when the remanufacturing cost is interrupted. They showed that the manufacturer modifies the production strategy when there is large scale interruption and that the revenue sharing contract can coordinate CLSC effectively. Xiong et al. [
32] analyzed remanufacturing performance when the manufacturer competes with the supplier in decentralized supply chains and showed that the consumers favor the manufacturer engaging in remanufacturing when the unit remanufacturing cost is high. Zheng et al. [
33] investigated the impacts of forward channel competition and power structure on a CLSC composed of manufacturers, retailers and collectors, and they also explore the pricing strategies in the centralized and decentralized models relating to power structures of different channels. Wang et al. [
34] investigated competitive recycling markets in closed-loop supply chains and noted that the manufacturer always chooses to recycle and remanufacture used products, while the recycling channel depends on the unit cost of recycling and compensation for outsourcing.
Much research on pricing and recycling decisions of closed-loop supply chains incorporates government subsidies and carbon tax on consumer behavior. Abbey et al. [
35] examined consumer views on remanufactured products in closed-loop supply chains and the results show that discounts exert a positive effect continuously on attracting consumers of remanufactured and green consumers believe that remanufactured products are more appealing. Miao et al. [
36] explored the manufacturer’s optimal pricing and production decisions with carbon tax and trade plans, and the results show that carbon regulations can boost the sales of remanufactured products and reduce the demand for new products, and the negative effects of implementing carbon regulations on the manufacturer’s profits can decline with the policy of government subsidies. Dai et al. [
37] constructed CLSL with government subsidies under the constraints of carbon emissions. Manufacturers sell new and remanufactured products through direct and retail channels. Feng and Govindan [
17] examined the strategic planning of optimal design and coordination decisions of CLSC. They constructed a model of recycling channel depending on consumer willingness and show that consumer preference plays a vital role in the coordination mechanism selection of dealers.
The discussion above shows that the recent research on pricing decisions and coordination centers on dual-channel or decentralized channels, which is the result of rapid development in e-commerce. Few studies are concerned with decisions on interruptions of closed-loop supply chains, and much research involves revenue sharing contracts which coordinate conflicts in supply chains. A growing number of studies in pricing and recycling strategies in closed-loop supply chains integrates government subsidies with carbon tax, considering consumer behavior, which can be the future research orientation for pricing decisions in closed-loop supply chains. Therefore, under the constraints of carbon emissions government reward and punishment, the study of the closed-loop supply chains with social responsibility conforms to the trend and expands the existing research.
2.2. Constraints of Carbon Emissions
With the increasing severity of global climate change, researchers integrate environment impacts into the operations strategies of low-carbon enterprises, investigating the role of carbon emission policy in managing supply chains. In terms of pricing and the strategy of emission reduction, Hammami et al. [
38] developed a multiple-layer production-inventory model with carbon emission constraints and compared the impacts of individual carbon emission caps and global emission caps on the total carbon emissions. Cheng et al. [
39] constructed a nonlinear planning model to analyze the impacts of carbon emission regulations on the inventory routing problem (IRP) and note that a smaller carbon quota may lead to greater carbon emissions. Qi et al. [
40] investigated the optimal pricing decisions with the limits of total carbon emissions of supply chains consisting of one supplier and two competitive retailers. Yang et al. [
41] considered the impacts of cap-and-trade and consumer preference on the manufacturer’s channel choices, and with the rise of the consumer’s online shopping, the government can formulate stricter policies of carbon emissions. In terms of collaboration among members and coordination of channels, Yang et al. [
42] compared four low-carbon policies (the basic model, the carbon emission model, carbon trade model, and carbon tax model) and showed that the policy of trading carbon emissions can be an effective mechanism to reduce carbon emissions in supply chains. Ding et al. [
43] developed a framework of collaborative supply chains with environmental constraints and carbon emission caps and found that collaboration among supply chain members can boost environmental performance remarkably. Xu et al. [
44] looked at production, pricing, and coordination of supply chains and showed that the manufacturer can apply green technology to cut carbon emissions, suggesting that wholesale prices and cost-sharing contracts may coordinate supply chains. Ji et al. [
45] introduced consumer preference for low carbon into the dual-channel supply chains and studied the impacts of low-carbon collaboration between the manufacturer and the retailer on channels. Zhou et al. [
46] examined whether the policy of carbon tax can change pricing decisions and social welfare of supply chain members and show that the carbon tax regulation with the government’s optimal tax rates can improve social welfare effectively.
Compared with traditional manufacturing, remanufacturing is conducive to energy conservation and emissions reduction [
47,
48], and therefore, research is centered on carbon emissions in closed-loop supply chains. Chang et al. [
49] showed that only the carbon quota and carbon trade mechanism in the alternative demand market can induce enterprises to choose low-carbon remanufacturing technology by studying production and remanufacturing decisions of enterprises. Miao et al. [
36] looked at trade-old-for-new (TON) with carbon emission regulations and showed that the introduction of carbon emission regulations can accelerate the sales of remanufactured products and curb the demand for new products. Bazan et al. [
20] examined the impacts of energy and carbon emissions on models of supply chains in closed-loop supply chains under different coordination mechanisms. Wang et al. [
2] investigated the optimal production decision of enterprises with carbon emission constraints and capital constraints, and the results show that capital constraints can encourage the manufacturer to remanufacture at a higher level of quality and significantly reduce carbon emissions. Chai et al. [
50] explored the possibility of achieving profitability in a single period when a monopoly manufacturer is involved in production and remanufacturing, and the results show that the control of total carbon emissions and carbon trade are of great significance in remanufacturing in the normal and green markets. When there are differences between new and remanufactured products, Wang et al. [
51] investigated the impacts of carbon tax on the optimal production decisions on manufacturing and remanufacturing and showed that the government can choose proper carbon tax to stimulate the manufacturer to invest in technologies that help reduce carbon emissions. With product differences, Turki et al. [
48] studied random machine faults and varying random demands of two products and showed that lower carbon emission caps or higher carbon trading prices can boost recycling and remanufacturing and curb carbon emissions from enterprises. Kundu et al. [
52] assumed that the quality of remanufactured products is inferior and established models under different carbon regulation mechanisms when the company sold new products and remanufactured products in two different markets. Haddad-Sisakht et al. [
5] investigated the uncertainty of demand and carbon tax rates, and found that capacity adjustment of modes of transportation can replace the construction of additional facilities to cope with the uncertainty of carbon taxes. Zhou et al. [
46] considered the uncertainty of quality in closed-loop supply chains with carbon emission constraints and showed that taking into account the impact of uncertain quality on carbon emissions can boost corporate profits and curb the total carbon emissions.
It can be seen that with a growing body of literature on closed-loop supply chains, some researchers consider the uncertainty of demand, tax rate and quality, while others integrate capital constraints and consumer preferences. However, this article introduces CSR in the model to explore impacts of CSR on carbon emissions, which is the particular contribution of this study to the current literature.
2.3. Social Responsibility and Sustainable Supply Chain
CSR is not only about corporate value, but also the embodiment of corporate sustainable development. Some literature has reported quantitative and empirical studies of applications and impacts of CSR. Carter and Jennings [
53] investigated the value of CSR in decisions in supply chains through case studies and found that a supplier with CSR can draw more attention from the society. CSR is generally associated with corporate performance and Carter and Jennings [
54] pointed out that the implementation of CSR tends to contribute to the performance of suppliers. Asgary et al. [
55] investigated into the economic impacts of CSR on operations of supply chains of multinational corporations and evaluated the special bullwhip effect due to unethical operations through expanding the bullwhip effect in managing supply chains into a moral operational environment. Additionally, some researchers have investigated into the impact of CSR on supply chains or explored ways to achieve a sustainable supply chain. Panda [
56] discussed pricing decision and coordination of CSR manufacturers and retailers. He found that the revenue sharing contract can be the maximum motivation to improve CSR of retailers. Modak et al. [
57] looked at dual-channel supply chains and integrated CSR impacts in the form of consumer surplus into CSR profit function, investigating CSR impacts on the successful operation of dual-channel supply chains. Liu et al. [
58] segment tourism supply chains and they found that environmental treatment efficiency or sales increase with the rise in CSR and that members’ profits grow with the rise in CSR of tourism operators. From the perspective of enterprise profitability, Panda and Modak [
59] showed that through the practice of corporate social responsibility, the motivation of maximizing non-profitability of channels creates greater profits than maximizing the target when sub-game perfect equilibrium substitutes quotation negotiation. Esfahbodi et al. [
60] proposed a sustainable supply chain management model. Through empirical comparison of this model, they found that sustainable supply chain management can improve environmental performance, but it will not gain economic benefits in the short term. Ding et al. [
43] studied the interaction of sustainable constraints and their influence on the cooperative decision-making of supply chain enterprises, and found that the government’s policy incentives have a significant impact on the sustainable development of the supply chain. Fritz et al. [
61] provided suggestions for the establishment of supply chain sustainability assessment indicators through qualitative and quantitative research on sustainability reports. They point out the importance of the governance dimension in a sustainable supply chain. Gouda et al. [
62] explored the impact of sustainable practices on supply chain risk through empirical analysis, and found that sustainability efforts can reduce supply chain risk, which provides impetus for sustainable supply chain practice.
Prior research has shown that there is a growing body of literature on the impacts of CSR on the performance of supply chains, but the literature related to CSR and sustainable closed-loop supply chain is relatively rare. Hamid et al. [
63] studied the network design in closed-loop supply chains, and developed three different target functions to create job opportunities by considering social factors such as total cost, environment and equity. Pedram et al. [
64] designed a closed-loop supply chain and claimed that job opportunities can be created to reduce unemployment rates; in addition, they developed a multiple-layer integer linear programming system to maximize profits and job opportunities. Panda and Modak [
24] explored channel coordination of CSR in closed-loop supply chains and showed that recycling rates are directly proportional to the manufacturer’s CSR strength and recycling rates are restricted within a certain range, while the revenue sharing contract can resolve channel conflicts. Wells et al. [
65] designed a closed-loop supply chain system for the automotive industry to explore the relationship between the new business model and the closed-loop system, and proposed the transition to sustainable production and consumption. Using the in-depth interview method, Jonas [
66] discussed how 3PL provides green logistics services to promote the sustainable development of enterprises and reveals the benefits of green logistics. Recently, Jonas [
67] established the Extend Producer Responsibility (EPR) model in the case of OEM recycling, and provided a sustainable development strategy for enterprises in the closed-loop supply chain. To enrich the research on CSR in closed-loop supply chains, this article expands the model by Panda and Modak (2017) to carbon emission constraints, and further explored into the impacts of CSR on carbon emissions. Following Nie et al. [
68] and Wang et al. [
69], this article introduces government reward and punishment mechanisms to control carbon emissions from enterprises. In terms of social welfare in social responsibility, Park et al. [
70], Yang et al. [
71] and Zhou et al. [
72] considered the impacts of CSR on social welfare. This article draws on their research and compares optimal decisions in different models.
Table 1 shows the summary of extant literature related to this article. Unlike prior research, this article highlights the following findings. Firstly, prior research on CSR supply chains focuses on pricing decisions and coordination of channels, while CSR in closed-loop supply chains has been under-researched. This article introduces government reward and punishment mechanisms into CSR in closed-loop supply chains, which enriches the research on CSR closed-loop supply chains and explores into the impacts of carbon emission constraints and government policy on pricing strategy, recycling strategy, profits of channel members and carbon emissions. Secondly, prior empirical and quantitative research concentrates on the role of CSR in the exterior and interior of enterprises, such as corporate reputation, staff employment and corporate profits, among many others. Therefore, this article deals with the impacts of CSR on carbon emissions, and mathematical models are deployed to prove the role of CSR on the environment. Finally, this article differs from prior research in that it constructs a model of maximizing social welfare; it examines the contribution of CSR to society from the perspective of social welfare, which is compared with the model of maximizing the manufacturer’s total profits; and it also discusses differences in economic and environmental benefits of these two models.
3. Model Description and Assumptions
This article considers a closed-loop supply chain composed of a single manufacturer and a single retailer. The manufacturer makes new products from components and raw materials, and remanufactures used products. The manufacturer collects used products through the retailer, sets the wholesale price of unit products, and pays the retailer the recycling price of unit-used products. In line with prior research, this article assumes that used products can be successfully remanufactured for secondary sales. The quality of remanufactured products is no different from that of new products and remanufactured products are sold at the same price as new products in the same market [
13,
73]. The retailer purchases products from the manufacturer and then sells them to consumers. Additionally, the retailer collects used products from the consumer and provides them to the manufacturer as raw materials. The retailer determines the recycling rate through controlling the recycling investment. The government sets a cap on carbon emissions to reduce the negative impacts of production and distribution on environment. If the total carbon emissions exceeds the critical value, the government would punish the manufacturer; if the total carbon emissions are below this critical value, the government would reward the manufacturer. Three cases are considered in this study: (1) the benchmark model, in which the manufacturer does not consider CSR, aiming to maximize profits; (2) the CSR model, in which the manufacturer focuses on CSR, aiming to maximize total profits; and (3) the model of maximizing social welfare, in which the manufacturer and the retailer make optimal decisions from the perspective of social welfare. By comparing the optimal pricing strategies, recycling strategies, and channel members’ profits in the three cases, this article investigates into the impacts of carbon emission constraints and CSR on supply chains and explores the correlation between CSR and carbon emissions.
3.1. Model Notations
Table 2 illustrates variables and notations used in this article.
3.2. Model Construction
This article constructs the Stackelberg game with a single period when the manufacturer and the retailer make decisions. This assumption is in line with the conventional research on supply chains. The manufacturer determines the wholesale price of the unit product, while the pricing strategy of the retailer and recycling strategy are influenced by the wholesale price. In supply chains, the unit cost of making a new product is , and the manufacturer charges the retailer a wholesale price of , while the retailer sells the products to the customers at retail price of . The market demand is the linear function of the retail price, and the form is , in which is the maximum market demand and is the sensitivity coefficient of the retail price, with . However, shows that the market demand is always negative in any circumstances, which is common in the literature relating to supply chains.
In the reverse channel, the retailer collects used products from the consumer, and pays the consumer unit price of
. Subsequently, the retailer transfers the used products to the manufacturer for remanufacturing, and now the manufacturer pays the retailer unit price of
in terms of used products. If the unit cost of new products made by the manufacturer from used products is
, then the unit cost of making new products from raw materials is greater than that of remanufactured products from used products, namely
[
74]. The cost saving that the manufacturer obtains from making remanufactured products is
[
75,
76], and we claim that the assumption is reasonable.
The recycling rate of used products
represents the willingness of consumers to get involved in recycling, and the retailer has to make efforts to motivate consumers to participate in collection activities. In other words,
is associated with the retailer’s investment
in recycling,
, in which
is the parameter of the investment scale [
13]. As a result, the retailer’s total cost of recycling used products includes the fees paid to the consumer for recycling and the investment into recycling,
[
24].
is the carbon emissions per unit product manufactured from raw materials by the manufacturer, while is the remanufacturing emission reduction coefficient, in which . A rise in means less impact of remanufacturing through recycling on reducing carbon emissions, and the carbon emissions from making remanufactured products is . is the upper limit set by the government on the total carbon emissions from enterprises making all products, and is the government reward and punishment coefficient set by the government, with . The carbon emissions from enterprises making products from raw materials exceeds the upper limit set by the government on carbon emissions, while the carbon emissions from enterprises remanufacturing products from used products are below the upper limit set by the government on carbon emissions, hence satisfying . This hypothesis is in line with the characteristics of environmental protection and energy conservation in remanufacturing.
It is assumed that according to the stakeholder theory, business operations should be accountable for all stakeholders in CSR enterprises, including governments, employees, suppliers, retailers and consumers. Consumers are the critical component of all stakeholders, and therefore, CSR is reflected by consumer surplus in the model, in line with the majority of studies [
24].
Consumer surplus is the gap between the maximum price the consumers are willing to pay for the product and the market price they actually pay for the products. Therefore, below is the consumer surplus.
CSR strength is introduced, and the consumer surplus of CSR enterprises is . shows that the manufacturer gets the maximum profits traditionally. shows that enterprises prioritize the interest of stakeholders, which does not happen in reality. The analyses below also prove this result.
Based on the parameter settings and assumptions above, this article constructs models in three cases and compares the optimal decisions.
4. Model Decisions
4.1. The Benchmark Model
As the leader in the Stackelberg game, the manufacturer takes the lead to sell the products to the retailer at the wholesale price, and then the retailer sells them to the consumer at the retail price. Also, the retailer collects used products from the consumer, and then the manufacturer remanufactures. As the follower in the Stackelberg game, the retailer maximizes profits by making optimal decisions according to the manufacturer’s strategies. The retailer’s earnings are mainly from selling new products and recycling used products, while the retailer’s cost is primarily concerned with recycling activities. So below is the retailer’s revenue function:
The profit function of the manufacturer includes the sales revenue, the income of remanufacturing used products and the recycling cost that the manufacturer pays to the retailer. Also, the manufacturer can receive corresponding government incentives or penalties in the case of carbon constraints. Now, below is the manufacturer’s profit function:
After the manufacturer determines the wholesale price of
, the retailer decides the optimal decision according to the wholesale price. To solve the Stackelberg game equilibrium, it is assumed that
and
; below is the retailer’s optimal pricing decision:
Substituting the optimal retail price
and recycling rates
into the manufacturer’s revenue function and assuming
, below is the manufacturer’s optimal wholesale price:
Proposition 1. In the benchmark model, the necessary condition for the existence of the optimal solution for the profits function of channel members is , and the optimal retail price is: The optimal recycling rate is: Proof. The Hessian matrix of retailer’s profit function is:
To maximize the profit function of the retailer, it needs to satisfy:
On the other hand, to maximize the manufacturer’ profits, it needs to satisfy:
Since
, and
, then
Substituting the optimal wholesale price
into Equations (3)–(5), the optimal retail price
, recycling rates
, and the retailer’s and the manufacturer’s optimal profits can be solved. According to
and
, the average carbon emissions and total carbon emissions of each unit product can be solved when the carbon emission constraint is considered.
Table 3 shows the results. □
Proposition 1 describes that under the benchmark model, only when the investment scale parameter satisfies certain conditions, can the retailer and manufacturer’s profit functions get the maximum value. The investment scale parameter affects the optimal decision of the channel members. When the investment scale parameter satisfies the condition, as the scale parameter increases, the cost of the recycling increases. Manufacturers will reduce costs by reducing recycling and reducing the amount of remanufactured products to minimize losses from increased costs. As the cost increases, the selling price will increase, resulting in a decrease in total production and a decrease in expected profit. At the same time, when the scale parameter of the recovery cost is increased to a certain extent, the expected profit is almost no longer reduced. This is mainly because the manufacturer cannot obtain profit from remanufacturing when the cost of the recycled product is large, so the recycle rate is close to zero; the expected profit at this time has nothing to do with the cost of recycling, and it tends to be fixed. As the scale parameter is gradually reduced, the smaller the recovery input, the more advantageous it is to remanufacture. Therefore, manufacturers set lower sales prices to obtain more sales and increase recycle rate, and through these two strategies to increase the amount of remanufacturing, thereby reducing costs and achieving higher profits. If the investment scale parameter does not satisfy this condition, manufacturers and retailers will not be able to make optimal decisions. The influence of other parameters such as carbon emission constraints and CSR on optimal decision cannot be explored naturally. However, the scale parameters of recycling cost in real life are large enough, which is consistent with the actual application.
4.2. Model of Maximizing Total Profits
In the CSR model, the manufacturer has social responsibility. The impact of CSR is denoted by consumer surplus, integrating consumer surplus into the manufacturer’s decision model. The retailer’s decision model is fixed; the retailer’s revenue function is
, and the manufacturer’s net profit function is
, while below is the manufacturer’s total profit function:
Assuming
and
, below is the retailer’s optimal decision:
Substituting the optimal retail price
and recycling rates
into the manufacturer’s total revenue function, and assuming
, below is the manufacturer’s optimal wholesale price.
Proposition 2. In the CSR model, the necessary condition for the existence of the optimal solution for the profits function of channel members is , and the optimal retail price is: The optimal recycling rate is: Proof. The Hessian matrix of retailer’s profit function is .
To maximize the profit function of the retailer, it needs to satisfy:
To maximize the manufacturer’ profits, it needs to satisfy:
According to Proposition 1, we can obtain:
Substituting the optimal wholesale price
into Equations (18)–(20), the optimal retail price
, recycling rates
, and the retailer’s and the manufacturer’s optimal revenues can be solved.
Table 3 shows the results. □
Proposition 2 describes the conditions that the parameter of investment scale should satisfy when the profit function of channel members can obtain the maximum value under the CSR model. The manufacturer in case 1 does not consider CSR, so the constraints on investment scale parameters do not involve the intensity of CSR. Proposition 2 shows that when the manufacturer considers the CSR, the value range of the investment scale parameter changes and it is related to the intensity of CSR. The lower limit of the investment scale parameter in case 2 is larger than case 1. Corporate social responsibility affects the value of investment scale parameters. When the CSR intensity increases, the value of the investment scale parameter also becomes larger. Under this model, manufacturers believe that CSR is the embodiment of recycling more used products. Therefore, when the intensity of CSR increases, the investment of enterprises in recycling used products needs to increase. At this time, the investment scale parameters also need to increase. When the CSR intensity is 0, this model becomes the benchmark model, the value range of the investment scale parameter is also consistent with the benchmark model. This is in line with the actual situation and lays the foundation for the analysis of the following text.
4.3. Model of Maximizing Social Welfare
The existence of enterprises is not only for profit, but also for maintaining social justice and fairness, protecting resources and environment, and assuming the responsibility of social security and welfare undertakings. Consequently, this part analyses the social welfare of CSR with carbon emission constraints, constructs the model of maximizing social welfare and investigates the optimal decision of CSR closed-loop supply chains with carbon emission constraints.
Social welfare amounts to the sum of corporate profits (producer surplus) and consumer surplus, and the producer surplus is the total profits of supply chain channels. In addition to the total profits of supply chain channels and consumer surplus, social welfare includes government expenditure or revenue (in this article, this means that when carbon emissions exceed the upper limit, the government punishes the manufacturer and obtains the revenue; when carbon emissions are below the upper limit, the government rewards the manufacturer), and subtracts the external disbursement caused by the manufacturers’ carbon emissions. Hence, the social welfare is calculated as follows.
Proposition 3. In the model of maximizing social welfare, the necessary condition for the existence of the optimal solution of the social welfare function is , and the optimal retail price is: The optimal recycling rate is: The optimal social welfare is: Proof. The Hessian matrix of retailer’s profit function is:
To maximize the profit function, it needs to satisfy:
To solve the Stackelberg game equilibrium, assuming and , the optimal retail price and recycling rate can be obtained as (30) and (31). Substituting the optimal retail price and the recycling rate into the function of social welfare, the optimal social welfare can be obtained as (32). □
Proposition 3 describes the necessary conditions for a social welfare function to derive an optimal solution. Under the social welfare maximization model, manufacturers, retailers, and governments make joint efforts to achieve the goal of maximizing social welfare. Therefore, the function does not involve the wholesale price and the unit recycling price set by the manufacturer for the retailer. Compared with the other two cases, the constraint of the investment scale parameter does not involve the unit recycling price . However, we can find that the lower limit of the investment scale parameter in case 3 is larger than the other two cases through comparative analysis. Under the social welfare maximization model, the lower limit of the investment scale parameter is larger. Social welfare maximization pursues greater economic and environmental benefits, and remanufacturing is an activity that is beneficial to both. In this case, the manufacturer will increase the amount of remanufacturing products, which requires greater recycling investment, so the lower limit of the scale of the recycling investment scale parameter will be greater. Which proves the proposition is of practical economic significance.
5. Discussion
The preceding part deals with optimal decisions of three different models in closed-loop supply chains with carbon emission constraints. This part aims to reveal the impacts of carbon emission constraints and CSR on the optimal decisions in the model of maximizing total profits through analyzing the impacts on the optimal recycling rate, the retailer’s and the manufacturer’s profits, and carbon emissions.
5.1. Impacts of Carbon Emission Constraints on Optimal Decisions
The carbon emissions generated by the products produced by the manufacturers using raw materials are higher than the government’s carbon emission caps, and the carbon emissions of products obtained by recycling the used products are lower than the upper limit namely . The carbon emission cap established by the government should be between the carbon emissions of the two products, so as to effectively control the carbon emissions of manufacturing enterprises. The production proportion of the two products depends on the retailer’s recycling efforts, and therefore the manufacturers must regulate the wholesale price of products to motivate the retailer to make decisions to maximize their own interest.
The optimal decisions of channel members are affected by the product remanufacturing emission reduction coefficient. According to
Table 3, we obtain:
Since
and
, we obtain:
Let
,
, then:
With a rise in the product remanufacturing emission reduction coefficient, the recycling rate of used products drops gradually; the profits of channel members decline gradually; while the average carbon emissions accumulate.
With an increasingly active role of remanufacturing in curbing carbon emissions, the manufacturer tends to remanufacture and encourage the retailer to collect used products to maximize profits with carbon emission constraints. Consequently, the retailer makes greater efforts to recycle. Meanwhile, the manufacturer’s and the retailer’s optimal profits increase to a certain degree, and the average carbon emissions decrease. When producing the same amount of products, the government’s carbon emission policy will bring more rewards to manufacturing enterprises. It shows that the remanufacturing industry not only brings profits to all members of the supply chain, but also creates environmental benefits. Although the recycling rate of used products has been improved, the increased total demand of products will lead to increased total carbon emissions. Therefore, under the carbon emission constraint, when the remanufacturing emission reduction effect is relatively small, the enterprise remanufacturing benefit may not be very ideal. At this point, it is necessary for the government to actively formulate policies.
The government reward-penalty coefficient has an impact on the optimal decision of channel members. From the above analysis, we obtain:
Let
, then:
With a rise in the government’s reward-penalty coefficient, the recycling rate of waste products drops; the retailer’s profits decline; the average carbon emission increases; while the total carbon emissions decreases.
When the government increases the reward-penalty coefficient for emission reduction, manufacturers will control the production of remanufactured products in order to reduce the penalty cost. Therefore, the retailer’s recycling efforts are correspondingly reduced, leading to a fall in the demand for products and the retailer’s profits. A rise in the reward-penalty coefficient decreases the retailer’s profits, and thereby the retailer may lose the motivation of recycling. In terms of the manufacturer, the initial loss due to a fall in the demand for products is much greater than the income from the government reward, and thus the manufacturer’s profits decrease gradually. With a rise in the government reward-penalty coefficient, the production diminishes gradually, and the total carbon emissions drop. The manufacturer’s reward from the government increases, exceeding the loss caused by a reduction in the demand for products. When the government reward-penalty coefficient increases to a certain level, the manufacturer’s profits start to augment gradually. In terms of carbon emissions, despite a fall in total carbon emissions from the manufacturer with a rise in the reward-penalty coefficient, a reduction in the total carbon emissions from enterprises can be mostly attributed to a fall in the production. A rise in the government reward-penalty coefficient can lead to a rise in average carbon emissions. The government can adopt different reward-penalty policies for different types of manufacturers and increase the incentives for enterprises with obvious emission reduction effects for recycling and remanufacturing, thus enhancing the control of greenhouse gases.
5.2. Impacts of Corporate Social Responsibility on Optimal Decisions
CSR is closely associated with carbon emissions, and a growing number of enterprises regard carbon emissions as an index to evaluate CSR. In this model, when CSR is introduced with carbon emission constraints, CSR is quantified in the form of consumer surplus, and is conducive to quantitative analyses in greater detail.
Table 3 shows that the optimal decision variable is the function of
.
Since
,
and
, we can obtain:
As the recycling rate is proportional to the CSR strength. When
,
is maximum; when
,
is maximum, but
. When
,
is likely to be greater than 1, while
is unlikely to be greater than 1 in the premise. As a result, the optimal decision on the recycling rate is restricted:
When , , which is obviously inadvisable. So the manufacturer will set the recycling rate as 1, and the recycling rate reaches maximum. Therefore, the recycling rate is proportional to CSR strength, while the recycling rate can rise within a range.
In the CSR supply chain, the manufacturer’s recycling activities show corporate social responsibility. When the CSR intensity is greater, the manufacturer tends to remanufacture. As a response, the retailer makes greater efforts to recycle used products, and the recycling rate increases. Also, the retailer reduces the retail price to encourage the customer to purchase more products. In the case of a rise in demand, the retailer’s profits and the manufacturer’s total profits increase, and the CSR strength influences the corporate decisions. Despite a fall in the manufacturer’s net profits, the consumer surplus gained is greater than the loss of net profits. The manufacturer’s total profits increase, benefiting channel members generally. Due to the limited scope of the recycling rate of used products, the intensity of CSR also has a certain level of restriction. When this range is exceeded, the increase in the intensity of the manufacturer’s CSR will not continue to bring higher profits to the members of the supply chain channel. Therefore, companies can develop the most appropriate social responsibility strategy based on the type of remanufactured products and the recycling rate of used products. After that, we analyze the impact of CSR on carbon emissions.
Since
,
and
, we can obtain:
With a rise in CSR strength, the average carbon emissions from manufacturing products decrease, while the total carbon emissions increase. When CSR awareness is higher, manufacturers will reduce wholesale prices to motivate retailers to invest more in recycling activities. However, the reduction in wholesale prices and retail prices has led to an increase in demand for products. The increase in the number of products produced by enterprises has increased the carbon emissions of enterprises. As the scale of production of enterprises increases, the increase in carbon emissions is greater than the reduction in carbon emissions from remanufacturing activities, so the total carbon emissions of enterprises increase. On the other hand, the retailer increases the recycling rate of used products, and therefore more used products are deployed for remanufacturing. The positive effect of remanufacturing on the environment can decrease the carbon emissions per unit product, leading to a fall in the average carbon emission from enterprises making products. The main reason for the increase in total carbon emissions of enterprises is the increase in the number of products, rather than the weak awareness of CSR. For manufacturing the same quantity of products, enterprises with CSR generate less emissions. For this reason, enterprises with CSR can curb carbon emissions per unit product effectively, and they gain profits while protecting environment. Meanwhile, the government should reward the enterprises with a rise in CSR, and the government punishes enterprises if they exceed the upper limit on carbon emissions, which is contradictory. The manufacturer should reasonably formulate the level of corporate social responsibility in order to achieve win-win economic and environmental benefits. This echoes the analyses mentioned above.
6. Numerical Examples
Numerical examples are deployed to show the analyses presented above. Firstly, a comparison is made between the total profits maximization model and the social welfare maximization model. Secondly, the benchmark model and CSR model are compared to show the impact of carbon emission constraints and CSR on optimal decision-making.
6.1. Comparison between Social Welfare Maximization Model and Total Profits Maximization Model
To show the differences between the optimal decisions of the model of maximizing social welfare and the model of maximizing the manufacturer’s total revenues more visually, the numerical analyses of these two models are deployed for comparison, assuming
,
,
,
,
,
,
, and
,
,
, and
. The optimal recycling rate, revenues, average carbon emissions, and the total carbon emissions are compared in these two models, and the results are shown in
Figure 1,
Figure 2 and
Figure 3.
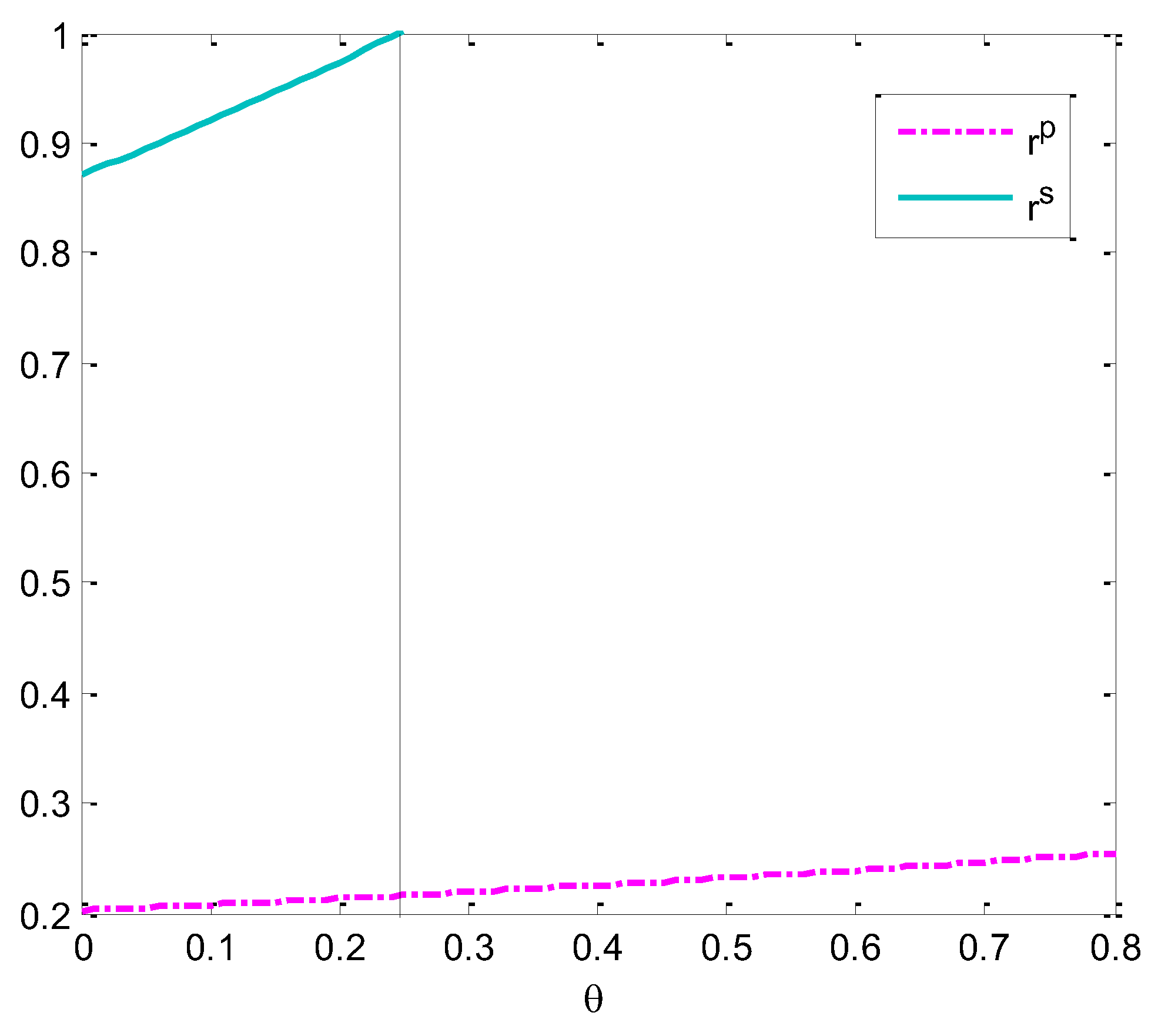
Figure 1 shows the changes of optimal recycling rates in two models with a rise in CSR strength. It can be seen that CSR strength rises from 0 to 0.8, and the recycling rate increases from 0.87 in the model of maximizing social welfare, which is far greater than the recycling rate in the model of maximizing the manufacturer’s total revenues. When
, the recycling rate is 1. Subsequently, if CSR strength continues to increase, the recycling rate can remain at 1, which suggests that CSR strength is restricted within a certain range.
This conforms to the original intention of the model of maximizing social welfare, considering the interest of a number of parties including the producer, the consumer and the government, with a focus on environmental benefits. In this circumstance, the manufacturer is involved in more remanufacturing, and a fall in retail prices of channels leads to a rise in the consumer surplus. Also, the retailer increases recycling, and thus the recycling rate steps up. Recycling and remanufacturing as an activity that can create environmental benefits, the greater the intensity of its activities, the greater the intensity of energy conservation and emission reduction, and the higher the social welfare. The social welfare maximization model can significantly improve the recovery rate of used products, thus increasing the utilization rate of resources and facilitating the establishment of the image of enterprises with CSR. At the same time, the recovery rate of used products is consistent with the government’s will, and more remanufacturing activities will reduce carbon emissions. For consumers, the reduction of retail price is the most directly beneficial to them, and the maximization of social welfare realizes higher expectations of consumers.
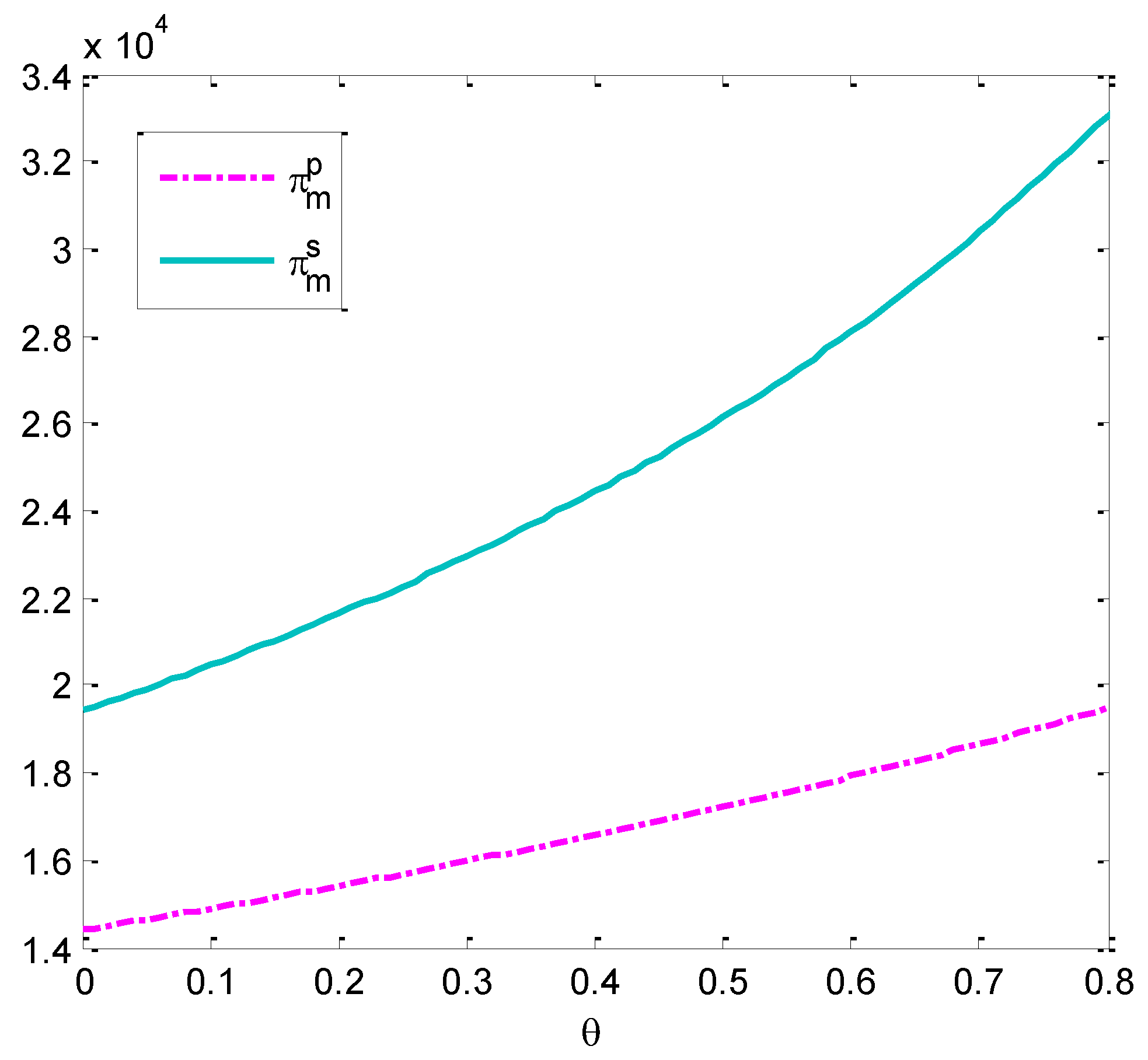
Figure 2 shows that the total revenues change in the two models with a rise in CSR strength when other conditions are identical. Clearly, when CSR strength rises from 0 to 0.8, social welfare increases from 19,200 to 33,000, whereas the revenues grow from 14,500 to 19,200 in the model of maximizing the manufacturer’s total profits. In the models of maximizing social welfare and maximizing the manufacturer’s total profits, the revenues tend to increase with a rise in CSR strength. The revenues in the model of maximizing social welfare are greater than those in the model of maximizing the manufacturer’s total profits.
It is manifest that the manufacturer’s total profits maximization model does not maximize the total profits of channels. With a rise in CSR strength, social welfare increases, which is greater than the total revenues of channels in the model of maximizing the manufacturer’s total profits. This change mainly comes from a lower retail price and a higher recycling rate in the model of maximizing social welfare; the customers purchase more products due to a lower retail price, and thus the total revenues of channels increase. The higher recycling rate reflects higher environmental benefits, so the social welfare increases and is higher than the total profits of channels under the manufacturer’s total profits maximization model. On the other hand, the model of maximizing social welfare can be considered as the model of centralized decisions. When the supply chain channel is considered as a unity for decisions, the total revenues are always greater than those in decentralized decisions, due to the fact that dual marginal effects are eliminated. This provides new managerial insights for enterprises to make decisions.
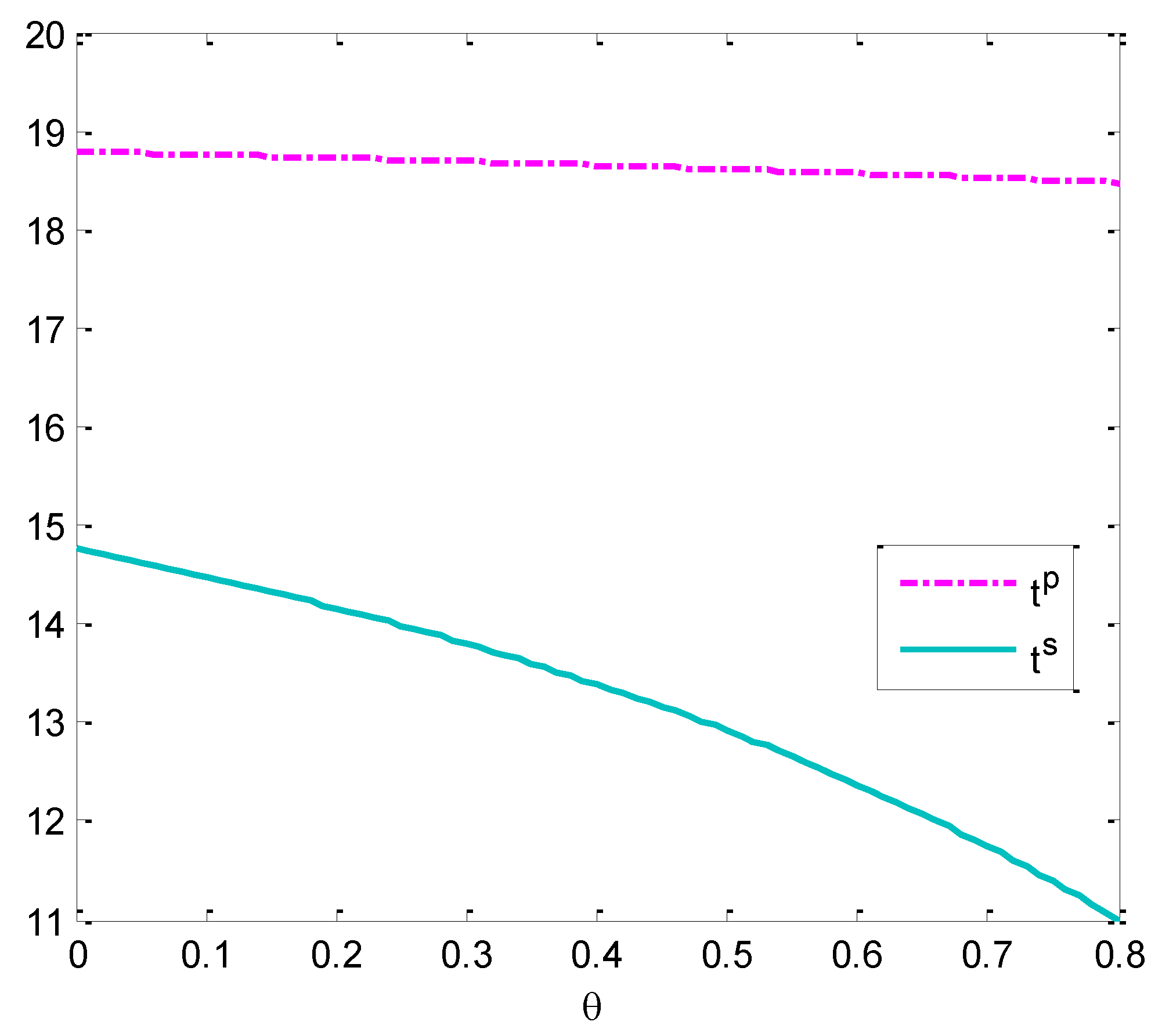
Figure 3 illustrates that the average carbon emission in the two models changes with a rise in CSR strength when other conditions are identical. It can be seen from
Figure 3, that as CSR strength increases from 0 to 0.8, the average carbon emissions drop from 14.8 to 11 in the model of maximizing social welfare. In the model of maximizing the manufacturer’s total revenues, the average carbon emissions decline from 18.8 to 18.5. The average carbon emissions fall with a rise in CSR strength.
A greater fall indicates that the model of maximizing social welfare can effectively curb the average carbon emissions from products, reflecting the environmental benefits. The recycling rate of used products is very high under this model. More used products have been recycled and remanufactured. In addition, remanufacturing has a positive effect on carbon emissions, so the average carbon emissions are less. Comparatively, the model of maximizing social welfare has a positive effect on the environment.
Based on the comparative analysis of two models, we found that compared with the manufacturer’s total profits, the recycling rate of used products and total profits of the channel are higher under the model of maximizing social welfare. Also, it can effectively curb the average carbon emissions from products. Starting from maximizing social welfare, focusing on CSR and environmental benefits facilitates sustainable development of enterprises and provides new orientation for enterprises to be profitable.
6.2. Comparison between Benchmark Model and Corporate Social Responsibility Model
The optimal profits of each supply chain member are compared in two cases of enterprises with and without CSR under the carbon emission constraint. The basic parameters are set as follows: , , , , , and . It is assumed that demand is the linear function of prices, and , , and .
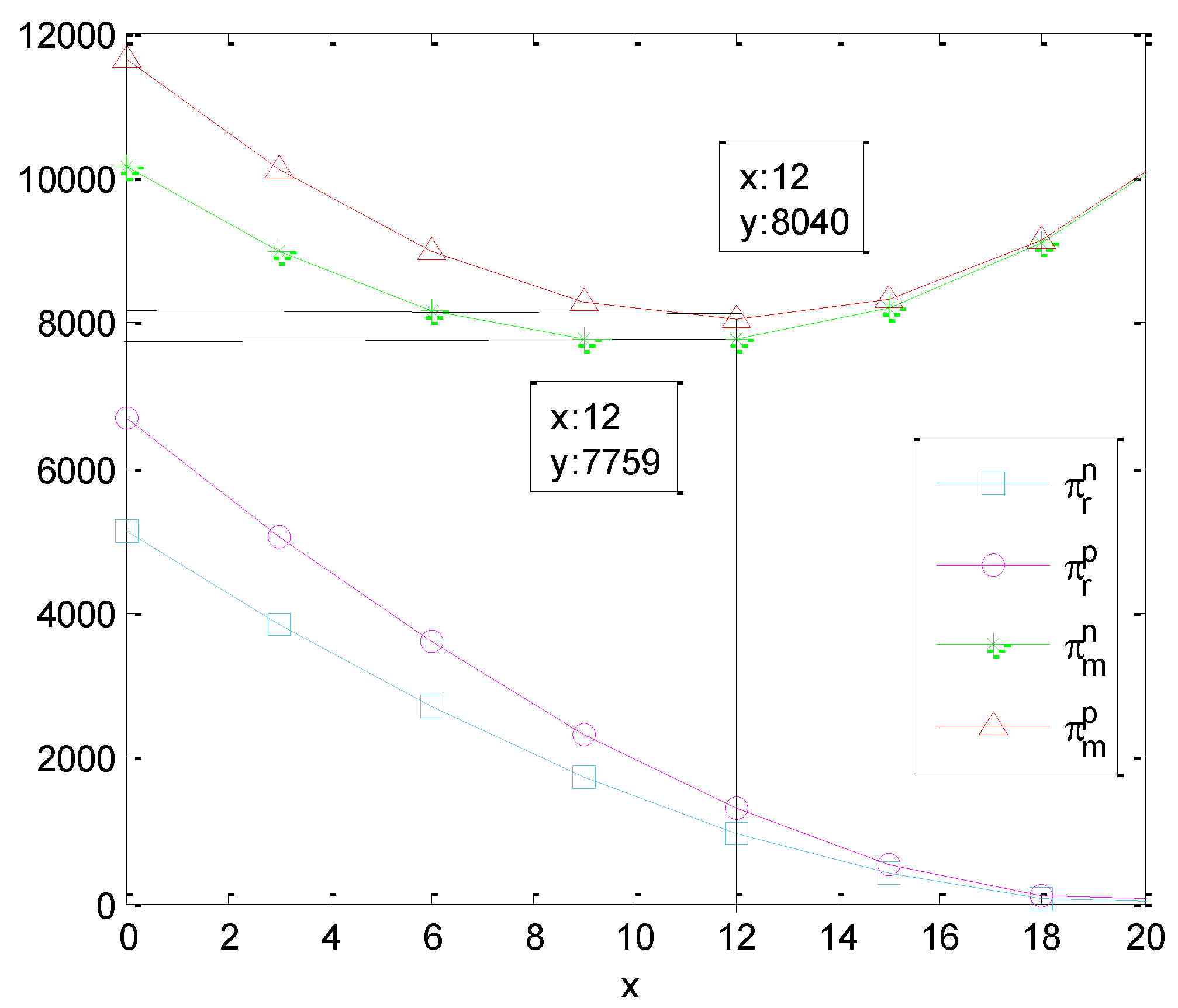
Figure 4 illustrates the impacts of the reward-penalty coefficient on the optimal profits of channel members. With a rise in the reward-penalty coefficient, the retailer’s profits tend to fall. The government reward-penalty coefficient is negatively correlated with the retailer’s optimal profits, while the manufacturer’s profits drop first and rise subsequently. With a rise in the reward-penalty coefficient, the total carbon emissions tend to decrease, and the manufacturer gains more reward from the government, exceeding the loss caused by the initial fall in the product’s demand. Consequently, when the reward-penalty coefficient increases to a certain level, the manufacturer’s profits start to step up.
Figure 5 illustrates the impacts of CSR strength on the average carbon emissions. In Case 1, with a rise in CSR strength, the average carbon emission is 18.94. In Case 2, the average carbon emission drops from 18.94 to 18.63. In Case 2, the average carbon emissions drop with a rise in CSR strength. A rise in the demand leads to an increase in the total carbon emissions, whereas a rise in the recycling rate means that a growing number of used products are used in remanufacturing. Remanufacturing plays a positive role in carbon emissions, so the average carbon emissions fall. The results of these numerical examples are consistent with discussions in
Section 5.
7. Conclusions
This article examines the optimal decisions in CSR closed-loop supply chains with the policy of government carbon emission constraints; discusses the impacts of carbon emission constraints and CSR strength on recycling and remanufacturing decisions; and compares the model of maximizing the manufacturer’s total revenues and the model of maximizing social welfare. Here, the manufacturer makes new and remanufactured products, while the retailer collects waste products from the consumer. This study integrates CSR in the form of consumer surplus into the model.
Based on the results of this study, a number of findings and implications are presented as follows. (1) The product remanufacturing emission reduction coefficient is positively correlated with the recycling rate of used products. For enterprises with different remanufacturing emission reduction factors, the government’s carbon emission restraint policy should be appropriately adjusted. (2) The increase of the government’s reward-penalty coefficient leads to a fall in the recycling rate, and the manufacturer’s profits drop initially and then increase. Therefore, in order to limit the carbon emissions under the conditions of ensuring the company’s income, the government needs to set a reasonable carbon emission cap and formulate different reward-penalty factors for different types of enterprises to achieve a win-win situation between economic interests and environmental benefits. (3) The recycling rate of used products and the profit of channel members are directly proportional to the intensity of corporate social responsibility. The increase in the intensity of corporate social responsibility has reduced the average carbon emissions of products, but the total carbon emissions of enterprises have increased. Therefore, the government needs to balance the rewards and penalties between corporate social responsibility and carbon emissions. (4) In terms of economic and environmental benefits, the social welfare maximization model is superior to the manufacturer’s total profits maximization model. This provides new management implications for corporate decision makers.
This article provides some recommendations for enterprises with CSR in closed-loop supply chains with carbon emission constraints. However, there are some limitations which can be expanded and improved on in future research. (1) It is assumed that demand is the linear function of prices, whereas the demand function can be expressed in more than one form in reality. Therefore, future research can be based on the stochastic demand function or a more complex form. (2) In this paper, CSR is discussed in the form of consumer surplus. In fact, some scholars have applied CSR directly to the demand function in other forms, which provides new ideas for future research. (3) The government reward-penalty coefficient and carbon emission cap have a significant impact on the profits of enterprises. The government needs to formulate the reward-penalty coefficient and carbon emission cap rationally, but this paper does not analyze and discuss it in detail. Therefore, the in-depth study of the reward-penalty coefficient and carbon emission cap is of practical significance. (4) With the increase of CSR intensity, the total carbon emissions will increase. The government needs to reward socially responsible enterprises reasonably under the constraint of carbon emissions, and punish those enterprises whose carbon emissions exceed the upper limit. Therefore, how to balance the incentives and penalties between social responsibility and carbon emissions is a problem worthy of further study. (5) The Social welfare maximization model is the model of maximizing total channel revenue. How to formulate an effective coordination contract to enable manufacturers and retailers to maximize channel total revenue is also one of the future research directions. (6) This paper only discusses the situation in which manufacturers have CSR. In fact, retailers may also have a sense of CSR. Therefore, future research can explore the issue of both manufacturers and retailers with a sense of social responsibility. Despite some assumptions and premises which limit the application of this model, our findings are practical, having a positive impact on the formulation of carbon emission constraints and the management of enterprises with CSR in closed-loop supply chains.