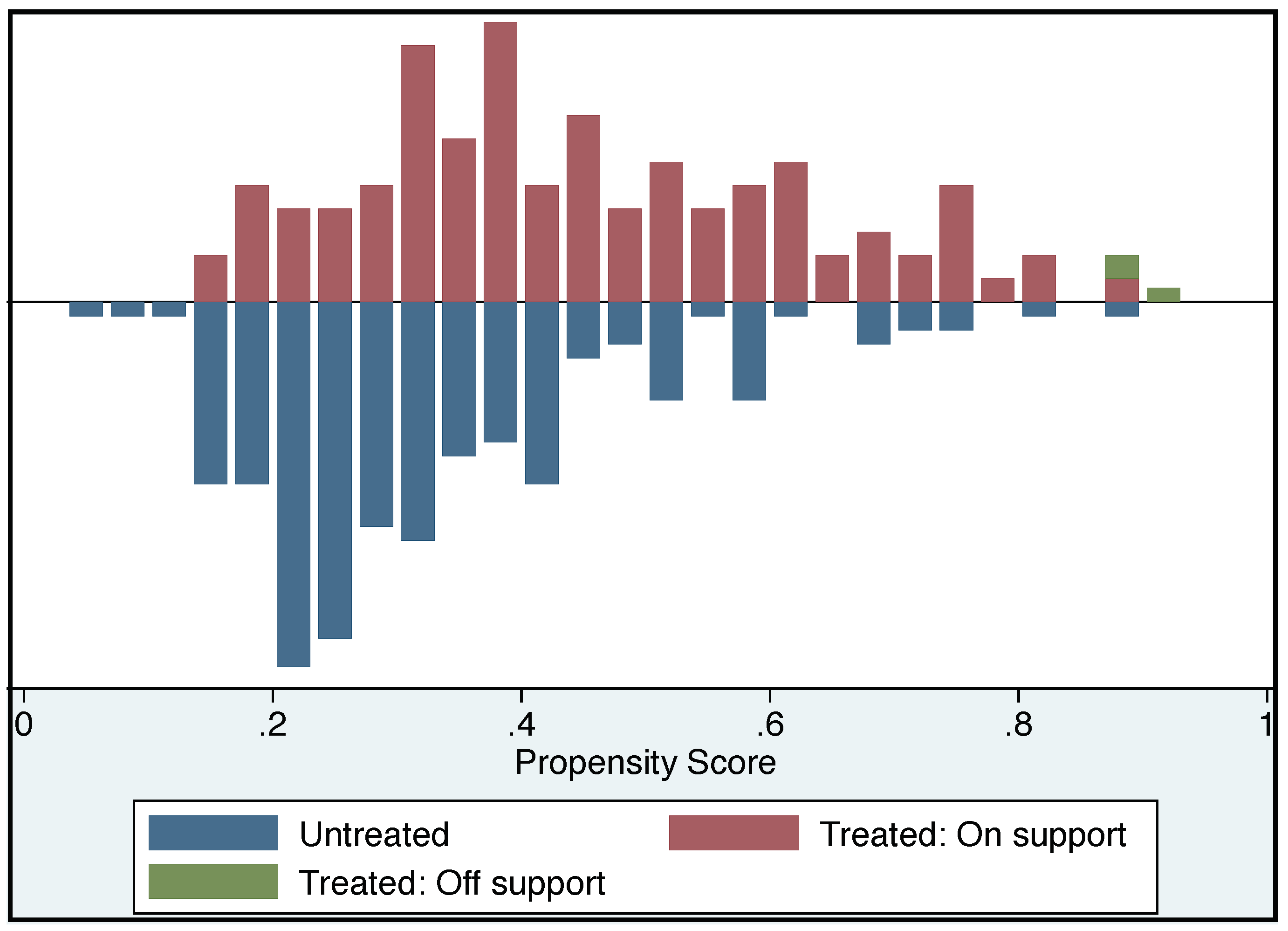1. Introduction
Environmental-related measures play a key role in the 2014–2020 Common Agricultural Policy (CAP), fostering the production of public goods (PGs) by EU agriculture and forestry. The so-called Pillar I of the CAP (the part mainly related to income support) has included since 2005 environmental cross-compliance, i.e., compliance with environmental practices that are conditional to the payment of CAP income support. In addition, the 2014–2020 CAP introduced a greening measure, which is a component of the direct payment rewarding farmers for respecting three obligatory agricultural practices (namely, maintenance of permanent grassland, ecological focus areas, and crop diversification). The greening payment accounts for 30% of the national direct payment envelope. The so-called Pillar II of the CAP is focused on rural development plans (RDPs). RDPs work typically with voluntary measures addressing a large set of objectives related to local development and natural resources. Among these measures, the RDPs reserve at least 30% of their budget for agri-environmental schemes (AESs), promoting the provision of environmental public goods such as biodiversity protection and climate change mitigation [
1]. AESs include voluntary measures that provide payments for farmers that assume practices going beyond cross-compliance and greening. AESs were first introduced at the beginning of the 1990s and gained growing importance over time, already playing a key role in the 2007–2013 CAP, where they accounted for the highest share of the public budget allocated [
2]. They are expected to remain in the proposal for the 2021–2027 CAP currently under discussion, which also introduces a voluntary environmental payment in Pillar I [
3]. The specific measures and sub-measures included in the AESs may vary substantially from country to country, but they mostly concern support for organic, integrated, and low-input farming, with agro-ecological practices, grassland management, and long term set-aside.
The assessment of the impact of these measures on the agricultural output and the agri-environmental services and PGs provided is a key challenge related to the CAP. The European Commission highlights the importance of policy evaluation exercises for CAP improvement and programming [
4], hence stimulating an intense demand for research in this field. Uthes and Matzdorf [
5], reviewing the literature on the AESs, note that most of the papers address their environmental effects, whereas few residual works approach the analysis of the impacts that are less directly linked to the environment (such as the impacts on the farms’ structural characteristics). Three main aspects of the AESs are analysed in the literature: farmers’ participation [
6], effectiveness in the environment [
7,
8,
9], and effects on farm revenues [
2,
10,
11].
Despite the fact that a great attention is given by the EU to impact assessment and policy evaluation, few studies on the CAP are based upon statistically rigorous analysis, and their evaluation results are often uncertain and theoretically questionable [
12], leading to few broad recommendations rather than providing valuable information for improved policy design. Jaraite and Kažukauskas [
13] point out that most of the existing studies are based either on expert judgements or simulation models rather than being based on empirical measurements. Similarly, Arata and Sckokai [
2] point out that only few studies are based on empirical measures by means of statistical and econometric tools.
Two main challenges contribute to limit the impact assessment of the AESs: the non-experimental conditions in which the impact assessment is implemented, and the availability of data.
The first limiting factor is the intrinsic framework of the observational studies. Usually, individuals, enterprises, and agricultural holdings cannot be merely assigned to a treatment or be the control (such as a policy measure) by means of a randomized experiment [
14]. In these cases, then, researchers must resort to the observed contingency. Due to the fact that it is not possible to simultaneously observe on the same unit of analysis two complementary statuses, the case of “what would have happened if had the unit of analysis not had the treatment” is not observable. This means that treated and control units cannot be directly compared due to the self-selection bias. If we cannot compare one unit that decides to uptake the treatment with another unit that decides otherwise, we have to set up a counterfactual group for the treated units by constructing it artificially. The propensity score matching (PSM) methodology serves this purpose; few authors investigating the impact of the AESs have applied it, often combining PSM with a difference-in-differences (DID) estimator (see, for example, [
2,
7,
8,
11,
13]).
Propensity score matching is applied to emulate the conditions of a randomized experiment in an observational studies context by constructing a proper counterfactual group for the observed treated units. This counterfactual group is built by means of the similarities existing among the observed covariates [
15]. The emulated experimental conditions are statistically significant and lead to unbiased results only if the two groups of treated and control units are the most similar with respect to the observed covariates. The latter units must not be influenced by the treatment assignment [
16]. In order to construct a statistically significant counterfactual group, researchers need a considerable number of observed covariates gathering specific information on the units of analysis. In the specific case of the agricultural holdings, we usually need: (1) general information such as altitude, location, size, economic size, legal status, specialization, etc.; (2) structural information such as total agricultural area (TAA), utilized agricultural area (UAA), hectares (ha) of land owned, and rented-in, rented-out, and individual crops in terms of UAA, etc.; (3) policy information such as the AES uptake, the single farm payment (SFP), etc.; (4) socio-demographic information on the farm household such as owner’s gender, age, educational level, agricultural education, income from agriculture, production for self-consumption, etc.; and, (5) information on agricultural inputs and outputs such as labour, costs, yields, etc.
The aforementioned amount of information needed to carry out a proper counterfactual analysis suggests the second limiting factor: data shortage. Even though there is not a mandatory number of necessary covariates (the number depends on the specific object of the analysis, the overall data quality, the sample representativeness, etc.), richer, more comprehensive and more timely data help to construct a better counterfactual, hence leading to more accurate analysis and more statistically significant and robust results [
17]. Indeed, many authors (see, for example, [
2,
12,
13,
18,
19]) suggest that the lack of comprehensive and timely data is the most impelling issue limiting the policy impact assessment in agricultural and environmental economics by means of well-founded evaluation methods.
Primary data such as ad hoc project surveys are difficult to collect due to both the high costs and the time needs of the new surveys. Moreover, ad hoc surveys can be rarely comprehensive in terms all the variables of interest needed for the research purposes, and they can hardly be used to compose a time series (i.e., to have a time span). Nevertheless, they have some advantages: they can be more focused on the specific research topic, and are more recent and more up-to-date with respect to the policy issue under analysis.
Secondary data are instead more comprehensive and they can have a time span. The national agricultural census, for example, collects, all together, general, structural, socio-demographic and technical information. Unfortunately, these data sources are collected and updated every decade. Hence, they are not collected in a timely manner and they do not collect specific information on a research topic (e.g., the uptake of a relatively new policy, respondents’ opinions, etc.). Moreover, due to privacy constraints, socio-demographic information on the farm households are often not available for research purposes or they are released at a very aggregated level. Farm Accountancy Data Network (FADN) data can suffer from the lengthiness of data collection. Indeed, often, data collected with respect to a specific reference year are available only at the beginning of the successive one. FADN data are also affected by sample representativeness issues: only the farms that are bigger than a minimal size in terms of both the UAAs or livestock units and standard output are represented by the sample. There is a weak or even non-existent representation of farm types and geographical areas, while large farms can be over-represented compared to small and medium ones, as suggested by several authors (see, for example, [
20,
21,
22,
23]).
The aforementioned limits could be tackled by means of data integration strategies such as record linkage (RL), statistical up(down)scaling (SUD), and statistical matching (SM). All these strategies allow to overcome, in different ways, the general problem of “missing data”. RL was originally implemented with the specific purpose of duplicated record identification in data sets where unique identifiers are unavailable. Lately, it has been progressively applied to observations matching among different data sets [
24]. Hence, it evolved from a practical “data cleaning” procedure to a complex “entity resolution” methodology. SUD is mainly used to enlarge or to narrow information referred to a specific territorial and/or aggregate level; it has been developed mainly in the environmental and meteorological research fields in order to represent and adapt data collected at different space levels and time scales [
25].
Statistical matching, the most up-to-date methodology among those aforementioned, allows us to impute information in one data set defined as the “recipient” from one (or more) data set(s) defined as “donor(s)”. This information is observed exclusively in the donor(s) while it is missing in the recipient data set. We stress that, in the present paper, we refer to a specific kind of missing information represented by entire variables. In other words, we do not observe entire data set columns that are, ideally, relevant (if not essential) for the research purposes. Within the general “missing data” scenario then, the present study differs from the usual cases of counterfactual analysis with missing values. We do not deal with a single (or more) variable(s) subject to missingness (to be imputed using a regression model), as in the case of the usual issues tackled by means of the multiple imputation methodology [
26]. The missing information that we want to deal with is represented by the “empty columns”of an ideally observable data set. Applying the SM methodology, the imputation procedure is carried out on the basis of the information that the donor(s) and the recipient do share. We use the covariates jointly observed between the donor and the recipient data sets (which are not the same covariates successively used for the PSM analysis) as a “bridge” for the imputation of the missing variables of interest for the impact evaluation purposes. SM is divided between the parametric and non-parametric approaches [
27] and the latter offers some relevant advantages with respect to the parametric one due to the fact that: (1) the data integration is based on “real” observed data; (2) the potential model misspecification bias can be avoided; and (3) the computational effort required for the whole imputation procedure is much lighter [
28]. Moreover, since the non-parametric SM allows researchers to use real observed data, it benefits the causal-effects analysis related to decision-making processes, which is the case of the policy evaluation exercises. Non-parametric micro SM (i.e., the so-called “hot deck” techniques) allows us to quickly and “easily” integrate primary and secondary data. For example, SM allows to enrich the information collected by ad hoc (project) surveys (which are both timely carried out and referred to the specific research topic) with the comprehensive but not timely information collected in the official statistics.
The objective of the paper is to explore the feasibility of combining SM methodology and PSM counterfactual approach analysis and to test the usefulness and practicability on a case study represented by selected impacts of the AESs in Emilia-Romagna.
The main novelties of the paper are with respect to the methodological grounding and the combined application of SM and PSM to policy impact evaluation. To the best of our knowledge, SM has been seldom applied in agricultural economics ([
19,
29]) and there are no PSM analyses carried out on newly-generated data sets built by means of different farm data source integration. Our proposed combination of methods fills this gap and aims to exploit the potentialities of different data sources integration in the context of impact evaluation within the non-experimental (observational) studies framework. On the operational side, this offers a valuable strategy to avoid new data collection costs and to take advantage from both the specificity of the information collected by means of ad hoc surveys and the elementary data knowledge acquired by means of the official statistics.
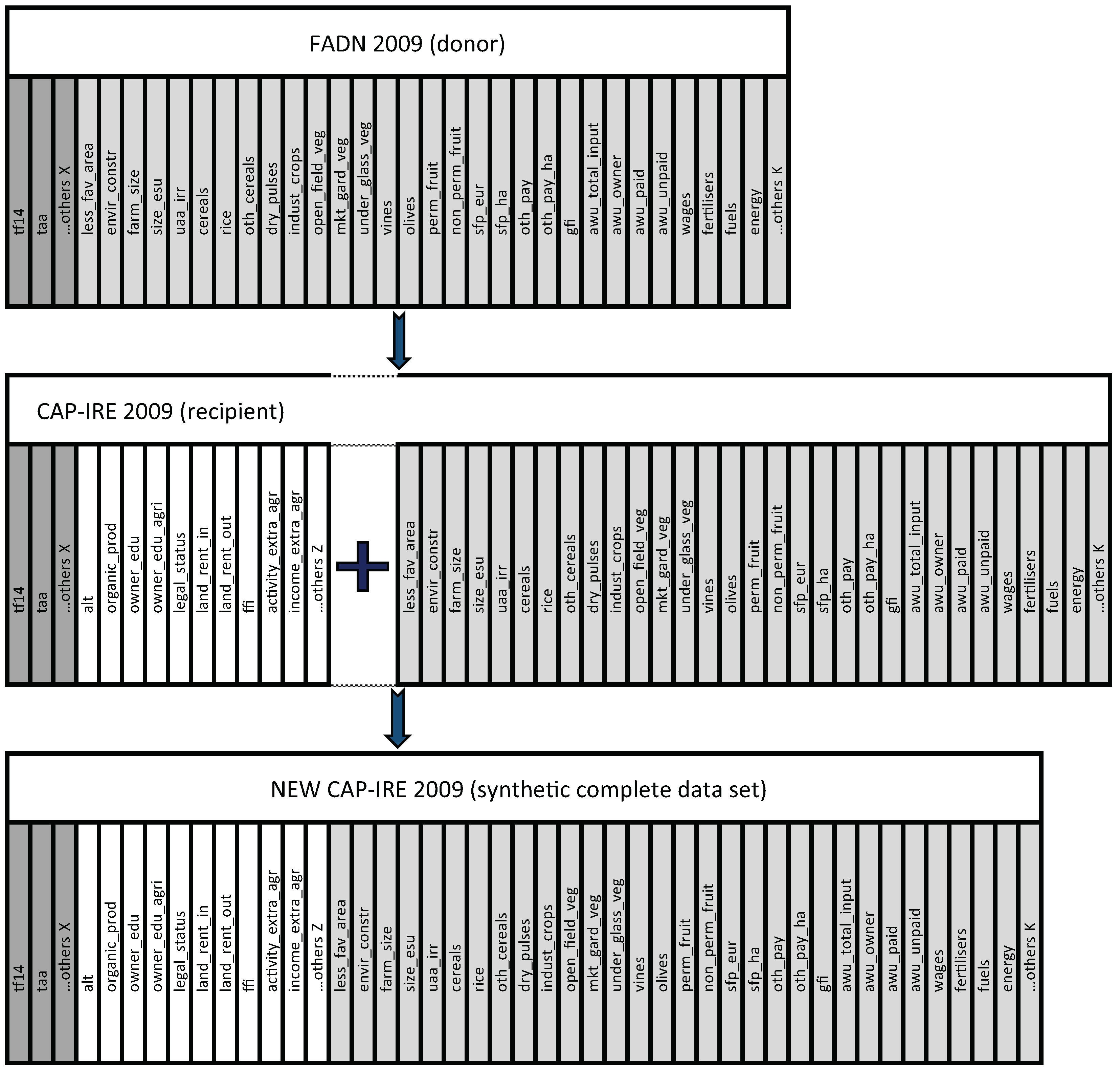
The present paper comprises two steps. First, we apply the hot deck techniques to integrate the information that is observed exclusively in a secondary data source (the FADN 2009 data set) into a primary data source (the CAP-IRE 2009 data set, acronym of the EU project “Assessing the multiple Impacts of the Common Agricultural Policies -CAP- on Rural Economies”). These are both already at our disposal. In this way, we enrich the specific information collected by an ad hoc EU project survey (CAP-IRE 2009) with the information collected by the FADN data source. The variables of interest are then imputed from the FADN 2009 donor data set to the CAP-IRE 2009 recipient data set. The imputation brings at the building of a new synthetic (complete) data set named the NEW CAP-IRE 2009. Second, this latter data set is used for a policy evaluation exercise concerning the AESs. The PSM analysis benefits from the integration of the aforementioned two data sources for two main reasons. First, by means of the CAP-IRE 2009 data set alone, it cannot be possible to construct, rigorously, a statistically significant model for the propensity score (PS) estimation (and hence to provide an unbiased and statistically significant estimation of the AESs effects on the outcomes variables). Second, the PSM analysis cannot be applied for investigating the effects of the treatment on the farms crop mix. The related model, indeed, needs a bigger set of covariates (e.g., including the individual crop UAA) which cannot be considered if the two data sets already at our disposal are used individually. The evaluation exercise focuses on the analysis of the Emilia-Romagna region (Italy) AESs and their effects on agricultural holdings. The exercise proposed here is based on the analysis of the AESs impact on the amount of the rent-in land and the diversity of the farm crop mix, two effects produced on farms by AESs uptake. The choice of this case study is to some extent data-driven due to both the availability of survey data and the accessibility of FADN individual data for the area.
The work is structured as follows. An essential overview of the literature related to both SM and PSM is presented in
Section 2. In this section we describe both the chosen combination of the non-parametric micro SM hot deck technique and distance function applied for data integration purposes, and the PSM estimator. Data used and the empirical applications of both data integration and the PSM analysis are described in
Section 3. In
Section 4 we present the results, discussing them in detail in
Section 5. Finally, in
Section 6, we conclude.
2. Methods
2.1. Statistical Matching Background
The integration of different data sources can be pursued resorting to several methods, among which statistical matching is the most up-to-date one [
27]. Particularly, the non-parametric micro SM allows us to create, from two or more different data sets, a synthetic (complete) data set by avoiding the assumption of any variables family distribution and/or the definition of any model parameters, such that all the real observed covariates which are relevant for the research purposes can be preserved and the model misspecification bias can be avoided [
28].
In particular, the non-parametric micro SM techniques are useful within the missing data scenarios characterised by the lack of entire variable(s). Hence, the targeted missing data scenario is not that of variable(s) subject to missingness, as in the case of the multiple imputation framework.
SM dates back to Okner [
30] and Kadane [
31] who proposed a first parametric approach to data integration. Successively, Rubin [
32] and Paass [
33] developed the SM techniques and the latter focused specifically on the non-parametric approach. Nevertheless, SM was only later coherently and unequivocally defined by several authors (see, for example, [
27,
34,
35]). Indeed, for decades, similar data integration procedures were indifferently addressed by practitioners as data fusion, record matching, and object identification, being finally formalized within the existing SM theoretical framework [
36].
In economics, SM has been applied mainly to integrate information from household surveys and official administrative registers (see [
37] and references therein). To the best of our knowledge, few applications concern agricultural holdings (and environmental-related measures), proposing the integration of the Italian FADN with the Italian Farm Structure Survey (FSS) [
29], and the combination of the Swiss FADN and FSS [
19]. Both these applications are based on the parametric SM approach. Hence, agricultural economics lacks of farm data applications where the hot deck techniques are applied, while no works present data integration applications aiming at supporting policy evaluation or policy impact assessment related to the AESs.
2.2. Statistical Matching and Propensity Score Matching Combined
The impact assessment of a policy that concerns voluntary measures such as the AESs (where farmers can voluntarily decide to uptake them or not) implies taking into account a relevant issue: the self-selection bias. For example, farms with the lowest compliance costs (e.g., low agricultural productivity) are expected to be more inclined to integrate the AESs. The rigorous construction of a statistically significant counterfactual for the farms which integrate the policy is then an essential condition for the robust assessment of its impact.
PSM serves this primal purpose and has been largely applied to several research topics ranging from medical to educational sciences and economics (see for example, [
14,
38,
39,
40,
41,
42] and references therein). In agricultural economics, PSM has been largely applied to investigate the effects of different policy treatments on the agricultural system, namely, to evaluate the effects generated by different farm programmes in different EU member states [
7,
43], to assess the impacts of different land preservation programs [
15,
44], to measure the effect of farmland preservation on farm profitability [
45], to estimate the capitalization of the Single Payment Scheme into land values [
46], to explore the effects generated on farms by the improvement of farm competitiveness and modernisation [
47,
48], and to evaluate effects of specific agricultural development programmes in developing countries (see, for example, [
49,
50,
51]).
There are instead few PSM applications concerning the AESs; Jaraite and Kažukauskas [
13] investigate the impact of AESs on farm expenditure for pesticide and fertilisers, considering these latter as proxies for the environmental effects of AESs. They apply a DID estimator to FADN data, finding neither a statistically significant effect on the outcome variables nor proving that there is a link between a larger share of subsidies and a stronger farmers’ motivation to improve their environmental performances. It is worth noting that the work highlights the data-driven nature of the analysis and the inappropriate aggregate level of the information used.
Chabé-Ferret and Subervie [
8] study the windfall effects on farms of some individual French AES measures, firstly deriving an economic model of utility maximisation for the farmers to test the assumptions under the DID approach, secondly testing for crossover effects, and thirdly applying the estimates in a cost-benefit modelling framework. They found that AES measures directly affect the diversification of the crop mix additionally with respect to the compliance of the requirements in absence of payments.
Udagawa et al. [
11] evaluate the AESs costs with respect to the Entry Level Stewardship on cereal farm incomes in Eastern England. Statistically significant effects on income (both including and not including the Entry Level Stewardship) are found. The work uses a data set generated by an official national survey contributing to FADN, highlighting the existence of three main issues: (1) the data set is neither a longitudinal survey nor a census; (2) the sample is hardly representative of the cereal farms population; and (3) there are several data limitations. The authors state also that the applied method is quite data-intensive and that available data present issues of missing covariates (e.g., on costs and socio-demographic information) and few observed units (e.g., the resulting sample of farms pairs in the common support region applying the most significant PSM estimator is composed of only 78 farms) [
11].
Arata and Sckokai [
2] compare aggregated AESs effects on the environment and the economic performance of farms among five EU member states. They found that in some EU member states there are positive effects of AESs, mainly concerning the reduction of farm expenditure for pesticides and fertilizers, crop diversification, total farm output, and hired labour. This work highlights also the difficulties arising from the fact that some information is too aggregated in the original accounts (e.g., for payments concerning different measures) and from the impossibility to sufficiently consider the heterogeneity of farms.
2.3. Hot Deck Technique and Distance Function Applied
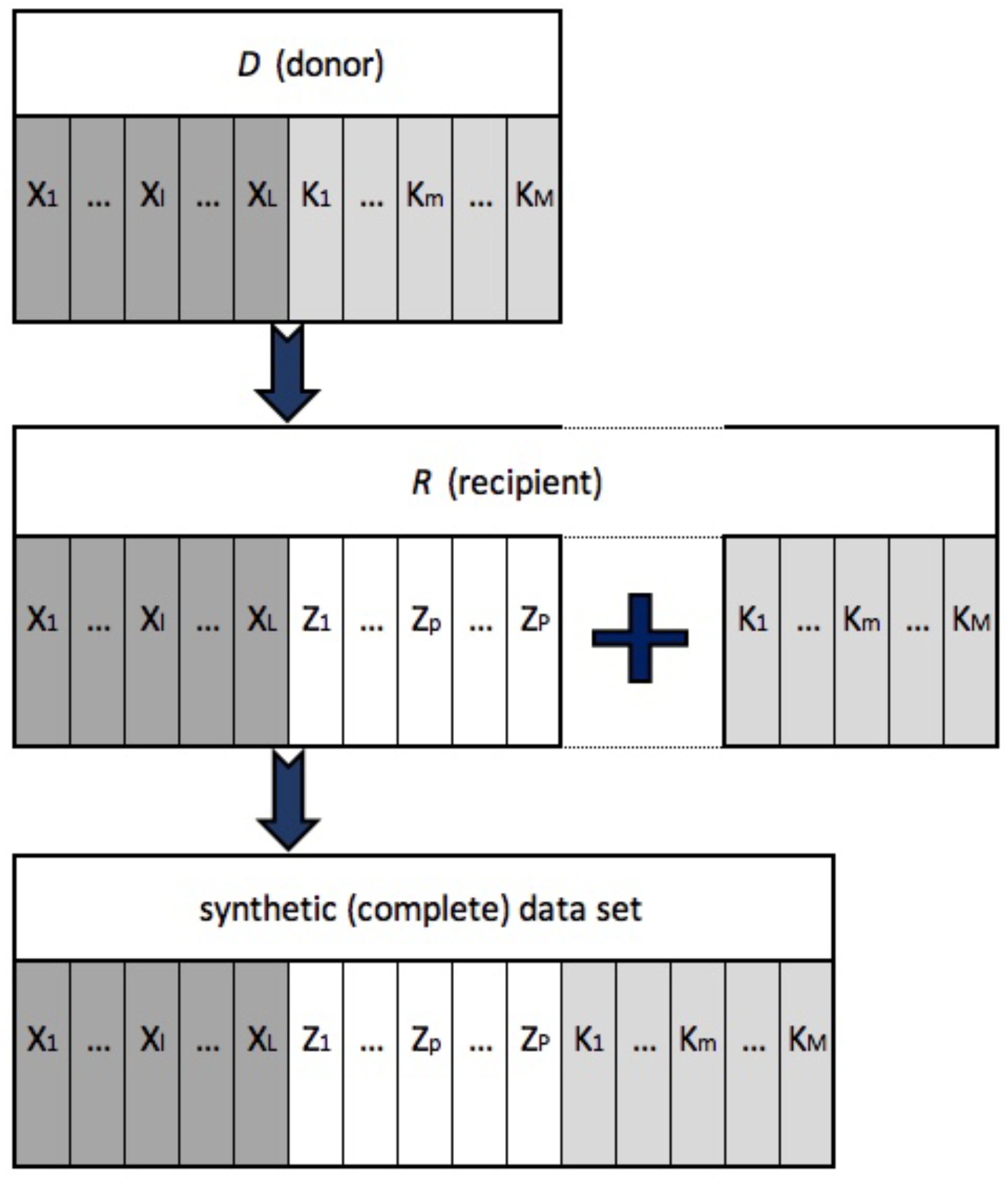
Let be the case that we have two data sets at our disposal. One is defined as the “recipient” data set (R) while the other is defined as the “donor” data set (D). Let X = (with being the vector of dimension, () and the vector of dimension ()), reflecting the set of variables which is observed both in R and D. (with being the vector of dimension ()) and (with being the vector of dimension ()) are two sets of variables which are observed either in R or in D, respectively. Hence, in two different data sets (R and D), we have at our disposal a set of jointly observed variables (X) and two sets of variables that are exclusively observed (Z and K). Therefore, let {, } be the recipient data set R and {, } the donor data set D. Finally, let the i-th and the j-th units (i.e., observations) be collected in R and D, respectively, with and . The aim is to integrate the recipient data set with some variables of interest observed only in the donor in order to have, in the most general case, the resulting synthetic (complete) data set: {, , }.
Figure 1 shows, in the most general case, the integration procedure by means of the SM methodology. The covariates jointly observed between the donor and the recipient data sets are used as a “bridge” for the imputation of the missing variables relevant for the impact evaluation purposes. Observed units are indeed matched in terms of their “proximity” with respect to the observed covariates.
The SM imputation holds upon the following assumptions:
R and
D are two data sets containing information on two representative samples of the same target population [
27].
R ∪
D must be considered as a unique sample of the
i.i.d. observations from the joint distribution of (
X,
Z,
K) [
27].
R and
D can have any dimensionality, i.e.,
and
must not be bounded to the condition
≤
[
52].
The proximity between two units is calculated by applying the constrained nearest neighbour distance hot deck (Nndc) technique [
27] combined with the Mahalanobis (Ms) distance function [
53]. For the sake of simplicity, let
, i.e., let
X be a single (continuous) variable jointly observed in
R and
D. The Nndc technique allows us to recursively exclude an already matched unit from the available pattern of donor units. Indeed, we match the
i-th and
j-th units as follows. Firstly:
so that we select the
j*-th unit to be the matched one; and, secondly:
Hence, we discard the already matched
j*-th unit from the pattern of donor ones. The Nndc technique is applied in combination with the Ms distance function. We refer to [
53] for a detailed discussion of both the distance functions and metrics. For the sake of brevity, we define the Ms distance function as follows:
where
is the covariance matrix of the jointly observed variables
X.
First, we apply the Nndc–Ms combination of the hot deck technique and distance function to integrate the information collected exclusively in data sets
R and
D. Second, we assess the imputation goodness, i.e., the goodness of the synthetic (complete) data set created, by means of the validation strategy proposed by [
52]. For the sake of brevity, the applied validation strategy is not discussed in detail here. In order to provide the reader of an easy tool for the quick evaluation of the imputation goodness, we also calculate the Hellinger distance index [
54], applied to quantify the similarity between two distributions.
2.4. The PSM Estimator
Let the i-th unit (with ) be a generic observation of the new synthetic (complete) data set generated by means of the Nndc–Ms combination, i.e., the recipient data set R enriched by the variables of interest originally collected only in the donor data set D.
We apply the PSM methodology to this new generated data set. Let be T a dichotomous variable indicating the assignment of the units to the treatment, so that = 0 indicates a control unit and = 1 indicates a treated one. Let Y be the outcome variable such that the outcome for the control unit and is the outcome for the treated one. In our application to the AESs, let T be the dichotomous variable which indicates the uptake of the AESs by the Emilia-Romagna farms; = 0 indicates that the i-th farm does not uptake the AESs, whereas = 1 indicates that the i-th farm does uptake the policy.
Let X be a sub-set of the variables observed in the new synthetic (complete) data set generated. These variables can be chosen among all the ones originally observed in R and the ones imputed from D but the variables that have been used for the previous imputation procedure by means of the SM methodology. Hence, if the new synthetic (complete) data set is {, , }, the variables can be chosen among these sets of variables with the exception of the previously used matching variables. In our application, for example, we observe both in the recipient data set R and the donor data set D several variables. Among these, the matching variables chosen for the imputation procedure by means of the SM are the farm specialization and the farm TAA, meaning that the sub-set could potentially consist of all the variables originally observed in R and the variables imputed from D with the exception of the farm specialization and the farm TAA (and the treatment and outcome variables selected).
Our interest is to estimate the treatment effect on the i-th unit, i.e., the impact of the uptake of the whole AESs package on the i-th farm. This could be done easily if we had at our disposal the information on the two different treatments for the outcome variable Y. Due to the fact that it is not possible to simultaneously observe both these potential outcomes on the same unit, in order to assess the treatment effect we have to measure the counterfactual mean difference in the outcome variables, i.e., the average treatment effect on treated (ATT). In other words, we have to estimate the effect of the treatment between a unit which undergoes it and its corresponding counterfactual, meaning that we have to consider the effect of the AESs uptake on the farms which uptake it and their counterfactual.
We assume that:
- 4.
The assignment to the treatment is independent of the potential outcomes conditional on the covariates [
38]:
i.e., we assume that there is unconfoundedness, meaning that we are assigning the treatment to units “ignoring” how they respond to the treatment (in other words ignoring the counterfactual potential outcomes). Therefore, we try to structure the analysis of the observational data so that what we observe can be thought of as if it has arisen from a regular assignment mechanism; i.e., if when we randomize, we pick the treated at random. This means we did not check their potential responses to the treatment to select them. Hence, we assume that the assignment to treatment is unconfounded given the pre-treatment characteristics observed in the units of analysis (i.e., the
covariates).
- 5.
The probability of the treatment assignment is bounded from 0 to 1 [
38]:
i.e., we assume overlap (or the so-called common support condition).
Due to the large number of covariates, we resort to the propensity score (PS) on the basis of which we match the donor and the recipient units. The PS is a balancing score [
16] and it is defined as follows:
where
is a potential balancing score. It is defined as the probability to be assigned to the treatment given some observed characteristics generically defined
X, i.e.:
If the treatment is ignorable given some covariates
X, then it is strongly ignorable given any balancing score and, at any value of a balancing score, the difference in means between treatment and control units is an unbiased estimate of the average treatment effect [
16].
We remove all the bias due to the observed covariates by conditioning on the PS, such that . Holding the hypothesis on the balancing score, all the observations which have the same PS have the same distribution of both the observable and unobservable characteristics, with them being independent from the treatment status. Hence, we assume the exposure to the treatment as if it were random.
The ATT is defined as follows:
and it is estimated such that:
where
indicates the observed outcomes of the treated units,
are their counterfactual outcomes, and
are the matched-treated units in the sample.
5. Discussion
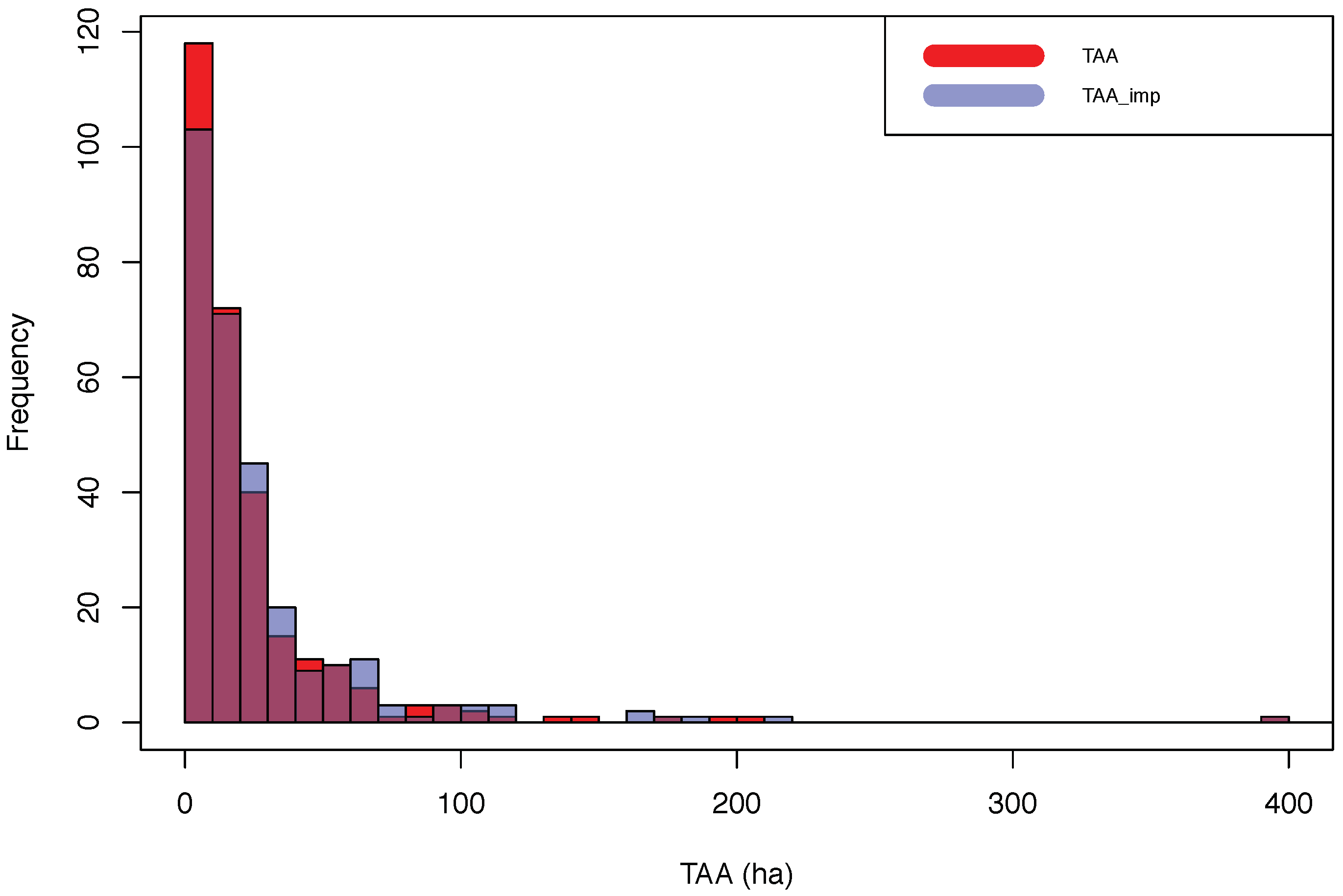
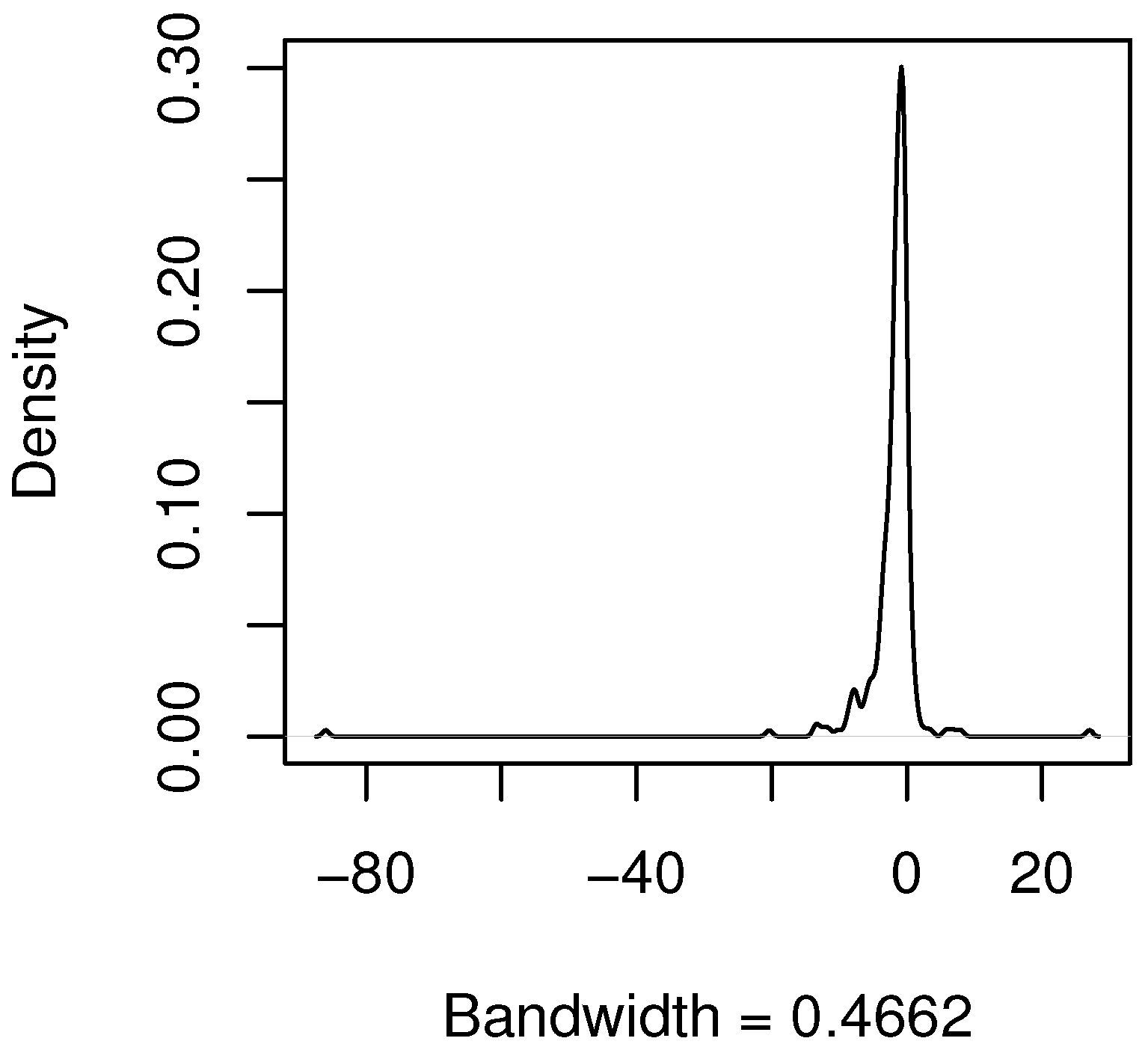
The application of the SM methodology in order to integrate the information collected exclusively in the FADN 2009 data set with that collected exclusively in the CAP-IRE 2009 data set led to the generation of a synthetic (complete) data set (i.e., NEW CAP-IRE 2009) resulting from an optimal imputation goodness. This latter data set can be used for the PSM analysis. Obviously, the integration of data from different sources can potentially lead to biased results. The magnitude of the uncertainty resulting in the final integrated data set can be increased by several factors, such as the initial sampling error that is spread by means of imputation, and the error in the imputation procedure itself (in other words, a poor imputation goodness). We have to add to these sources of uncertainty also the potential issues represented by the small dimension of the sample that will be finally taken into account for the PSM application. These sources of uncertainty can, together, lead to biased PSM analysis and represent an issue in terms of results interpretation. Hence, the assessment of the imputation goodness is a fundamental step to be carried out in order to ensure, at least, the lowest level of uncertainty in the integrated data, previous to the PSM application.
Results from the PSM application show that the estimated PS holds upon a model in which at least some of the most relevant covariates (significant at the 5%) were related to the AESs uptake and suggested by the literature are included. Exceptions are constituted by the agricultural education of the owner, the irrigated UAA and the family farm income that are significant at the 10% level. Thus, 279 final valid farms are considered for the estimation of the AESs effect on the rent-in land and crop diversity. We discarded six untreated farms which were laying outside the PS region of common support, included in the interval (0.152536, 0.928727). Six PS blocks are identified for each treated and control unit in order to guarantee the balance of the covariates and, consequently, of the estimated PS. Without the previous integration of the available data, i.e., by means of the solely CAP-IRE 2009 data set, such a model on the PS estimation could not be constructed in a statistically significant way. As
Table 5 shows, the covariates used only from the CAP-IRE 2009 data set (i.e., without the data integration that generated the NEW CAP-IRE 2009) are not statistically significant. No significant model could then be used for the PS estimation and the consequent estimation of the ATT.
The results from the ATT estimation show a statistically significant negative effect of the treatment on the rent-in land by farms. This result is inconsistent with most of the existing literature on the AESs. Indeed, Pufahl and Weiss [
7] show that there is a statistically significant effect of the AESs uptake on the farm size, which increases by 5.6% (mainly due to the fact that farms rent-in additional land). The aforementioned work also points out that treatment effects are heterogeneous among farms of different sizes and they vary both according to programme duration and payments per hectare. It is worth noting that Pufahl and Weiss [
7] highlight also how sample representativeness issues could have probably affected their results: large-scale intensive livestock farms that are over-represented in the farm sample they use tend to increase the farm size in order to reduce the cattle livestock densities and consequently become eligible for AES payment.
Arata and Sckokai [
2] find that the sub-sample of farms with a share of the AES payments on farm revenue higher than 5% tends to increase their size by means of the rented land both in the United Kingdom and Italy. As the authors point out, this increase could be linked either to the fact that “less favoured area” payments (which explicitly encourage farm extensification) foster the increase of the average farm size, or to the fact that farms attempt to offset the decrease in output value per hectare as a consequence of the participation in the organic farming. Moreover, Arata and Sckokai [
2] stress how both the well-known FADN representativeness issues and the aggregate level of information on the AES uptake could have biased their results. Indeed, a statistically significant positive effect of the AES on rent-in land is found only in 2 out of 10 sub-samples of the EU member states considered.
To the best of our knowledge, no other works focus on the AESs effects on farm production choices in relation to the amount of the rent-in land. Our results on the negative effect on rent-in land could be due to the fact that our farm sample, albeit small, does not suffer from the over-representation of larger and bigger farms both in terms of hectares and farm revenue as occurs, instead, for the data applications of the two aforementioned works and some others (see, for example, [
11,
13]). It is worth noting that even in our results (as for the aforementioned applications), treatment heterogeneity is not considered, but in contrast to these works, the potential bias due to the over-representation of: (1) the most involved farms (considered in terms of the payment per hectares); (2) the sub-sample considered [
2]; and (3) certain types of specialized farms [
7] is inconsistent.
The significant effect of the AESs on the reduction of crop diversity, albeit small, is relatively difficult to compare with the existing studies. Chabé-Ferret and Subervie [
8] found a small, significant, positive effect of the AESs on crop diversity, but the AES measures considered in their study explicitly require an increase in crop diversity. Arata and Sckokai [
2] also found a positive effect, but on the absolute number of crops. Our results are compatible with the fact that some of the prevailing AES measures in the area do not require longer crop rotation, while they may have had an insurance effect due to income stabilisation, hence inducing a simplification of the crop mix. There is also some anecdotal evidence in the area that AES measures tend to induce farms to focus on crops with higher returns from the participation in AESs, hence providing incentives to simplification of crop mixes (personal communication). While surely deeper analyses are required, the results of this model suggest that if crop diversity is a desired goal, it should be explicitly mentioned in the design of the AESs, which could otherwise could have a negative effect on it.
6. Conclusions
To address the sustainability of the agricultural sector, the EU has allocated a significant share of the CAP budget to the AESs, whose main goal is to incentivise the provision of environmental public goods in rural areas. However, their actual impact is debated and little evaluated. Data shortage, missing information, and sample representativeness issues can severely limit the potentialities of the counterfactual analysis approach and weaken the application of the PSM methodology for AES evaluation purposes. In this paper, we explore the feasibility of assessing the impacts of the AESs on farms of the Emilia-Romagna region by means of a PSM estimator applied to a new integrated data set (NEW CAP-IRE 2009) generated by means of the SM methodology application. Indeed, we aggregate the information collected by two different farm data sources (FADN data and the ad hoc project survey CAP-IRE 2009) with the non-parametric micro SM techniques.
The presented methodology consists in two steps. First, we use the SM methodology (namely the Nndc hot deck technique combined with the Ms distance function) to create a new data set which combines both the accounting and the structural information collected by the FADN data and the socio-demographic and policy information collected by the CAP-IRE 2009 survey. In the second step, we apply the PSM estimator to the new generated synthetic (complete) NEW CAP-IRE 2009 data set which collects, by means of integration, all the variables of interest relevant for a rigorous counterfactual analysis on the AESs. Otherwise, neither the information collected exclusively in the donor data set nor that collected exclusively in the recipient were alone, albeit necessary, sufficient for the PSM application.
Data integration performs well considering both the results obtained from the application of the validation strategy [
52] and the value of the Hellinger distance index. The assessment of the imputation goodness and the validation of the integration results show that the NEW CAP-IRE 2009 data set has been optimally constructed. The low level of uncertainty of the observed covariates in the NEW CAP-IRE 2009 data set suggests that its use for the PSM application must not be negatively recommended, at least not more so than all the other data sources on farms that are currently used for similar research purposes (such as the FADN data). However, the NEW CAP-IRE 2009 data set has, compared with the FADN data, an important advantage that is relevant for the consequent PSM analysis: it allows for us to (potentially) take into account all the information of interest that is necessary and sufficient for the counterfactual approach.
Results of the PSM estimator applied to the synthetic (complete) data set highlight that there is a statistically significant impact of the AESs on the decision of farmers to decrease both the rent-in land and the crop diversity of farms. Despite the fact that these results can be hardly generalised to discrepancies with the few works available from the literature, they show the scope for a better investigation of the impact of AESs on farm management parameters at the boundary with structural change, and not exclusively the impact of AESs on PG production and environmental service provision. Our results are statistically significant and benefit from the fact that the recipient data set does not suffer from the sample representativeness issues characterising similar works (e.g., [
2,
7]).
The present work has also some limitations. First, from the point of view of both the SM application and the impact evaluation of the AESs, due to the binding availability of data, and taking into account the need for differentiating the matching variables used for the imputation procedure from the variables successively used for the PS estimation and the ATT estimation, we carry out a somehow more limited imputation procedure compared to the one that we could ideally perform having planned and collected some others key relevant variables by means of a survey. This limitation hints at a potential trade off between using a wider number of variables, explicitly collected for impact evaluation purposes in an existing data set, versus the imputation of additional information, facing the need to have a more complete set of variables to assess the impact. Due to the unavailability of data specifically referring to the single measures that the Italian farms uptake within the overall AES package, our treatment variable takes into account just the uptake of the AESs package as a whole. This binary treatment could lead to biased results due to the fact that the heterogeneity of the measures (and hence the heterogeneous results that they can generate in terms of different impacts on the treated farms) cannot be properly taken into account. Nevertheless, this highlights even more the potentialities of the proposed combination of SM and PSM; such key information on the uptake of the single AES measures could be collected by means of specific survey and/or administrative register and official statistics in order to be then easily integrated with the yet existing data.
Second, the proposed PSM application led to a counterfactual analysis that lacks a time span, with the previous integration carried out while not having at our disposal different data sets referring to different years of the CAP programming. A further improvement of the present work could hence consist in the application of our combined SM-PSM methodology to data sets which collect information at different times of CAP programming, integrated so as to apply a PSM DID estimator.
Third, from the point of view of the SM methodology, the application could be fruitfully improved by trying to properly exploit the information on the sample structure and representativeness, resorting to the sample weights collected by the official data sources. This could help to overcome the assumption that R and D are two data sets containing information on two representative samples of the same target population. Indeed, the aforementioned assumption responds more to theoretical needs rather than being truly believed. It is commonly adopted but often not verified in practice; while using the sample weights, the researcher could explicit relax this assumption, making it possible to integrate the information collected with different sampling designs.
In spite of the aforementioned limits, this work aims to present and discuss the potentiality of integrating different data sources to perform more rigorous policy impact assessments. Through the use of the SM methodology, the overall information collected separately by means of two (or more) different data sets can be enriched. Hence, by generating a more comprehensive source of information that is necessary and sufficient for the PSM application, in the present paper we are able to jointly consider both the socio-demographic information and policy uptake variables originally observed in CAP-IRE 2009 and the structural and technical ones originally observed in FADN 2009. This benefits the overall PSM analysis due to the fact that, thanks to the SM, the PS estimation and the consequent ATT estimation could be performed using a wider range of variables, better covering the many determinants reported in the literature on the impact assessment of the AES and the CAP effects evaluation, including the socio-demographic characteristics of the farmer and the farm household, the geographical information on the farm, and its structural characteristics, etc.
The further development of the conjoint application of SM and PSM has several implications from the point of view of both policy impact assessment and research design. The importance of behavioural (risk aversion, trust, inequality aversion, etc.) and social characteristics are deemed to be more and more important in relation to the policy uptake and thus its effect. These features are usually collected and estimated through limited and expensive ad hoc project surveys and/or experiments. On one hand, the SM implementation would enable us to integrate the structural characteristics collected in the official statistics with specific information on individuals’ behaviour, thoughts, PG perceptions, willingness-to-pay for the provision of PGs, etc., and also on their socio-demographic characteristics. This would greatly improve the quantity and the quality of the available data and ameliorate the impact assessment exercise. In addition, this exercise also hints at the need for a more careful design of data collection together with policy monitoring and evaluation schemes, in such a way as to allow later matching and, altogether, a better exploitation of available results. There is the need for a systematic collection of the key relevant covariates to be included in the EU-financed project surveys in order to properly integrate them with the already collected FADN data. Finally, there is the need for the provision of quick and unbiased integration standards related to the FADN data and the several ad hoc project surveys carried out in the EU-financed projects. For example, it could be useful to include in the ad hoc project surveys on farms and farmers a few key questions on farms’ UAA, TAA, location, specialization, economic dimensions, and class of UAA, plus some relevant socio-demographic information on the farmers. This will allow the integration of the information collected by the FADN data “easily” and quickly, in order to be more recent and up-to-date but also more comprehensive.
Altogether, this study represents a suitable solution to tackle data shortage challenges but also to rigorously approach a counterfactual analysis by means of PSM on already available data. SM and PSM can be successfully combined and applied to allow researchers to deal with major practical issues (e.g., lack of data, surveys costs, time needs, etc.) but also to properly account for the often overlooked features of the observational studies context, e.g., self-selection bias, unconfoundedness reliability, etc.