A Countermeasure for Preventing Flexibility Deficit under High-Level Penetration of Renewable Energies: A Robust Optimization Approach
Abstract
1. Introduction
2. Materials and Methods
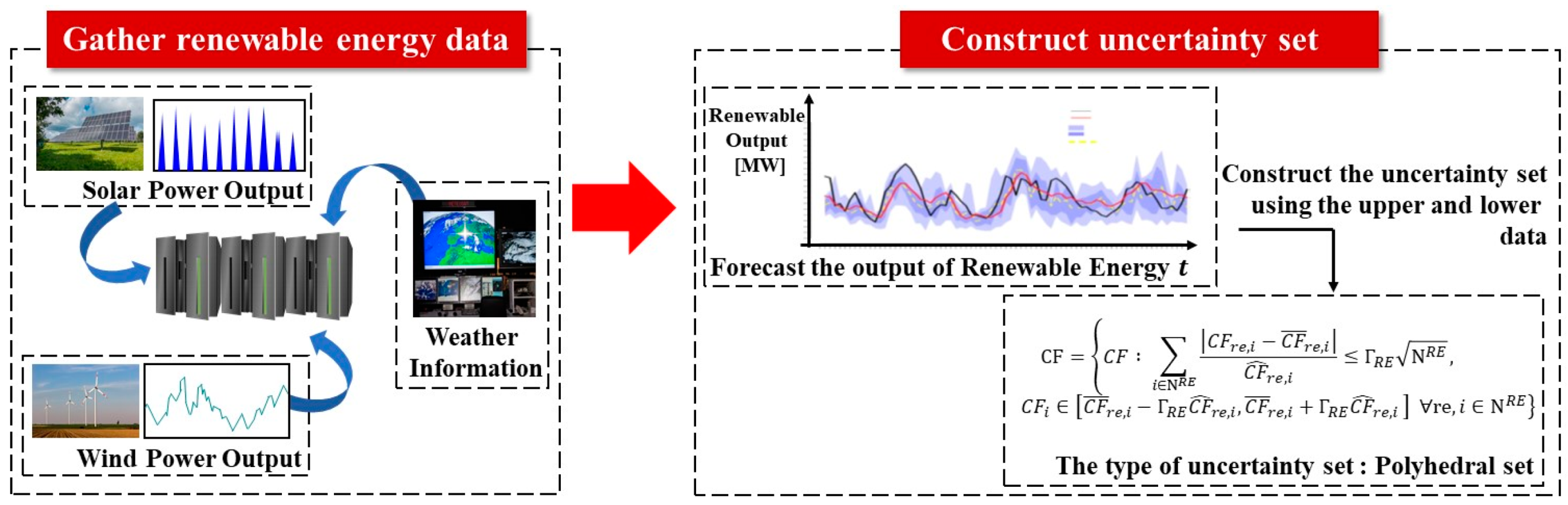
2.1. Uncertain Parameter
2.2. Mathematical Formulation
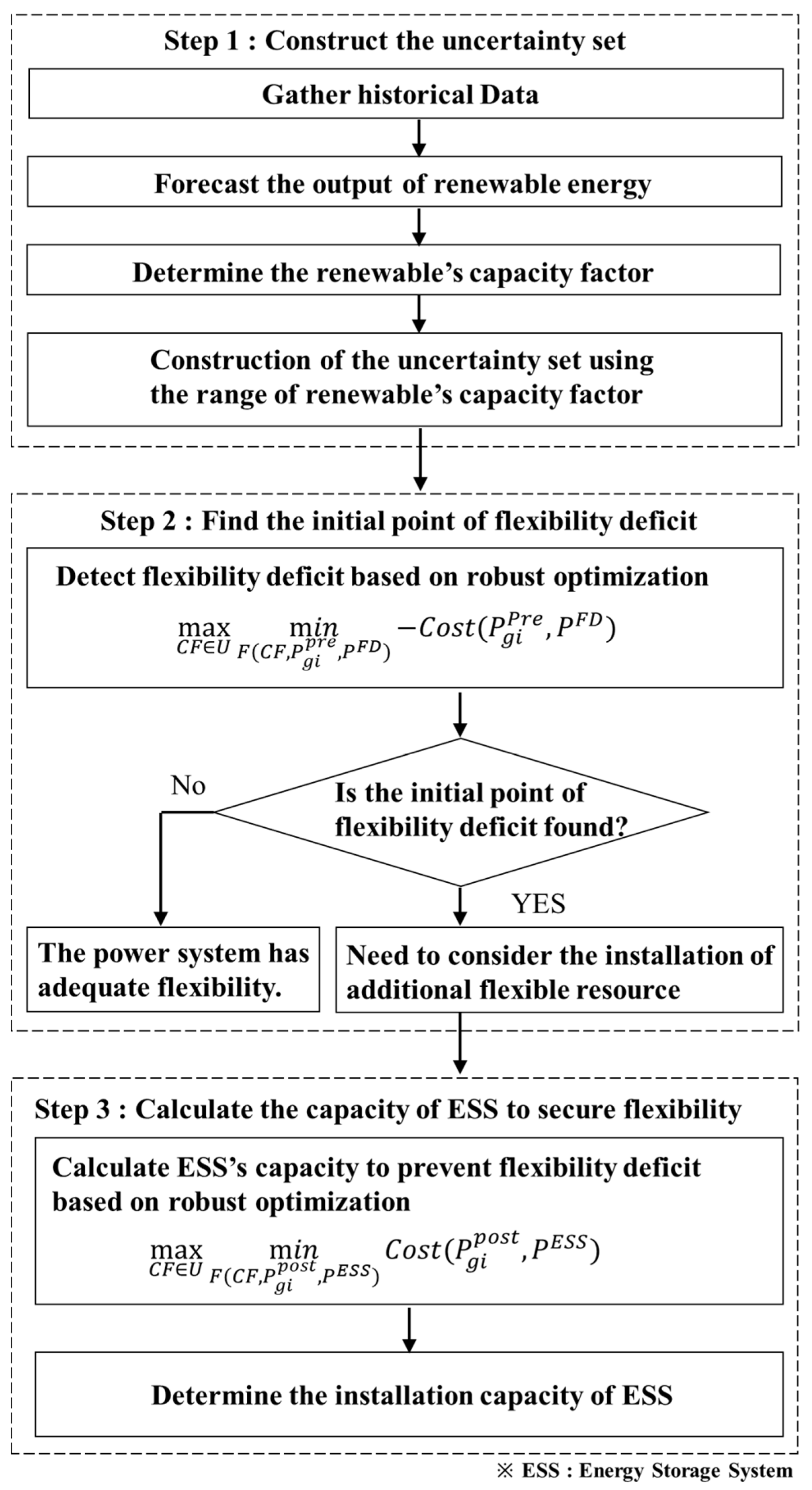
2.2.1. Searching for the Initial Point of Flexibility Deficit within the Uncertainty Set
Objective Function
Constraints
2.2.2. Determining the Capacity of Flexible Resources to Ensure Nonnegative Flexibility
Objective Function
Constraints
2.3. Description of the Proposed Method
3. Simulation and Results
3.1. Data Description
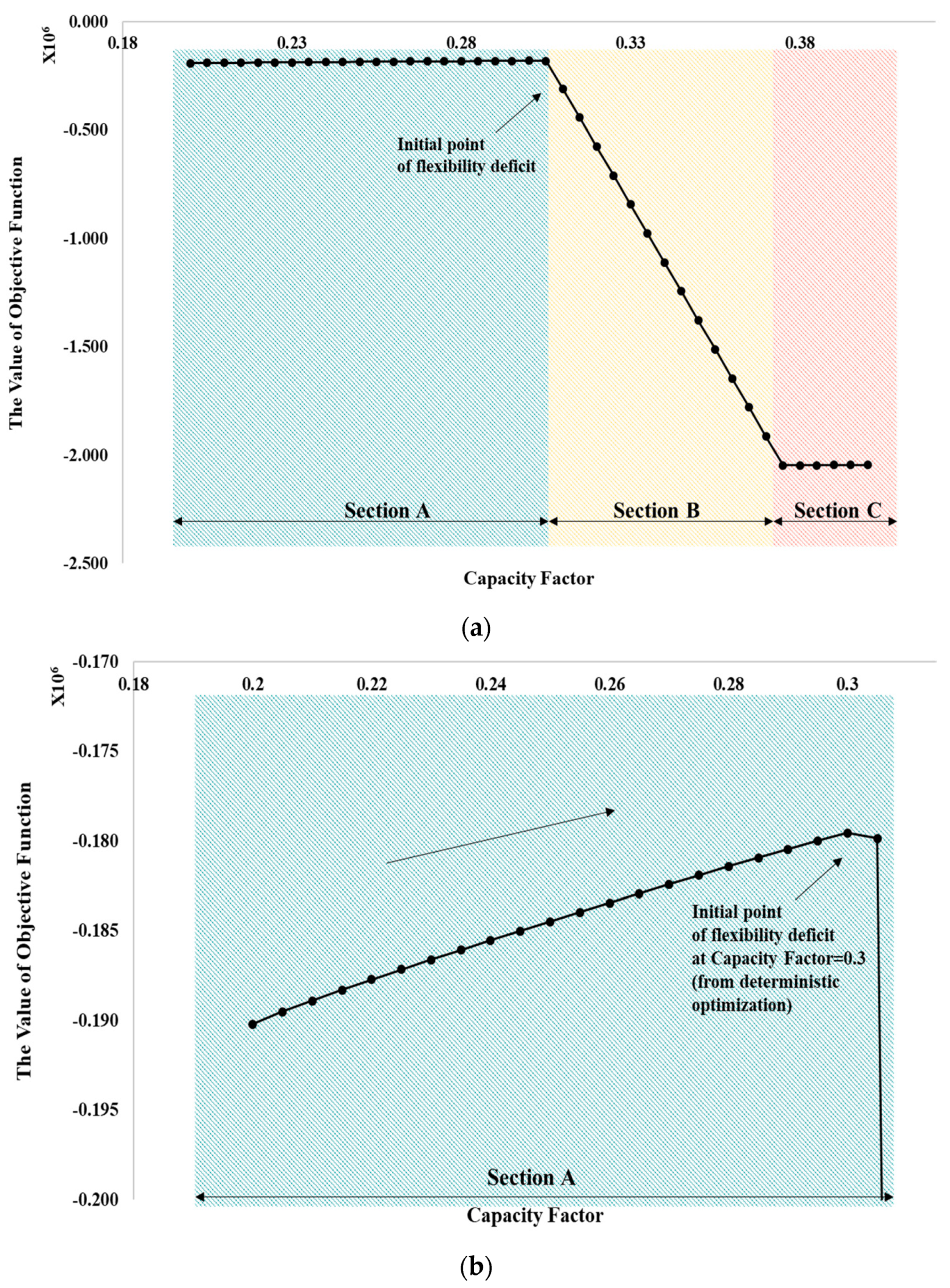
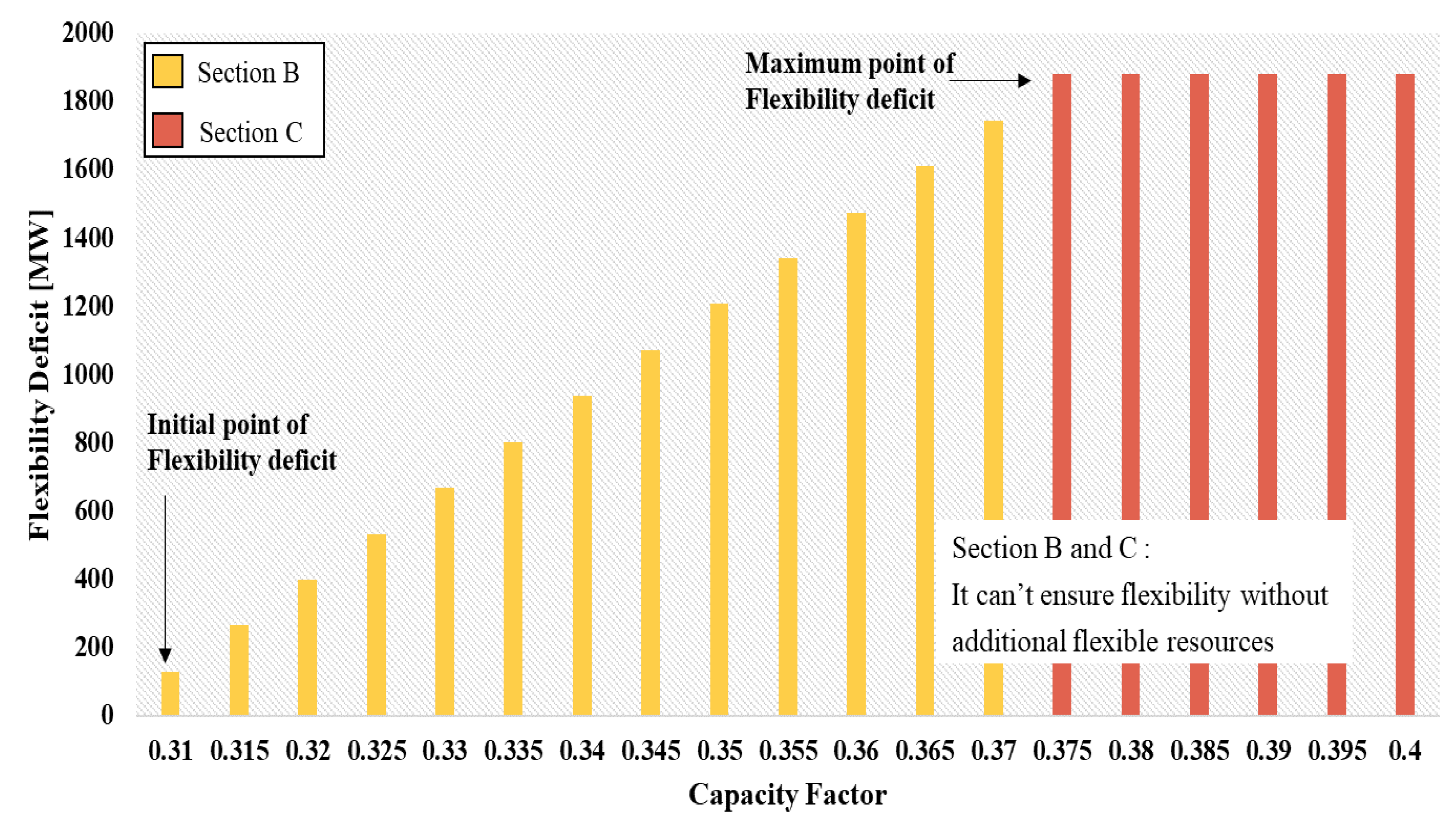
3.2. Searching for the Initial Point of Flexibility Deficit with Robust Optimization
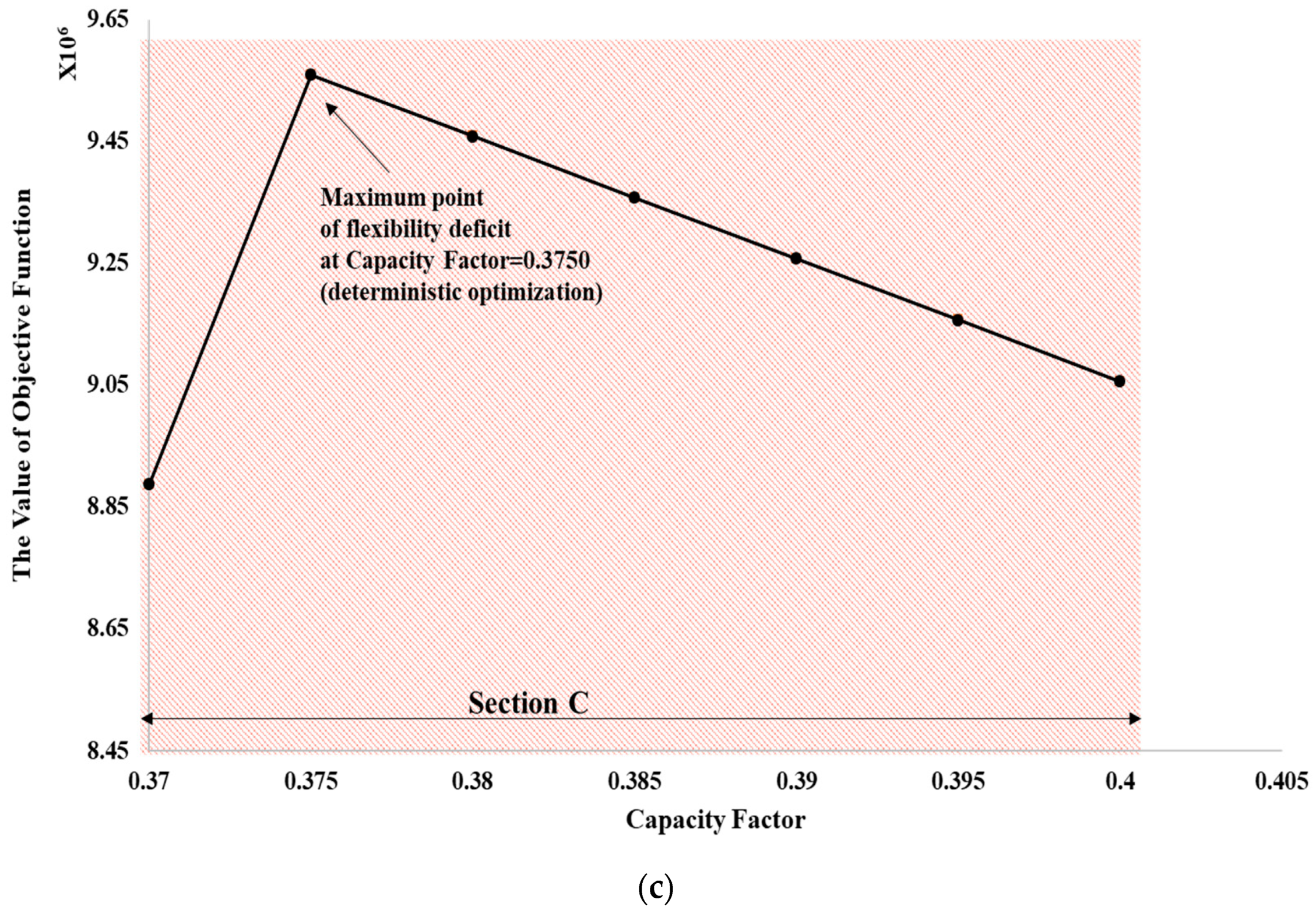
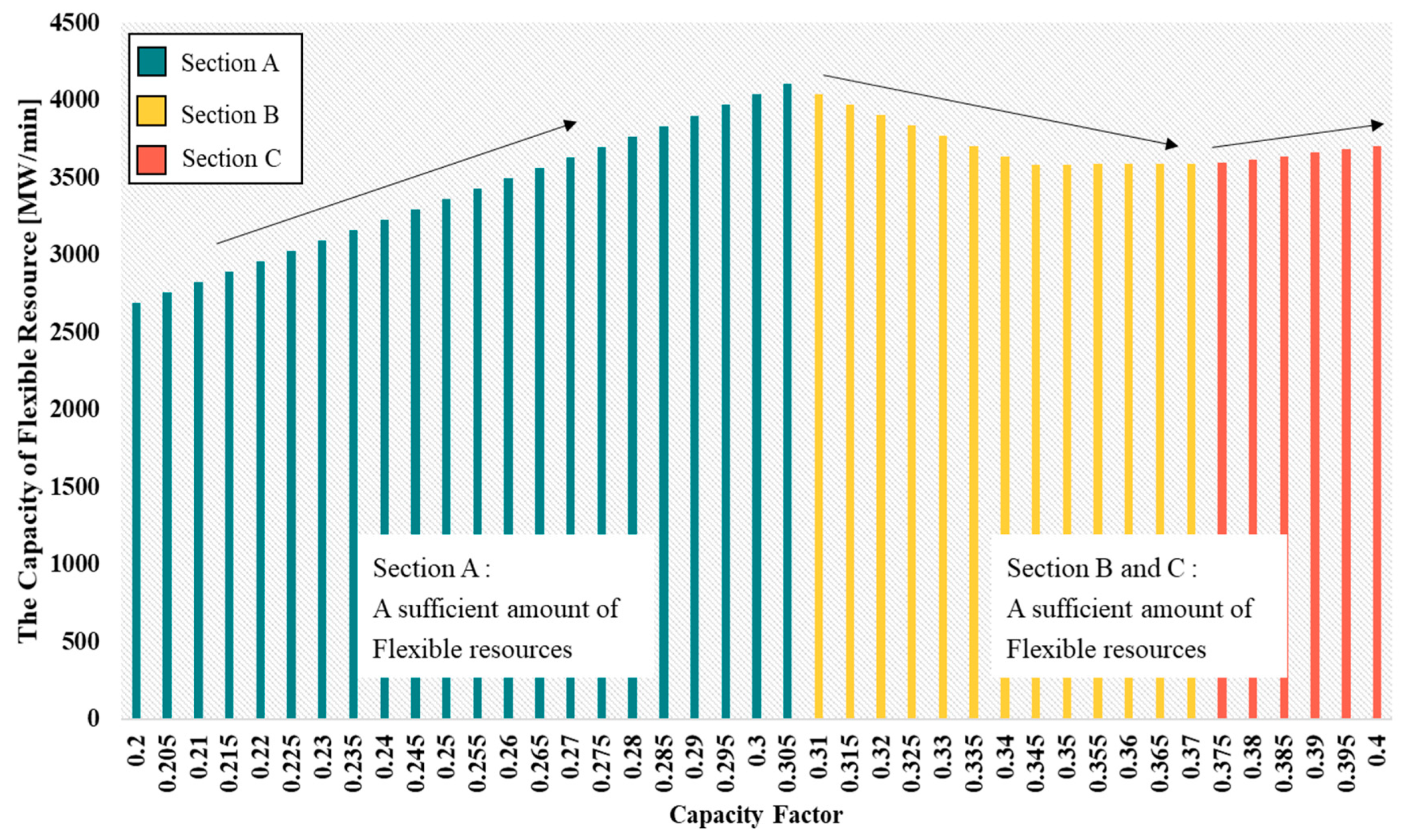
3.3. Determining the Capacity of Eenergy Storage System(ESS) to Ensure Nonnegative Flexibility
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- The Ministry of Trade, Industry and Energy. New and Renewable Energy 3020 Implementation Plan; The Ministry of Trade, Industry and Energy: Sejong-si, Korea, 2017. (In Korean)
- The Ministry of Trade, Industry and Energy. The 8th Basic Plan for Long-Term Electricity Supply and Demand (2017–2031); The Ministry of Trade, Industry and Energy: Sejong-si, Korea, 2017. (In Korean)
- Stram, B.N. Key challenges to expanding renewable energy. Energy Policy 2016, 96, 728–734. [Google Scholar] [CrossRef]
- Kunz, H.; Hagens, N.; Balogh, S. The Influence of Output Variability from Renewable Electricity Generation on Net Energy Calculations. Energies 2014, 7, 150–172. [Google Scholar] [CrossRef]
- Haas, J.; Cebulla, F.; Cao, K.; Nowak, W.; Palma-Behnke, R.; Rahmann, C.; Mancarella, P. Challenges and trends of energy storage expansion planning for flexibility provision in low-carbon power systems—A review. Renew. Sustain. Energy Rev. 2017, 80, 603–619. [Google Scholar] [CrossRef]
- Bae, M.; Lee, H.; Lee, B. An Approach to Improve the Penetration of Sustainable Energy Using Optimal Transformer Tap Control. Sustainability 2017, 9, 1536. [Google Scholar]
- Liu, Z.; Chen, Y.; Luo, Y.; Zhao, G.; Jin, X. Optimized Planning of Power Source Capacity in Microgrid, Considering Combinations of Energy Storage Devices. Appl. Sci. 2016, 6, 416. [Google Scholar] [CrossRef]
- Shigenobu, R.; Noorzad, A.; Muarapaz, C.; Yona, A.; Senjyu, T. Optimal Operation and Management of Smart Grid System with LPC and BESS in Fault Conditions. Sustainability 2016, 8, 1282. [Google Scholar] [CrossRef]
- Tuohy, A. Flexibility in Transmission and Resource Planning; EPRI: Palo Alto, CA, USA, 2014. [Google Scholar]
- EPRI. Metrics for Quantifying Flexibility in Power System Planning; EPRI: Palo Alto, CA, USA, 2014. [Google Scholar]
- Cochran, J.; Miller, M.; Zinaman, O.; Milligan, M.; Arent, D.; Palmintier, B.; O’Malley, M.; Mueller, S.; Lannoye, E.; Tuohy, A.; et al. Flexibility in 21st Century Power Systems; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2014. [Google Scholar]
- Danish Energy Agency. Flexiblity in the Power System—Danish and European Experience, 2015. Available online: https://ens.dk/sites/ens.dk/files/Globalcooperation/flexibility_in_the_power_system_v23-lri.pdf (accessed on 9 November 2018).
- Poncela, M.; Purvins, A.; Chondrogiannis, S. Pan-European Analysis on Power System Flexibility. Energies 2018, 11, 1765. [Google Scholar] [CrossRef]
- Lannoye, E.; Daly, P.; Tuohy, A.; Flynn, D.; O’Malley, M. Assessing Power System Flexibility for Variable Renewable Integration: A Flexibility Metric for Long-Term System Planning. CIGRE Sci. Eng. J. 2015, 3, 26–39. [Google Scholar]
- California ISO. Final Flexible Capacity Needs Assessment for 2019, 2018. Available online: http://www.caiso.com/informed/Pages/StakeholderProcesses/FlexibleCapacityNeedsAssessmentProcess.aspx (accessed on 9 November 2018).
- California ISO. Flexible Ramping Product Uncertainty Calculation and Implementation Issues, 2018. Available online: https://www.caiso.com/Documents/FlexibleRampingProductUncertaintyCalculationImplementationIssues.pdf (accessed on 9 November 2018).
- Rodrigues, E.M.G.; Godina, R.; Santos, S.F.; Bizuayehu, A.W.; Contreras, J.; Catalão, J.P.S. Energy storage systems supporting increased penetration of renewables in islanded systems. Energy 2014, 75, 265–280. [Google Scholar] [CrossRef]
- Denholm, P. Energy storage to reduce renewable energy curtailment. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–4. [Google Scholar]
- Jirutitijaroen, P.; Singh, C. Reliability Constrained Multi-Area Adequacy Planning Using Stochastic Programming with Sample-Average Approximations. IEEE Trans. Power Syst. 2008, 23, 504–513. [Google Scholar] [CrossRef]
- Hajipour, E.; Bozorg, M.; Fotuhi-Firuzabad, M. Stochastic Capacity Expansion Planning of Remote Microgrids with Wind Farms and Energy Storage. IEEE Trans. Sustain. Energy 2015, 6, 491–498. [Google Scholar] [CrossRef]
- Zhan, Y.; Zheng, Q.P.; Wang, J.; Pinson, P. Generation Expansion Planning with Large Amounts of Wind Power via Decision-Dependent Stochastic Programming. IEEE Trans. Power Syst. 2017, 32, 3015–3026. [Google Scholar] [CrossRef]
- Alharbi, H.; Bhattacharya, K. Stochastic Optimal Planning of Battery Energy Storage Systems for Isolated Microgrids. IEEE Trans. Sustain. Energy 2018, 9, 211–227. [Google Scholar] [CrossRef]
- Ruiz, C.; Conejo, A.J. Robust transmission expansion planning. Eur. J. Oper. Res. 2015, 242, 390–401. [Google Scholar] [CrossRef]
- Dehghan, S.; Amjady, N. Robust Transmission and Energy Storage Expansion Planning in Wind Farm-Integrated Power Systems Considering Transmission Switching. IEEE Trans. Sustain. Energy 2016, 7, 765–774. [Google Scholar] [CrossRef]
- Liu, D.; Shang, C.; Cheng, H. A two-stage robust optimization for coordinated planning of generation and energy storage systems. In Proceedings of the 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 26–28 November 2017; pp. 1–5. [Google Scholar]
- Thatte, A.A.; Sun, X.A.; Xie, L. Robust Optimization Based Economic Dispatch for Managing System Ramp Requirement. In Proceedings of the 2014 47th Hawaii International Conference on System Sciences, Waikoloa, HI, USA, 6–9 January 2014; pp. 2344–2352. [Google Scholar]
- Ampatzis, M.; Nguyen, P.H.; Kamphuis, I.R.; van Zwam, A. Robust optimisation for deciding on real-time flexibility of storage-integrated photovoltaic units controlled by intelligent software agents. IET Renew. Power Gener. 2017, 11, 1527–1533. [Google Scholar] [CrossRef]
- Lorca, A.; Sun, X.A. Adaptive Robust Optimization with Dynamic Uncertainty Sets for Multi-Period Economic Dispatch Under Significant Wind. IEEE Trans. Power Syst. 2015, 30, 1702–1713. [Google Scholar] [CrossRef]
- Yi, J.; Lyons, P.F.; Davison, P.J.; Wang, P.; Taylor, P.C. Robust Scheduling Scheme for Energy Storage to Facilitate High Penetration of Renewables. IEEE Trans. Sustain. Energy 2016, 7, 797–807. [Google Scholar] [CrossRef]
- Kim, J.; Choi, Y.; Ryu, S.; Kim, H. Robust Operation of Energy Storage System with Uncertain Load Profiles. Energies 2017, 10, 416. [Google Scholar] [CrossRef]
- Ben-Tal, A.; El Ghaoui, L.; Nemirovski, A. Robust Optimization; Princeton University Press: Princeton, NJ, USA, 2009; Volume 28. [Google Scholar]
- Ben-Tal, A.; Nemirovski, A. Robust optimization—Methodology and applications. Math. Program. 2002, 92, 453–480. [Google Scholar] [CrossRef]
- Steuben, J.C.; Turner, C.J. Robust optimization of mixed-integer problems using NURBs-based metamodels. J. Comput. Inf. Sci. Eng. 2012, 12, 041010. [Google Scholar] [CrossRef]
- Bertsimas, D.; Sim, M. The price of robustness. Oper. Res. 2004, 52, 35–53. [Google Scholar] [CrossRef]
- Bertsimas, D.; Dunning, I.; Lubin, M. Reformulation versus cutting-planes for robust optimization. Comput. Manag. Sci. 2016, 13, 195–217. [Google Scholar] [CrossRef]
- Yuan, Y.; Li, Z.; Huang, B. Robust optimization under correlated uncertainty: Formulations and computational study. Comput. Chem. Eng. 2016, 85, 58–71. [Google Scholar] [CrossRef]
- Bertsimas, D.; Brown, D.B.; Caramanis, C. Theory and Applications of Robust Optimization. SIAM Rev. 2011, 53, 464–501. [Google Scholar] [CrossRef]
- Löfberg, J. Automatic robust convex programming. Optim. Methods Softw. 2012, 27, 115–129. [Google Scholar] [CrossRef]
| Total Number | Ramp Rate (MW/h) | Pmin (MW) | Pmax (MW) | ai (₩/h) | bi (₩/MWh) | ci (₩/MW2h) | |
|---|---|---|---|---|---|---|---|
| Gas turbine | 18 | 26.669 | 259.500 | 627.044 | 370.5158 | 1.29171 | 0.000976 |
| Hydro | 22 | 119.154 | 90.227 | 280.727 | 16.54394 | 1.70669 | 0.006959 |
| Coal-fuel | 60 | 15.702 | 357.353 | 649.480 | 164.3439 | 1.82554 | 0.000317 |
| LNG | 25 | 25.564 | 230.800 | 614.139 | 94.9775 | 1.43732 | 0.000270 |
| Nuclear | 18 | 1.766 | 973.111 | 1188.333 | 473.3557 | 1.69536 | 0.000296 |
| Capacity Factor | Value of Objective Function | |
|---|---|---|
| Robust | 0.3051 | −179,890 |
| Capacity Factor | Value of Objective Function | Installation of ESS (MW) | |
|---|---|---|---|
| Deterministic | 0.2000 | 215,279 | 0 |
| Deterministic | 0.4000 | 9,056,140 | 1777.4 |
| Robust | 0.3749 | 9,545,556 | 1875.7 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, J.; Shin, H.; Song, H.; Lee, B. A Countermeasure for Preventing Flexibility Deficit under High-Level Penetration of Renewable Energies: A Robust Optimization Approach. Sustainability 2018, 10, 4159. https://doi.org/10.3390/su10114159
Jeong J, Shin H, Song H, Lee B. A Countermeasure for Preventing Flexibility Deficit under High-Level Penetration of Renewable Energies: A Robust Optimization Approach. Sustainability. 2018; 10(11):4159. https://doi.org/10.3390/su10114159
Chicago/Turabian StyleJeong, Jinwoo, Heewon Shin, Hwachang Song, and Byongjun Lee. 2018. "A Countermeasure for Preventing Flexibility Deficit under High-Level Penetration of Renewable Energies: A Robust Optimization Approach" Sustainability 10, no. 11: 4159. https://doi.org/10.3390/su10114159
APA StyleJeong, J., Shin, H., Song, H., & Lee, B. (2018). A Countermeasure for Preventing Flexibility Deficit under High-Level Penetration of Renewable Energies: A Robust Optimization Approach. Sustainability, 10(11), 4159. https://doi.org/10.3390/su10114159





