In most remote islands, centralized generation of electricity is nearly impossible due to their unique conditions, and it makes diesel generation the primary source for power generation. High dependence on diesel price puts a huge economic and environmental burden on Small Island Developing States (SIDS). Reducing heavy reliance on imported diesel for power generation has been an important agenda for SIDS. This challenge has been encouraging SIDS to increase the deployment of renewable energy systems [
1]. The recent technology development provides opportunities for the Maldives to deploy more renewable energy systems by reducing the costs of solar photovoltaics (PV) with or without energy storage systems (ESS) as well as increasing their efficiencies [
2]. However, adopting renewable energy systems is still burdensome for the Maldives because of its initial costs and insufficient financial resources. Also, the countries lack understanding about whether a renewable system is an economically feasible option compared to conventional energy systems. Since the countries have limited financial resources and capacity, the economic feasibility is inevitably an important factor for the selection of energy systems. Therefore, achieving grid parity where the cost of renewables becomes the same or less than that of conventional sources is an important milestone for the successful diffusion of renewables in SIDS.
Reducing high diesel dependence and adopting renewable systems are also an important national agenda for the Maldives, one of the SIDS. The Maldives is in the Indian Ocean and is composed of more than 1000 islands. Due to its location in tropical zones, the Maldives has a high potential for solar systems. The country reached 100% electrification rate, but the dominant system is still off-grid diesel generation. The Maldives has established an ambitious target of achieving 100% renewable energy by 2020 in 2009 and encouraged the deployment of renewable systems [
3]. However, the pace of the deployment of renewable systems has been slow, and only 1.28% of electricity generated is provided by renewables [
4].
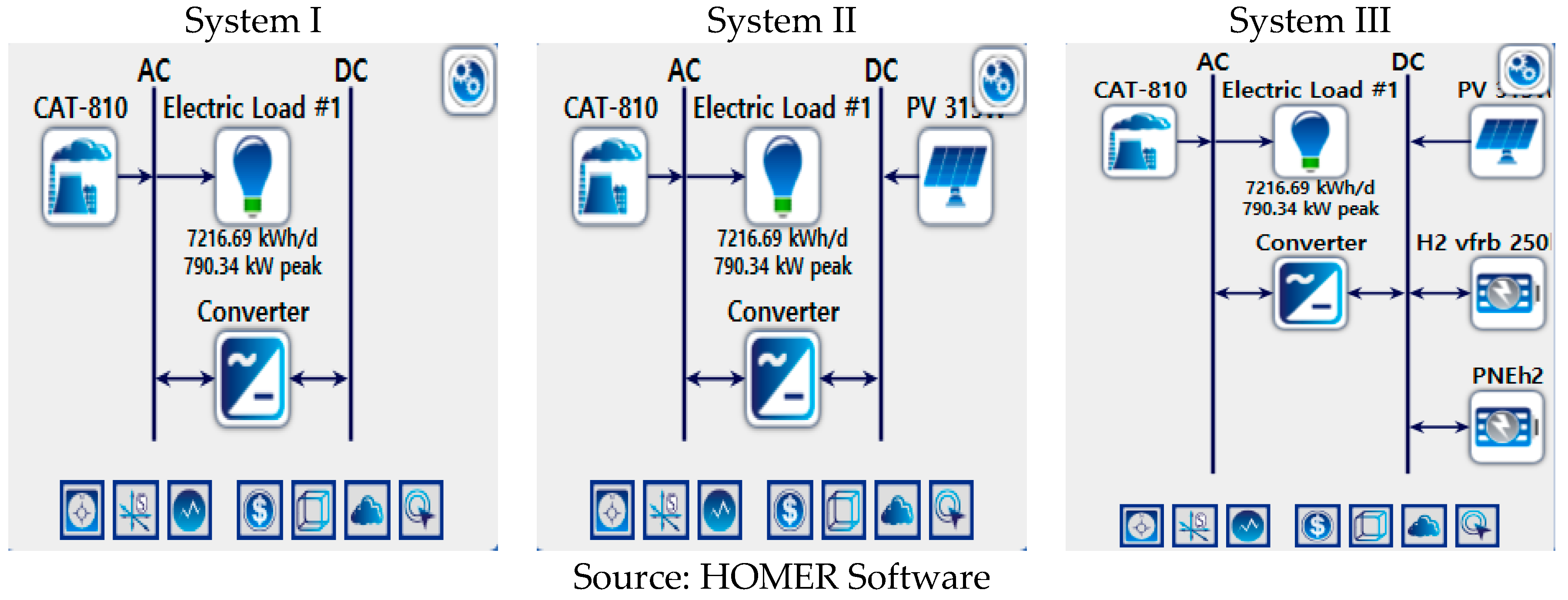
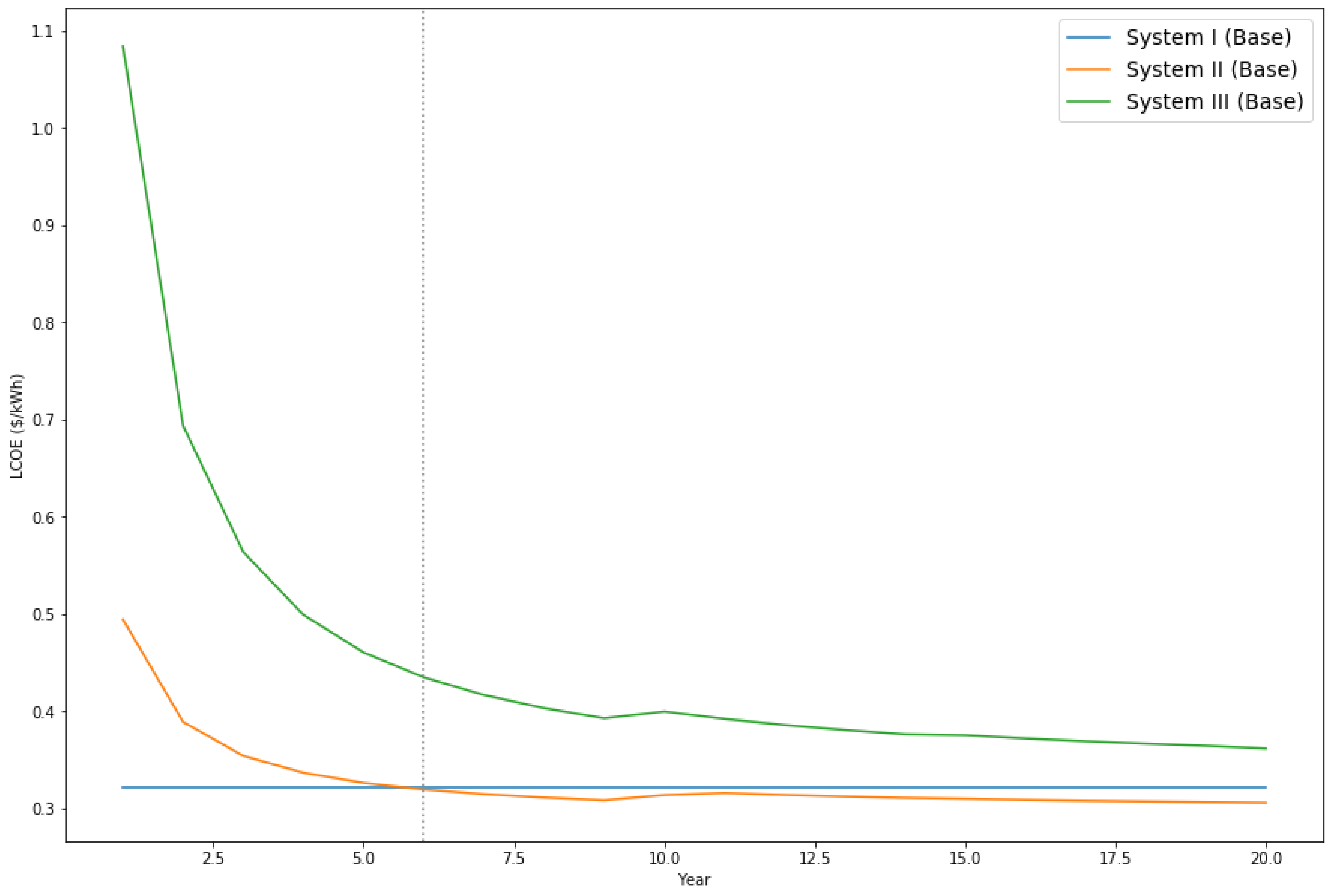
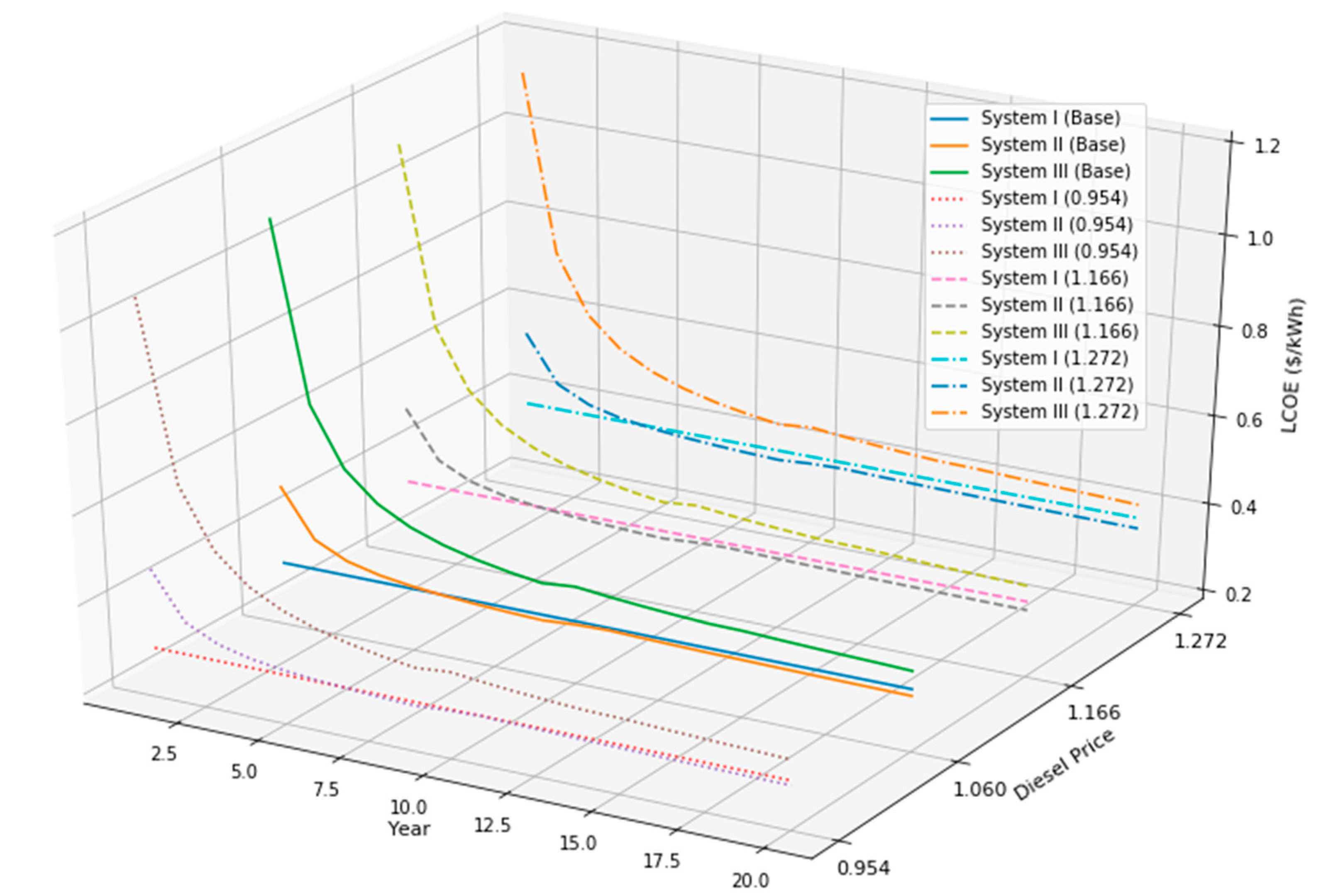
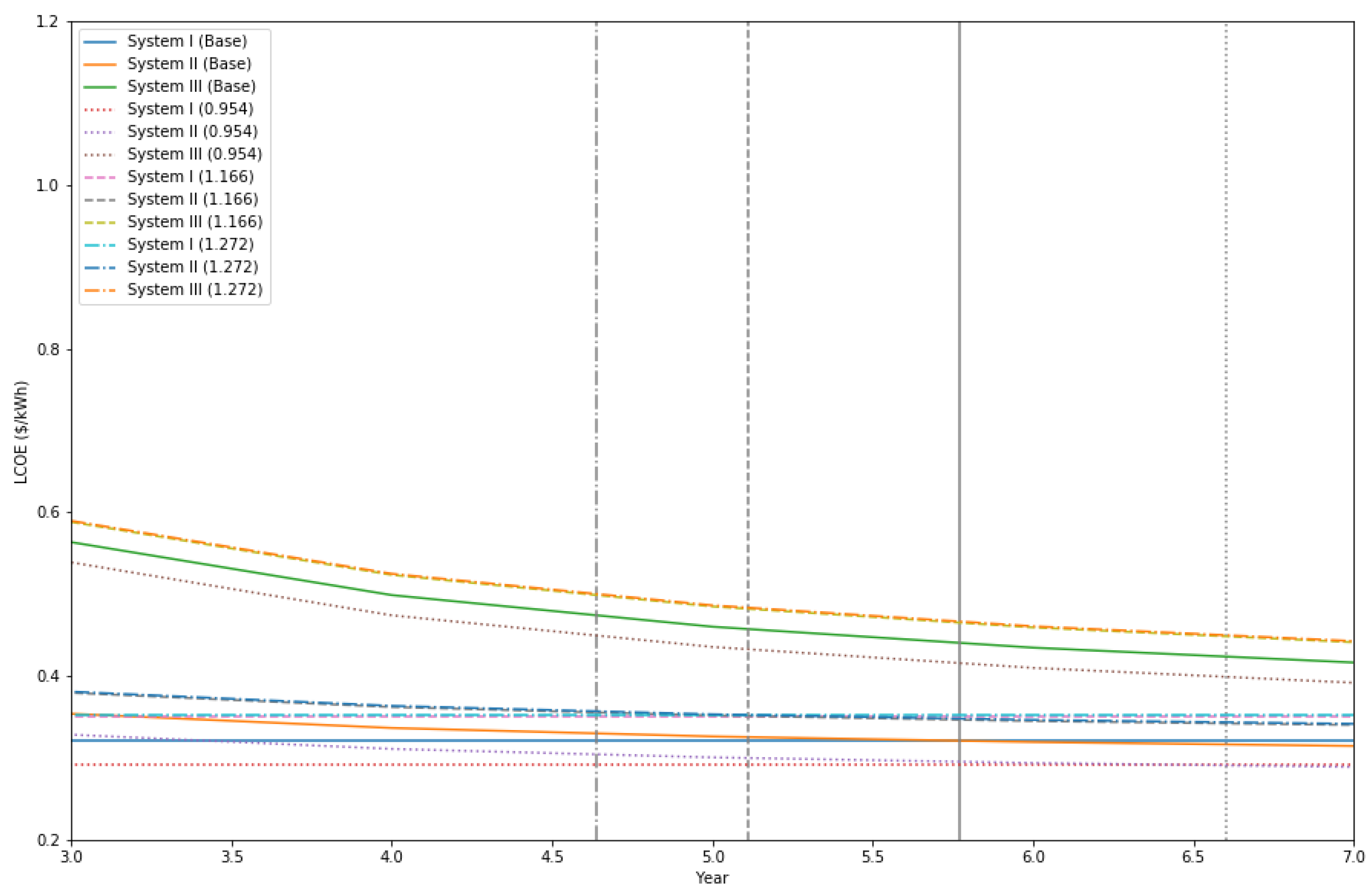
The paper examines the possible timeframe for reaching grid parity in a SIDS country from the case project of replacing an existing diesel generator to photovoltaic power generation with ESS in a resort on Kuda Bandos Island, Maldives. Kuda Bandos Island is located near Male, the capital of the Maldives. The main economic activity of the island is tourism, so the resort on the island has demands for establishing a sustainable energy system. Also, this small island is remote from other islands, and the resort is the only demand source for energy. Thus, both the reliability and economic feasibility of the energy system are important. The project is funded by the Korea Institute of Energy Technology Evaluation and Planning and the Ministry of Trade, Industry, and Energy of the Republic of Korea. The purpose of the project is to replace the existing diesel generator to PV with ESS and diesel generator. The project implements the installation of PV 290 kW with Power Conversion System (PCS) 295 kW, 728 kWh Lithium battery and 250 kWh Vanadium Redox Flow Battery (VRFB). The objective of the project is to develop advanced VRFB and implement the independent renewable system on the island. Thus, the paper tests the system’s technical feasibility and compares levelized cost of energy (LCOEs) of three different systems, which are existing diesel generation, solar photovoltaic systems with diesel generators, and solar photovoltaic systems with ESSs based on the information given from the resort and the companies providing system components. The study uses costs, such as logistics, technology, construction, and operations costs, and system specifications from the case project. Since the project site is a remote island and requires a self-sufficient energy system, the project contains additional issues, such as including logistics costs and operations and maintenance issues. Thus, the concept of grid parity would be applied to the comparison among LCOEs of feasible options. The study examines the timeframe for reaching grid parity for those renewable systems compared to the existing diesel generation. Examining LCOEs of different system settings, including ESS, and their timeframe for reaching grid parity, can contribute to accelerating deployment of renewable systems in the Maldives as well as other SIDS countries. Furthermore, the results can provide further implications to other islands in the Maldives, those have similar characteristics, such as remote island and a self-sufficient diesel generation, to the case projects.
Literature Review
In the literature, various papers studied the economic and technical feasibility of sustainable energy systems in developing countries and SIDS. The objectives of the studies were to find the optimal independent renewable system and demonstrate the economic and financial feasibility of the selected system. (Jung et al. (2017) [
5]; Ali et al. (2018) [
6]; and Kaldellis et al. (2009) [
7]) Jung et al. (2017) and Ali et al. (2018) both examined technical and economic feasibilities of independent PV systems on the islands of the Maldives by Hybrid Optimization of Multiple Electric Renewables (HOMER) simulations and demonstrated that the PV system is a feasible option to replace the diesel generation of the small islands in the Maldives. In addition, Kalidellis et al. (2009) found the optimal PV-ESS system configuration, as Jung et al. (2017) did, for small remote islands and conducted a cost-benefit analysis. The study also confirmed that the optimal renewable system with ESS can be considered as an effective option for solving electrification issues on remote islands, especially located in high and medium-high solar potential regions [
7]. Though those studies demonstrated the technical and economic feasibility of the independent renewable systems, those analyses limitedly consider the timeframe for reaching grid parity condition of renewable systems. Therefore, the analysis of the paper can contribute to providing additional information when the grid parity condition of independent renewable systems can be reached in remote islands.
Moreover, the optimal selection and the management of renewable systems are essential parts for understanding economic feasibility of the renewable systems. In particular, the recent progress in computational simulation capacity allowed the introduction of the advanced methodologies in achieving optimal management of renewable systems with ESSs. Though this paper analyzes based on a project with a pre-determined renewable system configuration, Rangel et al. (2018) presented a methodology for choosing an optimal size, type, and site of ESS. The purpose of the study was to obtain the optimal charge and discharge strategy and find the best cost option [
8]. Ghanaatian and Lotfifard (2018) proposed a method for the optimal control of the flywheel ESS by using a tube-based Model Predictive Control (MPC) model. The study included uncertainties and external disturbances in the model and conducted simulations to show the effectiveness of the model [
9]. Li and Hennessy (2013) conducted a study to reduce grid dependence of midsize European town by adopting a large-scale PV, Wind, and VRFB. The study targeted to reduce grid dependence, grid purchase, and spilled wind lost and achieve shorter payback periods for the ESS. By considering different size of VRB-ESS, the study found the optimal size and technical specification of ESS that satisfies the objectives [
10]. These studies were to find the optimal selection and management of the battery system that satisfy the optimal operation and the reliability of the renewable system. In addition, the advanced methodologies are presented for the management of multiple micro grid systems. Tavakoli et al. (2018) proposed a way to find an optimal management system of battery energy for the commercial building microgrid using a linear optimization programming with the Conditional Value at Risk (CVaR). This approach considers maximizing the management of microgrid photovoltaic system and battery energy while reducing key uncertainties, such as electricity price and power generation, in operating photovoltaic energy system with battery. It not only improves the efficient use of renewable energy system but also enhances the resilience of the commercial microgrid [
11]. Marzband et al. (2018a) and Marzband et al. (2018b) demonstrated a smart Transactive Energy (TE) framework that established a coalition of multiple home microgrids and found an optimal resource management and profit sharing among the participants [
12,
13]. Marzband et al. (2018a) showed a smart TE framework that builds a coalition of multiple home microgrids and found an optimal way to achieve fair allocation of coalition profit. The study used a multi-stage stochastic programming based on artificial bee colony (MSSP-ABC) algorithm to simulate the formation of possible coalitions and find a “fair” distribution of profits. The simulation result demonstrated that the coalition encourages the participation of home microgrid owners and consumers in the deregulated market and contributes to mitigating electric load fluctuations [
12]. Marzband et al. (2018b) used improved optimization techniques to solve the non-linear and non-convex Market Operator Transactive Energy (MO-TE) structure issue. The method proposed by the study was used to find the home microgrids’ optimal electricity and thermal resources and maximize home microgrids owners’ profits. This approach enables to find the optimal timing for home microgrids owners to exchange electricity and provides a chance to reduce the exploitation cost of home microgrids owners [
13]. However, the case project used in this paper is a resort in a remote island with no grid connections to other islands, and the resort operates its self-sufficient energy system. Also, the pre-determined renewable system design was implemented in the resort. Thus, these advanced methodologies for optimal management of multiple home-grid systems as well as the selection of ESS are hard to be implemented in this case.
Along with feasibility studies of on-grid and off-grid renewable energy systems, various research has been undertaken on grid parity analysis. To compare the different types of energy technologies, LCOE calculation method is widely used in the grid party analysis. In the early 2010s, the studies showed that a solar PV system showed a great potential to be a feasible option in the future but reaching grid parity condition needed much more time. (Branker et al. (2011) [
14]; Yang (2010) [
15]; Lund (2011) [
16]) However, the continued technological development made the on-grid and off-grid solar PV systems more attractive options, and the recent studies expected shorter timeframes for reaching grid parity of PV systems. Though the recent studies found that both off-grid and on-grid solar systems are still expensive options for developing countries (Baurzhan and Jenkins (2016) [
17]; Zou et al. (2017) [
18]), many studies found the grid parity of solar PV systems can be reached in countries within the next few decades. For instance, Zou et al. (2017) and Mundada et al. (2016) studied whether the off-grid PV systems can reach the grid parity condition in China and the US Zou et al. (2017) found optimal solar PV systems in five different Chinese cities and applied learning curves for calculating LCOEs. It found that the grid parity condition of off-grid PV systems in those Chinese cities can be reached in between about 2026 and 2050 [
18]. Mundada et al. (2016) chose a residential sector in Houston, MI with an unfavorable environment for solar systems as a case study and calculated LCOE of off-grid PV with ESSs and combined heat and power (CHP) systems. The study showed that LCOEs of the hybrid system are lower than grid costs in many cases and argued that the hybrid system can be developed further in the US in the near future [
19]. Moreover, there has been in-depth studies which included uncertainties in calculating LCOEs of PV systems. (Biondi and Moretto (2015) [
20]; and Said et al. (2015) [
21]) Biondi and Moretto (2015) examined solar grid parity in Italy by using a real option approach. The study evaluated uncertainties, such as energy prices and PV module costs, and demonstrated how those uncertainties affect the PV market in Italy. It showed that PV systems seem to achieve grid parity soon thanks to relatively high electricity tariffs and good solar radiation, but the uncertainties may delay grid parity condition in Italy for several years [
20]. Said et al. (2015) presented an improved modeling of LCOE that used the effective lifetime of different types of PV technologies and different environmental or technical conditions. The study included the input data’s uncertainties in the analysis and examined whether PV technologies reached grid parity in Egypt. It found the use of the effective lifetime affects LCOE and the total electricity generation during the lifetime [
21].
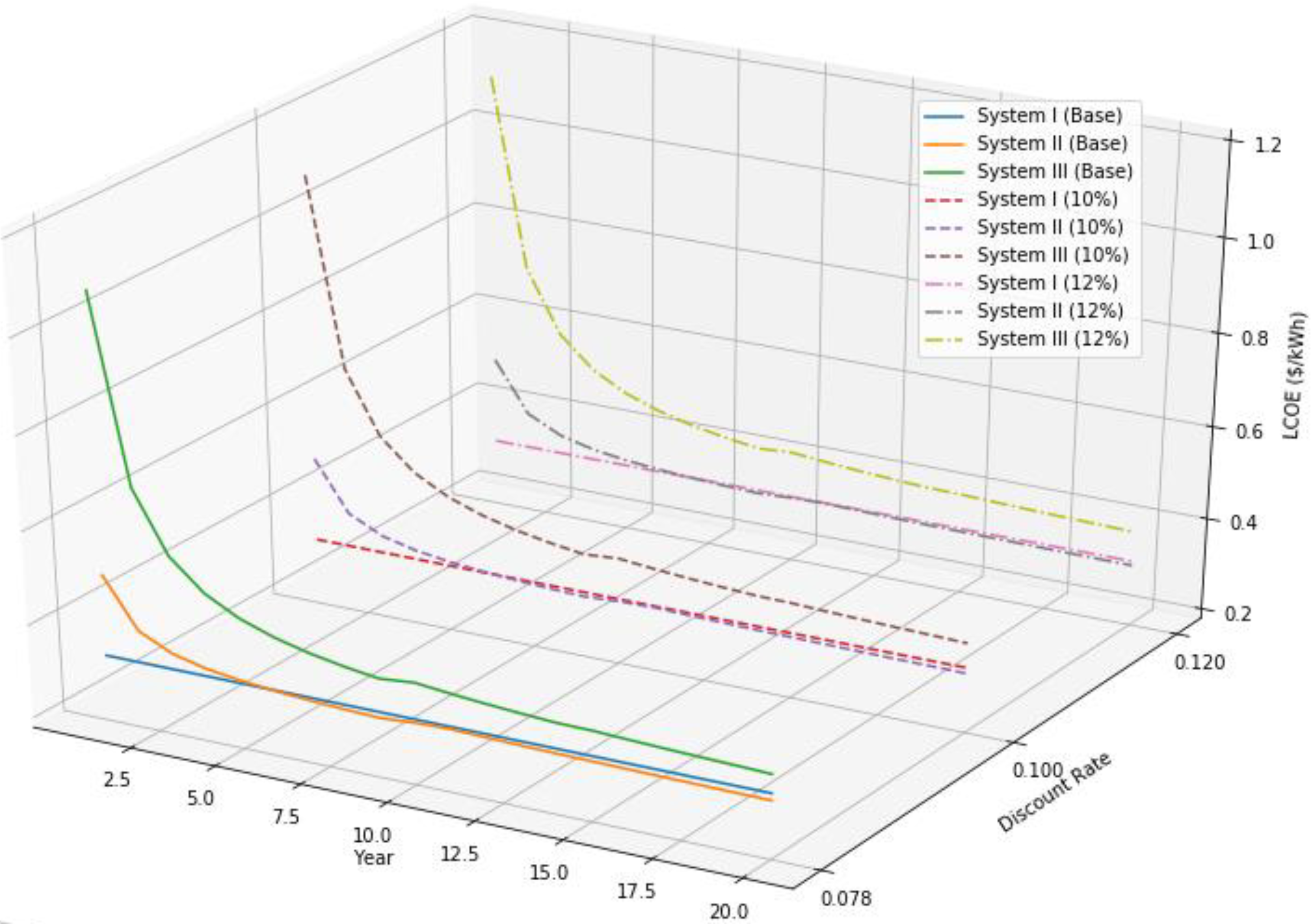
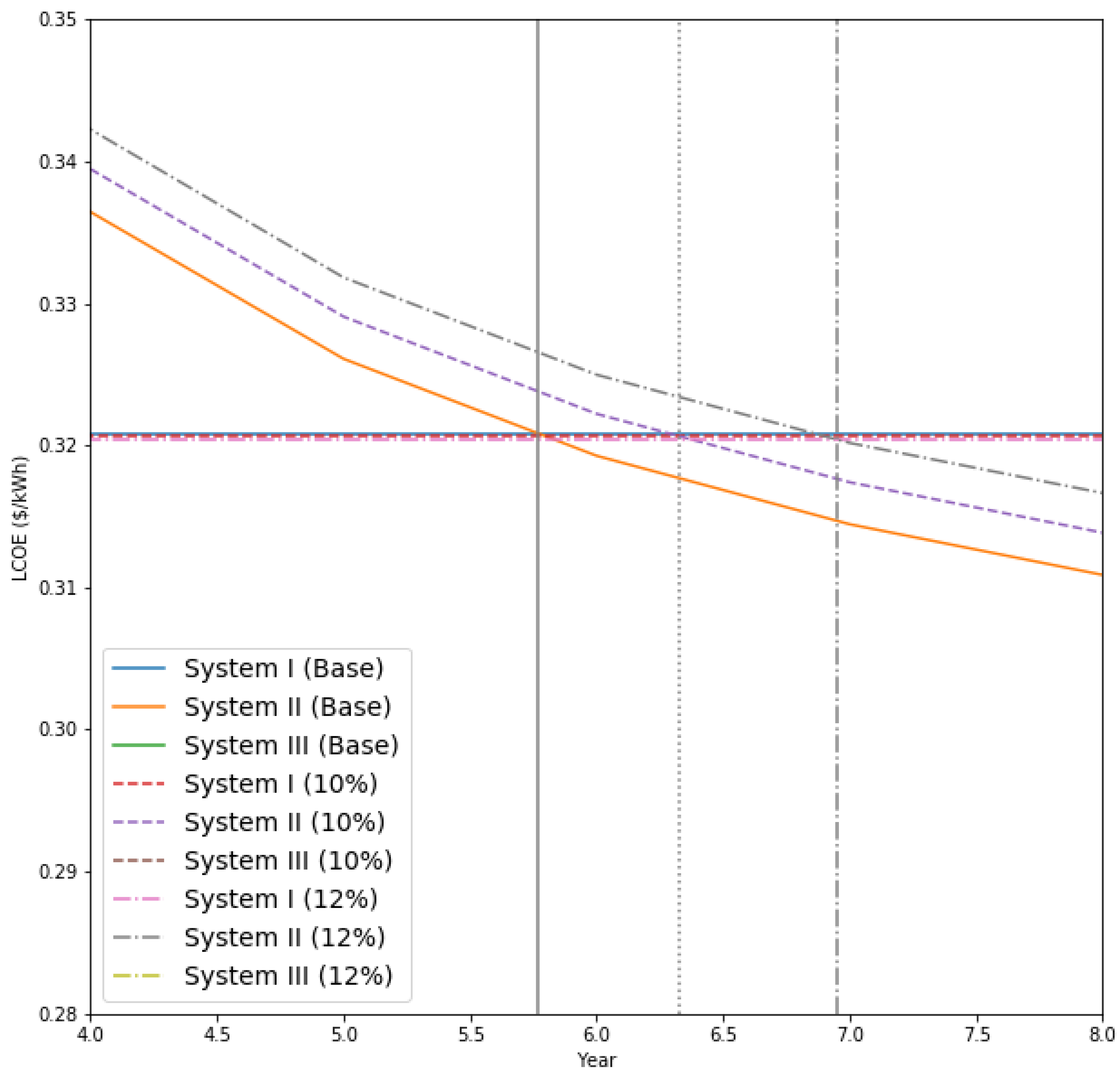
Various studies on the levelized cost of energy are conducted on comparing LCOEs of different technologies in national level and on comparing LCOEs of grid-connected renewable systems to other conventional energy systems. However, in the countries composed of many islands, such as the Maldives, the grid connection among systems is nearly impossible, and the deployment of independent renewable systems have additional risk factors. This paper uses actual technology, logistics, construction, and operations costs from the project. Also, the paper applies the concept of the grid parity to the project in a remote island in the Maldives where the central grid system cannot be established. The findings from the paper can be further applied to other remote islands. Moreover, the paper conducts sensitivity analysis on key risk factors, such as changes in discount rate and diesel price, to examine how the external risk factors can affect the economic feasibilities and the grid parity conditions of renewable energy systems in the Maldives.