Long-Term Decision on Wind Investment with Considering Different Load Ranges of Power Plant for Sustainable Electricity Energy Market
Abstract
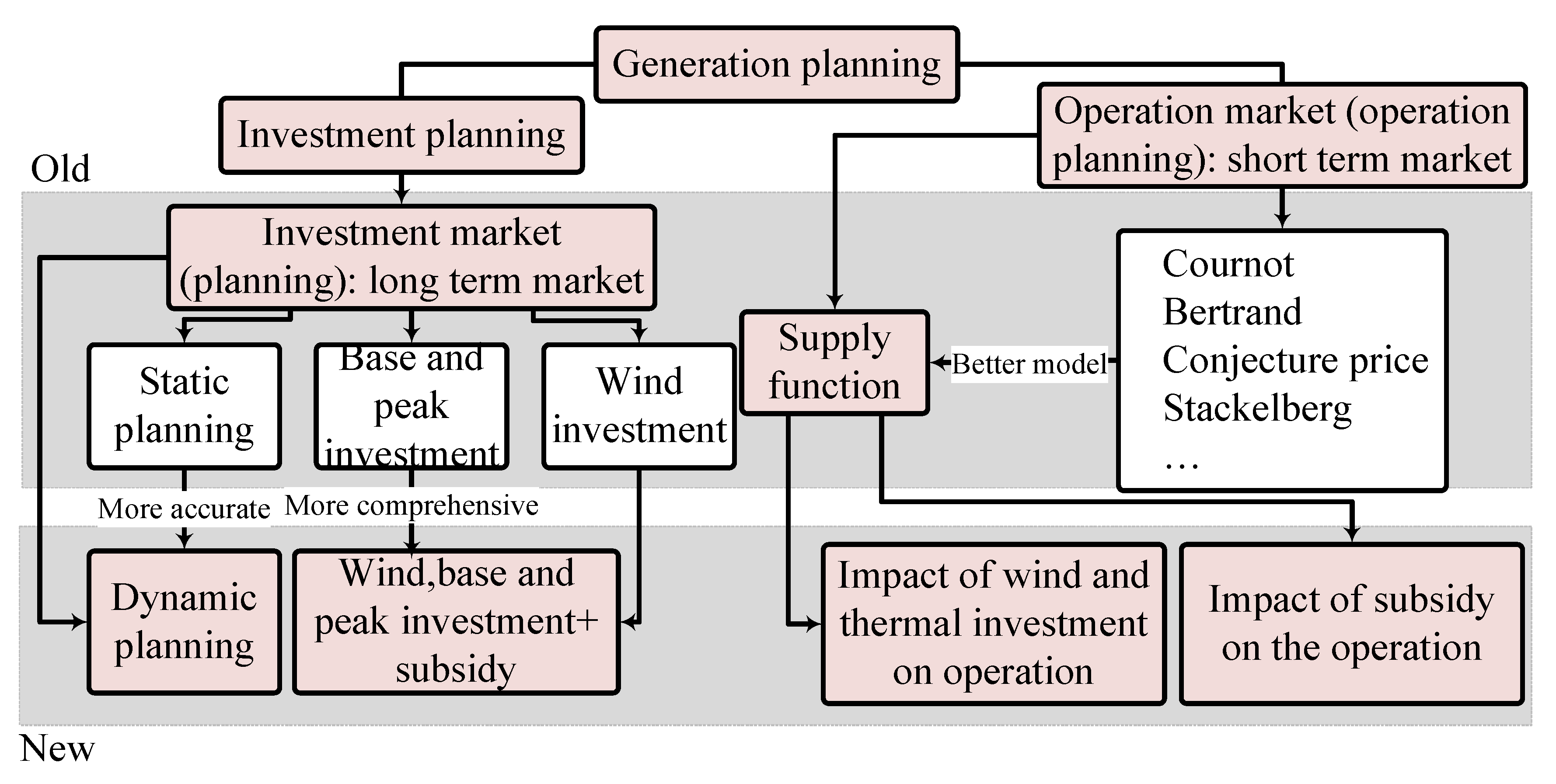
1. Introduction
- The model presents more reliable and better results if those that are intended for the short-term market include the market clearing aspect, whereas those intended for the longer term take into account investment. Therefore, the investment problem in this paper is bi-level; however, those presented in [5,18,19,20,21,22,23,24] are not bi-level.
- In this paper, three different load range technologies, including base, peak and wind plant are considered as the candidate units for investment and each technology has different options for investment capacity. However, candidate units for investment in [5,21,25,27,30] are wind unit and in [14,19,20,22,26,31,32,33,34,35,36,37,38,39] are other technologies. In addition, in this paper, the subsidy is considered in order to stimulate investment in the wind unit. This approach is more in line with reality, whilst largely overlooked in previous cases;
- The proposed model is a dynamic one, whilst the dynamic nature of investment decisions has not been considered in papers concerning wind energy [3,25,40,41] and other technologies [19,20,22,26,32,34,35,36,37,38,39]. Therefore, the multi-period stochastic model consisting of transmission network constraints is presented here;
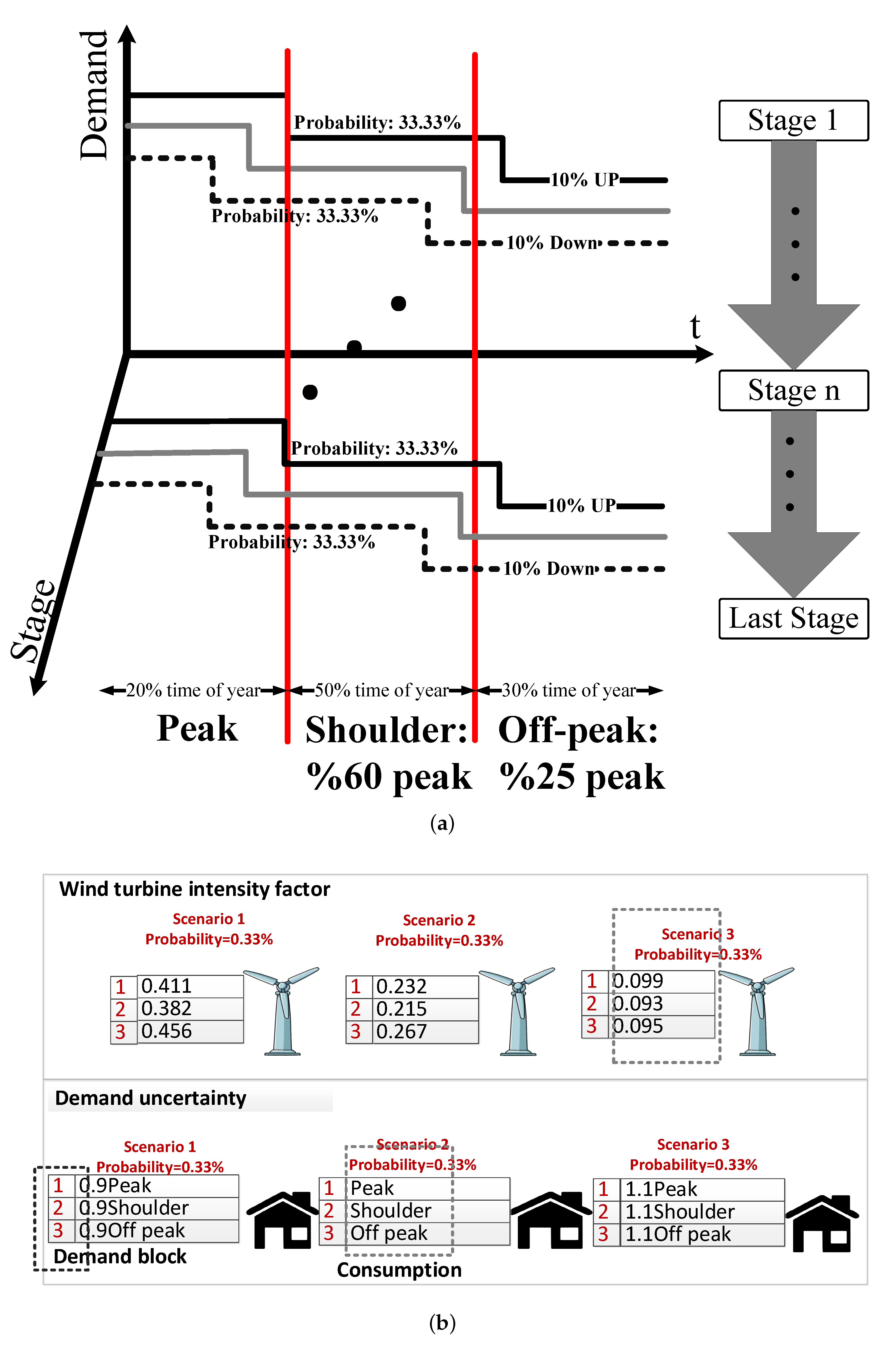
- In this network, consideration is given to the uncertainty in the generation of electricity from wind power along with demand consumption. These uncertainties are modeled by means of a scenario based approach.
- In addition, conventional producers are assumed to be competitive, i.e., they offer their respective productions at their marginal costs.
- to propose a wind investment model considering different load ranges of power plants so that the best production technology in the optimized location are offered.
- to envelope a wind investment multi-stage model for sustainable electricity energy markets
- to provide a methodology to investigate subsidies in both planning and operating planning in a network-constrained electricity market as a game-theoretic model.
- To implement the proposed model to Mazandaran Regional Electric Company (MREC) as a real power network and comprehensively analyze the related results.
2. Planning Features
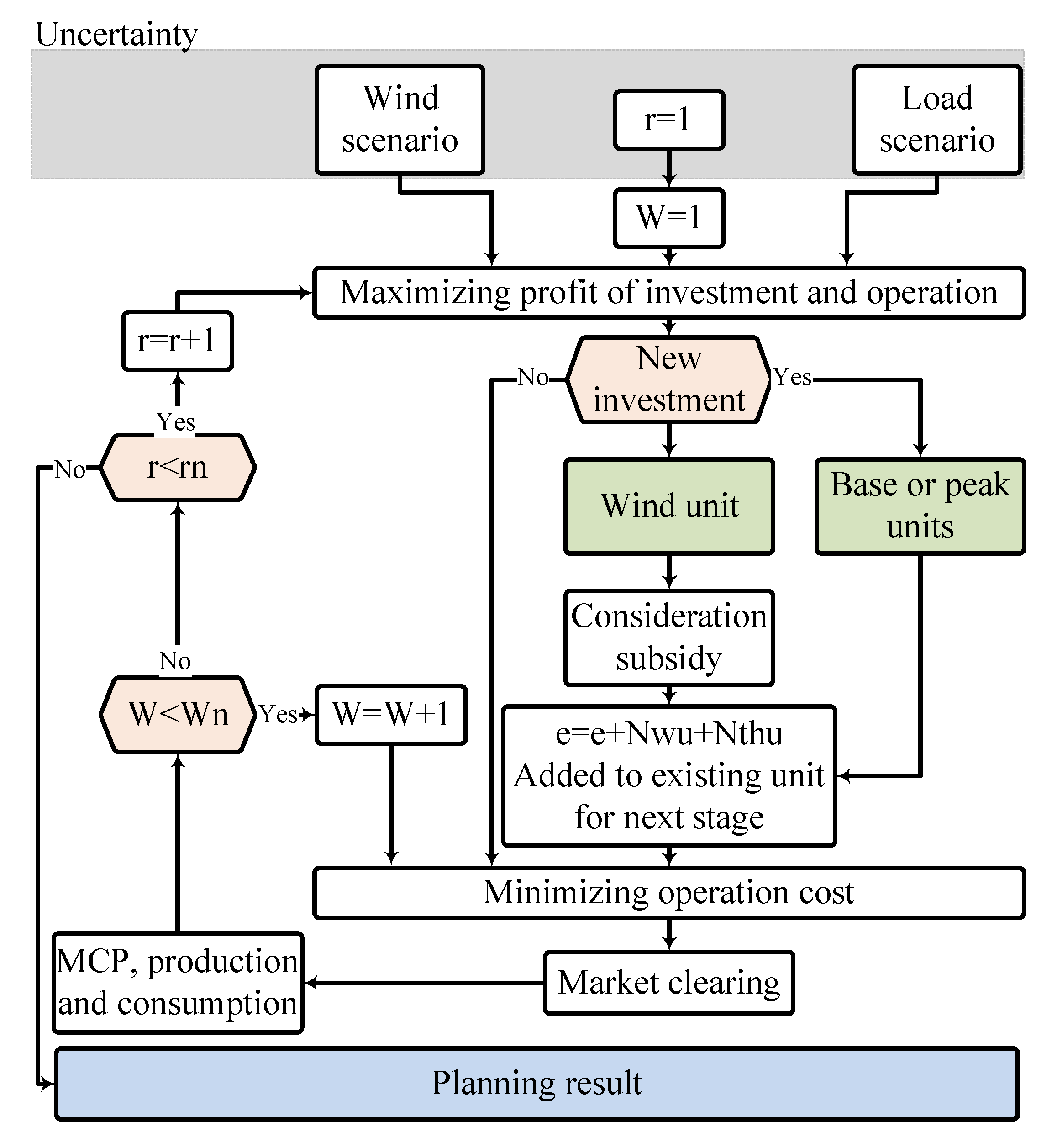
3. The Proposed Algorithm
3.1. Inputs and Outputs
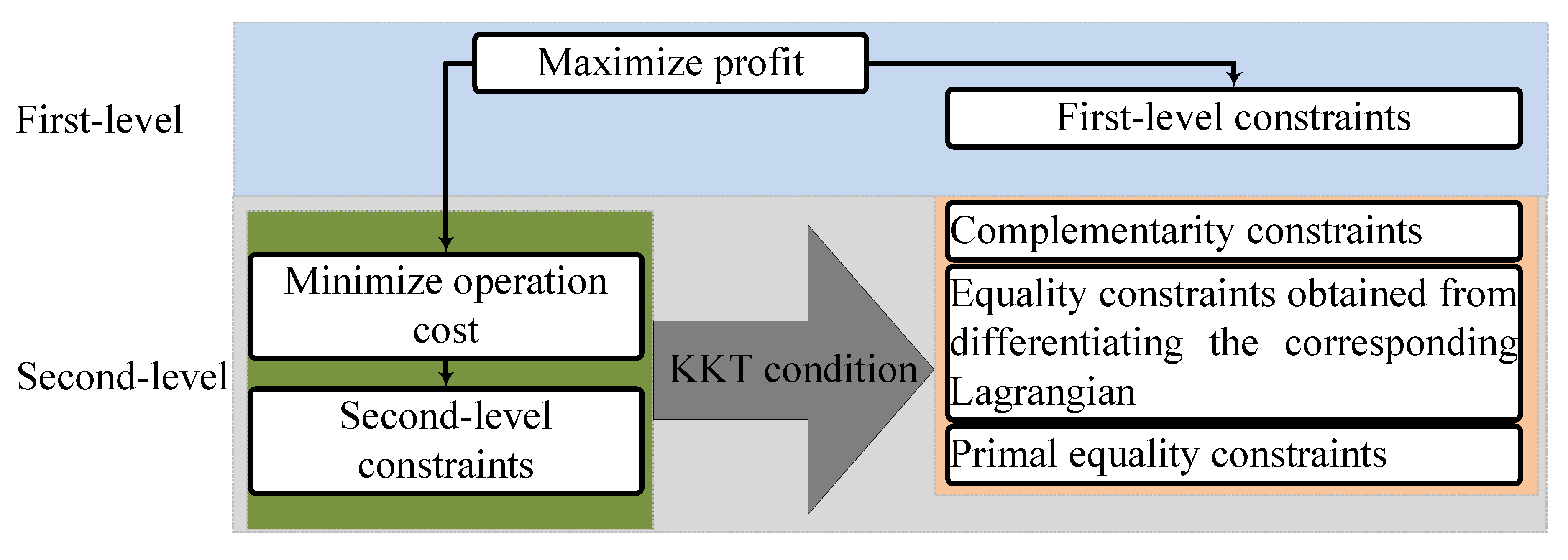
3.2. Converting Two Level Model to One Level Model
4. Mathematical Formulation
4.1. The Bi-Level Model
MPEC
- Equality constraints obtained from differentiating the corresponding Lagrangian:
- Complimentary constraints by KKT:
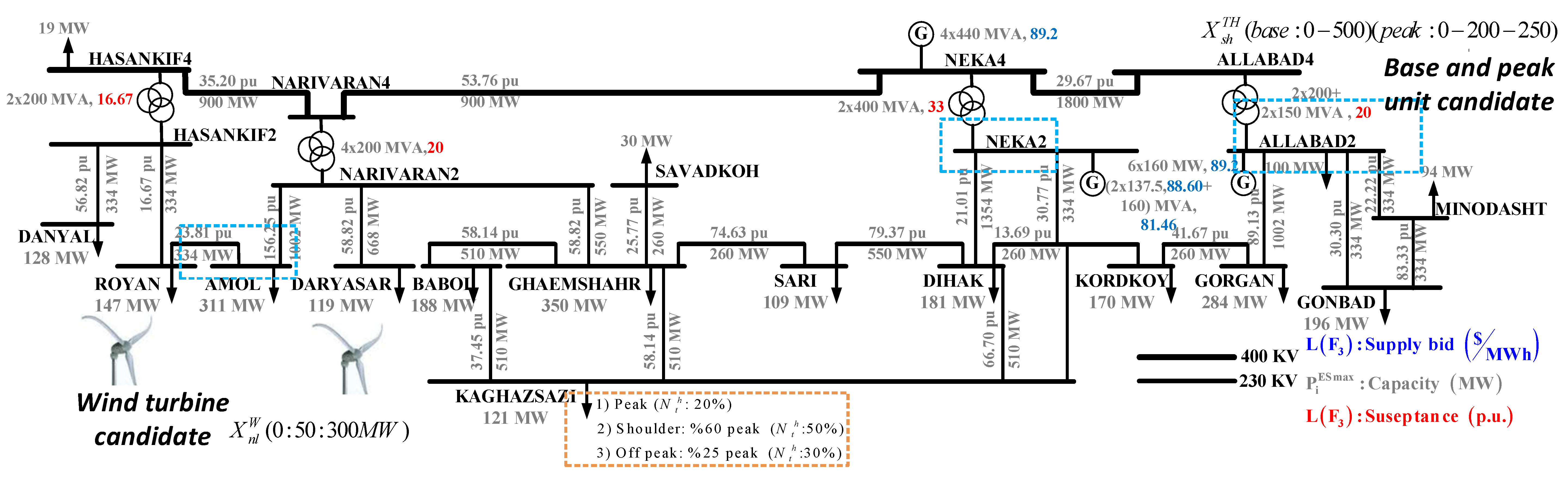
5. Case Studies
Case Study: MREC Network
- Case #1
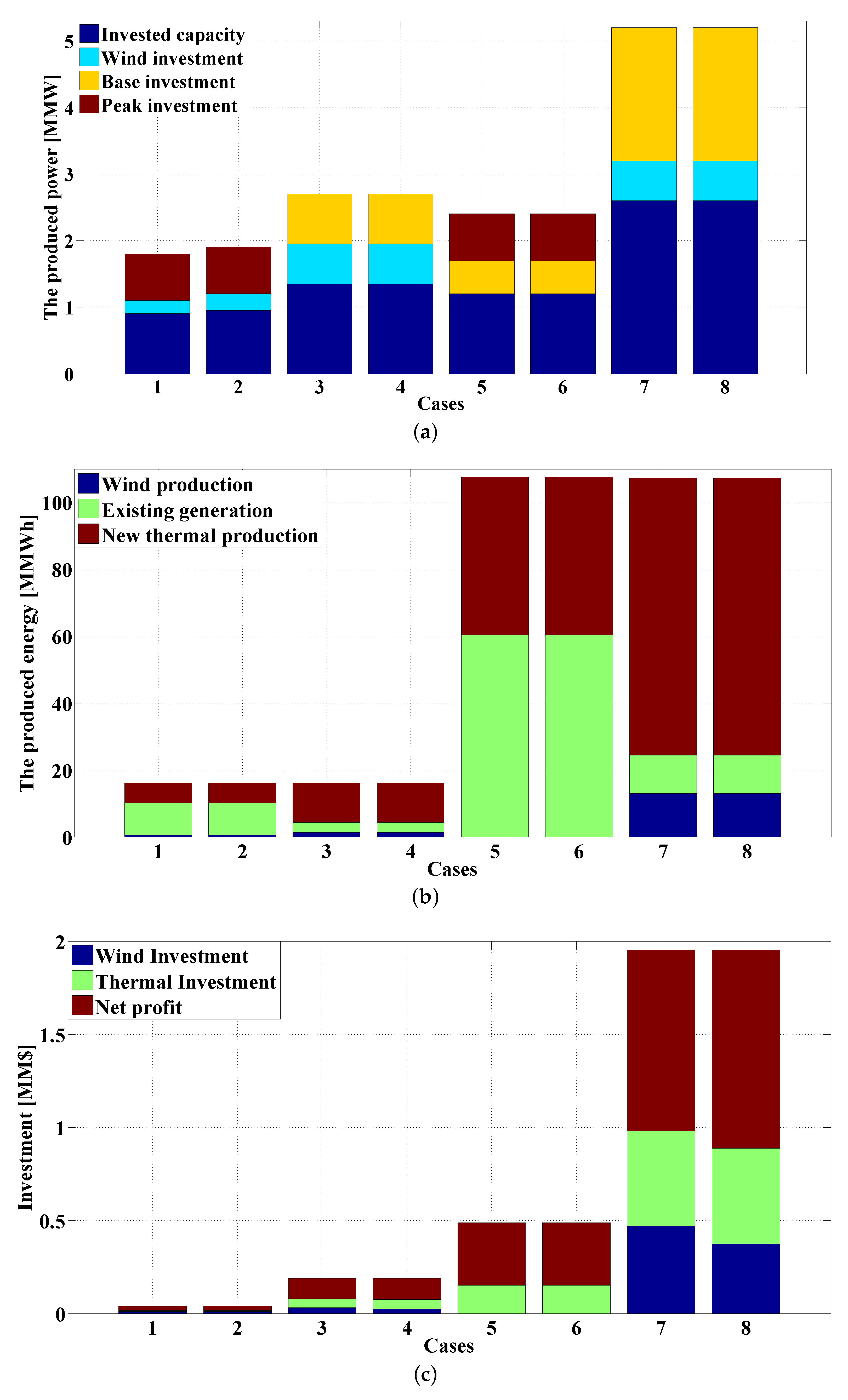
- total thermal investment is equal to 700 MW in the peak technology due to budget limitations and offset by their investment cost with respect to base technology. In this case, the total capacity added by the producer in the planning horizon has been established at 900 MW, resulting in the producer investing 200 MW in the wind technology and 700 MW in the peak technology. In this case, total thermal investment is attributable to peak technology due to budget limitation and less their investment cost with respect to base technology. The existing units supply 9.78 MMWh of the energy consumed by the network and thereby play an important role in the provision of energy to the MREC network;
- Case #2
- Investment in wind units in this case is increased by 50 MW compared with Case #1 due to a 20% subsidy. In addition, the investment cost of wind units is the same as Case #1. In this case, the production of wind units has increased by 25.58%. Therefore, the net profit in Case #2 has increased by 18.44% with respect to Case #1;
- Case #3
- The total capacity added by the producer in Case #3 has increased by 450 MW compared with Case #1 by increasing the budget from 15 M$ to 150 M$. Investment in wind units in this case has increased by 400 MW compared with the Case #1 due to an increase in the budget. In addition, the total thermal investment is base technology so that 750 MW is added to the MREC network. In Case #3, the production of wind and new thermal units have been increased by 201.62% and 98.15% compared with Case #1, respectively. In addition, the net profit in the planning horizon has been obtained equal to 108 M$ that it has been increased by 389.35% with respect to Case #1;
- Case #4
- In Case #4, investment in wind and thermal units is the same as Case #3. In this case, subsidy has no effect on wind investment because the total capacity of wind units added to network is the same as in Case #3. In addition, the production of different units is the same as Case #3. However, the investment cost of wind units has decreased by 20% due to the 20% subsidy. As a result, the investor’s net profit has increased by 5.56% compared with Case #3;
- Case #5
- In this case, the total capacity added by the producer in the planning duration has been determined to be 1200 MW, resulting in the producer investing 500 MW in the base technology and 700 MW in the peak technology, while no wind unit was constructed in the MREC network. This is the result of the desire to invest in units that have a lower investment cost due to the budget limitations. In addition, distribution of the investment are as follows: 200 MW on peak technology in the first year, 500 MW on base technology in the fifth year, 250 MW on peak technology in the eighth year and 250 MW on peak technology in the ninth and tenth years. Due to lack of generation in the western region, the total capacity has been constructed in AMOL located in this region.
- Case #6
- All output of Case #6 is the same as Case #5; consequently, the consideration of a 20% subsidy has no influence on the desire to invest in wind units. It can be observed that the 20% subsidy is not enough to encourage investment in wind units and therefore the capacity of wind units is zero in this network.
- Case #7
- In Case #3, the total capacity added by the investor has increased by 1400 MW compared with Case #5 and Investment in wind units in this case have been increased by 600 MW compared with the Case #1. In addition, total thermal investment is base technology so that 2000 MW base technologies are added to the MREC network. In Case #7, the production of new thermal units has been increased by 75.89% compared with Case #5, while the production of existing units decreased by 81.04%. In addition, the production of wind units has been increased from 0 MMWh to 12.97 MMWh with respect to Case #5. Thus, the total net profit in the planning duration is predicted to be 973.28 M$, an increase of 188.86% with respect to Case #5.
- Case #8
- In this case, investment in wind and thermal units, and the production of different units, is the same as Case #7. However, investment cost of wind units has been decreased by 20% due to the 20% subsidy. As a result, the investor’s net profit has been increased by 9.62% compared with Case #3.
6. Conclusions
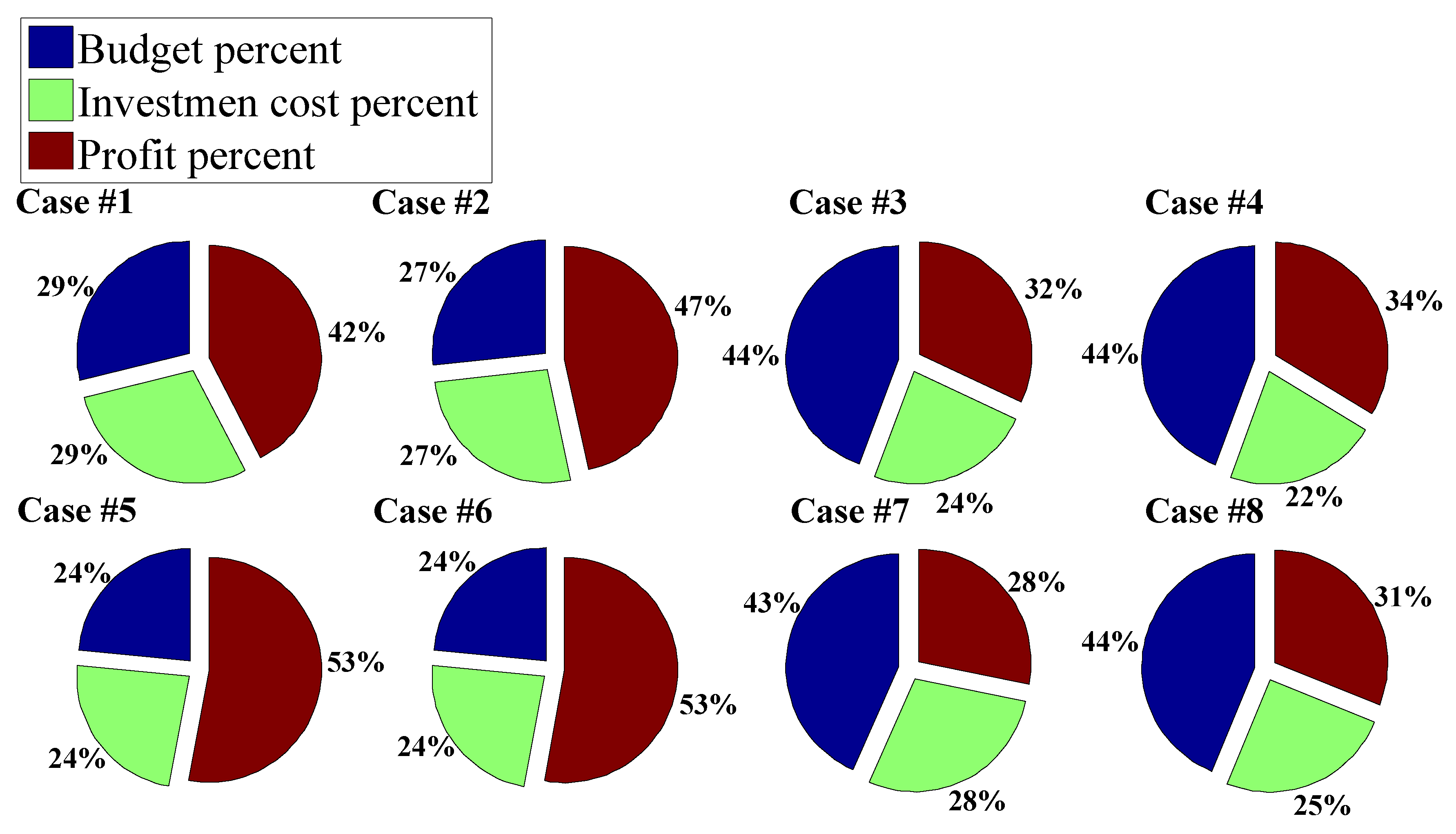
- It can be seen that the percentage profit decreases as a result of increasing the available budget for both static and dynamic planning. At a lower budgetary level, the percentage profit yielded by the dynamic approach is more than that of the static approach so that the investment cost of the dynamic approach is less than the static. However, when the budgetary level is higher, the percentage profit in the static approach exceeds that of the dynamic approach while the static approach has a lower investment cost. The effect of a subsidy is to increase investor profit if the subsidy encourages investment on the wind technologies. In addition, the investment cost decreases in these cases. It can be seen that the total investor contribution has been increased in the dynamic approach with respect to the static one. Moreover, using the dynamic versus static approach in the planning of generation capacity leads to accurate and realistic results in the expansion planning.
- Additional work is underway to represent the strategic behaviour of market participants other than wind and new thermal producers. The proposed model can be adapted to consider the impact of transmission expansion plans, availability of gas transmission networks, tax policy, DSM plans and uncertainty in the demand growth.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| w | index for scenario |
| y/y | indexes for stage (year) |
| t | index for demand blocks |
| s/i/j | indexes for new base or peak units/existing generation unit and demand |
| h/l | investment capacity of new base or peak unit s/wind power at bus n (MW) |
| n/m | indexes for bus |
| weight of demand block t in year y | |
| weight of scenario w in demand block t | |
| / | annualized investment cost of base or peak units/wind power (€/MW) |
| investment cost of wind power at bus n | |
| maximum wind capacity that can be installed at bus n | |
| / | option h/l for investment capacity of new base or peak units s/wind power at bus n (MW) |
| capacity of existing generation unit i of strategic producer (MW) | |
| load of demand j in block t and year y (MW) | |
| / | price offered by new base or peak units/existing unit producer (€/MWh) |
| susceptance of line n-m (p.u.) | |
| transmission capacity of line n-m (MW) | |
| f | Discount rate |
| S | Subsidy percent |
| / | capacity investment of new unit s/wind power at bus n (MW) |
| / | binary variable that is equal to 1 if the h/lth investment option determines the base or peak unit/wind power is selected in year y |
| / | available capacity of new unit s/wind power at bus n in year y’, in the years after the installation in year y (MW) |
| // | power produced by new base or peak units s/existing unit i/wind power at bus n, in year y, demand block t and scenario w (MW) |
| // | power produced by new base or peak units s/wind power at bus n, in year y’, in the years after the installation in year y (MW) |
| price offered by new base or peak units producer a, in year y’, In the years after the installation in year y (€/MWh) | |
| voltage angle of bus n, in year y, demand block t and scenario w | |
References
- Bagheri, A.; Monsef, H.; Lesani, H. Renewable power generation employed in an integrated dynamic distribution network expansion planning. Electr. Power Syst. Res. 2015, 127, 280–296. [Google Scholar] [CrossRef]
- Kahraman, C.; Onar, S.C.; Oztaysi, B. A Comparison of Wind Energy Investment Alternatives Using Interval-Valued Intuitionistic Fuzzy Benefit/Cost Analysis. Sustainability 2016, 8, 118. [Google Scholar] [CrossRef]
- Lumbreras, S.; Ramos, A.; Banez-Chicharro, F. Optimal transmission network expansion planning in real-sized power systems with high renewable penetration. Electr. Power Syst. Res. 2017, 149, 76–88. [Google Scholar] [CrossRef]
- Gan, L.; Li, G.; Zhou, M. Coordinated planning of large-scale wind farm integration system and regional transmission network considering static voltage stability constraints. Electr. Power Syst. Res. 2016, 136, 298–308. [Google Scholar] [CrossRef]
- Kamalinia, S.; Shahidehpour, M.; Khodaei, A. Security-constrained expansion planning of fast-response units for wind integration. Electr. Power Syst. Res. 2011, 81, 107–116. [Google Scholar] [CrossRef]
- You, S.; Hadley, S.W.; Shankar, M.; Liu, Y. Co-optimizing generation and transmission expansion with wind power in large-scale power grids—Implementation in the US Eastern Interconnection. Electr. Power Syst. Res. 2016, 133, 209–218. [Google Scholar] [CrossRef]
- Syed, I.M.; Raahemifar, K. Predictive energy management, control and communication system for grid tied wind energy conversion systems. Electr. Power Syst. Res. 2017, 142, 298–309. [Google Scholar] [CrossRef]
- Saboori, H.; Hemmati, R. Considering Carbon Capture and Storage in Electricity Generation Expansion Planning. IEEE Trans. Sustain. Energy 2016, 7, 1371–1378. [Google Scholar] [CrossRef]
- Nosair, H.; Bouffard, F. Flexibility Envelopes for Power System Operational Planning. IEEE Trans. Sustain. Energy 2015, 6, 800–809. [Google Scholar] [CrossRef]
- Valinejad, J.; Marzband, M.; Busawona, K.; Kyyrä, J.; Pouresmaeil, E. Investigating Wind Generation Investment Indices in Multi-Stage Planning. In Proceedings of the 5th International Symposium on Environment Friendly Energies and Applications (EFEA), Rome, Italy, 24–26 September 2018. [Google Scholar]
- Marzband, M.; Azarinejadian, F.; Savaghebi, M.; Pouresmaeil, E.; Guerrero, J.M.; Lightbody, G. Smart transactive energy framework in grid-connected multiple home microgrids under independent and coalition operations. Renew. Energy 2018, 126, 95–106. [Google Scholar] [CrossRef]
- Tavakoli, M.; Shokridehaki, F.; Akorede, M.F.; Marzband, M.; Vechiu, I.; Pouresmaeil, E. CVaR-based energy management scheme for optimal resilience and operational cost in commercial building microgrids. Int. J. Electr. Power Energy Syst. 2018, 100, 1–9. [Google Scholar] [CrossRef]
- Momoh, J.; Mili, L. Economic Market Design and Planning for Electric Power Systems; Wiley-IEEE Press: New York, NY, USA, 2009. [Google Scholar]
- Valinejad, J.; Marzband, M.; Akorede, M.F.; Barforoshi, T.; Jovanović, M. Generation expansion planning in electricity market considering uncertainty in load demand and presence of strategic GENCOs. Electr. Power Syst. Res. 2017, 152, 92–104. [Google Scholar] [CrossRef]
- Marzband, M.; Fouladfar, M.H.; Akorede, M.F.; Lightbody, G.; Pouresmaeil, E. Framework for smart transactive energy in home-microgrids considering coalition formation and demand side management. Sustain. Cities Soc. 2018, 40, 136–154. [Google Scholar] [CrossRef]
- Marzband, M.; Javadi, M.; Pourmousavi, S.A.; Lightbody, G. An advanced retail electricity market for active distribution systems and home microgrid interoperability based on game theory. Electr. Power Syst. Res. 2018, 157, 187–199. [Google Scholar] [CrossRef]
- Olsen, D.; Byron, J.; DeShazo, G.; Shirmohammadi, D.; Wald, J. Collaborative Transmission Planning: California’s Renewable Energy Transmission Initiative. IEEE Trans. Sustain. Energy 2012, 3, 837–844. [Google Scholar] [CrossRef]
- Soroudi, A.; Rabiee, A.; Keane, A. Information gap decision theory approach to deal with wind power uncertainty in unit commitment. Electr. Power Syst. Res. 2017, 145, 137–148. [Google Scholar] [CrossRef]
- Baringo, L.; Conejo, A. Wind Power Investment: A Benders Decomposition Approach. IEEE Trans. Power Syst. 2012, 27, 433–441. [Google Scholar] [CrossRef]
- Xiong, P.; Singh, C. Optimal Planning of Storage in Power Systems Integrated With Wind Power Generation. IEEE Trans. Sustain. Energy 2016, 7, 232–240. [Google Scholar] [CrossRef]
- Sun, C.; Bie, Z.; Xie, M.; Jiang, J. Assessing wind curtailment under different wind capacity considering the possibilistic uncertainty of wind resources. Electr. Power Syst. Res. 2016, 132, 39–46. [Google Scholar] [CrossRef]
- Li, S.; Coit, D.W.; Felder, F. Stochastic optimization for electric power generation expansion planning with discrete climate change scenarios. Electr. Power Syst. Res. 2016, 140, 401–412. [Google Scholar] [CrossRef]
- Tavakoli, M.; Shokridehaki, F.; Mousa Marzband, R.G.; Pouresmaeil, E. A two stage hierarchical control approach for the optimal energy management in commercial building microgrids based on local wind power and PEVs. Sustain. Cities Soc. 2018, 41, 332–340. [Google Scholar] [CrossRef]
- Hinojosa, V.H.; Velásquez, J. Improving the mathematical formulation of security-constrained generation capacity expansion planning using power transmission distribution factors and line outage distribution factors. Electr. Power Syst. Res. 2016, 140, 391–400. [Google Scholar] [CrossRef]
- Valenzuela, J.; Wang, J. A probabilistic model for assessing the long-term economics of wind energy. Electr. Power Syst. Res. 2011, 81, 853–861. [Google Scholar] [CrossRef]
- Zhang, T.; Baldick, R.; Deetjen, T. Optimized generation capacity expansion using a further improved screening curve method. Electr. Power Syst. Res. 2015, 124, 47–54. [Google Scholar] [CrossRef]
- Pineda, S.; Morales, J.; Ding, Y.; Østergaard, J. Impact of equipment failures and wind correlation on generation expansion planning. Electr. Power Syst. Res. 2014, 116, 451–458. [Google Scholar] [CrossRef]
- Brandi, R.B.S.; Ramos, T.P.; David, P.A.M.S.; Dias, B.H.; Marcato, A.L.M. Maximizing hydro share in peak demand of power systems long-term operation planning. Electr. Power Syst. Res. 2016, 141, 264–271. [Google Scholar] [CrossRef]
- Jabr, R. Robust Transmission Network Expansion Planning With Uncertain Renewable Generation and Loads. IEEE Trans. Power Syst. 2013, 28, 4558–4567. [Google Scholar] [CrossRef]
- Munoz, F.D.; Mills, A.D. Endogenous Assessment of the Capacity Value of Solar PV in Generation Investment Planning Studies. IEEE Trans. Sustain. Energy 2015, 6, 1574–1585. [Google Scholar] [CrossRef]
- Valinejad, J.; Barforoushi, T. Generation expansion planning in electricity markets: A novel framework based on dynamic stochastic MPEC. Int. J. Electr. Power Energy Syst. 2015, 70, 108–117. [Google Scholar] [CrossRef]
- Baringo, L.; Conejo, A. Strategic Wind Power Investment. IEEE Trans. Power Syst. 2014, 29, 1250–1260. [Google Scholar] [CrossRef]
- Valinejad, J.; Marzband, M.; Barforoushi, T.; Kyyrä, J.; Pouresmaeil, E. Dynamic stochastic EPEC model for Competition of Dominant Producers in Generation Expansion Planning. In Proceedings of the 5th International Symposium on Environment Friendly Energies and Applications (EFEA), Rome, Italy, 24–26 September 2018. [Google Scholar]
- Kim, J.-Y.; Kim, K.S. Integrated Model of Economic Generation System Expansion Plan for the Stable Operation of a Power Plant and the Response of Future Electricity Power Demand. Sustainability 2018, 10, 2417. [Google Scholar] [CrossRef]
- Khaligh, V.; Buygi, M.O.; Anvari-Moghaddam, A.; Guerrero, J. A Multi-Attribute Expansion Planning Model for Integrated Gas–Electricity System. Energies 2018, 11, 2573. [Google Scholar] [CrossRef]
- Ko, W.; Park, J.K.; Kim, M.K.; Heo, J.H. A Multi-Energy System Expansion Planning Method Using a Linearized Load-Energy Curve: A Case Study in South Korea. Energies 2017, 10, 1663. [Google Scholar] [CrossRef]
- Hong, S.; Cheng, H.; Zeng, P. An N-k Analytic Method of Composite Generation and Transmission with Interval Load. Energies 2017, 10, 168. [Google Scholar] [CrossRef]
- Zhou, X.; Guo, C.; Wang, Y.; Li, W. Optimal Expansion Co-Planning of Reconfigurable Electricity and Natural Gas Distribution Systems Incorporating Energy Hubs. Energies 2017, 10, 124. [Google Scholar] [CrossRef]
- Li, R.; Ma, H.; Wang, F.; Wang, Y.; Liu, Y.; Li, Z. Game Optimization Theory and Application in Distribution System Expansion Planning, Including Distributed Generation. Energies 2013, 6, 1101–1124. [Google Scholar] [CrossRef]
- Meng, K.; Yang, H.; Dong, Z.Y.; Guo, W.; Wen, F.; Xu, Z. Flexible Operational Planning Framework Considering Multiple Wind Energy Forecasting Service Providers. IEEE Trans. Sustain. Energy 2016, 7, 708–717. [Google Scholar] [CrossRef]
- Flores-Quiroz, A.; Palma-Behnke, R.; Zakeri, G.; Moreno, R. A column generation approach for solving generation expansion planning problems with high renewable energy penetration. Electr. Power Syst. Res. 2016, 136, 232–241. [Google Scholar] [CrossRef]
- Duong, M.Q.; Grimaccia, F.; Leva, S.; Mussetta, M.; Le, K.H. Improving transient stability in a grid-connected squirrel-cage induction generator wind turbine system using a fuzzy logic controller. Energies 2015, 8, 6328–6349. [Google Scholar] [CrossRef]
- Conejo, A.J.; Carrión, M.; Morales, J.M. Decision Making under Uncertainty in Electricity Markets; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Kazempour, S.; Conejo, A.; Ruiz, C. Strategic Generation Investment Using a Complementarity Approach. IEEE Trans. Power Syst. 2011, 26, 940–948. [Google Scholar] [CrossRef]
- Drud, A. CONOPT. Available online: https://ampl.com/products/solvers/solvers-we-sell/conopt/ (accessed on 31 July 2012).
- Valinejad, J.; Oladi, Z.; Barforoshi, T.; Parvania, M. Stochastic Unit Commitment in the Presence of Demand Response Program Under Uncertainties. IJE Trans. B Appl. 2017, 30, 1134–1143. [Google Scholar]
- Brooke, D.; Kendrick, A.; Meeraus, R.; Raman, R. GAMS: A User’s Guide; GAMS Development Corp.: Washington, DC, USA, 1998. [Google Scholar]


| Cases | Planning | Subsidy (%) | Budget (M$) |
|---|---|---|---|
| #1 | Static | 0 | 15.0 |
| #2 | Static | 20 | 15.0 |
| #3 | Static | 0 | 150 |
| #4 | Static | 20 | 150 |
| #5 | Dynamic | 0 | 150 |
| #6 | Dynamic | 20 | 150 |
| #7 | Dynamic | 0 | 1500 |
| #8 | Dynamic | 20 | 1500 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valinejad, J.; Marzband, M.; Funsho Akorede, M.; D Elliott, I.; Godina, R.; Matias, J.C.d.O.; Pouresmaeil, E. Long-Term Decision on Wind Investment with Considering Different Load Ranges of Power Plant for Sustainable Electricity Energy Market. Sustainability 2018, 10, 3811. https://doi.org/10.3390/su10103811
Valinejad J, Marzband M, Funsho Akorede M, D Elliott I, Godina R, Matias JCdO, Pouresmaeil E. Long-Term Decision on Wind Investment with Considering Different Load Ranges of Power Plant for Sustainable Electricity Energy Market. Sustainability. 2018; 10(10):3811. https://doi.org/10.3390/su10103811
Chicago/Turabian StyleValinejad, Jaber, Mousa Marzband, Mudathir Funsho Akorede, Ian D Elliott, Radu Godina, João Carlos de Oliveira Matias, and Edris Pouresmaeil. 2018. "Long-Term Decision on Wind Investment with Considering Different Load Ranges of Power Plant for Sustainable Electricity Energy Market" Sustainability 10, no. 10: 3811. https://doi.org/10.3390/su10103811
APA StyleValinejad, J., Marzband, M., Funsho Akorede, M., D Elliott, I., Godina, R., Matias, J. C. d. O., & Pouresmaeil, E. (2018). Long-Term Decision on Wind Investment with Considering Different Load Ranges of Power Plant for Sustainable Electricity Energy Market. Sustainability, 10(10), 3811. https://doi.org/10.3390/su10103811









