Innovative Energy Islands: Life-Cycle Cost-Benefit Analysis for Battery Energy Storage
Abstract
1. Introduction
2. Materials and Methods
2.1. Cost-Benefit Analysis
2.1.1. Cost Estimation
- is the initial cost of battery storage (€);
- is the energy cost of battery storage (€/kWh);
- is the energy capacity of battery storage (kWh);
- is the power cost of battery storage (€/kW);
- is the nominal output power of battery storage (kW).
- is the battery storage system energy capacity (kWh);
- is the operating time of the battery storage (hours);
- is the total energy supply from battery storage (kWh);
- is the roundtrip efficiency of the battery storage (%);
- is the maximum level of depth of discharge (%).
- is the input energy cost (€);
- is the amount of energy input (kWh);
- is the unit cost of energy input (€/kWh).
- is the starting value of the loan;
- is the annual interest rate;
- is the total number of interest periods.
2.1.2. Benefit Estimation
- is the energy output income (€);
- is the amount of energy input (kWh);
- is the roundtrip efficiency of the battery storage system (%);
- is the maximum level of depth of discharge (%);
- is unit income of energy output (€/kWh).
2.2. Addressing the Life-Cycle Emissions from Battery Storage System
2.3. Output Indicators
- is the initial investment;
- is the net cash flow in period 1;
- is the net cash flow in period 2;
- is the net cash flow in period t;
- is the discount rate (the rate used to discount future cash flows to the present value).
2.4. Data
3. Results
3.1. Key Output Indicators
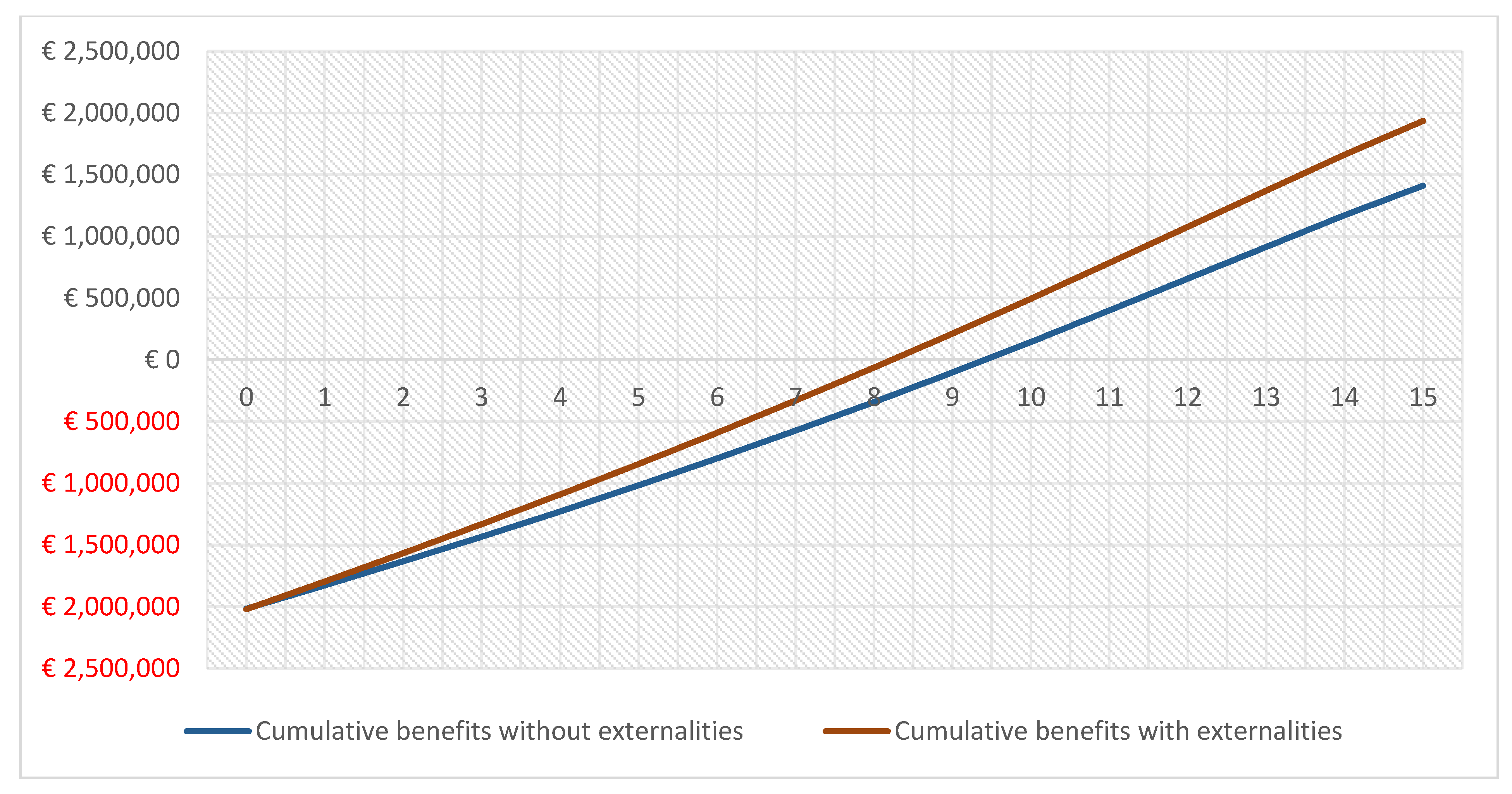
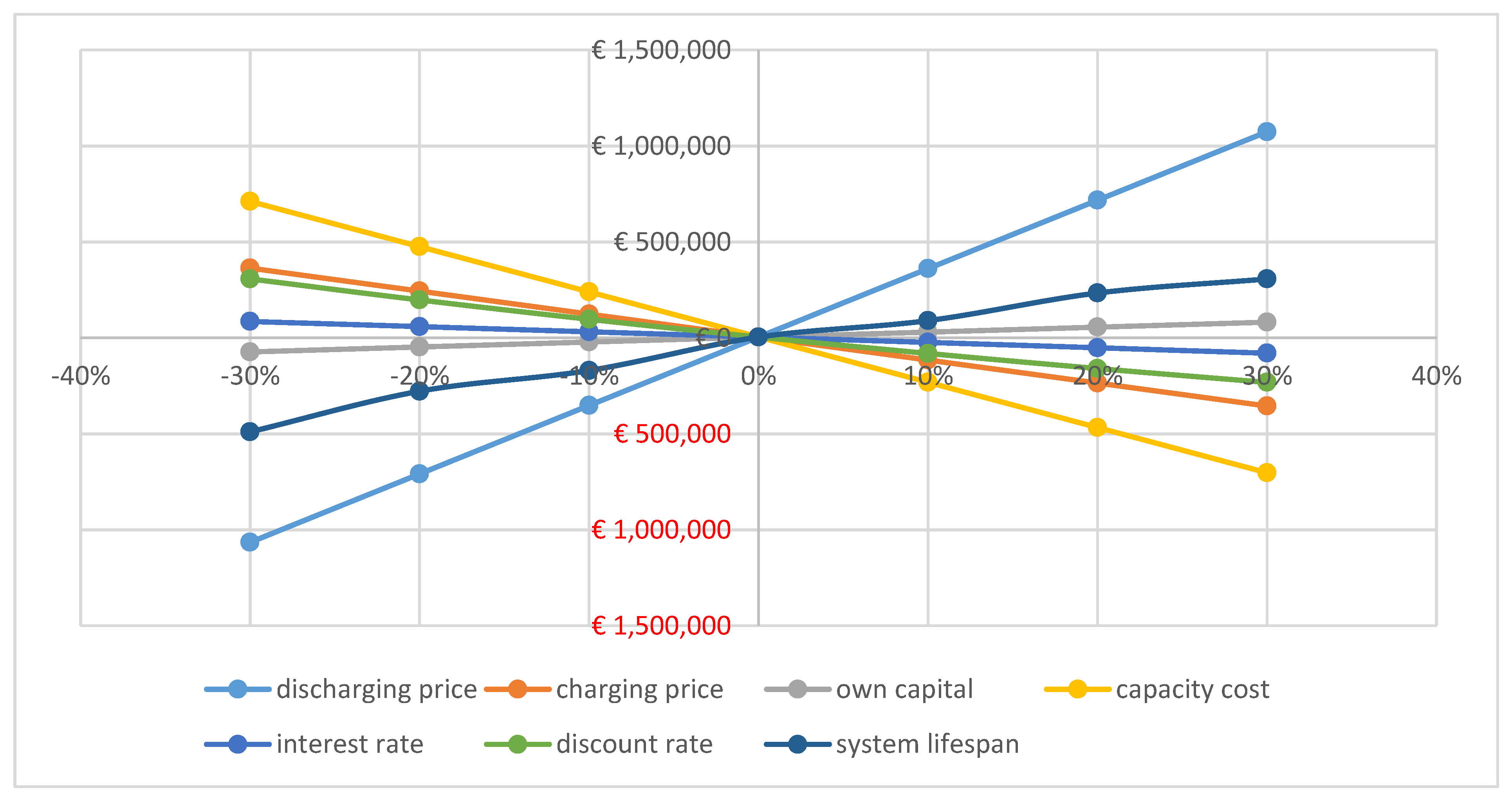
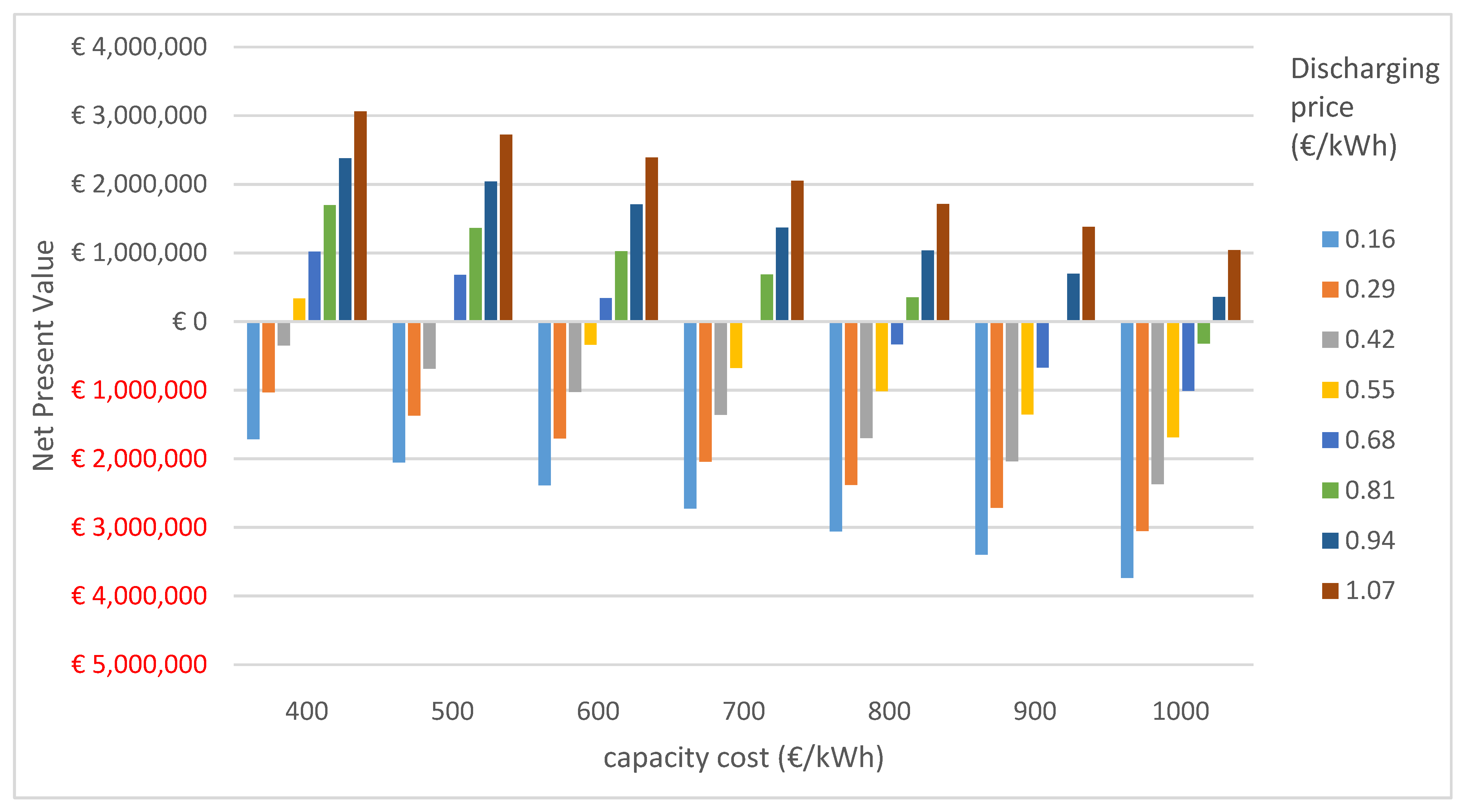
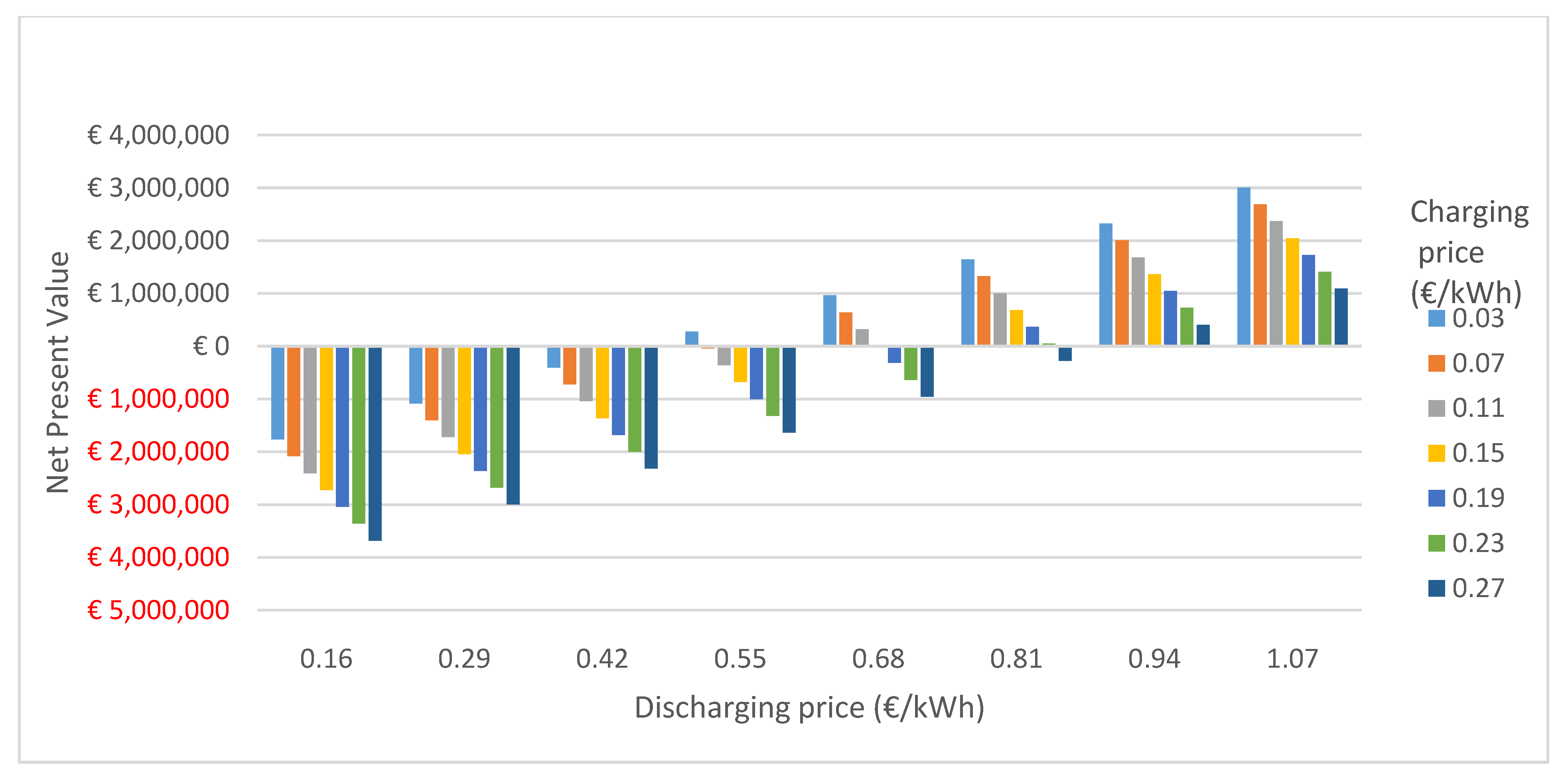
3.2. Changes in Net Present Value Associated with Changes in Different Parameters without Externalities
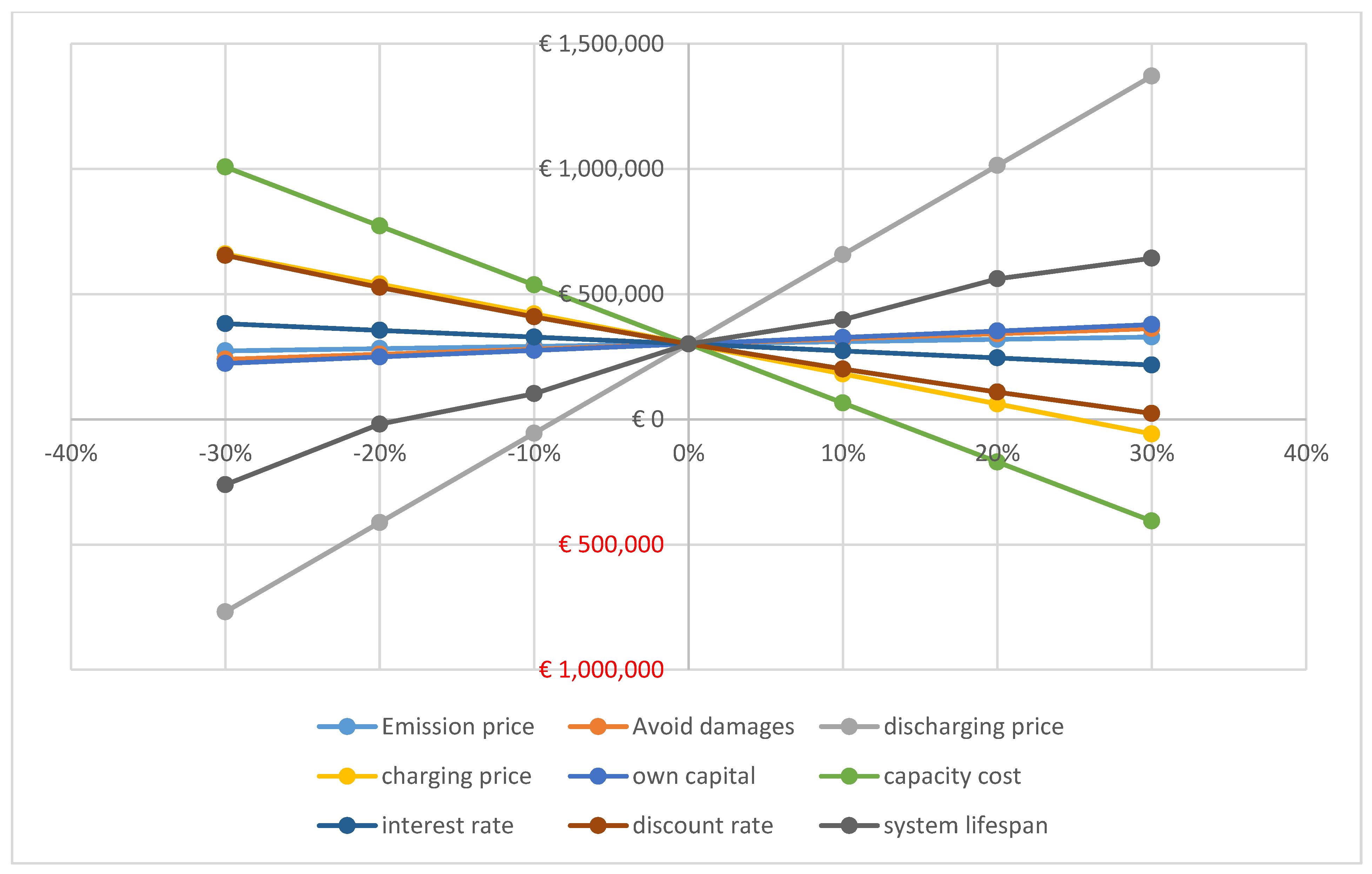
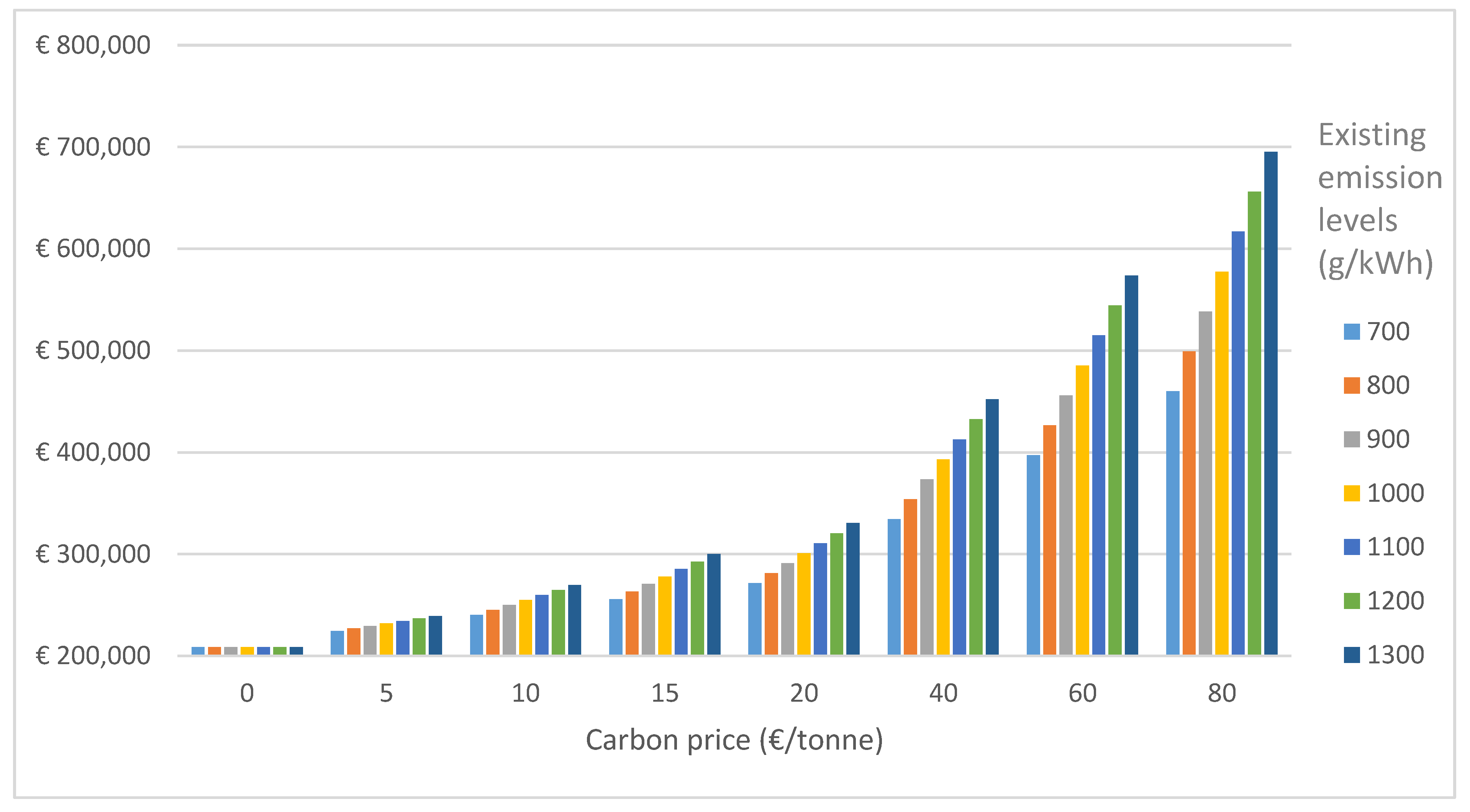
3.3. Changes in Net Present Value Associated with Changes in Different Parameters with Externalities
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- IRENA. Renewable Energy in Cities; International Renewable Energy Agency: Abu Dhabi, UAE, 2016. [Google Scholar]
- Chalvatzis, K.J. Electricity generation development of eastern europe: A carbon technology management case study for poland. Renew. Sustain. Energy Rev. 2009, 13, 1606–1612. [Google Scholar] [CrossRef]
- Kaldellis, J.K.; Spyropoulos, G.; Chalvatzis, K. The impact of greek electricity generation sector on the national air pollution problem. Fresenius Environ. Bull. 2004, 13, 647–656. [Google Scholar]
- Chalvatzis, K.J.; Ioannidis, A. Energy supply security in the eu: Benchmarking diversity and dependence of primary energy. Appl. Energy 2017, 207, 465–476. [Google Scholar] [CrossRef]
- Chalvatzis, K.J.; Ioannidis, A. Energy supply security in southern europe and ireland. Energy Proced. 2017, 105, 2916–2922. [Google Scholar] [CrossRef]
- CDP. Cities Are Harnessing the Power of Renewable Energy: Here’s How. Available online: https://www.cdp.net/en/articles/cities/cities-are-harnessing-the-power-of-renewable-energy (accessed on 19 September 2018).
- Eizenberg, E.; Jabareen, Y. Social sustainability: A new conceptual framework. Sustainability 2017, 9, 68. [Google Scholar] [CrossRef]
- Pothitou, M.; Hanna, R.F.; Chalvatzis, K.J. Ict entertainment appliances’ impact on domestic electricity consumption. Renew. Sustain. Energy Rev. 2017, 69, 843–853. [Google Scholar] [CrossRef]
- Zafirakis, D.; Chalvatzis, K.J. Wind energy and natural gas-based energy storage to promote energy security and lower emissions in island regions. Fuel 2014, 115, 203–219. [Google Scholar] [CrossRef]
- Chalvatzis, K.J.; Malekpoor, H.; Mishra, N.; Lettice, F.; Choudhary, S. Sustainable resource allocation for power generation: The role of big data in enabling interindustry architectural innovation. Technol. Forecast. Soc. Chang. 2018. [Google Scholar] [CrossRef]
- Malekpoor, H.; Chalvatzis, K.; Mishra, N.; Mehlawat, M.K.; Zafirakis, D.; Song, M. Integrated grey relational analysis and multi objective grey linear programming for sustainable electricity generation planning. Ann. Oper. Res. 2018, 269, 475–703. [Google Scholar] [CrossRef]
- Li, X.; Chalvatzis, K.J.; Pappas, D. Life cycle greenhouse gas emissions from power generation in china’s provinces in 2020. Appl. Energy 2018, 223, 93–102. [Google Scholar] [CrossRef]
- Sartori, D.; Catalano, G.; Genco, M.; Pancotti, C.; Sirtori, E.; Vignetti, S.; Del Bo, C. Guide to Cost-Benefit Analysis of Investment Projects–Economic Appraisal Tool for Cohesion Policy 2014–2020; European Commission: Brussels, Belgium, 2014. [Google Scholar]
- Strantzali, E.; Aravossis, K. Decision making in renewable energy investments: A review. Renew. Sustain. Energy Rev. 2016, 55, 885–898. [Google Scholar] [CrossRef]
- Feuillette, S.; Levrel, H.; Boeuf, B.; Blanquart, S.; Gorin, O.; Monaco, G.; Penisson, B.; Robichon, S. The use of cost–benefit analysis in environmental policies: Some issues raised by the water framework directive implementation in france. Environ. Sci. Policy 2016, 57, 79–85. [Google Scholar] [CrossRef]
- OECD. Cost-Benefit Analysis and the Environment; OECD publishing: Paris, France, 2018. [Google Scholar]
- Maresova, P.; Sobeslav, V.; Krejcar, O. Cost–benefit analysis–evaluation model of cloud computing deployment for use in companies. Appl. Econ. 2017, 49, 521–533. [Google Scholar] [CrossRef]
- Mateo, C.; Reneses, J.; Rodriguez-Calvo, A.; Frías, P.; Álvaro, S. Cost-benefit analysis of battery storage in medium-voltage distribution networks. IET Gener. Transm. Distrib. 2016, 10, 815–821. [Google Scholar] [CrossRef]
- Liu, W.; Niu, S.; Xu, H. Optimal planning of battery energy storage considering reliability benefit and operation strategy in active distribution system. J. Mod. Power Syst. Clean Energy 2017, 5, 177–186. [Google Scholar] [CrossRef]
- Zucker, A.; Hinchliffe, T.; Spisto, A. Assessing Storage Value in Electricity Markets; European Commission: Brussels, Belgium, 2013. [Google Scholar]
- Kaldellis, J.K.; Zafirakis, D.; Kaldelli, E.L.; Kavadias, K. Cost benefit analysis of a photovoltaic-energy storage electrification solution for remote islands. Renew. Energy 2009, 34, 1299–1311. [Google Scholar] [CrossRef]
- Spyropoulos, G.; Chalvatzis, K.; Paliatsos, A.; Kaldellis, J.K. Sulphur dioxide emissions due to electricity generation in the aegean islands: Real threat or overestimated danger? In Proceedings of the 9th International Conference on Environmental Science and Technology, Rhodes Island, Greece, 3–6 September 2005. [Google Scholar]
- Ioannidis, A.; Chalvatzis, K.J. Energy supply sustainability for island nations: A study on 8 global islands. Energy Proced. 2017, 142, 3028–3034. [Google Scholar] [CrossRef]
- Kaldellis, J.K.; Zafirakis, D.; Kondili, E. Optimum sizing of photovoltaic-energy storage systems for autonomous small islands. Int. J. Electr. Power Energy Syst. 2010, 32, 24–36. [Google Scholar] [CrossRef]
- Chauhan, A.; Saini, R.P. Techno-economic feasibility study on integrated renewable energy system for an isolated community of india. Renew. Sustain. Energy Rev. 2016, 59, 388–405. [Google Scholar] [CrossRef]
- Hills, J.M.; Μichalena, E.; Chalvatzis, K.J. Innovative technology in the pacific: Building resilience for vulnerable communities. Technol. Forecast. Soc. Chang. 2018, 129, 16–26. [Google Scholar] [CrossRef]
- Malekpoor, H.; Chalvatzis, K.; Mishra, N.; Ramudhin, A. A hybrid approach of vikor and bi-objective integer linear programming for electrification planning in a disaster relief camp. Ann. Oper. Res. 2018, 269, 1–27. [Google Scholar] [CrossRef]
- De Sisternes, F.J.; Jenkins, J.D.; Botterud, A. The value of energy storage in decarbonizing the electricity sector. Appl. Energy 2016, 175, 368–379. [Google Scholar] [CrossRef]
- Leou, R.-C. An economic analysis model for the energy storage system applied to a distribution substation. Int. J. Electr. Power Energy Syst. 2012, 34, 132–137. [Google Scholar] [CrossRef]
- Lin, B.; Wu, W. Economic viability of battery energy storage and grid strategy: A special case of china electricity market. Energy 2017, 124, 423–434. [Google Scholar] [CrossRef]
- Kaldellis, J.K.; Zafirakis, D.; Kavadias, K. Techno-economic comparison of energy storage systems for island autonomous electrical networks. Renew. Sustain. Energy Rev. 2009, 13, 378–392. [Google Scholar] [CrossRef]
- Sullivan, J.L.; Gaines, L. Status of life cycle inventories for batteries. Energy Convers. Manag. 2012, 58, 134–148. [Google Scholar] [CrossRef]
- Denholm, P.; Kulcinski, G.L. Life cycle energy requirements and greenhouse gas emissions from large scale energy storage systems. Energy Convers. Manag. 2004, 45, 2153–2172. [Google Scholar] [CrossRef]
- Van den Bossche, P.; Vergels, F.; Van Mierlo, J.; Matheys, J.; Van Autenboer, W. Subat: An assessment of sustainable battery technology. J. Power Sources 2006, 162, 913–919. [Google Scholar] [CrossRef]
- Sullivan, J.L.; Gaines, L. A Review of Battery Life-Cycle Analysis: State of Knowledge and Critical Needs; Argonne National Laboratory–Energy Systems Division: Oak Ridge, TN, USA, 2010. [Google Scholar]
- Hiremath, M.; Derendorf, K.; Vogt, T. Comparative life cycle assessment of battery storage systems for stationary applications. Environ. Sci. Technol. 2015, 49, 4825–4833. [Google Scholar] [CrossRef] [PubMed]
- Longo, S.; Antonucci, V.; Cellura, M.; Ferraro, M. Life cycle assessment of storage systems: The case study of a sodium/nickel chloride battery. J. Clean. Prod. 2014, 85, 337–346. [Google Scholar] [CrossRef]
- IRENA. Renewable Power Generation Costs in 2017; International Renewable Energy Agency: Abudabi, UAE, 2018. [Google Scholar]
- Eurostat. Electricity Prices for Household Consumers (Taxes included), Second Half 2017 (Eur Per kwh). Available online: http://ec.europa.eu/eurostat/statistics-explained/index.php/Electricity_price_statistics (accessed on 26 July 2018).
- BNEF. Lithium-Ion Battery Costs and Market–Squeezed Margins Seek Technology Improvements & New Business Models; Bloomberg New Energy Finance: New York, NY, USA, 2017. [Google Scholar]
- Newbery, D.; Strbac, G. What is needed for battery electric vehicles to become socially cost competitive? Econ. Transp. 2016, 5, 1–11. [Google Scholar] [CrossRef]
- Zafirakis, D.; Chalvatzis, K.J.; Baiocchi, G.; Daskalakis, G. Modeling of financial incentives for investments in energy storage systems that promote the large-scale integration of wind energy. Appl. Energy 2013, 105, 138–154. [Google Scholar] [CrossRef]
- Kintner-Meyer, M.; Balducci, P.; Colella, W.; Elizondo, M.; Jin, C.; Nguyen, T.; Viswannathan, V.; Zhang, Y. National Assessment of Energy Storage for Grid Balancing and Arbitrage: Phase 1 WECC; Pacific Northwest National Laboratory: Oak Ridge, TN, USA, 2012. [Google Scholar]
- Eyer, J.; Corey, G. Energy Storage for the Electricity Grid: Benefits and Market Potential Assessment Guide; Sandia National Laboratories: California, CA, USA, 2010. [Google Scholar]
- Fitzgerald, G.; Mandel, J.; Morris, J.; Touati, H. The Economics of Battery Energy Storage: How Multi-Use, Customer-Sited Batteries Deliver the Most Services and Value to Customers and the Grid; Rocky Mountain Institute: New York, NY, USA, 2015. [Google Scholar]
- Newbery, D. A Simple Introduction to the Economics of Storage: Shifting Demand and Supply over Time and Space; University of Cambridge: Cambridge, UK, 2016. [Google Scholar]
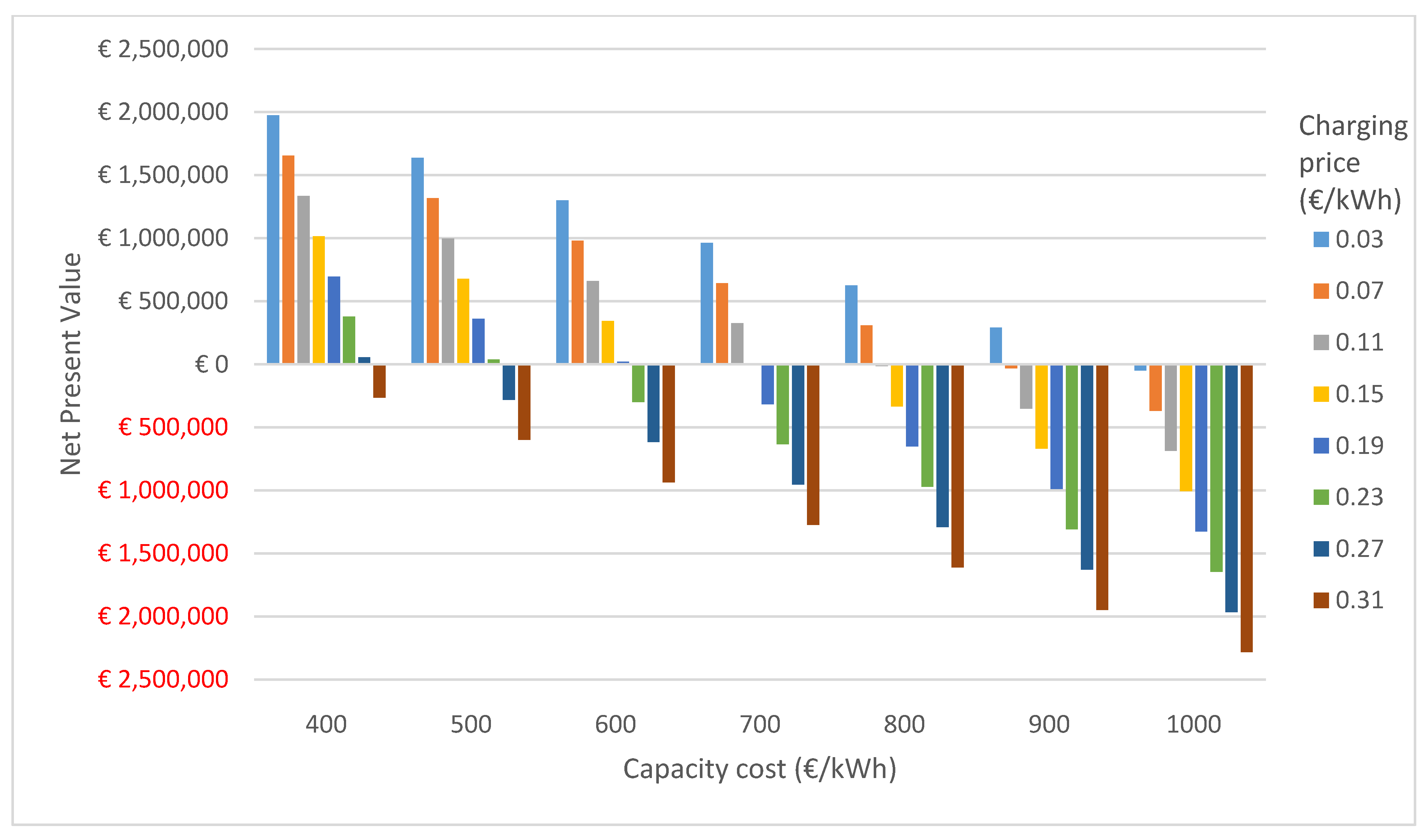
| Type of Battery | FIAMM SONICK 48TL 200 |
|---|---|
| Nominal Voltage | 48 V |
| Nominal capacity | 200 Ah |
| Nominal Energy | 9600 Wh |
| Scenario 1 | Scenario 2 | |
|---|---|---|
| Total cycles during lifetime | 3000 | 2500 |
| Useful life | 1500 | 2187 |
| Roundtrip efficiency (%) | 90 | 90 |
| Depth of discharge (%) | 95 | 95 |
| Global Warming Potential (kg CO2-eq) of which: Manufacturing (%) Operation (%) End-of-life (%) | 2000 75.5% (or 1510) 20.4% (or 408) 4.1% (or 82) | 2100 70.4% (or 1478) 25.8% (or 542) 3.8% (or 80) |
| Scenario 1 | Scenario 2 | |
|---|---|---|
| Total power output (kWh) 1 | 24,624 | 28,728 |
| Total emissions (kg) | 2000 | 2100 |
| Emissions per kWh (g CO2-e per kWh) of which: Manufacturing Operation End-of-life | 81.2 61.3 16.6 3.3 | 73.1 51.5 18.9 2.8 |
| Number of units | 2 |
| Energy storage capacity per unit (kWh) | 1440 |
| Maximum charge duration (h) | 3 |
| Maximum discharge duration (h) | 3 |
| Roundtrip efficiency (%) | 85 |
| Depth of discharge (%) | 80 |
| Rate of storage performance declines (%/yr) | 0.5 |
| Capacity cost of energy storage (€/kWh) | 700 |
| Insurance rate (%) | 0.25% |
| Maintenance cost (€/yr) | 10,000 |
| Installation cost (€/unit) | 30,000 |
| Labor cost (€/yr) | 10,000 |
| Charging cost (€/kWh) | 0.15 |
| Charging cost escalator (%/yr) | 1% |
| Cost of recycling (unit) | 10,000 |
| Own capital ratio (%) | 50% |
| Own capital (€) | 1,008,000 |
| Loan amount (€) | 1,008,000 |
| Loan period (yrs) | 10 |
| Loan interest rate (%) | 6.0% |
| Discount rate (%) | 7% |
| System lifespan (yrs) | 15 |
| Discharge income (€/kWh) | 0.75 |
| Discharge income escalator (%/yr) | 1% |
| Subsidies (€/unit) | 30,000 |
| Environmental Externalities of Storage System | |
| Emissions from manufacturing (CO2-e ton/unit) | 226.5 |
| Emissions from operation (CO2-e g/kWh) | 16.6 |
| Emissions after lifespan (CO2-e ton/unit) | 12.3 |
| Environmental Externalities of Existing Power System | |
| CO2 emissions (g/kWh) | 1000 |
| Pollution Fee | |
| Unit cost of CO2 emissions (€/ton) | 20 |
| Other benefits 1 | |
| TV (€400/unit) | 8000 |
| Fridge (€300/unit) | 8000 |
| Air conditioner (€500/unit) | 6000 |
| Output Indicators | Value without Externalities | Value with Externalities |
|---|---|---|
| Net Present Value | €4533 | €301,014 |
| Benefit-Cost Ratio | 1.00 | 1.08 |
| Internal rate of return | 7.0% | 9.3% |
| Discounted payback period | 9.4 | 8.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Chalvatzis, K.J.; Stephanides, P. Innovative Energy Islands: Life-Cycle Cost-Benefit Analysis for Battery Energy Storage. Sustainability 2018, 10, 3371. https://doi.org/10.3390/su10103371
Li X, Chalvatzis KJ, Stephanides P. Innovative Energy Islands: Life-Cycle Cost-Benefit Analysis for Battery Energy Storage. Sustainability. 2018; 10(10):3371. https://doi.org/10.3390/su10103371
Chicago/Turabian StyleLi, Xin, Konstantinos J. Chalvatzis, and Phedeas Stephanides. 2018. "Innovative Energy Islands: Life-Cycle Cost-Benefit Analysis for Battery Energy Storage" Sustainability 10, no. 10: 3371. https://doi.org/10.3390/su10103371
APA StyleLi, X., Chalvatzis, K. J., & Stephanides, P. (2018). Innovative Energy Islands: Life-Cycle Cost-Benefit Analysis for Battery Energy Storage. Sustainability, 10(10), 3371. https://doi.org/10.3390/su10103371





