Monte Carlo Simulation of Pesticide Toxicity for Rainbow Trout (Oncorhynchus mykiss) Using New Criteria of Predictive Potential
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
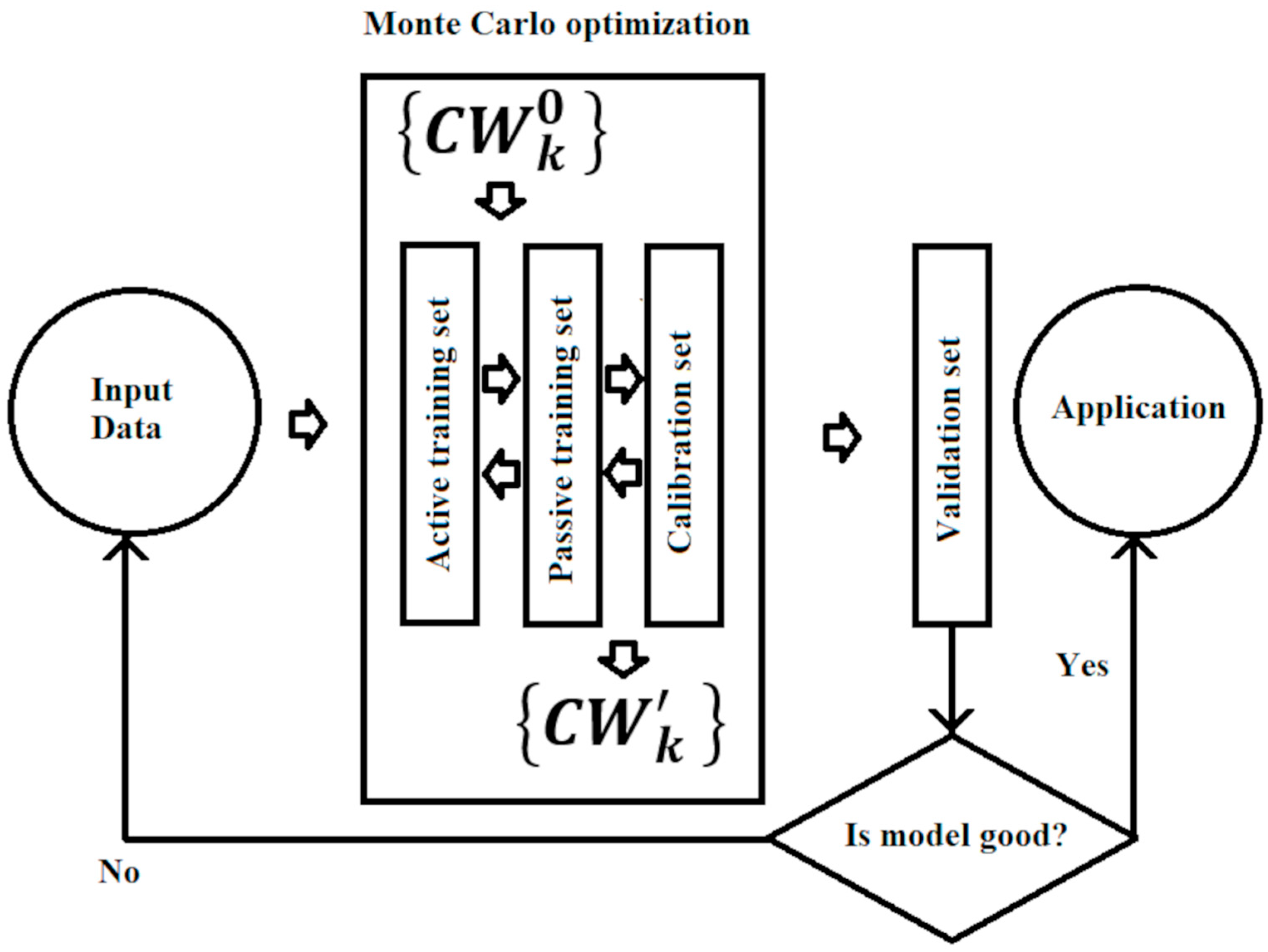
2.2. Simulation Scheme
2.3. Optimal Descriptors
2.4. Optimization of Correlation Weights
2.5. Applicability Domain
2.6. Mechanistic Interpretation
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Auñón-Calles, D.; Pinciroli, M.; Nicolás, E.; Gil-Izquierdo, A.; Gabaldón, J.A.; Sánchez-Iglesias, M.P.; Carbonell-Barrachina, A.A.; Ferreres, F.; García, C.J.; Romero-Trigueros, C. Agronomic and metabolic responses of citrus clementina to long-term irrigation with saline reclaimed water as abiotic factor. Int. J. Mol. Sci. 2025, 26, 3450. [Google Scholar] [CrossRef]
- Arias, A.; Feijoo, G.; Moreira, M.T. Agri-food waste to phenolic compounds: Life cycle and eco-efficiency assessments. J. Environ. Manag. 2025, 380, 124935. [Google Scholar] [CrossRef] [PubMed]
- Avioz, D.; Linker, R.; Raveh, E.; Baram, S.; Paz-Kagan, T. Multi-scale remote sensing for sustainable citrus farming: Predicting canopy nitrogen content using UAV-satellite data fusion. Smart Agric. Technol. 2025, 11, 100906. [Google Scholar] [CrossRef]
- Heshmati, A.; Sadati, R.; Ghavami, M.; Mousavi Khaneghah, A. The concentration of potentially toxic elements (PTEs) in muscle tissue of farmed Iranian rainbow trout (Oncorhynchus mykiss), feed, and water samples collected from the west of Iran: A risk assessment study. Environ. Sci. Pollut. Res. 2019, 26, 34584–34593. [Google Scholar] [CrossRef] [PubMed]
- Barrientos, C.; Tapia, J.; Bertrán, C.; Peña-Cortés, F.; Hauenstein, E.; Fierro, P.; Vargas-Chacoff, L. Is eating wild rainbow trout safe? The effects of different land-uses on heavy metals content in Chile. Environ. Pollut. 2019, 254, 112995. [Google Scholar] [CrossRef]
- Tveterås, S.; Asche, F.; Bellemare, M.F.; Smith, M.D.; Guttormsen, A.G.; Lem, A.; Lien, K.; Vannuccini, S. Fish is food—The FAO’s fish price index. PLoS ONE 2012, 7, e36731. [Google Scholar] [CrossRef]
- Føre, M.; Frank, K.; Norton, T.; Svendsen, E.; Alfredsen, J.A.; Dempster, T.; Eguiraun, H.; Watson, W.; Stahl, A.; Sunde, L.M.; et al. Precision fish farming: A new framework to improve production in aquaculture. Biosyst. Eng. 2018, 173, 176–193. [Google Scholar] [CrossRef]
- LeDoux, M. Analytical methods applied to the determination of pesticide residues in foods of animal origin. A review of the past two decades. J. Chromatogr. A 2011, 1218, 1021–1036. [Google Scholar] [CrossRef]
- Friedman, M.; Juneja, V.K. Review of antimicrobial and antioxidative activities of chitosans in food. J. Food Prot. 2010, 73, 1737–1761. [Google Scholar] [CrossRef]
- Gephart, J.A.; Pace, M.L. Structure and evolution of the global seafood trade network. Environ. Res. Lett. 2015, 10, 125014. [Google Scholar] [CrossRef]
- D’Amore, T.; Chaari, M.; Falco, G.; De Gregorio, G.; Zaraî Jaouadi, N.; Ali, D.S.; Sarkar, T.; Smaoui, S. When sustainability meets health and innovation: The case of citrus by-products for cancer chemoprevention and applications in functional foods. Biocatal. Agric. Biotechnol. 2024, 58, 103163. [Google Scholar] [CrossRef]
- Pacini, T.; D’Amore, T.; Sdogati, S.; Verdini, E.; Bibi, R.; Caporali, A.; Cristofani, E.; Maresca, C.; Orsini, S.; Pelliccia, A.; et al. Assessment of alternaria toxins and pesticides in organic and conventional tomato products: Insights into contamination patterns and food safety implications. Toxins 2025, 17, 12. [Google Scholar] [CrossRef] [PubMed]
- Smaoui, S.; Hosseini, E.; Tsegay, Z.T.; D’Amore, T.; Varzakas, T. Sustainable valorisation of seafood-derived proteins: Current approaches for recovery and applications in biomedical and food systems. Food Biosci. 2024, 62, 105450. [Google Scholar] [CrossRef]
- Tulcan, R.X.S.; Ouyang, W.; Gu, X.; Lin, C.; Tysklind, M.; Wang, B. Typical herbicide residues, trophic transfer, bioconcentration, and health risk of marine organisms. Environ. Int. 2021, 152, 106500. [Google Scholar] [CrossRef]
- Khoshnood, Z. A review on toxic effects of pesticides in Zebrafish, Danio rerio and common carp, Cyprinus carpio, emphasising Atrazine herbicide. Toxicol. Rep. 2024, 13, 101694. [Google Scholar] [CrossRef]
- Khoshnood, Z. Effects of environmental pollution on fish: A short review. Transylv. Rev. Syst. Ecol. Res. 2017, 19, 49–60. [Google Scholar] [CrossRef]
- Stehle, S.; Schulz, R. Agricultural insecticides threaten surface waters at the global scale. Proc. Natl. Acad. Sci. USA 2015, 112, 5750–5755. [Google Scholar] [CrossRef]
- Damalas, C.A.; Eleftherohorinos, I.G. Pesticide exposure, safety issues, and risk assessment indicators. Int. J. Environ. Res. Public Health 2011, 8, 1402–1419. [Google Scholar] [CrossRef]
- Horzmann, K.A.; Lin, L.F.; Taslakjian, B.; Yuan, C.; Freeman, J.L. Anxiety-related behavior and associated brain transcriptome and epigenome alterations in adult female zebrafish exposed to atrazine during embryogenesis. Chemosphere 2022, 308, 136431. [Google Scholar] [CrossRef]
- Kucka, M.; Pogrmic-Majkic, K.; Fa, S.; Stojilkovic, S.S.; Kovacevic, R. Atrazine acts as an endocrine disrupter by inhibiting cAMP-specific phosphodiesterase-4. Toxicol. Appl. Pharmacol. 2012, 265, 19–26. [Google Scholar] [CrossRef]
- Olsvik, P.A.; Larsen, A.K.; Berntssen, M.H.G.; Goksøyr, A.; Karlsen, O.A.; Yadetie, F.; Sanden, M.; Kristensen, T. Effects of agricultural pesticides in aquafeeds on wild fish feeding on leftover pellets near fish farms. Front. Genet. 2019, 10, 794. [Google Scholar] [CrossRef] [PubMed]
- Takata, M.; Lin, B.-L.; Xue, M.; Zushi, Y.; Terada, A.; Hosomi, M. Predicting the acute ecotoxicity of chemical substances by machine learning using graph theory. Chemosphere 2020, 238, 124604. [Google Scholar] [CrossRef] [PubMed]
- Austin, T.; Denoyelle, M.; Chaudry, A.; Stradling, S.; Eadsforth, C. European chemicals agency dossier submissions as an experimental data source: Refinement of a fish toxicity model for predicting acute LC50 values. Environ. Toxicol. Chem. 2015, 34, 369–378. [Google Scholar] [CrossRef] [PubMed]
- Raimondo, S.; Barron, M.G. Application of interspecies correlation estimation (ICE) models and QSAR in estimating species sensitivity to pesticides. SAR QSAR Environ. Res. 2020, 31, 1–18. [Google Scholar] [CrossRef]
- Veldman, M.B.; Lin, S. Zebrafish as a developmental model organism for pediatric research. Pediatr. Res. 2008, 64, 470–476. [Google Scholar] [CrossRef] [PubMed]
- Lessman, C.A. The developing zebrafish (Danio rerio): A vertebrate model for high-throughput screening of chemical libraries. Birth Defects Res. Part C Embryo Today Rev. 2011, 93, 268–280. [Google Scholar] [CrossRef]
- Hill, A.J.; Teraoka, H.; Heideman, W.; Peterson, R.E. Zebrafish as a Model Vertebrate for Investigating Chemical Toxicity. Toxicol. Sci. 2005, 86, 6–19. [Google Scholar] [CrossRef]
- OECD. Test No. 203: Fish Acute Toxicity Testing; Guideline for the Testing of Chemicals, Section 2; OECD Publishing: Paris, France, 2019. [Google Scholar] [CrossRef]
- OECD. Test No. 210: Fish, Early-Life Stage Toxicity Test; OECD Publishing: Paris, France, 2009; pp. 1–24. Available online: https://www.oecd.org/en/publications/test-no-210-fish-early-life-stage-toxicity-test_9789264203785-en.html (accessed on 27 May 2025).
- OECD. Test No. 212: Fish, Short-Term Toxicity Test on Embryo and Sac-Fry Stages; Guidelines for the Testing Chemicals, Section 2: Effects on Biotic Systems; OECD Publishing: Paris, France, 1998; pp. 1–20. Available online: https://www.oecd.org/en/publications/test-no-212-fish-short-term-toxicity-test-on-embryo-and-sac-fry-stages_9789264070141-en.html (accessed on 27 May 2025).
- OECD. Test No. 236: Fish Embryo Acute Toxicity (FET) Test; OECD Guidelines for the Testing of Chemicals, Section 2; OECD Publishing: Paris, France, 2013; pp. 1–22. Available online: https://www.oecd.org/en/publications/test-no-236-fish-embryo-acute-toxicity-fet-test_9789264203709-en.html (accessed on 27 May 2025).
- Pulido-Reyes, G.; Moreno-Martín, G.; Gómez-Gómez, B.; Navas, J.M.; Madrid, Y.; Fernández-Cruz, M.L. Fish acute toxicity of nine nanomaterials: Need of pre-tests to ensure comparability and reuse of data. Environ. Res. 2024, 245, 118072. [Google Scholar] [CrossRef]
- Zercher, M.; Coral, J.A.; Nabb, D.; Powers, G.; Jones, A.; Johanning, K. A Comparison of in vitro metabolic clearance of various regulatory fish species using hepatic S9 fractions. Environ. Toxicol. Chem. 2024, 43, 1390–1405. [Google Scholar] [CrossRef]
- Bueso-Bordils, J.I.; Antón-Fos, G.M.; Martín-Algarra, R.; Alemán-López, P.A. Overview of computational toxicology methods applied in drug and green chemical discovery. J. Xenobiotics 2024, 14, 1901–1918. [Google Scholar] [CrossRef]
- McKim, J.M. Physiological and Biochemical Mechanisms that Regulate the Accumulation and Toxicity of Environmental Chemicals in Fish. In Bioavailability: Physical, Chemical, and Biological Interactions; CRC Press: Boca Raton, FL, USA, 2024; pp. 179–201. [Google Scholar] [CrossRef]
- Jia, Q.; Liu, T.; Yan, F.; Wang, Q. Norm index–based QSAR model for acute toxicity of pesticides toward Rainbow Trout. Environ. Toxicol. Chem. 2020, 39, 352–358. [Google Scholar] [CrossRef] [PubMed]
- Toropova, A.P.; Toropov, A.A. Hybrid optimal descriptors as a tool to predict skin sensitization in accordance to OECD principles. Toxicol. Lett. 2017, 275, 57–66. [Google Scholar] [CrossRef] [PubMed]
- Toropova, A.P.; Toropov, A.A. Does the Index of Ideality of Correlation Detect the Better Model Correctly? Mol. Inform. 2019, 38, 1800157. [Google Scholar] [CrossRef]
- Toropov, A.A.; Toropova, A.P.; Benfenati, E. QSAR model for pesticides toxicity to Rainbow Trout based on “ideal correlations”. Aquat. Toxicol. 2020, 227, 105589. [Google Scholar] [CrossRef]
- Toropova, A.P.; Toropov, A.A.; Roncaglioni, A.; Benfenati, E. Monte Carlo simulation of aromatic molecule adsorption on multi-walled carbon nanotube surfaces using coefficient of conformism of a correlative prediction (CCCP). C-J. Carbon Res. 2025, 11, 7. [Google Scholar] [CrossRef]
- Khan, K.; Khan, P.M.; Lavado, G.; Valsecchi, C.; Pasqualini, J.; Baderna, D.; Marzo, M.; Lombardo, A.; Roy, K.; Benfenati, E. QSAR modeling of Daphnia magna and fish toxicities of biocides using 2D descriptors. Chemosphere 2019, 229, 8–17. [Google Scholar] [CrossRef]
- Vopson, M.M. The second law of infodynamics and its implications for the simulated universe hypothesis. AIP Adv. 2023, 13, 105308. [Google Scholar] [CrossRef]
- Drefahl, A. CurlySMILES: A chemical language to customize and annotate encodings of molecular and nanodevice structures. J. Cheminformatics 2011, 3, 1. [Google Scholar] [CrossRef]
- Iovine, N.; Toropova, A.P.; Toropov, A.A.; Roncaglioni, A.; Benfenati, E. Simulation of the long-term toxicity towards Bobwhite Quail (Colinus virginianus) by the Monte Carlo method. J. Xenobiotics 2025, 15, 3. [Google Scholar] [CrossRef]
- Usmani, S.M.; Bremer-Hoffmann, S.; Cheyns, K.; Cubadda, F.; Dumit, V.I.; Escher, S.E.; Fessard, V.; Gutleb, A.C.; Léger, T.; Liu, Y.-C.; et al. Review of new approach methodologies for application in risk assessment of nanoparticles in the food and feed sector: Status and challenges. EFSA Support. Publ. 2024, 21, EN-8826. [Google Scholar] [CrossRef]
- Bearth, A.; Roth, N.; Jansen, T.; Holden, L.; Čavoški, A.; Di Consiglio, E.; Hauzenberger, I.; Lee, R.; Mombelli, E.; Tcheremenskaia, O.; et al. New approach methodologies in human health risk assessment across European regulatory frameworks: Status quo, barriers and drivers for regulatory acceptance and use. Environ. Int. 2025, 196, 109279. [Google Scholar] [CrossRef] [PubMed]

| TF1 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Split | Set * | n | R2 | CCC | IIC | CII | Q2 | CCCP | RMSE | F | NA |
| 1 | A | 79 | 0.476 | 0.645 | 0.549 | 0.746 | 0.443 | 0.024 | 1.18 | 70 | |
| P | 77 | 0.544 | 0.652 | 0.545 | 0.750 | 0.524 | 0.159 | 1.32 | 89 | ||
| C | 78 | 0.576 | 0.748 | 0.759 | 0.775 | 0.541 | 0.301 | 0.76 | 103 | ||
| V | 77 | 0.844 | - | - | - | - | - | 0.66 | - | 61 | |
| 2 | A | 78 | 0.409 | 0.581 | 0.608 | 0.738 | 0.377 | −0.019 | 1.28 | 53 | |
| P | 78 | 0.409 | 0.542 | 0.608 | 0.701 | 0.377 | −0.235 | 1.43 | 53 | ||
| C | 77 | 0.687 | 0.826 | 0.829 | 0.808 | 0.664 | 0.386 | 0.52 | 165 | ||
| V | 78 | 0.805 | - | - | - | - | - | 0.57 | - | 60 | |
| 3 | A | 78 | 0.419 | 0.590 | 0.555 | 0.723 | 0.388 | −0.107 | 1.41 | 55 | |
| P | 77 | 0.381 | 0.543 | 0.589 | 0.710 | 0.348 | −0.209 | 1.32 | 46 | ||
| C | 78 | 0.785 | 0.874 | 0.883 | 0.856 | 0.772 | 0.536 | 0.47 | 277 | ||
| V | 78 | 0.837 | - | - | - | - | - | 0.57 | - | 58 | |
| 4 | A | 79 | 0.361 | 0.531 | 0.586 | 0.784 | 0.328 | 0.164 | 1.33 | 44 | |
| P | 77 | 0.362 | 0.493 | 0.460 | 0.717 | 0.325 | −0.182 | 1.49 | 43 | ||
| C | 78 | 0.738 | 0.839 | 0.859 | 0.842 | 0.715 | 0.474 | 0.53 | 214 | ||
| V | 77 | 0.831 | - | - | - | - | - | 0.51 | - | 61 | |
| 5 | A | 78 | 0.453 | 0.624 | 0.640 | 0.765 | 0.425 | 0.177 | 1.37 | 63 | |
| P | 78 | 0.414 | 0.615 | 0.499 | 0.740 | 0.384 | −0.092 | 1.29 | 54 | ||
| C | 78 | 0.633 | 0.792 | 0.795 | 0.809 | 0.609 | 0.413 | 0.56 | 131 | ||
| V | 77 | 0.827 | - | - | - | - | - | 0.57 | - | 62 | |
| TF2 | |||||||||||
| 1 | A | 79 | 0.554 | 0.713 | 0.656 | 0.769 | 0.527 | 0.240 | 1.09 | 96 | |
| P | 77 | 0.594 | 0.678 | 0.585 | 0.779 | 0.576 | 0.140 | 1.30 | 110 | ||
| C | 78 | 0.366 | 0.576 | 0.573 | 0.760 | 0.310 | 0.063 | 1.08 | 44 | ||
| V | 77 | 0.632 | - | - | - | - | - | 1.10 | - | 61 | |
| 2 | A | 78 | 0.498 | 0.665 | 0.706 | 0.751 | 0.469 | 0.090 | 1.18 | 75 | |
| P | 78 | 0.497 | 0.640 | 0.689 | 0.740 | 0.473 | −0.014 | 1.32 | 75 | ||
| C | 77 | 0.659 | 0.800 | 0.623 | 0.837 | 0.636 | 0.466 | 0.62 | 145 | ||
| V | 78 | 0.810 | - | - | - | - | - | 0.70 | - | 60 | |
| 3 | A | 78 | 0.497 | 0.664 | 0.705 | 0.757 | 0.472 | 0.203 | 1.31 | 75 | |
| P | 77 | 0.497 | 0.623 | 0.675 | 0.733 | 0.467 | 0.005 | 1.20 | 74 | ||
| C | 78 | 0.753 | 0.837 | 0.623 | 0.868 | 0.733 | 0.591 | 0.57 | 232 | ||
| V | 78 | 0.826 | - | - | - | - | - | 0.64 | - | 58 | |
| 4 | A | 79 | 0.482 | 0.651 | 0.677 | 0.761 | 0.4537 | 0.218 | 1.19 | 72 | |
| P | 77 | 0.515 | 0.656 | 0.628 | 0.768 | 0.4897 | 0.223 | 1.28 | 79 | ||
| C | 78 | 0.642 | 0.801 | 0.790 | 0.835 | 0.6105 | 0.465 | 0.65 | 136 | ||
| V | 77 | 0.720 | - | - | - | - | - | 0.78 | - | 61 | |
| 5 | A | 78 | 0.529 | 0.692 | 0.657 | 0.768 | 0.505 | 0.097 | 1.27 | 85 | |
| P | 78 | 0.521 | 0.706 | 0.704 | 0.776 | 0.496 | 0.179 | 1.21 | 83 | ||
| C | 78 | 0.583 | 0.742 | 0.545 | 0.832 | 0.543 | 0.484 | 0.66 | 106 | ||
| V | 77 | 0.778 | - | - | - | - | - | 0.72 | - | 62 | |
| TF3 | |||||||||||
| 1 | A | 79 | 0.440 | 0.611 | 0.646 | 0.744 | 0.406 | 0.052 | 1.22 | 60 | |
| P | 77 | 0.458 | 0.629 | 0.547 | 0.741 | 0.429 | 0.093 | 1.41 | 63 | ||
| C | 78 | 0.696 | 0.823 | 0.741 | 0.827 | 0.675 | 0.530 | 0.64 | 174 | ||
| V | 77 | 0.886 | - | - | - | - | - | 0.62 | - | 61 | |
| 2 | A | 78 | 0.437 | 0.608 | 0.661 | 0.752 | 0.405 | 0.079 | 1.25 | 59 | |
| P | 78 | 0.437 | 0.586 | 0.651 | 0.710 | 0.405 | −0.140 | 1.40 | 59 | ||
| C | 77 | 0.799 | 0.890 | 0.803 | 0.899 | 0.785 | 0.749 | 0.44 | 297 | ||
| V | 78 | 0.886 | - | - | - | - | - | 0.47 | - | 60 | |
| 3 | A | 78 | 0.456 | 0.627 | 0.610 | 0.740 | 0.429 | 0.080 | 1.36 | 64 | |
| P | 77 | 0.456 | 0.567 | 0.611 | 0.726 | 0.425 | −0.134 | 1.25 | 63 | ||
| C | 78 | 0.867 | 0.919 | 0.869 | 0.921 | 0.858 | 0.796 | 0.37 | 495 | ||
| V | 78 | 0.887 | - | - | - | - | - | 0.46 | - | 58 | |
| 4 | A | 79 | 0.397 | 0.568 | 0.614 | 0.759 | 0.368 | 0.064 | 1.29 | 51 | |
| P | 77 | 0.397 | 0.544 | 0.549 | 0.730 | 0.362 | −0.039 | 1.43 | 49 | ||
| C | 78 | 0.858 | 0.906 | 0.777 | 0.926 | 0.847 | 0.827 | 0.40 | 459 | ||
| V | 77 | 0.883 | - | - | - | - | - | 0.42 | - | 61 | |
| 5 | A | 78 | 0.470 | 0.639 | 0.651 | 0.764 | 0.442 | 0.208 | 1.35 | 67 | |
| P | 78 | 0.453 | 0.652 | 0.614 | 0.749 | 0.424 | −0.043 | 1.27 | 63 | ||
| C | 78 | 0.781 | 0.872 | 0.617 | 0.898 | 0.765 | 0.776 | 0.43 | 271 | ||
| V | 77 | 0.881 | - | - | - | - | - | 0.48 | - | 62 |
| No. | SMILES Attributes | CWs Probe 1 | CWs Probe 2 | CWs Probe 3 | NA | NP | NC | dk |
|---|---|---|---|---|---|---|---|---|
| 1 | 1........... | 0.353 | 1.271 | 0.414 | 70 | 65 | 61 | 0.0011 |
| 2 | =........... | 0.460 | 0.181 | 0.482 | 62 | 65 | 62 | 0.0006 |
| 3 | c...1....... | 0.823 | 0.266 | 0.290 | 57 | 44 | 56 | 0.0019 |
| 4 | c...c....... | 0.484 | 0.355 | 0.005 | 55 | 44 | 50 | 0.0017 |
| 5 | (...(....... | 0.904 | 0.393 | 0.512 | 39 | 33 | 36 | 0.0012 |
| 6 | Cl.......... | 1.433 | 0.096 | 0.788 | 38 | 30 | 32 | 0.0018 |
| 7 | S........... | 1.643 | 1.467 | 1.151 | 22 | 28 | 21 | 0.0027 |
| 1 | O...(....... | −0.128 | −0.600 | −0.306 | 59 | 55 | 56 | 0.0004 |
| 2 | N........... | −0.885 | −0.481 | −0.966 | 51 | 39 | 45 | 0.0021 |
| 3 | N...(....... | −0.685 | −0.089 | −0.094 | 37 | 28 | 33 | 0.0021 |
| 4 | C...=....... | −0.243 | −0.087 | −0.460 | 31 | 37 | 28 | 0.0025 |
| 5 | 1...(....... | −0.506 | −0.122 | −0.522 | 29 | 24 | 24 | 0.0015 |
| 6 | n........... | −0.063 | −0.402 | −0.277 | 26 | 13 | 21 | 0.0053 |
| 7 | n...c....... | −0.807 | −0.276 | −0.770 | 24 | 11 | 21 | 0.0057 |
| The Number of Compounds in the Training Set | Determination Coefficient for Training Set | The Number of Compounds in Validation Set | Determination Coefficient for Validation Set | Reference |
|---|---|---|---|---|
| 249 | 0.80 | 62 | 0.81 | [36] |
| 233 | 0.67 | 78 | 0.86 | [39] |
| 66 | 0.80 | 22 | 0.74 | [41] |
| 234 | 0.53 | 77 | 0.89 | In this work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toropova, A.P.; Toropov, A.A.; Benfenati, E. Monte Carlo Simulation of Pesticide Toxicity for Rainbow Trout (Oncorhynchus mykiss) Using New Criteria of Predictive Potential. J. Xenobiot. 2025, 15, 82. https://doi.org/10.3390/jox15030082
Toropova AP, Toropov AA, Benfenati E. Monte Carlo Simulation of Pesticide Toxicity for Rainbow Trout (Oncorhynchus mykiss) Using New Criteria of Predictive Potential. Journal of Xenobiotics. 2025; 15(3):82. https://doi.org/10.3390/jox15030082
Chicago/Turabian StyleToropova, Alla P., Andrey A. Toropov, and Emilio Benfenati. 2025. "Monte Carlo Simulation of Pesticide Toxicity for Rainbow Trout (Oncorhynchus mykiss) Using New Criteria of Predictive Potential" Journal of Xenobiotics 15, no. 3: 82. https://doi.org/10.3390/jox15030082
APA StyleToropova, A. P., Toropov, A. A., & Benfenati, E. (2025). Monte Carlo Simulation of Pesticide Toxicity for Rainbow Trout (Oncorhynchus mykiss) Using New Criteria of Predictive Potential. Journal of Xenobiotics, 15(3), 82. https://doi.org/10.3390/jox15030082








