A Switched Algorithm for Adaptive Feedback Cancellation Using Pre-Filters in Hearing Aids
Abstract
:1. Introduction
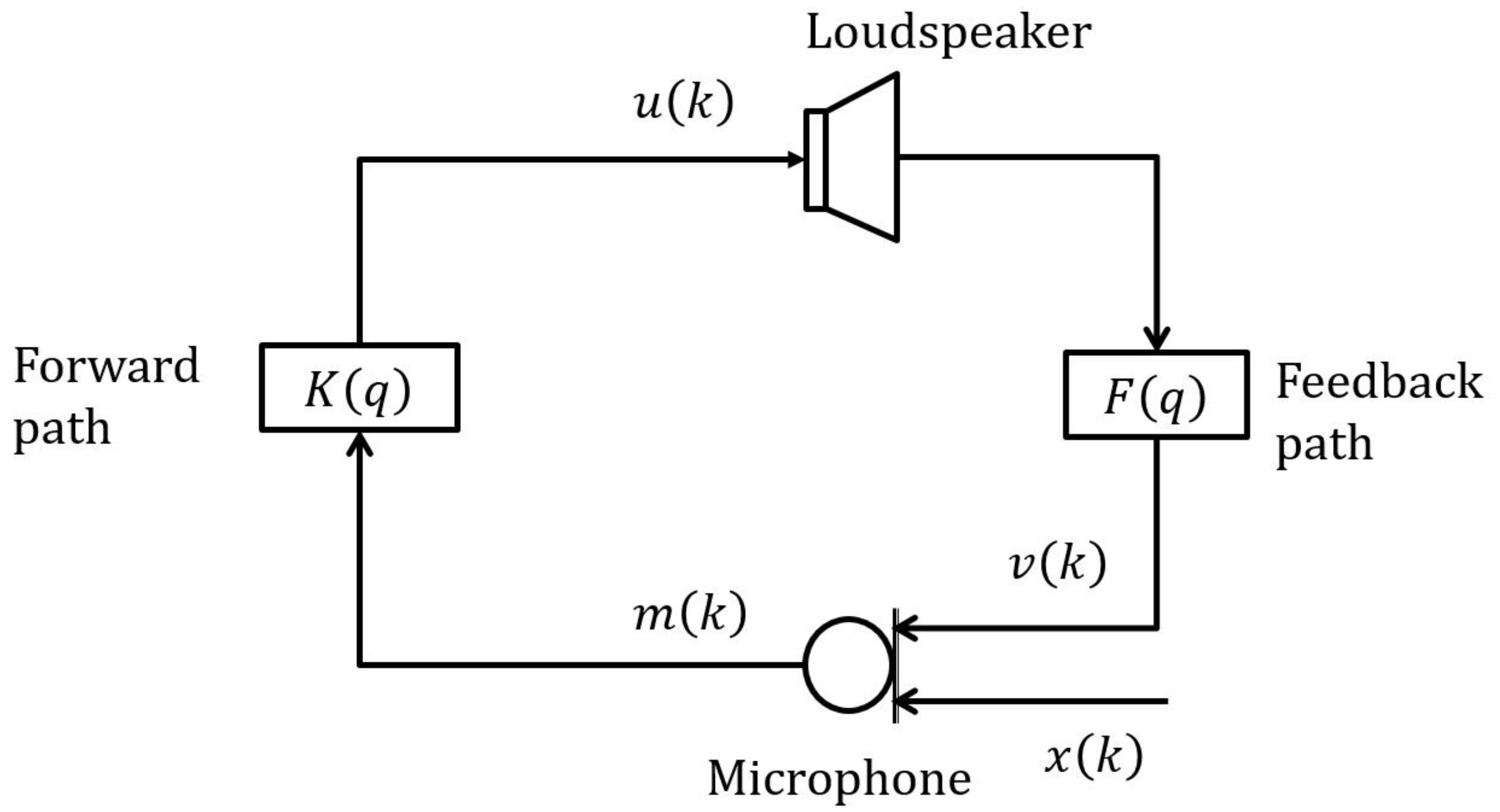
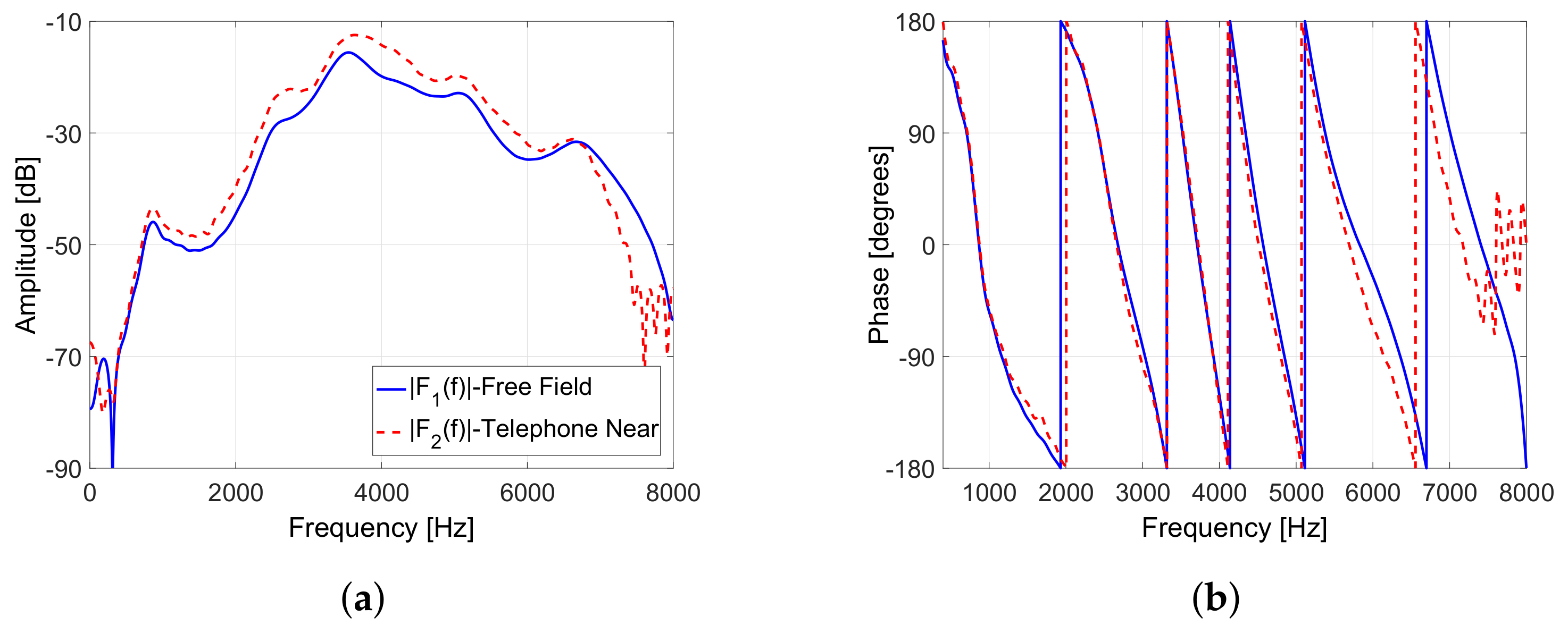
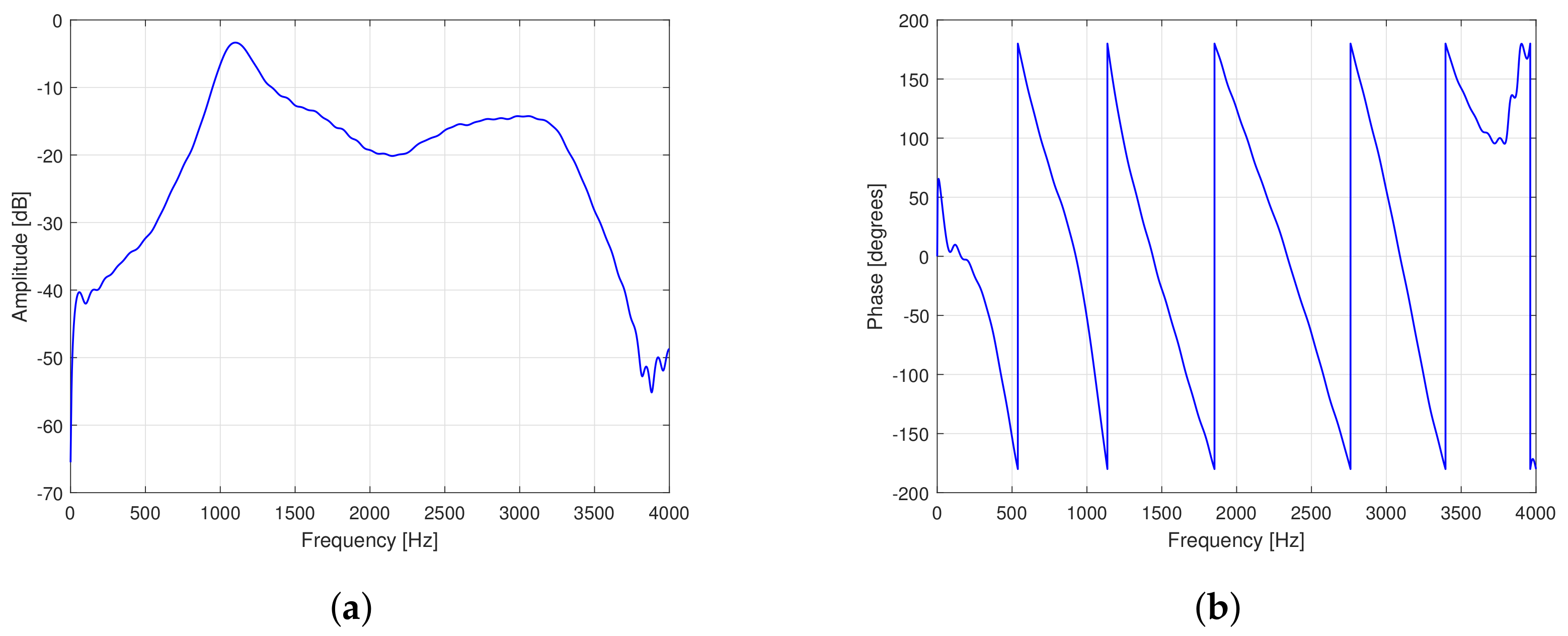
2. Hearing Aids and Acoustic Feedback Problem
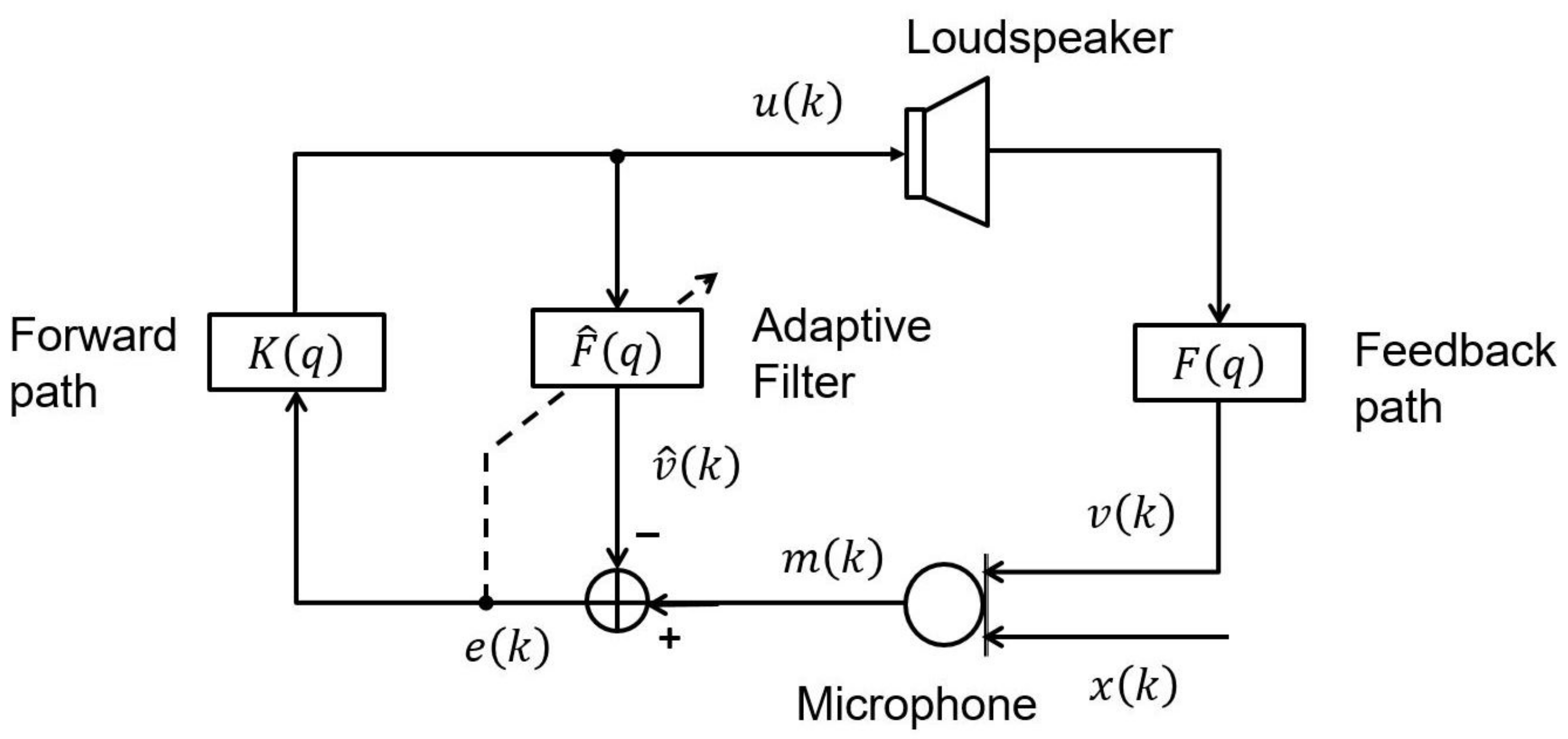
3. Standard AFC Approach
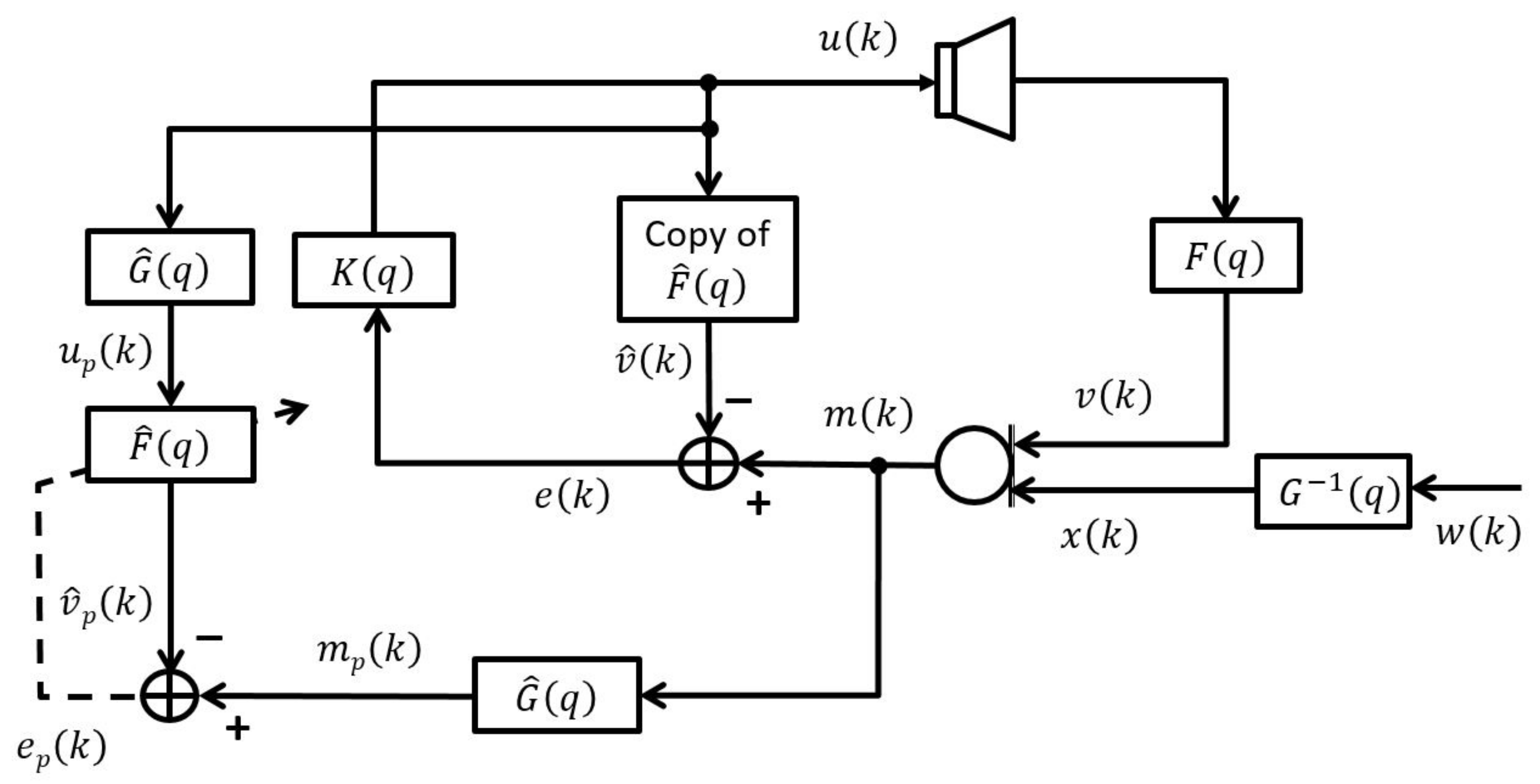
4. PEM-AFC
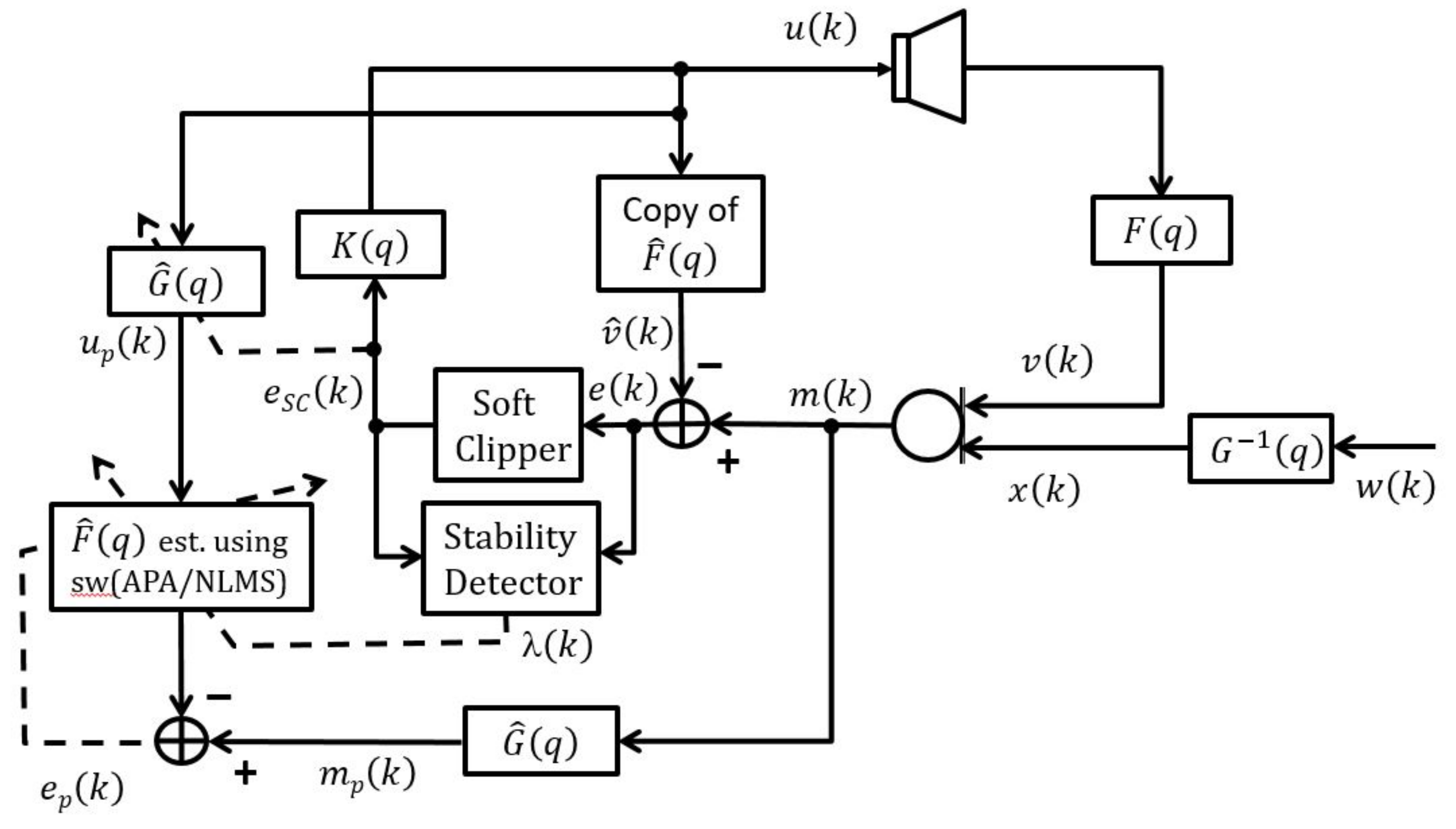
5. Proposed Method
6. Computational Complexity
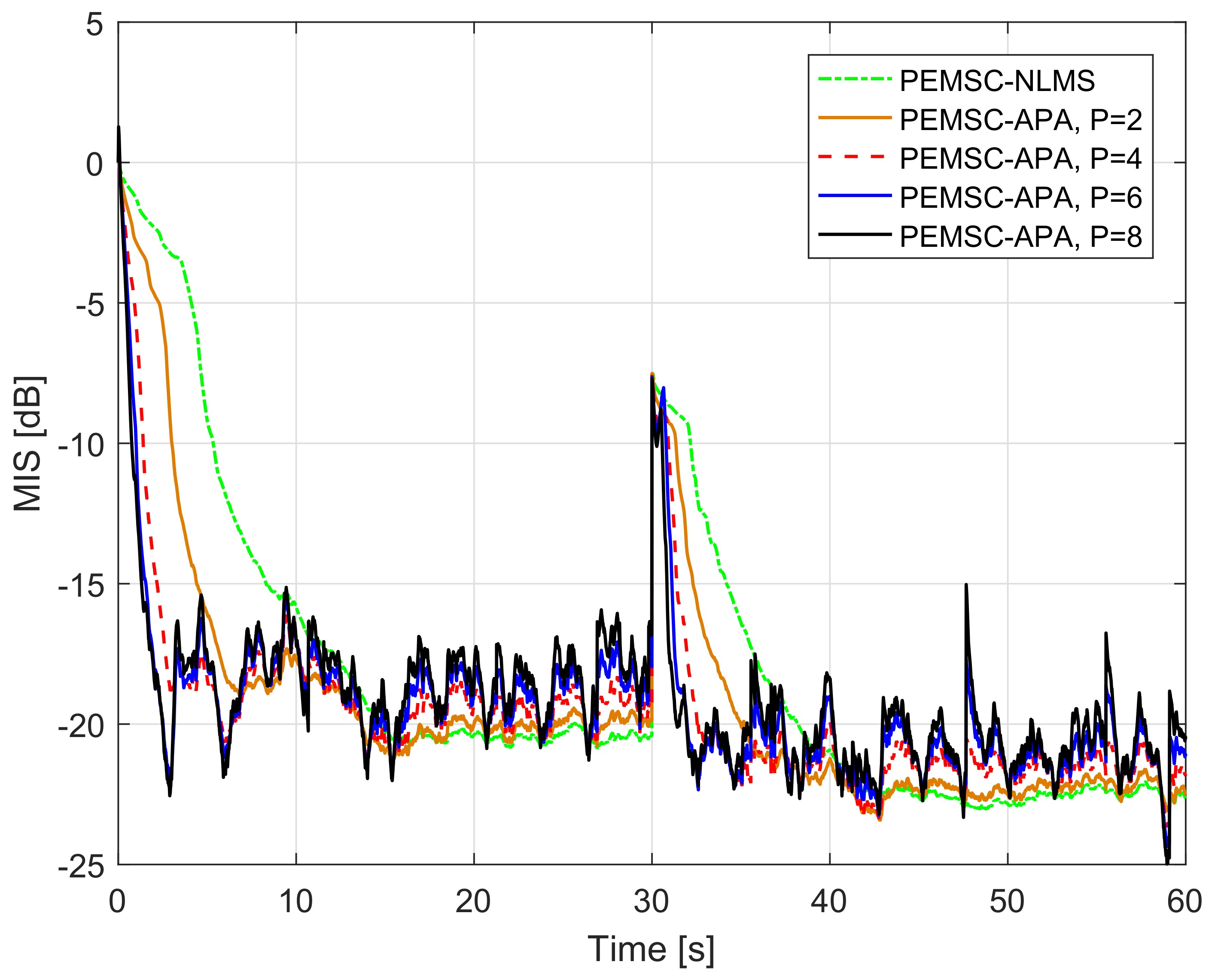
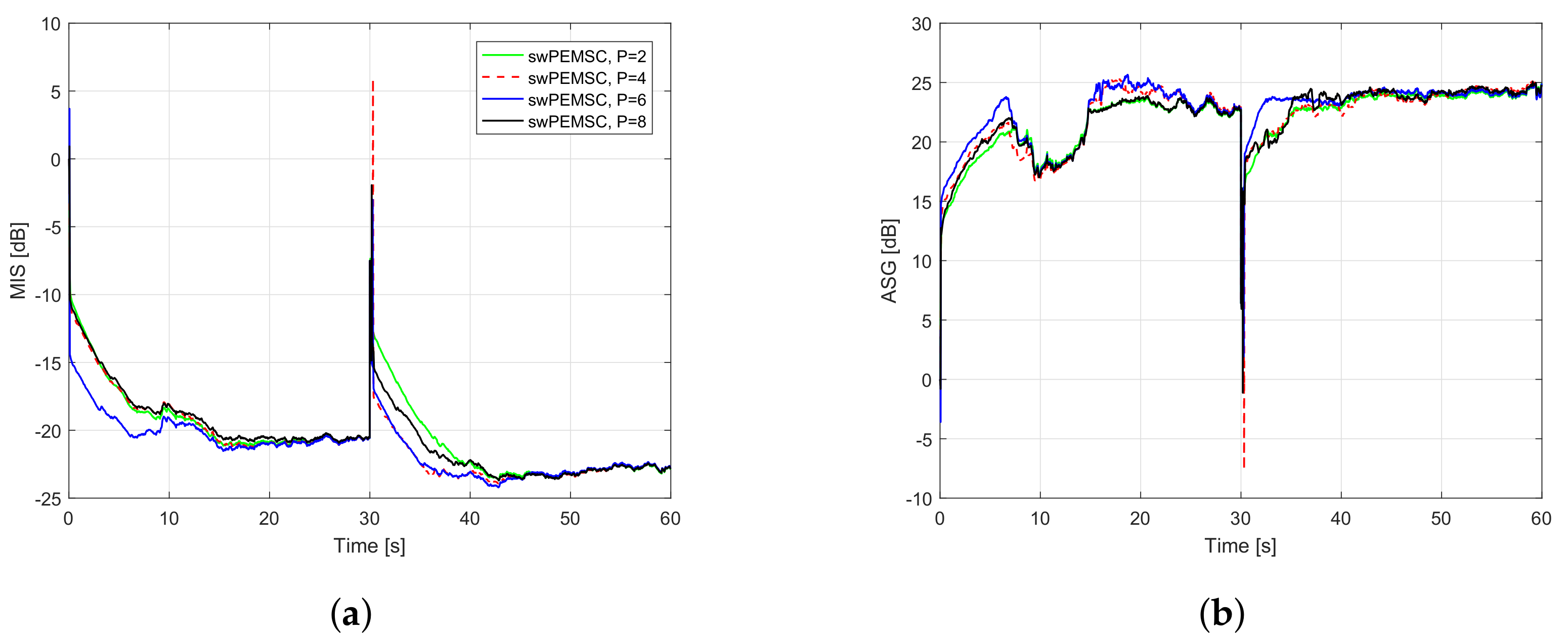
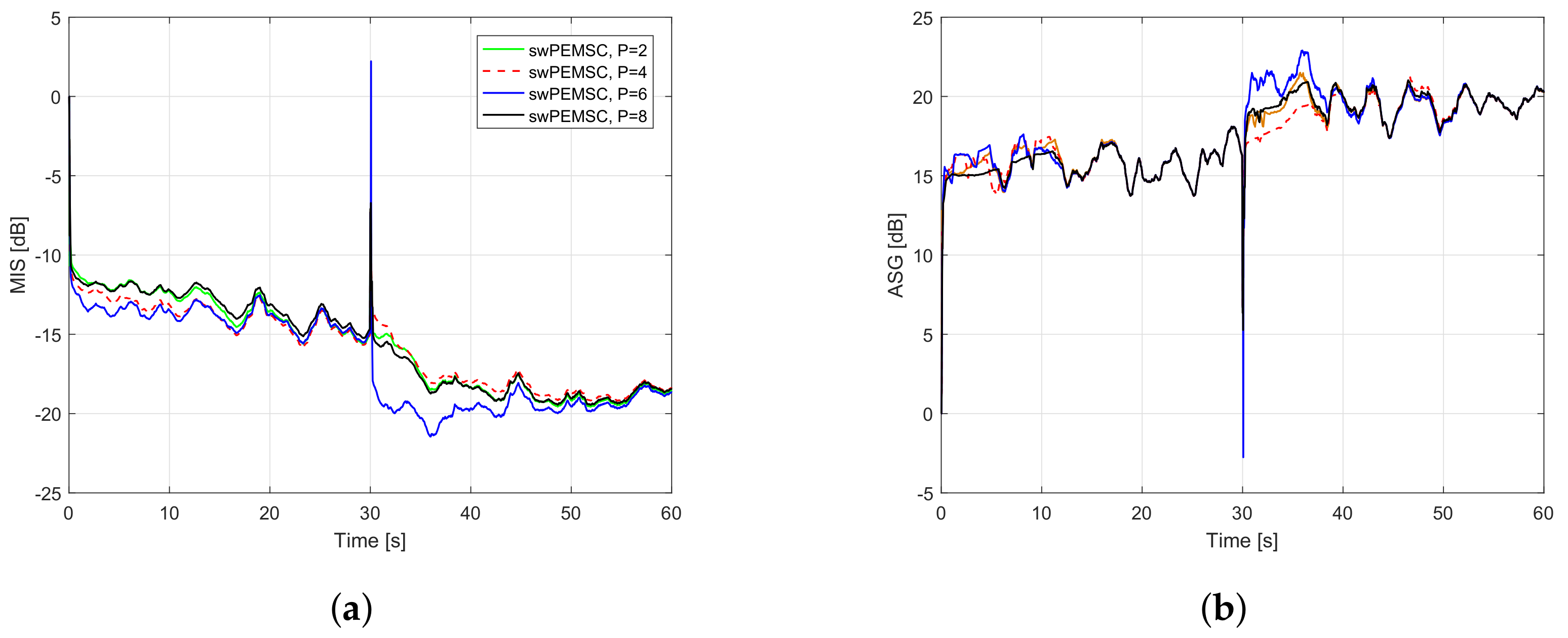
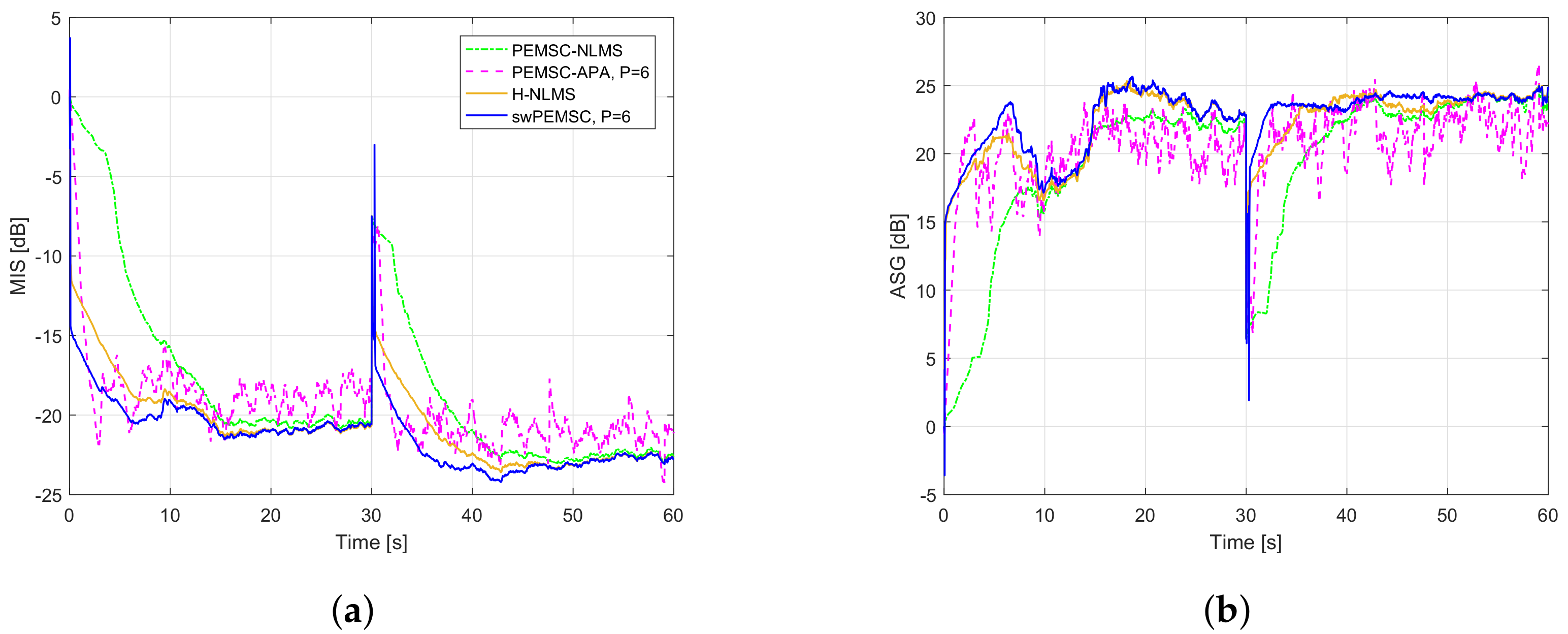
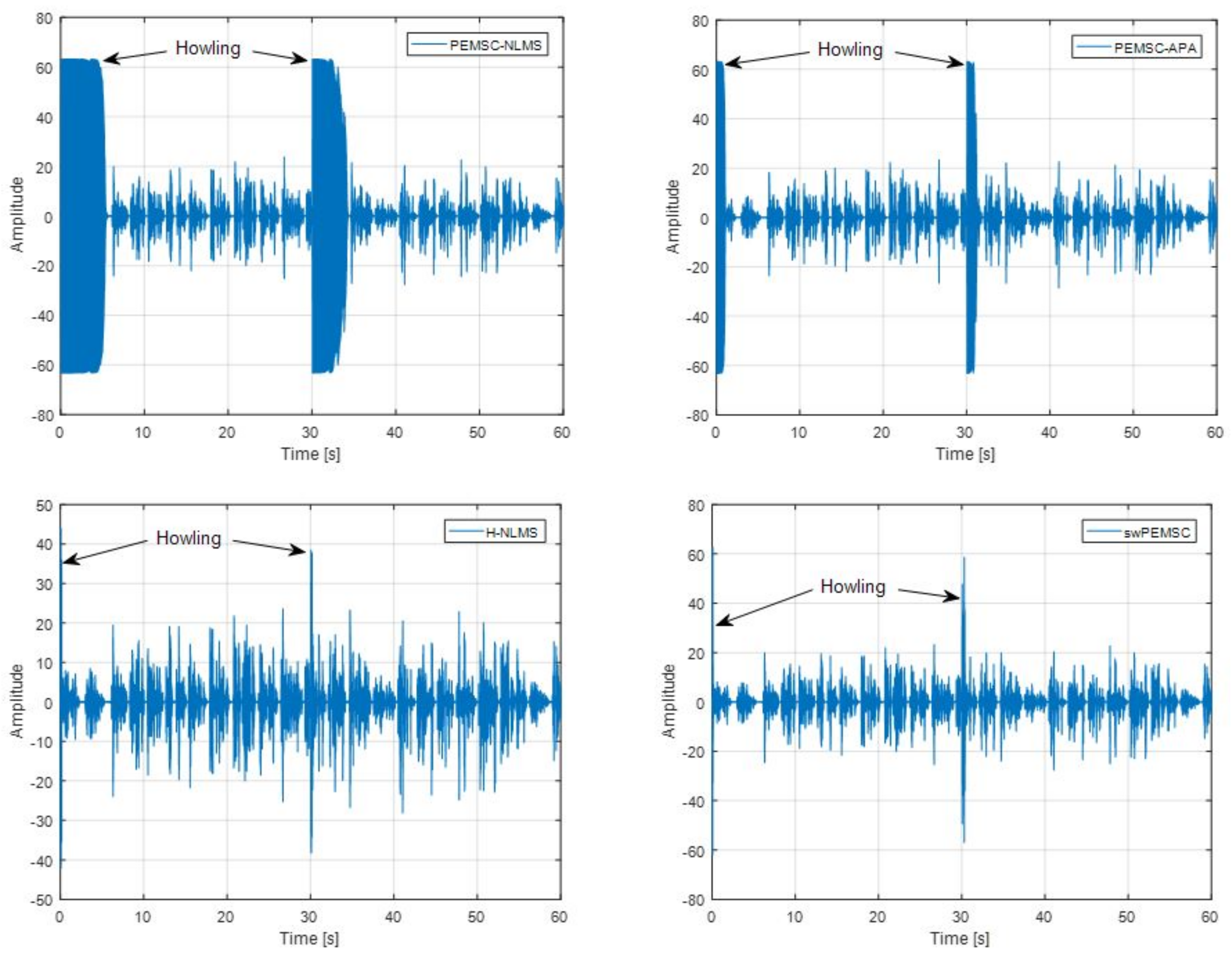
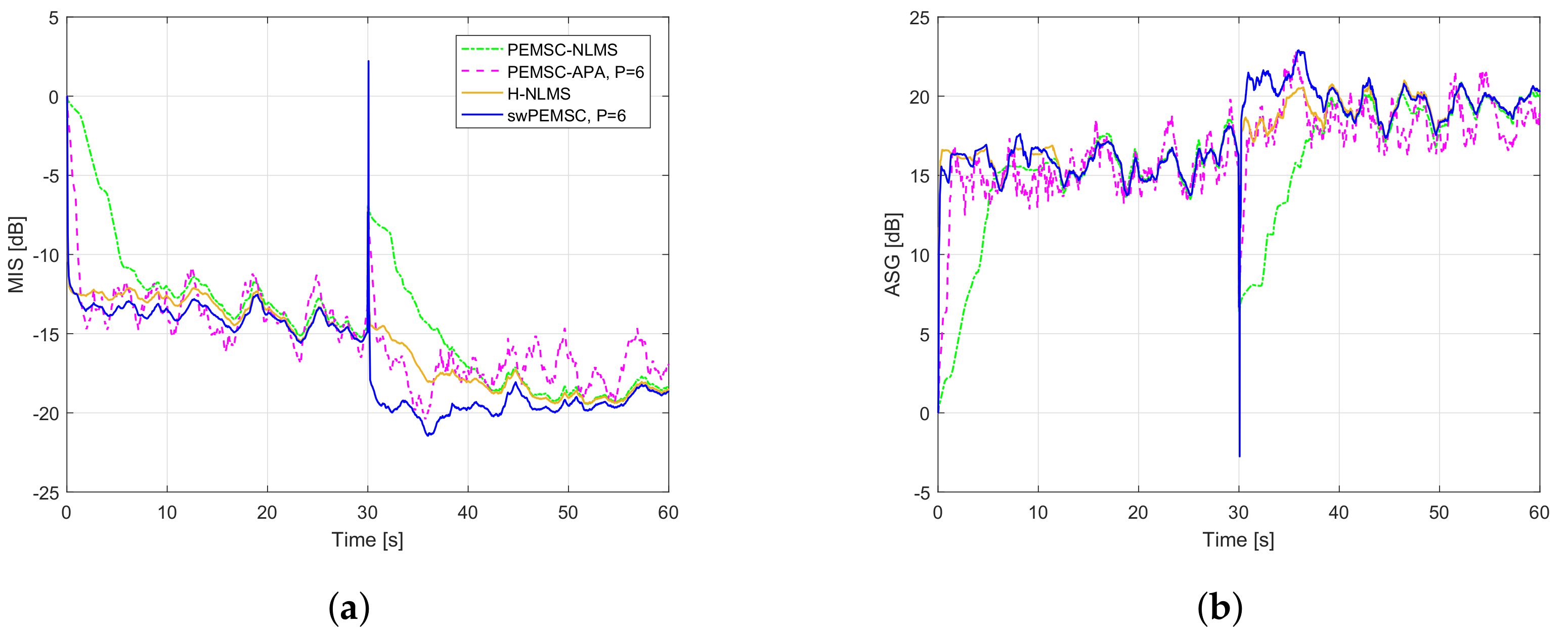
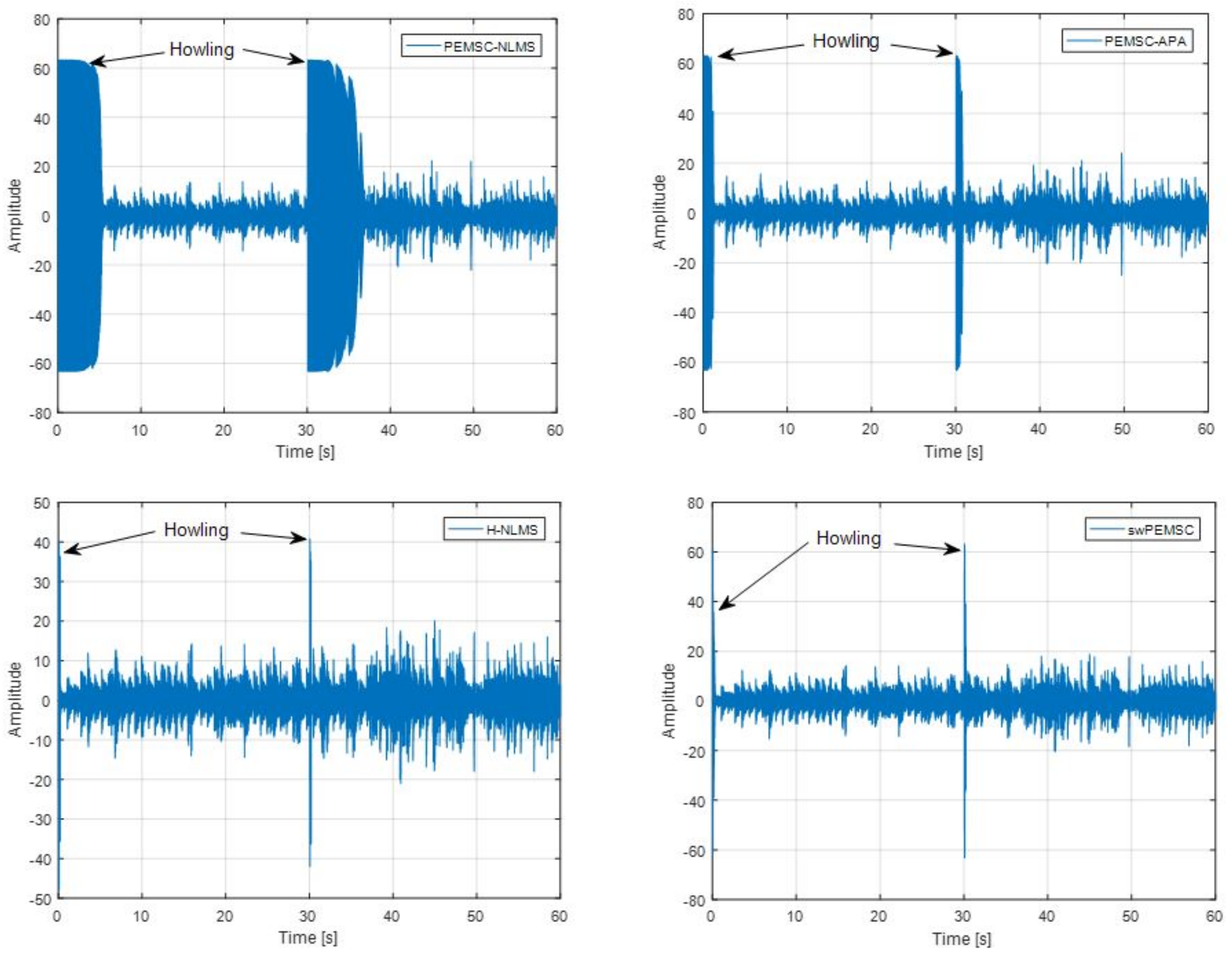
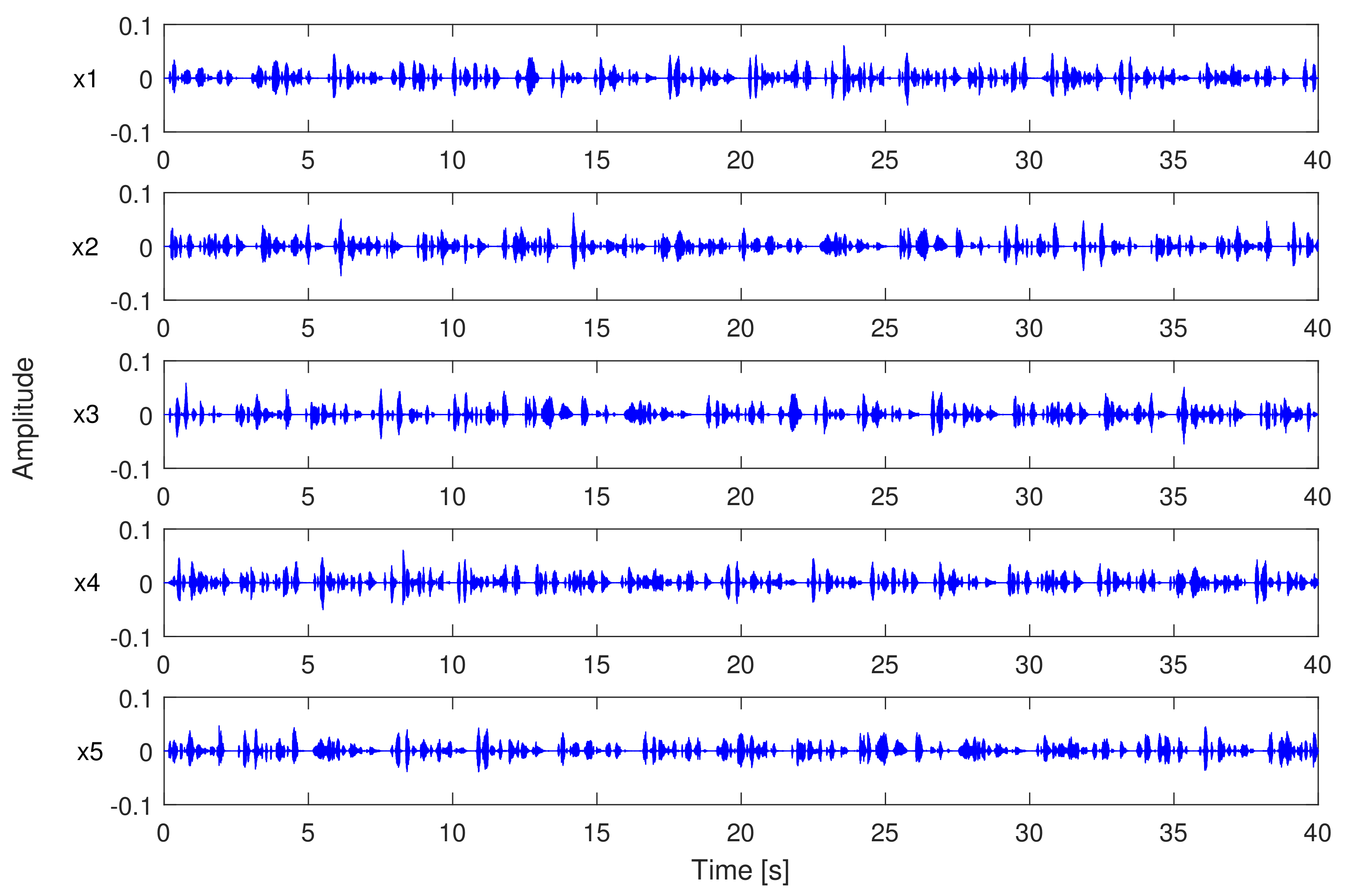
7. Experimental Results
- For PEMSC-NLMS: for Experiments 1–3 and for Experiment 4.
- For PEMSC-APA: .
- For H-NLMS and swPEMSC: , .
8. Discussion
9. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Siqueira, M.G.; Alwan, A. Steady-state analysis of continuous adaptation in acoustic feedback reduction systems for hearing-aids. IEEE Trans. Speech Audio Process. 2000, 8, 443–453. [Google Scholar] [CrossRef]
- Spriet, A.; Doclo, S.; Moonen, M.; Wouters, J. Feedback control in hearing aids. In Springer Handbook of Speech Processing; Springer: Berlin/Heidelberg, Germany, 2008; pp. 979–1000. [Google Scholar]
- Van Waterschoot, T.; Moonen, M. Fifty Years of Acoustic Feedback Control: State of the Art and Future Challenges. Proc. IEEE 2011, 99, 288–327. [Google Scholar] [CrossRef]
- Hellgren, J.; Forssell, U. Bias of feedback cancellation algorithms in hearing aids based on direct closed loop identification. IEEE Trans. Speech Audio Process. 2001, 9, 906–913. [Google Scholar] [CrossRef]
- Laugesen, S.; Hansen, K.V.; Hellgren, J. Acceptable delays in hearing aids and implications for feedback cancellation. J. Acoust. Soc. Am. 1999, 105, 1211–1212. [Google Scholar] [CrossRef]
- Kates, J. Feedback cancellation in hearing aids. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Albuquerque, NM, USA, 3–6 April 1990; pp. 1125–1128. [Google Scholar]
- Guo, M.; Jensen, S.H.; Jensen, J. Novel acoustic feedback cancellation approaches in hearing aid applications using probe noise and probe noise enhancement. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 2549–2563. [Google Scholar] [CrossRef]
- Guo, M.; Elmedyb, T.B.; Jensen, S.H.; Jensen, J. On acoustic feedback cancellation using probe noise in multiple-microphone and single-loudspeaker systems. IEEE Signal Process. Lett. 2012, 19, 283–286. [Google Scholar] [CrossRef]
- Nakagawa, C.R.C.; Nordholm, S.; Yan, W.Y. Feedback cancellation with probe shaping compensation. IEEE Signal Process. Lett. 2014, 21, 365–369. [Google Scholar] [CrossRef]
- Schroeder, M.R. Improvement of Acoustic-Feedback Stability by Frequency Shifting. J. Acoust. Soc. Am. 1964, 36, 1718–1724. [Google Scholar] [CrossRef]
- Strasser, F.; Puder, H. Adaptive feedback cancellation for realistic hearing aid applications. IEEE/ACM Trans. Audio Speech Lang. Process. 2015, 23, 2322–2333. [Google Scholar] [CrossRef]
- Guo, M.; Jensen, S.H.; Jensen, J.; Grant, S.L. On the use of a phase modulation method for decorrelation in acoustic feedback cancellation. In Proceedings of the European Signal Processing Conference (EUSIPCO), Bucharest, Romania, 27–31 August 2012; pp. 2000–2004. [Google Scholar]
- Hellgren, J. Analysis of feedback cancellation in hearing aids with filtered-X LMS and the direct method of closed loop identification. IEEE Trans. Speech Audio Process. 2002, 10, 119–131. [Google Scholar] [CrossRef]
- Spriet, A.; Proudler, I.; Moonen, M.; Wouters, J. Adaptive feedback cancellation in hearing aids with linear prediction of the desired signal. IEEE Trans. Signal Process. 2005, 53, 3749–3763. [Google Scholar] [CrossRef]
- Tran, L.T.T.; Dam, H.H.; Nordholm, S. Affine Projection Algorithm For Acoustic Feedback Cancellation Using Prediction Error Method In Hearing Aids. In Proceedings of the IEEE International Workshop on Acoustic Signal Enhancement (IWAENC), Xi’an, China, 13–16 September 2016. [Google Scholar]
- Rombouts, G.; Van Waterschoot, T.; Moonen, M. Robust and Efficient Implementation of the PEM-AFROW Algorithm for Acousic Feedback Cancellation. J. Audio Eng. Soc. 2007, 55, 955–966. [Google Scholar]
- Tran, L.T.T.; Schepker, H.; Doclo, S.; Dam, H.H.; Nordholm, S. Proportionate NLMS for adaptive feedback control in hearing aids. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, New Orleans, LA, USA, 5–9 March 2017. [Google Scholar]
- Gil-Cacho, J.M.; van Waterschoot, T.; Moonen, M.; Jensen, S.H. Transform domain prediction error method for improved acoustic echo and feedback cancellation. In Proceedings of the European Signal Processing Conference (EUSIPCO), Bucharest, Romania, 27–31 August 2012; pp. 2422–2426. [Google Scholar]
- Tran, L.T.T.; Nordholm, S.E.; Schepker, H.; Dam, H.H.; Doclo, S. Two-microphone hearing aids using prediction error method for adaptive feedback control. IEEE/ACM Trans. Audio Speech Lang. Process. 2018, 26, 909–923. [Google Scholar] [CrossRef]
- Spriet, A.; Rombouts, G.; Moonen, M.; Wouters, J. Adaptive feedback cancellation in hearing aids. Elsevier J. Frankl. Inst. 2006, 343, 545–573. [Google Scholar] [CrossRef]
- Bernardi, G.; van Waterschoot, T.; Wouters, J.; Moonen, M. An all-frequency-domain adaptive filter with PEM-based decorrelation for acoustic feedback control. In Proceedings of the Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, USA, 18–21 October 2015; pp. 1–5. [Google Scholar]
- Bernardi, G.; van Waterschoot, T.; Wouters, J.; Hillbratt, M.; Moonen, M. A PEM-based frequency-domain Kalman filter for adaptive feedback cancellation. In Proceedings of the 23rd European Signal Processing Conference (EUSIPCO), Nice, France, 31 August–4 September 2015; pp. 270–274. [Google Scholar]
- Schepker, H.; Tran, L.T.T.; Nordholm, S.; Doclo, S. Improving Adaptive Feedback Cancellation in Hearing Aids Using an Affine Combination of Filters. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Shanghai, China, 20–25 March 2016. [Google Scholar]
- Tran, L.T.T.; Schepker, H.; Doclo, S.; Dam, H.H.; Nordholm, S. Frequency Domain Improved Practical Variable Step-Size for Adaptive Feedback Cancellation Using Pre-Filters. In Proceedings of the 2018 16th International Workshop on Acoustic Signal Enhancement (IWAENC), Tokyo, Japan, 17–20 September 2018; pp. 171–175. [Google Scholar]
- Yang, F.; Wu, M.; Ji, P.; Yang, J. An improved multiband-structured subband adaptive filter algorithm. IEEE Signal Process. Lett. 2012, 19, 647–650. [Google Scholar] [CrossRef]
- Strasser, F.; Puder, H. Sub-band feedback cancellation with variable step sizes for music signals in hearing aids. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Florence, Italy, 4–9 May 2014; pp. 8207–8211. [Google Scholar]
- Khoubrouy, S.A.; Panahi, I.M.S. An Efficient Delayless Sub-band Filtering for Adaptive Feedback Compensation in Hearing Aid. J. Signal Process. Syst. 2016, 83, 401–409. [Google Scholar] [CrossRef]
- Pradhan, S.; Patel, V.; Somani, D.; George, N.V. An improved proportionate delayless multiband-structured subband adaptive feedback canceller for digital hearing aids. IEEE/ACM Trans. Audio Speech Lang. Process. 2017, 25, 1633–1643. [Google Scholar] [CrossRef]
- Nakagawa, C.R.C.; Nordholm, S.; Yan, W.Y. Dual microphone solution for acoustic feedback cancellation for assistive listening. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Kyoto, Japan, 25–30 March 2012; pp. 149–152. [Google Scholar]
- Nakagawa, C.R.C.; Nordholm, S.; Yan, W.Y. Analysis of Two Microphone Method for Feedback Cancellation. IEEE Signal Process. Lett. 2015, 22, 35–39. [Google Scholar] [CrossRef]
- Tran, L.T.T.; Nordholm, S.; Dam, H.H.; Yan, W.Y.; Nakagawa, C.R. Acoustic Feedback Cancellation in hearing aids using two microphones employing variable step size affine projection algorithms. In Proceedings of the IEEE International Conference on Digital Signal Processing (DSP), Singapore, 21–24 July 2015; pp. 1191–1195. [Google Scholar]
- Albu, F.; Nakagawa, R.; Nordholm, S. Proportionate algorithms for two-microphone active feedback cancellation. In Proceedings of the 23rd European Signal Processing Conference (EUSIPCO), Nice, France, 31 August–4 September 2015; pp. 290–294. [Google Scholar]
- Schepker, H.; Nordholm, S.E.; Tran, L.T.T.; Doclo, S. Null-steering beamformer-based feedback cancellation for multi-microphone hearing aids with incoming signal preservation. IEEE/ACM Trans. Audio Speech Lang. Process. 2019, 27, 679–691. [Google Scholar] [CrossRef]
- Schepker, H.; Nordholm, S.; Doclo, S. Acoustic Feedback Suppression for Multi-Microphone Hearing Devices Using a Soft-Constrained Null-Steering Beamformer. IEEE/ACM Trans. Audio Speech Lang. Process. 2020, 28, 929–940. [Google Scholar] [CrossRef]
- Lee, S.; Kim, I.Y.; Park, Y.C. Approximated affine projection algorithm for feedback cancellation in hearing aids. Comp. Methods Programs Biomed. 2007, 87, 254–261. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.; Baik, Y.h.; Park, Y.; Kim, D.; Sohn, J. Robust adaptive feedback canceller based on modified pseudo affine projection algorithm. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 3760–3763. [Google Scholar]
- Pradhan, S.; Patel, V.; Patel, K.; Maheshwari, J.; George, N.V. Acoustic feedback cancellation in digital hearing aids: A sparse adaptive filtering approach. Appl. Acoust. 2017, 122, 138–145. [Google Scholar] [CrossRef]
- Thipphayathetthana, S.; Chinrungrueng, C. Variable step-size of the least-mean-square algorithm for reducing acoustic feedback in hearing aids. In Proceedings of the IEEE Asia-Pacific Conference on Circuits and Systems, Tianjin, China, 4–6 December 2000; pp. 407–410. [Google Scholar]
- Rotaru, M.; Albu, F.; Coanda, H. A variable step size modified decorrelated NLMS algorithm for adaptive feedback cancellation in hearing aids. In Proceedings of the International Symposium on Electronics and Telecommunications, Timisoara, Romania, 15–16 November 2012; pp. 263–266. [Google Scholar]
- Tran, L.T.T.; Schepker, H.; Doclo, S.; Dam, H.H.; Nordholm, S. Improved Practical Variable Step-Size Algorithm For Adaptive Feedback Control in Hearing Aids. In Proceedings of the IEEE International Conference on Signal Processing and Communication Systems, Surfers Paradise, QLD, Australia, 19–21 December 2016. [Google Scholar]
- Albu, F.; Tran, L.T.T.; Nordholm, S. A combined variable step size strategy for two microphones acoustic feedback cancellation using proportionate algorithms. In Proceedings of the Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Kuala Lumpur, Malaysia, 12–15 December 2017; pp. 1373–1377. [Google Scholar]
- Tran, L.T.T.; Schepker, H.; Doclo, S.; Dam, H.H.; Nordholm, S.E. Adaptive feedback control using improved variable step-size affine projection algorithm for hearing aids. In Proceedings of the 2017 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Kuala Lumpur, Malaysia, 12–15 December 2017; pp. 1633–1640. [Google Scholar]
- Bhattacharjee, S.S.; George, N.V. Fast and Efficient Acoustic Feedback Cancellation based on Low Rank Approximation. Signal Process. 2021, 182, 107984. [Google Scholar] [CrossRef]
- Nordholm, S.; Schepker, H.; Tran, L.T.T.; Doclo, S. Stability-controlled hybrid adaptive feedback cancellation scheme for hearing aids. J. Acoust. Soc. Am. 2018, 143, 150–166. [Google Scholar] [CrossRef]
- Ozeki, K.; Umeda, T. An adaptive filtering algorithm using an orthogonal projection to an affine subspace and its properties. Electron. Commun. Jpn. 1984, 67, 19–27. [Google Scholar] [CrossRef]
- Paleologu, C.; Benesty, J.; Ciochina, S. A variable step-size affine projection algorithm designed for acoustic echo cancellation. IEEE Trans. Audio Speech Lang. Process. 2008, 16, 1466–1478. [Google Scholar] [CrossRef]
- Sayed, A.H. Fundamental Adaptive Filtering; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Shynk, J.J. Frequency-domain and multirate adaptive filtering. IEEE Signal Process. Mag. 1992, 9, 14–37. [Google Scholar] [CrossRef]
- Sankowsky-Rothe, T.; Blau, M.; Schepker, H.; Doclo, S. Reciprocal measurement of acoustic feedback paths in hearing aids. J. Acoust. Soc. Am. 2015, 138, EL399–EL404. [Google Scholar] [CrossRef]
- Kates, J.M. Room reverberation effects in hearing aid feedback cancellation. J. Acoust. Soc. Am. 2001, 109, 367–378. [Google Scholar] [CrossRef]
- Loizou, P.C. Speech Enhancement: Theory and Practice; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Deller, J.R.; Proakis, J.G.; Hansen, J.H. Discrete Time Processing of Speech Signals; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1993. [Google Scholar]


| AFC Methods | Computational Complexity | # |
|---|---|---|
| PEMSC-NLMS | 263 | |
| PEMSC-APA | 3363 | |
| H-NLMS | 457 | |
| swPEMSC | 3557 |
| AFC Methods | Incoming Signals | [dB] | [dB] | [s] | [dB] | [dB] | [s] |
|---|---|---|---|---|---|---|---|
| PEMSC-NLMS | −16.023 | 17.656 | 8.312 | −20.115 | 21.194 | 4.780 | |
| PEMSC-APA | recorded speech | −18.176 | 19.586 | 1.545 | −20.562 | 21.385 | 1.180 |
| H-NLMS [44] | −19.278 | 21.260 | 2.715 | −21.750 | 23.175 | 1.186 | |
| swPEMSC | −20.016 | 21.786 | 0.304 | −22.487 | 23.638 | 0.367 | |
| PEMSC-NLMS | −11.493 | 14.066 | 6.540 | −16.568 | 17.354 | 6.149 | |
| PEMSC-APA | recorded music | −13.341 | 14.970 | 1.205 | −17.073 | 18.406 | 0.779 |
| H-NLMS [44] | −13.358 | 15.860 | 0.193 | −17.946 | 19.278 | 0.441 | |
| swPEMSC | −13.847 | 15.804 | 0.144 | −19.465 | 19.837 | 0.105 | |
| PEMSC-NLMS | −14.655 | 15.034 | 2.103 | −14.339 | 14.424 | 3.088 | |
| PEMSC-APA | 5 speech segments | −14.768 | 14.906 | 1.775 | −14.417 | 14.175 | 2.795 |
| H-NLMS [44] | −15.254 | 15.897 | 0.203 | −15.446 | 15.662 | 0.169 | |
| swPEMSC | −16.810 | 17.936 | 0.251 | −16.043 | 17.227 | 0.131 |
| AFC Methods | Incoming Signals | ||
|---|---|---|---|
| PEM-NLMS | 1.652 | 3.013 | |
| PEM-APA | recorded speech | 2.067 | 3.448 |
| H-NLMS [44] | 4.167 | 4.047 | |
| swPEMSC | 4.218 | 3.729 | |
| PEM-NLMS | 4.132 | 1.646 | |
| PEM-APA | 5 speech segments | 4.124 | 1.890 |
| H-NLMS [44] | 4.077 | 4.129 | |
| swPEMSC | 4.134 | 4.075 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, L.T.T.; Nordholm, S.E. A Switched Algorithm for Adaptive Feedback Cancellation Using Pre-Filters in Hearing Aids. Audiol. Res. 2021, 11, 389-409. https://doi.org/10.3390/audiolres11030037
Tran LTT, Nordholm SE. A Switched Algorithm for Adaptive Feedback Cancellation Using Pre-Filters in Hearing Aids. Audiology Research. 2021; 11(3):389-409. https://doi.org/10.3390/audiolres11030037
Chicago/Turabian StyleTran, Linh Thi Thuc, and Sven Erik Nordholm. 2021. "A Switched Algorithm for Adaptive Feedback Cancellation Using Pre-Filters in Hearing Aids" Audiology Research 11, no. 3: 389-409. https://doi.org/10.3390/audiolres11030037
APA StyleTran, L. T. T., & Nordholm, S. E. (2021). A Switched Algorithm for Adaptive Feedback Cancellation Using Pre-Filters in Hearing Aids. Audiology Research, 11(3), 389-409. https://doi.org/10.3390/audiolres11030037






