Allometric Models to Estimate Aboveground Biomass of Individual Trees of Eucalyptus saligna Sm in Young Plantations in Ecuador
Abstract
1. Introduction
2. Materials and Methods
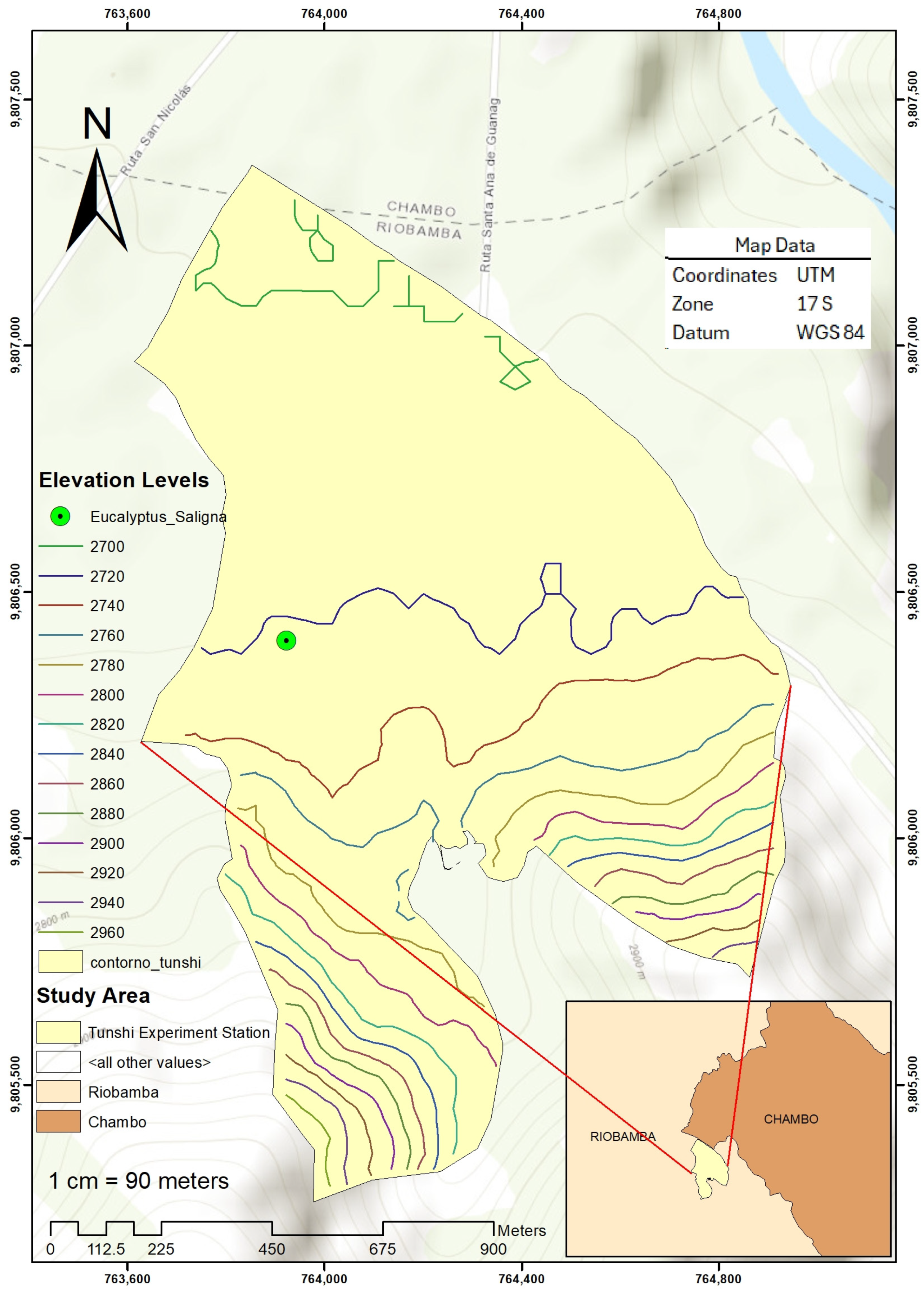
2.1. Site Description
2.2. Selection of Individual Trees
2.3. Cutting, Measurement, and Estimation of Total Aboveground Biomass
2.4. Statistical Analysis
3. Results
3.1. Normality of Variables and Correlation Between Aboveground Biomass and Dendrometric Tree Variables
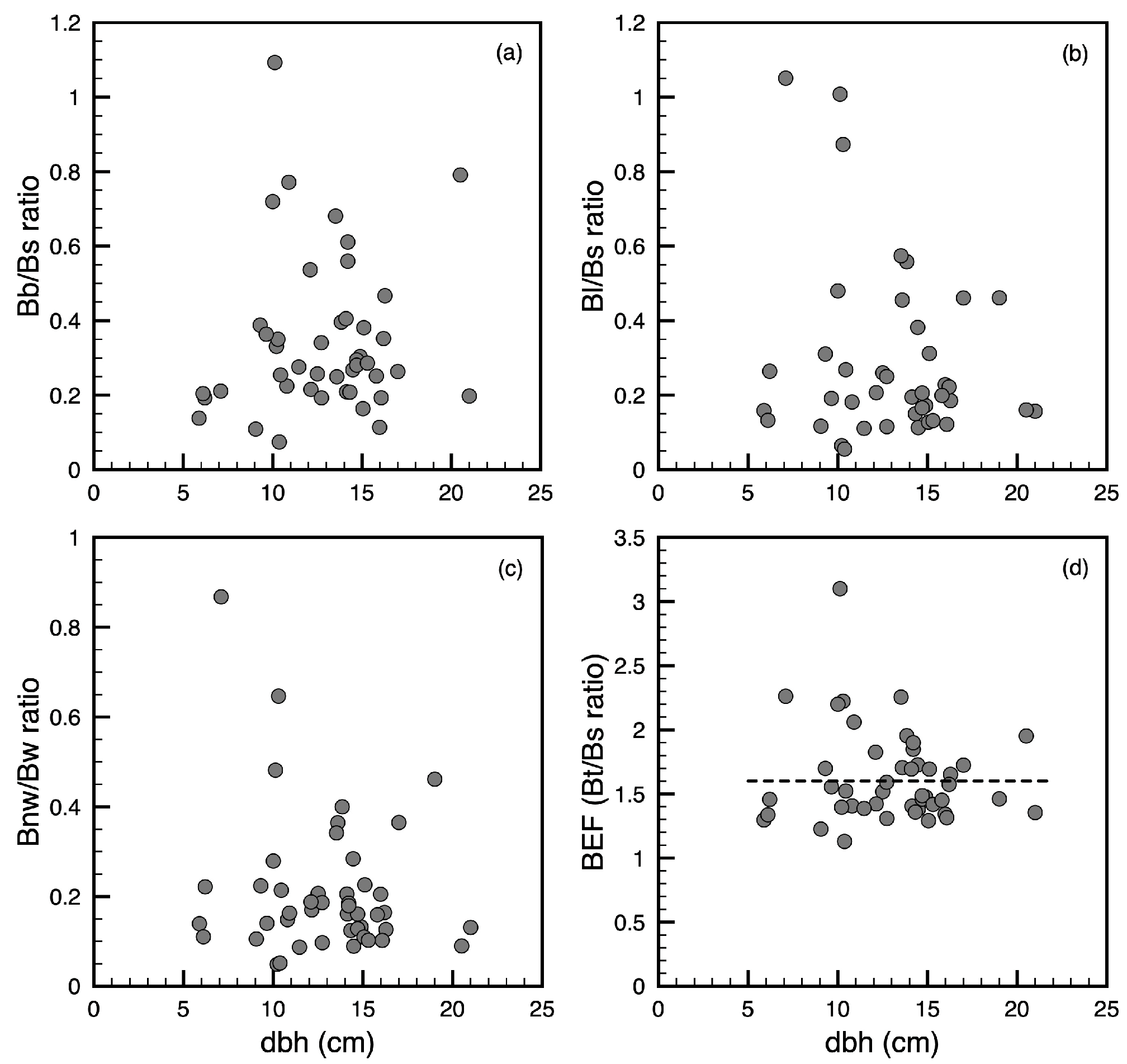
3.2. Biomass Expansion Factor and Other Biomass Ratios
3.3. Allometric Biomass Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- UN Environment Program, UNEP. Annual Report UNEP 2022; The Global Authority for the Environment with Programs Focusing on Climate, Nature, Pollution, Sustainable Development; UNEP: Nairobi, Kenia, 2023; Available online: https://reliefweb.int/report/world/unep-2022?gclid=Cj0KCQjwib2mBhDWARIsAPZUn_lpAGFnd5tTDqYtc76C_BcGF7Z4oFV7tHUzbKjLdYA9HJIE-GhtZhYaAsV3EALw_wcB (accessed on 23 April 2023).
- Reyns, W.; Rineau, F.; Spaak, J.W.; Franken, O.; Berg, M.P.; Van der Plas, F.; Bardgett, R.D.; Beenaerts, N.; De Laender, F. Food web uncertainties influence predictions of climate change effects on soil carbon sequestration in heathlands. Microb. Ecol. 2020, 79, 686–693. [Google Scholar] [CrossRef]
- Costello, A.; Mustafa, A.; Adriana, A.; Sarah, B.; Sarah, B.; Richard, B.; Sharon, F.; Nora, G.; Anne, J.; Maria, K.; et al. Managing the health effects of climate change. Lancet and University College London Institute for Global Health Commission. Lancet 2009, 373, 1693–1733. Available online: https://www.researchgate.net/publication/40724209_Managing_the_Health_Effects_of_Climate_Change (accessed on 14 August 2023). [PubMed]
- Favier, T.; Ceballos, M.; Dehesa, L.; Veranes, M. Efectos del cambio climático en la salud. Rev. Inf. Cient. 2019, 98, 272–282. Available online: https://revinfcientifica.sld.cu/index.php/ric/article/view/2276 (accessed on 10 February 2024).
- Ojeda, R.; Murray, G. La huella del cambio climático en la vida. Rev. Digit. Univ. (Rdu) 2023, 24, 1–11. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Cambio Climático 2023: Informe de Síntesis; Informe del Panel Intergubernamental sobre Cambio Climático. Contribución de los Grupos de Trabajo I, II y III al Sexto Informe de Evaluación del Panel Intergubernamental sobre Cambio Climático [Equipo central de redacción]; Lee, H., Romero, J., Eds.; IPCC: Ginebra, Switzerland, 2023; Available online: https://www.ipcc.ch/report/ar6/syr/downloads/report/IPCC_AR6_SYR_SPM.pdf (accessed on 10 January 2024).
- Intergovernmental Panel on Climate Change (IPCC). Summary for Policymakers. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; IPCC: Ginebra, Switzerland, 2021; Available online: https://www.ipcc.ch/report/ar6/wg1/downloads/report/IPCC_AR6_WGI_SPM_final.pdf (accessed on 23 April 2023).
- Intergovernmental Panel on Climate Change (IPCC). Cambio Climático 2014: Mitigación del Cambio Climático. Resumen para Responsables de Políticas. Contribución del Grupo de trabajo III al Quinto Informe de Evaluación del Grupo Intergubernamental de Expertos sobre el Cambio Climático; IPCC: Ginebra, Switzerland, 2015; Available online: https://www.ipcc.ch/site/assets/uploads/2018/03/WGIIIAR5_SPM_TS_Volume_es-1.pdf (accessed on 14 August 2023).
- Waring, B.; Neumann, M.; Prentice, I.C.; Adams, M.; Smith, P.; Siegert, M. Forests and Decarbonization—Roles of Natural and Planted Forests. Front. For. Glob. Change 2020, 3, 1–6. [Google Scholar] [CrossRef]
- Samaniego, J.; Lorenzo, S.; Rondón, E.; Krieger, L.; Herrera, J.; Rouse, P.; Harrison, N. Soluciones Basadas en la Naturaleza y Remoción de Dióxido de Carbono; Documentos de Proyectos (LC/TS.2022/224); Comisión Económica para América Latina y el Caribe (CEPAL): Santiago, Chile, 2022; Available online: https://repositorio.cepal.org/bitstream/handle/11362/48615/1/S2201074_es.pdf (accessed on 14 August 2023).
- Constitución de la República del Ecuador. Ciudad Alfaro: Asamblea Constituyente. Ecuador. 2008. Available online: https://www.oas.org/juridico/pdfs/mesicic4_ecu_const.pdf (accessed on 14 February 2025).
- MAE. National Biodiversity Strategy and Its Action Plan 2016–2030; Ministry of the Environment of Ecuador (MAE): Quito, Ecuador, 2016; Available online: https://www.cbd.int/doc/world/ec/ec-nbsap-v2-p01-es.pdf (accessed on 6 August 2023).
- Lewis, S.L.; Lopez, G.G.; Sonké, B.; Affum, K.B.; Baker, T.R.; Ojo, L.O.; Phillips, O.L.; Reitsma, J.M.; White, L.; Comiskey, J.A.; et al. Increasing carbon storage in intact African tropical forests. Nat. Lett. 2009, 457, 1003–1007. [Google Scholar] [CrossRef]
- Pandey, S.S.; Maraseni, T.N.; Cockfield, G. Carbon stock dynamics in different vegetation dominated community forests under REDD+: A case from Nepal. For. Ecol. Manag. 2014, 327, 40–47. [Google Scholar] [CrossRef]
- Yadav, R.P.; Bisht, J.K.; Bhatt, J.C. Biomass, carbon stock under different production systems in the mid hills of Indian Himalaya. Trop. Ecol. 2017, 58, 15–21. [Google Scholar]
- Food and Agricultural Organization (FAO). Plantations and Wood Energy; Report Based on the Work of D. J. Mead; Forest Plantation Thematic Papers, Working Paper 5; FAO: Rome, Italy, 2001; 20p. [Google Scholar]
- Guariguata, M.; Arce, J.; Ammourt, T.; Capella, J. Las Plantaciones Forestales en el Perú: Reflexiones, Estatus Actual y Perspectivas a Futuro; Documento Ocacional 169; CIFOR: Bogor, Indonecia, 2017. [Google Scholar]
- Castillo, V.D.; Gavilanes, M.A. Challenges Faced by the Ecuadorian Forests and Forest Industry. Rev. Pădurilor 2020, 135, 1–56. [Google Scholar]
- Corporación Financiera Nacional. Ficha Sectorial: Explotación de Viveros Forestales y Madera en pie; Corporación Financiera Nacional: Quito, Ecuador, 2017; Available online: https://www.cfn.fin.ec/wp-content/uploads/2017/10/Ficha-Sectorial-Viveros-y-Madera-en-Pie.pdf (accessed on 14 August 2023).
- Food and Agricultural Organization (FAO). El Eucalipto en la Repoblación Forestal; Colección FAO: Montes, Roma, 1981. [Google Scholar]
- Food and Agricultural Organization (FAO). The State of Food Insecurity in the World; Food and Agriculture Organization of the United Nations: Rome, Italy, 2001. [Google Scholar]
- Kasekete, D.K.; Ligot, G.; Mweru, J.P.; Drouet, T.; Rousseau, M.; Moango, A.; Bourland, N. Growth, Productivity, Biomass and Carbon Stock in Eucalyptus saligna and Grevillea robusta Plantations in North Kivu, Democratic Republic of the Congo. Forests 2022, 13, 1508. [Google Scholar] [CrossRef]
- Turnbull, J.W. Eucalypt plantations. New For. 1999, 17, 37–52. Available online: https://link.springer.com/article/10.1023/A:1006524911242 (accessed on 18 August 2023). [CrossRef]
- Restrepo, C.; Alviar, M. Tasa de descuento y rotación forestal: El caso del Eucalyptus saligna. Lect. Econ. 2010, 73, 149–164. Available online: http://www.scielo.org.co/scielo.php?script=sci_arttext&pid=S0120-25962010000200006&lng=en&tlng=es (accessed on 5 May 2023). [CrossRef]
- Boland, J.; Brooker, M.; Chippendale, G.; Hall, N.; Hyland, B. Forest Trees of Australia; CSIRO: Melbourne, Australia, 1984. [Google Scholar]
- Jovanovic, T.; Booth, T. Improved Species Climatic Profiles: A Report for the RIRDC/L&W Australia/FWPRDC/MDBC Joint Venture Agroforestry Program; RIRDC Publication: Hobart, Australia, 2002. [Google Scholar]
- Henry, M.; Besnard, A.; Asante, W.A. Wood density, phytomass variations within and among trees, and allometric equations in a tropical rainforest of Africa. For. Ecol. Manag. 2010, 260, 1375–1388. Available online: https://www.sciencedirect.com/science/article/abs/pii/S037811271000424X (accessed on 22 February 2023). [CrossRef]
- Wang, Z.; Liu, L.; Peng, D.; Liu, X.; Zhang, S.; Wang, Y. Estimating woody aboveground biomass in an area of agroforestry using airborne light detection and ranging and compact airborne spectrographic imager hyperspectral data: Individual tree analysis incorporating tree species information. J. Appl. Remote Sens. 2016, 10, 036007. Available online: https://spie.org/Publications/Journal/10.1117/1.JRS.10.036007 (accessed on 2 March 2024). [CrossRef]
- Zhao, D.; Kane, M.; Markewitz, D.; Teskey, R.; Clutter, M. Additive tree biomass equations for midrotation loblolly pine plantations. For. Sci. 2015, 61, 613–623. [Google Scholar] [CrossRef]
- Picard, N.; Saint-André, L.; Henry, M. Manual de Construcción de Ecuaciones Alométricas para Estimar el Volumen y la Biomasa de los árboles: Del Trabajo de Campo a la Predicción; Las Naciones Unidas para la Alimentación y la Agricultura y el Centre de Coopération Internationale en Recherche Agronomique pour le Développement: Rome, Italy; Montpellier, France, 2012; 223p, Available online: http://www.globallometree.org/media/cms_page_media/6/tarifs_sp_web_19jun.pdf (accessed on 2 March 2023).
- Schlegel, B.; Gayoso, J.; Guerra, J. Manual de Procedimientos para Inventarios de Carbono en Ecosistemas Forestales; Proyecto FONDEF D98I1076; Universidad Austral de Chile: Santiago de Chile, Chile, 2001. [Google Scholar]
- Risio, A.L.; Bravo, F.; Bogino, S. Cuantificación de Biomasa y Carbono en Bosques Nativos de Prosopis caldenia (Burkhart) en la Pampa Semiárida Argentina. 2012. Available online: https://uvadoc.uva.es/bitstream/handle/10324/1593/TFM-L%2043.pdf?sequence=1&isAllowed=y (accessed on 23 April 2023).
- Henry, M.; Bombelli, A.; Trotta, C.; Alessandrini, A.; Birigazzi, L.; Sola, G.; Vieilledent, G.; Santenoise, P.; Longuetaud, F.; Valentini, R.; et al. GlobAllomeTree: International platform for tree allometric equations to support volume, biomass and carbon assessment. iFor. Biogeosci. For. 2013, 6, 326–330. Available online: https://iforest.sisef.org/pdf/?id=ifor0901-006 (accessed on 5 August 2022). [CrossRef]
- Martínez, L.A.; De los Santos, H.M.; Fierros, A.M.; Fierros, R.M.; Pérez, R.M.; Hernández, A.R.; Hernández, J.R. Factores de expansión y sistema de partición de biomasa aérea para Pinus chiapensis (Martínez) Andresen. Rev. Mex. Cienc. For. 2018, 10, 1–26. [Google Scholar] [CrossRef]
- Andrade, H.J.; Segura, M.; Somarriba, E. Above-ground biomass models for dominant trees species in cacao agroforestry systems in Talamanca, Costa Rica. Agrofor. Syst. 2022, 96, 787–797. [Google Scholar] [CrossRef]
- Hassan, A.; Jahangir, M.; Shaban, S.J. Allometric Models and Biomass Conversion and Expansion Factors to Predict Total Tree-level Aboveground Biomass for Three Conifers Species in Iran. For. Sci. 2023, 69, 355–379. [Google Scholar]
- Magalhães, T.M.; Mate, R.S. Least squares-based biomass conversion and expansion factors best estimate biomass tan ratio-based ones: Statistical evidences based on tropical timber species. MethodsX 2018, 5, 30–38. [Google Scholar] [CrossRef]
- Senelwa, K.; Sims, R. Tree biomass equations for short rotation eucalypts grown in New Zealand. Biomass Bioenergy 1998, 13, 133–140. Available online: https://www.sciencedirect.com/science/article/abs/pii/S0961953497000263 (accessed on 24 October 2022). [CrossRef]
- MacFarlane, D.W.; Kuyah, S.C.; Mulia, R.M.; Dietz, J.; Muthuri, C.; Noordwijk, M.V. Evaluating a non-destructive method for calibrating tree biomass equations derived from tree branching architecture. Trees 2014, 28, 807–817. [Google Scholar] [CrossRef]
- Momolli, D.R.; Valdir, M.; Ludvichak, A.A.; Araújo, A.A. Modeling and Biomass Quantification in Euc alyptus saligna Smith Stand at the End Rotation in the South of Brazil. J. Exp. Agric. Int. 2019, 33, 1–10. [Google Scholar] [CrossRef]
- Ngomanda, A.; Obiang, N.L.; Lebamba, J.; Mavouroulou, Q.; Gomat, H.; Mankou, G.S.; Loumeto, J.; Midoko, D.; Kossi, F.; Zinga, K.R.; et al. Site-specifc versus pantropical allometric equations: Which option to estimate the biomass of a moist central African forest? For. Ecol. Manag. 2014, 312, 1–9. Available online: https://www.sciencedirect.com/science/article/abs/pii/S0378112713007160 (accessed on 18 August 2023). [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Guidelines for National Greenhouse Gas Inventories; Institute for Global Environmental Strategies (IGES): Tokyo, Japan, 2006; Available online: https://www.ipcc-nggip.iges.or.jp/public/2006gl/ (accessed on 23 April 2023).
- Lott, J.E.; Howard, S.B.; Black, C.R.; Ong, C.K. Allometric estimation of above-ground biomass and leaf area in managed Grevillea robusta agroforestry systems. Agrofor. Syst. 2000, 49, 1–15. [Google Scholar] [CrossRef]
- Albrecht, A.; Kandji, S.T. Carbon sequestration in tropical agroforestry systems. Agric. Ecosyst. Environ. 2003, 99, 15–27. [Google Scholar] [CrossRef]
- Holdridge, L.R. Ecología Basada en Zonas de Vida; Instituto Interamericano de Cooperación para la Agricultura: San José, Costa Rica, 1982; pp. 8–12. [Google Scholar]
- Vera, R.V.; Grijalva, J.O.; Ramos, R.V.; Sigcha, F.M.; Limongi, R.A. Respuesta de tres especies maderables de rápido crecimiento a diferentes bioclimas en Ecuador. Trop. Subtrop. Agroecosyst. 2023, 12, 1–10. [Google Scholar] [CrossRef]
- Guilcapi, B.D. Estudio de Adaptabilidad de Tres Especies Forestales del Género Paulownia (P. elongata, P. fortunei, y el híbrido P. elongata × P. fortunei) A las Condiciones de sitio “Estepa Espinosa” de Tunshi, Cantón Riobamba, Provincia de Chimborazo. Bechelor’s Thesis, Escuela Superior Politécnica de Chimborazo, Facultad de Recursos Naturales, Escuela de Ingeniería Agronómica, Riobamba, Ecuador, 2015. Available online: http://dspace.espoch.edu.ec/handle/123456789/3954 (accessed on 22 February 2022).
- Segura, M.; Andrade, H. ¿Cómo construir modelos alométricos de volumen, biomasa o carbono de especies leñosas perennes? Agrofor. Am. 2008, 46, 89–96. [Google Scholar]
- Fonseca, W.; Alice, F.; Rey, J.B. Modelos para estimar la biomasa de especies nativas en plantaciones y bosques secundarios en la zona Caribe de Costa Rica. Bosque 2009, 30, 36–47. [Google Scholar] [CrossRef]
- Sione, S.; Silvia, G.; Rosenberger, L.J.; Oszust, J.D.; Andrade, H.J.; Castañeda, G.O.; Wilson, M.G.; Sasal, M.C. Ecuaciones alométricas de biomasa aérea para Prosopis nigra (Griseb.) Hierón. “Algarrobo negro” (fabaceae) en bosques de entre Ríos (Argentina). Rev. Fac. Agron. UBA 2020, 40, 63–76. [Google Scholar]
- Piñeiro, G.; Perelman, S.; Guerschman, J.P.; Paruelo, J.M. How to evaluate models: Observed vs. predicted or predicted vs. observed? Ecol. Model. 2008, 216, 316–322. [Google Scholar] [CrossRef]
- Loetsch, F.; Zohrer, F.; Haller, K.E. Forest Inventory; BLV Verlagsgesellschaft: Munich, Germany, 1973. [Google Scholar]
- Cifuentes, J.M.; Henry, M.; Réjou, M.; Wayson, C.; Zapata, M.; Piotto, D.; Guie, A.G.; Alicer, F.; Castañeda, L.H.; Castellanos, L.E.; et al. Guidelines for documenting and reporting tree allometric equations. Ann. For. Sci. 2015, 72, 763–768. Available online: https://annforsci.biomedcentral.com/articles/10.1007/s13595-014-0415-z (accessed on 24 November 2024). [CrossRef]
- Correia, A.C.; Faias, S.P.; Ruiz, P.R.; Chianucci, F.; Cutini, A.; Fontes, L.; Manetti, M.C.; Montero, G.; Soares, P.; Tomé, M. Generalized biomass equations for Stone pine (Pinus pinea L.) across the Mediterranean basin. For. Ecol. Manag. 2018, 429, 425–436. [Google Scholar] [CrossRef]
- Sanquetta, C.R.; Dalla, C.A.; Behling, A.; Oliveira, L.R.; Péllico, S.; Rodrigues, A.L.; Inoue, M.N. Selection criteria for linear regression models to estimate individual tree biomasses in the Atlantic Rain Forest, Brazil. Carbon Balance Manag. 2018, 13, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Hammer, Ø.; Harper, D.A.; Ryan, P.D. PAST: Paleontological Statistics Software package for education and data analysis. Paleontol. Electron. 2001, 4, 1–9. Available online: https://n9.cl/nb7vmt (accessed on 14 August 2023).
- Clutter, J.L.; Fortson, J.C.; Pienaar, L.V.; Brister, G.H.; Bailey, R.L. Timber Management: A Quantitative Approach; Wiley: New York, NY, USA, 1983. [Google Scholar]
- Sileshi, G.W. A critical review of forest biomass estimation models, common mistakes and corrective measures. For. Ecol. Manag. 2014, 329, 237–254. [Google Scholar] [CrossRef]
- Van, B.M.; Ransijn, J.; Craven, D.; Bongers, F.; Hall, J.S. Estimating carbon stock in secondary forests: Decisions and uncertainties associated with allometric biomass models. For. Ecol. Manag. 2011, 262, 1648–1657. [Google Scholar]
- Baskerville, G.L. Use of Logarithmic Regression in the Estimation of Plant Biomass. Can. J. For. Res. 1972, 2, 49–53. [Google Scholar] [CrossRef]
- Sprugel, D.L. Correcting for bias in log-transformed allometric equations. Ecology 1983, 64, 209–210. [Google Scholar] [CrossRef]
- Clifford, D.; Cressie, N.; England, J.R.; Roxburgh, S.H.; Paul, K.I. Correction factors for unbiased, efficient estimation and prediction of biomass from log–log allometric models. For. Ecol. Manag. 2013, 310, 375–381. [Google Scholar] [CrossRef]
- Dossa, E.; Fernández, E.C.; Reid, W.S.; Ezui, K. Above-and belowground biomass, nutrient and carbon stocks contrasting an open-grown and a shaded coffee plantation. Agrofor. Syst. 2008, 72, 103–115. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Cambio Climático 2013: Bases Físicas. Contribución del Grupo de Trabajo I al Quinto Informe de Evaluación del Grupo Intergubernamental de Expertos Sobre el Cambio Climático; IPCC: Ginebra, Switzerland, 2013. [Google Scholar]
- Kalkanlı Genç, S.; Diamantopoulou, M.J.; Özçelik, R. Tree Biomass Modeling Based on the Exploration of Regression and Artificial Neural Networks Approaches. Forests 2023, 14, 2429. [Google Scholar] [CrossRef]
- Quirós, S. Modelos de Volumen Comercial, Perfil de Fuste y Crecimiento Para Plantaciones Clonales de Gmelina Arborea Roxb., ex Sm., en Costa Rica. Bechelor’s Thesis, Ingeniería Forestal, Instituto Tecnológico de Costa Rica, Cartago, Costa Rica, 2015. Available online: https://repositoriotec.tec.ac.cr/bitstream/handle/2238/6659/Modelos_volumen_comercial_perfil_fuste_crecimiento_plantaciones_clonales%20_gmelina_arborea.pdf?sequence=1 (accessed on 23 April 2023).
- Jiménez, E.; Fonseca, W.; Pazmiño, L. Sistemas silvopastoriles y cambio climático: Estimación y predicción de biomasa arbórea. Granja Rev. Cienc. Vida 2019, 29, 45–55. [Google Scholar] [CrossRef]
- Fonseca, G.W.; Murillo, C.R.; Ávila, A.C.; Rojas, V.M.; Spínola, P.R. Modelos de biomasa y carbono para árboles de Gmelina arborea en plantaciones clonales. Rev. Cienc. Ambient. 2021, 55, 143–159. [Google Scholar] [CrossRef]
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.A.; Eamus, D.; Folster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stock and balance in tropical forest. Oecological 2005, 145, 87–99. [Google Scholar] [CrossRef]
- Segura, M.; Kanninen, M.; Suárez, D. Allometric models for estimating aboveground biomass of shade trees and cofee bushes grown together. Agrofor. Syst. 2006, 68, 143–150. [Google Scholar] [CrossRef]
- Brown, S. Estimating Biomass and Biomass Change of Tropical Forests: A Primer; FAO Forestry Paper-134; FAO: Rome, Italy, 1997. [Google Scholar]
- Segura, M.; Kanninen, M. Allometric models for tree volume and total aboveground biomass in a tropical humid forest in Costa Rica. Biotropica Sci. J. ATBC 2005, 37, 2–8. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). State of Knowledge of Climate Change. Synthesis Report (SYR) of the IPCC Sixth Assessment Report (AR6); IPCC: Ginebra, Switzerland, 2023; Available online: https://www.ipcc.ch/report/sixth-assessment-report-cycle/ (accessed on 6 August 2023).
- Ubuy, M.H.; Eid, T.; Bollandsås, O.M.; Birhane, E. Aboveground biomass models for trees and shrubs of exclosures in the drylands of Tigray, northern Ethiopia. J. Arid. Environ. 2018, 156, 9–18. [Google Scholar]
- Vorster, A.G.; Evangelista, P.H.; Stovall, A.E.; Ex, S. Variability and uncertainty in forest biomass estimates from the tree to landscape scale: The role of allometric equations. Carbon. Bal. Manag. 2020, 15, 1–20. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Good Practice Guidance for Land Use, Land-Use Change and Forestry; Penman, J., Gytarsky, M., Hiraishi, T., Krug, T., Kruger, D., Pipatti, R., Buendia, L., Miwa, K., Ngara, T., Tanabe, K., et al., Eds.; IPCC Good Practice Guidance for LULUCF; IPCC: Hayama, Japan, 2003; Volume 4, pp. 113–116. [Google Scholar]
- Duncanson, L.; Armston, J.; Disney, M.; Avitabile, V.; Barbier, N.; Calders, K.; Carter, S.; Chave, J.; Herold, M.; Crowther, T.W.; et al. The importance of consistent global forest aboveground biomass product validation. Surv. Geophys. 2019, 40, 979–999. [Google Scholar]
- Henry, M.; Cifuentes, J.M.; Réjou-Méchain, M.; Piotto, D.; Michel, F.J.M.; Wayson, C.; Alice, G.F.; Castañeda, L.H.; Castellanos, L.E.; Cuenca, L.R.; et al. Recommendations for the use of tree models to estimate national forest biomass and assess their uncertainty. Ann. For. Sci. 2015, 72, 769–777. [Google Scholar]
- MacFarlane, D.W. A generalized tree component biomass model derived from principles of variable allometry. For. Ecol. Manag. 2015, 354, 43–55. [Google Scholar] [CrossRef]
- Piza, P.A.; Suárez, J.C.; Andrade, H.J. Litter decomposition and nutrient release in different land use located in Valle del Cauca (Colombia). Agrofor. Syst. 2021, 95, 257–267. [Google Scholar] [CrossRef]



| No. | Allometric Model |
|---|---|
| 1 | B = a + b∗dbh |
| 2 | B = a + b∗h |
| 3 | B = a + b∗dbh + c∗h |
| 4 | B = a + b∗dbh∗h |
| 5 | B = a + b∗dbh2 |
| 6 | B = a + b∗d + c∗dbh2 |
| 7 | Ln(B) = a + b∗Ln(dbh) |
| 8 | B = a + b∗h2 |
| 9 | B = a + b∗d + c∗dbh2∗h |
| 10 | B = a + b∗dbh + c∗h2 |
| 11 | B = a + b∗dbh2∗h |
| 12 | B = a + b∗Ln(dbh) |
| 13 | B = a + b∗dbh2 + c∗dbh2∗h + d∗h |
| 14 | B = a + b∗Ln(dbh) + c∗Ln(h) |
| 15 | B = a + b∗dbh2 + c∗dbh∗h + d∗dbh2∗h |
| 16 | Ln(B) = a + b∗Ln(dbh) + c∗Ln(h) |
| Component | Allometric Model | Standard Errors | R2 | AdjR2 | AIC | BIC | RMSE | MSE | FI | Breusch–Pagan Test (p) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Intercept (a) | Slope (b) | ||||||||||
| Stem | Ln(B) = −1.49 + 2.00∗Ln(dbh) | 0.13 | 0.34 | 0.80 | 0.83 | 12.00 | 17.50 | 0.258 | 0.07 | 9.10 | 0.90 |
| Branches | Ln(B) = −3.63 + 2.37∗Ln(dbh) | 0.29 | 0.74 | 0.60 | 0.59 | 80.10 | 85.50 | 0.551 | 0.32 | 5.60 | 0.43 |
| Leaves | Ln(B) = −2.61 + 1.86∗Ln(dbh) | 0.32 | 0.81 | 0.40 | 0.43 | 91.40 | 96.90 | 0.612 | 0.39 | 5.00 | 0.05 |
| Total | Ln(B) = −0.952 + 1.97∗Ln(dbh) | 0.14 | 0.36 | 0.80 | 0.81 | 17.10 | 22.60 | 0.273 | 0.08 | 15.00 | 0.41 |
| Component | Allometric Model | MRE (%) | ME | |
|---|---|---|---|---|
| Stem | With CF | B = e(−1.49+2.00∗Ln(dbh))∗1.002 | 20.9 | 0.79 |
| Without CF | B = e(−1.49+2.00∗Ln(dbh)) | 21.0 | 0.79 | |
| Branches | With CF | B = e(−3.63+2.37∗Ln(dbh))∗1.047 | 51.0 | 0.45 |
| Without CF | B = e(−3.63+2.37∗Ln(dbh)) | 53.5 | 0.46 | |
| Leaves | With CF | B = e(−2.61+1.86∗Ln(dbh))∗1.073 | 55.1 | 0.26 |
| Without CF | B = e(−2.61+1.86∗Ln(dbh)) | 59.4 | 0.29 | |
| Total | With CF | B = e(−0.952+1.97∗Ln(dbh))∗1.003 | 23.2 | 0.80 |
| Without CF | B = e(−0.952+1.97∗Ln(dbh)) | 23.3 | 0.80 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramos-Veintimilla, R.; Andrade, H.J.; Vera-Velez, R.; Esparza-Parra, J.; Panama-Perugachi, P.; Segura, M.; Grijalva-Olmedo, J. Allometric Models to Estimate Aboveground Biomass of Individual Trees of Eucalyptus saligna Sm in Young Plantations in Ecuador. Int. J. Plant Biol. 2025, 16, 39. https://doi.org/10.3390/ijpb16020039
Ramos-Veintimilla R, Andrade HJ, Vera-Velez R, Esparza-Parra J, Panama-Perugachi P, Segura M, Grijalva-Olmedo J. Allometric Models to Estimate Aboveground Biomass of Individual Trees of Eucalyptus saligna Sm in Young Plantations in Ecuador. International Journal of Plant Biology. 2025; 16(2):39. https://doi.org/10.3390/ijpb16020039
Chicago/Turabian StyleRamos-Veintimilla, Raúl, Hernán J. Andrade, Roy Vera-Velez, José Esparza-Parra, Pedro Panama-Perugachi, Milena Segura, and Jorge Grijalva-Olmedo. 2025. "Allometric Models to Estimate Aboveground Biomass of Individual Trees of Eucalyptus saligna Sm in Young Plantations in Ecuador" International Journal of Plant Biology 16, no. 2: 39. https://doi.org/10.3390/ijpb16020039
APA StyleRamos-Veintimilla, R., Andrade, H. J., Vera-Velez, R., Esparza-Parra, J., Panama-Perugachi, P., Segura, M., & Grijalva-Olmedo, J. (2025). Allometric Models to Estimate Aboveground Biomass of Individual Trees of Eucalyptus saligna Sm in Young Plantations in Ecuador. International Journal of Plant Biology, 16(2), 39. https://doi.org/10.3390/ijpb16020039






