Abstract
Inverter-fed drive systems are mostly optimized to operate at the best efficiency, neglecting the possibility of acoustic optimization. The chosen operating point can lead to undesired harmonics involving vibrations and noises of the electrical drive. In order to optimize the system with respect to acoustics, the given operating point for best efficiency is left and a noise, vibration and harshness (NVH)-optimized operating point is chosen. This paper shows the influence of the operating point on NVH, describes an NVH-optimized control and draws a comparison between simulation and measurement.
1. Introduction
The operating points of induction machines are often optimized for lowest machine or drive losses. These points especially show an advantage in the thermal behavior of the drive system. However, the harmonic excitation of the drive system is not taken into account. In order to consider the harmonics, which lead to vibrations on the surface of the electrical drive and audible noises, a new operating strategy, for noise, vibration and harshness, is defined, shown in Figure 1. As this diagram shows, the operating points for one given torque are operable for different induction machine slip frequencies, changing the stator d-q-axis current operating strategy. The electromagnetic force excitation behavior is influenced in order to subsequently reduce noises. This paper shows these operating strategies, explains the theoretical background of the machine behavior changing the operating strategy and draws a comparison between the simulation of a vibration synthesis model [1,2,3,4,5,6] and measurements on the surface of the electrical drive.
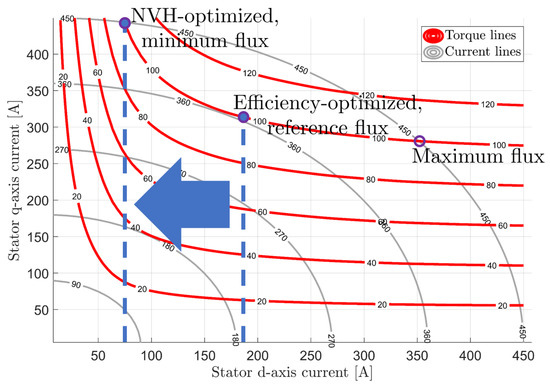
Figure 1.
Schematic diagram of noise-optimized and efficiency-optimized operating points.
2. Theoretical Background
This section imparts the general understanding of the electromagnetic behavior of the electrical machine and, subsequently, to the electromagnetic force excitation, which causes noise emissions. Assuming the radial electromagnetic force excitation , mainly depending on the radial component of the magnetic flux density , over a given surface area and the vacuum permeability , defined in (1). The magnetic flux density including the stator and rotor mmfs, and , as well as the magnetic permeance is calculated as shown in (2) [1,2,4].
Considering the slotting of the stator and rotor, as well as the saturation in the magnetic permeance , both the mmfs of stator and rotor, and , and their spatial position are the main focused parts for changing the operating points and subsequently the noise emissions. In Figure 2b,c the magneto motive forces are calculated for three different d-q-axis currents for 60 Nm of torque, as shown in the d-q-diagram in Figure 1. It is shown that the position and the amplitude of the magneto motive forces (mmfs) depend on the slip of the induction machine.
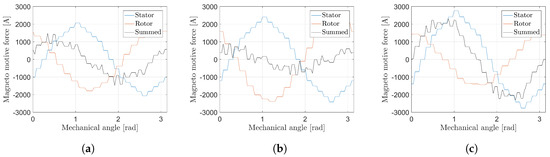
Figure 2.
Mmfs for (a) reference, (b) minimum and (c) maximum stator d-axis current at 60 Nm of torque.
The schematic for the fundamental electromagnetic are shown in Figure 3a–c, where
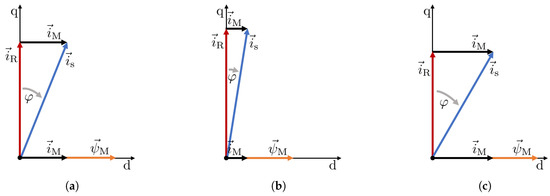
Figure 3.
Schematic diagrams for (a) reference, (b) minimum and (c) maximum stator d-axis current at 60 Nm of torque.
Decreasing the stator d-axis current, decreases the flux and the magnetic flux density, similar to the field weakening area of the machine operating range. Due to this behavior, the induction machine slip frequency is increased in order to hold the desired electromagnetic torque. Increasing the slip, increases the induced voltage into the rotor bars and, with it, the rotor bar currents. As the rotor bar currents produce the rotor mmf in order to act against its origin, a field is built from the rotor side in order to damp the stator field. Increasing the induction decreases the spatial position difference between stator and rotor mmfs in comparison to the referenced system in Figure 3a. This reduces the summed mmf, as well as the resultant magnetic flux density, shown in Figure 3b. Decreasing the slip decreases the induction into the rotor bars. This decreases the occurring rotor bar currents and the rotor mmf decreases. This implicates the less opposing field from the rotor side. Due to this behavior, the rotor mmf damps the system less than the reference operating in Figure 3a and the summed mmf, as well as the magnetic flux density in Figure 3c increases. The angle between stator and rotor mmf is related to the stator and rotor currents and and are defined as,
The harmonics content of each operating set at 60 Nm of torque is shown for simulated speed run-ups in the Campbell diagrams in Figure 4a–c. These Figures show the temporal frequency decomposition of the radial forces over the mechanical machine rotor speed. Since the voltage is produced by a pulse width modulation (PWM) inverter, thus the voltage supply is non-sinusoidal and same given to each operating system. It is shown, that the d-q-axis operating point and subsequently the magneto-motive force, as well as the saturation of the magnetic permeance have a huge influence on the electromagnetic force excitation, as explained in the following.
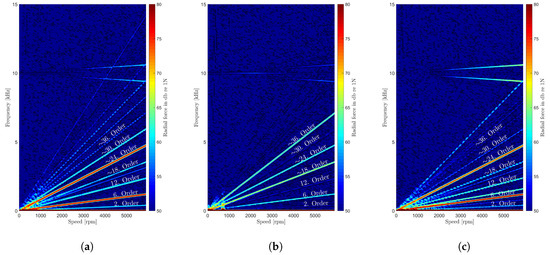
Figure 4.
Radial force spectrum for (a) reference, (b) minimum and (c) maximum stator d-axis current at 60 Nm of torque.
Keeping Figure 4a as reference, the operation in the minimum d-axis stator current in Figure 4b shows less harmonics coming from the non-sinusoidal voltage excitation. Due to the small spatial angle difference of the stator and rotor mmfs, the rotor is able to damp more harmonics than in the reference system. This small angle and the increased rotor current reduces the fundamental amplitude of 2. Order and the saturation harmonics, 6. and 12. Order. The mechanical harmonics, like the rotor slotting harmonics of ∼18. and ∼36. Order, due to 36 rotor bars and machine pole pair number 2, are more prominent. Harmonics, like ∼24. and ∼30. Order, caused by the interaction of saturation and slotting are reduced, due to the less saturation [3,4,7].
Comparing the reference operation from Figure 4a with the operating points from Figure 4c, the PWM-beat is more prominent due to the less damping from the cage rotor. This causes higher flux and increases the saturation harmonics, 6., 8. and 12. Order, but reduces mechanical harmonics from the rotor slotting, ∼18. and ∼26. Order, because the tooth saturation decreases the electromagnetic slotting effect. The interaction harmonics from the saturation and slotting is partly increased, like ∼24. Order, and partly decreased, like the ∼30. Order, depending on the spatial position of the saturation to the slotting harmonics [3,4,7].
The simulation of the radial force decomposition can also be viewed as the force levels in Figure 5, calculated as the summed magnitudes over all frequencies for each rotor speed. It is shown, that the radial force level in the minimum d-axis current and subsequently in the minimum flux is always lower than the radial force levels of the reference and maximum flux operating, caused by the reduced amplitudes of saturation, PWM harmonics as well as the reduction of the fundamental flux. The calculation of the level of the radial force neglects the damping of the structural dynamics system of the stator and a A-weighting in order to validate the noise perception of the humans hearing. However, the force decomposition in minimum flux operation gives a strong indication for noise reduction.
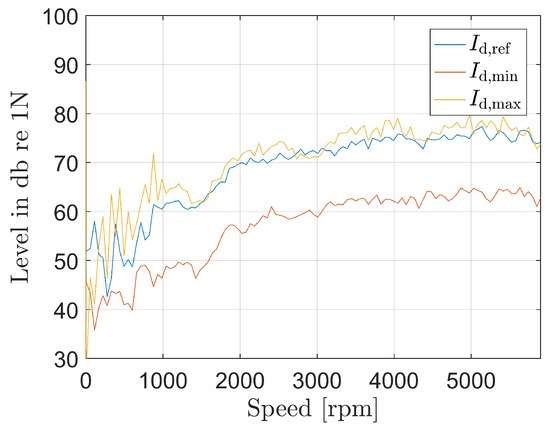
Figure 5.
Radial force levels for speed run-ups at 60 Nm of torque.
The structural dynamic of the stator is also important in order to reduce noise emissions. The structural dynamics systems damps the forces depending on its temporal frequency decomposition. Thus, the noise emissions are depending on the ratio of force excitation and the damping of the structure. Relating to the temporal harmonics of the spatial radial force order, the damping on the system can be defined for the stator structure with a transfer function for each spatial force mode, as shown in Figure 6.
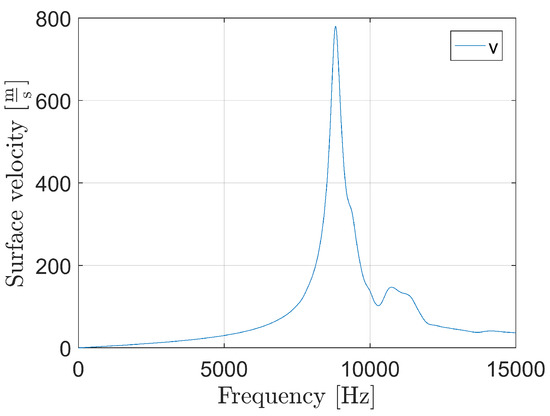
Figure 6.
Structural transfer function for the 0th spatial force mode at one spatial point on the surface.
Here, temporal frequencies in the 0th spatial force mode are mostly damped, but frequencies which are in the range of 7–11 kHz, are much less damped than others. This effect is very important to reduce noises. In general, the procedure introduced in this paper relates to reduce force excitation. Reducing high amplitudes of force harmonics, which occur in the range of natural frequencies of the structural dynamic, have the highest potential to reduce the noise emissions of induction machine [5,6,8].
Finally, the radial velocity on the surface of the induction machine is defined, with the radial force in the spatial and temporal frequency domain u and f, as well as the structural transfer function , as
Since the sound pressure level is mainly explained in the spatial and temporal time domain and t, the radial surface velocity is transformed back with an 2-dimensional Fast Fourier transform (FFT) [3,5,6].
3. Acoustic Measurements
In order to validate the simulation results obtained from Section 2, measurements were performed. To receive accurate results, the surface velocity of the induction machine is recorded, using an acceleration sensor on the surface of the induction machine. In general, the radial surface velocity shows a direct impact on the sound pressure level with the sound power P [6,8], where
with the mean-square surface radial velocity for an infinite axial length defined as,
The Velocity levels, in the following, are rated with A weighting curve in order to get a ratio of the sound pressure level and the perception of human hearing.
The measured surface velocity levels are shown in Figure 8a for speed run-ups at 20 Nm of torque. The reference, minimum and maximum flux operating shows huge differences. As described in Section 2, the minimum flux operation has mainly the lowest velocity level, but there are also operating points, where the operation in reference flux is beneath the minimum flux curve. These points can be explained with the Campbell diagrams in Figure 7a–c. The saturation in this operating point is less, increasing the d-current, increases the flux and the saturation, as well as the PWM-harmonics. This causes the high level of surface velocity for the maximum flux operating. Due to the operating in minimum flux, the PWM-harmonics, as well as the saturation harmonics are minimized, but the slotting harmonics are increased. If the slotting harmonics in this operating come up with the natural frequencies of the system, the slotting harmonics become prominent and increase the velocity level over the reference level.
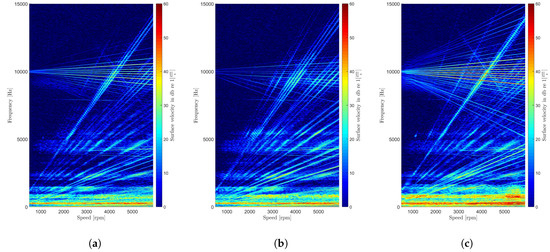
Figure 7.
Surface velocity spectrum for (a) reference, (b) minimum and (c) maximum stator d-axis current at 20 Nm of torque.
The measured surface velocity levels for speed run-ups of 60 Nm and 100 Nm of torque are shown in Figure 8b,c. The reference, minimum and maximum flux operating differences are not as big as in the measurements for 20 Nm of torque. The theses from Section 2 are also approved for these operating points. Relating to the slotting, saturation and PWM-harmonics, the measurements picture same behavior, as shown for the 20 Nm of torque measurements, shown in the Campbell diagrams for 60 Nm of torque in Figure 9a–c and 100 Nm of torque in Figure 10a–c. Due to the stator current limitation, the operating range for higher torques gets more and more limited, which reduces the difference between the choosable flux range and shrinks the differences between the measurements.
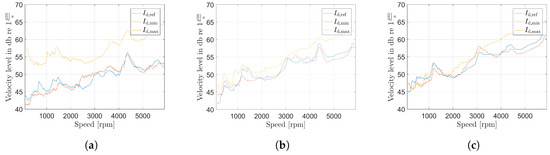
Figure 8.
Surface velocity levels for speed run-ups at (a) 20 Nm, (b) 60 Nm and (c) 100 Nm of torque.
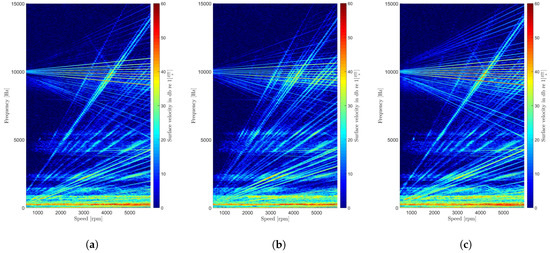
Figure 9.
Surface velocity spectrum for (a) reference, (b) minimum and (c) maximum stator d-axis current at 60 Nm of torque.
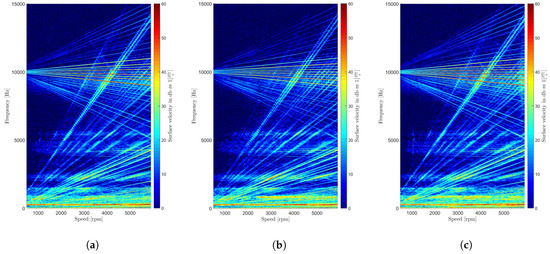
Figure 10.
Surface velocity spectrum for (a) reference, (b) minimum and (c) maximum stator d-axis current at 100 Nm of torque.
The potential velocity differences on the induction machine surface are shown for 20 Nm of torque in Figure 11a, for 60 Nm of torque in Figure 11b and for 100 Nm of torque in Figure 11c. The measurements are performed for different stator d-axis currents, including a bigger range of d-axis operating currents, as shown in the comparison above. This potential analysis shows the maximum reducibility of the surface velocity for each rotor speed. Especially at partial load, the operating area has the biggest influence and subsequently the highest potential for noise reduction. Due to the current limitation, the operating range for higher torque is limited as well. Nevertheless it shows especially for the beginning field weakening area at 3500 rpm a possibility for reducing noise emissions.
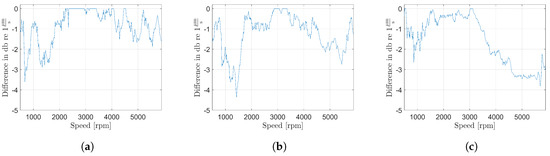
Figure 11.
Maximum of velocity level difference for different stator d-axis current at (a) 20 Nm, (b) 60 Nm and (c) 100 Nm of torque.
At higher torques, the system temperature increases much faster in comparison to lower torques, influencing the acoustic measurements. This fact blurs the measurement and the potential at higher torques. Shown in Figure 11c, the potential has to be rated lower, than shown especially for speed above 4000 rpm.
4. Calculation of the Operating Points
A model is defined in order to calculate the complete operating area of the induction machine. The fundamental machine behavior can be described in the d-q-axis system, which is referencing on the rotor flux [9]. Additionally measurements or a vibration syntheses model is used to optimize the electrical drive. The calculation of operating points depend mainly on the optimization criteria, that is most of the time used for efficiency. This section compares an efficiency optimized operating strategy and a possible NVH-optimization.
4.1. Operating Points for Best Efficiency
In order to calculate the best efficiency of the machine, the machine loss equations from [10,11,12], or test bench measurements are used to calculate the losses for the induction machine operating range. This loss calculation is taken in order to find the minimum of power losses for each torque and stator d-current. The results are shown in Figure 12a for different torques in dependency on power losses of the e-drive and the stator d-currents. With this information of stator d-axis currents at different torques, the machine’s best efficiency trace is calculated, as shown in Figure 12b.
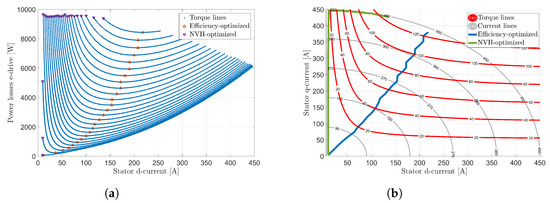
Figure 12.
Optimized (a) stator d-currents changing with torque reference and (b) operating points at the fundamental speed range.
4.2. Operating Points for Best NVH-Behavior
The calculation for the best NVH-behavior is based on the sound pressure level, or surface velocity measurements, from the above sections. This calculation can also be performed with a vibration syntheses model. It is shown that the surface velocity and, subsequently, the sound pressure level can be mainly reduced for low stator d-axis currents. This effect can be explained by the proportionality of the stator d-axis current and the machine magnetization flux [9]. As already explained, in minimum flux regions, saturation is minimized and the slip frequency, and, subsequently, the rotor current has its maximum for the given torque. With the reduction of saturation, saturation harmonics are less stimulated. Increasing the induction in the rotor bars, due to the slip maximum, helps to compensate harmonics in the magnetic flux density in the air-gap of the machine. Noises which occur due to this excitation are hence reduced. Due to the slotting harmonics, the operation in the minimum flux region is not the best solution for every operating point.
For the optimization criteria, the power losses of the electrical drive for different stator d-currents are shown in the minimal flux operating strategy in Figure 12a, the operation in the stator d-q-axis system shown in Figure 12b. These diagrams show, that with changing the operating strategy, the efficiency of the e-drive decreases and can cause thermal issues, when operating permanently in these operating points. These information is very important in order to define the optimization criteria for the NVH-optimization.
As shown in the potential analysis for the maximum surface velocity difference between the strategies, the optimization criteria is defined as shown in (8). In order to reduce the efficiency decrease in case of the flux reduced operating, the strategy for best efficiency operating is not changed till a threshold of the surface velocity difference of −2 dB, meaning 20% improvement, is reached. Reducing fast switching of different d-axis currents are additionally reduced by adding a second condition. The operating points are not changed if there is no operating point nearby, that shows an improvement of −0.5 dB, meaning 5% improvement, of velocity difference.
The optimized operating is shown for 20 Nm–60 Nm of torque in Figure 13a–c and for 80 Nm–120 Nm of torque in Figure 13d–f. It is shown, how the operating is changed from the NVH-optimized to the Efficiency-optimized curves in Figure 12b. These operating strategies show an improvement for reaching field weakening area, because the minimum flux region is directly supporting this behavior. However, the stator d-axis current is changed very quickly, which can have an influence on the dynamics of the operating system.
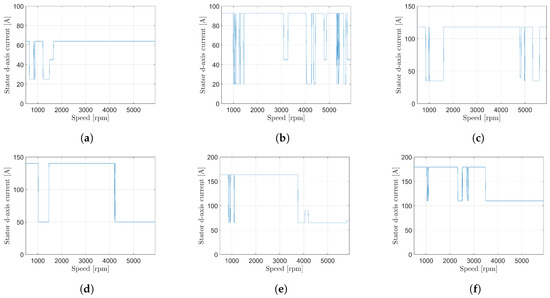
Figure 13.
Stator d-axis current for noise optimized operating at (a) 20 Nm, (b) 40 Nm, (c) 60 Nm, (d) 80 Nm, (e) 100 Nm and (f) 120 Nm of torque.
5. Validation of the Optimization
The optimized strategy is validated with a surface velocity measurement speed run-up at 40 Nm of torque. Figure 14 shows the comparison of the measured NVH-optimized and efficiency-optimized strategy. Because of the influences of temperature, the velocity levels at low speeds are not completely matching. After reaching the same operation temperature, the NVH-optimized strategy follows the efficiency-optimized velocity level, but changes the flux level in order to reduce the velocity levels for the given optimization criteria. The operating points 3500 rpm and 4300 rpm of rotor speed illustrate and support the validity of changing the operating strategy in order to reduce the noise emission of the electrical drive.
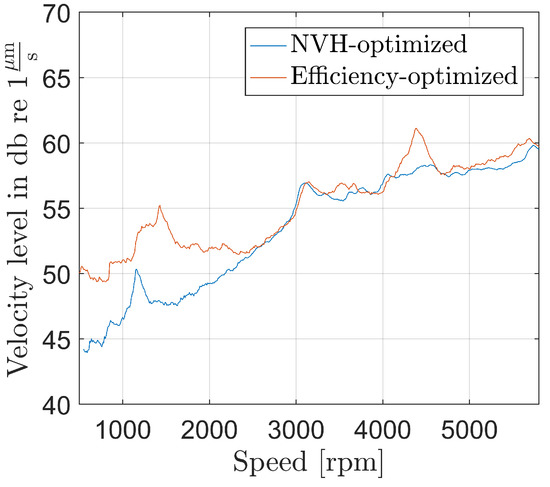
Figure 14.
Measured surface velocity with NVH- and Efficiency-optimized operating strategies.
6. Conclusions
As it is shown in Section 2, influencing the electromagnetic force excitation and, subsequently, the noise emissions, the effects of the occurring harmonics are explainable, and can be simulated. The acoustic measurements support these theories and their validity, and help to create the optimization for the best suitable NVH-optimized behavior. It is also shown that the NVH optimization leads to less efficiency depending on the optimization criteria and can cause thermal issues. The temperature has a big influence on noise emissions, which complicates the calculation of the NVH-optimized operating points. Nevertheless, this paper proposes the cause–effect relationship between the induction machine operating system and the harmonic force stimulation, and shows a procedure in order to optimize the electrical drive in the discrepancy of efficiency and noise excitation.
7. Patents
Resulting and referring to this work, patents are applied for various countries: Control device for an asynchronous machine and method for operating an asynchronous machine, Robert Bosch GmbH, US20180026564A1, DE102015203524A1, CN107251403A, JP2018506956A.
Author Contributions
The contributions of this work can be split up into following parts: Conceptualization, M.D.H. and W.M.B.; Software, W.M.B.; Validation, W.M.B., M.D.H. and F.D.; Investigation, W.M.B., M.D.H. and F.D.; Writing—Review & Editing, W.M.B., F.D., M.D.H. and R.M.K.; Visualization, W.M.B.; Supervision, R.M.K. and M.D.H.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Le Besnerais, J. Reduction of Magnetic Noise in PWM-Supplied Induction Machines-Low-Noise Design Rules and Multi-Objective Optimization. Ph.D. Dissertation, Ecole Centrale de Lille, Laboratoire d’Eletcricité et d’Electronique de Puissance, Lille, France, 2008. [Google Scholar]
- Bischof, W.M.; Hennen, M.D.; Kennel, R.M. Synthesized Magnetic Flux Density in Three-Phase Cage Induction Machines with MATLAB & Simulink. In Proceedings of the 18th International Conference on Electrical Machines and Systems (ICEMS), Pattaya City, Thailand, 25–28 October 2015. [Google Scholar]
- Bischof, W.M.; Chatterjee, B.; Boesing, M.; Hennen, M.D.; Kennel, R.M. Modeling Radial Air-Gap Forces of Three-Phase Cage Induction Machines in Spatial Frequency Domain. In Proceedings of the 19th International Conference on Electrical Machines and Systems (ICEMS), Chiba, Japan, 13–16 November 2016. [Google Scholar]
- Bischof, W.M.; Chatterjee, B.; Boesing, M.; Hennen, M.D.; Kennel, R.M. Modeling Inverter-Fed Three-Phase Squirrel-Cage Induction Machines including Spatial and Temporal Harmonics. In Proceedings of the International Electric Machines and Drives Conference (IEMDC), Miami, Florida, USA, 21–24 May 2017. [Google Scholar]
- Kotter, P.; Koepf, C.; Bischof, W.M.; Wegener, K. Efficient Noise-Vibration-Harshness-modeling for squirrel-cage induction drives in EV applications. In Proceedings of 17. Internationales Stuttgarter Symposium; Springer: Wiesbaden, Germany, 2017. [Google Scholar]
- Kotter, P.; Callan-Bartkiw, B.; Boesing, M.; Wegener, K.; Berkemer, J.; Zirn, O. Noise-Vibration-Harshness simulation of ultralight vehicle traction drives based on a universal modelling approach. In Proceedings of the 8th International Conference on Power Electronics, Machines and Drives, PEMD, Glasgow, UK, 19–21 April 2016. [Google Scholar]
- Müller, G.; Ponick, B. Theorie Elektrischer Maschinen; WILEY-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2009. [Google Scholar]
- Bösing, M. Acoustic Modeling of Electrical Drives. Dissertation, Institut für Stromrichtertechnik und Elektrische Antriebe, RWTH Aachen, Aachen, Germany, 2013. [Google Scholar]
- De Doncker, R.; Pulle, D.W.; Veltman, A. Advanced Electrical Drives—Analysis, Modeling, Control, 1st ed.; Springer Science + Business Media B.V.: Dordrecht, The Netherlands, 2011. [Google Scholar]
- Müller, G.; Vogt, K.; Ponick, B. Berechnung Elektrischer Maschinen; WILEY-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2008. [Google Scholar]
- Von Pfingsten, G.; Steentjes, S.; Hameyer, K. Transient approach to model operating point dependent losses in saturated induction machines. In Proceedings of the XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016. [Google Scholar]
- Andersson, A. Electric Machine Control for Energy Efficient Electric Drive Systems. Dissertation, Chalmers University of Technology Goeteburg, Department of Energy and Environment, Göteborg, Sweden, 2015. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).