Investigation of Flow Channel Configurations in Liquid-Cooled Plates for Electric Vehicle Battery Thermal Management
Abstract
1. Introduction
2. Materials and Methods
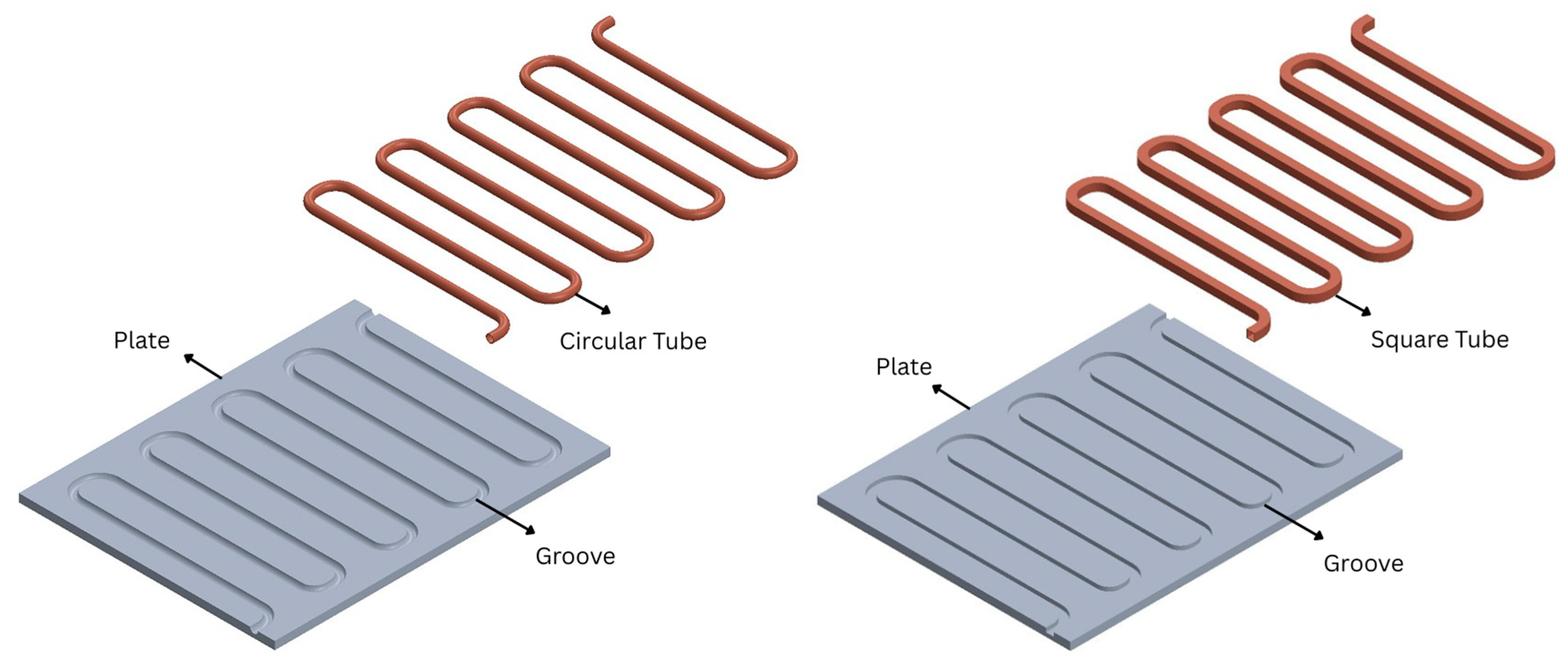
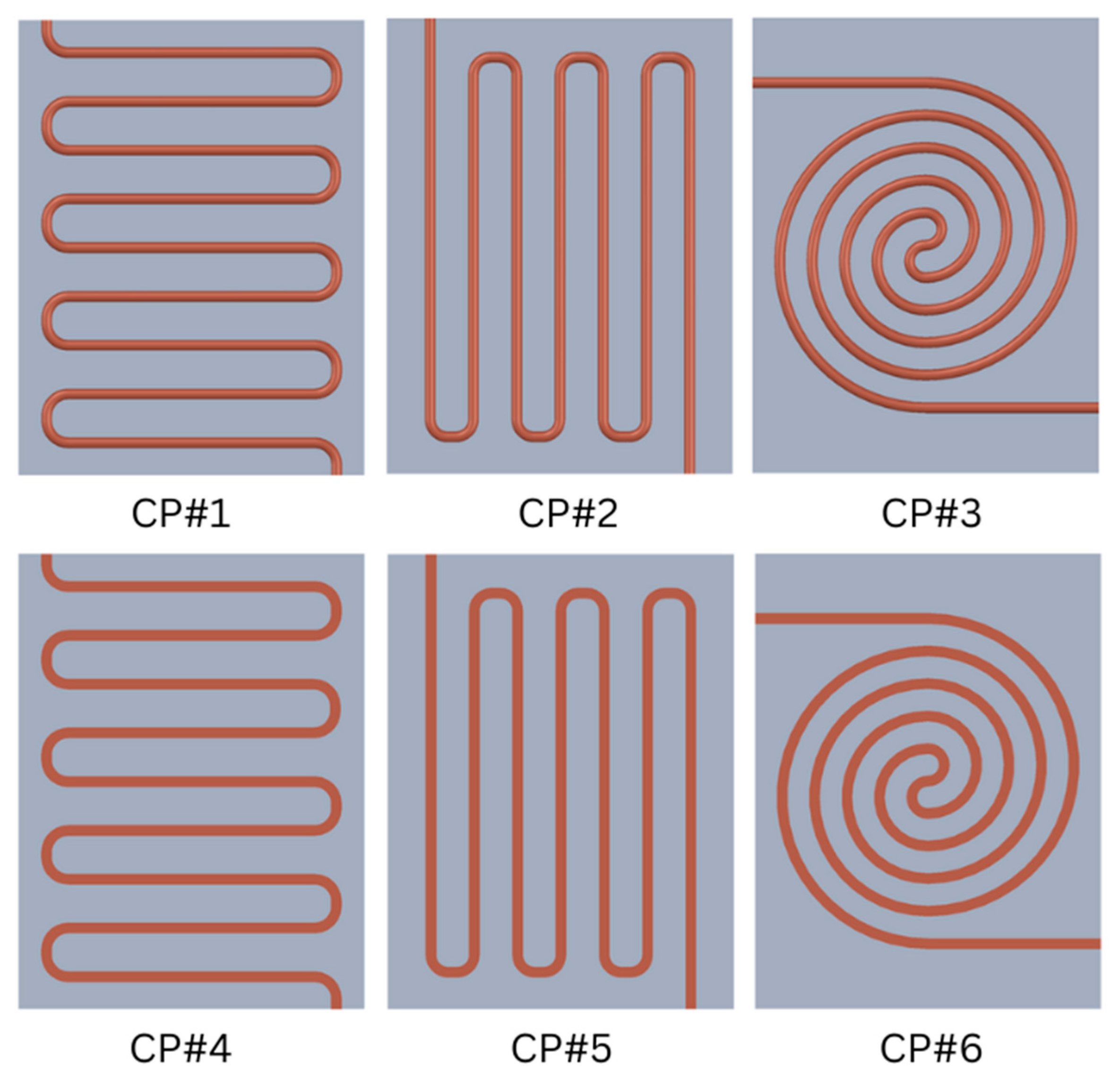
2.1. Geometry and Design Variations
2.2. Mesh Generations and Grid Independence
2.3. Computational Model Setup
- is fluid density ;
- is a fluid velocity vector ;
- is time (s).
- is pressure ;
- is the effective dynamic viscosity, including the contribution of turbulence ;
- are other forces (e.g., gravity).
- is the total enthalpy ;
- is an effective thermal conductivity ;
- is temperature (K);
- is the heat source due to viscosity or pressure work.
- is turbulence energy production;
- is turbulent viscosity;
- is model constants;
- is blending function;
- is thermal conductivity ;
- is the specific heat capacity ;
- is thermal diffusivity .
- is heat flux ;
- is the convection heat transfer coefficient ;
- is surface temperature (wall/copper tube);
- is fluid temperature (water).
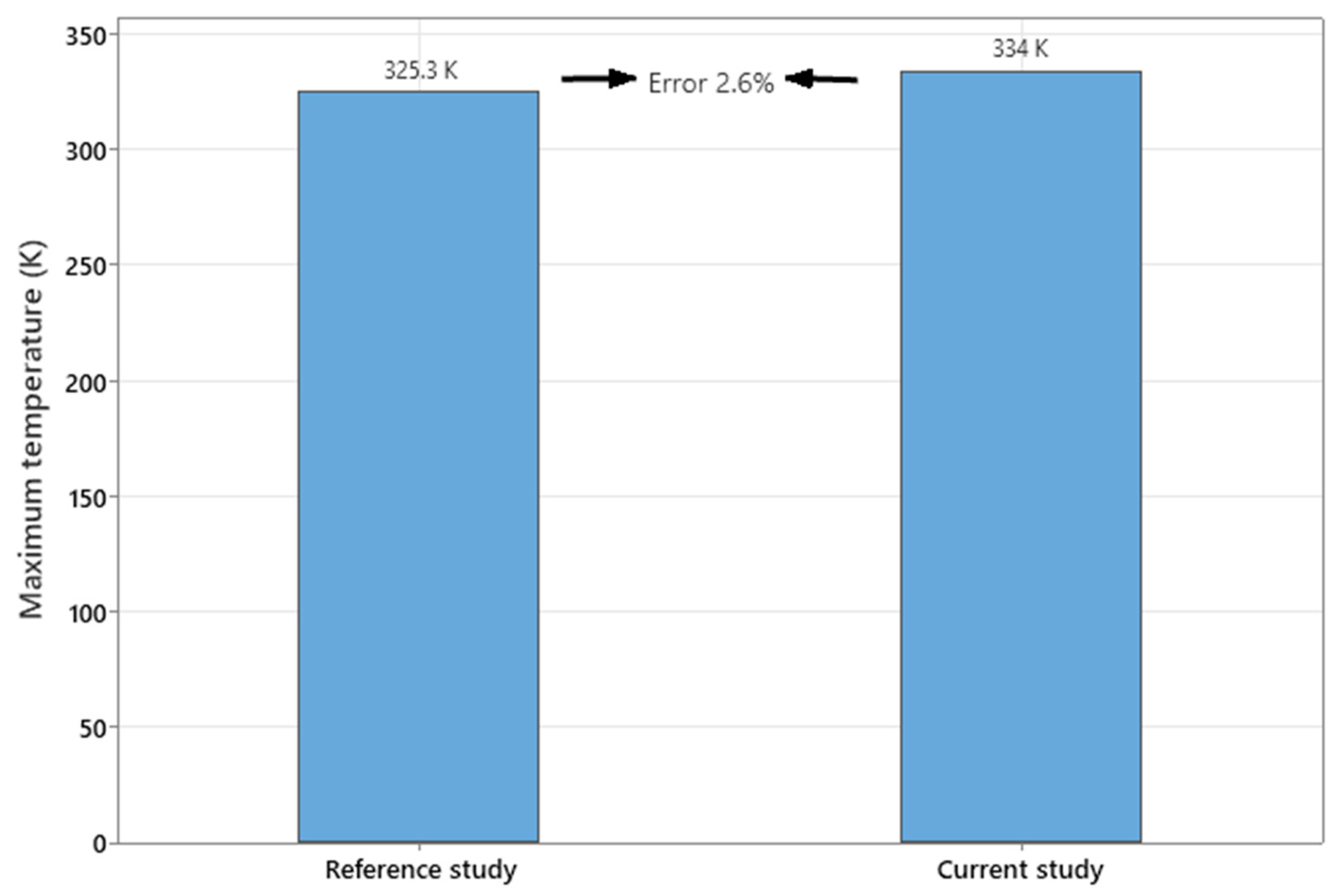
2.4. Model Validation
2.5. Assumptions and Limitations
3. Results and Discussion
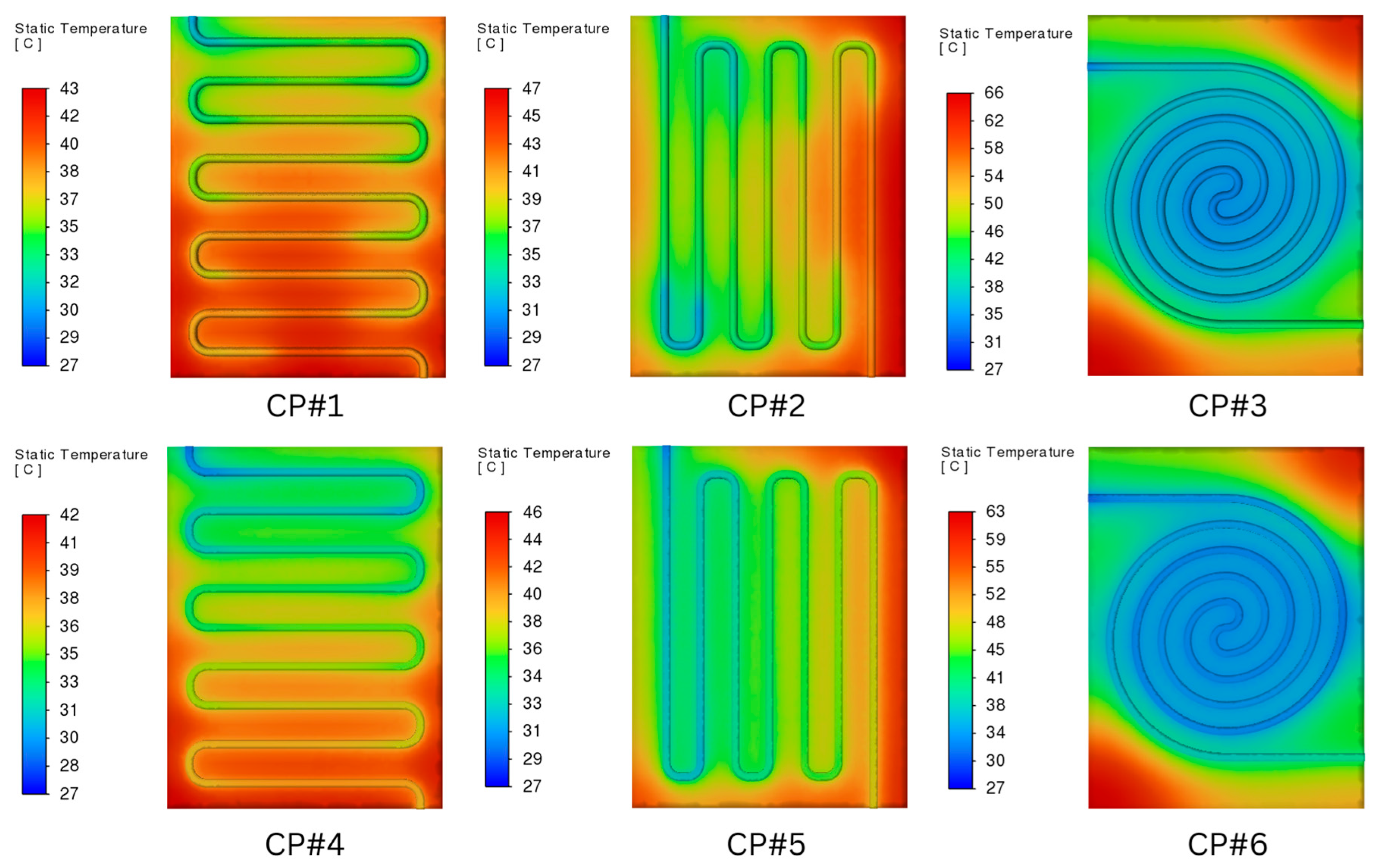
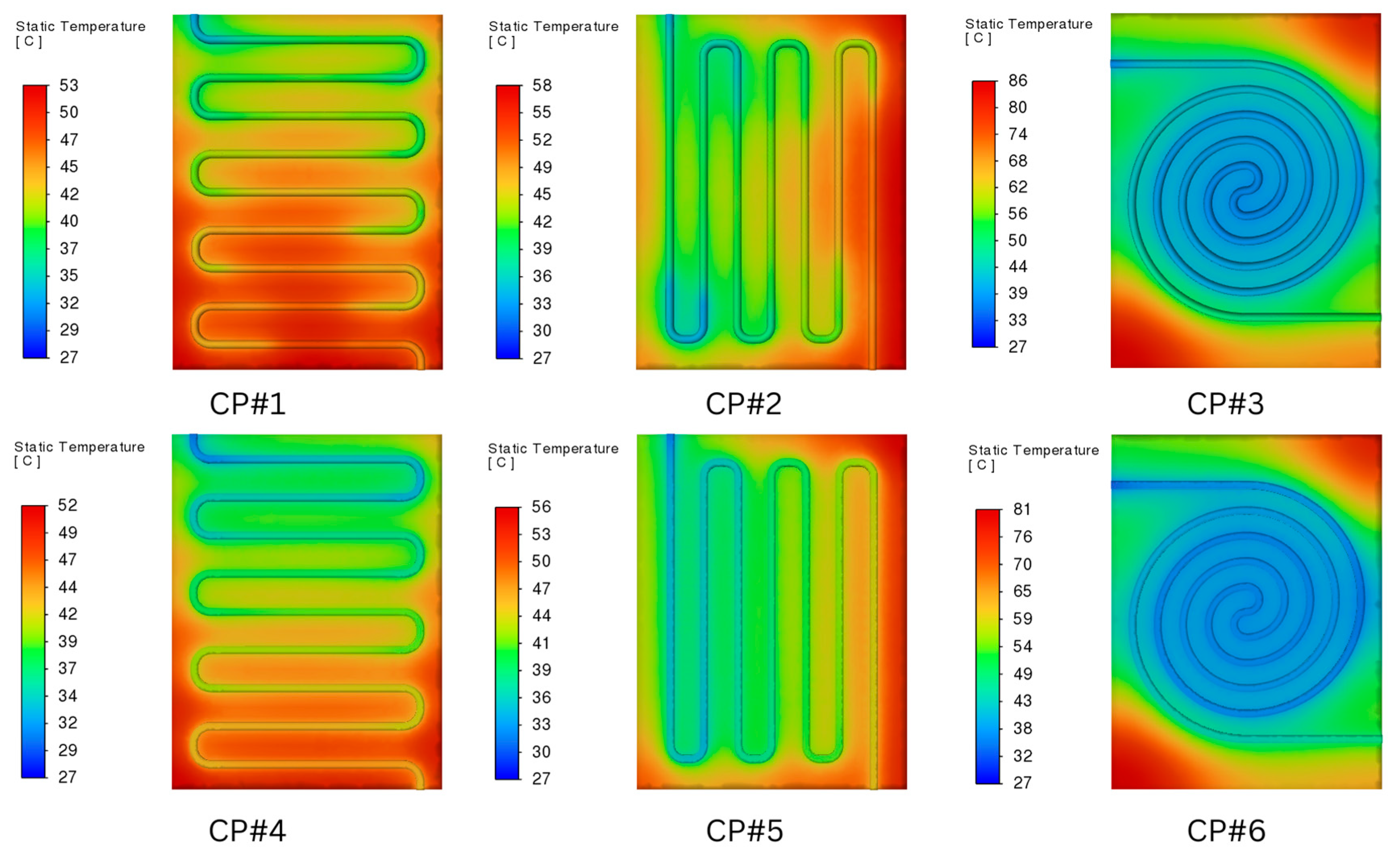
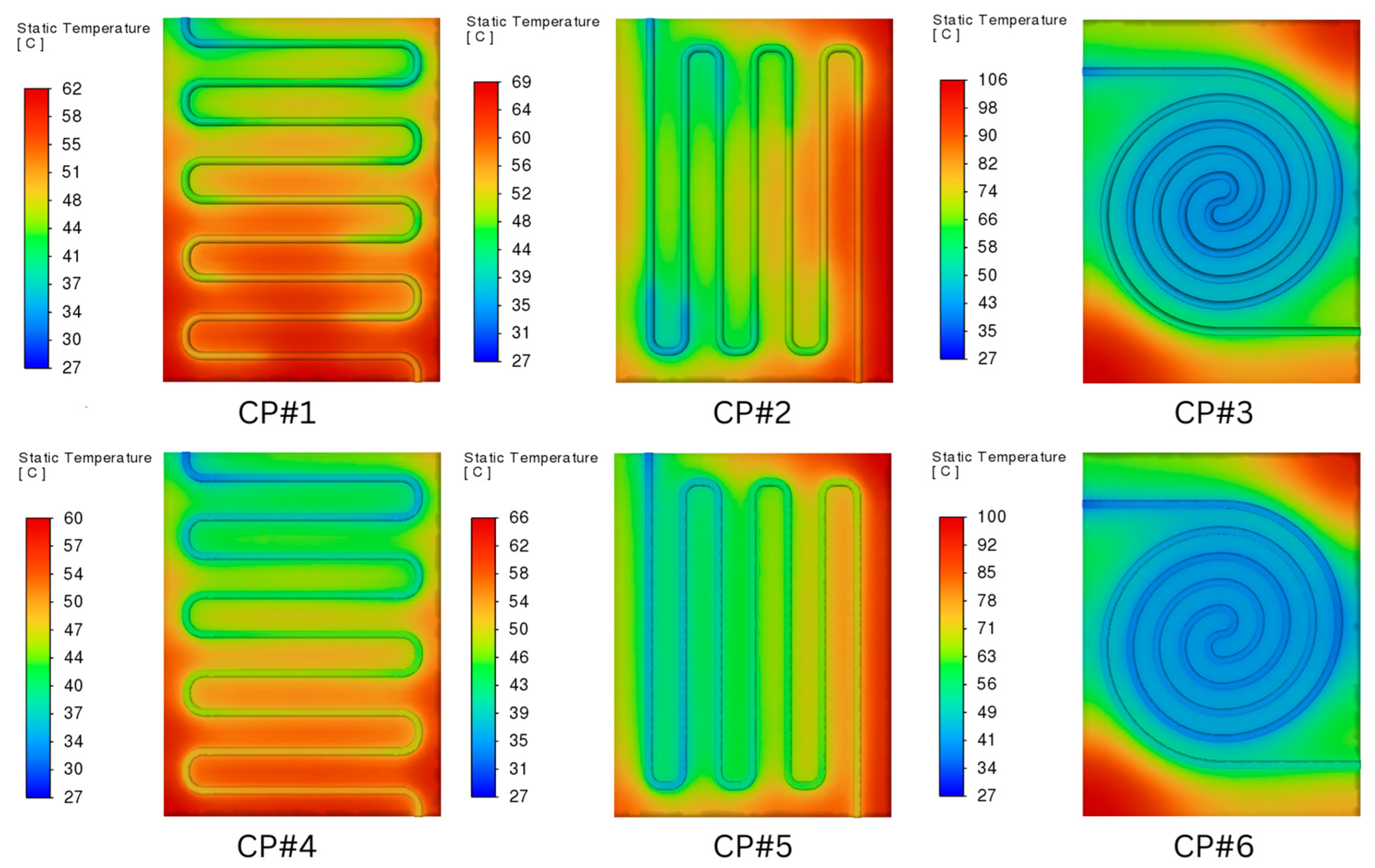
3.1. Temperature Distribution
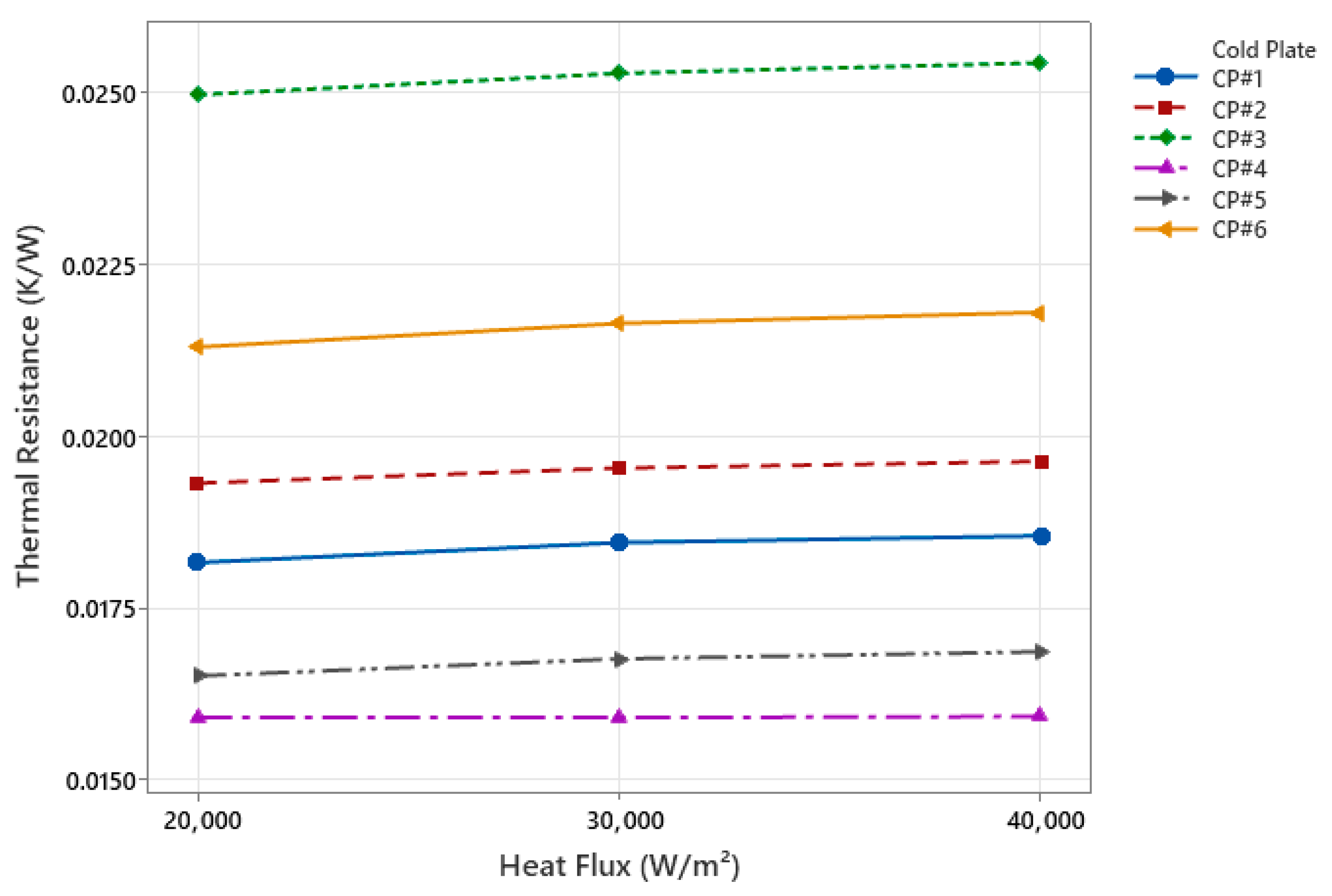
3.2. Thermal Resistance
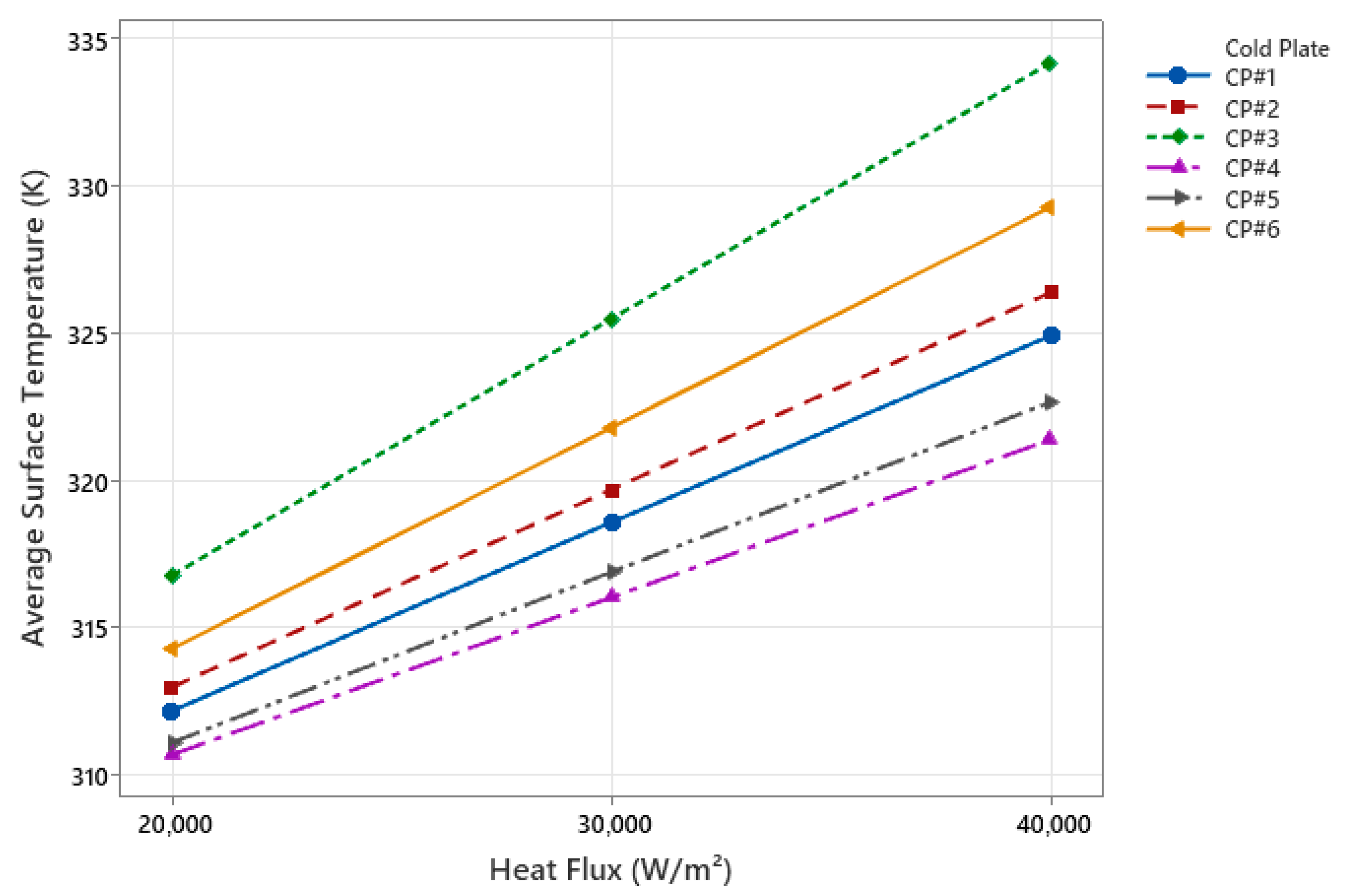
3.3. Average Surface Temperature
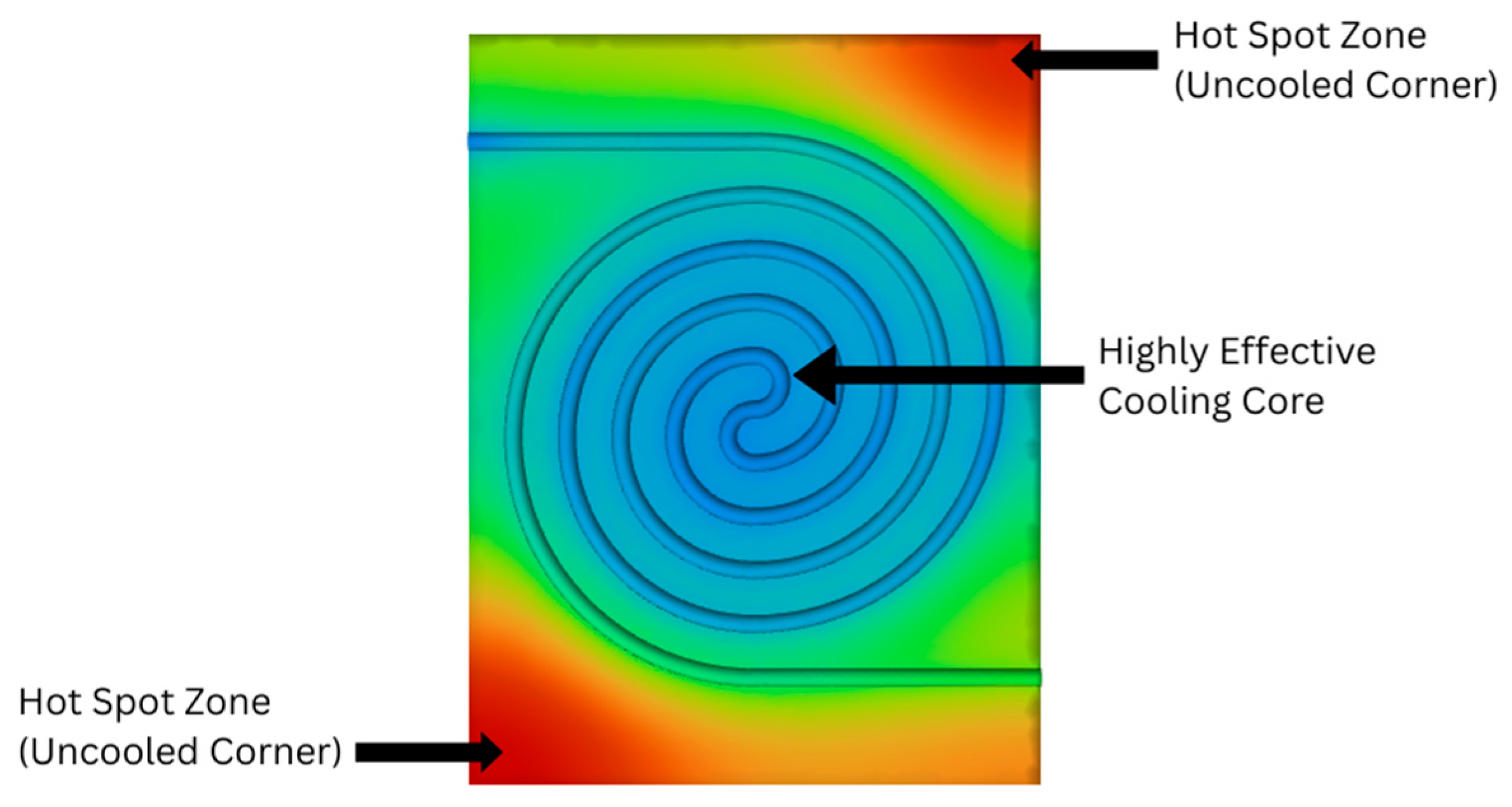
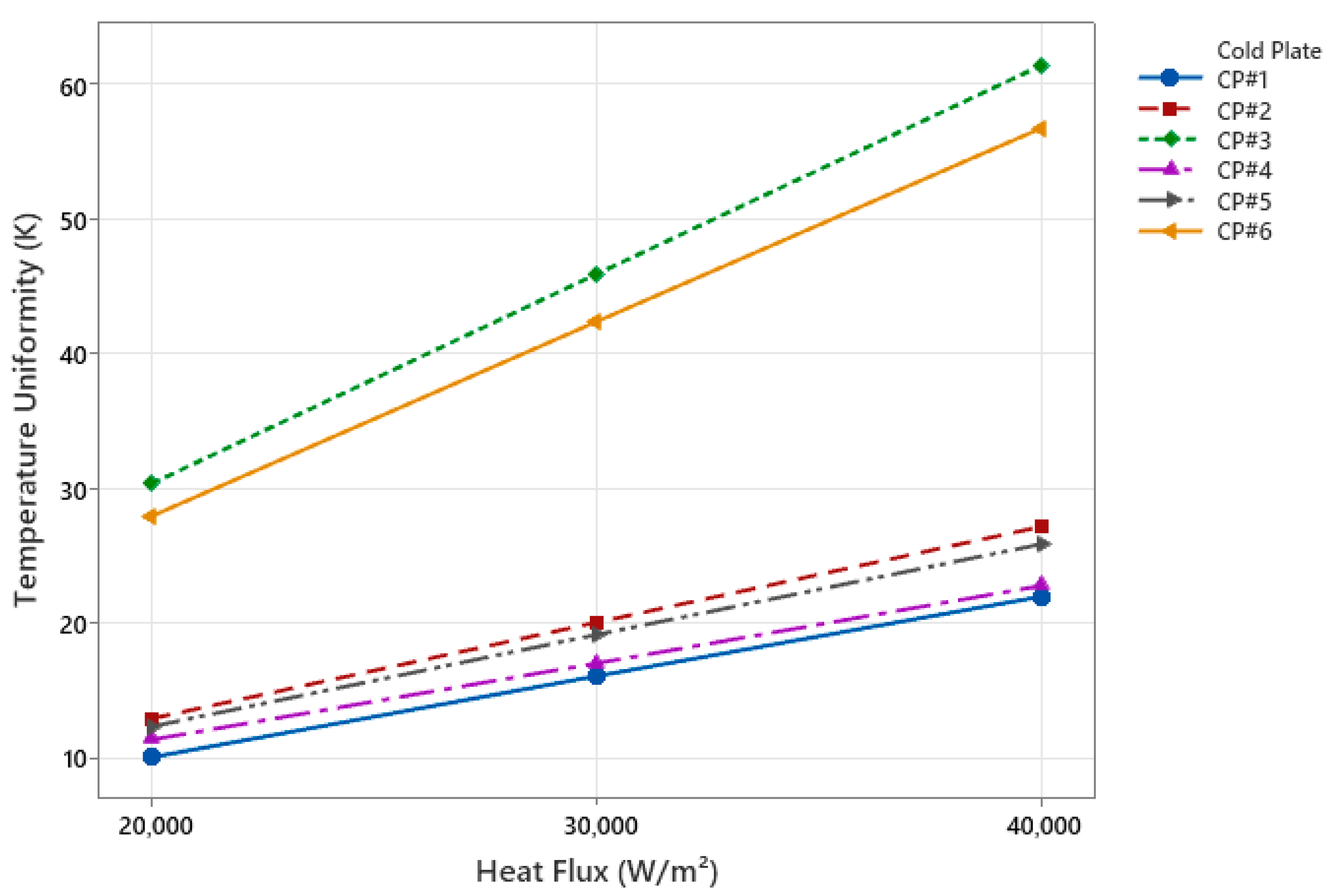
3.4. Temperature Uniformity
3.5. Temperature Uniformity Index
3.6. Pressure Contour
3.7. Pressure Drop
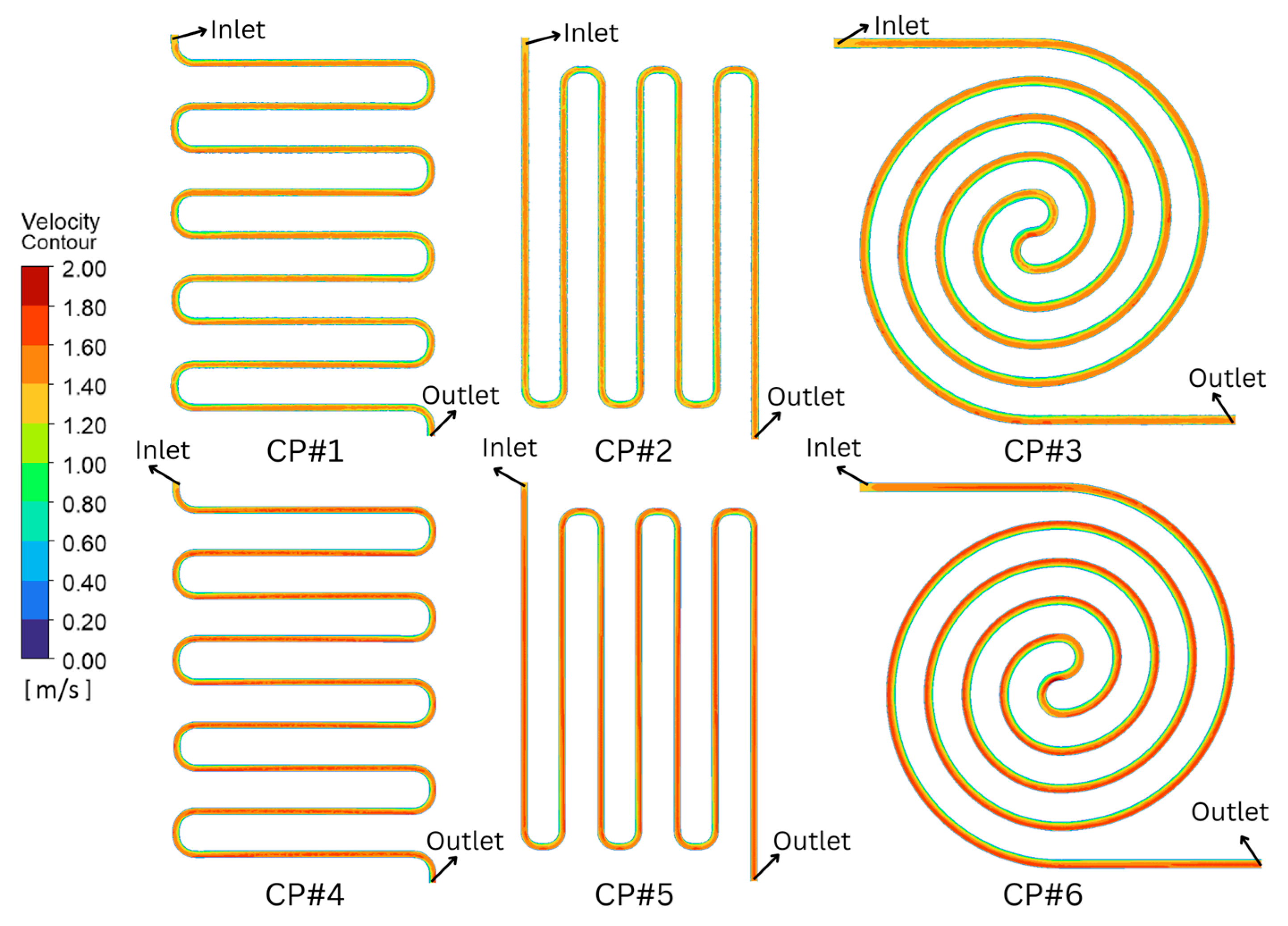
3.8. Velocity Contour
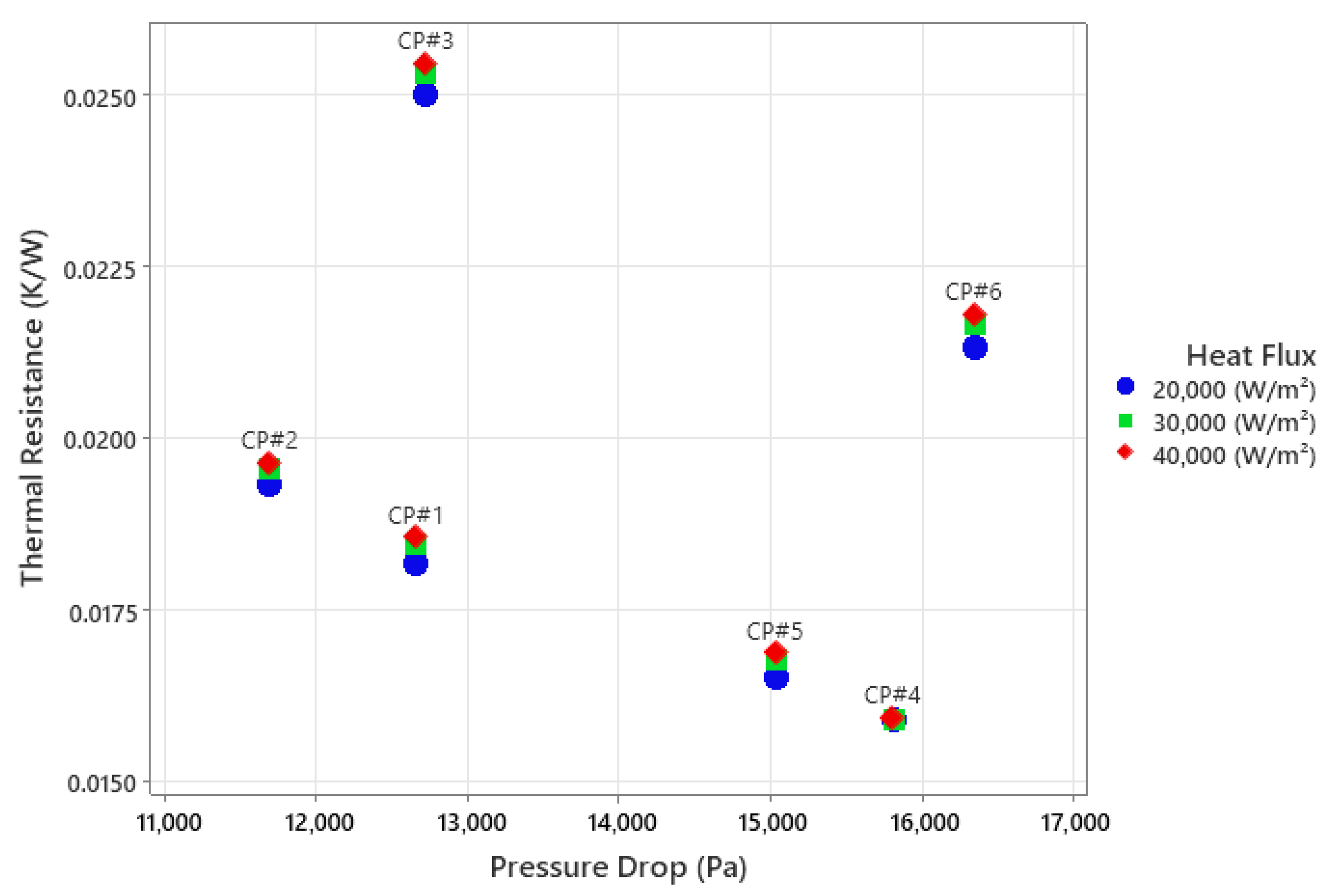
3.9. The Relationship Between Thermal Resistance and Pressure Drop
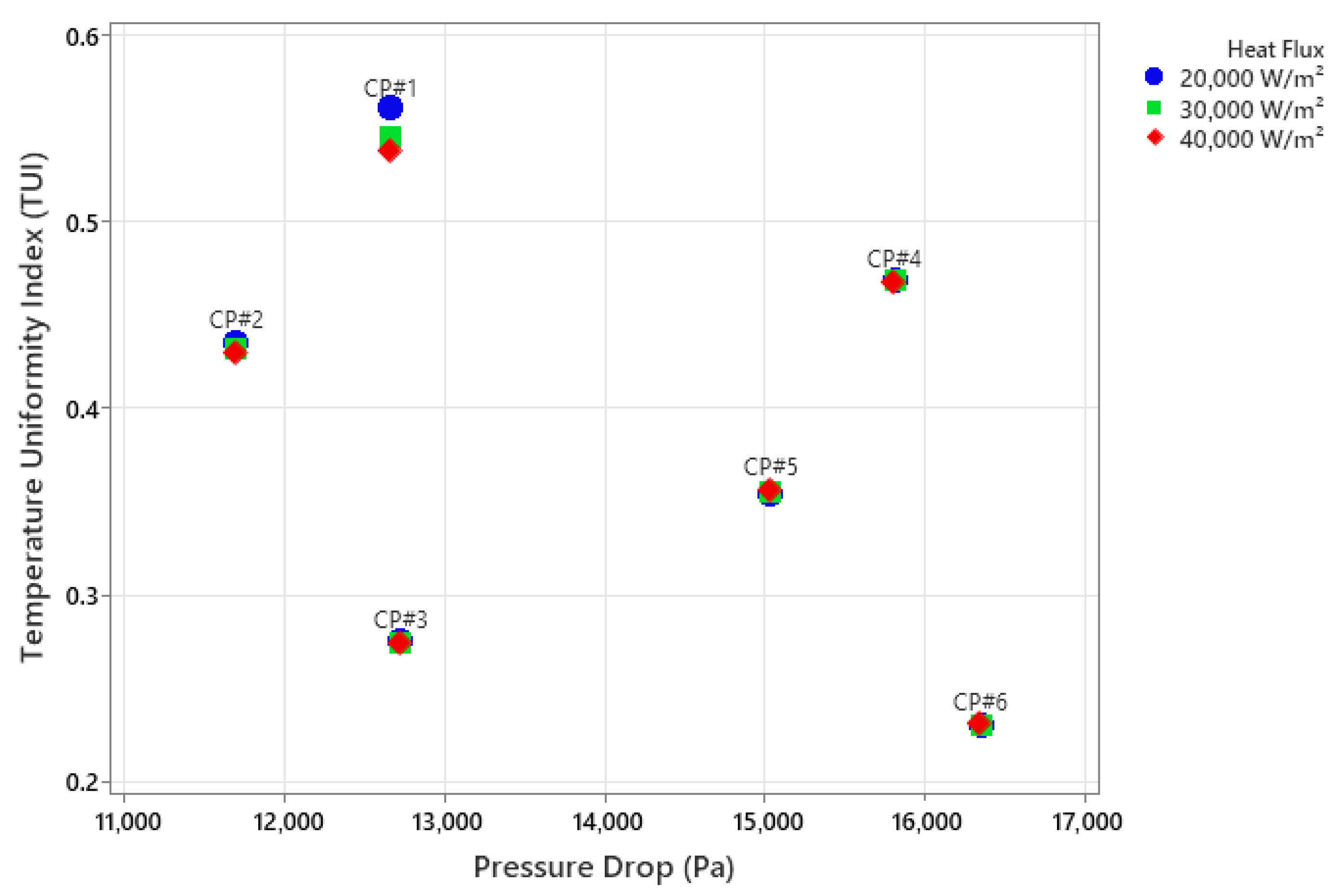
3.10. The Relationship Between TUI and Pressure Drop
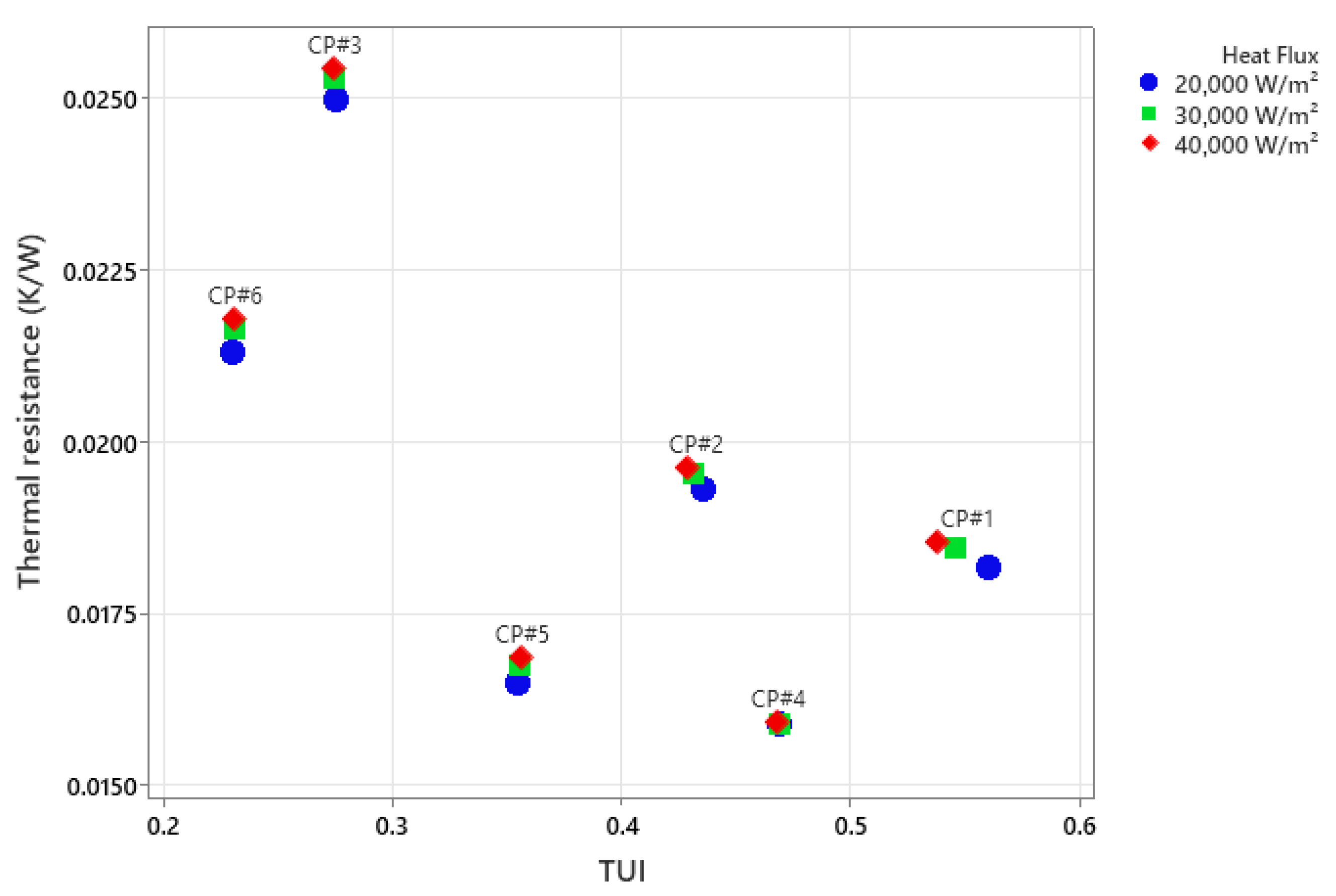
3.11. The Relationship Between TUI and Thermal Resistance
3.12. Implications for BTMS Design Guidelines
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, H.; Yu, S.; Wang, T.; Li, J.; Wang, Y. A systematic review on sustainability assessment of internal combustion engines. J. Clean. Prod. 2024, 451, 141996. [Google Scholar] [CrossRef]
- Zimm, C. Improving the understanding of electric vehicle technology and policy diffusion across countries. Transp. Policy 2021, 105, 54–66. [Google Scholar] [CrossRef]
- Jiang, F.; Yuan, X.; Hu, L.; Xie, G.; Zhang, Z.; Li, X.; Hu, J.; Wang, C.; Wang, H. A comprehensive review of energy storage technology development and application for pure electric vehicles. J. Energy Storage 2024, 86, 111159. [Google Scholar] [CrossRef]
- Lipu, M.S.; Mamun, A.A.; Ansari, S.; Miah, M.S.; Hasan, K.; Meraj, S.T.; Abdolrasol, M.G.M.; Rahman, T.; Maruf, M.H.; Sarker, M.R.; et al. Battery Management, Key Technologies, Methods, Issues, and Future Trends of Electric Vehicles: A Pathway toward Achieving Sustainable Development Goals. Batteries 2022, 8, 119. [Google Scholar] [CrossRef]
- Koroma, M.S.; Costa, D.; Philippot, M.; Cardellini, G.; Hosen, M.S.; Coosemans, T.; Messagie, M. Life cycle assessment of battery electric vehicles: Implications of future electricity mix and different battery end-of-life management. Sci. Total Environ. 2022, 831, 154859. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Lv, Y.; Qu, J.; Sun, Q.; Grachev, D. Performance evaluation of hybrid oscillating heat pipe with carbon nanotube nanofluids for electric vehicle battery cooling. Appl. Therm. Eng. 2021, 196, 117300. [Google Scholar] [CrossRef]
- Afzal, A.; Mohammed Samee, A.D.; Abdul Razak, R.K.; Ramis, M.K. Thermal management of modern electric vehicle battery systems (MEVBS). J. Therm. Anal. Calorim. 2021, 144, 1271–1285. [Google Scholar] [CrossRef]
- Senol, M.; Bayram, I.S.; Naderi, Y.; Galloway, S. Electric Vehicles Under Low Temperatures: A Review on Battery Performance, Charging Needs, and Power Grid Impacts. IEEE Access 2023, 11, 39879–39912. [Google Scholar] [CrossRef]
- Kang, J.; Rizzoni, G. Study of relationship between temperature and thermal energy, operating conditions as well as environmental factors in large-scale lithium-ion batteries. Int. J. Energy Res. 2014, 38, 1994–2002. [Google Scholar] [CrossRef]
- Feng, X.; Xu, C.; He, X.; Wang, L.; Zhang, G.; Ouyang, M. Mechanisms for the evolution of cell variations within a LiNixCoyMnzO2/graphite lithium-ion battery pack caused by temperature non-uniformity. J. Clean. Prod. 2018, 205, 447–462. [Google Scholar] [CrossRef]
- Khan, M.R.; Swierczynski, M.J.; Kær, S.K. Towards an Ultimate Battery Thermal Management System: A Review. Batteries 2017, 3, 9. [Google Scholar] [CrossRef]
- Pesaran, A.A. Battery thermal models for hybrid vehicle simulations. J. Power Sources 2002, 110, 377–382. [Google Scholar] [CrossRef]
- Chen, S.; Wei, X.; Zhang, G.; Wang, X.; Zhu, J.; Feng, X.; Dai, H.; Ouyang, M. All-temperature area battery application mechanism, performance, and strategies. Innovation 2023, 4, 100465. [Google Scholar] [CrossRef]
- Buidin, T.I.; Mariasiu, F. Battery Thermal Management Systems: Current Status and Design Approach of Cooling Technologies. Energies 2021, 14, 4879. [Google Scholar] [CrossRef]
- Olabi, A.G.; Maghrabie, H.M.; Adhari, O.H.K.; Sayed, E.T.; Yousef, B.A.A.; Salameh, T.; Kamil, M.; Abdelkareem, M.A. Battery thermal management systems: Recent progress and challenges. Int. J. Thermofluids 2022, 15, 100171. [Google Scholar] [CrossRef]
- Akbarzadeh, M.; Kalogiannis, T.; Jaguemont, J.; Jin, L.; Behi, H.; Karimi, D.; Beheshti, H.; Van Mierlo, J.; Berecibar, M. A comparative study between air cooling and liquid cooling thermal management systems for a high-energy lithium-ion battery module. Appl. Therm. Eng. 2021, 198, 117503. [Google Scholar] [CrossRef]
- Deng, Y.; Feng, C.; E, J.; Zhu, H.; Chen, J.; Wen, M.; Yin, H. Effects of different coolants and cooling strategies on the cooling performance of the power lithium ion battery system: A review. Appl. Therm. Eng. 2018, 142, 10–29. [Google Scholar] [CrossRef]
- Arora, S. Selection of thermal management system for modular battery packs of electric vehicles: A review of existing and emerging technologies. J. Power Sources 2018, 400, 621–640. [Google Scholar] [CrossRef]
- Behi, H.; Behi, M.; Karimi, D.; Jaguemont, J.; Ghanbarpour, M.; Behnia, M.; Berecibar, M.; Van Mierlo, J. Heat pipe air-cooled thermal management system for lithium-ion batteries: High power applications. Appl. Therm. Eng. 2021, 183, 116240. [Google Scholar] [CrossRef]
- Behi, H.; Karimi, D.; Behi, M.; Ghanbarpour, M.; Jaguemont, J.; Sokkeh, M.A.; Gandoman, F.H.; Berecibar, M.; Van Mierlo, J. A new concept of thermal management system in Li-ion battery using air cooling and heat pipe for electric vehicles. Appl. Therm. Eng. 2020, 174, 115280. [Google Scholar] [CrossRef]
- Shahjalal, M.; Shams, T.; Islam, M.E.; Alam, W.; Modak, M.; Hossain, S.B.; Ramadesigan, V.; Ahmed, M.R.; Ahmed, H.; Iqbal, A. A review of thermal management for Li-ion batteries: Prospects, challenges, and issues. J. Energy Storage 2021, 39, 102518. [Google Scholar] [CrossRef]
- Lu, M.; Zhang, X.; Ji, J.; Xu, X.; Zhang, Y. Research progress on power battery cooling technology for electric vehicles. J. Energy Storage 2020, 27, 101155. [Google Scholar] [CrossRef]
- Al-Zareer, M.; Dincer, I.; Rosen, M.A. Novel thermal management system using boiling cooling for high-powered lithium-ion battery packs for hybrid electric vehicles. J. Power Sources 2017, 363, 291–303. [Google Scholar] [CrossRef]
- Jaguemont, J.; Van Mierlo, J. A comprehensive review of future thermal management systems for battery-electrified vehicles. J. Energy Storage 2020, 31, 101551. [Google Scholar] [CrossRef]
- Kumar Thakur, A.; Sathyamurthy, R.; Velraj, R.; Saidur, R.; Pandey, A.K.; Ma, Z.; Singh, P.; Hazra, S.K.; Wafa Sharshir, S.; Prabakaran, R.; et al. A state-of-the art review on advancing battery thermal management systems for fast-charging. Appl. Therm. Eng. 2023, 226, 120303. [Google Scholar] [CrossRef]
- Zhao, G.; Wang, X.; Negnevitsky, M.; Li, C. An up-to-date review on the design improvement and optimization of the liquid-cooling battery thermal management system for electric vehicles. Appl. Therm. Eng. 2023, 219, 119626. [Google Scholar] [CrossRef]
- Li, W.; Garg, A.; Xiao, M.; Gao, L. Optimization for Liquid Cooling Cylindrical Battery Thermal Management System Based on Gaussian Process Model. J. Therm. Sci. Eng. Appl. 2020, 13, 021015. [Google Scholar] [CrossRef]
- Xu, Y.; Li, X.; Liu, X.; Wang, Y.; Wu, X.; Zhou, D. Experiment investigation on a novel composite silica gel plate coupled with liquid-cooling system for square battery thermal management. Appl. Therm. Eng. 2021, 184, 116217. [Google Scholar] [CrossRef]
- Jarrett, A.; Kim, I.Y. Influence of operating conditions on the optimum design of electric vehicle battery cooling plates. J. Power Sources 2014, 245, 644–655. [Google Scholar] [CrossRef]
- Monika, K.; Chakraborty, C.; Roy, S.; Dinda, S.; Singh, S.A.; Datta, S.P. An improved mini-channel based liquid cooling strategy of prismatic LiFePO4 batteries for electric or hybrid vehicles. J. Energy Storage 2021, 35, 102301. [Google Scholar] [CrossRef]
- Mousavi, S.; Siavashi, M.; Zadehkabir, A. A new design for hybrid cooling of Li-ion battery pack utilizing PCM and mini channel cold plates. Appl. Therm. Eng. 2021, 197, 117398. [Google Scholar] [CrossRef]
- Sheng, L.; Su, L.; Zhang, H.; Li, K.; Fang, Y.; Ye, W.; Fang, Y. Numerical investigation on a lithium ion battery thermal management utilizing a serpentine-channel liquid cooling plate exchanger. Int. J. Heat Mass Transf. 2019, 141, 658–668. [Google Scholar] [CrossRef]
- Patil, M.S.; Seo, J.-H.; Panchal, S.; Jee, S.-W.; Lee, M.-Y. Investigation on thermal performance of water-cooled Li-ion pouch cell and pack at high discharge rate with U-turn type microchannel cold plate. Int. J. Heat Mass Transf. 2020, 155, 119728. [Google Scholar] [CrossRef]
- Li, X.; Zhao, J.; Duan, J.; Panchal, S.; Yuan, J.; Fraser, R.; Fowler, M.; Chen, M. Simulation of cooling plate effect on a battery module with different channel arrangement. J. Energy Storage 2022, 49, 104113. [Google Scholar] [CrossRef]
- Wang, N.; Li, C.; Li, W.; Chen, X.; Li, Y.; Qi, D. Heat dissipation optimization for a serpentine liquid cooling battery thermal management system: An application of surrogate assisted approach. J. Energy Storage 2021, 40, 102771. [Google Scholar] [CrossRef]
- Mousavi, S.; Zadehkabir, A.; Siavashi, M.; Yang, X. An improved hybrid thermal management system for prismatic Li-ion batteries integrated with mini-channel and phase change materials. Appl. Energy 2023, 334, 120643. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, T.; Zhou, L.; Gong, J.; Li, J. A parametric study of a hybrid battery thermal management system that couples PCM with wavy microchannel cold plate. Appl. Therm. Eng. 2023, 219, 119625. [Google Scholar] [CrossRef]
- Khan, S.A.; Eze, C.; Dong, K.; Shahid, A.R.; Patil, M.S.; Ahmad, S.; Hussain, I.; Zhao, J. Design of a new optimized U-shaped lightweight liquid-cooled battery thermal management system for electric vehicles: A machine learning approach. Int. Commun. Heat Mass Transf. 2022, 136, 106209. [Google Scholar] [CrossRef]
- Tang, Z.; Liu, Z.; Li, J.; Cheng, J. A lightweight liquid cooling thermal management structure for prismatic batteries. J. Energy Storage 2021, 42, 103078. [Google Scholar] [CrossRef]
- Zhao, D.; An, C.; Jia, Z.; Lei, Z. Structure optimization of liquid-cooled plate for electric vehicle lithium-ion power batteries. Int. J. Therm. Sci. 2024, 195, 108614. [Google Scholar] [CrossRef]
- Wu, C.; Ni, J.; Shi, X.; Huang, R. A new design of cooling plate for liquid-cooled battery thermal management system with variable heat transfer path. Appl. Therm. Eng. 2024, 239, 122107. [Google Scholar] [CrossRef]
- Rabiei, M.; Gharehghani, A.; Andwari, A.M. Enhancement of battery thermal management system using a novel structure of hybrid liquid cold plate. Appl. Therm. Eng. 2023, 232, 121051. [Google Scholar] [CrossRef]
- Karthik, A.; Pankaj, K.; Akhil, G.; Liang, G.; Siqi, C.; Peng, X. A Novel MOGA approach for power saving strategy and optimization of maximum temperature and maximum pressure for liquid cooling type battery thermal management system. Int. J. Green Energy 2021, 18, 80–89. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, J.; Cheng, D.; Mao, J.; Zhang, K. Numerical investigation and parameter optimization on a rib-grooved liquid-cooled plate for lithium battery thermal management system. J. Energy Storage 2024, 85, 111085. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, X.; Zeng, Q.; Gao, K.; Jiang, S. Bidirectional heat transfer characteristics of cavity cold plate battery thermal management system: An experimental study. Appl. Therm. Eng. 2023, 225, 120242. [Google Scholar] [CrossRef]
- Shen, J.; Chen, X.; Xu, X.; Kong, J.; Song, Z.; Wang, X.; Zhou, F. Thermal performance of a hybrid cooling plate integrated with microchannels and PCM. Appl. Therm. Eng. 2024, 236, 121917. [Google Scholar] [CrossRef]
- Li, P.; Zhao, J.; Zhou, S.; Duan, J.; Li, X.; Zhang, H.; Yuan, J. Design and Optimization of a Liquid Cooling Thermal Management System with Flow Distributors and Spiral Channel Cooling Plates for Lithium-Ion Batteries. Energies 2023, 16, 2196. [Google Scholar] [CrossRef]
- Khoshvaght-Aliabadi, M.; Ghodrati, P.; Kang, Y.T. Performance analysis of supercritical carbon dioxide as a coolant in cold plate systems. Energy 2025, 314, 134301. [Google Scholar] [CrossRef]
- Ansys, I. Ansys Fluent, 2025 R1; Ansys, Inc.: Canonsburg, PA, USA, 2025. [Google Scholar]
- Ma, G.; Tian, L.; Song, Y.; Zhao, N. Effects of Turbulence Modeling on the Simulation of Wind Flow over Typical Complex Terrains. Appl. Sci. 2024, 14, 11438. [Google Scholar] [CrossRef]
- Shaheed, R.; Mohammadian, A.; Shaheed, A.M. Numerical Simulation of Turbulent Flow in River Bends and Confluences Using the k-ω SST Turbulence Model and Comparison with Standard and Realizable k-ε Models. Hydrology 2025, 12, 145. [Google Scholar] [CrossRef]
- Hailu, G.; Henke, M.; Petersen, T. Stationary Battery Thermal Management: Analysis of Active Cooling Designs. Batteries 2022, 8, 23. [Google Scholar] [CrossRef]
- Gu, W.B.; Wang, C.Y. Thermal-Electrochemical Modeling of Battery Systems. J. Electrochem. Soc. 2000, 147, 2910. [Google Scholar] [CrossRef]
- Li, H.; Li, L.; Li, Q.; Tang, Z.; Zhang, Z.; Chen, R. Coupling characteristics and simplification analysis method of laminated cooling configuration between external and internal cooling. Int. J. Therm. Sci. 2023, 187, 108159. [Google Scholar] [CrossRef]
- Fan, L.; Li, J.; Chen, Y.; Zhou, D.; Jiang, Z.; Sun, J. Study on the cooling performance of a new secondary flow serpentine liquid cooling plate used for lithium battery thermal management. Int. J. Heat Mass Transf. 2024, 218, 124711. [Google Scholar] [CrossRef]
- Yu, Z.-Q.; Li, M.-T.; Cao, B.-Y. A comprehensive review on microchannel heat sinks for electronics cooling. Int. J. Extrem. Manuf. 2024, 6, 022005. [Google Scholar] [CrossRef]
- Yang, H.; Wang, Z.; Li, M.; Ren, F.; Ma, B. Numerical Study on Cross-Linked Cold Plate Design for Thermal Management of High-Power Lithium-Ion Battery. Batteries 2023, 9, 220. [Google Scholar] [CrossRef]
- Mubashir, M.; Xu, J.; Guo, Z.; Wang, X.; Wang, H.; Qiao, F.; Li, E.; Mei, X. Numerical investigation of a novel cold plate design with uniform circular hollow fins for battery thermal management systems. Appl. Therm. Eng. 2024, 237, 121791. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, Y.; Hou, L.; Hu, J.; Shang, Y. In-situ analysis and estimation of temperature distribution for large-format lithium-ion batteries based on distributed optical fiber sensors. eTransportation 2025, 100425, in press. [Google Scholar] [CrossRef]
- Wang, H.; Gan, Y.; Luo, Q.; Li, Y.; Feng, J. A study on the effect of channel structures on flow and heat transfer performance of cold plate with double-layer serpentine microchannel. Appl. Therm. Eng. 2025, 259, 124944. [Google Scholar] [CrossRef]
- Albana, M.H.; Batubara, N.H.; Novebriantika, N.; Silalahi, M.T.; Yogantara, Y.; Guntur, H.L. Dataset supporting the article: Investigation of Flow Channel Configurations in Liquid-Cooled Plates for Electric Vehicle Battery Thermal Management. Zenodo 2025. [Google Scholar] [CrossRef]
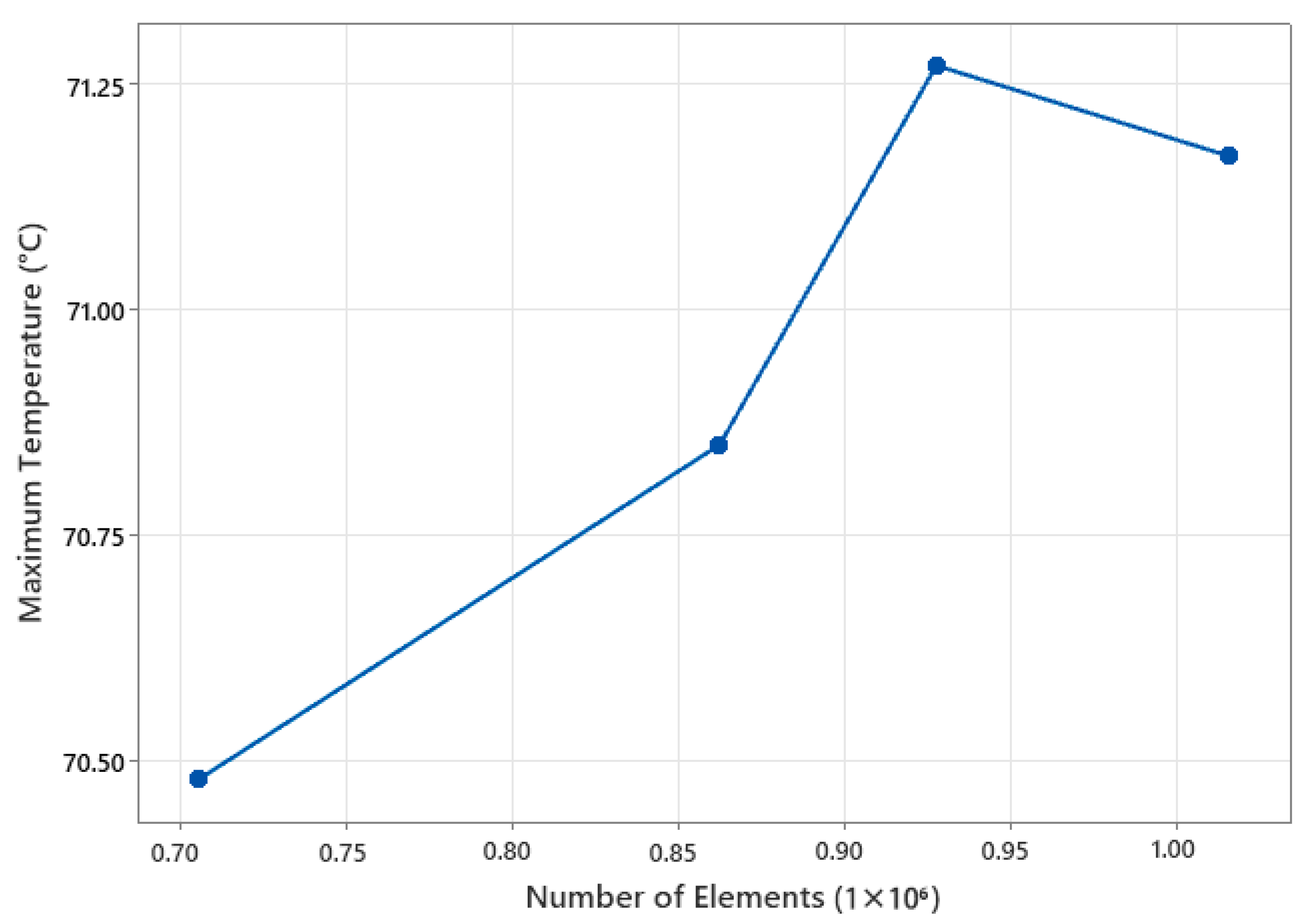





| Mesh No. | Elements | Maximum Temperature (°C) | Pressure Drop (Pa) |
|---|---|---|---|
| 1. | 705,891 | 70.48 | 13,125.42 |
| 2. | 862,639 | 70.85 | 13,125.15 |
| 3. | 927,875 | 71.27 | 12,658.75 |
| 4. | 1,015,787 | 71.17 | 12,801.71 |
| Component | Material | |||
|---|---|---|---|---|
| Plate | Aluminum | 2179 | 871 | 202.4 |
| Tube | Copper | 8978 | 381 | 387.6 |
| Coolant | Water | 998.2 | 4182 | 0.6 |
| Cold Plate Configuration | Maximum Temperature (°C) at 20,000 W/m2 | Maximum Temperature (°C) at 40,000 W/m2 | Ascension (%) |
|---|---|---|---|
| CP#1 | 43 | 62 | 30.65 |
| CP#2 | 47 | 69 | 31.88 |
| CP#3 | 66 | 106 | 37.74 |
| CP#4 | 42 | 60 | 30 |
| CP#5 | 46 | 66 | 30.3 |
| CP#6 | 63 | 100 | 37 |
| Heat Flux (W/m2) | CP#1 Temperature Uniformity Values |
|---|---|
| 20,000 | 10.9% lower than CP#4 |
| 30,000 | 5.2% lower than CP#4 |
| 40,000 | 3.2% lower than CP#4 |
| Design Priorities | Recommended Geometry | Recommended Cross-Section | Advantage | Drawback |
|---|---|---|---|---|
| Maximum Cooling | Serpentine (8 U-turns) | Square | Lowest Thermal Resistance | High Pressure Drop |
| Temperature Uniformity | Serpentine (8 U-turns) | Circular | Highest TUI | Moderate Cooling Performance and Pressure Drop |
| Hydraulic Efficiency | Serpentine (6 U-turns) | Circular | Lowest Pressure Drop | Less Effective Cooling Performance |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albana, M.H.; Batubara, N.H.; Novebriantika, N.; Silalahi, M.T.; Yogantara, Y.; Guntur, H.L. Investigation of Flow Channel Configurations in Liquid-Cooled Plates for Electric Vehicle Battery Thermal Management. World Electr. Veh. J. 2025, 16, 536. https://doi.org/10.3390/wevj16090536
Albana MH, Batubara NH, Novebriantika N, Silalahi MT, Yogantara Y, Guntur HL. Investigation of Flow Channel Configurations in Liquid-Cooled Plates for Electric Vehicle Battery Thermal Management. World Electric Vehicle Journal. 2025; 16(9):536. https://doi.org/10.3390/wevj16090536
Chicago/Turabian StyleAlbana, Muhammad Hasan, Ninda Hardina Batubara, Novebriantika Novebriantika, Meschac Timothee Silalahi, Yogantara Yogantara, and Harus Laksana Guntur. 2025. "Investigation of Flow Channel Configurations in Liquid-Cooled Plates for Electric Vehicle Battery Thermal Management" World Electric Vehicle Journal 16, no. 9: 536. https://doi.org/10.3390/wevj16090536
APA StyleAlbana, M. H., Batubara, N. H., Novebriantika, N., Silalahi, M. T., Yogantara, Y., & Guntur, H. L. (2025). Investigation of Flow Channel Configurations in Liquid-Cooled Plates for Electric Vehicle Battery Thermal Management. World Electric Vehicle Journal, 16(9), 536. https://doi.org/10.3390/wevj16090536






