A Resilience Entropy-Based Framework for V2G Charging Station Siting and Resilient Reconfiguration of Power Distribution Networks Under Disasters

Abstract

In the post-disaster recovery of power distribution networks (PDNs), electric vehicles (EVs) possess a great potential as mobile energy storage units. When supported by vehicle-to-grid (V2G)-enabled charging stations, EVs can provide effective supplementary power for disaster-stricken areas. However, most existing stations only support unidirectional charging, limiting the resilience-enhancing potential of V2G. To address this gap, this paper proposes a resilience-oriented restoration optimization model that jointly considers the siting of V2G-enabled charging stations and PDN topology reconfiguration. A novel metric—Resilience Entropy—is introduced to dynamically characterize the recovery process. The model explicitly describes fault propagation and circuit breaker operations, while incorporating power flow and radial topology constraints to ensure secure operation. EV behavioral uncertainty is also considered to enhance model adaptability under real-world post-disaster conditions. The optimal siting scheme is obtained by solving the proposed model. Case studies demonstrate the model’s effectiveness in improving post-disaster supply and recovery efficiency, and analyze the impact of user participation willingness on V2G-based restoration.

1. Introduction

In recent years, the increasing frequency of extreme weather events and natural disasters has posed severe challenges to the secure and stable operation of power distribution networks (PDNs) [1,2,3]. These events often lead to large-scale power outages, with devastating impacts on critical infrastructure and public services. For instance, in April 2025, a massive blackout in Spain and Portugal left approximately 50 million people without electricity, severely disrupting transportation, healthcare, and communication systems. Therefore, enhancing the resilience of PDNs and enabling rapid power restoration in the aftermath of disasters has become a vital focus of modern distribution system research.

By 2030, the global number of electric vehicles (EVs) is projected to reach 120 million [4]. Vehicle-to-Grid (V2G) technology has demonstrated great potential in improving electricity demand management, mitigating load fluctuations, and enhancing the sustainability of smart grids [5]. Consequently, leveraging EVs and V2G technology to enable rapid post-disaster power recovery and support critical loads has become a crucial research direction for enhancing PDN resilience.

With the increasing frequency of extreme weather events such as typhoons, earthquakes, and floods, the concept of “resilience” has been introduced into the operation of PDNs. PDN resilience refers to the ability of the system to anticipate the development of extreme events, prepare resources in advance, adjust topology and operation strategies, mitigate the impacts of disasters, and recover services rapidly [6,7]. In China, the physical infrastructure of the power distribution network—including power lines, transformers, and various types of switches—is owned by the power supply bureau, which is also responsible for their operation and maintenance, as well as post-disaster service restoration. Restoring power after disasters is considered both a legal obligation and an important performance metric for the power supply bureau. The electricity supply to all types of charging stations is guaranteed by the power supply bureau; however, the ownership and daily operation of these charging stations typically belong to third-party operators. Some of these third-party companies generally have agreements with the power supply bureau to coordinate and support power supply as needed during emergency or resilience-oriented operations. This enables V2G resources to contribute to disaster recovery, even without direct utility ownership.

According to [8], the resilience process of a PDN can generally be divided into four stages: pre-event, degradation, fault isolation, and service restoration. The pre-event stage mainly includes resource allocation and network topology optimization [9,10]. The degradation and fault isolation stages are relatively short and are combined in this paper as a single phase. This phase refers to the period immediately after the disaster, when the power utility has not yet started fault repairs [11,12], and is the main focus of this study. The service restoration stage refers to the gradual repair of faults and recovery of supply by the utility company [13]. In Ref. [14], mainstream resilience evaluation methods primarily use load loss as the assessment metric, typically based on the assumption that load conditions remain constant within each phase. However, such static assessments overlook the dynamic evolution of resilience over time and fail to fully capture the variations in power supply performance during different stages. In resilience assessment, it is often necessary to jointly consider the reliability of infrastructure systems. For example, the recent review [15] provides a comprehensive overview of applying graph neural networks (GNNs) to the reliability and resilience evaluation of critical infrastructure systems, highlighting their capability to capture potential cascading effects. Current mainstream resilience evaluation methods primarily use load loss as the assessment metric, typically based on the assumption that load conditions remain constant within each phase. However, such static assessments overlook the dynamic evolution of resilience over time and fail to fully capture the variations in power supply performance during different stages. Recent studies have explored multi-resource coordination to enhance PDN resilience. For instance, Ref. [16] considers the integration of renewable energy, energy storage, and V2G within a two-stage stochastic programming framework, but it does not address the siting problem of V2G charging stations. Similarly, another work [17] formulates a two-stage stochastic MILP model that coordinates investments in line hardening, distributed generation, mobile emergency generators, and switching devices, while explicitly accounting for uncertainties in wind fields, line damage, and load fluctuations, thereby reducing post-event recovery costs and improving resilience. Compared with these approaches, our study explicitly incorporates the siting and sizing of V2G charging stations into the resilience enhancement framework, and further quantifies resilience through the proposed Resilience Entropy metric, offering a new perspective on the spatial-temporal allocation of V2G resources.

With the growing number of EVs, their potential as mobile energy storage resources has attracted increasing attention. In particular, supported by charging infrastructure with V2G capabilities, EVs can serve as controllable backup power sources during post-disaster periods, supplying electricity to local areas or critical loads [18]. Recent studies and real-world cases also provide evidence of EV owners’ willingness to participate in V2G during disaster conditions. For instance, researchers at the Australian National University (ANU) demonstrated in a February 2024 outage event that 16 EVs supplied a total of 107 kW of reverse power to the grid via V2G, successfully sustaining critical loads for several hours [19]. Survey-based evidence further indicates strong user acceptance: one study reports that 78% of EV owners are willing to participate in V2G during disasters, with response rates exceeding 90% when incentives are set at or above 0.5/kWh [20]. In addition, Ref. [21] investigated the role of existing charging stations in post-disaster support, showing that, with large-scale user participation, V2G can achieve superior restoration performance compared to mobile energy storage systems (MESs). These findings collectively suggest that EV-based resilience services are both technically feasible and socially acceptable, thereby supporting the practical applicability of V2G-enabled charging stations in disaster recovery. However, due to technical and cost limitations, most existing charging stations are still unidirectional and have not been planned with post-disaster support in mind. As a result, the full potential of V2G reverse power supply has not been realized.

In recent years, various studies have focused on charging station siting and construction. Ref. [22] has addressed EV charging station siting by incorporating multiple spatial, environmental, and technical criteria—such as land use, traffic flow, renewable resources, and grid accessibility—through a GIS-based multi-criteria decision-making framework. Ref. [23] considered uncertainties in EV inflow, charging port availability, and queueing time when addressing the Charging Station Siting and Sizing Problem (CSSSP), with the objective of minimizing unsatisfied charging demand. Some research built PV–storage–charging systems and aimed to maximize EV owner profits when planning charging station locations [24]. Others focused on the dynamic matching of photovoltaic generation and charging demand, balancing economic performance and energy efficiency in station deployment [25]. The mismatch between supply and demand of shared EV (SEV) charging infrastructure has also been studied [26]. Moreover, human behavioral factors are often considered in planning, such as arrival/departure times, trip purposes, parking duration, walking distance, and willingness to participate in V2G [27,28]. Some works addressed grid and traffic constraints to minimize total cost in station siting [29], while others adopted bilevel optimization to improve power system flexibility by determining optimal locations and sizes of charging stations [30]. In terms of charging efficiency, some studies aimed to reduce user waiting time during siting decisions [31], while others built PV–storage–charging regulation networks to minimize power losses in distribution systems [32].

However, these studies generally overlook the potential of V2G-enabled stations to support post-disaster power restoration. The lack of modeling for V2G reverse supply functions limits the role of EVs in enhancing the resilience of distribution networks.

To address the aforementioned research gap, this paper proposes a resilience enhancement optimization model for disaster scenarios. A unified framework is established to jointly optimize the siting of V2G charging stations and the reconfiguration of PDN topology via tie-lines. Moreover, a novel metric called “Resilience Entropy” is introduced to dynamically quantify the recovery process from both temporal and spatial perspectives, capturing the evolution of supply satisfaction at each node. To handle the inherent uncertainty of disaster events, the proposed framework adopts a Monte Carlo-based scenario generation method, where probabilistic line failure rates are used to simulate multiple outage scenarios.

On this basis, a multi-objective optimization model is formulated, jointly considering V2G charging stations siting, circuit breaker (CB) operations, and network reconfiguration. To enhance the adaptability of the model under uncertain disaster scenarios, a probabilistic approach is adopted to describe the spatiotemporal uncertainty of electric vehicle behavior, thereby improving the model’s applicability and effectiveness in real-world conditions. The main contributions of this paper are as follows:

1.

A novel resilience metric—Resilience Entropy—is proposed. This metric is constructed based on the power supply satisfaction degree S of each node over time, incorporating a time-weighted factor to dynamically reflect the characteristics of the restoration process. Compared to traditional static resilience metrics centered on load loss, Resilience Entropy enables a more comprehensive and dynamic evaluation of restoration strategies.

2.

A resilience-oriented optimization model is developed for power distribution network (PDN) recovery under disaster scenarios, jointly considering the siting of V2G charging stations and the reconfiguration of PDN topology. Guided by the proposed Resilience Entropy, the model explicitly describes fault propagation and isolation mechanisms, while incorporating the spatiotemporal uncertainty of EV behaviors and post-disaster operational constraints. This supports coordinated energy supply and resilience enhancement.

3.

The effectiveness and policy sensitivity of the proposed model are validated through numerical simulations. The case studies demonstrate the model’s ability to improve post-disaster power supply capacity and recovery efficiency. Furthermore, the influence of varying EV owner participation willingness in V2G activities on charging station siting and support capabilities is analyzed, offering practical insights for policy formulation.

2. Location and Operation Model of V2G Charging Stations

In our study, the considered disasters mainly refer to extreme weather events in Southern China that have historically caused widespread distribution network outages, such as typhoons, heavy rainfall and flooding, and secondary disasters like landslides. While conventional approaches such as network hardening (e.g., power lines reinforcement, pole replacement) and the deployment of mobile energy storage (MES) or diesel generators are widely adopted, they often involve high investment costs and limited flexibility. In contrast, V2G-enabled charging stations provide a complementary solution, leveraging existing EV resources to supply critical loads with rapid and distributed support during the restoration phase.

Modern V2G-enabled chargers allow real-time power adjustment. If the total V2G discharge from EVs temporarily exceeds the power system’s demand, the surplus can either be curtailed by reducing the discharge output or redirected to charge other EVs that require energy. Conversely, if the available power is insufficient, the control strategy prioritizes supply to critical loads. This mechanism provides operational flexibility to balance varying EV contributions against actual resilience demand.

2.1. Investment Cost and Installation Limit Constraints of V2G Stations

To enhance the energy support capability of the PDN during post-disaster restoration, this study considers the deployment of V2G-enabled charging stations at critical nodes. A binary decision variable $a_i^{\mathrm{V}2\mathrm{G}}$ is introduced to indicate whether a V2G station is installed at node i, where $a_i^{\mathrm{V}2\mathrm{G}}=1$ denotes the presence of a V2G facility, and $a_i^{\mathrm{V}2\mathrm{G}}=0$ otherwise.

In our study, the investment cost of constructing V2G-enabled charging stations is generally assumed to be borne by third-party charging service companies, which are responsible for infrastructure deployment and daily operation. Meanwhile, the compensation for EV owners participating in V2G services—particularly during disaster recovery—is typically provided by the power supply bureau, as it is responsible for ensuring post-disaster power restoration.

The investment cost of a V2G charging station primarily depends on its supported maximum reverse power output. Accordingly, the cost model is formulated as follows in Equation (1):

$$C_{\mathrm{INV}}={\alpha }^{\mathrm{V}2\mathrm{G}}·\sum _{i\in N}{P}_{i,\max }^{\mathrm{V}2\mathrm{G}}{a}_i^{\mathrm{V}2\mathrm{G}}$$

(1)

where ${\alpha }^{\mathrm{V}2\mathrm{G}}$ represents the unit investment cost coefficient, and $P_{i,\max }^{\mathrm{V}2\mathrm{G}}$ denotes the maximum reverse discharge power that the V2G station at node i can support.

Considering the high cost of V2G infrastructure, and in order to keep the investment within budgetary constraints while ensuring feasibility, the total number of newly installed V2G stations is limited by the following constraint (2):

$$\sum _{i\in N}{a}_i^{\mathrm{V}2\mathrm{G}}\le N_{\mathrm{V}2\mathrm{G}}^{max}$$

(2)

where $N_{\mathrm{V}2\mathrm{G}}^{max}$ indicates the maximum allowable number of V2G station installations. This constraint ensures that the V2G facilities are deployed only at strategically selected nodes, thus balancing system resilience enhancement with economic investment control.

2.2. Operational Constraints of V2G Charging Stations

During real-time scheduling, the operating status of V2G charging stations may vary across time periods and tasks. Some stations may be in discharge mode to support grid recovery, while others may be charging EVs. Since each charging connector can only operate in either charging or discharging mode at any given time, the actual charging and discharging power at node i must be constrained by the maximum capacity of the station, as expressed below:

$$0\le P_{i,t}^{\mathrm{EV},\mathrm{ch}}\le P_{i,\max }^{\mathrm{V}2\mathrm{G}}$$

(3)

$$0\le P_{i,t}^{\mathrm{EV},\mathrm{dis}}\le P_{i,\max }^{\mathrm{V}2\mathrm{G}}$$

(4)

where $P_{i,t}^{\mathrm{EV},\mathrm{ch}}$ and $P_{i,t}^{\mathrm{EV},\mathrm{dis}}$ denote the total charging and discharging power at node i at time t, respectively. Equations (3) and (4) define the upper bounds for the charging power $P_{i,t}^{\mathrm{EV},\mathrm{ch}}$ and discharging power $P_{i,t}^{\mathrm{EV},\mathrm{dis}}$ at node i and time t, both constrained by the station’s capacity $P_{i,\max }^{\mathrm{V}2\mathrm{G}}$. While each charging port has mutually exclusive operating modes, the station-level power can be flexibly scheduled to dynamically respond to grid demands.

In practice, the charging/discharging capability is also constrained by the number of connected EVs and their individual power capacities. To reflect this, we define the feasible power range as follows:

The maximum charging power at node i and time t depends on the number of EVs in charging mode and their rated power:

$$0\le P_{i,t}^{\mathrm{EV},\mathrm{ch}}\le \sum _{j=1}^{N_{i,t}^{\mathrm{ch}}}{p}_j^{\mathrm{ch}}$$

(5)

where $N_{i,t}^{\mathrm{ch}}$ denotes the number of EVs charging at time t, and $p_j^{\mathrm{ch}}$ is the rated charging power of vehicle j. Since power flow constraints must be satisfied and V2G systems can monitor and dispatch each EV individually, a batch charging strategy is employed when total demand exceeds grid capacity. Hence, the inequality form is adopted.

Similarly, the maximum discharging power is subject to both the station’s technical limit and the total capability of discharging EVs:

$$P_{i,t}^{\mathrm{EV},\mathrm{dis}}=min\left\{P_i^{\mathrm{V}2\mathrm{G},\max },\sum _{j=1}^{N_{i,t}^{\mathrm{dis}}}{p}_j^{\mathrm{dis}}\right\}$$

(6)

For linear optimization purposes, this constraint is relaxed as:

$$0\le P_{i,t}^{\mathrm{EV},\mathrm{dis}}\le \sum _{j=1}^{N_{i,t}^{\mathrm{dis}}}{p}_j^{\mathrm{dis}}$$

(7)

where $N_{i,t}^{\mathrm{dis}}$ is the number of EVs discharging at time t, $p_j^{\mathrm{dis}}$ denotes the discharging power of vehicle j, and $P_i^{\mathrm{V}2\mathrm{G},\max }$ is the station’s maximum discharge capacity.

This modeling approach enables a more accurate representation of EV group flexibility during disaster recovery and highlights their auxiliary role in supporting the resilience of the distribution network.

2.3. Behavioral Modeling of Electric Vehicles

During post-disaster restoration, the number of EVs at each node varies dynamically over time. To capture this behavior, we model three key aspects of EV dynamics at each node and time step: arrival, participation in V2G services, and departure behavior.

Let $A_{i,t}^{\mathrm{EV}}$ denote the number of EVs arriving at node i at time t, which follows a truncated normal distribution (restricted to non-negative integers):

$$A_{i,t}^{\mathrm{EV}}\sim max\left(0,⌊\mathcal{N}({\mu }_i^{\mathrm{in}},{\sigma }_i^{\mathrm{in}})⌉\right)$$

(8)

where ${\mu }_i^{\mathrm{in}}$ and ${\sigma }_i^{\mathrm{in}}$ are the mean and standard deviation of EV arrivals at node i, respectively.

Among the arriving vehicles, a fraction $\beta \in [0,1]$ is assumed to participate in V2G services. The number of new V2G participants $A_{i,t}^{\mathrm{V}2\mathrm{G}}$ is given by

$$A_{i,t}^{\mathrm{V}2\mathrm{G}}=⌊\beta ·A_{i,t}^{\mathrm{EV}}⌉$$

(9)

The remaining vehicles, which only perform charging $A_{i,t}^{\mathrm{ch}}$, are

$$A_{i,t}^{\mathrm{ch}}=A_{i,t}^{\mathrm{EV}}-A_{i,t}^{\mathrm{V}2\mathrm{G}}$$

(10)

The temporal evolution of V2G-participating vehicles is modeled as

$$N_{i,t+1}^{\mathrm{dis}}=N_{i,t}^{\mathrm{dis}}+A_{i,t}^{\mathrm{V}2\mathrm{G}}-D_{i,t}^{\mathrm{V}2\mathrm{G}}$$

(11)

where $N_{i,t}^{\mathrm{dis}}$ represents the number of V2G vehicles at node i and time t, and $D_{i,t}^{\mathrm{V}2\mathrm{G}}$ is the number of vehicles departing from V2G participation.

Considering the dependency of vehicle departure behavior on state of charge (SOC), we define the average SOC of V2G vehicles at node i and time t as ${\mu }_{i,t}^{\mathrm{SOC}}\in [0,1]$. The probability of departure is then

$${\rho }_{i,t}^{\mathrm{out}}={\rho }_0-\gamma ·{\mu }_{i,t}^{\mathrm{SOC}}$$

(12)

here, ${\rho }_0$ is the base departure probability and $\gamma$ is a sensitivity coefficient indicating that lower SOC increases the likelihood of departure.

Accordingly, the number of departing V2G vehicles $D_{i,t}^{\mathrm{V}2\mathrm{G}}$ follows a binomial distribution:

$$D_{i,t}^{\mathrm{V}2\mathrm{G}}\sim \mathrm{Binomial}(x_{i,t}^{\mathrm{V}2\mathrm{G}},{\rho }_{i,t}^{\mathrm{out}})$$

(13)

For non-V2G charging vehicles, the departure behavior is also modeled using a truncated normal distribution:

$$D_{i,t}^{\mathrm{ch}}\sim max\left(0,⌊\mathcal{N}({\mu }_i^{\mathrm{out}},{\sigma }_i^{\mathrm{out}})⌉\right)$$

(14)

where ${\mu }_i^{\mathrm{out}}$ and ${\sigma }_i^{\mathrm{out}}$ denote the expected value and standard deviation of departures for charging-only EVs at node i.

The population of charging-only EVs $N_{i,t+1}^{\mathrm{ch}}$ then evolves as

$$N_{i,t+1}^{\mathrm{ch}}=N_{i,t}^{\mathrm{ch}}+A_{i,t}^{\mathrm{ch}}-D_{i,t}^{\mathrm{ch}}$$

(15)

In summary, this modeling framework captures the dynamic EV behavior during disaster recovery by integrating stochastic arrival patterns, V2G participation rates, and SOC-dependent departure dynamics. It provides a reliable foundation for subsequent scheduling and optimization tasks.

2.4. Assumptions on Public EV Charging Post-Disaster

During post-disaster restoration, the number of EVs at each node varies dynamically over time. To capture this behavior, we model stochastic arrival patterns, V2G participation rates, and SOC-dependent departure dynamics, which provide a reliable foundation for subsequent scheduling and optimization tasks.

It is worth noting that, under normal operating conditions, public fast-charging stations are typically used for short-duration, in-transit charging, whereas residential or workplace charging points allow longer connection times that are more suitable for V2G. However, in the disaster recovery context considered in this paper, the behavioral modeling departs from conventional daily commuting assumptions. Instead, EVs already present at or mobilized to designated charging stations may intentionally remain to provide resilience services. Through utility-operator coordination platforms (e.g., the “One-Grid Service” of Hainan Province affiliated with China Southern Power Grid), charging operators can monitor real-time usage and remotely dispatch V2G-enabled chargers to supply critical loads, thereby temporarily transforming some public charging sites into resilience hubs.

In this framework, we do not assume that random in-transit EV drivers will immediately participate, but rather that available EVs are aggregated and dispatched as part of the resilience strategy. While stationary energy storage devices also represent a valuable resilience option, EVs provide a widely distributed, mobile, and flexible resource that can be leveraged immediately after disasters.

3. Distribution Network Operation and Disaster Impact Modeling

In the operation of a PDN, a series of operational constraints must be satisfied. In this paper, we assume that the V2G system only participates in active power regulation and does not provide reactive power support, while reactive power support is ensured by conventional devices already existing in the distribution system, such as capacitor banks and on-load tap changers. Specifically, the discharging behavior of EVs is modeled as a type of distributed generation and incorporated into the active power balance equation, while EV charging loads are treated as part of the nodal total demand.

3.1. Power Balance Constraints

Equations (16) and (17) represents the nodal active/reactive power balance constraint, respectively:

$$P_{j,t,c}^L-P_{j,t,c}^{DG}-P_{j,t,c}^{Sub}=a_j^{\mathrm{V}2\mathrm{G}}·P_{j,t,c}^{\mathrm{EV},\mathrm{dis}}+\sum _{i\in \pi \left(j\right)}{P}_{ij,t,c}-\sum _{s\in \delta \left(j\right)}{P}_{js,t,c},\forall j\in N,t\in T,c\in C$$

(16)

$$Q_{j,t,c}^L-Q_{j,t,c}^{DG}-Q_{j,t,c}^{Sub}=\sum _{i\in \pi \left(j\right)}{Q}_{ij,t,c}-\sum _{s\in \delta \left(j\right)}{Q}_{js,t,c},\forall j\in N,t\in T,c\in C$$

(17)

where P and Q denote active power and reactive power, respectively; $P_{j,t,c}^L$ represents the total load power at node j at time t under scenario c; $P_{j,t,c}^{DG}$ and $Q_{j,t,c}^{DG}$ denote the active and reactive power outputs of distributed generation at node j in the given time and scenario; $P_{j,t,c}^{Sub}$ and $Q_{j,t,c}^{Sub}$ represent the active and reactive power supplied by the substation to node j; $P_{j,t}^{\mathrm{EV},\mathrm{dis}}$ is the active power discharged by electric vehicles at node j; $P_{ij,t,c}$ and $Q_{ij,t,c}$ are the active and reactive power flows on the line from node i to node j; $\pi \left(j\right)$ and $\delta \left(j\right)$ represent the sets of upstream and downstream nodes of node j, respectively.

Equation (18) defines the total demand $P_{j,t,c}^{\mathrm{demand}}$ at each node as the sum of conventional load $P_{j,t,c}^{\mathrm{normal}}$ and EV charging load.

$$P_{j,t,c}^{\mathrm{demand}}=P_{j,t,c}^{\mathrm{normal}}+a_j^{\mathrm{V}2\mathrm{G}}·\sum _{j=1}^{N_{i,t}^{\mathrm{ch}}}{p}_j^{\mathrm{ch}},\forall j\in N,t\in T,c\in C$$

(18)

here, the indicator $a_j^{\mathrm{V}2\mathrm{G}}$ identifies whether a V2G station is installed at node j; otherwise, its charging/discharging power is zero. In the power balance equations, $P_{j,t,c}^L$ denotes the actual power delivered by the grid, constrained to be no more than the total demand $P_{j,t}^{\mathrm{demand}}$.

3.2. Nodal Voltage Constraints

To ensure system-wide voltage stability and power quality, nodal voltage magnitudes must be maintained within acceptable operational ranges. Accordingly, the voltage at each node is constrained as follow:

$$0.95U_R\le U_{j,t,c}\le 1.05U_R,\forall j\in N,t\in T,c\in C$$

(19)

Equation (19) enforces that the nodal voltage magnitude remains within $\pm 5\%$ of the nominal voltage $U_R$, thereby guaranteeing voltage stability across all nodes under various time periods and contingency scenarios.

Furthermore, the voltage difference between adjacent nodes is governed by the power flow and line impedance. To capture this, the following pair of constraints are introduced to model the voltage drop across distribution lines:

$$U_{i,t,c}-U_{j,t,c}-{\displaystyle \frac{r_{ij}{P}_{ij,t,c}+x_{ij}{Q}_{ij,t,c}}{U_R}}\le M(1-z_{ij,t,c}),\forall (i,j)\in E,t\in T,c\in C$$

(20)

$$U_{i,t,c}-U_{j,t,c}-{\displaystyle \frac{r_{ij}{P}_{ij,t,c}+x_{ij}{Q}_{ij,t,c}}{U_R}}\ge -M(1-z_{ij,t,c}),\forall (i,j)\in E,t\in T,c\in C$$

(21)

Equations (20) and (21) jointly define the permissible voltage drop between node pairs connected by distribution lines. The term ${\displaystyle \frac{r_{ij}{P}_{ij,t,c}+x_{ij}{Q}_{ij,t,c}}{U_R}}$ reflects the voltage deviation caused by active and reactive power flow over a line with resistance $r_{ij}$ and reactance $x_{ij}$. The binary variable $z_{ij,t,c}$ indicates the operational status of the line: when $z_{ij,t,c}=1$, line-$ij$ is connected and the constraint is enforced; otherwise, it is relaxed through the big-M method to deactivate the voltage drop expression when the line is out of service due to damage or disconnection, and M should be sufficiently large to ensure constraint feasibility.

3.3. Power Flow Limit Constraints

The power flow in transmission lines must respect thermal limits to ensure secure operation. Accordingly, we introduce constraints on active power, reactive power, and apparent power flow as follows:

$$-S_{ij}^{max}{z}_{ij,t,c}\le P_{ij,t,c}\le S_{ij}^{max}{z}_{ij,t,c},\forall (i,j)\in E,t\in T,c\in C$$

(22)

$$-S_{ij}^{max}{z}_{ij,t,c}\le Q_{ij,t,c}\le S_{ij}^{max}{z}_{ij,t,c},\forall (i,j)\in E,t\in T,c\in C$$

(23)

$$-\sqrt{2}{S}_{ij}^{max}{z}_{ij,t,c}\le P_{ij,t,c}\pm Q_{ij,t,c}\le \sqrt{2}{S}_{ij}^{max}{z}_{ij,t,c},\forall (i,j)\in E,t\in T,c\in C$$

(24)

where $S_{ij}^{max}$ denotes the maximum apparent power capacity of line-$ij$. Equations (22)–(24) represent the active, reactive, and apparent power flow constraints, respectively. These constraints ensure that line flows do not exceed the thermal capacity and incorporate the line availability status through the binary variable $z_{ij,t,c}$.

3.4. Constraints for DG and Substations

In post-disaster scenarios, the power output of Distributed Generators (DGs) and substations (Subs) is affected by the operational state of their corresponding nodes. Specifically, if a node is in failure status, its associated DG or Sub is not permitted to generate power. The constraint is given as Equations (25) and (26):

$$\begin{array}{c}\hfill (1-n_{j,t,c})P_{j,min}^{\mathrm{DG}/\mathrm{Sub}}\le P_{j,t,c,\mathrm{PoD}}^{\mathrm{DG}/\mathrm{Sub}}\le (1-n_{j,t,c})P_{j,max}^{\mathrm{DG}/\mathrm{Sub}},\forall j\in {\Omega }_{\mathrm{DG}/\mathrm{Sub}},\forall t\in T,\forall c\in C\end{array}$$

(25)

$$\begin{array}{c}\hfill (1-n_{j,t,c})Q_{j,min}^{\mathrm{DG}/\mathrm{Sub}}\le Q_{j,t,c,\mathrm{PoD}}^{\mathrm{DG}/\mathrm{Sub}}\le (1-n_{j,t,c})Q_{j,max}^{\mathrm{DG}/\mathrm{Sub}},\forall j\in {\Omega }_{\mathrm{DG}/\mathrm{Sub}},\forall t\in T,\forall c\in C\end{array}$$

(26)

here, the parameter $n_{j,t,c}$ represents the fault status of node j at time t under scenario c, where $n_{j,t,c}=1$ indicates a fault at node j and $n_{j,t,c}=0$ indicates normal operation. The terms $P_{j,min}^{\mathrm{DG}/\mathrm{Sub}}$ and $P_{j,max}^{\mathrm{DG}/\mathrm{Sub}}$ denote the lower and upper bounds of the active power output for the DG or substation located at node j, respectively, while $Q_{j,min}^{\mathrm{DG}/\mathrm{Sub}}$ and $Q_{j,max}^{\mathrm{DG}/\mathrm{Sub}}$ correspond to the respective limits for reactive power. The variables $P_{j,t,c,\mathrm{PoD}}^{\mathrm{DG}/\mathrm{Sub}}$ and $Q_{j,t,c,\mathrm{PoD}}^{\mathrm{DG}/\mathrm{Sub}}$ describe the actual active and reactive power injections at time t under scenario c. These constraints ensure that DGs and substations can only operate when their corresponding nodes status remain functional.

3.5. Fault Propagation Model

When disasters occur, faults can propagate through distribution lines and cause cascading failures across the network. To suppress fault spread and enhance system resilience, it is crucial to construct a model that accurately captures both line disconnections and node fault states under various scenarios. This subsection presents a fault propagation and isolation model considering the role of circuit breakers (CBs).

First, the line status under post-disaster conditions is constrained by both its fault status and breaker configuration:

$$(1-f_{ij,c})z_{ij,PD}\le z_{ij,c}\le (1-f_{ij,c})(z_{ij,PD}+b_{ij}),\forall ij\in E,\forall c\in C$$

(27)

Next, the propagation of faults from lines to connected nodes is described using the following constraints:

$$n_{i,t,c}\ge f_{ij,c}(1-a_{ij})+z_{ij,PD}-1,\forall ij\in E,\forall c\in C$$

(28)

$$n_{j,t,c}\ge f_{ij,c}(1-a_{ij})+z_{ij,PD}-1,\forall ij\in E,\forall c\in C$$

(29)

To ensure consistency between the fault state of nodes and their neighboring lines, we enforce the following coupling constraints:

$$n_{i,t,c}\ge n_{j,t,c}+z_{ij,c}-1,\forall ij\in E,\forall c\in C$$

(30)

$$n_{j,t,c}\ge n_{i,t,c}+z_{ij,c}-1,\forall ij\in E,\forall c\in C$$

(31)

here, $f_{ij,c}$ is a binary parameter indicating whether line $ij$ is damaged under scenario c, with 1 representing a fault and 0 otherwise; $z_{ij,PD}$ denotes the line’s status before the disaster; $b_{ij}$ is a binary parameter indicating whether line $ij$ is a tie-line with breaker capability; $a_{ij}$ indicates the presence of a circuit breaker on line $ij$; and $n_{i,t,c}$, $n_{j,t,c}$ represent the fault state of nodes i and j at time t and scenario c, respectively.

The role of circuit breakers in isolating faults is illustrated in Figure 1. When line-3 (L3) is damaged ($f_{3,c}=1$), and no breaker is present, the fault propagates along L2 and L1, resulting in all connected nodes (N1–N4) becoming faulty ($n_{j,t,c}=1,j=1,2,3,4$). In contrast, if L2 is equipped with a circuit breaker, it trips upon detecting fault current, isolating the fault. In this case, N1 and N2 remain operational ($n_{j,t,c}=0,j=1,2$), while N3 and N4 experience faults ($n_{j,t,c}=1,j=3,4$).

The operational rules under disaster scenarios can be summarized as follows:

• If line $ij$ is damaged, then constraint (27) enforces $z_{ij,c}=0$, i.e., forced line $ij$ disconnection;
• For lines that are neither tie lines ($b_{ij}=0$) nor equipped with breakers ($a_{ij}=0$), if they were in a connected state prior to the disaster ($z_{ij,\mathrm{PD}}=1$), then they are assumed to remain connected after the disaster ($z_{ij,c}=1$) during fault state determination;
• Tie lines ($b_{ij}=1$) may be flexibly switched ($z_{ij,c}\in \{0,1\}$) in response to system status, provided the radial topology is maintained;
• For lines without circuit breakers that were closed before the disaster ($z_{ij,PD}=1,a_{ij}=0$) and are damaged in scenario-c, both terminal nodes become faulty ($n_{i,t,c}=n_{j,t,c}=1$);
• For lines that were open pre-disaster ($z_{ij,PD}=0$), node fault status must be recursively determined based on neighboring line conditions, similar to breaker-protected lines.

3.6. Tie-Line Connection and Radiality Constraints

To ensure radial topology in distribution networks, special consideration must be given during the switching of tie-lines, as arbitrary connection of tie-lines may lead to closed loops, thereby violating the radiality constraint.

Radial structure is maintained by introducing directional flow variables $X_{ij,t,c}$ and $X_{ji,t,c}$, which are non-negative continuous variables representing the directional contribution of line $ij$ in scenario c and time period t [33]. These variables are constrained by the following equation:

$$X_{ij,t,c}+X_{ji,t,c}=z_{ij,c},\forall ij\in E,\forall c\in C,\forall t\in T$$

(32)

$$\sum _{i\in \pi \left(j\right)}{X}_{ij,t,c}+\sum _{s\in \delta \left(j\right)}{X}_{js,t,c}\le {\displaystyle \frac{\left|N\right|-\left|S\right|}{\left|N\right|-\left|S\right|+1}},\forall j\in N\setminus S,\forall t\in T$$

(33)

$$\sum _{j\in S}\left(\sum _{i\in \pi \left(j\right)}{X}_{ij,t,c}+\sum _{s\in \delta \left(j\right)}{X}_{js,t,c}\right)\le {\displaystyle \frac{\left|N\right|-\left|S\right|}{\left|N\right|-\left|S\right|+1}},\forall j\in S,\forall t\in T$$

(34)

where $z_{ij,c}$ is a binary variable indicating whether line $ij$ is closed; $\left|N\right|$ denotes the total number of nodes in the network, and $\left|S\right|$ represents the number of source nodes such as substations. The sets $\pi \left(j\right)$ and $\delta \left(j\right)$ denote the upstream and downstream neighboring nodes of node j, respectively. By incorporating these constraints, the network maintains radial connectivity post-disaster while avoiding the complexity of integer-based spanning tree formulations, thus enhancing computational efficiency.

4. Resilience Entropy Modeling

4.1. Power Supply Satisfaction

In post-disaster scenarios, the power supply satisfaction at each node serves as a significant indicator to assess the system’s recovery capability. It should be clarified that both $S_{i,t,c}$ and $P_{i,t,c}^{\mathrm{demand}}$ refer exclusively to active power. Active power is the component of electricity consumed by end-users to perform useful work (e.g., lighting, motors, and electronic devices), and thus directly reflects the effectiveness of post-disaster load restoration. In contrast, reactive power and voltage levels, though critical for network stability, are typically managed by voltage control equipment such as on-load tap changers, capacitors, or voltage source converters. Consequently, the proposed satisfaction metric focuses solely on active power restoration, which aligns with the primary objective of V2G-enabled EVs during the early recovery stage. In this paper, the supply satisfaction is defined as the ratio between the actual power supply received by node i and its power demand. It is formulated as follows (35):

$$S_{i,t,c}=(1-n_{i,t,c})·{\displaystyle \frac{P_{i,t,c}^L}{P_{i,t,c}^{\mathrm{demand}}}}\le 1$$

(35)

here, $S_{i,t,c}$ denotes the power supply satisfaction of node i at time t in scenario c; $P_{i,t,c}^L$ represents the supplied power received by node i from the grid, V2G discharge, and other sources, as mentioned in (16); $P_{i,t,c}^{\mathrm{demand}}$ is the power demand at the same time and scenario. When $S_{i,t,c}=1$, the load demand is fully met; if $S_{i,t,c}<1$, the node experiences an unmet demand; when the node is faulted ($n_{i,t,c}=1$), $S_{i,t,c}$ is enforced to zero.

Since the expression in (35) is nonlinear due to the variable in the denominator, we reformulate it into a linearized form using the following constraints:

$$\begin{array}{cccc}\hfill & P_{i,t,c}^L\le S_{i,t,c}·P_{i,t,c}^{\mathrm{demand}}\hfill & \hfill & \forall i\in \mathcal{N},t\in \mathcal{T},c\in \mathcal{C}\hfill \end{array}$$

(36)

$$\begin{array}{cccc}\hfill & S_{i,t,c}\le 1\hfill & \hfill & \forall i\in \mathcal{N},t\in \mathcal{T},c\in \mathcal{C}\hfill \end{array}$$

(37)

$$\begin{array}{cccc}\hfill & S_{i,t,c}\le 1-n_{i,t,c}\hfill & \hfill & \forall i\in \mathcal{N},t\in \mathcal{T},c\in \mathcal{C}\hfill \end{array}$$

(38)

These constraints ensure that the supplied power is bounded by demand and that supply satisfaction is automatically set to zero in case of a fault.

4.2. Entropy-Based Resilience Metric Using Recovery Probabilities

To evaluate the efficiency and balance of the recovery process, we introduce a resilience metric called “Resilience Entropy”, which quantifies the distribution of recovery across space and time. This entropy-based indicator helps identify whether recovery is concentrated and efficient. We first define the recovery probability for each node and time based on its supply satisfaction:

$$p_{i,t,c}={\displaystyle \frac{S_{i,t,c}}{{\sum }_{\tau \in \mathcal{T}}{\sum }_{j\in \mathcal{N}}{S}_{j,\tau ,c}+\epsilon }}$$

(39)

where $\mathcal{T}$ and $\mathcal{N}$ denote the set of time periods and nodes, respectively, and $\epsilon$ is a small positive number to avoid division by zero. The term $p_{i,t,c}$ represents the proportion of recovery effort concentrated at node i and time t within the overall recovery process in scenario c.

The weighted Resilience Entropy of the system across all scenarios is defined as

$$H=-\sum _{c\in \mathcal{C}}{P}_c\sum _{t\in \mathcal{T}}\sum _{i\in \mathcal{N}}{\omega }_{t,c}·p_{i,t,c}·log\left(p_{i,t,c}\right)$$

(40)

here, $P_c$ is the probability of scenario c, and ${\omega }_{t,c}$ denotes the importance weight of time t in scenario c. A lower entropy value indicates a more focused and faster recovery, reflecting stronger resilience.

In DNs, resilience and reliability represent two complementary aspects. In this study, we focus on resilience, specifically the post-disaster restoration of nodal load which is directly captured by the proposed Resilience Entropy metric. Voltage level is critical for overall grid reliability and stability, and voltage constraints have been incorporated into our optimization model to ensure feasible and secure operation during recovery. Therefore, the proposed metric provides a practical assessment of post-disaster load restoration, while operational constraints maintain system safety.

Compared with conventional resilience indicators that mainly focus on minimizing the total load shedding, the proposed Resilience Entropy provides a more detailed characterization of node-level resilience over time. By incorporating time-dependent weights, it enables the evaluation of supply satisfaction across different nodes and periods. In particular, the weighting mechanism allows critical periods (e.g., peak-load hours) to be prioritized, ensuring that supply adequacy during these key intervals is better captured in the resilience assessment. A simple example is shown in Appendix A.

4.3. Objective Function

To enhance post-disaster recovery in distribution networks, this study incorporates a dual-objective optimization framework that balances resilience improvement and economic cost. Specifically, the total cost comprises both investment expenses for V2G infrastructure and operational compensation for V2G discharge services, while resilience is quantified using Resilience Entropy.

The economic compensation cost for V2G services is modeled as

$$C_{\mathrm{OP}}=\sum _{c\in \mathcal{C}}{P}_c·\sum _{t\in \mathcal{T}}\sum _{i\in \mathcal{N}}{\rho }_{i,t}·P_{i,t,c}^{\mathrm{EV},\mathrm{dis}}$$

(41)

where ${\rho }_{i,t}$ is the electricity compensation price at node i and time t, and $P_{i,t,c}^{\mathrm{EV},\mathrm{dis}}$ denotes the V2G discharge power supplied by electric vehicles at node i under scenario c and time t. This cost formulation reflects the financial incentives needed to mobilize EV resources for grid support during the recovery phase.

The overall objective function is defined as

$$min{\lambda }_{1}H+{\lambda }_2(C_{\mathrm{INV}}+C_{\mathrm{OP}})$$

(42)

where H denotes the Resilience Entropy, reflecting the distribution of load restoration over time and space; $C_{\mathrm{INV}}$ is the capital investment cost for V2G infrastructure deployment; and ${\lambda }_1$, ${\lambda }_2$ are user-defined weighting factors used to trade off resilience and economic considerations.

In this study, a dual-objective formulation is employed to jointly account for resilience enhancement and economic cost. This type of formulation is well established in optimization research, where the objectives typically incorporate both the investment cost of infrastructure deployment and the operational cost of mobilizing V2G services, while system resilience is measured through appropriate indicators, such as the proposed Resilience Entropy metric [22]. This formulation ensures a coordinated decision-making process that not only enhances the resilience of the power distribution network in the aftermath of disasters but also accounts for the economic viability of mobilizing distributed V2G resources.

5. Case Studies

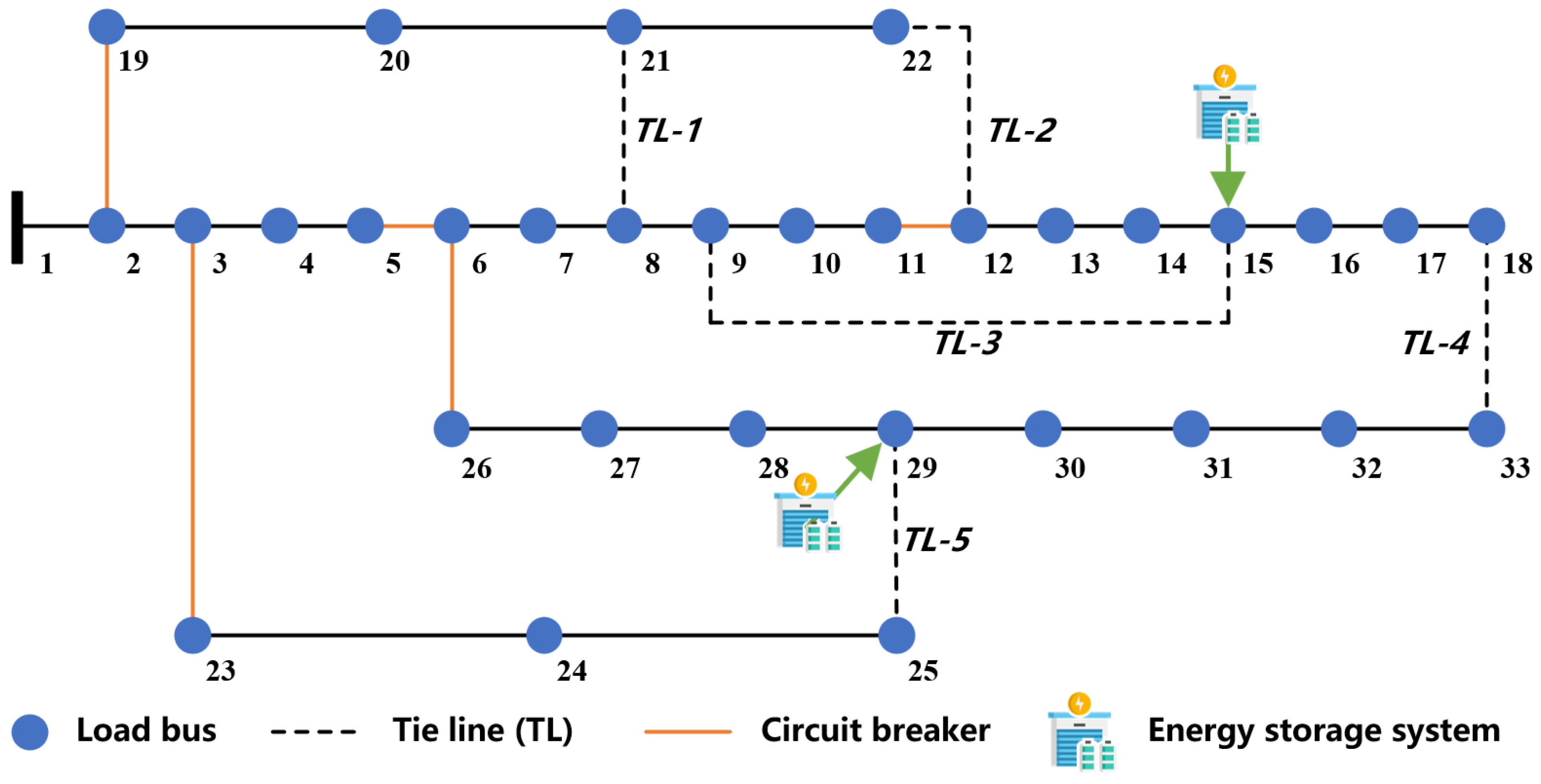
To verify the effectiveness of the proposed methodology, the classical IEEE-33 bus distribution system is adopted as a test case. The initial topology is illustrated in Figure 2. This system comprises 37 distribution lines, with tie-lines strategically deployed to enable network reconfiguration when necessary. In addition, circuit breakers are installed at key locations within the network, allowing for rapid fault isolation upon detecting abnormal currents, thus effectively preventing fault propagation. The proposed optimization model is formulated as a mixed-integer nonlinear programming (MINLP) problem, which is implemented and solved using Gurobi 9.5.2 on a standard desktop computer with Intel i5-12500H CPU and 16 GB of RAM.

5.1. Case Study Results and Analysis

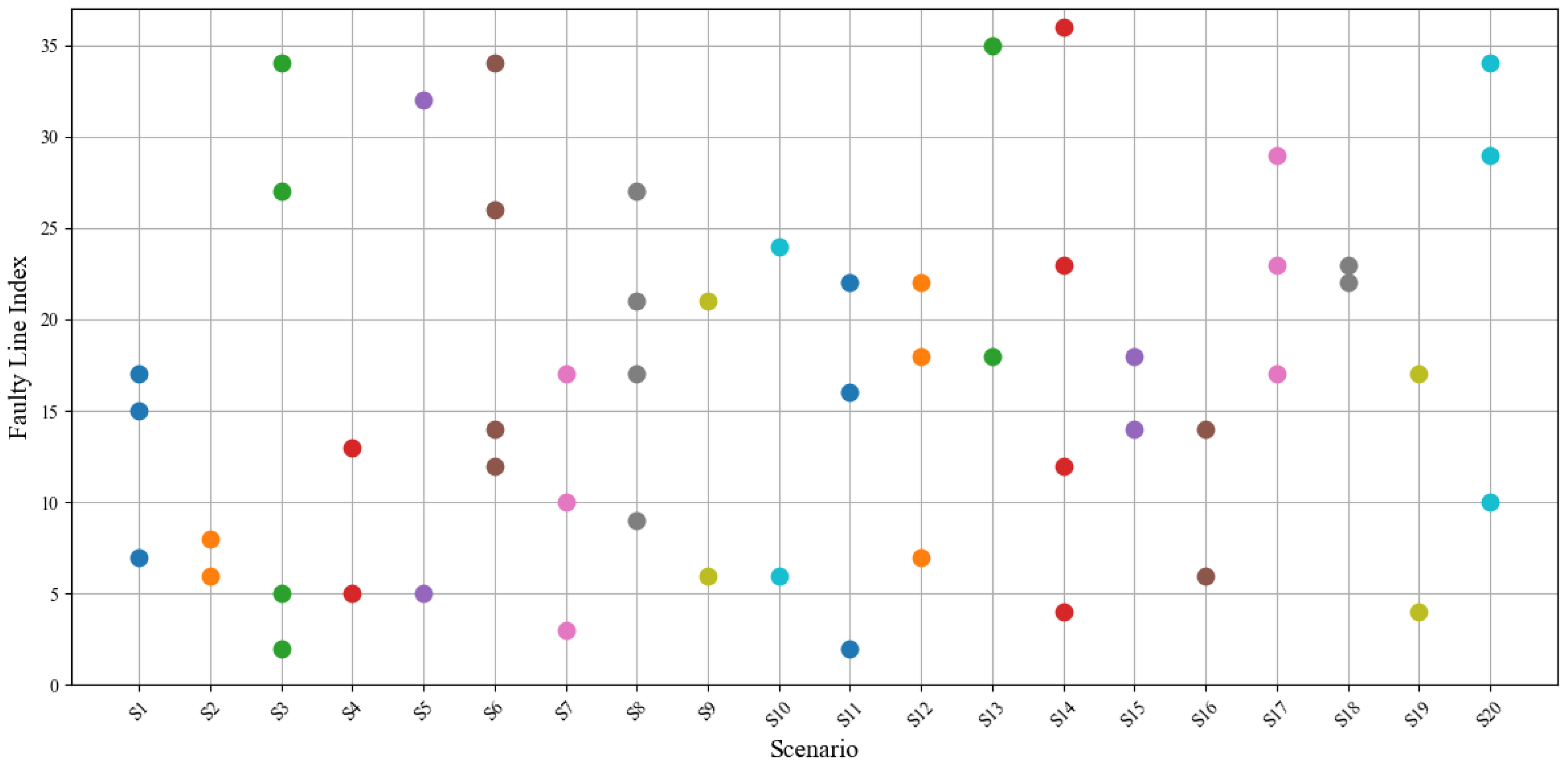
The simulation assumes a disaster recovery horizon of 3 h, with system status sampled every 15 min. The participation willingness of EV owners in V2G services $\beta$ is set at 40%. Based on large-scale Monte Carlo simulations, multiple disaster scenarios are generated, and their respective faulted line distributions are shown in Figure 3. In our study, each distribution line is assigned a failure probability ranging from 1% to 8%. Using Monte Carlo simulation, line outages are sampled independently according to these probabilities. From a large number of simulations, we selected 20 representative fault scenarios for the case study, each containing 2–4 failed lines, and assigned them equal scenario probabilities to ensure a balanced representation. 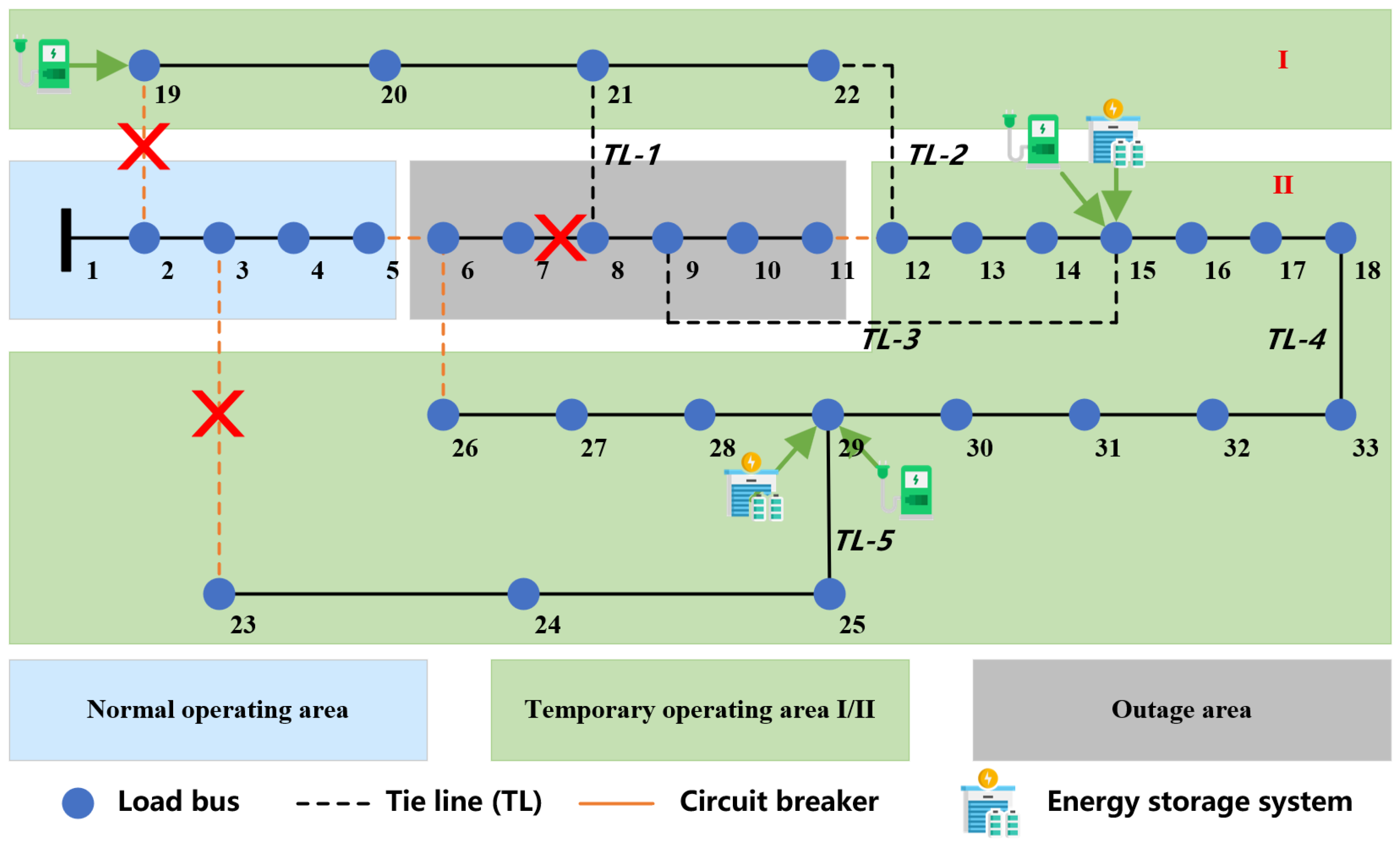When V2G stations and DGs jointly serve as power sources for temporary operating areas, the location of V2G integration leads to different power flow distributions across the system (i.e., variations in nodal voltages, line flows, and supplied power as shown in Equations (16)–(21)). Consequently, supply satisfaction varies among nodes, and the optimization model tends to select nodes that maximize overall satisfaction under the influence of the Resilience Entropy objective. According to the optimization results, three V2G charging stations are established at nodes 15, 19, and 29, respectively. The post-disaster operational states of different regions are visualized in Figure 4.

Among these scenarios, the damaged lines in scenario 12 are primarily located along the main feeder, which poses a significant risk of large-scale power outages. Therefore, it is selected for detailed analysis due to the disruption of critical power flow paths.

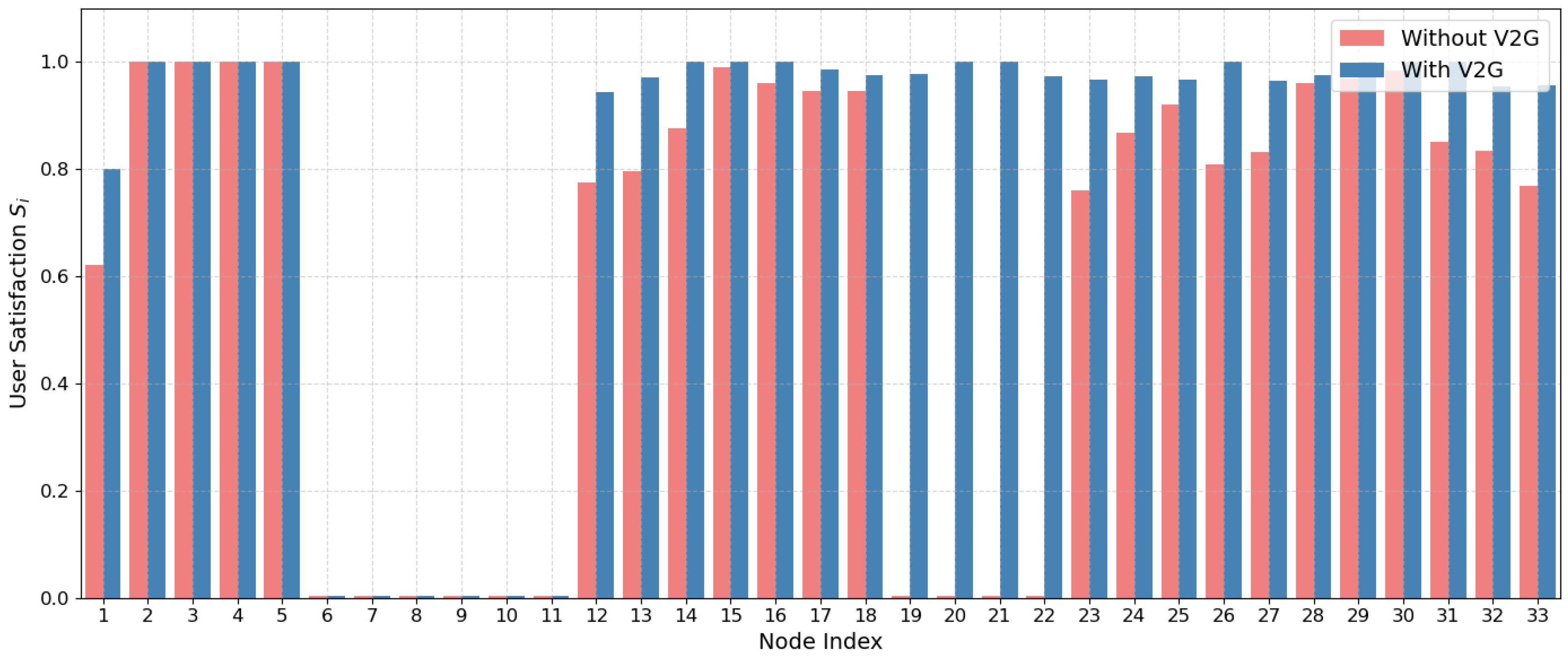
As shown in the figure, “Temporary Operating Areas” operate as islands that are formed by tie-line switching and supported by local distributed generation and V2G resources. The gray-shaded area indicates “Outage Areas”, which refers to zones without supply, i.e., neither grid connection nor local support. The faults in scenario 12 primarily affect the main feeder of the distribution network. Although the deployment of circuit breakers successfully contains the fault within a limited region (gray-shaded area), many downstream nodes become electrically isolated due to line outages. In the absence of V2G infrastructure, these nodes—such as nodes 19 to 22—would experience complete power loss, resulting in user satisfaction dropping to 0, as shown in Figure 5.

It is noteworthy that, although tie-line 2 (TL-2) is available in the network, it is not directly utilized in this scenario. This is because temporary operating area II relies mainly on local energy storage system and V2G stations for supply, whose capacity is significantly lower than that of the main feeder. If long-distance power transfer is attempted without additional support, voltage drops will become severe and trigger cascading failures. Consequently, deploying a V2G charging station at node 19 to supply temporary operating area I is a more effective and practical strategy. And it should be emphasized that the gray-shaded region represents the outage area where faults have not been cleared. Even if backup power exists, these areas remain non-operational until the damaged line (from node 7 to 8) is structurally restored.

Table 1. Comparison of resilience entropy and average supply satisfaction with and without V2G charging stations installation.

Method	Resilience Entropy H	Average Supply Satisfaction S
Without V2G charging stations installation	1479.3	0.658
With V2G charging stations installation	775.6	0.805

presents the overall resilience entropy indicators and average supply satisfaction, comparing scenarios with and without the installation of V2G charging stations. It can be observed that the introduction of the V2G charging station significantly reduces the Resilience Entropy from 1479.3 to 775.6, representing an approximate 47.6% improvement in the system’s resilience to maintain supply continuity and cope with disruptions. Simultaneously, the average supply satisfaction increases from 0.658 to 0.805, indicating a marked enhancement in the power delivery performance experienced by users. These results clearly demonstrate the effectiveness of integrating V2G charging stations into the post-disaster distribution network. The improved Resilience Entropy implies a more reliable and adaptive system, while the increase in supply satisfaction highlights the practical benefits from the end-user perspective.

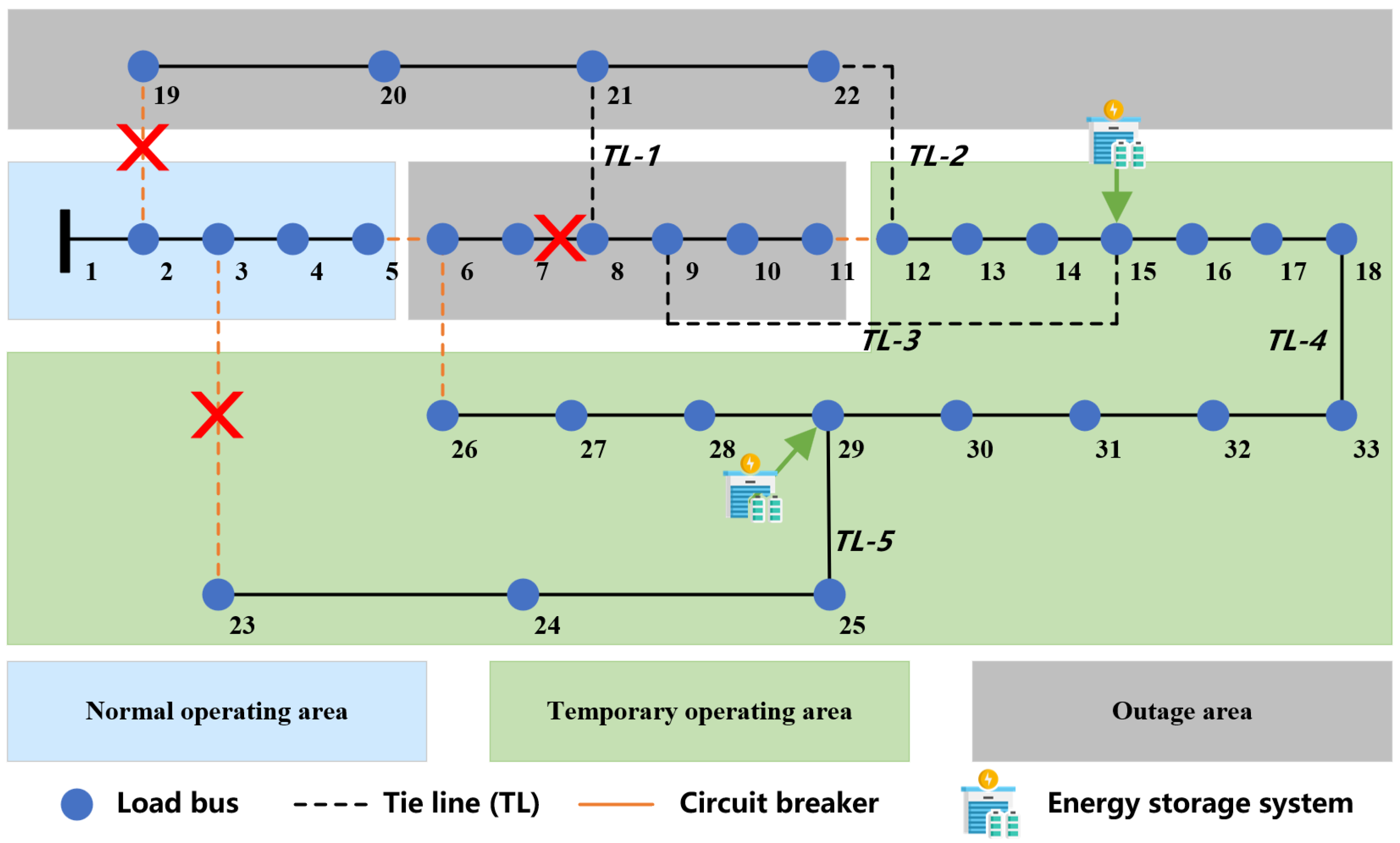
To further illustrate the temporal and spatial distribution of supply satisfaction, Figure 6 shows a comparison of power supply satisfaction at time $t=5$, i.e., one hour after the disaster event. Notably, Node 1 is the main power supply node without any connected loads; thus, the reported value for Node 1 represents the average power supply satisfaction across all load-serving nodes.

From Figure 6, it is observed that Nodes 2–5 are supplied directly by the main power source, maintaining a power supply satisfaction level of 1. In contrast, Nodes 6–11 fall within the fault-affected area and experience complete power loss; therefore, their satisfaction remains 0 regardless of the deployment of V2G charging stations. For Nodes 19–22, the integration of V2G charging stations improves their satisfaction levels, although full satisfaction ($S=1$) is not achieved under the current V2G participation rate. This limitation arises because these nodes rely solely on V2G as their power source, and the available power is constrained by the number of participating vehicles.

Furthermore, in temporary operating area 2, V2G stations serve as supplementary power sources, improving supply reliability and satisfaction in the affected area. Figure 7 depicts the power supply satisfaction at time $t=7$. In the absence of V2G infrastructure, conventional energy storage systems—typically limited in capacity—experience rapid depletion over extended periods, leading to a significant decline in satisfaction within temporary operating area 2. In contrast, with V2G stations deployment, continuous arrival of new EVs enables sustained power injection. This ensures higher and more stable satisfaction levels in the temporary operating area.

In conclusion, the deployment of V2G charging stations significantly mitigates power shortages and enhances the resilience of the distribution network, all while maintaining economic feasibility. This demonstrates that V2G integration effectively enhances both system-level performance and user-level supply experience.

5.2. Sensitivity Analysis

Furthermore, a sensitivity analysis was conducted on the willingness of EV owners to participate in V2G grid support, denoted by the parameter $\beta$. As shown in Figure 8, the Resilience Entropy decreases progressively as the value of $\beta$ increases, indicating improved user satisfaction with power supply and enhanced overall resilience of the distribution network.

Notably, when $\beta$ reaches 70%, a high level of power supply satisfaction can be achieved by installing V2G charging stations at only nodes 15 and 29, and activating the tie-line TL-2. Although the Resilience Entropy under this configuration is slightly higher than that in the case of $\beta =60\%$, the total construction cost is reduced due to the simplified infrastructure layout. This demonstrates a cost-effective and resilient configuration strategy. Therefore, enhancing EV owner participation in V2G operations not only strengthens the grid’s post-disaster recovery capability but also yields considerable economic benefits.

The IEEE-33 bus distribution system is adopted in this study as it is a widely recognized benchmark for distribution network analysis, providing a transparent and standard platform to validate new methodologies. It should be noted that the proposed framework is not restricted to this system; it can be readily extended to other distribution networks by updating the topology, line parameters, and load data, ensuring the general applicability of the approach.

Regarding the siting results, the optimization selects node 19 as a practical and robust location for deploying a V2G charging station. This is because, under post-disaster conditions, supplying active power from node 19 maximizes load recovery within the temporary operating area and improves overall supply satisfaction, as reflected in the Resilience Entropy objective. Although the V2G stations in this study are modeled to provide only active power, voltage and reactive power levels are maintained through conventional devices such as tap changers, capacitors, and voltage source converters. Therefore, the deployment at node 19 remains both practical and effective for enhancing post-disaster recovery.

In terms of practical considerations, although V2G stations only provide active power support, overall system reliability is preserved since voltage levels and reactive power are regulated by conventional devices such as tap-changing transformers and capacitor banks. The notion of “disaster” in this study refers to extreme events (e.g., typhoons, floods) that cause widespread distribution outages, under which V2G resources serve as auxiliary support for critical load recovery. Furthermore, all mathematical models are explicitly tied to nodes and lines of the IEEE-33 bus system, with system topology illustrated in Figure 2, ensuring clarity between theoretical formulation and physical implementation.

6. Conclusions

This paper proposes a resilience-oriented restoration model for post-disaster distribution networks, integrating the optimal siting of V2G charging stations. The model accounts for the spatiotemporal uncertainties of EV behavior, power flow constraints, and radial topology requirements, ensuring both physical feasibility and operational safety.

A key innovation lies in the introduction of Resilience Entropy—a dynamic metric that captures the spatiotemporal evolution of supply satisfaction by simultaneously considering both the speed and distribution of recovery across time and space. By incorporating time-weighting factors, it effectively addresses the limitations of conventional static indicators and enables a more comprehensive evaluation of restoration strategies.

Simulation studies based on the IEEE-33 bus system verify that the model effectively adapts to complex fault scenarios. It dynamically determines V2G station deployment and tie-line strategies, achieving adaptive local restoration and improved supply satisfaction. In particular, scenario 12 demonstrates successful island restoration without full tie-line activation. Sensitivity analysis shows that higher user willingness to participate in V2G significantly enhances recovery performance. Under high participation rates (e.g., 70%), the model further optimizes configurations to reduce reconfiguration costs, highlighting its controllability and economic efficiency.

Overall, the proposed model demonstrates strong adaptability, feasibility, and optimization capability, offering valuable insights for resilience-oriented planning in disaster-affected distribution systems.