Maximum Power Point Tracking Strategy for Fuel Cells Based on an Adaptive Particle Swarm Optimization Algorithm

Abstract

With the growing global demand for clean energy, fuel cells have been adopted as key components in renewable energy systems. Their high efficiency and environmentally friendly operation make them attractive. However, during maximum power point tracking (MPPT), traditional proportional–integral–derivative (PID) controllers often fail to maintain optimal power output. Dynamic load changes and complex operating conditions exacerbate this issue. As a result, system response is slowed, and tracking accuracy is reduced. To address these problems, an online identification method based on recursive least squares (RLS) is employed. A cubic power–current model is identified in real time. Polynomial fitting and the golden section search are then applied to estimate the current at the maximum power point. Following model-based estimation, adaptive particle swarm optimization (APSO) is utilized to tune the PID controller parameters. Precise regulation is thus achieved. The use of RLS enables real-time model identification. The golden section search improves the efficiency of current estimation. APSO enhances global optimization, while PID provides fast dynamic response. By integrating these methods, both tracking accuracy and system responsiveness are significantly improved in fuel cell MPPT applications. Simulation results demonstrate that the proposed strategy enhances maximum power output by up to 12.40% compared to conventional P&O, fuzzy logic control, GWO-PID, and PSO-PID methods, as well as maintaining a consistent improvement of 1.50% to 1.90% even when compared to other optimization algorithms.

1. Introduction

In today’s era, global energy crises and environmental pollution are becoming increasingly severe. This has made new energy technology research and development a key focus of international attention [1]. Among the many new energy technologies, fuel cells [2,3] have emerged as a focal point of research due to their unique advantages. As efficient and clean energy conversion devices [4,5], fuel cells directly convert chemical energy into electrical energy [6]. They are highly efficient and produce minimal environmental pollution [7,8]. Thus, they are widely regarded as a crucial component of future sustainable energy systems. It is anticipated that fuel cells will instigate profound changes in the energy sector, offering innovative solutions to global energy problems [9,10].

However, fuel cell applications and development face challenges, as performance is significantly affected by operating conditions. Particularly under dynamic load variations [11], achieving maximum power point tracking (MPPT) for fuel cells is a critical unresolved issue [12]. Continuous load changes cause fuel cell output power to fluctuate. Ineffective MPPT results in significant energy underutilization. This reduces energy conversion efficiency [13] and accelerates electrode material degradation, shortening service life. Successful MPPT implementation is crucial. It substantially improves energy conversion efficiency [14], enabling efficient energy use and reduced waste. It also extends operational lifespan and lowers maintenance costs [15,16]. Consequently, commercialization barriers are removed, promoting widespread practical adoption. This allows fuel cells to realize greater value and potential in the new energy sector [17,18].

P&O (Perturb and Observe) is widely employed in solar photovoltaic and fuel cell systems due to its simplicity and rapid response [19,20]. A novel hybrid artificial ecosystem-based optimization combined with the P&O MPPT algorithm, specifically designed for fuel cell MPPT in microgrid applications, is introduced in [21]. This algorithm integrates the artificial ecosystem approach with traditional P&O techniques to address limitations of existing MPPT methods in fuel cell applications. A flexible P&O-based control strategy, proposed in [22], ensures optimal power supply capability at the ideal load voltage/current and prevents overload during grid fault modes. Although these algorithms are simple to implement, oscillations or insufficient tracking accuracy may be induced under dynamic load variations. Consequently, these classical algorithms have been optimized. For example, a drift-free MPPT algorithm was proposed in [23] to eliminate incorrect decision-making by classical P&O under rapidly changing dynamic conditions.

Furthermore, intelligent control, recognized as an advanced control technique [24], is widely applied in complex systems due to its excellent adaptive and self-learning capabilities. In the field of fuel cells, intelligent control techniques offer novel approaches for solving MPPT problems [25,26]. MPPT control utilizing a fuzzy logic controller was implemented in [27]. This method requires only the output current and voltage signals of the PEMFC, reducing the number of sensors needed. Limitations of traditional MPPT algorithms in addressing the nonlinear characteristics of PEMFC systems were thereby addressed. A generalized predictive controller (NGPC) based on a multilayer perceptron (MLP) neural network was proposed in [28] to achieve maximum efficiency and power output from PEMFC. This approach addresses the challenge of precise PEMFC control under dynamic load variations, specifically the problem of MPPT under current constraints. Compared with traditional methods, this approach achieves a 10.23% improvement in output power. Literature [29] presented an MPPT control method utilizing an adaptive neuro-fuzzy inference system (ANFIS) and a modified fluid search optimization (MFSO) algorithm. Enhanced power output and tracking efficiency under varying temperature and membrane humidity conditions are achieved via two-stage power optimization and MPPT search. Compared with traditional methods, this approach achieves an improvement in output power ranging from 0.68% to 1.50%.

Although intelligent controllers demonstrate excellent performance in managing complex systems and nonlinear tasks, significant disadvantages are also recognized [30]. These include inherent structural complexity, which leads to high computational costs and difficulties in meeting real-time requirements. Guaranteeing stability is challenging, as these controllers are prone to convergence at local optima. Furthermore, insufficient adaptability to environmental changes necessitates parameter retuning or complete retraining for new conditions, something that is challenging to accomplish in real time.

In fuel cell MPPT, PID controllers offer advantages. Their structure is simple, and implementation is straightforward. They also provide effective power regulation under stable operating conditions. However, PID controllers exhibit limitations. Under dynamic load variations or complex conditions, they may fail to adjust system parameters rapidly and accurately. This failure leads to reduced tracking accuracy. Therefore, integrating optimization algorithms with PID controllers is considered to address these shortcomings.

To overcome these limitations, this study aims to present a novel integrated MPPT control strategy to achieve fast and accurate tracking of the maximum power point in fuel cells under complex operating conditions. The main innovations of this paper include:

(1) An online polynomial parameter identification method based on the Recursive Least Squares (RLS) algorithm, which updates the fuel cell power-current model in real time to accurately capture its dynamic characteristics;

(2) The introduction of the golden section search algorithm to perform efficient and precise interval search based on the model-derived initial estimate, rapidly locating the maximum power point current;

(3) The design of an Adaptive Particle Swarm Optimization (APSO) algorithm to dynamically adjust the parameters of the PID controller, significantly enhancing the system’s adaptability and robustness under changing loads and environmental conditions.

By integrating real-time modeling, accurate search, and adaptive control, the proposed strategy effectively improves the tracking speed, accuracy, and stability of the system.

2. PEMFC System Modeling

In this section, the working principle of fuel cells will first be outlined. Subsequently, a fuel cell model will be developed based on the polarization curve to predict performance under various operating conditions. Furthermore, the structure of the boost converter will be briefly introduced, as this component plays a significant role in improving energy efficiency within fuel cell systems. Through analysis of these key components, theoretical foundations and practical guidance for enhancing fuel cell system performance will be provided.

2.1. Principle and Modeling of PEMFCs

As shown in Figure 1, the basic principle of fuel cells is to utilize the electrochemical reaction between hydrogen (or other fuels) and oxygen (or air) [31,32,33]. Fuel cell efficiency is usually higher than that of traditional combustion processes, as they do not rely on heat engine cycles, thus reducing energy loss during conversion.

The MPPT of fuel cells is an effective way to enhance their energy conversion efficiency. Fuel cell modeling is conducted to accurately predict and control fuel cell performance, particularly under dynamically changing operating conditions. The performance output of fuel cells exhibits significant nonlinear behavior due to the combined effects of various internal and external factors. The intricate interplay among these variables leads to complex and nonlinear output characteristics in practical fuel cell systems. As shown in the single fuel cell model diagram in Figure 1, the output voltage characteristics of fuel cells can be calculated by the following mathematical expression [34,35]:

$$V_{cell}=E_{ner}-V_{act}-V_{ohm}-V_{con}$$

(1)

The output voltage of an individual fuel cell, denoted as $V_{cell}$, is determined by the balance of several distinct voltage components. Specifically, $E_{ner}$ refers to the theoretical reversible voltage derived from the Nernst equation. The actual operating voltage is reduced by multiple losses: $V_{act}$ corresponds to the activation overpotential caused by electrochemical reaction kinetics; $V_{ohm}$ accounts for internal resistance losses due to ionic and electronic conduction; and $V_{con}$ represents concentration overpotential arising from mass transport limitations at high current densities. These parameters can be further expressed through additional mathematical formulations.

$$\begin{array}{cc}\hfill E_{ner}& =1.229-0.85\times {10}^{-3}\times \left(T-298.15\right)\hfill \\ & +4.3085\times {10}^{-5}T\times \mathit{ln}\left(P_{H_2}\sqrt{P_{O_2}}\right)\hfill \end{array}$$

(2)

The operating temperature of the fuel cell, denoted by $T$, is expressed in Kelvin (K). The partial pressures of hydrogen and oxygen, represented by $P_{H_2}$ and $P_{O_2}$, are quantified in units of atmospheres (atm). These thermodynamic variables play a critical role in determining the electrochemical performance and are essential inputs for accurate modeling of fuel cell behavior.

The coefficients in this equation are derived from the Nernst equation for fuel cells. Specifically, the coefficient −0.85 × 10⁻³ represents the linear correction effect of temperature change on the theoretical voltage at standard state. The coefficient 4.3085 × 10⁻⁵ is derived from the Nernstian slope, which quantifies the influence of reactant partial pressures (concentrations) on the cell potential. These coefficients incorporate fundamental thermodynamic constants along with necessary empirical adjustments to accurately capture how the theoretical cell potential varies with temperature and reactant concentrations.

The activation voltage loss of fuel cells results from the slow reactions at the electrode surface. When electrochemical reactions drive electron transfer to or from the electrode, some reaction-generated voltage is lost. It can be calculated by the following equation:

$$V_{act}={\xi }_1+{\xi }_{2}T+{\xi }_{3}T\ln {{(C}_O}_2)+{\xi }_{4}T\ln \left(I\right)$$

(3)

Here, ${\xi }_1$ to ${\xi }_4$ are empirical parameters of the model. As their theoretical calculation is exceedingly complex, it is a common practice in engineering applications and modeling to adopt empirical values obtained by fitting experimental data. The parameter values utilized in this work are taken from Reference [35] and are listed in

Table 1. PEMFC Parameters.

Parameter	Value	Definition
$N$	35	Number of cells
$A$	232 cm2	Cell active area
$l$	0.0178 cm	Membrane thickness
${\xi }_1$	−0.944	Coefficients
${\xi }_2$	0.00354
${\xi }_3$	7.8 × 10−8
${\xi }_4$	−1.96 × 10−4
$n$	2	Number of electrons involved in the electrochemical reaction
$R$	8.31447 J/(mol K)	Universal gas constant
$F$	96,484,600 C/kmol	Faraday constant
$P_{H_2}$	2.6 (bar)	Hydrogen partial pressure
$P_{O_2}$	0.3 (bar)	Oxygen partial pressure
$R_c$	3 × 10−3 $\Omega$	Contact resistance
$j_{max}$	2.00 A cm−2	Peak current density

.

$C_{O_2}$ is the dissolved oxygen concentration at the cathode catalyst interface. $I$ represents the output current. The coefficient $5.08\times {10}^6$ is a comprehensive coefficient related to the solubility of oxygen in the Nafion membrane. It is essentially an empirical form of the Henry’s law constant. The value is obtained by regressing experimental data to establish the quantitative relationship between oxygen partial pressure and its equilibrium dissolved concentration in the membrane phase. The number 498 is related to the apparent activation energy associated with the dissolution process of oxygen. It appears in the exponential term $\exp \left({\displaystyle \frac{498}{T}}\right)$, quantitatively describing the trend of increasing dissolved oxygen concentration with rising temperature, which follows the form of the Arrhenius equation.

$$C_{O_2}={\displaystyle \frac{P_{O_2}}{5.08\times {10}^6}}\exp \left({\displaystyle \frac{498}{T}}\right)$$

(4)

The ohmic voltage loss in a fuel cell is primarily caused by the resistance of components such as the electrolyte and electrodes:

$$V_{ohm}=I(R_M+R_C)$$

(5)

The contact resistance ($R_C$) of a fuel cell is essentially constant. The equivalent membrane resistance ($R_M$) is determined by the proton exchange membrane’s specific resistivity (${\rho }_M$), thickness ($l$), and active area ($A$):

$$R_M={\displaystyle \frac{{\rho }_{M}l}{A}}$$

(6)

The following equation can be utilized to calculate ${\rho }_M$:

$${\rho }_M={\displaystyle \frac{181.6[1+0.03j+0.062{\left(\frac{T}{303}\right)}^2{j}^{2.5}]}{\left(\lambda -0.634-3j\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{4.18\left(T-303\right)}{T}\right)}}$$

(7)

In this equation, $\lambda$ represents the membrane water content. 181.6 represents the baseline resistivity of the membrane under reference conditions. 0.03 and 0.062 quantify the influence of the operating current density ($j)$ on membrane drying. An increase in j promotes membrane dehydration, thereby increasing resistance. These coefficients, determined through data fitting, describe the strength of this non-linear effect. 303 K is the reference temperature utilized in the formulation. All temperature-dependent terms are normalized relative to this temperature. 0.634 and 3 are empirical constants related to the critical membrane water content. The term $\left(\lambda -0.634-3j\right)$ defines a current density dependent threshold, modeling the physical phenomenon of a sharp decrease in conductivity when water content is too low. 4.18 is related to the apparent activation energy for proton conduction. It is located in the exponential term $\mathrm{e}\mathrm{x}\mathrm{p}\left({\displaystyle \frac{4.18\left(T-303\right)}{T}}\right)$, describing the Arrhenius relationship of how membrane conductivity improves with temperature and is a key parameter for capturing the temperature effect. The term $j$ can be calculated utilizing the subsequent equation:

$$j={\displaystyle \frac{I}{A}}$$

(8)

The concentration voltage loss ($V_{con}$) can also be determined by the following equation:

$$V_{con}=-{\displaystyle \frac{RT}{nF}}\ln (1-{\displaystyle \frac{j}{j_{max}}})$$

(9)

In this context, the parameter $j_{max}$ denotes the peak current density achievable by the fuel cell. The corresponding maximum current $I_{max}$ is calculated as the product of $j_{max}$ and the active area ($A$). The universal gas constant is represented by $R$. $n$ signifies the number of electrons involved in the electrochemical reaction. $F$ is Faraday’s constant. A fuel cell stack is typically conceptualized as a series of idealized single-cell units. Therefore, for a stack consisting of $N$ individual cells, the total stack voltage $V_{out}$ can be described by the following expression:

$$V_{out}=N\times V_{cell}$$

(10)

The output power is the product of the output voltage and current.

$$P=V_{out}\times I$$

(11)

The relationship between the fuel cell output power and current is inherently nonlinear and is commonly represented by the power density curve. As illustrated in Figure 2, under identical ambient conditions, the power density curve of a fuel cell typically exhibits a single peak. With the increase in current density, the output power rises and reaches its maximum at a specific current density, corresponding to the maximum power point. Beyond this point, further increases in current density cause a sharp voltage drop, resulting in reduced output power. This nonlinear characteristic makes the power density curve a key tool for analyzing fuel cell performance and identifying the optimal operating point.

In fuel cell system operation, the maximum power point current ($I_{mppt}$) under varying ambient parameters must be determined accurately and rapidly for effective maximum power point tracking. However, direct analytical solutions for $I_{mppt}$ are often computationally complex. They also lack real-time feasibility. This complexity arises due to the highly non-linear output characteristics of fuel cells. Environmental factors such as temperature, humidity, and pressure significantly impact these characteristics. In practical operation, fuel cell systems must dynamically adapt to changing ambient conditions. This further increases the difficulty of obtaining real-time solutions.

2.2. Boost Converter Modeling and Parameter Selection

In the fuel cell MPPT system, the power converter is utilized to regulate the fuel cell output voltage, keeping it operating stably in the maximum power point region. This improves energy extraction efficiency. Among various power converters, the boost converter [36,37], with its voltage-boosting characteristics and high efficiency, is the preferred choice for fuel cell MPPT applications. It is a DC voltage-boosting circuit that elevates the low and dynamic output voltage of fuel cells to the system-required stable voltage range Additionally, it boasts a simple structure and flexible duty cycle control. Therefore, the boost converter is utilized in this paper as the power interface to effectively convert energy in fuel cell MPPT control.

The relationship between the fuel cell output voltage ($V_{out}$) and the boost converter output voltage ($V_o$) is as follows:

$${\displaystyle \frac{V_o}{V_{out}}}={\displaystyle \frac{D}{1-D}}$$

(12)

The duty cycle is denoted by $D$. Considering the current ripple $∆I_L$, the minimum inductance $L_{min}$ can be calculated as follows:

$$L_{min}={\displaystyle \frac{D{V}_{out}}{f_s∆I_L}}$$

(13)

Here, $f_s$ represents the switching frequency of the boost converter. Similarly, the minimum capacitance $C_{min}$ is determined based on the voltage ripple $∆V_C$:

$$C_{min}={\displaystyle \frac{D{I}_o}{f_s∆V_C}}$$

(14)

Here, $I_o$ is the output current of the boost converter. It can be calculated as the ratio of the maximum power $P_{max}$ to the output voltage $V_o$:

$$I_o={\displaystyle \frac{P_{max}}{V_o}}$$

(15)

The load $R$ can be calculated utilizing the following formula:

$$R={\displaystyle \frac{V_o^2}{P_{max}}}$$

(16)

3. MPPT Strategy

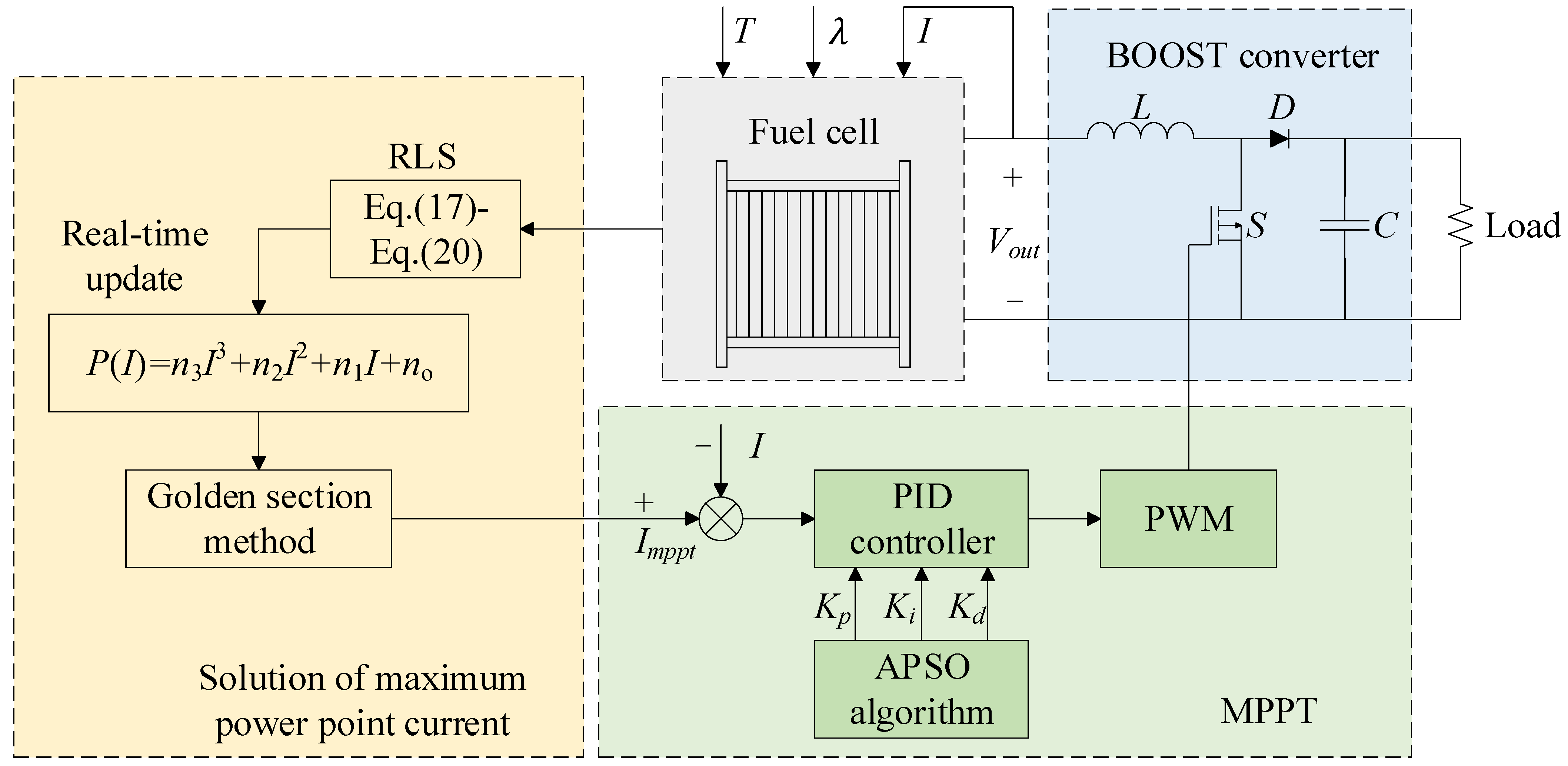
First, the RLS algorithm is utilized to identify a cubic power–current model of the fuel cell in real time. Based on the updated model, the golden section method is applied to iteratively locate the current corresponding to the maximum power point. Precise real-time tracking of the maximum power point is thus achieved. Next, the basic principle of the PID controller and its application in MPPT are briefly described. The limitations of traditional PID control under dynamic load variations are highlighted. Then, the particle swarm optimization (PSO) algorithm is introduced. Standard PSO may exhibit slow convergence and can become trapped in local optima. To address these issues, an adaptive PSO (APSO) algorithm is presented. APSO is expected to improve the efficiency and accuracy of PID parameter optimization. Enhanced adaptation to dynamic MPPT characteristics and improved system performance are thereby realized.

3.1. Real-Time Solution of Maximum Power Point Current

To address these issues, this paper presents a solution method combining polynomial fitting of the power—current relationship with recursive least squares (RLS). First, a mathematical model is established through polynomial fitting by analyzing the fuel cell’s power—current characteristic curve.

$$P\left(I\right)=n_3{I}^3+n_2{I}^2+n_1{I}^1+n_0$$

(17)

This model is rewritten in linear regression form for RLS updating [38]. In this form, the actual measured output power $P\left(k\right)$ of the fuel cell at time $k$ is expressed as:

$$P\left(k\right)=\phi {\left(k\right)}^T\theta \left(k-1\right)+v\left(k\right)$$

(18)

where $\phi \left(k\right)$ is the regression vector, $\theta$ is the parameter vector, and $v\left(k\right)$ is the parameter vector. Where $\phi \left(k\right)$ is the regression vector, $\theta$ is the parameter vector containing the polynomial coefficients to be identified, and $v\left(k\right)$ is a measurement noise with zero mean. The definitions of $\phi \left(k\right)$ and $\theta$ are as follows:

$$\left\{\begin{array}{c}\phi {\left(k\right)}^T=[I{\left(k\right)}^3,I{\left(k\right)}^2,I\left(k\right),1]\\ \theta ={\left[n_3,n_2,n_1,n_0\right]}^{\mathrm{T}}\end{array}\right.$$

(19)

The RLS update equations are given by:

$$\left\{\begin{array}{c}K\left(k\right)={\displaystyle \frac{P_{cov}(k-1)\phi \left(k\right)}{1+\phi {\left(k\right)}^T{P}_{cov}(k-1)\phi \left(k\right)}}\\ \theta \left(k\right)=\theta \left(k-1\right)+K\left(k\right)[P\left(k\right)-\phi {\left(k\right)}^T\theta \left(k-1\right)]\\ P_{cov}\left(k\right)=\left[S-K\left(k\right)\phi {\left(k\right)}^T\right]P_{cov}(k-1)\end{array}\right.$$

(20)

where $\theta \left(k\right)$ is the parameter estimate vector at time $k$, $P_{cov}\left(k\right)$ is the covariance matrix of the estimation error, $K\left(k\right)$ is the algorithm gain vector, and $S$ is the identity matrix (with dimensions matching $P_{cov}\left(k\right))$. The second line in Equation (20) clearly shows that the new parameter estimate $\theta \left(k\right)$ is obtained by updating the previous estimate $\theta \left(k-1\right)$ with a correction term proportional to the prediction error $P\left(k\right)-\phi {\left(k\right)}^T\theta \left(k-1\right)$.

The initial current solution can be obtained by taking the derivative of the polynomial and setting it to zero.

$${\displaystyle \frac{dP\left(I\right)}{dI}}={3n}_3{I}_{mppt,k}^2+{2n}_2{I}_{mppt,k}+n_1=0$$

(21)

This paper further introduces the golden section method [39] for efficient maximum power point current searching. Based on the power-current curve fitting model, it narrows the search interval stepwise for rapid convergence on the maximum point. With high-precision convergence in few iterations, this method meets the fuel cell’s real-time dynamic operation requirements.

First, an initial search interval $[a, b]$ containing the maximum power point is determined. Two golden section points within the interval are then calculated:

$$\left\{\begin{array}{c}{I}_{mppt-1}=b-(b-a)/1.618\\ I_{mppt-2}=a+(b-a)/1.618\end{array}\right.$$

(22)

The interval contraction direction is determined by comparing the power values at the two golden section points: when $P\left(I_{mppt-1}\right)>P(I_{mppt-2}$), the maximum lies in the interval $[a, I_{mppt-2}]$; otherwise, it lies in $[I_{mppt-1}, b]$. The search interval is then updated accordingly:

$$\left\{\begin{array}{c}b=I_{mppt-2},P\left(I_{mppt-1}\right)>P\left(I_{mppt-2}\right)\\ a=I_{mppt-1},P\left(I_{mppt-1}\right)\le P\left(I_{mppt-2}\right)\end{array}\right.$$

(23)

The iteration stops when the length of the search interval converges to a preset precision. The final maximum power point current is taken as the midpoint of the final interval:

$$I_{mppt,k}=(a+b)/2$$

(24)

3.2. PID Control

The PID controller is a classic feedback controller [40,41]. It is widely utilized in industrial control systems. It adjusts the control variable by performing proportional, integral, and derivative operations on the system error. In this way, it achieves precise system control. In fuel cell MPPT, the PID controller adjusts the DC/DC converter’s duty cycle ($d_{con}$). This ensures that the fuel cell operates at its maximum power point.

$$d_{con}\left(t\right)=K_{p}e\left(t\right)+K_i{\int }_0^{t}e\left(\tau \right)d\tau +K_d{\displaystyle \frac{de\left(t\right)}{dt}}$$

(25)

$$e\left(t\right)=I_{mppt}-I$$

(26)

Traditional PID controllers have limitations in fuel cell MPPT applications. Their parameters ($K_p$, $K_i$, $K_d$) are fixed and cannot adapt to the dynamic operating conditions of fuel cells. This can lead to suboptimal power output under varying loads and environmental conditions, affecting the efficiency and performance of fuel cells. To address this, the PID controller can be combined with an optimization algorithm. Particle swarm optimization (PSO) can be utilized to dynamically adjust the PID parameters. By optimizing these parameters, the controller can achieve optimal power point tracking under different operating conditions. The error ($e\left(t\right)$) is defined as the difference between the reference value of the maximum power point current ($I_{mppt}$) and the actual output current of the fuel cell stack ($I$). Here, $I_{mppt}$ is calculated online and in real-time by the aforementioned RLS algorithm and golden section method, serving as the reference target for the system. $I$ is the actual current measured by a sensor, providing feedback for the system.

In this process, the PID parameters $\theta$ become the objects to be optimized.

$$\theta =(K_p,K_i,K_d)$$

(27)

The objective function $E$ is designed as follows:

$$E=a_{1}e\left(t\right)+a_2{\int }_0^T\left|e\left(t\right)\right|dt+a_3{\int }_0^T{e}^2\left(t\right)dt$$

(28)

The objective function $E$ for optimization is composed of three parts: the instantaneous error term $e\left(t\right)$, the integral of absolute error term ${\int }_0^T\left|e\left(t\right)\right|dt$, and the integral of squared error term ${\int }_0^T{e}^2\left(t\right)dt$. The instantaneous error term reflects the tracking accuracy at the current moment. The integral of absolute error term measures the cumulative impact of long-term errors. The integral of squared error term emphasizes the penalty for larger errors. These terms enable the objective function to balance the system’s instantaneous response, steady-state performance, and sensitivity to large errors.

The parameters $a_1$, $a_2$, and $a_3$ control the weight of each part and can be set according to the actual situation. For instance, increasing the weight of the instantaneous error term can enhance response speed. Enlarging the weight of the integral of absolute error term can focus more on steady-state performance. Boosting the weight of the integral of squared error term can reduce the influence of large errors. By setting these parameters properly, the controller’s performance can be optimized for different operating conditions, ensuring good tracking accuracy.

To guarantee parameter stability during optimization, the PID controller’s parameters must meet certain constraints:

$$\left\{\begin{array}{c}{K}_{p-min}\le K_p\le K_{p-max}\\ K_{i-min}\le K_i\le K_{i-max}\\ K_{d-min}\le K_d\le K_{d-max}\end{array}\right.$$

(29)

The particle swarm optimization algorithm continuously adjusts the values of $K_p$, $K_i$, and $K_d$ to minimize the objective function $E$. This process optimizes the performance of the fuel cell MPPT system, improving the accuracy and stability of maximum power point tracking. Here, $K_{p-min}$, $K_{i-min}$, $K_{d-min}$ and $K_{p-max}$, $K_{i-max}$, $K_{d-max}$ represent the lower and upper search bounds for the proportional, integral, and derivative gains, respectively.

3.3. Particle Swarm Optimization Algorithm

The Particle Swarm Optimization (PSO) algorithm draws inspiration from the cooperative foraging behavior observed in bird flocks [42,43]. It leverages information-sharing among individuals to find the global optimum. With advantages like simple implementation and fast convergence, PSO has been widely utilized in complex optimization problems.

In this algorithmic framework, each individual entity, referred to as a “particle,” represents a potential solution within the multidimensional search space. The motion of each particle is influenced by two main factors: the best position it has personally encountered (termed personal best) and the best position found by the entire swarm (termed global best). By iteratively updating their velocity and position based on these benchmarks, particles gradually converge toward an optimal solution.

When employed to tune the parameters of a PID controller, each particle encodes a specific candidate set for the parameter vector $\theta$. The dynamics of the optimization process are governed by the following fundamental equations:

(1) Velocity update:

$$\begin{array}{c}{v}_i\left(t+1\right)=\omega v_i\left(t\right)+c_1{r}_1\left(p_i\left(t\right)-x_i\left(t\right)\right)\\ +c_2{r}_2\left(g\left(t\right)-x_i\left(t\right)\right)\end{array}$$

(30)

In the PSO framework, the term $v_i\left(t+1\right)$ represents the velocity of the $i$-th particle at iteration $t+1$. It governs both the direction and magnitude of its movement within the solution space. The parameter $\omega ,$ known as the inertia weight, plays a crucial role in regulating the trade-off between global exploration and local exploitation, thereby influencing the overall diversity of the swarm. The variable $p_i\left(t\right)$ refers to the best historical position discovered by particle $i$, and $g\left(t\right)$ is the global optimal position of the swarm. The interaction among these components guides the swarm dynamics, gradually steering particles toward regions with higher objective function values.

(2) Position update

$$x_i\left(t+1\right)=x_i\left(t\right)+v_i(t+1)$$

(31)

In each iteration, the position of particle $i$, denoted as $x_i\left(t+1\right)$ at iteration $t+1$, is updated to reflect the change in its parameter values.

Particles move based on their velocity and current position. The continuous updating of particle positions allows for the exploration of the optimal solution to the objective function. By evaluating the value of the objective function, PSO identifies a set of parameters that minimize the objective function.

3.4. Adaptive Particle Swarm Optimization Algorithm

The traditional PSO algorithm has some limitations. It may have a slow search speed and can also be prone to getting trapped in local optima. These issues are particularly evident under dynamic loads and complex environmental conditions. To overcome these limitations and enhance optimization efficiency and accuracy, an adaptive particle swarm optimization (APSO) algorithm is presented. It dynamically adjusts key parameters of the PSO to adapt to changing conditions.

In the APSO algorithm, the inertia weight $\omega \left(t\right)$ decreases gradually as iterations proceed. This strategy enables extensive searching in the early stages of the algorithm, preventing premature convergence to local optima. In the later stages, it focuses on more precise local searches to approach the global optimum. The update formula for the inertia weight is as follows:

$$\omega \left(t\right)={\omega }_{max}-{\displaystyle \frac{t({\omega }_{max}-{\omega }_{min})}{T_{max}}}$$

(32)

Here, ${\omega }_{max}$ and ${\omega }_{min}$ are the maximum and minimum inertia weights, and $T_{max}$ is the total number of iterations. As the inertia weight decreases gradually, the particles’ exploration ability in the search space diminishes, enabling more effective convergence of the optimization process.

The APSO algorithm dynamically adjusts the learning factors $c_1$ and $c_2$. These factors control the balance between the particles’ movement toward their personal best and the global best positions. When the swarm’s convergence is poor, the learning factors are increased to enhance global exploration. When the swarm is more converged, the learning factors are decreased to strengthen local search ability, thereby improving the algorithm’s precision during convergence. The update formulas for the learning factors are as follows:

$$c_1\left(t\right)=c_1\left(t-1\right)+{\alpha }_1(g\left(t\right)-p_i(t\left)\right)$$

(33)

$$c_2\left(t\right)=c_2\left(t-1\right)+{\alpha }_2(g\left(t\right)-p_i(t\left)\right)$$

(34)

In the APSO algorithm, ${\alpha }_1$ and ${\alpha }_2$ are dynamic adjustment coefficients for adaptively updating the learning factors based on the swarm’s convergence degree. This mechanism allows APSO to adjust flexibly according to the swarm’s convergence, avoiding premature convergence and local optima.

3.5. The Presented MPPT Control Strategy and Methodology

The overall presented MPPT strategy is shown in Figure 3, which primarily consists of four sequential stages to achieve efficient maximum power point tracking. First, the Recursive Least Squares (RLS) algorithm is employed to update the coefficients of the cubic power-current polynomial model online and in real time, ensuring the model dynamically reflects the actual output characteristics of the fuel cell. Second, based on the current polynomial fitting result, an initial estimate of the maximum power point current is calculated by solving the derivative. Subsequently, the golden section search method is introduced to establish a search interval around the initial estimate and precisely locate the maximum power point current $I_{mppt}$ through interval contraction. Finally, $I_{mppt}$ is utilized as the reference current for an Adaptive Particle Swarm Optimization (APSO) algorithm, which dynamically tunes the parameters ($K_p$, $K_i$, and $K_d$) of the PID controller to drive the boost converter for fast and accurate current tracking.

With these improvements, the APSO algorithm can better adapt to the complex conditions and dynamic load changes in fuel cell MPPT. During PID controller parameter optimization, APSO can find better parameter combinations in a shorter time, improving optimization efficiency and accuracy. This enables more efficient and stable maximum power point tracking. Consequently, the performance of the fuel cell system is enhanced across various operating conditions. The system can maintain stable operation at the maximum power point, improving the overall efficiency and stability of the fuel cell.

4. Results and Discussion

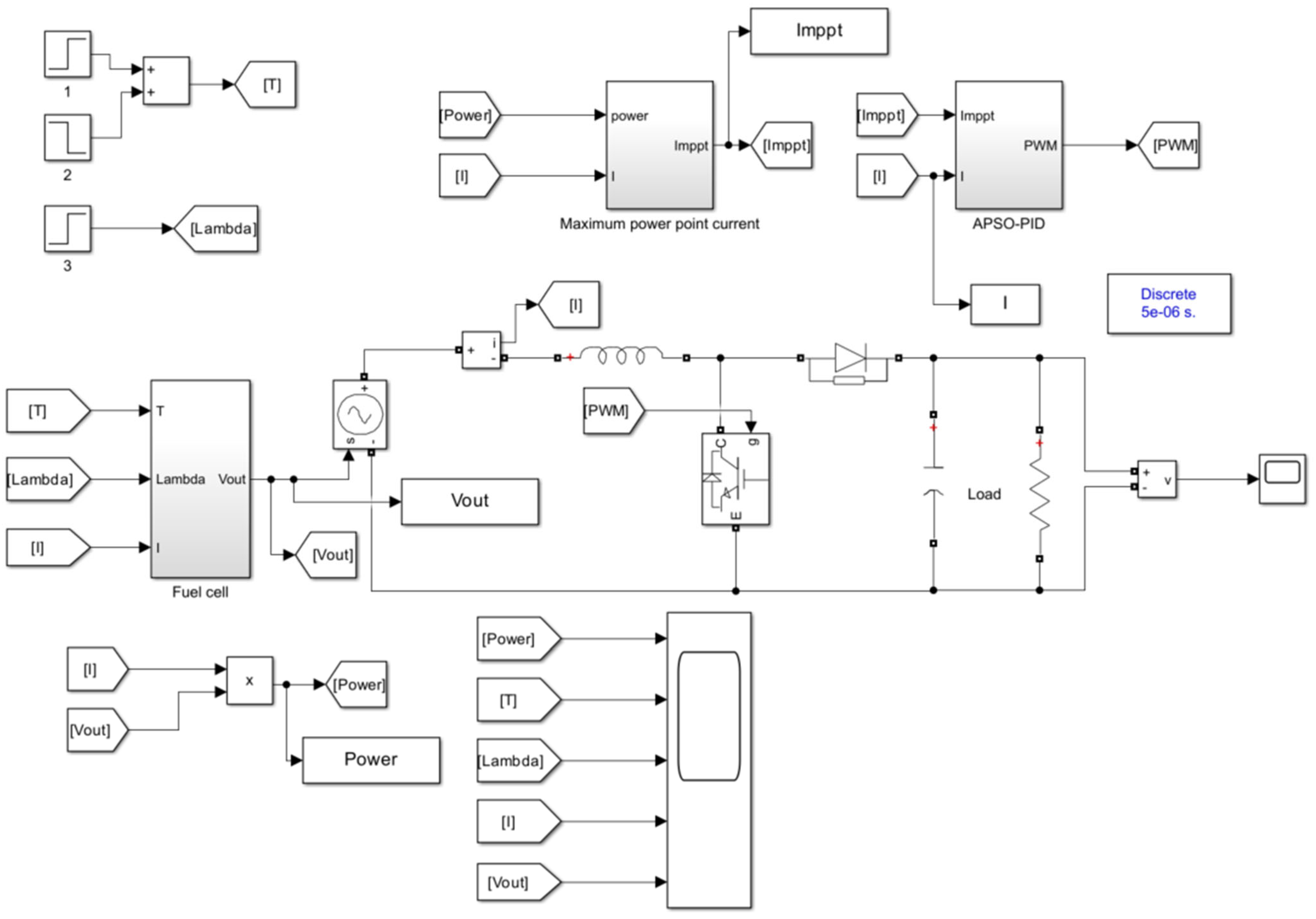
Based on the earlier modeling, a 7.2 kW fuel cell model was established in the MATLAB/Simulink R2024b environment. The detailed parameters of the model are listed in Table 1. The converter within the system operates at a switching frequency of 20 kHz. It has an inductance value of 0.5 mH, a capacitance value of 0.5 mF, and the output load is set to 10 Ω [44].

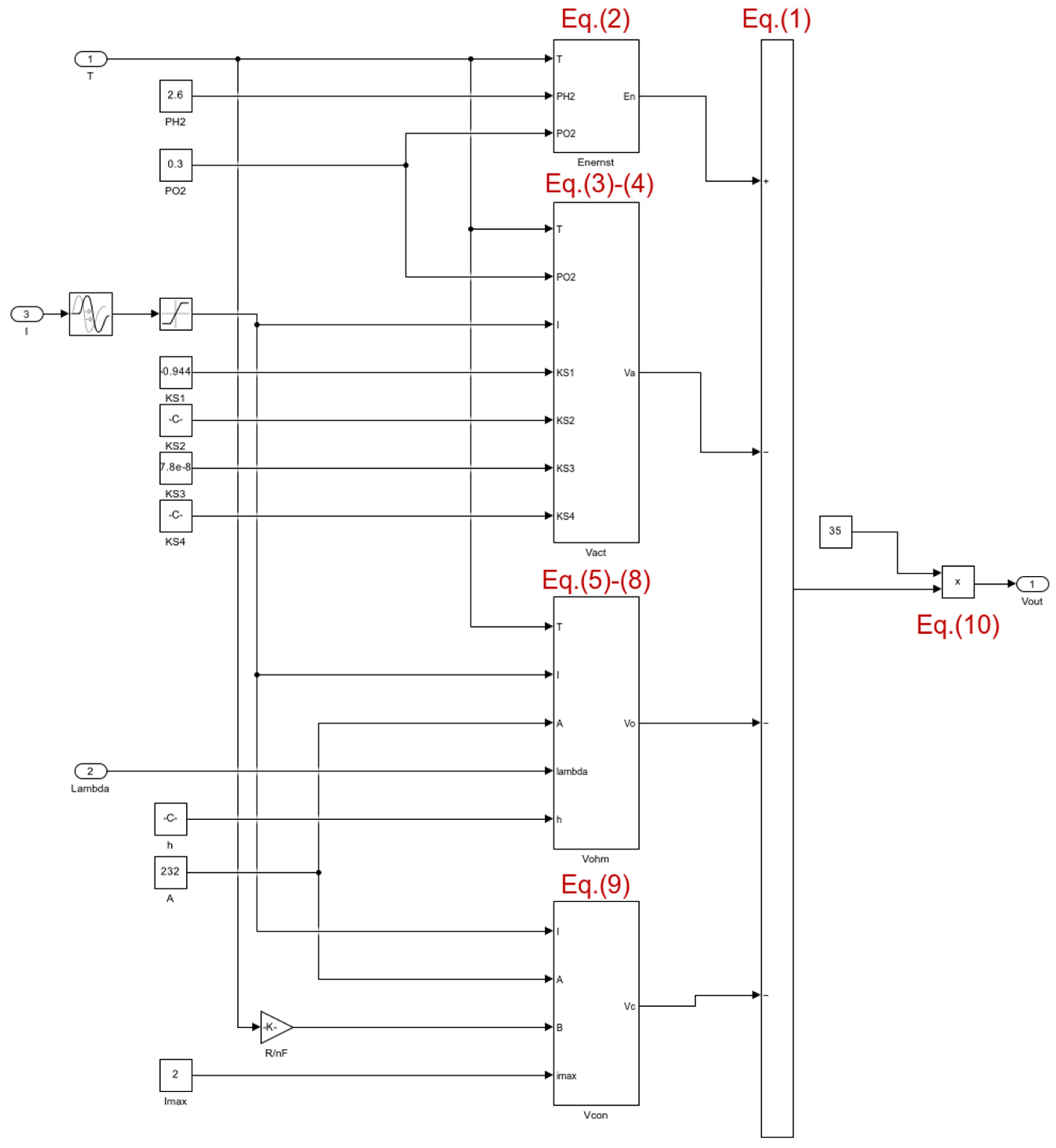
Figure 4 illustrates the specific modeling process and structure of the fuel cell. The comprehensive simulation of the entire fuel cell system, along with the implementation of the MPPT strategy, is depicted in Figure 5. These simulations are designed to test the efficiency of the presented MPPT strategy in maximizing power output under various operating conditions.

The performance of a fuel cell is highly dependent on its internal operating state, with membrane water content and temperature being two of the most critical parameters influencing its electrochemical characteristics and output performance. Membrane water content directly affects the proton conduction resistance, while temperature simultaneously influences reaction kinetics, gas diffusion rates, and membrane conductivity. As shown in Figure 6, variations in these two parameters significantly alter the fuel cell’s polarization curve and the location of the maximum power point. Therefore, different combinations of these two parameters were selected as dynamic operating conditions to conduct comprehensive and representative performance comparisons.

These results highlight that temperature and membrane water content are crucial parameters for fuel cell performance. Higher temperatures and optimal membrane hydration can optimize the fuel cell’s operating state and increase its output power. However, this also shows that MPPT strategies need to be more adaptive and flexible in different working conditions. To achieve efficient MPPT, real-time monitoring and analysis of these parameters are necessary. This allows for timely adjustments to the MPPT algorithm’s settings, ensuring accurate tracking of the maximum power point under various conditions. This dynamic adjustment is vital for enhancing the overall efficiency and stability of fuel cell systems, especially in complex and changing practical environments.

Therefore, the MPPT strategy presented in this paper combines an adaptive particle swarm optimization algorithm. It can adaptively optimize the PID controller parameters based on changes in temperature and membrane water content. This optimization not only improves the power-output efficiency of the fuel cell system under different conditions, but also enhances the system’s robustness against environmental changes. As a result, the system can operate stably and achieve maximum power output under various conditions.

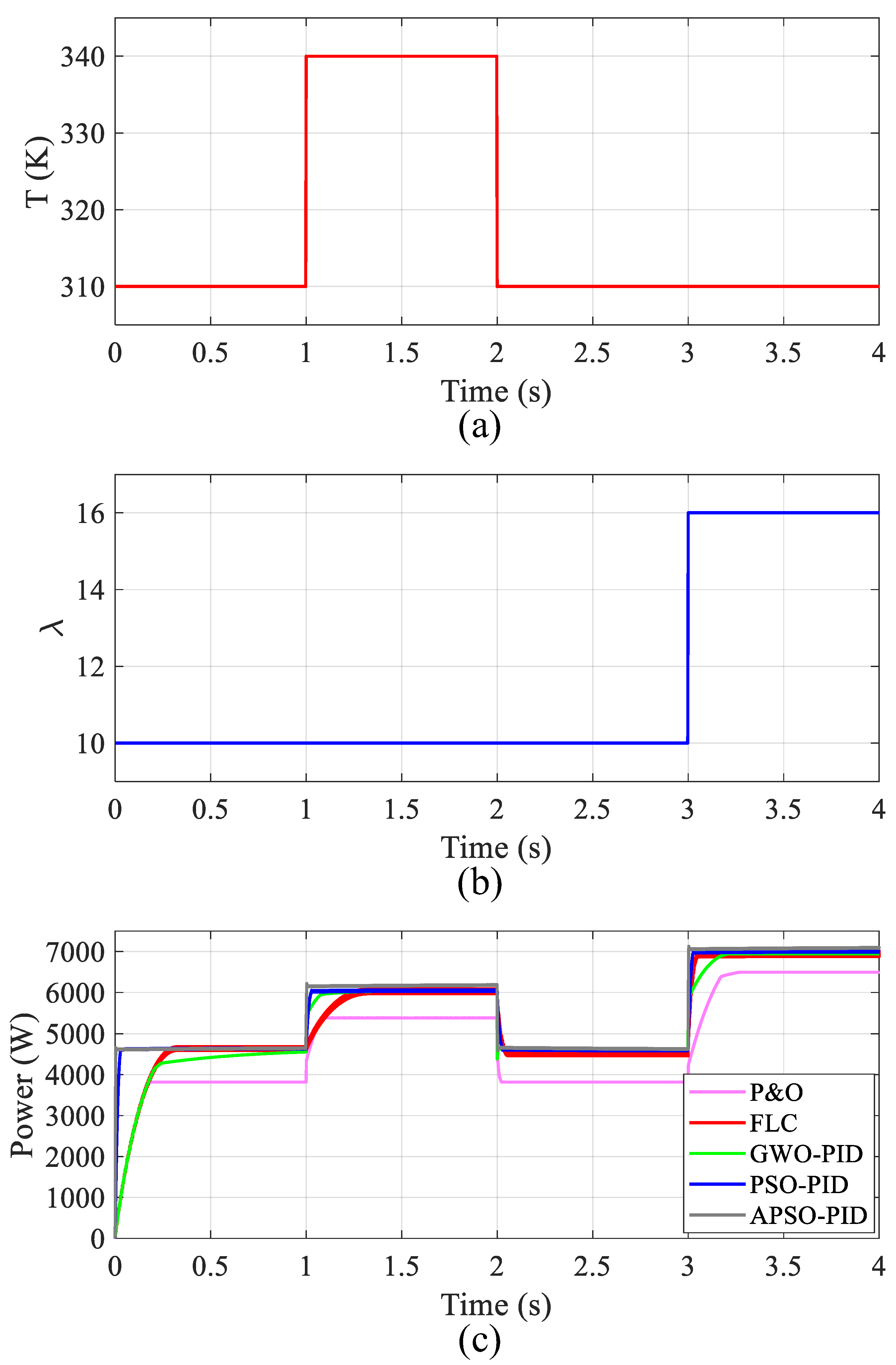
Experiments are designed for environments with dynamic changes in temperature $T$ and membrane water content $\lambda$. The performance of five methods—P&O, fuzzy logic control (FLC), GWO-PID, PSO-PID, and APSO-PID—is compared, as shown in Figure 7a,b. The specific experimental conditions are as follows:

0–1 s: $T=310 \mathrm{K}$, $\lambda =10$

1–2 s: $T=340 \mathrm{K}$, $\lambda =10$

2–3 s: $T=310 \mathrm{K}$, $\lambda =10$

3–4 s: $T=310 \mathrm{K}$, $\lambda =16$

In the temperature variation tests, the fuel cell’s output power increases significantly with rising temperature. This is because higher temperatures enhance the fuel cell’s electrochemical reaction activity, boosting its power output. From

Table 2. Comparison with other methods (output power).

Operating Conditions	Output Power (W)
	P&O	Fuzzy Logic Control	GWO-PID	PSO-PID	APSO-PID
T = 310 K, $\lambda =10$	3818	4619	4554	4626	4631
T = 340 K, $\lambda =10$	5377	6024	6029	6044	6136
T = 310 K, $\lambda =10$	3819	4520	4625	4601	4626
T = 310 K, $\lambda =16$	6493	6941	6946	6998	7045

and Figure 7c, the P&O method is shown to have the poorest tracking performance. When the membrane hydration is fixed at $\lambda =10$ and the temperature rises from 310 K to 340 K, the steady-state output power of all control methods increases. However, the APSO-PID method maintains the highest power output under both conditions. At 340 K, APSO-PID achieves 6136 W. This represents improvements of 12.40%, 1.86%, 1.77%, and 1.53% over P&O (5377 W), fuzzy logic control (6024 W), GWO-PID (6029 W), and PSO-PID (6044 W), respectively. This demonstrates the APSO-PID method’s ability to accurately track the fuel cell’s maximum power point under temperature changes, effectively improving output power. Its high control precision also gives it stronger adaptability in complex temperature environments, ensuring stable fuel cell operation under varying temperatures.

In the membrane water-content variation tests, the APSO-PID method again demonstrates superior performance. When the membrane water content increases from $\lambda =10$ to $\lambda =16$, with the temperature maintained at 310 K, the fuel cell’s power output shows further improvement. This reflects the performance enhancement under optimized humidity conditions. Under these conditions, a steady-state output of 7045 W is achieved by the APSO-PID method. This corresponds to improvements of 8.50%, 1.50%, 1.43%, and 0.67% over P&O (6493 W), fuzzy logic control (6941 W), GWO-PID (6949 W), and PSO-PID (6998 W), respectively. These results clearly indicate that the APSO-PID method possesses greater robustness and higher power tracking accuracy under varying humidity conditions. Consequently, it provides strong support for the efficient operation of fuel cells. Through precise control and continuous optimization, the APSO-PID method significantly enhances the overall performance of fuel cell systems in dynamic environments. This ensures maximum power output under diverse conditions, effectively meeting real-world energy demands.

Furthermore, as can be seen from Figure 7c and

Table 3. Comparison with other methods (convergence time).

Operating Conditions	Convergence Time (s)
	P&O	Fuzzy Logic Control	GWO-PID	PSO-PID	APSO-PID
T = 310 K, $\lambda =10$	0.18	0.30	0.45	0.03	Less than 0.03
T = 340 K, $\lambda =10$	0.08	0.31	0.23	0.03	Less than 0.03
T = 310 K, $\lambda =10$	0.02	0.05	0.02	0.03	Less than 0.03
T = 310 K, $\lambda =16$	0.27	0.05	0.21	0.03	Less than 0.03

, the results demonstrate that the APSO-PID controller achieves the fastest convergence speed (less than 0.03 s) under all tested conditions. Particularly under dynamic condition changes, APSO-PID maintains stable and rapid response characteristics, while other methods show considerable fluctuations in convergence time. Compared to PSO-PID, APSO-PID further optimizes convergence performance through its adaptive mechanism, verifying its superiority in complex operating conditions.

It is noted that the APSO-PID method achieves comprehensive improvements in dynamic response and steady-state accuracy. The P&O algorithm is characterized by low computational complexity and ease of implementation but delivers poor power output performance. In contrast, dynamic response is significantly enhanced in PSO-PID through PID parameter optimization via the particle swarm algorithm. However, limitations remain under complex operating conditions. Adaptive particle swarm optimization is incorporated in the APSO-PID method to adjust the search mechanism dynamically. Significant advantages are thus obtained in power output, dynamic tracking precision, and robustness.

Despite its advantages, the presented control strategy also has potential drawbacks and limitations regarding its applicability. First, the computational complexity of the method is significantly higher than that of conventional methods like P&O. The integration of online RLS identification, polynomial fitting, golden section search, and APSO optimization requires a relatively higher level of microprocessor computational power. This may increase hardware implementation costs and pose a challenge in applications with limited computational resources. Second, the effectiveness of the APSO algorithm is dependent on its initial parameter settings; inappropriate parameters may result in slower convergence speeds or convergence to local optima.

5. Conclusions

A novel strategy integrating online RLS identification, polynomial fitting, golden section search, and APSO-PID control is presented and validated for fuel cell MPPT. First, the recursive least squares algorithm is utilized to continuously update the parameters of a cubic power–current model. Polynomial fitting is then applied to obtain an initial estimate of the maximum power point current. Next, the golden section search is performed within the narrowed interval to efficiently locate the precise current $I_{mppt}$. Adaptive particle swarm optimization is subsequently employed to tune the PID controller parameters, achieving improved dynamic response and regulation. Experimental results demonstrate that the presented method delivers superior tracking accuracy and rapid response under dynamic loads and complex conditions.

Moreover, the integration of adaptive particle swarm optimization (APSO) with a PID controller allows for rapid adjustments and stable fuel cell operation under dynamic conditions. Experimental results demonstrate that the APSO-PID method reacts faster under complex conditions. It also shortens system adjustment time. Moreover, it outperforms conventional P&O, fuzzy logic control, GWO-PID, and PSO-PID methods in power output stability and efficiency. Specifically, in tests with varying temperature and membrane water content, the APSO-PID method achieves improvements of up to 12.40% compared to the P&O method. It also maintains a consistent performance enhancement of 1.50% to 1.90% over other intelligent control methods (fuzzy logic, GWO-PID, PSO-PID).

In summary, this study presents and validates an integrated strategy that combines real-time modeling, precise search, and adaptive control. Through the synergistic combination of RLS online identification, golden section search, and APSO-PID optimization, the presented strategy effectively addresses the MPPT challenges of fuel cells under complex operating conditions. It enables rapid tracking and stable control of the fuel cell’s maximum power point, offering a practical solution for efficient fuel cell operation. The results demonstrate that the proposed method not only significantly improves the dynamic response speed and tracking accuracy of the system but also provides new insights and technical approaches for fuel cell MPPT control.

A key limitation of this work is that the validation was performed solely through simulation, lacking experimental verification on a physical hardware platform. Furthermore, the impact of measurement noise and external disturbances on system performance was not thoroughly investigated in the current study, and its noise immunity requires further evaluation. To address this, future research will be directed toward establishing an experimental platform for model validation, followed by an investigation into its practical applications in real-world engineering contexts.