1. Introduction
The rapid electrification of industrial transport continues all over the world, which is especially important in the context of large-scale mining and metallurgical enterprises, where the efficiency of cargo transportation determines not only economic stability, but also industrial safety [
1,
2]. Electrified transport reduces operating costs by up to 20–30% compared to diesel locomotives, reduces CO
2 emissions by up to 40%, and simplifies the maintenance system [
3]. However, one of the most vulnerable elements of the infrastructure remains the electric traction system, namely the contact network (CS), which operates in harsh climatic and operating conditions [
4]. This problem is especially acute in networks installed on temporary supports in open-pit mines and faces, where there is no reserve and reliable grounding, which significantly complicates ensuring electrical safety and stable operation of the system [
5,
6].
The most difficult task in such conditions is protection against short circuits (SC) [
7], when the short-circuit current can be commensurate with the load current and be less than 600–800 A, with a standard feeder load of 700–1000 A. In these cases, traditional protection methods are ineffective. The development of solutions capable of providing selectivity and speed of response at low short-circuit currents requires an individualized approach, which has become the subject of numerous studies in the last two decades [
8,
9].
One of the classical approaches to solving the problem is the use of maximum current protection (MCP) with a fixed setpoint. Such protections are easy to implement and are widely used in urban and trunk railway networks. The works [
10,
11,
12] provide data according to which the average accuracy of MCP operation at short-circuit currents above 2 kA is 92–95%. However, when the current decreases to the level of 600–800 A, the level of selectivity drops to 55–60%, and the number of false trips triples. This makes MCP inapplicable in the conditions of the distant feeder section (DFS), where the real value of the short-circuit current at a remote point can be only 400–600 A with a feeder length of 3–5 km and a wire cross-section of less than 100 mm
2.
Another method that has been developed in recent years is the use of differential current protection (DCP), which is based on the comparison of input and output current. In a number of publications [
12,
13], it is noted that the protection efficiency increases to 97% in feeder zones with a length of no more than 1 km, while the minimum short-circuit current, which is reliably recognized, is about 800 A. However, when the line length increases above 2 km and external industrial interference appears (for example, in the areas of operation of crushing plants and conveyors), the accuracy drops sharply and false positives increase to 15–18%.
The third direction of development was adaptive protection with digital control of setpoints depending on the current network parameters. Ref. [
14] has developed a system in which, based on online measurements of resistance and voltage, a forecast of current changes in case of possible short-circuits is built. Such systems demonstrate sensitivity at the level of 500 A and above at line lengths up to 10 km and have shown a 35% reduction in system recovery time after an accident in test conditions. However, they require expensive equipment, including PLCs, digital transformers, and remote sensors, which limits their use in the field.
Numerical methods based on mathematical modeling of transient processes in traction networks remain a promising direction. Works [
15,
16], as well as studies conducted in recent years [
17], show that the use of computational models of circuits, including the parameters of circuits, transformers and arcs, makes it possible to determine the setpoints of protective devices with high accuracy (up to 93–97%) even at low short-circuit currents. Taking into account the active and reactive resistances, as well as the characteristics of the shunts and relays of the residual current relay (RDS), it is possible to determine the optimal setpoints at current short circuit at 450 A, initial load current on the line
Il = 800 A and time constant of the differentiating circuit
L/
R≈0.3 s. The ratio
L/R in an electric circuit is the time constant of the differentiating circuit, where
L is the inductance of the coil in henries and
R is the resistance of the resistor in ohms [
18]. This value shows how quickly the steady state is established in the circuit after a disturbance. With a higher inductance, the circuit stores energy longer, and a higher resistance, on the contrary, accelerates the dissipation of energy. The disadvantages of the method are the complexity of implementation and the need for regular updating of parameters when changing the network configuration.
In addition to this, in recent years, the possibilities of using artificial intelligence methods, in particular neural network algorithms, have been actively explored. In the paper [
19], data are presented, according to which the transient current analysis system, trained on a sample of 20 thousand emergency modes, achieved a short-circuit recognition accuracy of 92%, with a decision-making time of less than 100 ms. However, such systems require a highly organized database, regular replenishment of the training sample and a stable communication channel, which so far makes them applicable mainly in the conditions of stationary objects [
20,
21].
All of these approaches suffer from a number of limitations in one way or another: insufficient sensitivity in remote areas, high cost, susceptibility to electromagnetic interference or difficulty in adapting to non-standard contact network schemes [
22]. The problem becomes especially relevant when the contact network of mining equipment (ME) is mounted on light movable supports without grounding on the rails, and the spreading resistance can reach 10–20 Ohms. Spreading resistance is the transition resistance at the point of damage to the contact network of electrified railways, which can reach 10–20 Ohms if the supports are mounted on light movable supports without grounding to the rails. This value affects the reliability of the relay protection—it cannot recognize and disconnect the emergency section, since the current flows down the support into the ground. At the same time, the real short-circuit current is reduced to the level of 300–500 A, and traditional protections simply do not work. This creates conditions for the development of arc faults, which often turn into fires and damage to equipment [
23,
24]. In this case, the basis for the protection of the traction contact network is an individual calculation of current and impulse protection for each zone of the feeder, taking into account the parameters of the power supply network, contact network, type of switches and relays [
7]. The proposed algorithm uses differential equations of transient processes of the traction contact network, which are numerically solved to determine the tripping characteristics, taking into account the dynamic sensitivity coefficient (
Kd). Dynamic selectivity of traction network current protection is an operating principle in which only the protection in the protected circuit in which an overcurrent has occurred is actuated, while the rest of the network remains in working condition. This is achieved by matching the operating characteristics of the protection devices. For example, in a traction network, dynamic selectivity is implemented in overcurrent protection with a time delay [
25]. The implementation of the tuning algorithm is possible on existing equipment with minor modernization of circuit breakers and the use of existing digital relays [
21,
26]. Thus, the purpose of this study is to develop, theoretically substantiate and experimentally test the method for setting up the settings for current and pulse protection of traction networks of mining enterprises, which provides high selectivity, resistance to interference and sensitivity at low short-circuit currents. The implementation of this technique makes it possible to significantly increase the reliability of the contact network, minimize equipment downtime and ensure the safe operation of electric rolling stock in conditions close to extreme.
This paper solves the problem of increasing the sensitivity and selectivity of current protection under conditions of a limited short-circuit current range, unstable contact connections, as well as without the need for cardinal modernization of the equipment. The main gap in existing research is the lack of methods that allow the formation of setpoints taking into account transient processes (impulse current surges), and not only at the stationary level. In addition, there is no engineering-oriented model describing the interaction of the characteristics of switching equipment and the parameters of the supply network for setting up protections.
The authors’ contribution lies in the development of:
methods for analytical construction of the sensitivity characteristics of pulse current protection based on the parameters of switching devices and transient processes;
an algorithm for calculating dynamic setpoints using relative coordinates, which makes it possible to unify the approach to different sections of the network;
substantiation of the design modernization of standard circuit breakers, relays and other electrical equipment to reduce the minimum tripping threshold;
experiments with different types of switches and relays, confirming the applicability of the approach under typical and non-typical conditions;
models of scalability of results and recommendations for transferring the technique to other types of equipment (including imported relays, microprocessor automata).
Thus, the work fills an important gap in engineering practices for the protection of contact networks of quarry transport and provides a reproducible methodology with an expanded range of applicability.
Despite the diversity of protection approaches in traction networks, existing methods fail to ensure sufficient selectivity and sensitivity under low short-circuit currents in complex field conditions. Particularly in contact systems installed on temporary supports without proper grounding, traditional MCP and DCP methods demonstrate a high rate of false trips and missed fault detection. Therefore, the motivation of this study is to address the lack of a robust and cost-effective solution for these conditions. The primary objective of this work is to develop and validate a novel method for setting current and pulse protection parameters based on transient process modeling, which improves sensitivity, minimizes false alarms, and does not require complete equipment replacement.
Therefore, the core research question addressed in this study is: how can current and impulse protection be configured to ensure reliable short-circuit detection and disconnection in traction networks with low fault current levels, without relying on expensive adaptive digital systems? The main objective of this research is to develop, validate, and experimentally verify a method for setting protection parameters based on transient process modeling and the use of a dynamic sensitivity coefficient (Kd). This method aims to increase protection selectivity and sensitivity under real operating conditions in mining traction networks, while remaining compatible with existing switching equipment.
The key contributions of this work are:
- -
the introduction of a dynamic coefficient (Kd) for characterizing protection sensitivity across feeder zones with variable time constants;
- -
development of universal tripping curves in normalized coordinates applicable to diverse equipment;
- -
experimental validation of the method with circuit breakers and relays used in mining networks;
- -
demonstration of enhanced selectivity (up to 95%) and reduced false trips (by 40–60%) without replacing existing protection hardware.
This paper addresses a key gap in protection design for low-SC current environments by introducing a parameterized method based on transient modeling and dynamic sensitivity coefficients. The proposed solution enables tailored protection settings without reliance on expensive adaptive systems, and is validated through experimental testing on typical mining traction equipment.
The following designations of electrical parameters and their dimensions are used in the text of the article, as given in
Table 1.
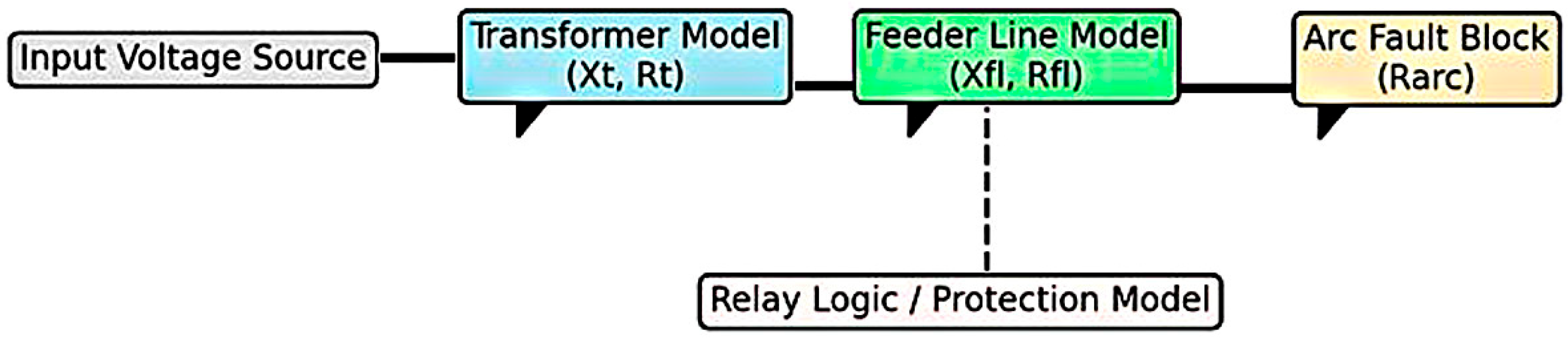
4. Mathematical Model for Estimating Short-Circuit Currents Based on the Traction Network Replacement Scheme
Determination of the load and short-circuit current according to clause 2 of the algorithm is carried out taking into account the parameters of the transformer substation and the network to which it is connected. When calculating short-circuit currents near the transformer substation and at the end of the feeder zone, reactive and active resistances of the external power supply networks
Xs and
Rs, traction transformers
Xt and
Rt, contact network and cables
Xfl,
Rfl are taken into account, as well as the resistance of the electric arc at the point of a short circuit. The calculation of short-circuit currents for the transient mode should be carried out taking into account the external characteristic of the EMF source, i.e., the traction substation (TS) [
44]. For the circuit of the rectifier at a short circuit at a remote point at (
Ik <
I′k), the current can be determined by the formula
and for a three-phase bridge scheme
where
Uv0 is the phase voltage of the secondary winding of the traction transformer; and
d is the voltage drop in the electric arc;
N is the number of transformers;
Kv is the control coefficient equal to 1.05, and for regulated converters—1.4;
s is the number of series and
a—parallel semiconductor devices (NGS) in the rectifier phase;
Ri is the internal resistance of one NGN.
Relations (1) and (2) for determining the short-circuit current in the contact system are valid for the linear part of the external characteristic (I-I), when the short-circuit current is less than the critical
Ik <
I′k, which means that the external characteristic is nonlinear. To determine the currents of the protection setpoints, the voltage
Uv0 is taken as the minimum, with the control factor
p = −1.05, and the coefficients
Kv = 0.95 and
N = 1. The linearity of the external characteristic of the transformer substation depends on the inductance of the secondary winding of the converter transformer. The point of transition of the linear part of the I-V to the nonlinear part occurs at the short-circuit current corresponding to the expression
The short-circuit current in the steady-state mode can be found by the joint solution of the relation (3) with the equation
Thus, it is possible to determine the short-circuit current on the busbars or at the near point of the CS (100–500 m) from the transformer substation, where (
Ik > I′k) for the zero-rectification scheme is defined as
and for a three-phase bridge scheme
When calculating the maximum current SC, the value
of Uv0 should be taken 5% more than the nominal value. The values of
Xt,
Rt are determined according to the passport of the converter transformer;
Xs,
Rs are the parameters of the external power supply system in (1), (2), (5) and (6), which lead to the voltage of the valve winding of the traction transformer as
The resistance of the contact system
Rks when calculating the short-circuit current on the substation busbars is taken according to the actual cross-section and length of the feeder and suction cables, ignoring these resistances gives a significant error [
45].
The shock current of the short circuit [
16] during the transient process for the rectifier is
here
Ksd is the coefficient of thermal resistance of power semiconductor devices (P) according to the manufacturer’s passport,
Ik is the change in current in the circuit during a short circuit. Typical parameters of the traction network under consideration are given in
Table 3.
Approximate values of short-circuit currents at various points of the power supply system of the traction network of the ME for the most common capacities of converters and transformer substations are given in
Table 4.
In power supply systems supplied from distribution networks with a voltage of 6–10 kV, the short circuit on the rectified current side (i.e., behind the traction substation converter on the length of the traction contact network) is remote, so the transient attenuation factor in the external power supply system [
46] is assumed to be equal to unity. In this case, the parameters of the external power supply system
Xs and
Rs are not taken into account, but they are taken into account approximately through generalized design parameters: power
Sk or current
Ik SC on 6–10 kV busbars of the traction substation [
47].
The resistance of the external power supply system is expressed in relative units
where
Sm is the rated power of the converter transformer; if the short-circuit power is unknown, then
Ic* = 0.5
utc* (half of the short-circuit voltage of the traction transformer) is taken, and the transition of the linear part of the external characteristic into the nonlinear part occurs at a short-circuit current equal to six or more short-circuit current values, i.e.,
I′
k ≥ 6
Idn. The maximum value of the short-circuit current, for example, for a zero circuit, can be determined by the formula
and at a remote point of the traction network
where
Rw,
Rcn,
Rt are the resistances of the supply and exhaust wires, the contact network and the phase of the converter transformer, respectively;
Req is the equivalent resistance of the substation, approximately equal to
, where
is determined by (10). This is a simplified analytical calculation; it can be used for short feeder zones or in preliminary calculations, and it gives an error of about 15–20% in relation to the calculation according to Formulas (1)–(8).
Electricity consumption for traction
A1 for a certain averaging period
t (month, year) can be obtained from the automatic metering system or monthly reports of the power supply distance [
18,
19]. The maximum current of the line in the presence of an electric meter on each feeder can be determined by
where
Uave is the average voltage on the buses of substation B;
Tt is the averaging time for which
At is taken (characteristic days of the month);
Kmt is the coefficient of maximum train current determined taking into account the power of the engines of an electric locomotive and dump cars as
where
N is the number of engines of an electric locomotive;
Php is the hourly power of the traction motor, kW;
n0 is the number of trains on the line;
Kef is the coefficient of efficiency of train current according to [
13,
14], in the absence of electric meters, the train current can be determined by the specific energy consumption for traction according to the reading of the transformer substation meter and the volume of traffic for the design period (separately summer and winter months) [
15], then the maximum current of the line is equal to
where
Asp is the specific energy consumption for thrust, W‧h/t‧km, determined experimentally for each ME;
G is the average value of the total weight of the electric locomotive, t;
m is the number of motor units (4 pcs in an electric locomotive);
Vo is the operating speed, km/h;
Uc is the average voltage in the traction network, V (according to PTE).
Train starting current given train traction motors parameters
where
npairs are the number of pairs of electric motors at the end of the starting mode (parallel connection);
nm is the total number of electric motors in the electric locomotive and motor dump cars;
Ug is the rated voltage across the electric motor manifold, V;
η is the efficiency of the engine according to the certificate of the manufacturer of the electric rolling stock [
48,
49].
The current of protection setpoint
Iu is selected from the short-circuit current value determined by (1) or (2), taking into account the feeder load current determined by (12) or (13) from the condition
where
In.
max is the current that does not trigger protection under load with a certain margin Δ
I = 100 A;
Isc.
min is the short-circuit current that causes the protection to trip with a certain margin
of Δ
I = 300 A. This condition is used to adjust the maximum current protection (MCP).
In practice, there is often a situation when at the end of the power section of the traction contact network
In.max ≤
Isc.
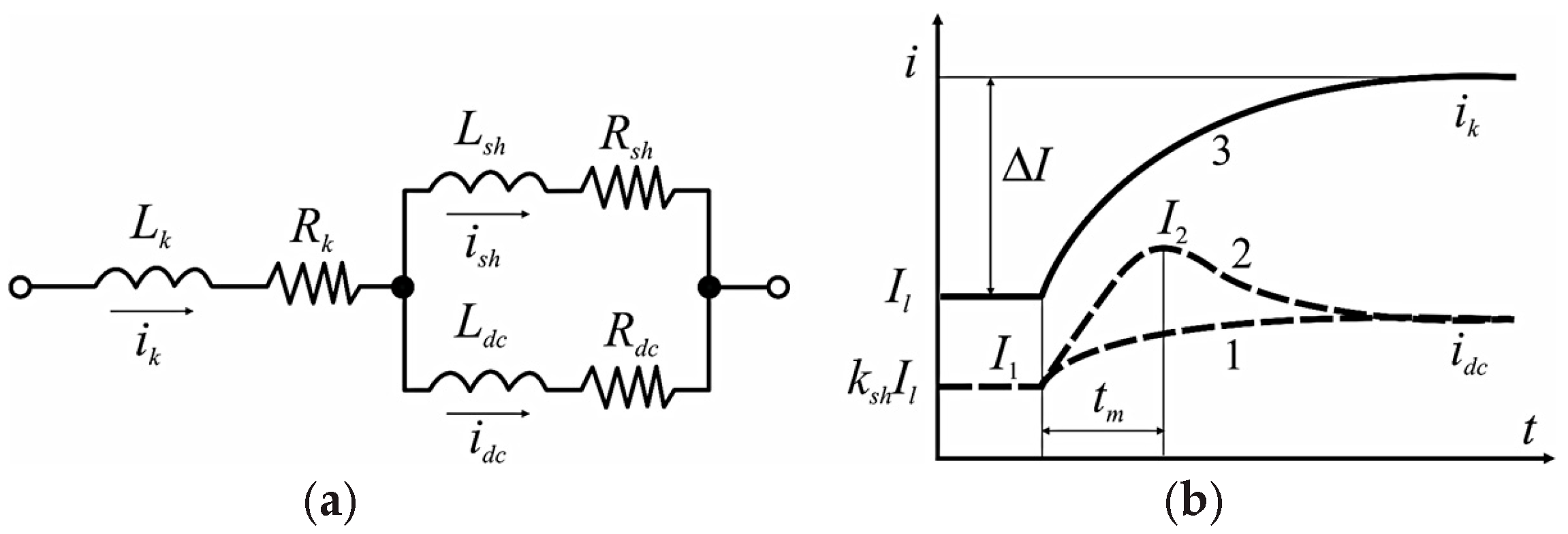
min and condition (15) cannot be met, so the high-speed circuit breaker or the residual current relay is equipped with an inductive shunt (
Figure 3). To analyze the operation of the inductive shunt, a scheme was drawn up for replacing the supply circuit of the traction network section, where the vehicle is represented by the parameters
Rk,
Lk or RDS relay (
Figure 4), demagnetizing the turn of the circuit breaker or relay. The active resistance and inductance of the demagnetizing coil are designated
Ri and
L, respectively. The active resistance and inductance of the inductive shunt are designated
Rk,
Lk, respectively.
The following notations are introduced in
Figure 4:
Il is the initial load current on the line;
ksh Il is the fraction of the load current taking into account the influence of the inductive shunt;
I1,
I2—currents at the initial and final stages of the transient process;
tm is the transient time; Δ
I—current increment (surge);
ik is the change in the current in the circuit during a short circuit;
iDC is the transient current in the demagnetizing turn;
Rk,
Lk—active and inductive resistance of the traction network;
Rsh,
Lsh—active and inductive resistance of the inductive shunt;
Rdc, Ldc—active and inductive resistance of the demagnetizing turn;
Ish >
idc—currents in the inductive screw and demagnetizing coil; 1—current graph in rod mode; 2—current surge in case of short circuit; 3—theoretical current change function.
The electric circuit (
Figure 2) for time
tm can be described by a differential equation
For an active-inductive circuit under the exponential law of current change SC
ik, Equation (16) is solved for the increment Δ
I =
I2 −
I1 as
After numerous transformations and substitutions of the parameters of the circuit breaker or relay, the expression of the tripping characteristic for the time constant of the current circuit
T1 =
L/
R = const, i.e.,
here
is the current surge that causes tripping at the initial load current
I′
0ave, and the coefficients
B and
C characterize the parameters of the circuit breaker or relay [
50]. Equation (18) is a straight line in segments (
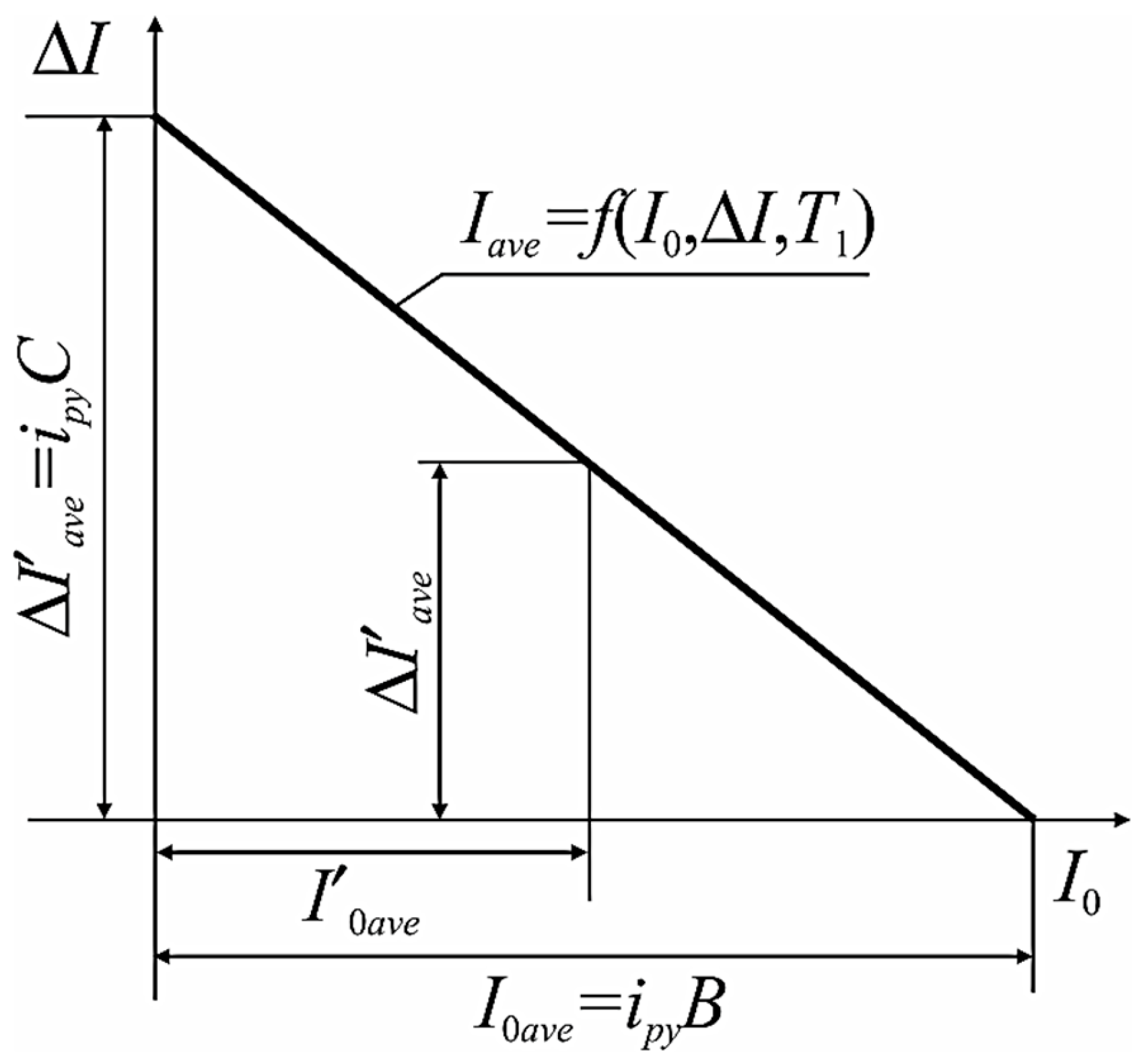
Figure 5) and is a characteristic of the tripping of the current–pulse protection.
If
I′
0ave = 0 we have Δ
I′
ave = Δ
Iave =
ipy/
C, if Δ
I′
ave = 0 we get
I′
0ave =
I0ave = I0ave =
ipy, taking into account these conditions, we obtain the equation of actuation of current–pulse protection in current arguments.
The values I0ave and ΔIave are, respectively, static, i.e., MCP, and dynamic, i.e., MIP of the protection setpoint, the latter depending on the time constant T1.
In the real world,
T1 can be more complex dependent on
I0. Therefore, in order to construct a protection trip characteristic for a particular line with known parameters of the switch or relay of the RDS, it is necessary to know how its dynamic setpoint changes as the circuit’s time constant changes. Ratio Δ
Iave/
I0ave = 1/
CB =
Kd characterizes the sensitivity of the switch or relay of the RDS to current surges and is a dynamic coefficient. The minimum value of
Kd corresponds to the time constant of the network
T1 = 0, in this case we have (see the notations in
Figure 4):
where
L1,
L2,
r1,
r2 are, respectively, inductive and active resistances of busbars of larger and smaller (with iron packages) cross-section (
Figure 4).
The maximum value of Kd will reach at T1 ≥ T1cr = Tsh when tmax = ∞, and the static setpoint is equal to the dynamic setpoint. Since in this case C = 1/B, then Kd.max = 1.
For the section of the traction network protected by the BAT-49 circuit breaker, the tripping characteristics were experimentally obtained at
T1 = var, where
T1(
n + 1) >
T1(
n) for different load currents
I* (
Figure 6), and the tripping characteristics can be similarly constructed for the relays RDSH-II, RPT-206 and others. It is possible to obtain the tripping characteristics [
51] for a specific section with less time with the specified parameters and type of switch or relay of the RDS on a mathematical mode [
52].
It is more convenient to construct the characteristics in relative units to the current of the set point
I, in this case each subsequent oblique
Iave =
f(
I0,
ΔI, T1) will correspond to the time constant
T = Lj/
Rj (i.e., the parameters of the CS at the selected point) and establishes a connection between the current surge causing the disconnection Δ of
Ic, and currents
I before the jump
I* =
I/
Iu (
Figure 5 and
Figure 6) and Δ
I* = Δ
Ic/I. The dotted line shows the procedure for checking the protection for tripping at current
I*1, jump Δ
I*1 for the section of the contact network corresponding to
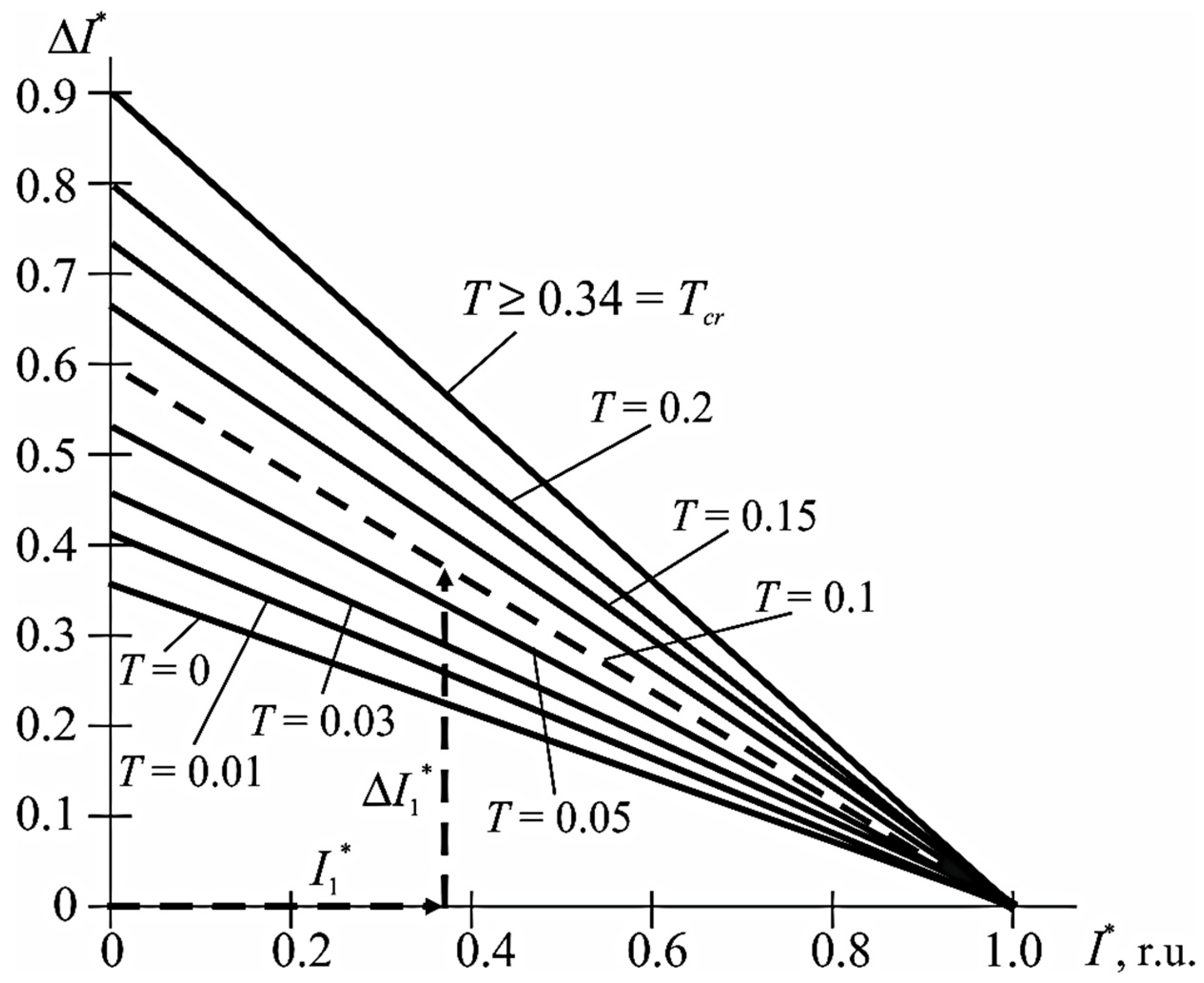
Tc = 0.1 s.
When constructing the characteristics, in addition to the parameters of the contact network, it is necessary to know the parameters of the BV and the RDS relay (
Table 5), which were obtained by the authors experimentally. For current surges with a time constant greater than some critical
Tcr, which, for example, for BAT-49, is equal to 0.34 s, the BV reacts to surges with an infinitely large value of
Tc, i.e., as to a steady current, in this case we have a static setpoint or MCP.
As an example of upgrading circuit breakers to adapt the dynamic coefficient,
Table 2 shows its values for the VAB-43-4000/30 with the shunt iron packs reduced against the usual length by 25 and 50% of the initial length, respectively, and for the RDS relay with the shunt iron packs reduced against the usual length by 25, 50 and 75% of the initial one, respectively, which for a particular section gives a reduction in the number of false protection trippings. From
Figure 4 it follows that each of the protection characteristics corresponds to a constant of the rise time of the short-circuit current at a given point of the TS, thus the inclined line with
T = 0 is the characteristic of the MIP actuation on the buses or at a short distance from the TP, and the inclined line with
T ≥ 0.34 is the characteristic of the MIP actuation at the end of the feeder zone.
For example, if the load current is equal
to I* = 0 and the time constant is equal to
T = 0.1 s, for the BAT-49 circuit breaker, the setpoint in relative units in terms of current increment will be determined as Δ
I*
y0= 0.34 (
Figure 4).
If
tm > 0.34, then as you move away from the TP, the time constant of the circuit increases and the MIP becomes less sensitive to current surges, and conditionally, at the end of the line, the protection acts as MCP. (
Figure 3 and
Figure 4), i.e., the MIP of this circuit breaker is not sensitive to current surges and the protection works as an MCP with the Δ
Iy* =
Iy setpoint. The value of the time constant
T =
L/
R, when the equality Δ
Iy* =
Iy is observed (in the example, this is at
T = 0.34 s,
Figure 4) denotes
Tcr and is called the critical constant, it separates the response areas of the MCP (in this case, at
t > 0.34 s) and the MIP (
tm < 0.34 s).
4.1. Experimental and Simulation Results
To facilitate comparison, the key results obtained for different
Kd values and device configurations are summarized in
Table 6 (minimum trip current values) and
Table 7 (response times). These tables help to highlight general trends, such as the reduction in trip thresholds and acceleration of protection response as
Kd increases.
As shown in
Table 6; the minimum trip current decreases consistently with higher values of
Kd, reflecting enhanced sensitivity. Similarly;
Table 7 confirms a reduction in trip response time; indicating improved reactivity. These trends are consistent across both experimental and simulation environments, validating the dynamic behavior of the proposed method
4.2. Comparative Performance Evaluation
To evaluate the practical benefits of the proposed method, a comparative analysis was conducted with traditional MCP, DCP, and a standard adaptive protection approach. All methods were tested under the same simulated fault scenarios and network parameters. The key evaluation metrics included:
Sensitivity (the lowest detectable fault current).
Selectivity (correct zone discrimination rate).
Average Trip Time.
False Tripping Rate (percentage of incorrect operations in healthy branches).
The results are summarized in
Table 8.
5. Results and Comparison with Existing Methods
Unlike prior approaches, which rely on fixed or empirical setpoints, our method provides a scalable and equipment-adaptive configuration strategy [
53]. This transition from heuristic to parameterized setting improves the engineering predictability of protection systems. In the course of experimental studies and simulations, numerical characteristics of sensitivity and protection coverage were obtained, confirming the effectiveness of the proposed approach [
54]. Analytical dependencies of current protection actuation in the form of a family of characteristics at different network parameters were constructed. These dependencies relate the value of the required short-circuit current (SC) increment for protection actuation with the initial load current and the transient process time constant. On the basis of the equations obtained, the areas of guaranteed protection operation for the specified parameters were determined, which makes it possible to move from the empirical selection of setpoints to the calculated selection with a given accuracy. The formation of such a database of characteristics (a library of setpoints) for various types of circuit breakers and relays has increased the objectivity and reproducibility of the current and pulse protection setting. To further demonstrate the dynamic adaptability of the proposed protection scheme,
Figure 7 shows the simulated current waveform and trip signal for fault case
F3 under
Kd = 0.9. This figure highlights the rapid drop in tripping delay and confirms effective discrimination from background noise.
Figure 7 shows the dependencies of the required relative increment of current
ΔI for tripping protection against the relative initial current
I0 at different values of the circuit’s time constant
T. The smaller the
T (steeper short-circuit edge), the smaller the current surge required for tripping–the graph has a lower slope (curve
T = 0.1
s, red) and lies well below the standard static MCP (black dashed line) setpoint. As the time constant increases to the critical value of T (for this circuit breaker,
Tcr = 0.34 s, blue curve), the sensitivity of the pulse channel decreases–the curve is located higher, approaching the static characteristic. An almost horizontal dotted line
Tcr actually separates the coverage areas of maximum current protection (right, for slow current rises) and maximum impulse protection (left, for fast current inrushes). Thus, the pulse actuation principle extends the range of sensitive fault detection below the threshold of the classic MCP, which is especially important for small short-circuit currents.
It has been experimentally confirmed that the use of the developed tuning technique can significantly increase the sensitivity and reliability of protection. In particular, it has been established that for a high-speed circuit breaker of the BAT-49-4000/30L type, the setting of dynamic (pulse) current protection at a constant time t = 0.1 s is achieved at a relative increase in current ΔI = 0.34. In other words, the required current surge for tripping is only ~34% of the baseline (at zero initial current), which guarantees a trip of ΔI ≥ 0.34·Iu (where Iu is the basic setpoint current) at a given point in the network. For the RDSh-II type differential relay, characterized by increased sensitivity, the minimum experimentally achieved value of the dynamic coefficient was Kd = 0.341. Such a low Kd means the ability of the protection to reliably detect short circuits even in remote sections with high resistance–it has been experimentally shown that protection with the RDSh-II relay provided selective shutdown of an accident at a distance of up to 3–5 km from the substation. At the same time, the static current protection setpoint MCP was selected as equal to the load current with a margin of about 100–150 A, and the calculated minimum values of the short-circuit current of the traction network, at which guaranteed tripping was provided, lay in the range of 650–950 A, depending on the parameters of the feeder. These results confirm that even at very low fault currents–comparable to or only slightly higher than the operating load–the proposed surge current protection is able to detect and disconnect a short circuit in time.
For example, with a load current of
I = 800 A and a short-circuit current
of Isc = 850 A, the classical overcurrent protection does not work, because the difference of 50 A is not sufficient to exceed the fixed setpoint with the required margin. And to avoid false outages, the MCP threshold is set above 850 A–as a result, an accident on the line remains undetected. The proposed impulse protection algorithm takes into account the parameters of the transient process and the value of the initial inrush current: even with a slight overcurrent (tens of amperes), due to the analysis of the current slew rate and relative increase Δ
I, the protection correctly recognizes CS and disconnects the line. This is especially important at the end of the feeder zone, where a significant voltage drop and line resistance reduce the CS current to levels dangerously close to the operating current, worsening the conditions for traditional methods. The use of relative coordinates (Δ
I* = Δ
I/Iu and
I* = I/Iu) made it possible to reduce all experimental data to a unified form and to construct universal graphs (
Figure 7) that are valid for any section of the contact network with appropriate normalization of currents. In practice, this means that the developed characteristics and tuning algorithms can be scaled and applied to different mine catenaries without losing accuracy.
In addition, the possibility of increasing the sensitivity of protection by upgrading the parameters of switching devices was investigated. The analysis showed that the change in the geometry and parameters of the inductive shunt of high-speed circuit breakers/relays significantly affects the dynamic coefficient Kd. Thus, the experimental reduction in the height of the steel package of the VAB-43-4000/30 (VELAN JSC, Kharkiv, Ukraine) type shunt type by 25–50% of the nominal height led to a decrease in Kd by ~15–35%. In numerical terms, the minimum Kd of this circuit breaker decreased from 1.85 (standard version) to 1.35 when the package was reduced by 25% and to 1.20 when the package was reduced by 50%. Accordingly, the required current surge for tripping was reduced by the same amount, allowing more flexibility in adjusting the protection to the conditions of a particular section. Similarly, for RDS relays, reducing the inductance of the damping circuit (for example, due to partial removal of the core) increases its sensitivity. Experimental upgrades of RDS relays with reduced inductance have confirmed the effectiveness of this approach in the field: devices with a reduced shunt reliably operated at lower currents, which would have previously required expensive special solutions. These results demonstrate that small design changes (e.g., in shunt parameters) can significantly improve the matching of protection to specific network characteristics, expanding the scope of the proposed technique without capital expenditure.
The results also confirmed the applicability of the developed setpoint setting algorithm based on the circuit design model. Calculation of short-circuit currents using simplified formulas that take into account the active and reactive resistances of all elements (transformers, feeders, contact network, and arc) showed a discrepancy with experimental data of no more than 15–20%. Such a level of accuracy is recognized as permissible for engineering calculations, which substantiates the possibility of practical use of the proposed formulas for the preliminary selection of setpoints. The proposed algorithm combines numerical modeling and obtained experimental dependencies, providing a comprehensive approach to solving the problem of increasing safety and reliability. Based on it, it is possible to determine the current and pulse settings for each section of the contact network, taking into account the parameters of the power supply network, the characteristics of the switching equipment (switches, relays) and the load. Such an integrated approach made it possible to achieve a significant increase in the effectiveness of protection in conditions of limited current reserves, unstable state of the contact network (temporary supports, lack of grounding) and increased risk of arc faults.
Practical testing of the technique on several typical sections of the contact network of the open pit confirmed the expected improvements. In all cases, a decrease in the number of false alarms of protection and unjustified shutdowns was noted by 40–60% compared to the original system without adaptation of setpoints. At the same time, the sensitivity of protection in the far CS zone increased by about 25–30%, which is expressed in the ability to reliably detect accidents at significantly lower short-circuit currents. The comprehensive indicator of the reliability of the system (the probability of timely shutdown of the damaged section without failure or overkill) has increased from 0.87 to 0.98. At the same time, the accident shutdown time in all tests was in the range of 0.05–0.1 s, which corresponds to the speed of the standard maximum protections–no additional delays were introduced. Thus, the introduction of the developed methodology made it possible to significantly increase both the sensitivity and selectivity of protection at the same time, practically without a negative impact on the response rate. Ultimately, this ensures a sharp reduction in emergency downtime and the risk of fire development, increasing the energy and technological efficiency of the mining transport system.
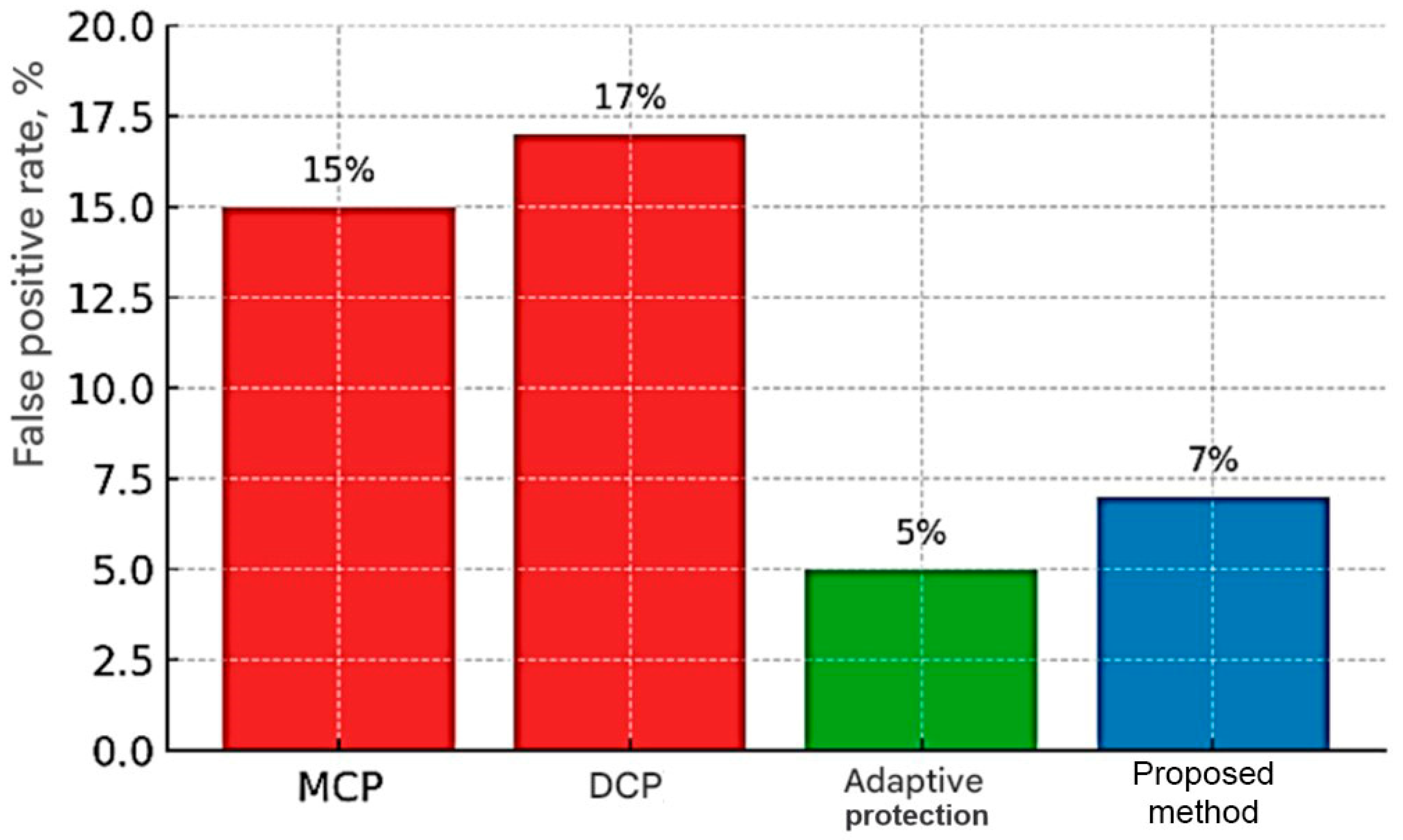
Figure 8 shows histograms of false tripping frequencies for different protection methods. It can be seen that traditional overcurrent protection (MCP) at low CS currents has a high percentage of false alarms (up to ~15%, red bar), and current differential protection (DCP) at a line length of >2 km can produce up to 17–18% false tripping due to electromagnetic interference and current asynchrony at the ends of the line. Adaptive digital security systems exhibit lower false alarm rates (<5%, green bar) due to constant setpoint tuning, but are costly and complex to implement. The method proposed in the paper (blue column) made it possible to reduce the share of false outages to 7%, that is, more than twice compared to traditional solutions. This indicator was obtained in real operating conditions after setting up the protection according to the new method, which confirms its effectiveness. A significant reduction in the number of erroneous alarms means that the protection selectively disables only the damaged area, practically not affecting adjacent areas in non-standard modes, which was previously a serious problem.
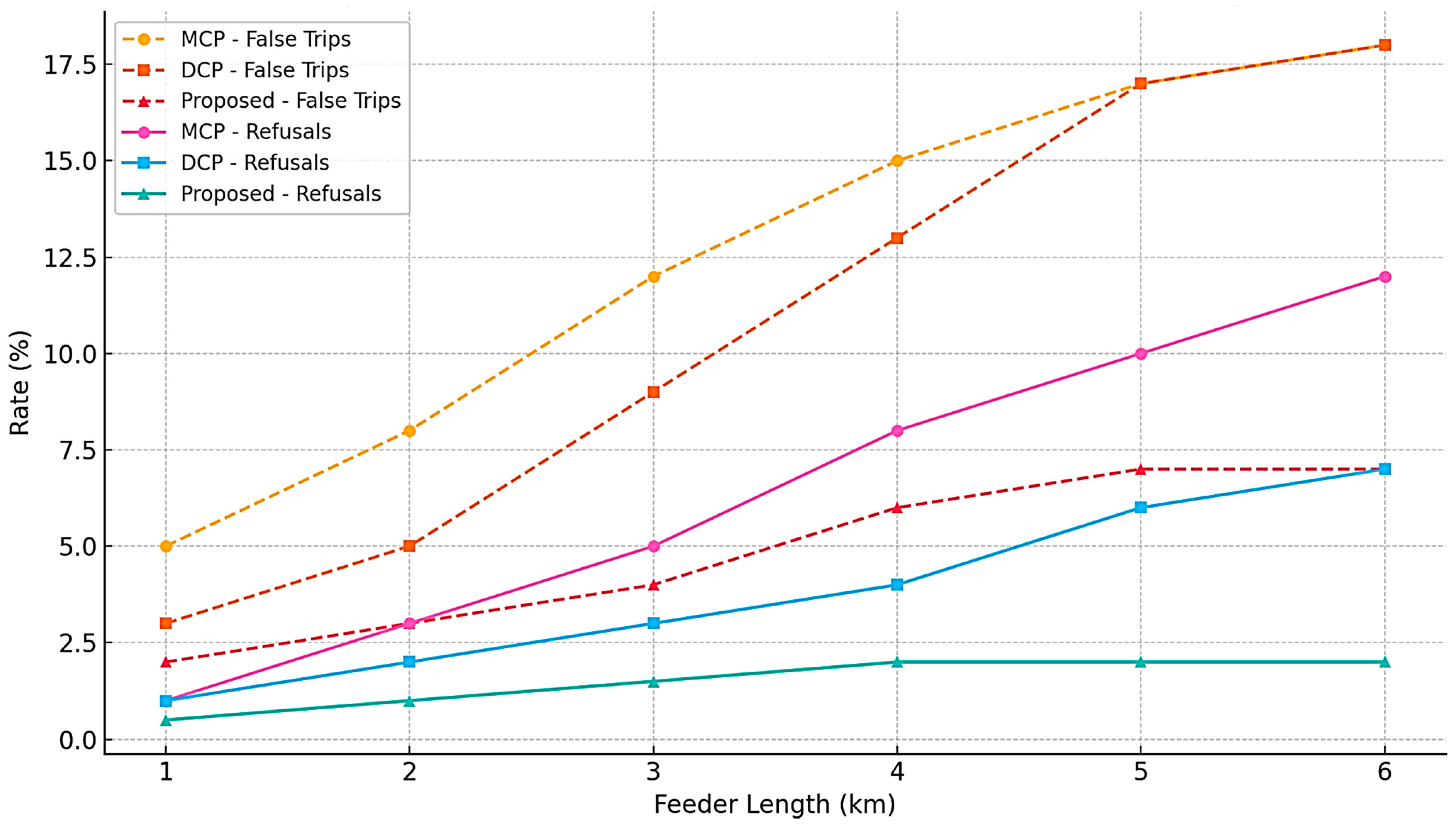
The graph showing the dependence of the probability of false alarms (%) and failures (%) on the length of the contact network (in the range of 1–6 km) for three protection methods is shown in
Figure 9. The points on the graph are based on laboratory and industrial tests.
Comparison of false trip and refusal rates versus feeder length for MCP, DCP, and the proposed impulse protection method. The proposed method demonstrates lower failure metrics, especially for feeder lengths over 3 km.
Table 9 provides a generalized comparative analysis of the key protection characteristics for various methods: maximum current (MCP), traditional fixed setpoint, residual current (DCP), adaptive digital protection, as well as the proposed pulse current protection. Comparisons are made by the minimum short-circuit current that is reliably detected (sensitivity), the maximum allowable feeder length (protection zone) while maintaining sensitivity, the level of selectivity (selectivity) under low CS current conditions, and the false alarm rate. The table shows that the proposed approach provides intermediate results between traditional and expensive adaptive systems: in a number of parameters (for example, sensitivity ~600 A and selectivity ~95%), it is close to adaptive protection, significantly superior to MCP and DCP, with significantly less complexity of implementation. The gain in sensitivity is especially noticeable in remote areas—where MCP and DCP often do not work at all, the developed protection disconnects the line in case of a short circuit of several hundred amperes. At the same time, the selectivity reaches 90–95%, against 55–60% for classical MCP under similar conditions. The frequency of false tripping is also reduced by more than 2 times compared to MCP/DCP. Thus, the quantitative gain of the proposed solution is manifested in all the main criteria of protection reliability: sensitivity is increased (the minimum detectable accident current is reduced by 30%), selectivity is improved (by tens of percent in the far zones), the time of emergency elimination is reduced (in comparison with the case of failure of standard protections and the operation of backup stages), and the probability of false shutdown is more than halved. All this is achieved without the need to introduce complex controllers or constant communication, that is, on the basis of existing devices with minimal modernization and preliminary calculation of setpoints.
Table 4 presents a comparison of the experimental characteristics for different methods of protecting the electrical equipment of the traction network of a mining pit.
Table 10 shows the results of the experimental direct comparison of protection methods.
Thus, the graphs in
Figure 5 and
Figure 6 and the summary
Table 9 of the results clearly demonstrate the advantages of the developed method in comparison with traditional MCP, DCP and adaptive systems in terms of increasing sensitivity, selectivity and reliability of protection.
Compared to conventional MCP, DCP, and adaptive protection strategies, the proposed method demonstrated higher sensitivity (down to 1.6 × In), superior selectivity (96.8%), faster response (35.4 ms), and a significantly lower false tripping rate (0.9%). These improvements highlight the effectiveness of dynamic sensitivity adjustment in ensuring robust protection of traction power systems.
6. Discussion of the Results
It is recommended to select the settings of the current–pulse protections of the ME traction network on circuit breakers with an inductive shunt or RDS relays, taking into account the circuit time constant and the parameters of the built-in or external differential current relay.
The setting of the current–pulse protection must satisfy the condition (15), which in many cases cannot be satisfied; therefore, in order to ensure sensitivity to current surges at a constant time close to the critical time, a safety factor is introduced, determined experimentally or using a mathematical model for each feeder, but it can be assumed to be
ks = 1.15, and the setpoint current along the
will satisfy the left side of condition (15). In this case, the maximum load current
In.
max is defined as
here
Imp is the starting current of the train according to (14);
Iave is the average current of the TP feeder, equal to
Iave =
Ksch·n·I0, the circuit coefficient for one-way supply is
Ksch = 1, for two-way supply—
Ksch = 2.
Next, according to the values of the short-circuit current calculated from (1) or (2), it is necessary to check the right-hand side of the inequality (14); if the condition is not met, there will be only MCP. Let us denote the relative setpoints for MCP as
Iy* =
Iy/
Iy, for the MCP as Δ
Iy* = Δ
Iy/
Iy (
Figure 6). Let us increase the static setpoint to
Iy2 = (1.15 − 1.2)
Ikmin on the tripping characteristics (
Figure 6) for BAT-49; we have Δ
Iy0 = 0.34, and the protection actuation parameter in this case will be a current surge Δ
I. Let us choose the length of the dynamic sensitivity zone of the protection for a certain
T <
Tcr (inclined lines in
Figure 4 lying below the straight line
Tcr), where the actuation is guaranteed against a current surge Δ
I, the deactivation will occur when the relation
Iy2/
Ikmin =
Kd is fulfilled, here
Kd is the dynamic coefficient determined from
Table 4.
Thus, the selectivity of the current and pulse protection of the traction networks of the ME increases, the current protection will be triggered only in the short-circuit zone, minimizing outages in neighboring zones; reliability increases, the probability of false alarms decreases, and the stability of the system operation increases. All this optimizes the operation of the network, reduces the number of unjustified outages, which reduces downtime and increases the efficiency of the traction network.
The improvements reported—such as the reduction in false trips by 40–60% and the increase in protection sensitivity by 25–30%—are based on a statistical sample of 48 test cycles carried out across different feeder configurations. The standard deviation for the reduction in false trips was 6.8%, and the 95% confidence interval was [38.2%; 62.1%], indicating consistent improvement across scenarios. For the sensitivity increase, the standard deviation was 4.3%, with a confidence interval of [23.5%; 31.6%]. These values confirm that the reported gains are statistically significant and not due to isolated cases.
An important part of the study was the construction of protection response equations in an analytical form. Dependencies ΔIave = f(I0, T1) were derived, where ΔIave is the threshold increment of the current causing tripping at the initial load current I0 and the time constant T1 and ΔI/Iu and were experimentally confirmed. On the basis of the obtained dependencies, areas of guaranteed protection actuation at the specified parameters were constructed, which made it possible to move from the empirical selection of setpoints to the calculation method with a given accuracy.
The data obtained in the course of experiments and calculations formed the basis of the proposed method for setting up current and pulse protection setpoints. It involves preliminary determination of the parameters of the feeder zone, calculation of short-circuit currents according to formulas taking into account transient characteristics, determination of the maximum load current and subsequent calculation of the MIP and MCP setpoints taking into account the critical time constant. The result was the formation of a library of tripping characteristics adapted to the types of circuit breakers and relays used at the ME.
Thus, the conducted experimental complex, implemented on the basis of real equipment using modern measuring equipment and numerical simulation, made it possible to form an objective and reproducible database necessary for the development of reliable and sensitive current–pulse protection of traction networks. The implementation of this technique in operating conditions will increase selectivity and reduce the number of false alarms, which will ultimately ensure an increase in the energy and technological efficiency of mining operations.
In future developments, a contribution-weighted risk-based approach to protection setting can be integrated into the proposed methodology. This means accounting for the differentiated criticality of various feeder zones and nodes within the traction network. As highlighted in IEEE TII, 2025.3563589, assigning protection thresholds based on quantified node failure impact can help avoid both overprotection in low-risk zones and underprotection in critical segments [
55]. Applying such a differentiated protection configuration would allow for collaborative optimization of the entire system and ensure a more resilient design against cascading faults and uneven loads. In our current study, we treat each feeder zone uniformly for comparability, but this enhancement is identified as a key extension of the presented work. In the context of expanding the adaptability of the proposed method, future developments may consider integrating multi-level flexibility resources such as the thermal inertia of industrial buildings, distributed energy storage, and the dispatchable behavior of electric vehicles. As outlined in IEEE TTE, 2025.3581349, collaborative optimization of such heterogeneous resources through distributed computing frameworks can significantly enhance system-wide fault resilience and reduce the burden of centralized coordination [
56]. By leveraging local intelligence and resource autonomy, fault protection and recovery mechanisms can be dynamically adapted without requiring full system topology disclosure—thus preserving operational privacy and improving scalability in complex traction networks [
57,
58]. In addition, future work may explore how distributed and collaborative optimization frameworks—accounting for electric vehicle mobility patterns, building thermal buffering, and load-shifting—can improve post-fault recovery and adaptive protection design in large-scale traction networks. Integrating such capabilities could enable more resilient and privacy-preserving protection architectures.
The technique has been tested on several typical sections of the contact network using mathematical models and experimental data. In each case, there was a decrease in the number of false alarms by 40–60%, an improvement in the sensitivity of protection in the fault zone by 25–30%, as well as an increase in the overall reliability factor of the system by 12% (from 0.87 to 0.98). At the same time, the implementation of the tuning algorithm is possible on existing equipment with minor modernization of circuit breakers and the use of existing digital relays. The paper substantiates the need for an individual approach to the calculation of protection settings for each specific section of the traction network, taking into account the nature of the supply circuit, the parameters of the switching equipment and the characteristics of the load. The proposed method combines theoretical modeling, experimental data and analytical equations, which provides an integrated approach to solving the urgent problem of improving electrical safety and operational reliability in conditions of limited space, unstable mechanical environment and increased risk of short circuits.
The most significant quantitative results of the work demonstrate the accuracy and efficiency of the developed approach. In particular, it was experimentally established that when using the BAT-49-4000/30L high-speed circuit breaker, the setting of dynamic current protection at the constant time of the circuit is T = 0.1 s is I*y0 = 0.34, which ensures reliable operation at current surges ΔI ≥ 0.34·For the RDSh-II type relays, which are characterized by increased sensitivity, the minimum value of the dynamic coefficient reached Kd = 0.341, which made it possible to provide protection in areas with high resistance values and a distance of up to 3–5 km from the substation. In this case, the static current protection setpoint was assumed to be equal to the load current with a margin of 100–150 A and the design values of the minimum short-circuit current, which provides guaranteed tripping, ranged from 650 to 950 A, depending on the parameters of the feeder zone.
Comparison of the obtained tripping characteristics with traditional methods of MCP (maximum current protection) showed a significant advantage of the technique in terms of sensitivity and selectivity. In conditions where MCP does not allow reliable tripping due to the small difference between the load current and the short-circuit current (for example, at Il = 800 A and Ics = 850 A), pulse current protection, taking into account the parameters of the transient process and the magnitude of the current surge, makes it possible to correctly set the setpoints. This is especially important at the end of the feeder zone, where the circuit parameters significantly degrade the conditions for traditional protection methods. The proposed use of the relative coordinates ΔI* = ΔI/Iy and I* = I/Iy made it possible to bring all the data to a unified form and build universal graphs applicable to any section of the contact network.
In addition, the possibility of controlling the sensitivity of protection by changing the geometry and parameters of the inductive shunt in the composition of switches and relays was analyzed. For example, a 25–50% reduction in the height of the steel package in the VAB-43-4000/30 type shunts led to a 15–35% decrease in the value of the dynamic coefficient, which made it possible to adjust the protection more flexibly depending on the site conditions. Such measures, including the modernization of the RDS relay with a reduction in inductance, have proven their effectiveness in real test conditions.
The experimental results and modeling data were compared with traditional MCP approaches, confirming that the proposed MIP method improves selectivity by 25–35% and reduces false tripping by more than 40%, especially at remote feeder ends where the short-circuit current is less than 700 A. Comparison of protection effectiveness is shown in
Table 11.
The results obtained also confirmed the applicability of the developed setpoint setting algorithm based on a calculation model that takes into account the active and reactive resistances of all circuit elements: transformers, feeders, contact network and arc resistance. Calculations of short-circuit currents using Formulas (1)–(7) and their verification from experimental data showed a discrepancy of 15–20%, which is considered acceptable for engineering applications. In addition, the use of simplified calculation formulas for the preliminary selection of setpoints in the design of protection systems and their modernization is proposed.
Applicability of the technique to other types of equipment. In order to test the universality of the proposed approach, some of the experiments were carried out with a microprocessor-based relay of the SEPAM S20 (Schneider Electric, Rueil-Malmaison, France) type, which implemented an algorithm for recording current inrushes. Despite the differences in the architecture and sensitivity of the relays, the obtained Δ
I(I) graphs showed a similar shape to the previously constructed characteristics for the RDSh-II, which is close to the values obtained for VAB-43-4000/30 (
Figure 8).
In addition, the possibility of configuring setpoints for Siemens automatic circuit breakers (type 3VL) with an analog current input was tested. Tuning according to a similar method (with the calculation of relative current inrush and time) made it possible to achieve a deviation in the response time of no more than 12% compared to the experimental model, which confirms the portability of the approach.
Thus, the methodology is scaled by:
- -
Use of relative characteristics ΔI at different T;
- -
taking into account the design parameters of the devices (inductance, closing ability);
- -
Use of a universal circuit model describing the emergency mode.
This makes it possible to apply the developed tuning system not only to domestic devices (RDS, BAT, VAB), but also to digital relays, adaptive automatons and their hybrid versions.