Development of a High-Switching-Frequency Motor Controller Based on SiC Discrete Components
Abstract
1. Introduction
2. Design of a High-Switching-Frequency Controller Using Discrete SiC MOSFET Devices
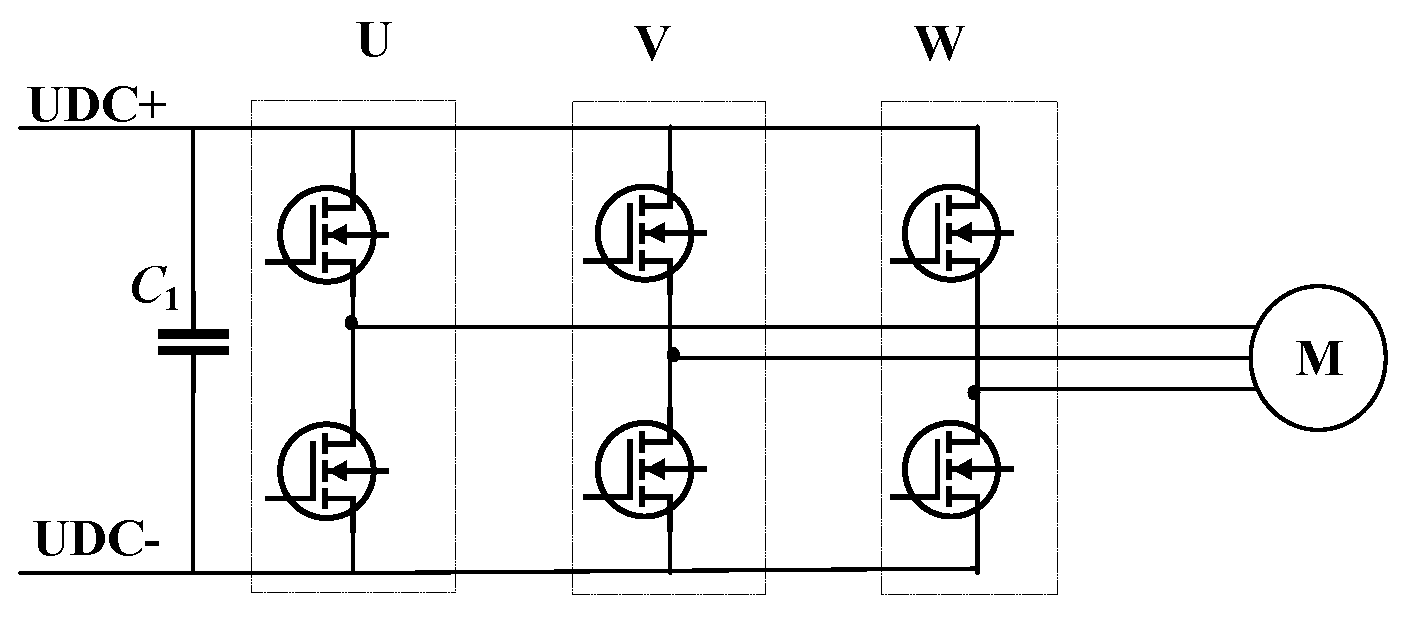
2.1. Design of Electrical Architecture for Controllers
2.2. Design of Key Power Units
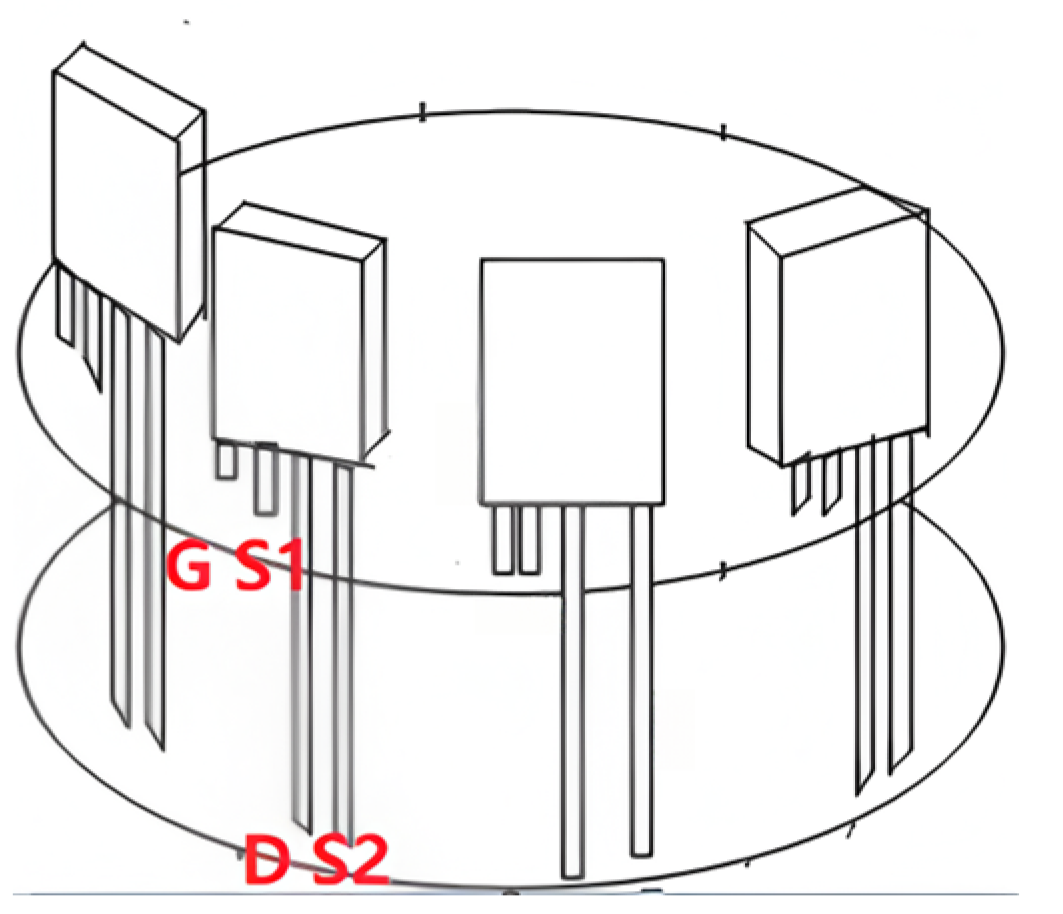
2.2.1. Module Selection and Design
2.2.2. Design of DC-Side Supporting Capacitor
2.3. Design of the Drive Unit
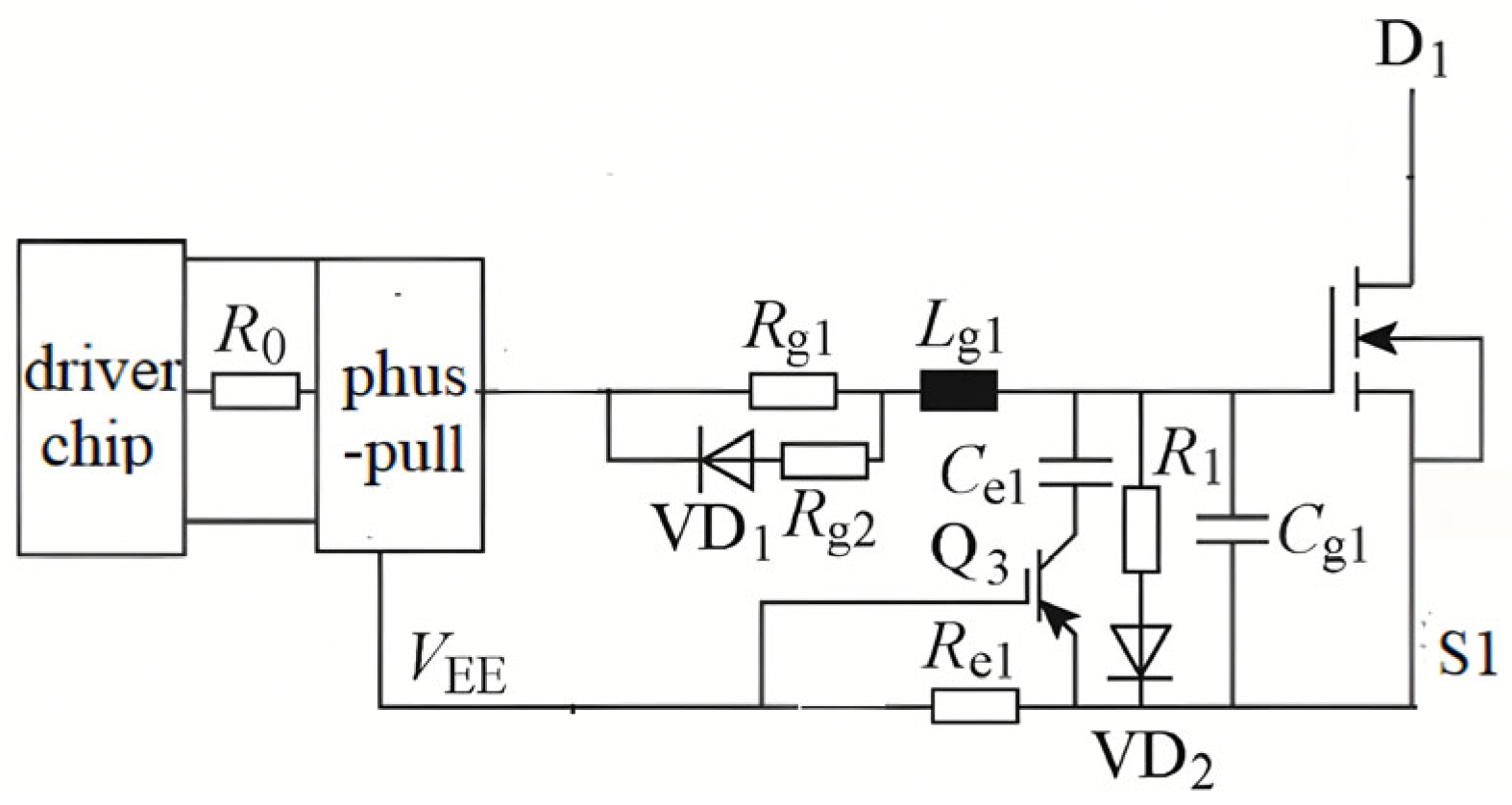
2.3.1. Design of the Drive Circuit
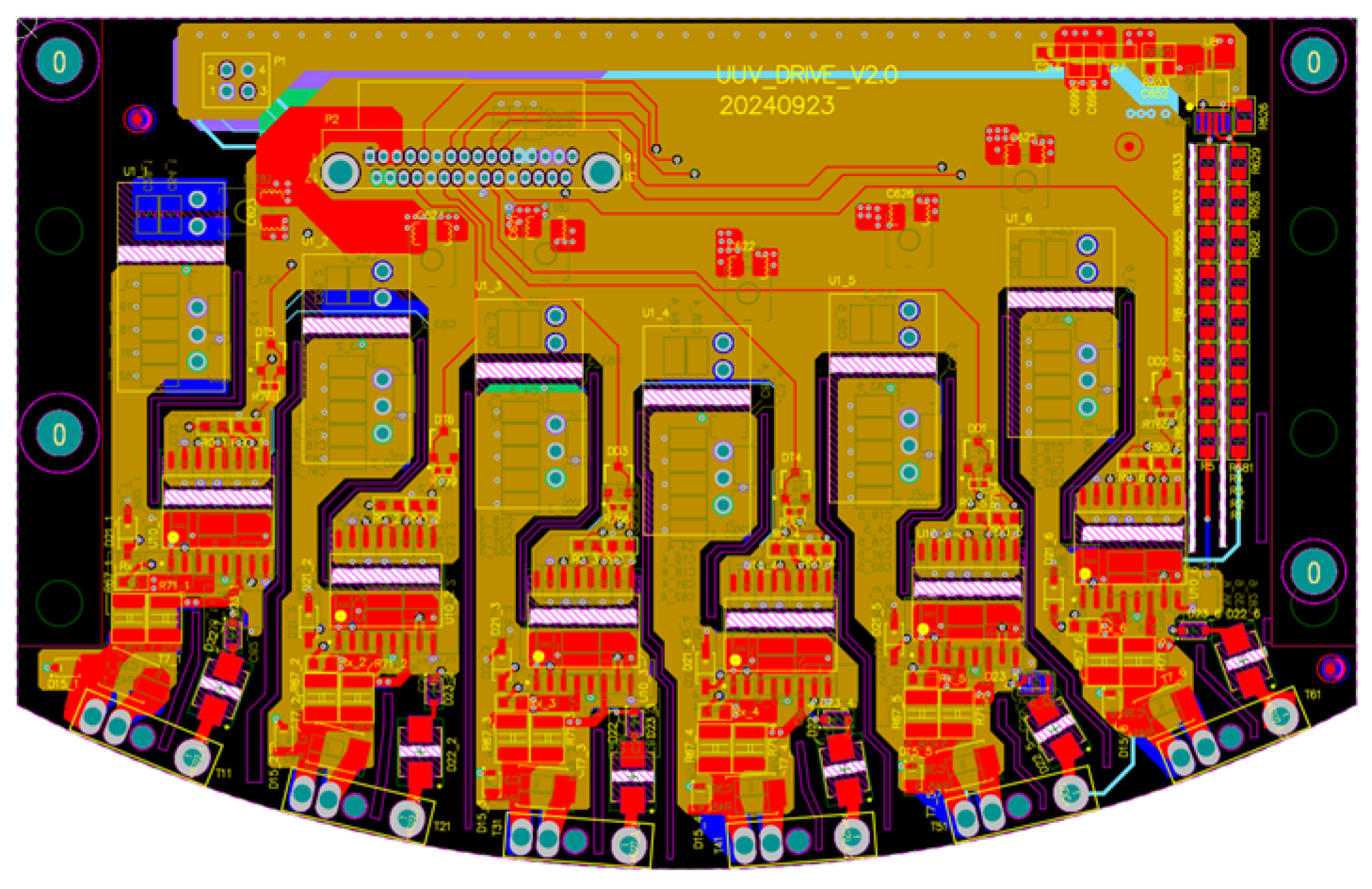
2.3.2. PCB Design of the Drive Circuit
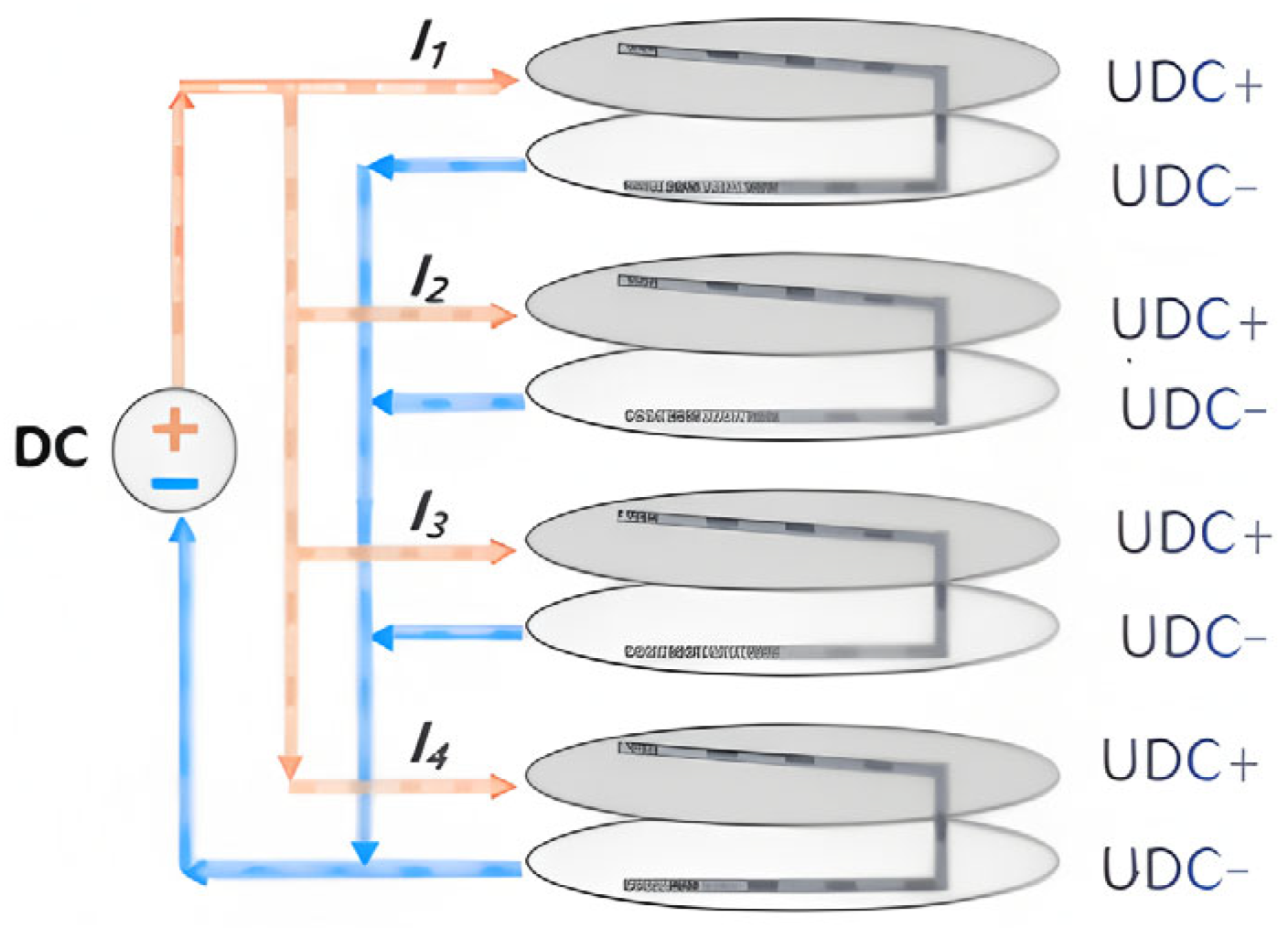
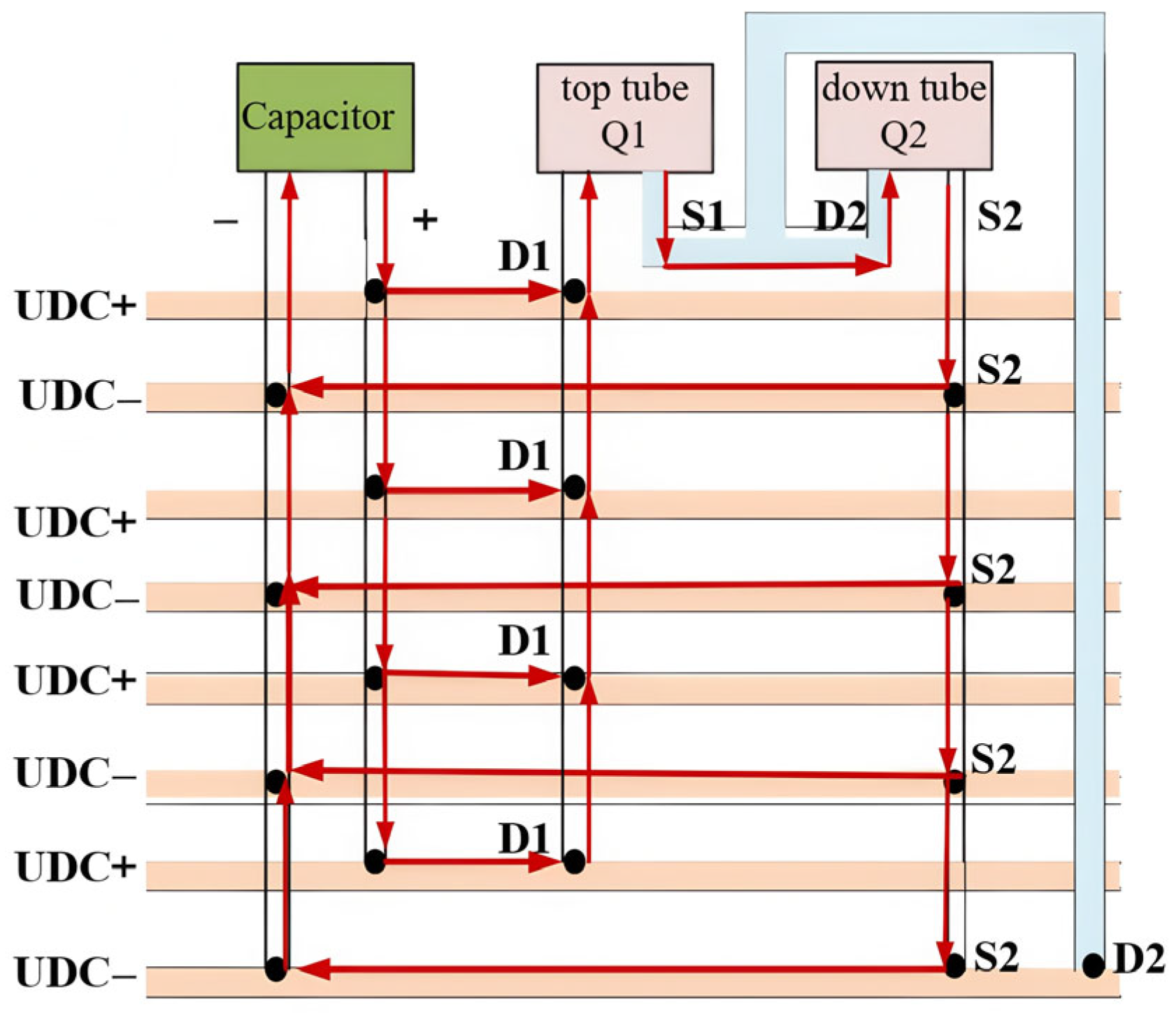
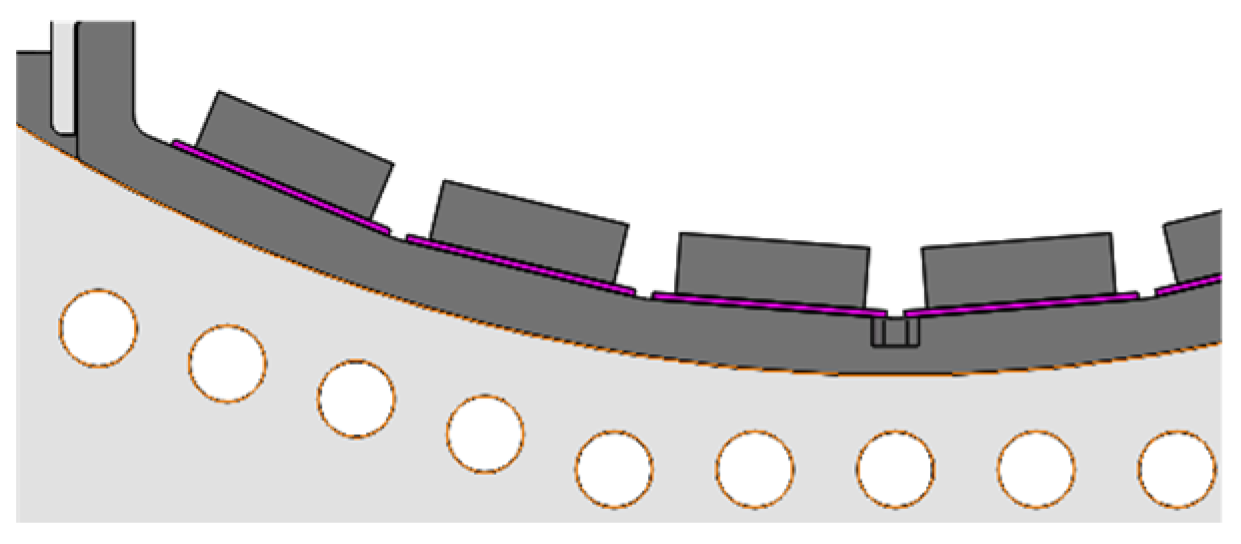
2.4. Design of PCB Busbar
2.4.1. Design of PCB Busbar Structure
2.4.2. Low-Hum Design for Busbars
2.4.3. The Inductance Test of Low-Inductance Laminated Busbars
2.5. Thermal Design
2.5.1. Loss Calculation
2.5.2. The Structural Design of Heat Dissipation
2.6. Software Algorithm Design
2.7. Design of Control Circuit
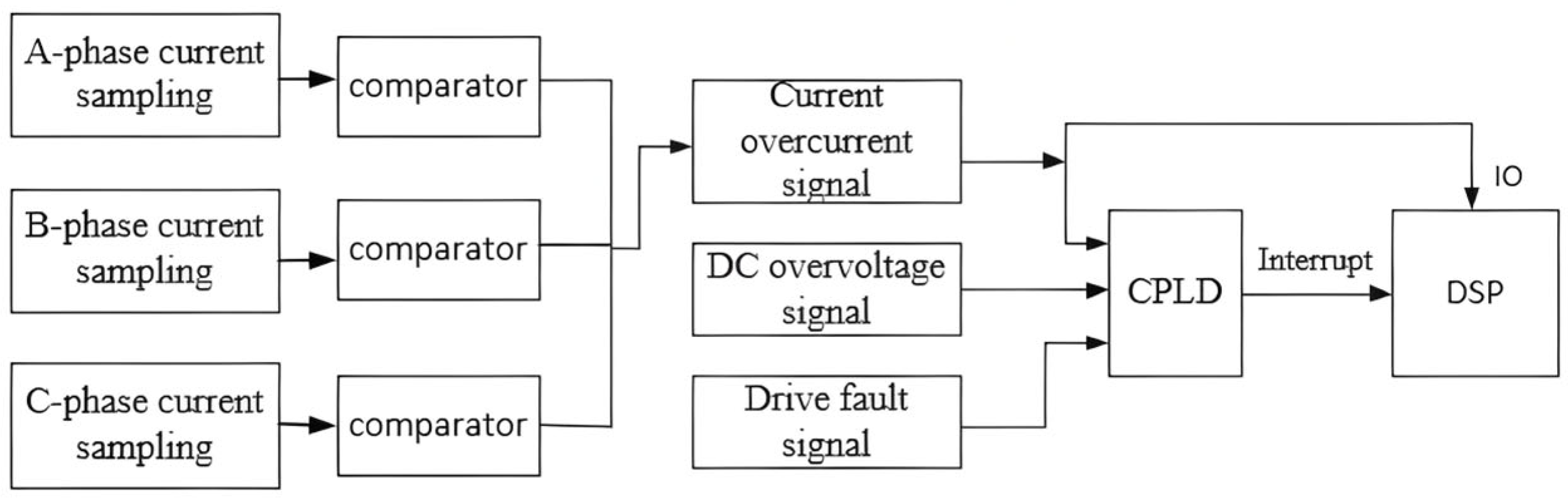
2.7.1. Design of Fault Protection
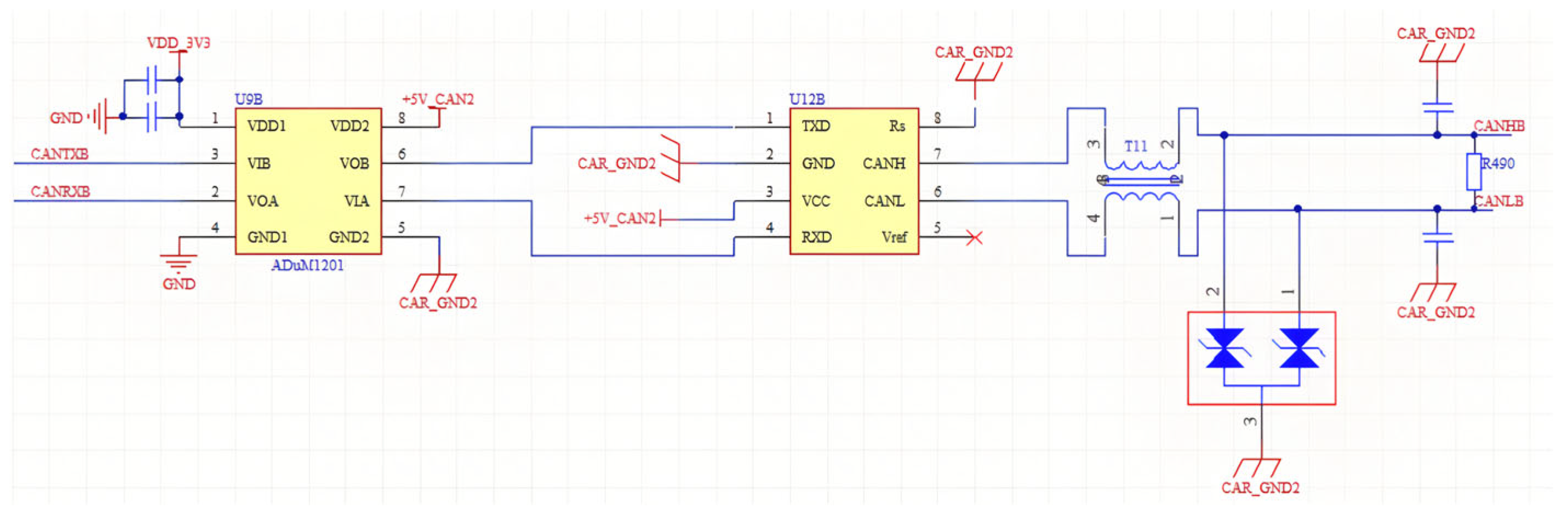
2.7.2. Design of CAN Communication Circuit
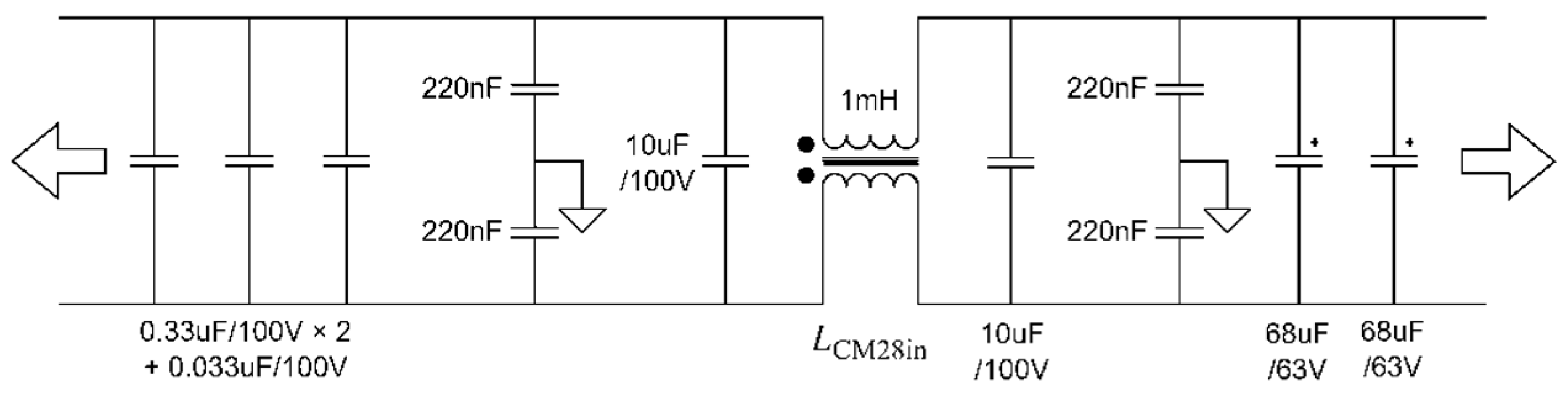
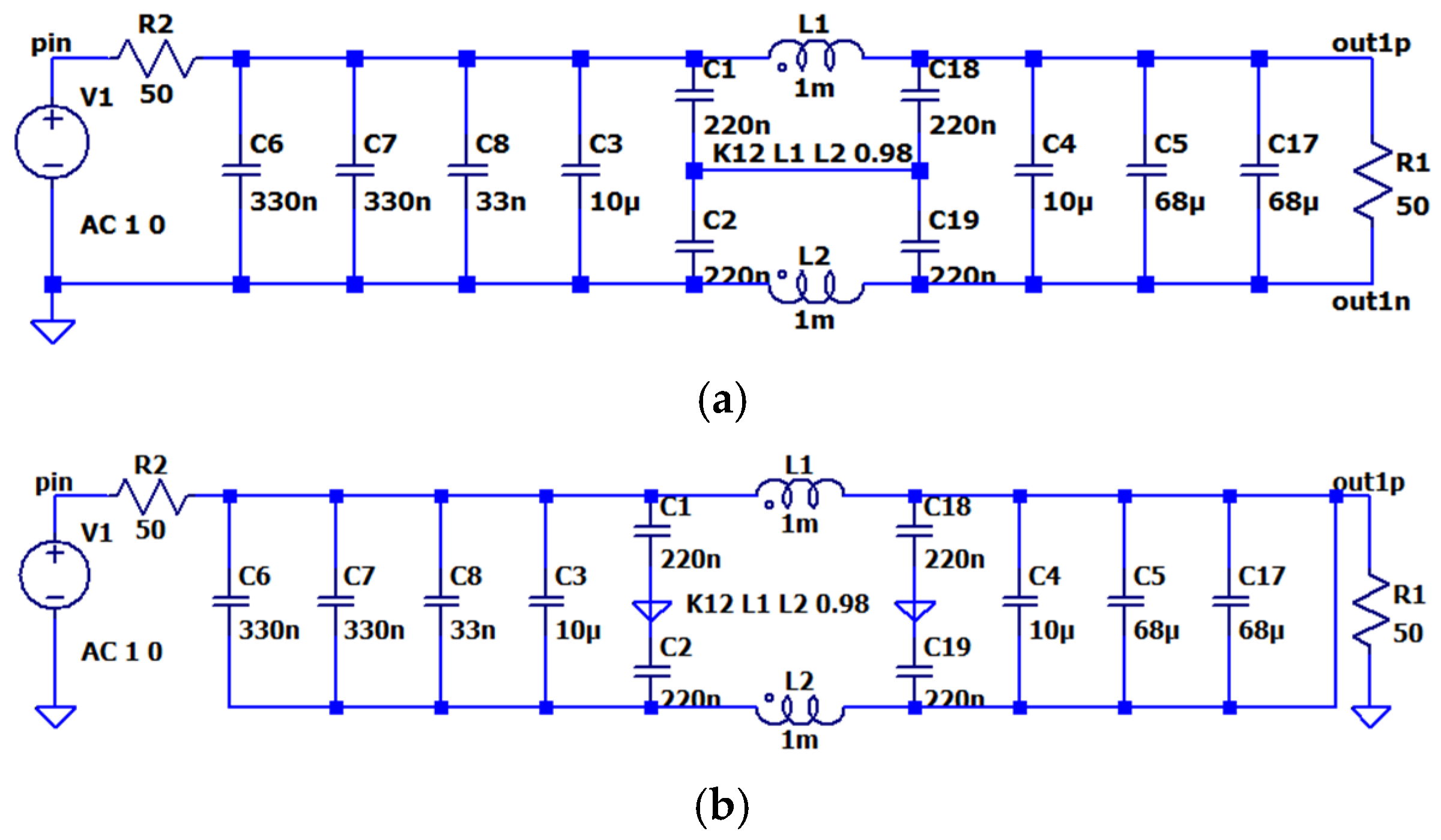
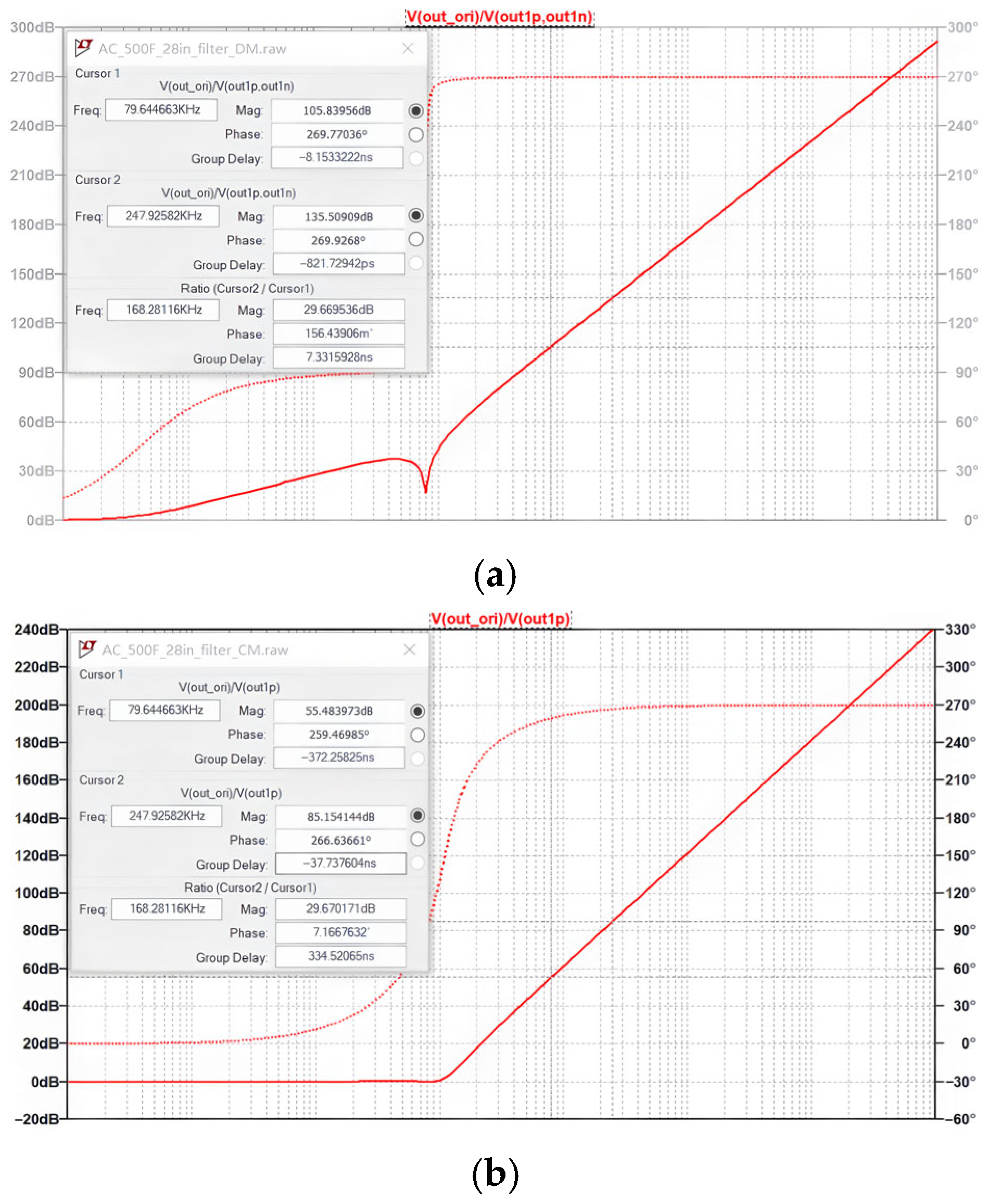
2.8. Design of Electrical Parameters for Filtering Components
3. The Prototype and Test of a High-Switching-Frequency Controller for SiC MOSFET Discrete Devices
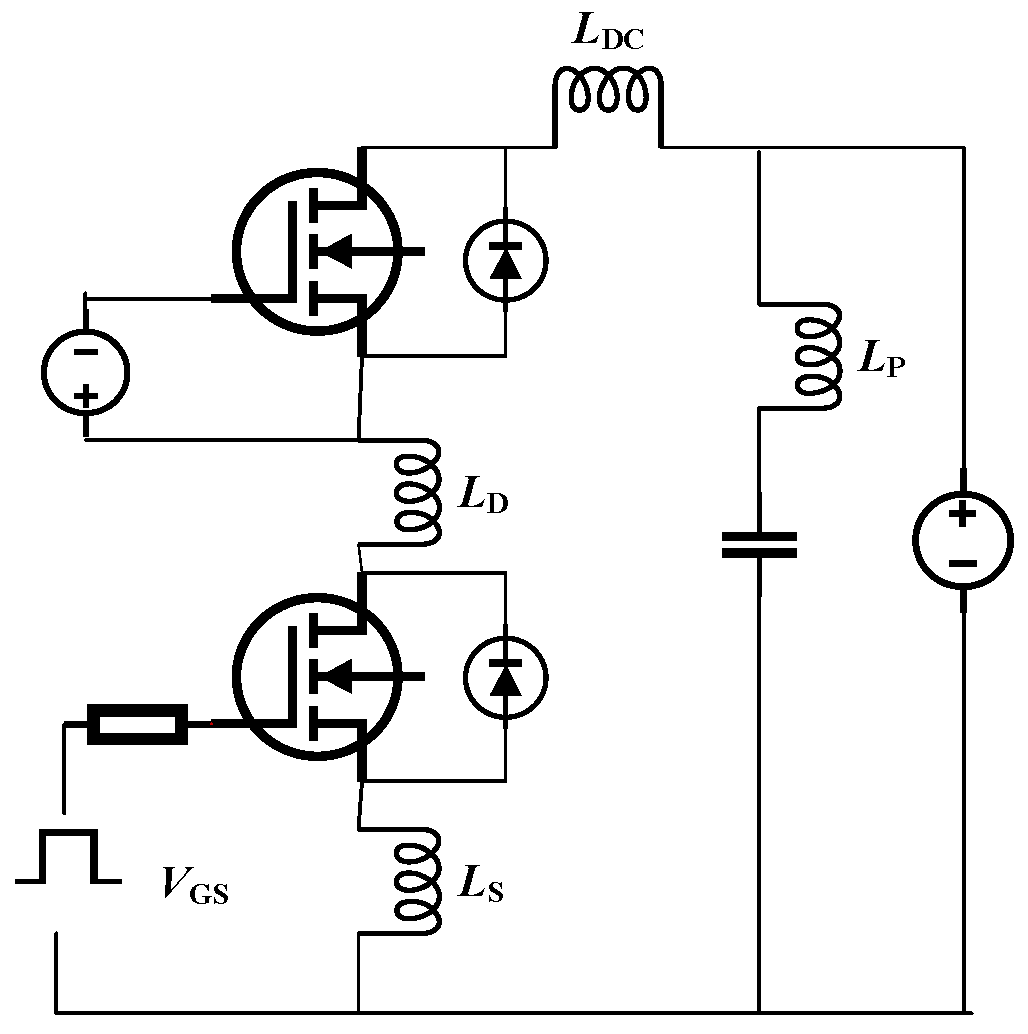
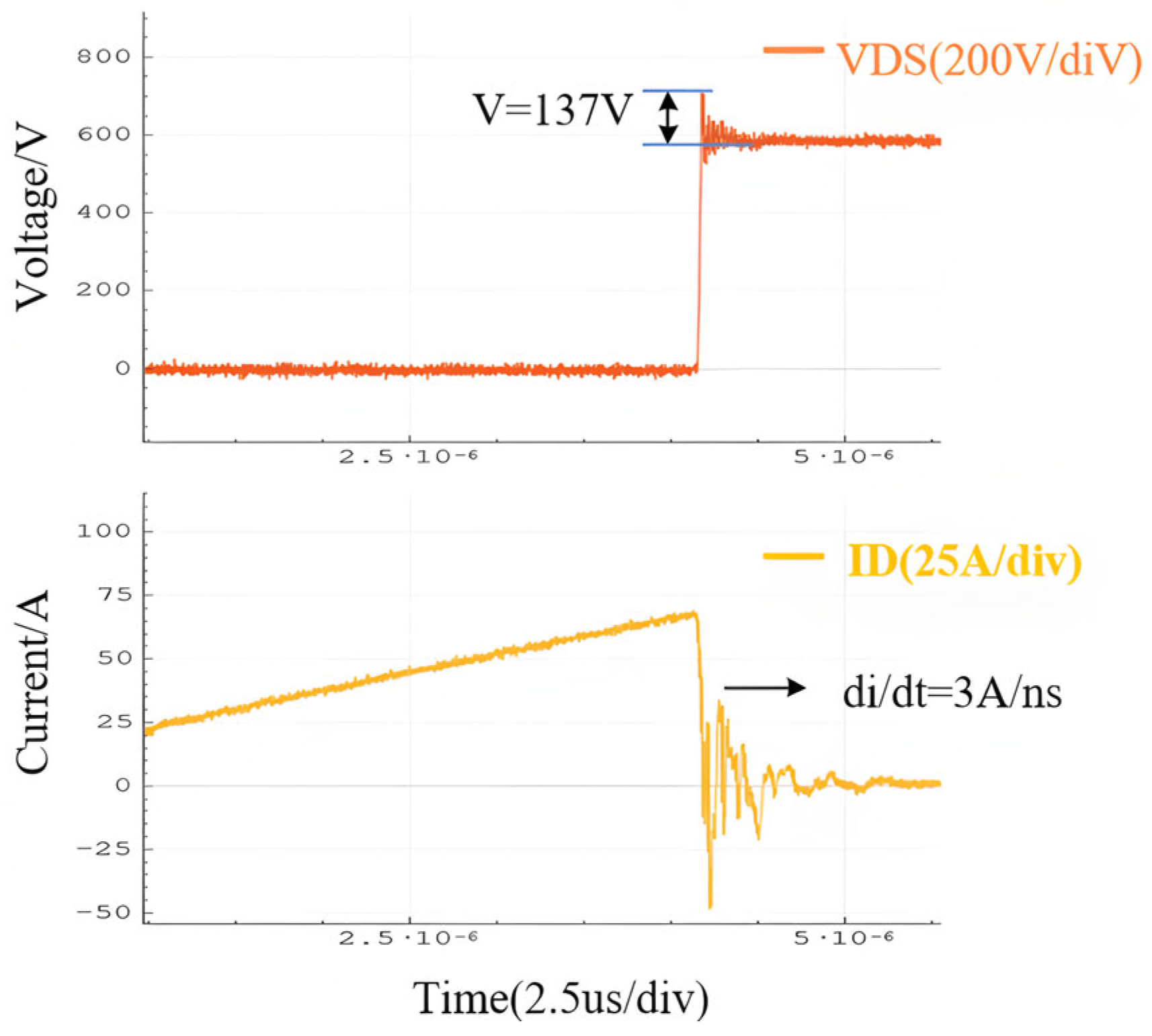
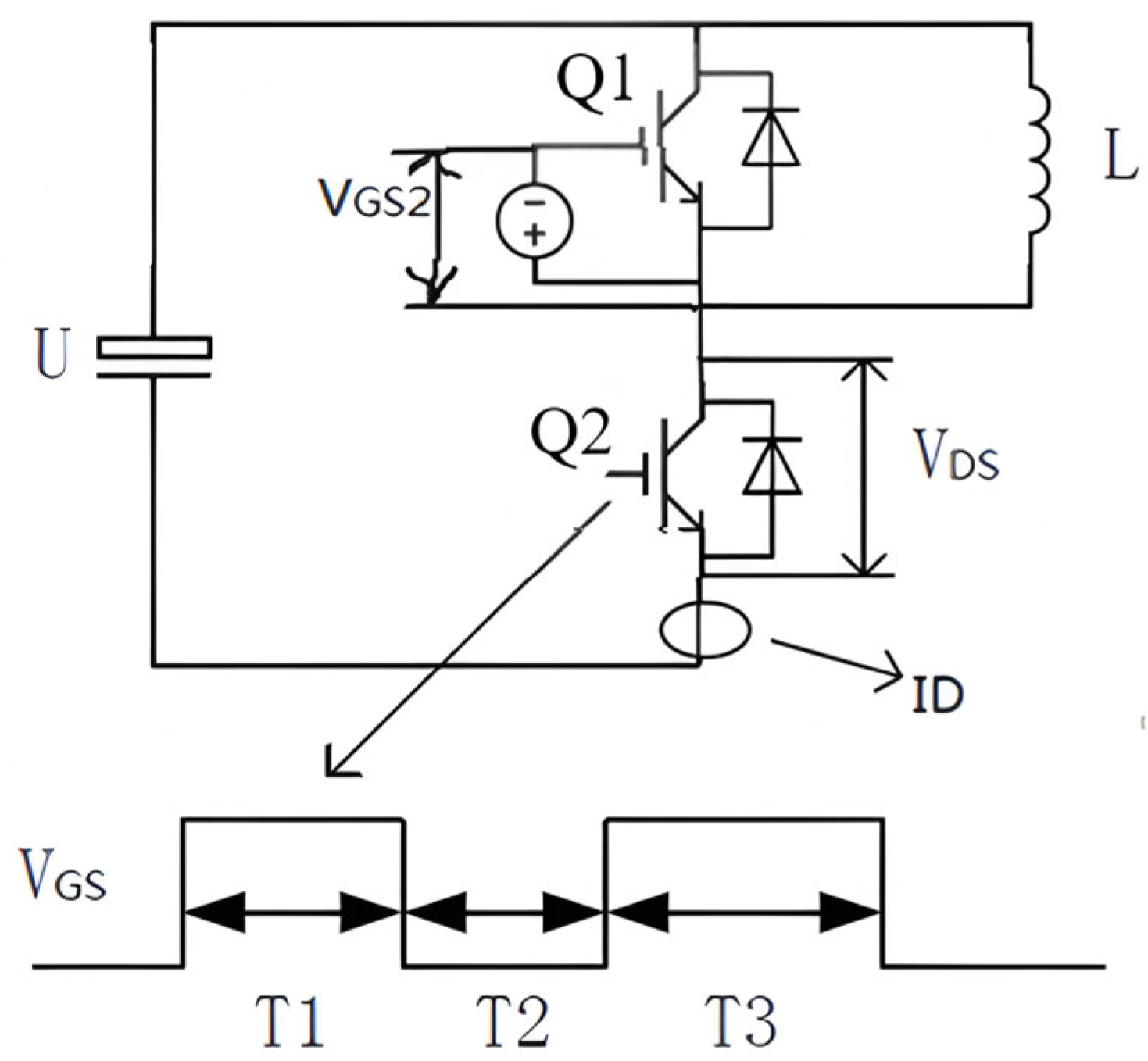
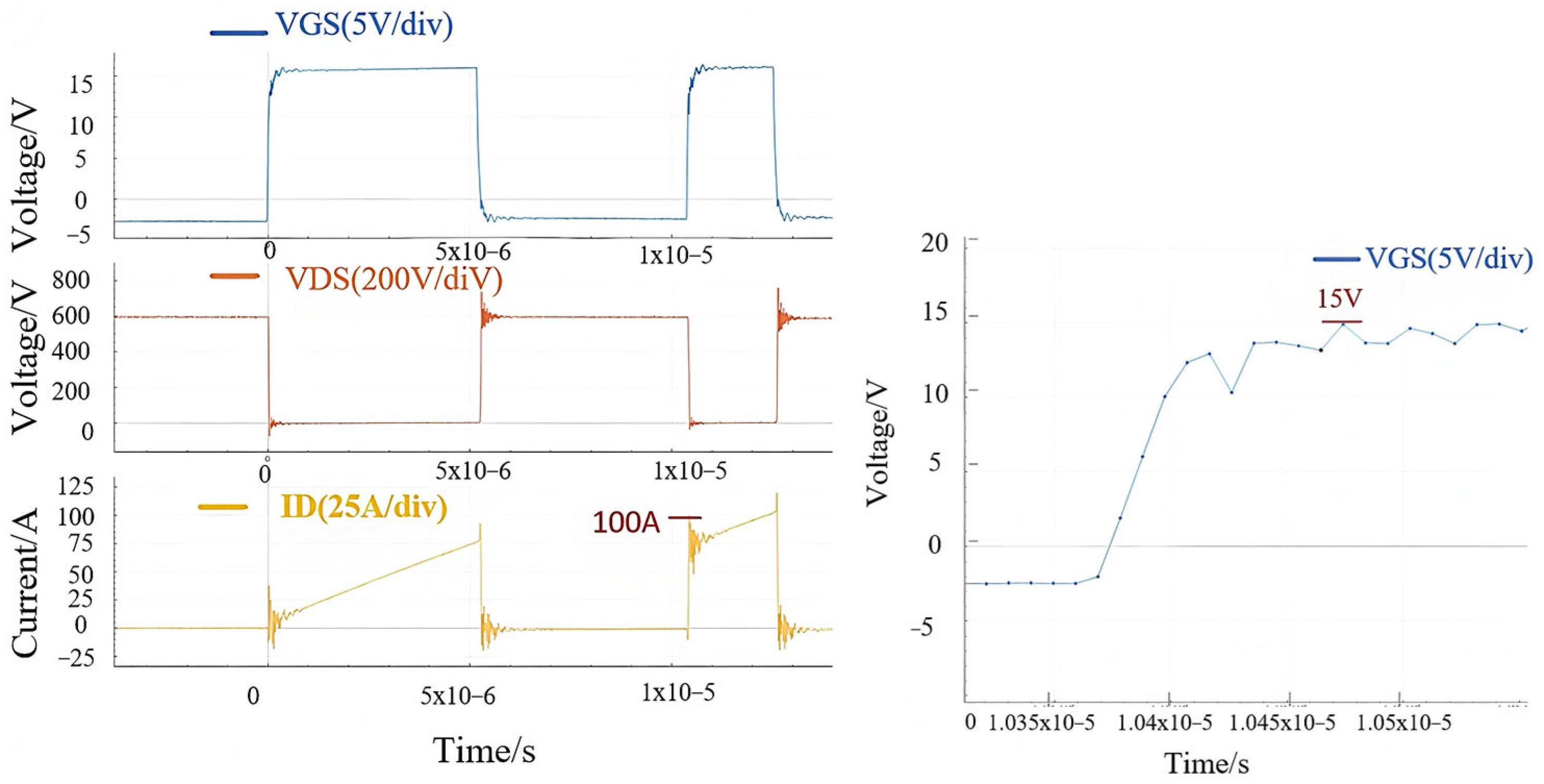
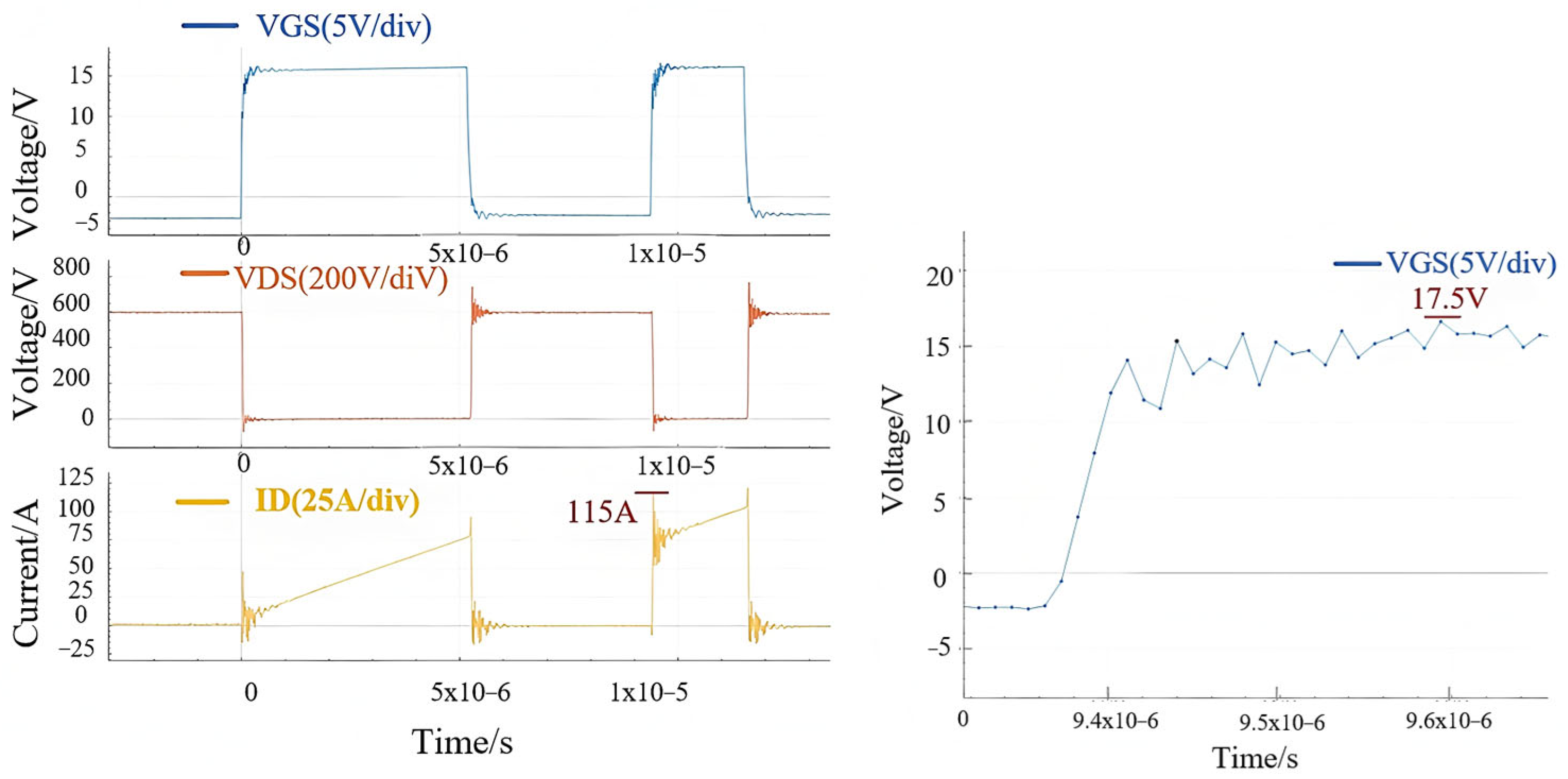
3.1. Dual-Pulse Test
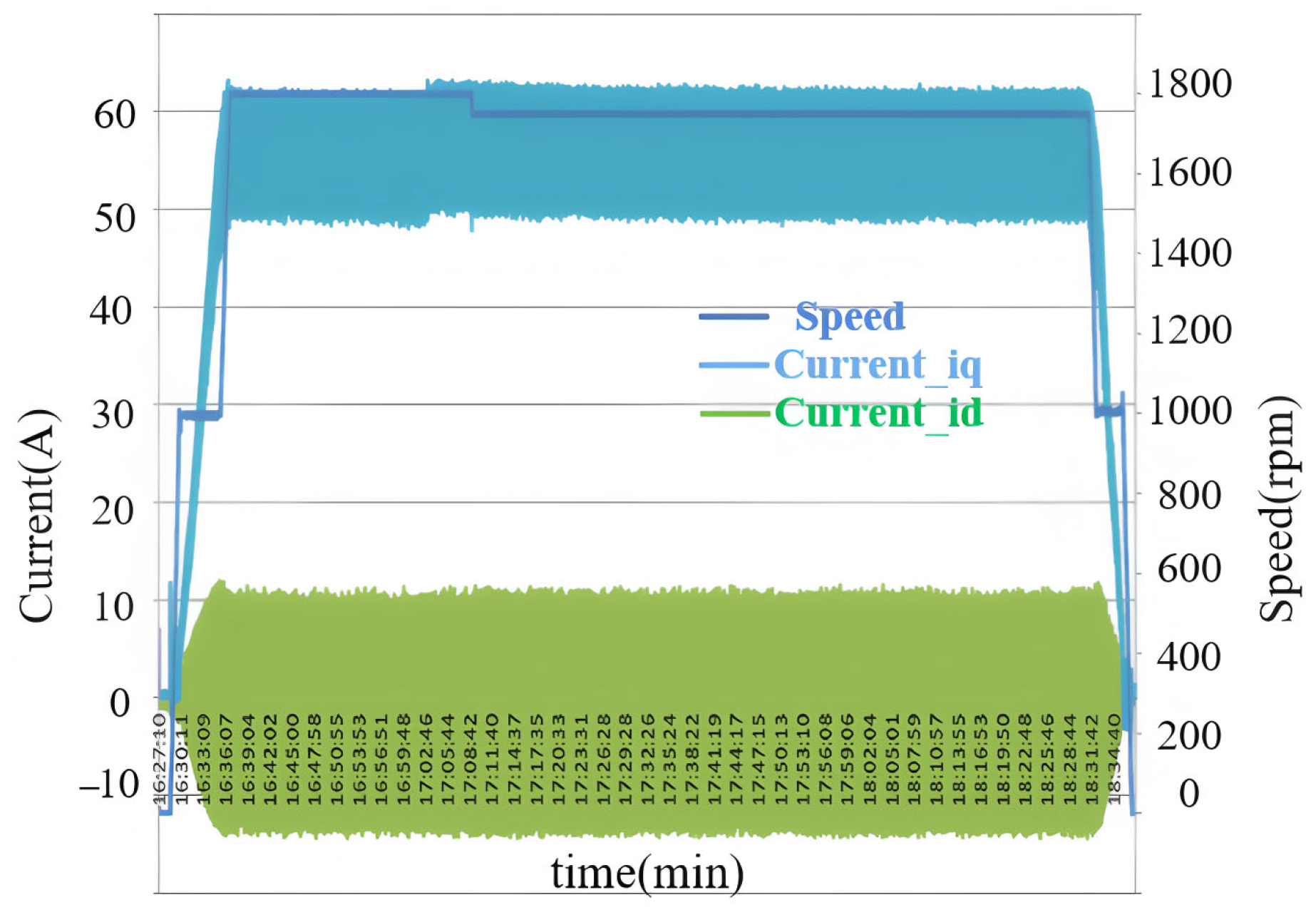
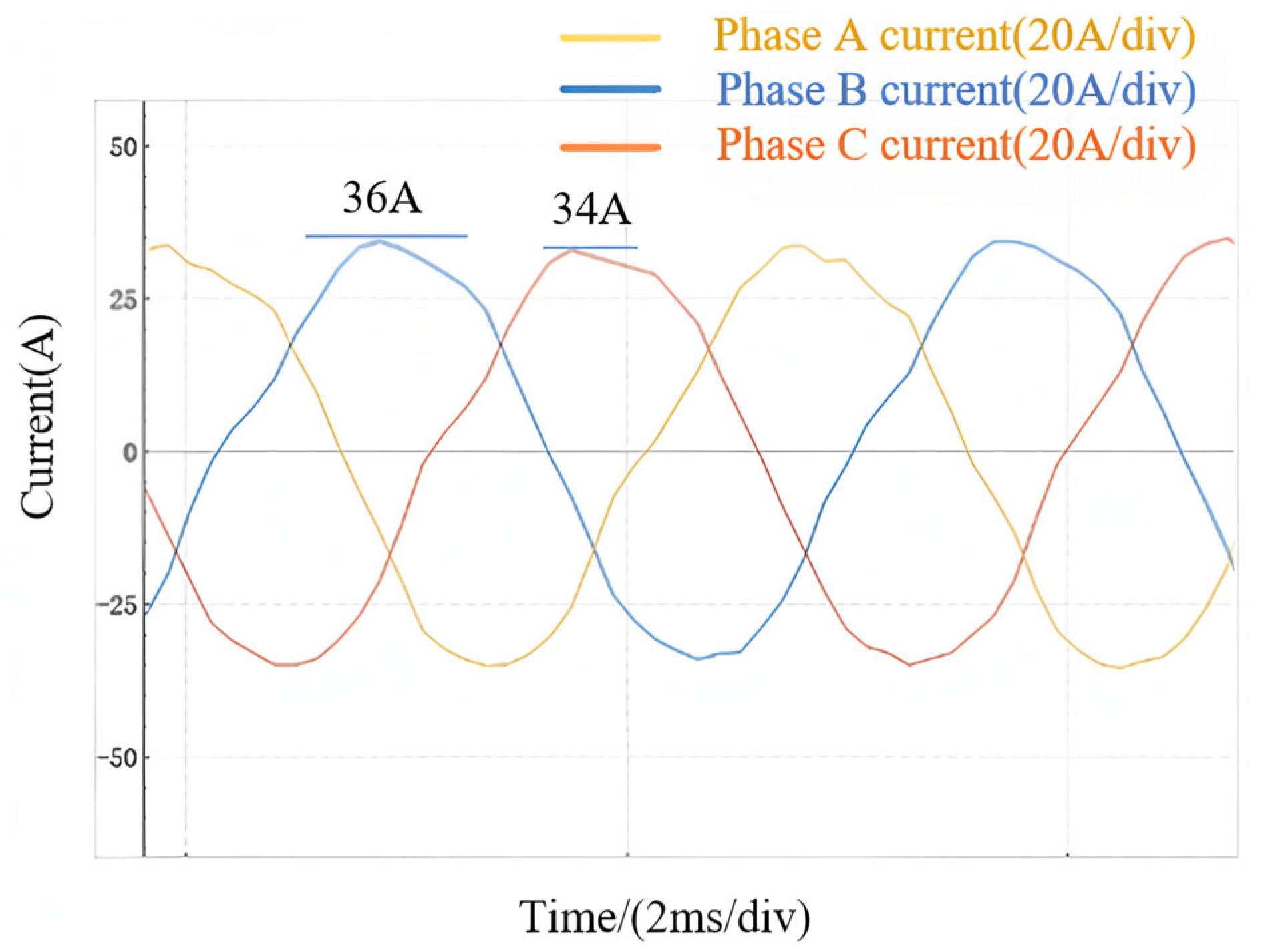
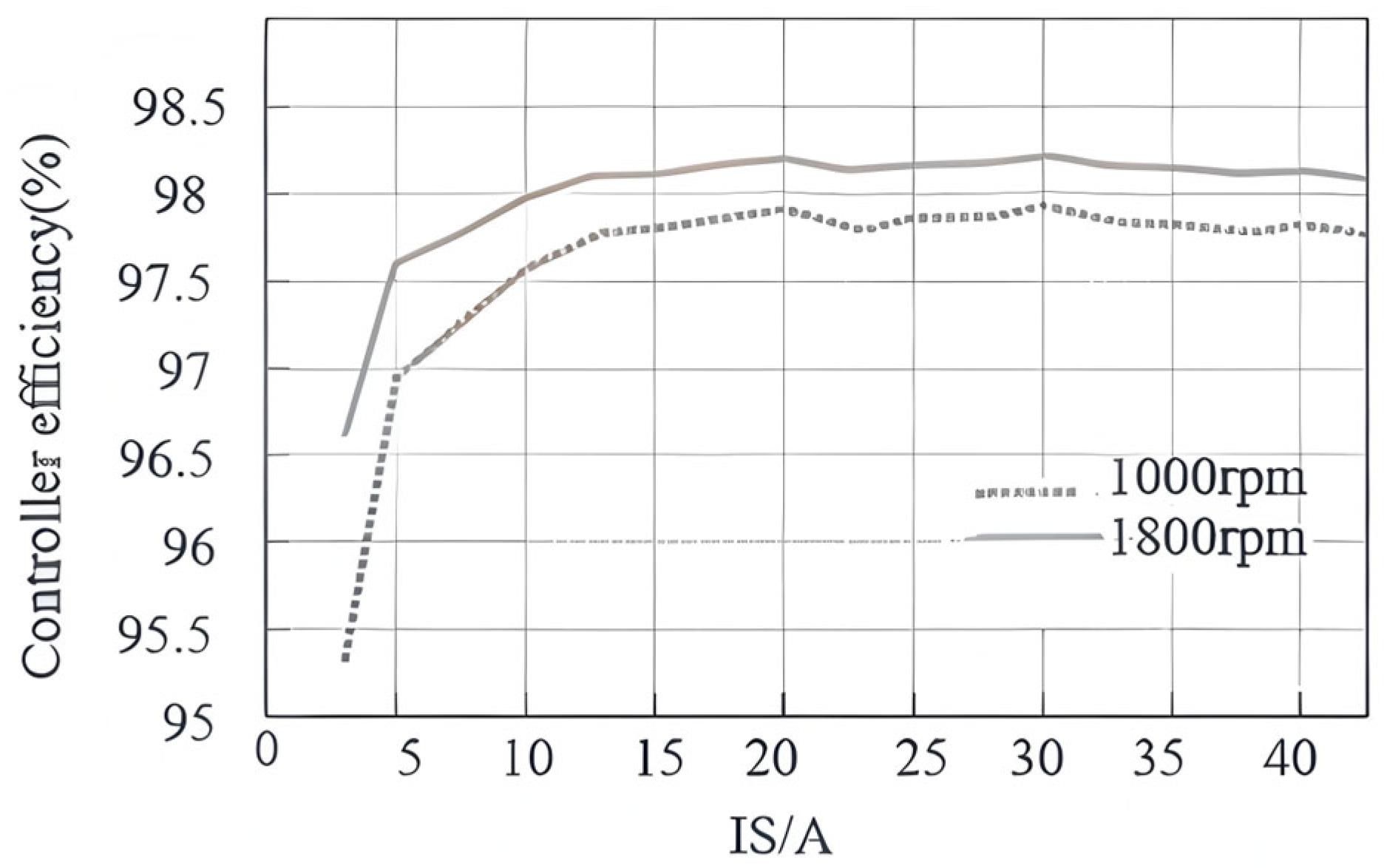
3.2. Power Experiment
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Liu, P.; Chen, Z.; Miao, Y. SiC MOSFET Active Driving Circuit Based on Switch Transient Feedback. J. Electr. Eng. 2022, 37, 4446–4457. [Google Scholar]
- Li, X.; Luo, Y.; Shi, Z. An Enhanced Circuit Model for SiC MOSFETs Based on Physics. J. Electr. Eng. 2022, 37, 5214–5226. [Google Scholar]
- Liu, B.; Liu, W.; Dong, K. Analytical Calculation Method for Stray Inductance of Converter Busbars Based on All Silicon Carbide Power Modules. J. Electr. Technol. 2021, 36, 2105–2114. [Google Scholar]
- Chen, J.; Deng, E.; Zhao, Z. Failure mechanism analysis of SiC MOSFET under different aging test methods. Trans. China Electrotech. Soc. 2020, 35, 5105–5114. [Google Scholar]
- Wang, L.; Zhao, C.; Zhang, T. Review of packaging technology for silicon carbide power modules. Trans. China Electrotech. Soc. 2023, 38, 4947–4962. [Google Scholar]
- Zou, M.; Zeng, Z.; Sun, P. Coordinated switching trajectory regulation of SiC device using variable resistance gate driver. Trans. China Electrotech. Soc. 2023, 38, 4286–4300. [Google Scholar]
- Chen, F.; Lee, S.; Jahns, T.M.; Sarlioglu, B. Comparative Investigation of Current-Source Inverters using SiC Discrete Devices and Power Modules. In Proceedings of the 2022 IEEE 9th Workshop on Wide Bandgap Power Devices & Applications (WiPDA), Redondo Beach, CA, USA, 7–9 November 2022; pp. 215–220. [Google Scholar]
- Liu, B.; Li, W.; Meng, D. Low-Stray Inductance Optimized Design for the Power Circuit of SiC-MOSFET-Based Inverters. IEEE Access 2020, 8, 20749–20758. [Google Scholar] [CrossRef]
- Li, Q.; Yang, Y.; Wen, Y.; Zhang, G.; Xing, W. Active Gate Driver With the Independent Suppression of Overshoot and Oscillation for SiC MOSFET Modules. IEEE Trans. Ind. Electron. 2025, 72, 2325–2335. [Google Scholar] [CrossRef]
- Shao, T.; Zheng, T.; Li, Z. SiC MOSFET Gate Driver Design Based on Interference Dynamic Response Mechanism. Trans. China Electrotech. Soc. 2021, 36, 4204–4214. [Google Scholar]
- Wang, N.; Zhang, J. Review of active gate driver for SiC MOSFET with switching trajectory optimization. Trans. China Electrotech. Soc. 2022, 37, 2523–2537. [Google Scholar]
- Ling, Y.; Zhao, Z.; Ji, S. Self-regulating control of IGBT switching characteristics with active gate drive. Trans. China Electrotech. Soc. 2021, 36, 2482–2494. [Google Scholar]
- Yue, Q.; Peng, H.; Tong, Q.; Kang, Y. A Novel Driving Current Control Approach in Enhanced Current-Source Gate Driver. IEEE Trans. Power Electron. 2023, 38, 10563–10568. [Google Scholar] [CrossRef]
- Zhao, S.; Zhao, X.; Wei, Y. A review of switching slew rate control for silicon carbide devices using active gate drivers. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 4096–4114. [Google Scholar] [CrossRef]
- Li, Z.; Chai, J.; Lu, H.; Li, Y. An Active Gate Driver for Suppressing the Current Oscillation of SiC MOSFET. In Proceedings of the 2021 IEEE 4th International Electrical and Energy Conference (CIEEC), Wuhan, China, 28–30 May 2021; pp. 1–5. [Google Scholar]
- Zhao, S.; Dearien, A.; Wu, Y. Adaptive multi-level active gate drivers for SiC power devices. IEEE Trans. Power Electron. 2020, 35, 1882–1898. [Google Scholar] [CrossRef]
- Yang, Y.; Wen, Y.; Gao, Y. Active gate driver for improving current sharing performance of paralleled high power SiC MOSFET modules. IEEE Trans. Power Electron. 2021, 36, 1491–1505. [Google Scholar]
- Sukhatme, Y.; Miryala, V.; Ganesan, P. Digitally controlled gate current source-based active gate driver for silicon carbide MOSFETs. IEEE Trans. Ind. Electron. 2020, 67, 10121–10133. [Google Scholar] [CrossRef]
- Lu, Y.; Yao, W. An Active Gate Driver Design to Reduce Voltage and Current Overshoots for SiC MOSFET Modules. In Proceedings of the 2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 29 November–2 December 2020; pp. 915–920. [Google Scholar]
- Zhao, D.; Qiu, J.; Wang, P.; Wang, W. Active Gate Drive Circuit with Auxiliary Drive Branch for SiC MOSFET. In Proceedings of the 2022 25th International Conference on Electrical Machines and Systems (ICEMS), Chiang Mai, Thailand, 29 November–2 December 2022; pp. 1–5. [Google Scholar]
- Wang, Z.; Wu, Y.; Mahmud, M.H.; Yuan, Z.; Zhao, Y.; Mantooth, H.A. Busbar Design and Optimization for Voltage Overshoot Mitigation of a Silicon Carbide High-Power Three-Phase T-Type Inverter. IEEE Trans. Power Electron. 2021, 36, 204–214. [Google Scholar] [CrossRef]
- Zhu, J.; Yuan, J.; Nie, Z. Optimum design of planer busbar based on all-silicon carbide power module. Proc. CSEE 2019, 39, 6383–6393. [Google Scholar]
- Mirdoddi, K.; Nag, S.S. A Vertically Stacked Bus-bar Design Approach for Equal Power Loop Inductance in Three—Phase Voltage Source Inverter. In Proceedings of the 2023 IEEE Transportation Electrification Conference & Expo (ITEC), Chiang Mai, Thailand, 28 November–1 December 2023; pp. 1–5. [Google Scholar]
- Li, C.; Liu, B.; Zhu, Q.; Qi, Y.; Cao, J.; Du, Y.; Jain, P.; Song, G. Comparative Study on Stray Inductance and Current Sharing of a 90kW Inverter Using Multiple Discrete IGBT Devices in Parallel. In Proceedings of the 2024 IEEE 2nd International Conference on Power Science and Technology (ICPST), Dali, China, 9–11 May 2024; pp. 135–140. [Google Scholar]
- Ou, H.; Li, B.; Fang, X. Analysis of Switching Oscillation for Different Packaging Structures of SiC MOSFETs. Power Electron. Technol. 2024, 58, 138–140. [Google Scholar]
- Solero, L.; Serrao, V.; Taglioni, P. Low-voltage power electronics building block for automotive applications. In Proceedings of the Twenty-First Annual IEEE Applied Power Electronics Conference and Exposition, Dallas, TX, USA, 19–23 March 2006; pp. 633–639. [Google Scholar]
- Xin, D.; Huo, Y.; Wang, Q. Development of a compact 60kW three-phase asymmetry half-bridge power convertor with specifically designed busbar for switched reluctance machines. In Proceedings of the 2015 IEEE NW Russia Young Research in Electrical and Electronic Engineering Conference, St. Petersburg, Russia, 2–4 February 2015; pp. 311–316. [Google Scholar]
- Guler, N.; Ben Hazem, Z. A K-Additive Fuzzy Logic Approach for Optimizing FCS Sizing and Enhanced User Satisfaction. World Electr. Veh. J. 2024, 15, 150. [Google Scholar] [CrossRef]
- Ben Hazem, Z. Study of Q-learning and deep Q-network learning control for a rotary inverted pendulum system. Discov. Appl. Sci. 2024, 6, 49. [Google Scholar] [CrossRef]



















| (nH) | /(nH) | /(nH) | /(nH) | Range of Temperature Increase (°C) | Error Range (%) | |
|---|---|---|---|---|---|---|
| Trial value | 45 | 15 | 15 | 15 | −10~50 | <5% |
| Name | /(nH) | Error Range(%) |
|---|---|---|
| Trial value | 15 | <5% |
| Q3D simulation value of the vertical multi-loop busbar structure | 17 | <5% |
| Q3D simulation value of the single-loop busbar structure | 29 | <5% |
| Name | Reference [21]/(nH) | Reference [22]/(nH) | Reference [23]/(nH) | In this paper/(nH) |
|---|---|---|---|---|
| Inductance of Busbar | 27 | 14.9 | 13.7 | 15 |
| Name | Material | Thermal Conductivity (W/mK) | Thickness (mm) | Thermal Resistance (K/W) |
|---|---|---|---|---|
| Module coating thermal resistance | ---- | ---- | ---- | 0.27 |
| Ceramic sheet | Alumina | 29.3 | 0.6 | 0.05 |
| Controller housing | Aluminum 6061 | 167 | 5.2 | 0.08 |
| Water channel shell | Aluminum 7075 | 130 | 19.0 | 0.39 |
| Thermal interface Material | Silicone grease | 2.5 | 0.3 | 0.32 |
| Convective heat transfer resistance | ---- | ---- | ---- | 0.40 |
| Entire thermal resistance | ---- | ---- | ---- | 1.52 |
| Item | The First Experiment | The Second Experiment | The Third Experiment | The Fourth Experiment | Mean Value | Variance | Confidence Interval |
|---|---|---|---|---|---|---|---|
| Is(max)/A | 35.8 | 35.4 | 35.6 | 35.7 | 35.625 | 0.021875 | [35.603, 35.646] |
| Speed/(r/min) | 995 | 1001 | 1003 | 998 | 999.25 | 9.1875 | [990.24, 1008.2] |
| Controller Temperature/(°C) | 42 | 40 | 41 | 41 | 41 | 0.5 | [40.51, 41.49] |
| Pointer Type | SiC Controller of BAIC New Energy Vehicle Co., Ltd. | SiC Controller of Fudi Power Company | SiC Controller of This Study |
|---|---|---|---|
| Switching frequency/Hz | 25 | <50 | 50 |
| Peak efficiency/% | 99.2% | 99.4% | 98.2% |
| Power density/(kW/L) | 43 | 45 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Guo, J.; Sun, W. Development of a High-Switching-Frequency Motor Controller Based on SiC Discrete Components. World Electr. Veh. J. 2025, 16, 474. https://doi.org/10.3390/wevj16080474
Zhang S, Guo J, Sun W. Development of a High-Switching-Frequency Motor Controller Based on SiC Discrete Components. World Electric Vehicle Journal. 2025; 16(8):474. https://doi.org/10.3390/wevj16080474
Chicago/Turabian StyleZhang, Shaokun, Jing Guo, and Wei Sun. 2025. "Development of a High-Switching-Frequency Motor Controller Based on SiC Discrete Components" World Electric Vehicle Journal 16, no. 8: 474. https://doi.org/10.3390/wevj16080474
APA StyleZhang, S., Guo, J., & Sun, W. (2025). Development of a High-Switching-Frequency Motor Controller Based on SiC Discrete Components. World Electric Vehicle Journal, 16(8), 474. https://doi.org/10.3390/wevj16080474






