Analytical Calculation and Verification of Radial Electromagnetic Force Under Multi-Type Air Gap Eccentricity of Hub Motor
Abstract
1. Introduction
2. Calculation of Multiple Eccentric Radial Force
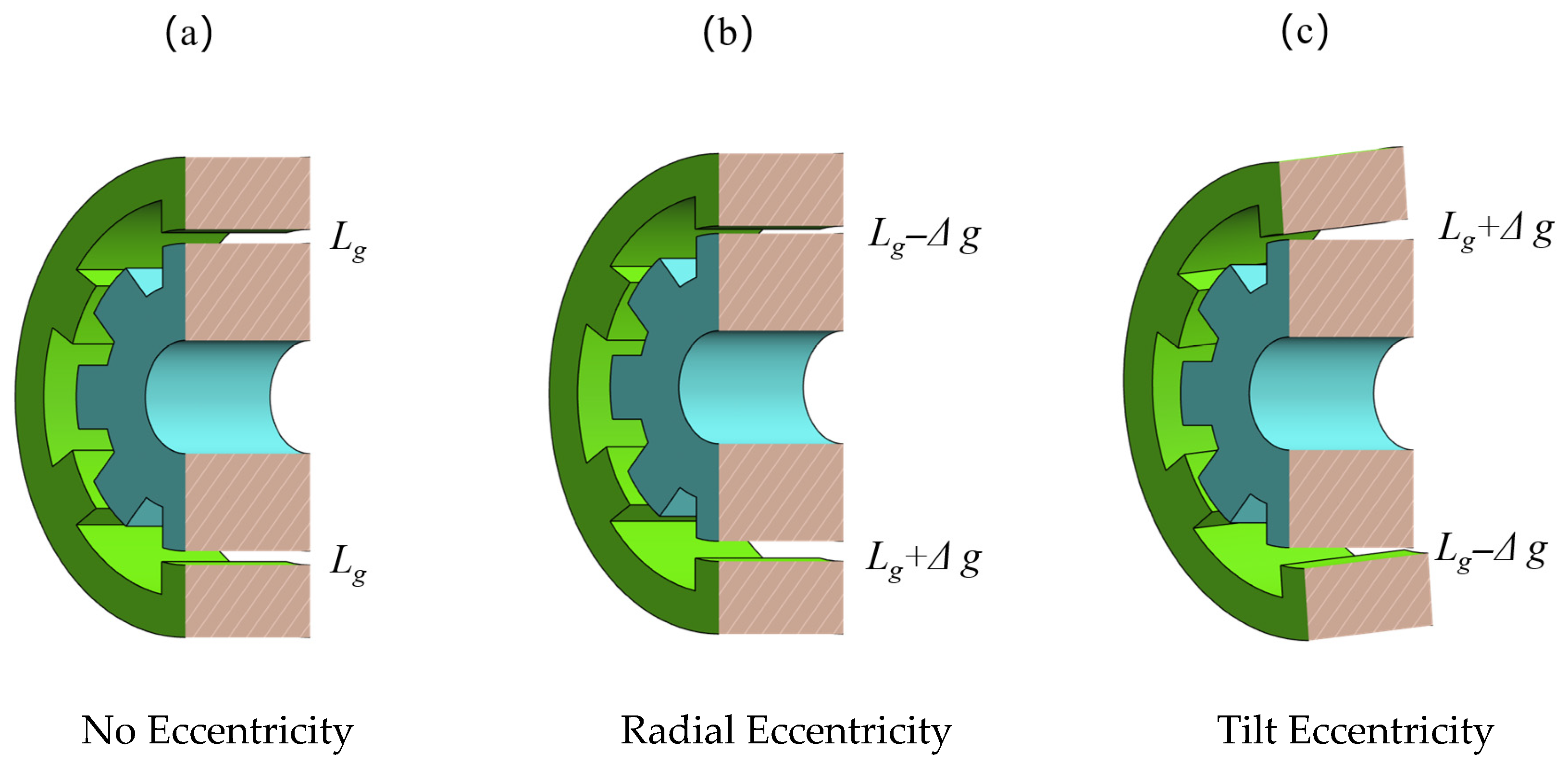
2.1. Type of Air-Gap Eccentricities
2.2. Nonlinear Model of Switched Reluctance Motor
2.3. Radial Force Calculation Under Radial Eccentricity
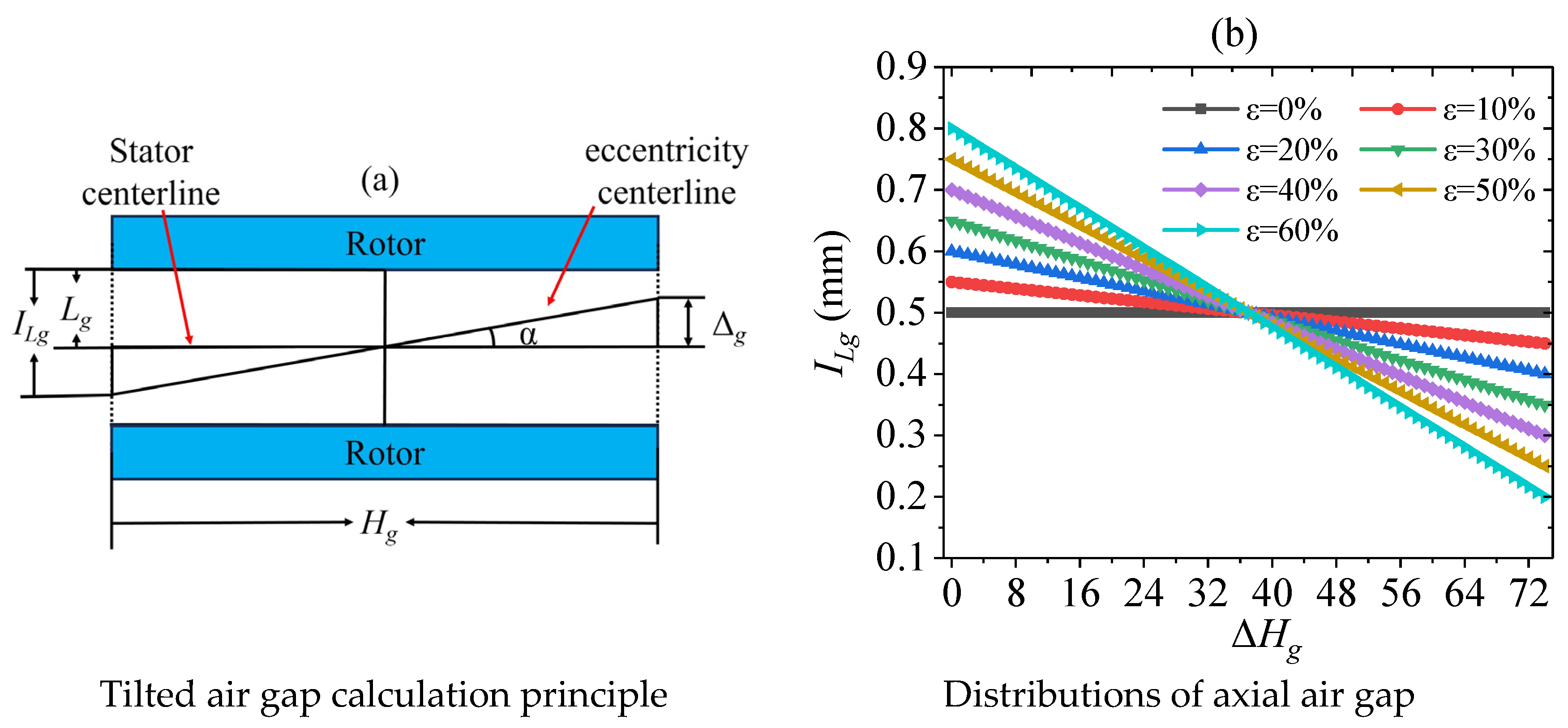
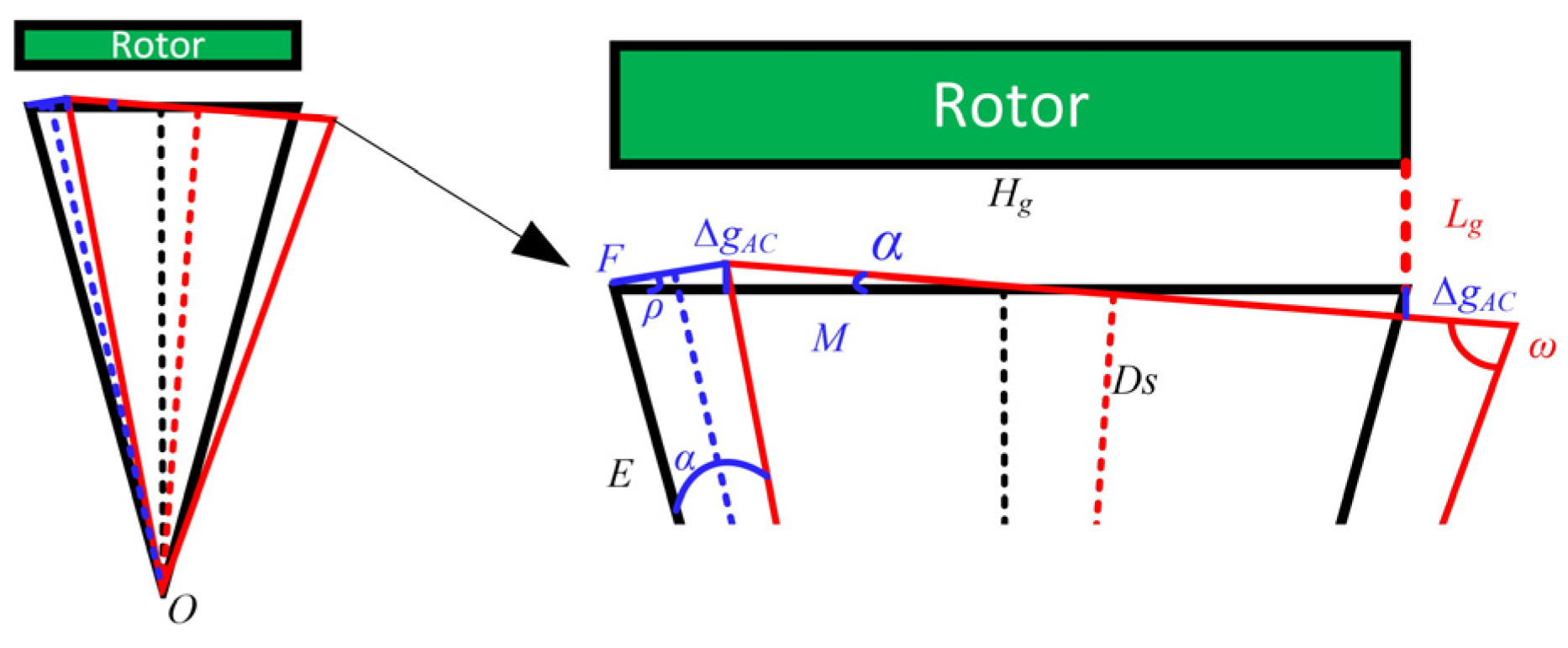
2.4. Radial Force Calculation Under Tilt Eccentricity
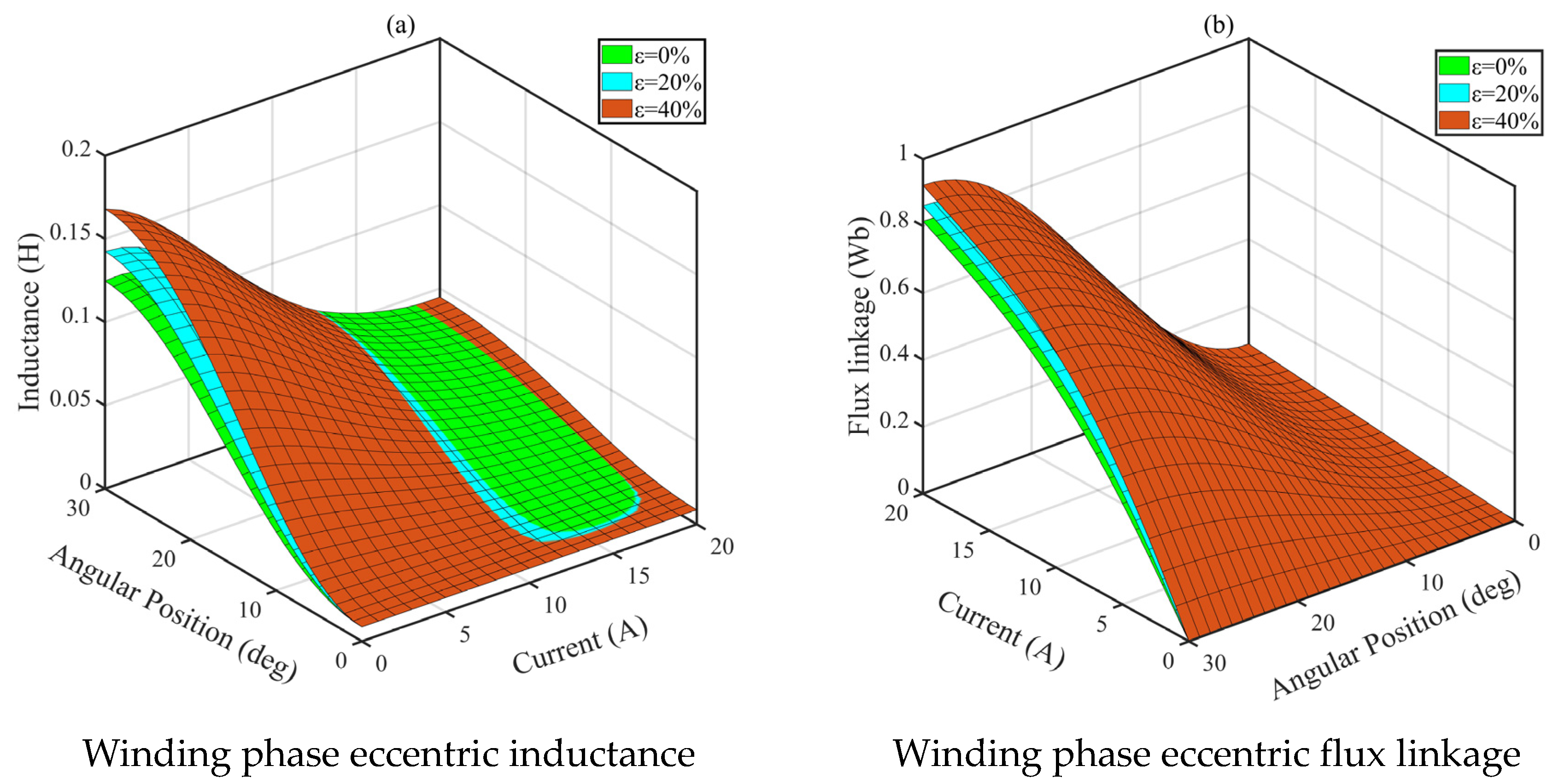
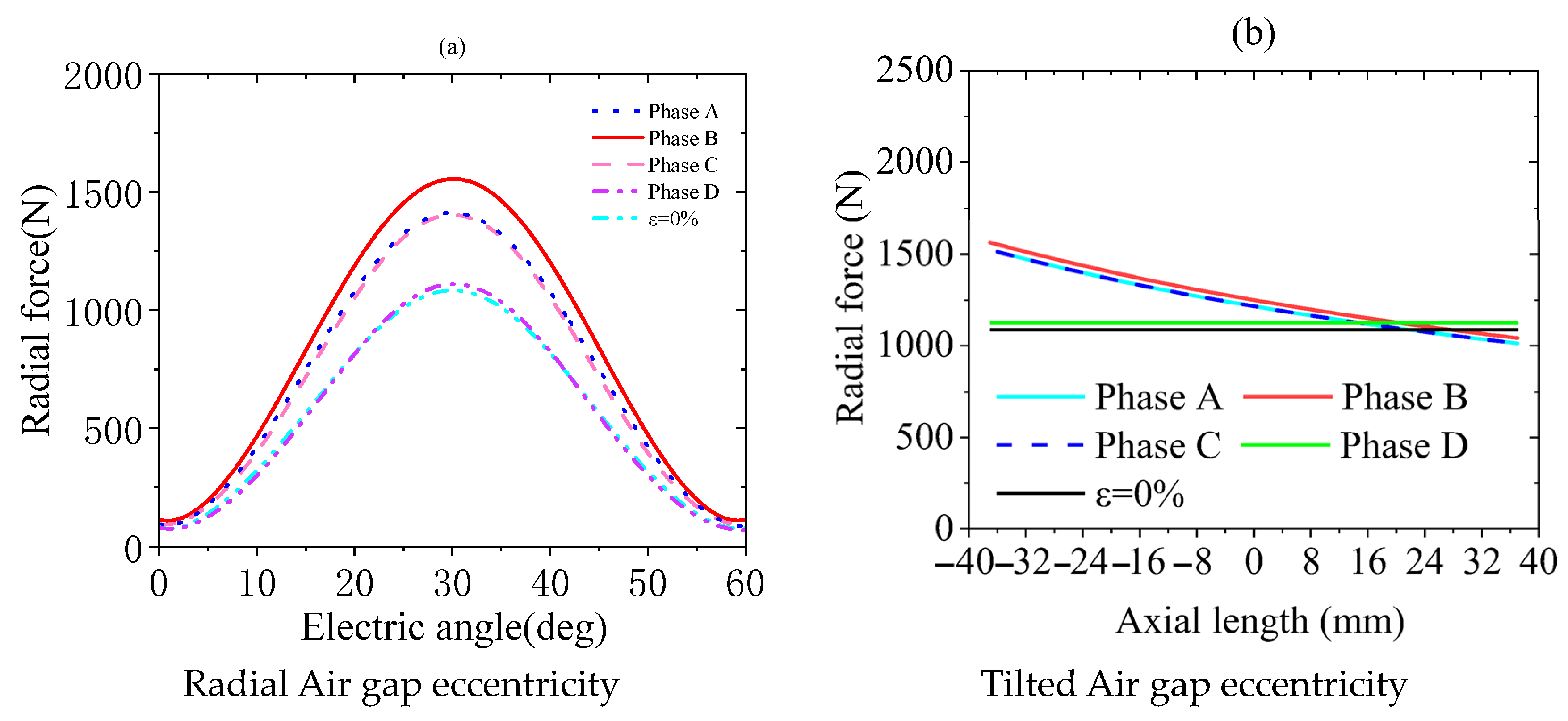
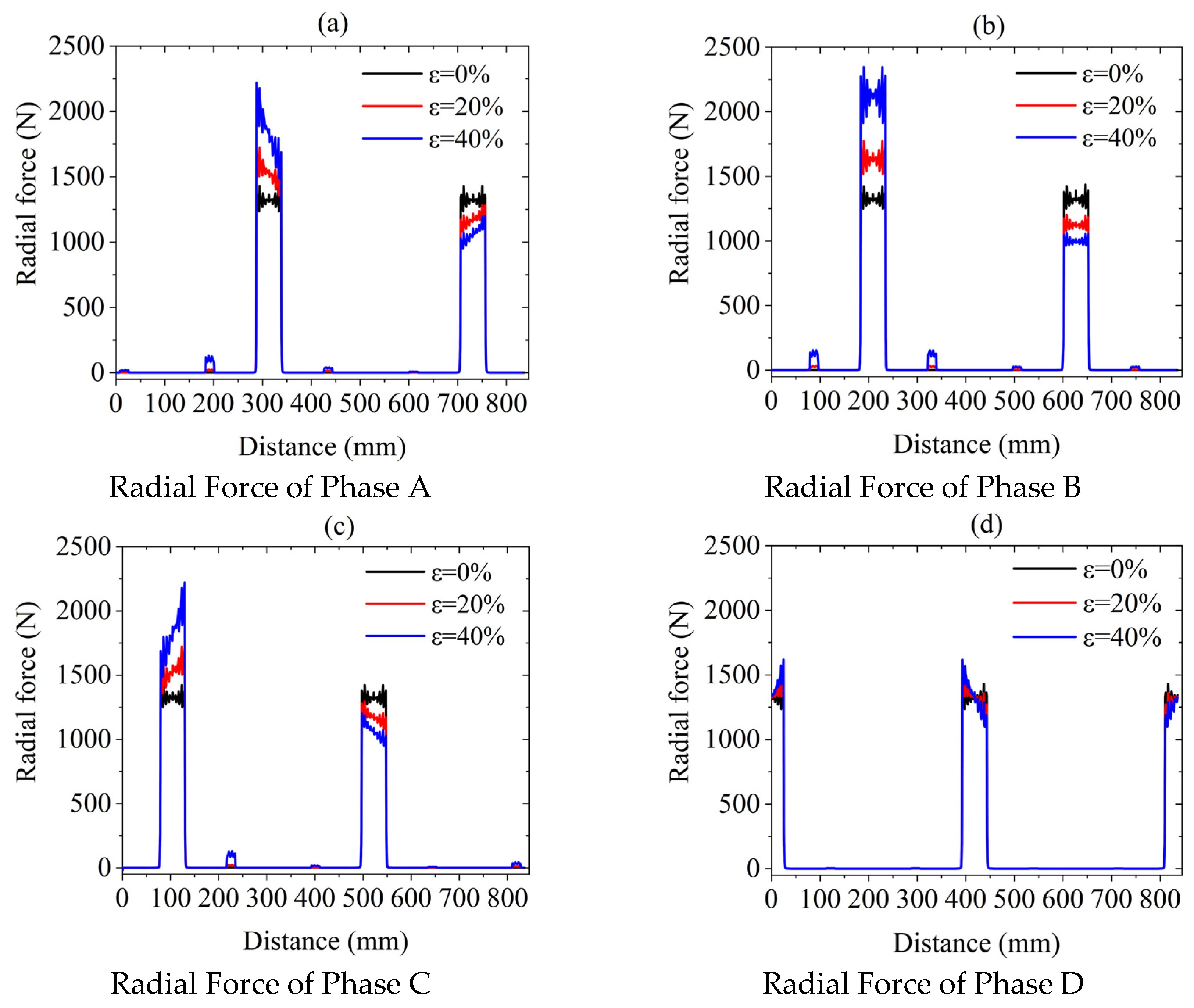
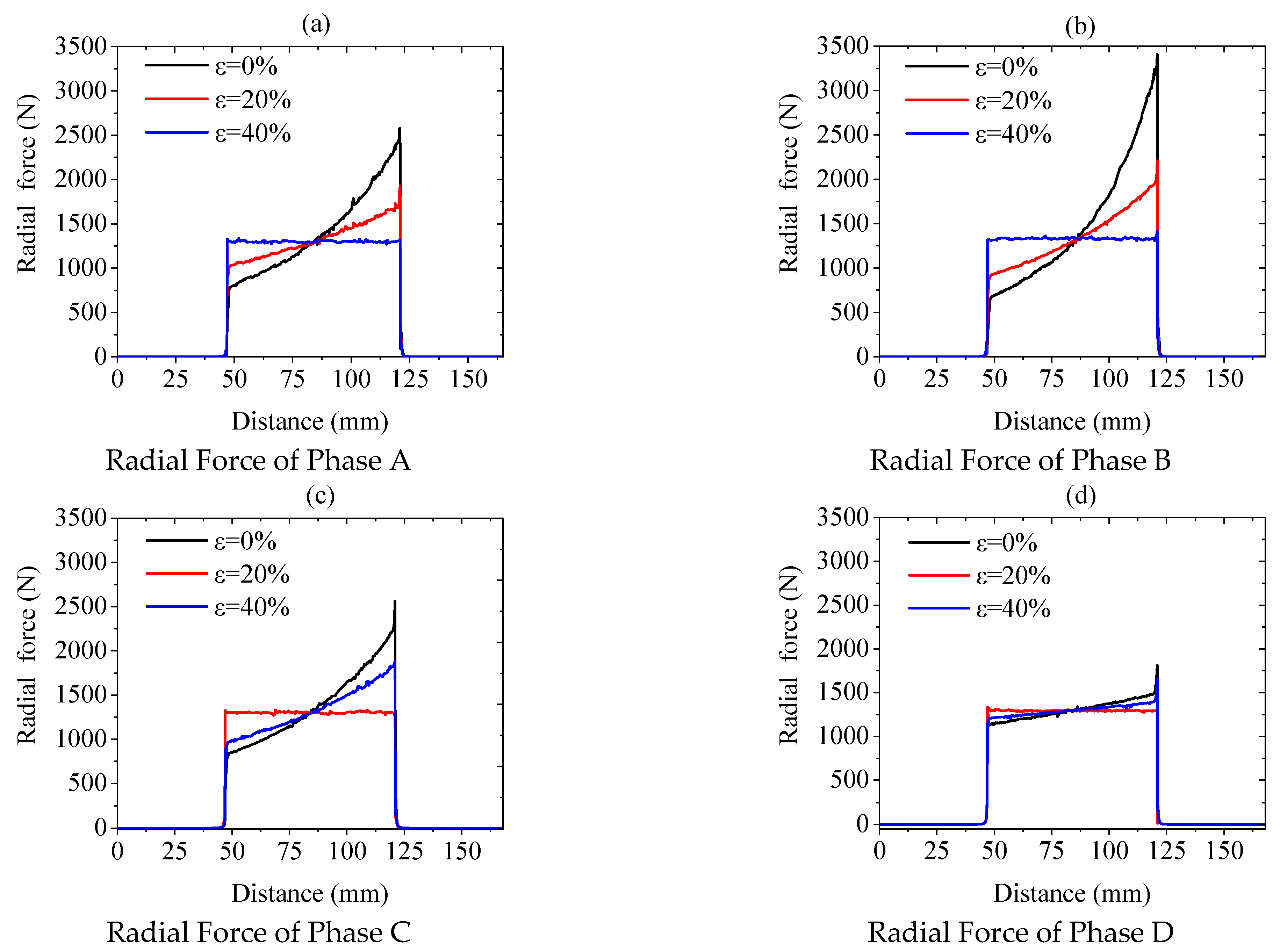
2.5. Radial Force Calculation of Each Winding Phase Under Eccentric Conditions
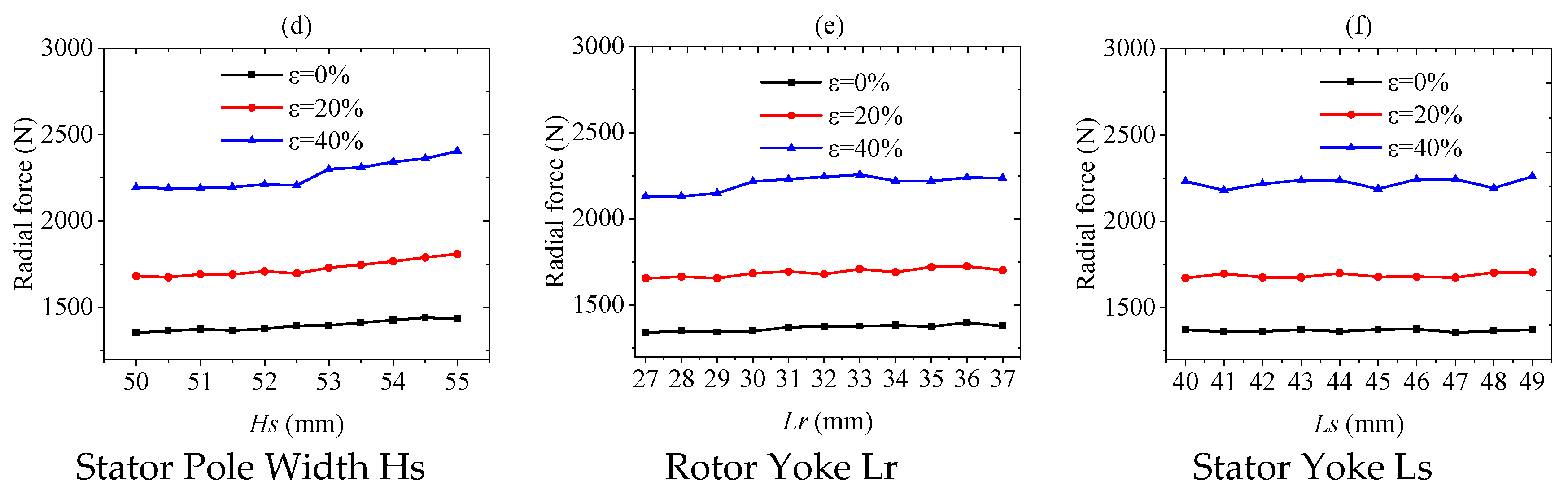
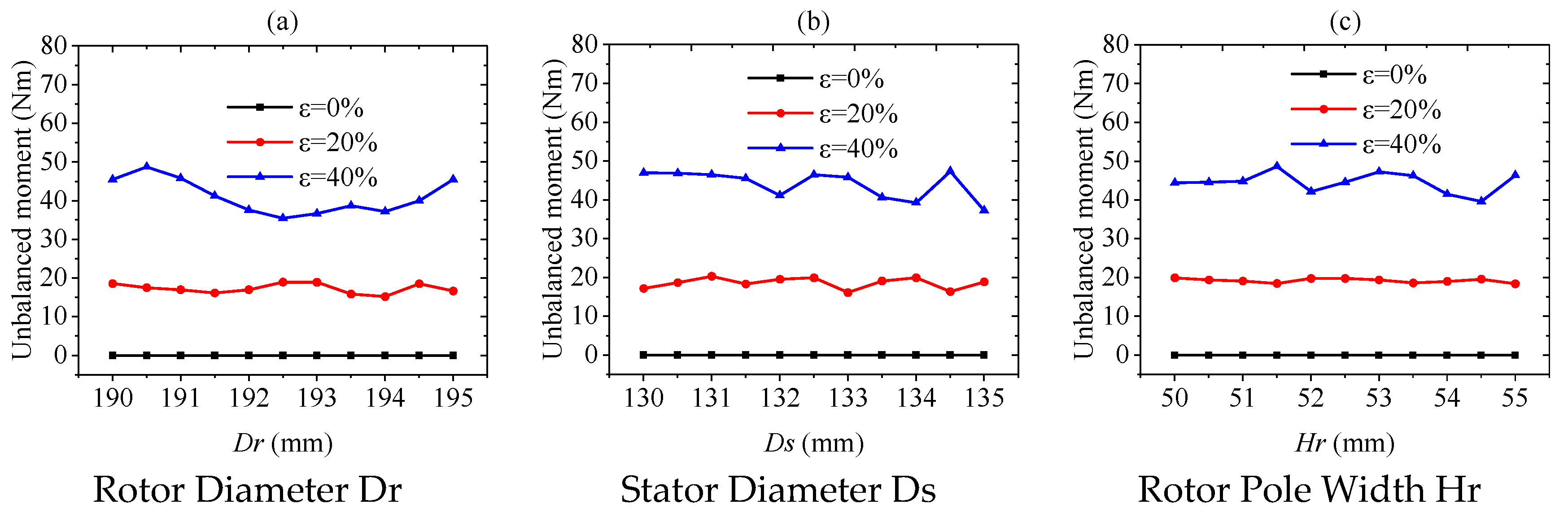
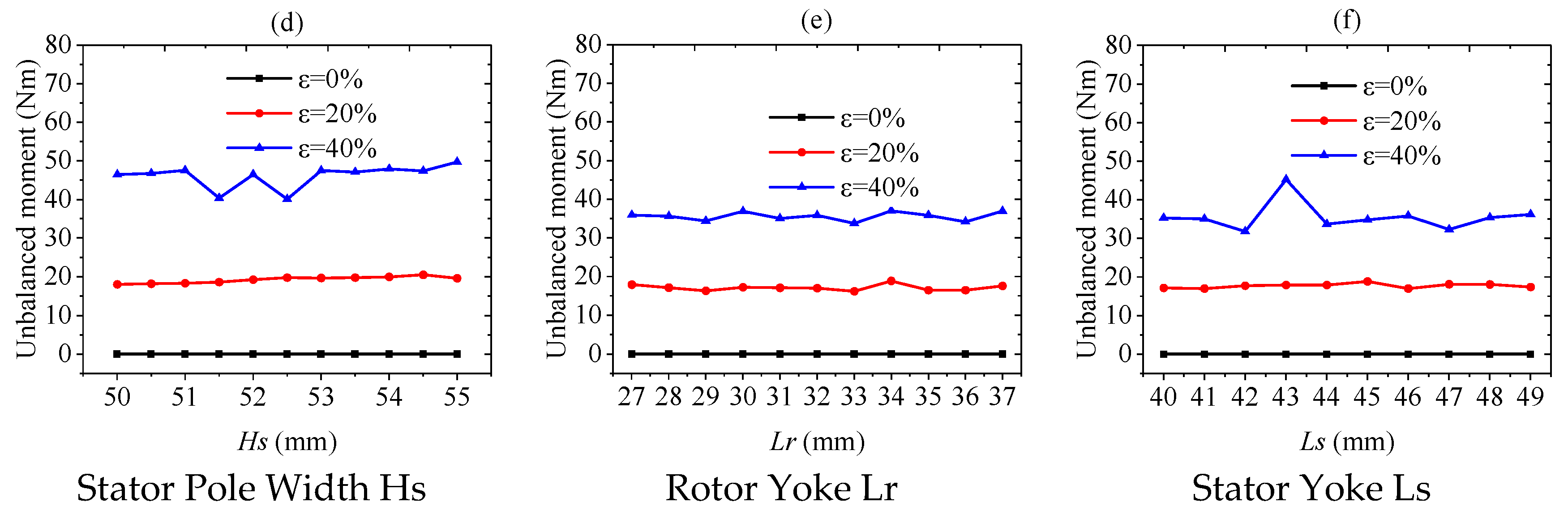
3. Influencing Factors of Radial Force Under Multi-Type Air Gap Eccentricity Conditions
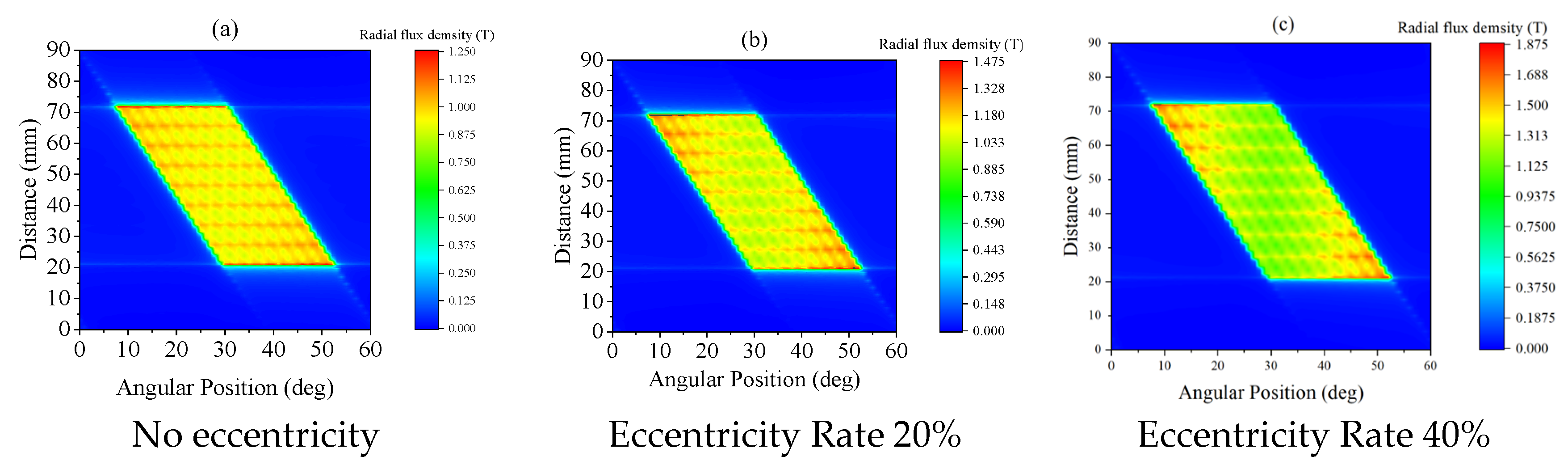
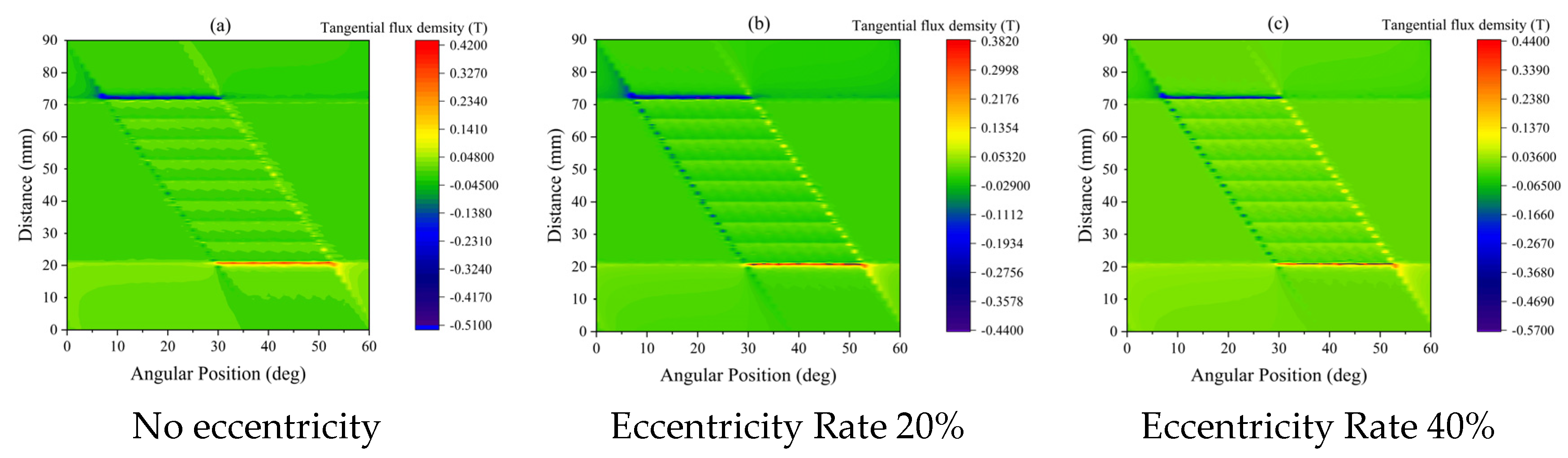
3.1. Analysis of SRM Magnetic Flux Density
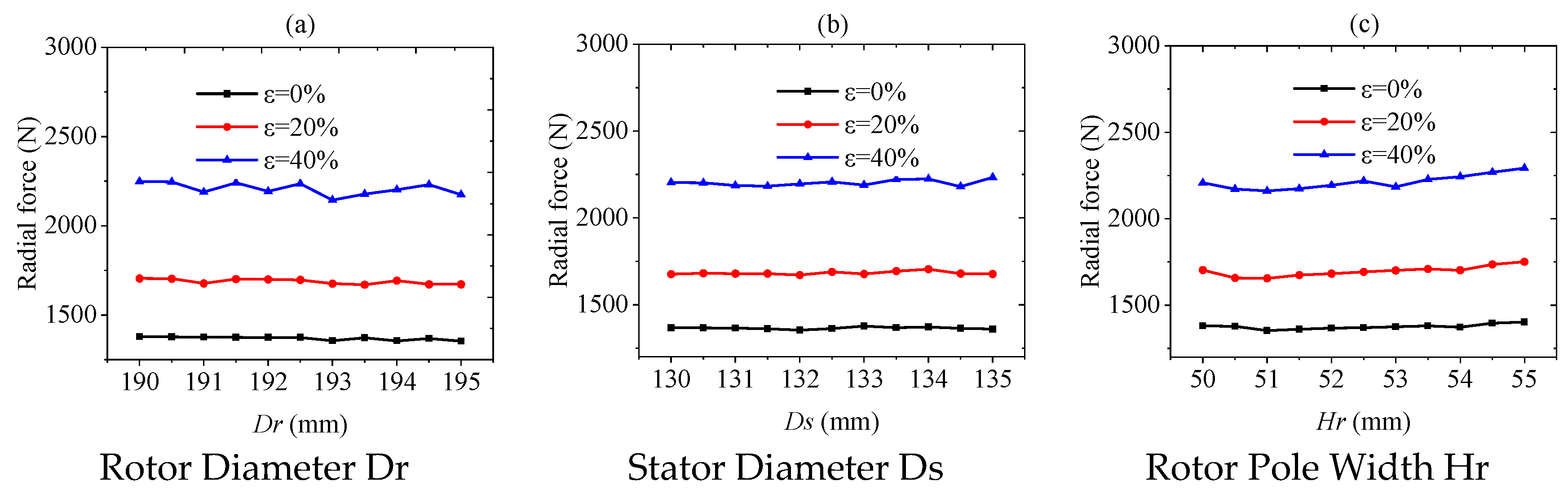
3.2. The Impact of Structural Parameters on Radial Force
3.3. Radial Force Characteristics of Each Winding Phase Under Eccentric Conditions
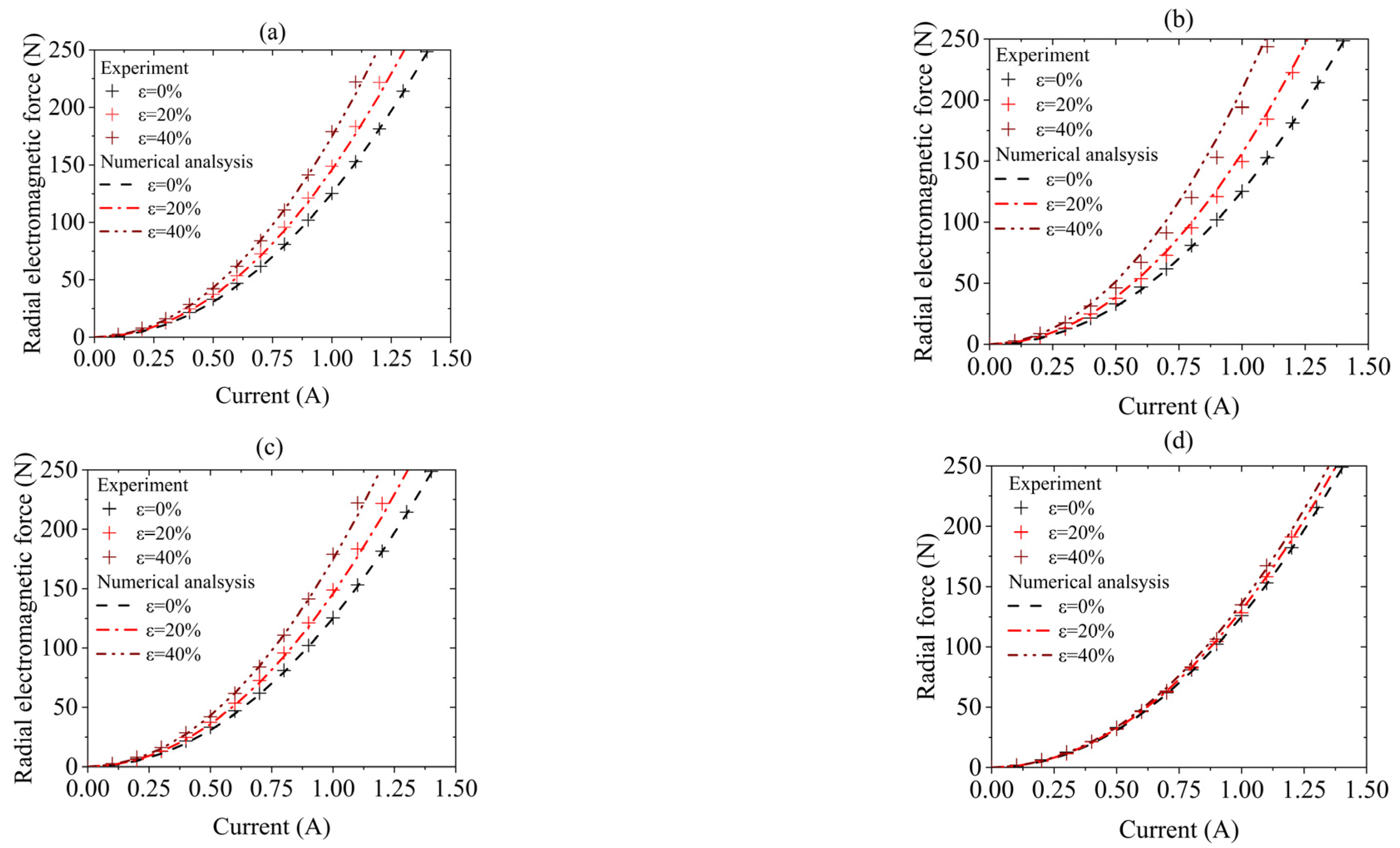
4. Experimental Verification of Radial Force Numerical Results
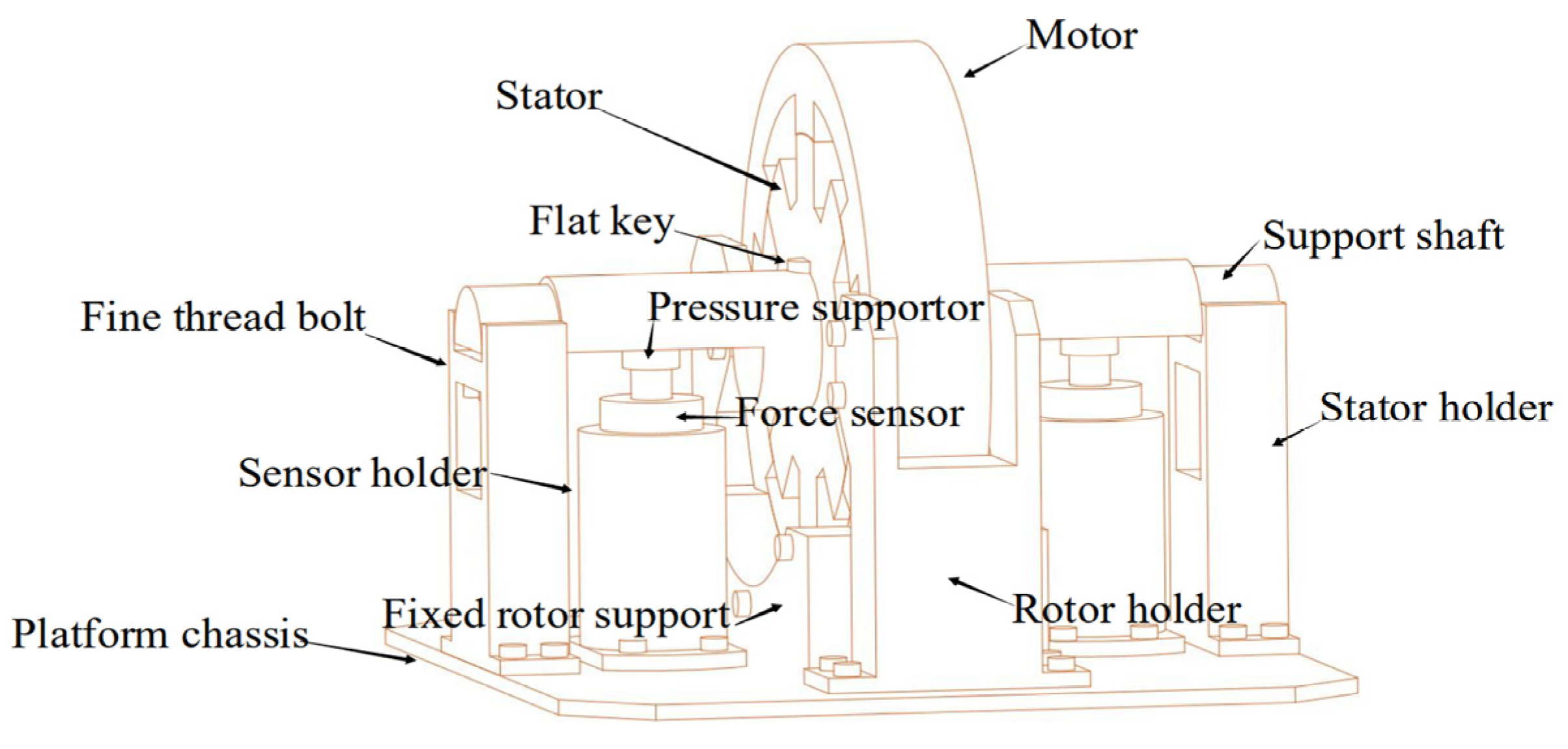
4.1. Develop Test Methods and Build Measurement Benches
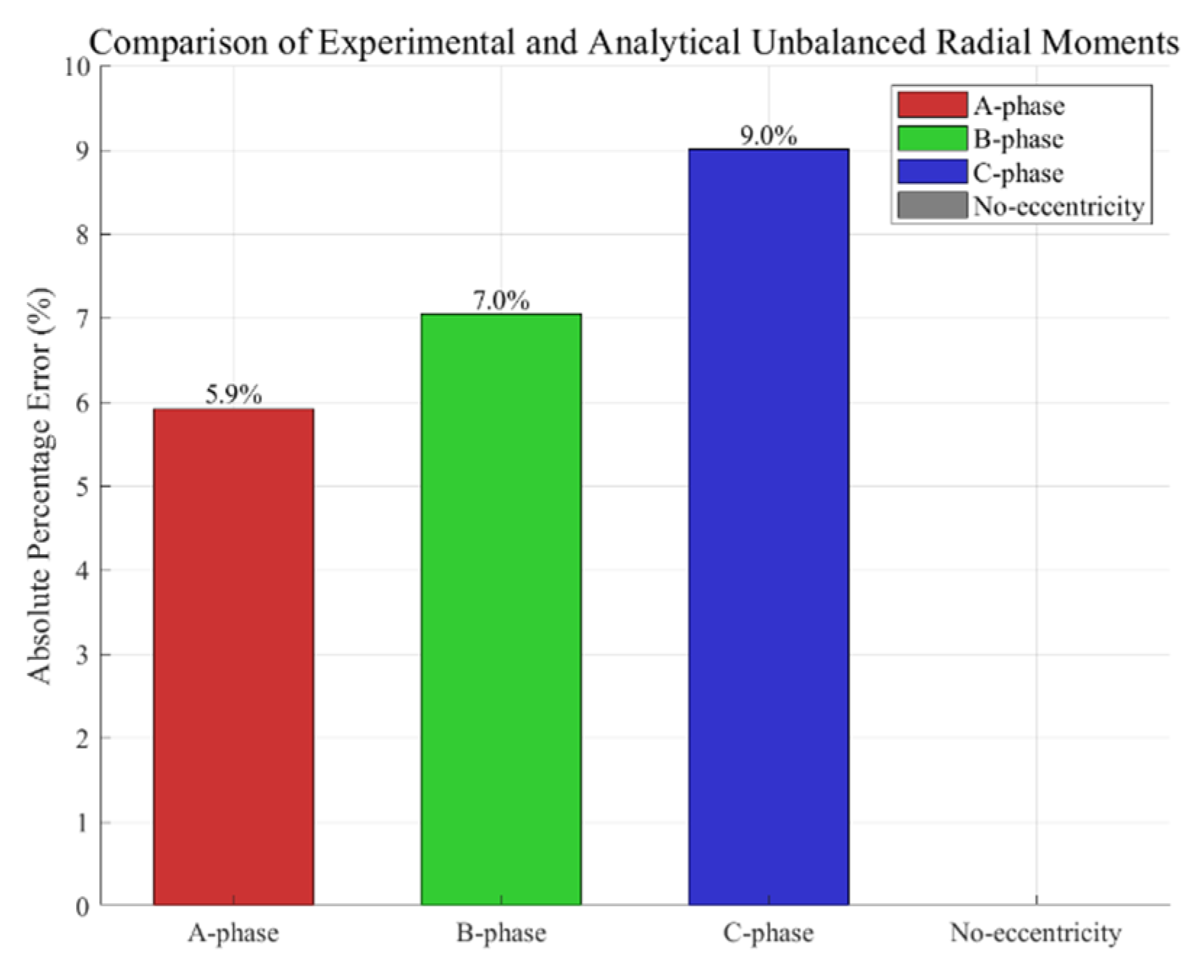
4.2. Experiment Result
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Martínez Lao, J.; Montoya, F.G.; Montoya, M.G.; Manzano-Agugliaro, F. Electric vehicles in Spain: An overview of charging systems. Renew. Sustain. Energy Rev. 2017, 77, 970–983. [Google Scholar] [CrossRef]
- Fernandes, J.C.M.; Gonçalves, P.J.P.; Silveira, M. Interaction between asymmetrical damping and geometrical nonlinearity in vehicle suspension systems improves comfort. Nonlinear Dyn. 2020, 99, 1561–1576. [Google Scholar] [CrossRef]
- Li, J.; Yang, S.; Li, Z.; Gou, L. An Energy Conservation Strategy Based on Drive Mode Switching for Multi-Axle In-wheel Motor Driven Vehicle. Energy Procedia 2019, 158, 2580–2585. [Google Scholar] [CrossRef]
- Wang, Q.; Li, R.; Zhu, Y.; Du, X.; Liu, Z. Integration design and parameter optimization for a novel in-wheel motor with dynamic vibration absorbers. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 1–12. [Google Scholar] [CrossRef]
- Fatemi, A.; Lahr, D. A Comparative Study of Cycloidal Reluctance Machine and Switched Reluctance Machine. IEEE Trans. Energy Convers. 2021, 36, 1852–1860. [Google Scholar] [CrossRef]
- Abdalmagid, M.; Sayed, E.; Bakr, M.H.; Emadi, A. Geometry and topology optimization of switched reluctance machines: A review. IEEE Access 2022, 10, 5141–5170. [Google Scholar] [CrossRef]
- Yang, X.; Song, H.; Shen, Y.; Liu, Y. Study on adverse effect suppression of hub motor driven vehicles with inertial suspensions. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 236, 767–779. [Google Scholar] [CrossRef]
- Yang, X.; Song, H.; Shen, Y.; Liu, Y.; He, T. Control of the vehicle inertial suspension based on the mixed skyhook and power-driven-damper strategy. IEEE Access 2020, 8, 217473–217482. [Google Scholar] [CrossRef]
- Hu, Y.; Li, Y.; Li, Z.; Zheng, L. Analysis and suppression of in-wheel motor electromagnetic excitation of IWM-EV. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 1552–1572. [Google Scholar] [CrossRef]
- Tan, D.; Wang, H.; Wang, Q. Study on the rollover characteristic of in-wheel-motor-driven electric vehicles considering road and electromagnetic excitation. Shock. Vib. 2016, 2016, 2450573. [Google Scholar] [CrossRef]
- Li, Z.; Liu, C.; Song, X.; Wang, C. Vibration suppression of hub motor electric vehicle considering unbalanced magnetic pull. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 3185–3198. [Google Scholar] [CrossRef]
- Guo, B.; Du, Y.; Peng, F.; Huang, Y. Magnetic field calculation in axial flux permanent magnet motor with rotor eccentricity. IEEE Trans. Magn. 2022, 58, 1–4. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, B. Analysis of magnetic forces in axial-flux permanent-magnet motors with rotor eccentricity. Math. Probl. Eng. 2021, 2021, 1–8. [Google Scholar] [CrossRef]
- Xu, M.X.; He, Y.L.; Zhang, W.; Dai, D.R.; Liu, X.A.; Zheng, W.J.; Wan, S.T.; Gerada, D.; Shi, S.Z. Impact of Radial Air-Gap Eccentricity on Stator End Winding Vibration Characteristics in DFIG. Energies 2022, 15, 6426. [Google Scholar] [CrossRef]
- He, Y.L.; Sun, Y.X.; Xu, M.X.; Wang, X.L.; Wu, Y.C.; Vakil, G.; Gerada, D.; Gerada, C. Rotor UMP characteristics and vibration properties in synchronous generator due to 3D static air-gap eccentricity faults. IET Electr. Power Appl. 2020, 14, 961–971. [Google Scholar] [CrossRef]
- He, Y.L.; Li, Y.; Zhang, W.; Xu, M.X.; Bai, Y.F.; Wang, X.L.; Shi, S.Z.; Gerada, D. Analysis of stator vibration characteristics in synchronous generators considering inclined static air gap eccentricity. IEEE Access 2022, 11, 7794–7807. [Google Scholar] [CrossRef]
- Xing, Z.; Wang, X.; Zhao, W. Electromagnetic Vibration Reduction of Surface-Mounted Permanent Magnet Synchronous Motors Based on Eccentric Magnetic Poles. J. Electr. Eng. Technol. 2023, 18, 3603–3614. [Google Scholar] [CrossRef]
- Galfarsoro, U.; McCloskey, A.; Zarate, S.; Hernández, X.; Almandoz, G. Influence of Manufacturing Tolerances and Eccentricities on the Electromotive Force in Permanent Magnet Synchronous Motors. In Proceedings of the 2022 International Conference on Electrical Machines (ICEM), Valencia, Spain, 5–8 September 2022. [Google Scholar]
- Teng, X.; Li, Y.; Zhang, B.; Feng, G.; Liu, Z. Analysis and weakening of radial electromagnetic forces in high-speed permanent magnet motors with external rotors based on shape functions. IET Electr. Power Appl. 2023, 17, 656–669. [Google Scholar] [CrossRef]
- Li, X.; Deng, Z.; Liu, T.; Zhao, S. Analytical representation and characteristics optimization for radial electromagnetic force of the switched reluctance motor under airgap eccentricity. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 7629–7640. [Google Scholar] [CrossRef]
- Liang, W.; Wang, J.; Luk, P.C.K.; Fei, W. Analytical study of stator tooth modulation on electromagnetic radial force in permanent magnet synchronous machines. IEEE Trans. Ind. Electron. 2020, 68, 11731–11739. [Google Scholar] [CrossRef]
- Wang, F.; Wu, Z.; Li, X. Analytical modelling of radial coupled vibration and superharmonic resonance in switched reluctance motor. J. Vib. Eng. Technol. 2021, 9, 449–467. [Google Scholar] [CrossRef]
- Deng, Z.; Luo, X.; Liao, X.; Li, X.; Du, Z.; Hou, M.; Wei, H. Analysis and suppression of the negative effect of electromagnetic characteristics of wheel hub motor drive system on vehicle dynamics performance. Nonlinear Dyn. 2025, 113, 4425–4445. [Google Scholar] [CrossRef]
- Khalil, A.; Husain, I. A fourier series generalized geometry-based analytical model of switched reluctance machines. IEEE Trans. Ind. Appl. 2007, 43, 673–684. [Google Scholar] [CrossRef]
- Ye, Z.Z.; Martin, T.W.; Balda, J.C. Modeling and nonlinear control of a switched reluctance motor to minimize torque ripple. In Proceedings of the Smc 2000 Conference Proceedings. 2000 IEEE International Conference on Systems, Man and Cybernetics. Cybernetics Evolving to Systems, Humans, Organizations, and Their Complex Interactions Cat, Nashville, TN, USA, 8–11 October 2000; Volume 5. [Google Scholar]
- Mahdavi, J.; Suresh, G.; Fahimi, B.; Ehsani, M. Dynamic modeling of nonlinear SRM drive with Pspice. In Proceedings of the IAS’97. Conference Record of the 1997 IEEE Industry Applications Conference Thirty-Second IAS Annual Meeting, New Orleans, LA, USA, 5–9 October 1997; Volume 1. [Google Scholar]
- Krishnamurthy, M.; Edrington, C.S.; Emadi, A.; Asadi, P.; Ehsani, M.; Fahimi, B. Making the case for applications of switched reluctance motor technology in automotive products. IEEE Trans. Power Electron. 2006, 21, 659–675. [Google Scholar] [CrossRef]






| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Rotor Diameter Dr/mm | 382 | Rotor Pole Arc βr/deg | 23 |
| Stator Diameter Ds/mm | 266 | Stator Pole Arc βs/deg | 22 |
| Shaft Diameter Dsh/mm | 90 | Rotor Yoke Lr/mm | 32 |
| Air-gap Length Lg/mm | 0.5 | Stator Yoke Ls/mm | 46 |
| Stack Length Hg/mm | 74 | Number of Turns Nc/- | 136 |
| Rotor Position | Parameters | ε = 0% | ε = 20% | ε = 40% |
|---|---|---|---|---|
| 30 deg | Radial Force | 1082.13 N/- | 1495.35 N/38.19% | 2243.96 N/107.37% |
| 15 deg | Static Torque | 1.80 Nm/- | 2.02 Nm/12.22% | 2.32 Nm/28.89% |
| Components | Functions |
|---|---|
| Regulated DC power supply | Supplies stable DC excitation voltage to the coil windings |
| DCC test leade | Connects the DC power source to the winding terminals |
| Load application point | Supports the stator shaft during force application |
| Spoke-type load cell (0 kg–800 kg) | Measures the radial force (RF) applied during testing |
| Force display controller | Displays and manages radial force readings |
| Digital multimeter | Monitors the current flowing through the winding coils |
| Precision feeler gauge (0.05 mm–1.00 mm) | Measures and verifies air-gap eccentricity |
| Angular protractor | Assists in adjusting winding phase and rotor-stator alignment |
| Laptop computer | Performs data acquisition, processing, and analysis |
| Phase | Value of Pressure Sensor | Numerical Value of Radial Force/N | Unbalanced Moment/Nm | |||
|---|---|---|---|---|---|---|
| Left | Right | Left | Right | Experimental | Numerical | |
| A | 119.8 | 152.5 | 99.89 | 227.85 | 2.227 | 2.367 |
| B | 117.9 | 152.1 | 102.7 | 239.6 | 2.309 | 2.484 |
| C | 120.1 | 153.5 | 99.90 | 227.83 | 2.153 | 2.366 |
| No ecc | 135.1 | 135.1 | 125.28 | 125.28 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Jia, S.; Ji, W.; Yang, C. Analytical Calculation and Verification of Radial Electromagnetic Force Under Multi-Type Air Gap Eccentricity of Hub Motor. World Electr. Veh. J. 2025, 16, 473. https://doi.org/10.3390/wevj16080473
Yang C, Jia S, Ji W, Yang C. Analytical Calculation and Verification of Radial Electromagnetic Force Under Multi-Type Air Gap Eccentricity of Hub Motor. World Electric Vehicle Journal. 2025; 16(8):473. https://doi.org/10.3390/wevj16080473
Chicago/Turabian StyleYang, Chao, Shudi Jia, Wujun Ji, and Chuanxing Yang. 2025. "Analytical Calculation and Verification of Radial Electromagnetic Force Under Multi-Type Air Gap Eccentricity of Hub Motor" World Electric Vehicle Journal 16, no. 8: 473. https://doi.org/10.3390/wevj16080473
APA StyleYang, C., Jia, S., Ji, W., & Yang, C. (2025). Analytical Calculation and Verification of Radial Electromagnetic Force Under Multi-Type Air Gap Eccentricity of Hub Motor. World Electric Vehicle Journal, 16(8), 473. https://doi.org/10.3390/wevj16080473




