A Novel Data-Driven Multi-Branch LSTM Architecture with Attention Mechanisms for Forecasting Electric Vehicle Adoption
Abstract
1. Introduction
2. Forecasting Methods for EV Adoption
2.1. Traditional Time-Series Forecasting Methods
2.2. Econometric and Diffusion Approaches
2.3. Machine Learning and Deep Learning Approaches
| Method | Study (Year) | Performance | Key Traits |
|---|---|---|---|
| Exponential Smoothing | Peng et al. [14] | MSPE = 1.8187 | Simplicity; lacks external inputs |
| Multiple Regression | Duan et al. [15] | MAPE = 22.7% | Linear assumption; interpretability |
| ARIMA | Dhankhar et al. [4] | MAPE = 44.7% | Autocorrelation; struggles with nonlinearity |
| Gray Prediction (GM) | Zhou et al. [22] | MAPE = 8.83% | Suited to small samples; moderate accuracy |
| SVR | Qu et al. [23] | Non-linear; requires parameter tuning | |
| ANN (MLP) | Ma et al. [24] | RMSE = 16.31 | Non-linear patterns; data intensive |
| GRU/LSTM | Rasheed et al. [18] | Adj. | Temporal dependencies; black box |
| CNN–LSTM | Simsek et al. [19] | Spatial–temporal features; superior accuracy | |
| Transformer | Zhou et al. [25] | 30–50% MSE gain over LSTM | Long-range dependencies; computationally intensive |
2.4. Alternative Forecasting Approaches and Future Directions
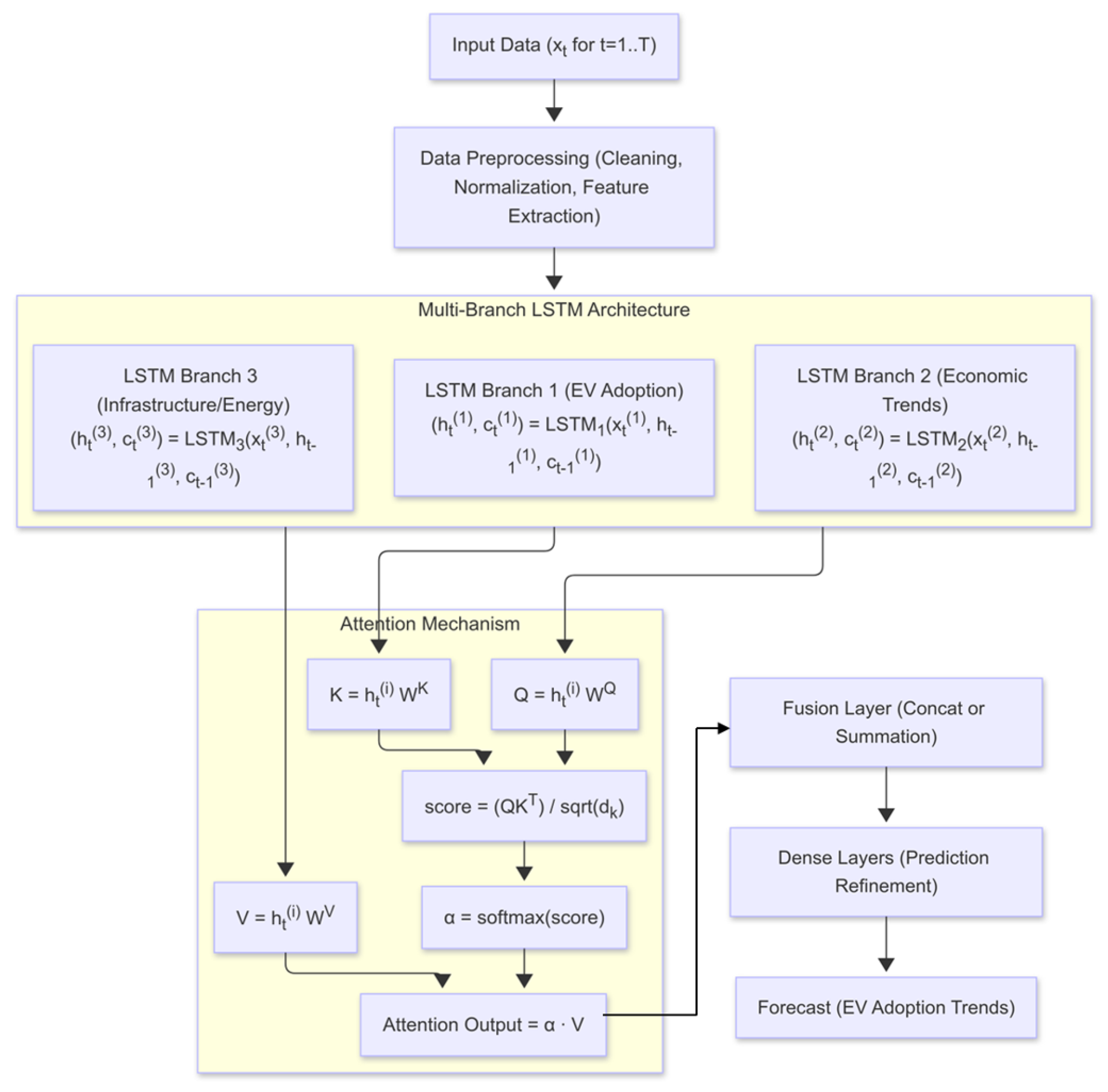
3. Multi-Branch LSTM Architectures and Attention Mechanisms
3.1. Multi-Branch LSTM Architecture
3.2. Attention Mechanisms in Time Series
3.3. Transformers for Time-Series Forecasting
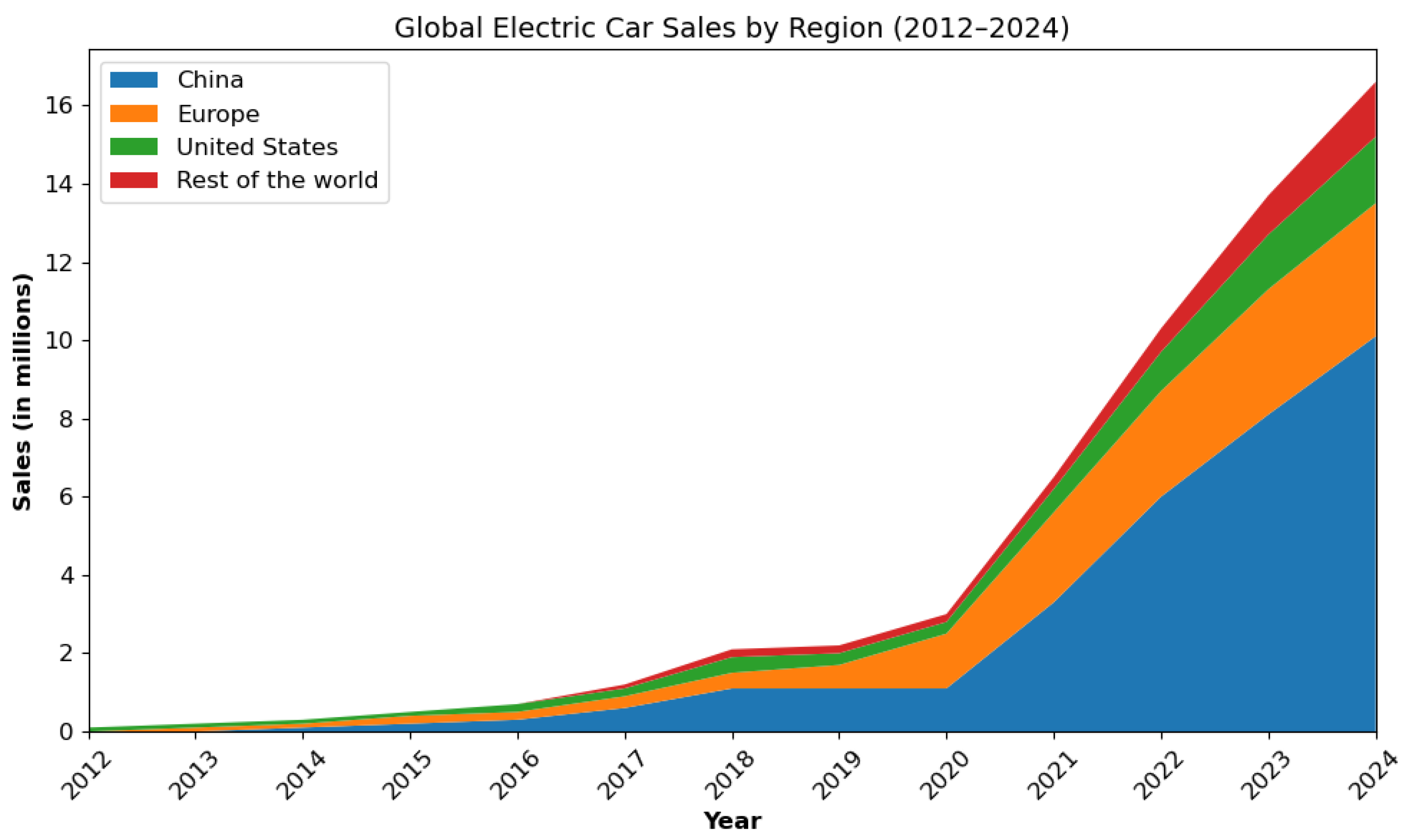
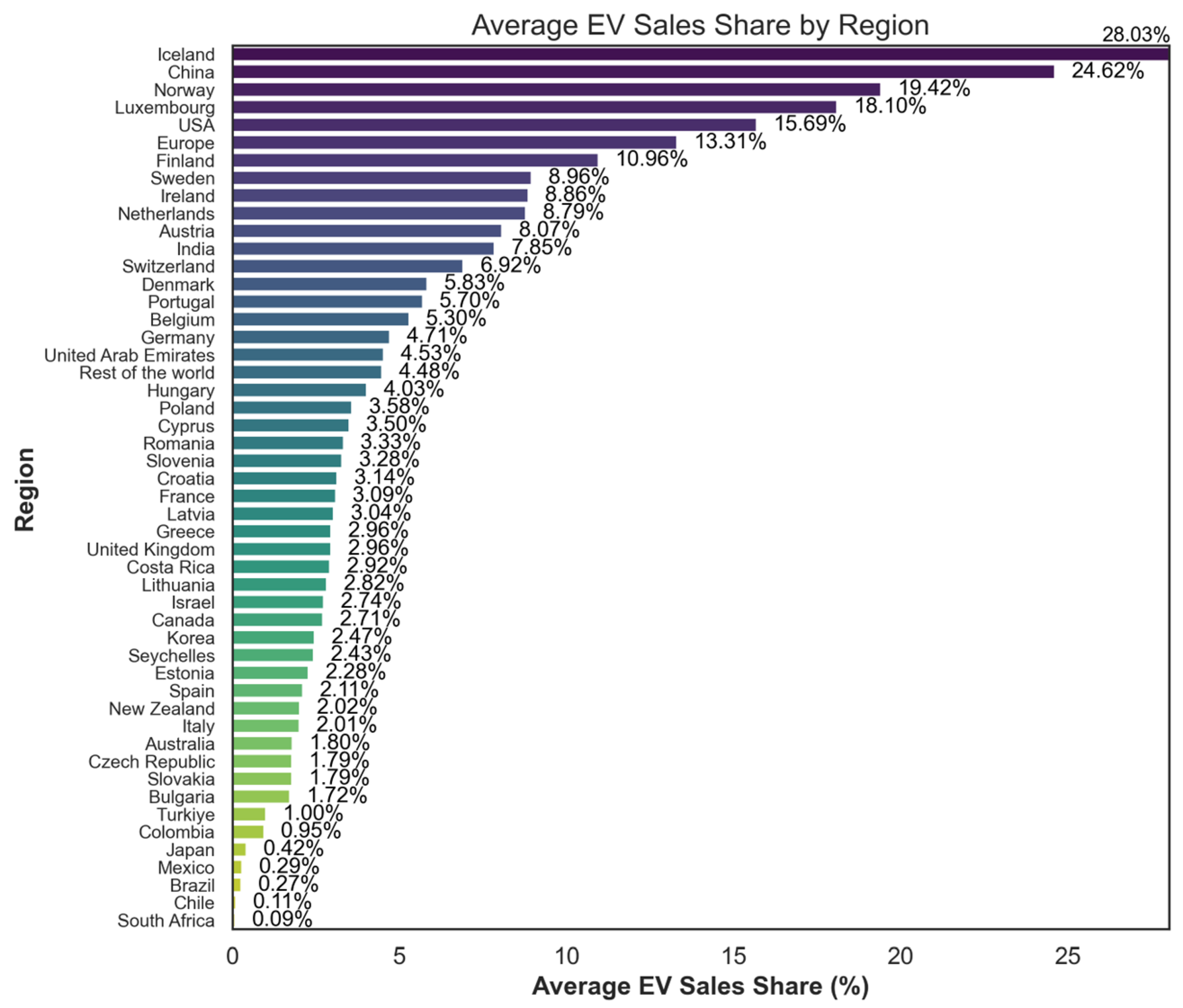
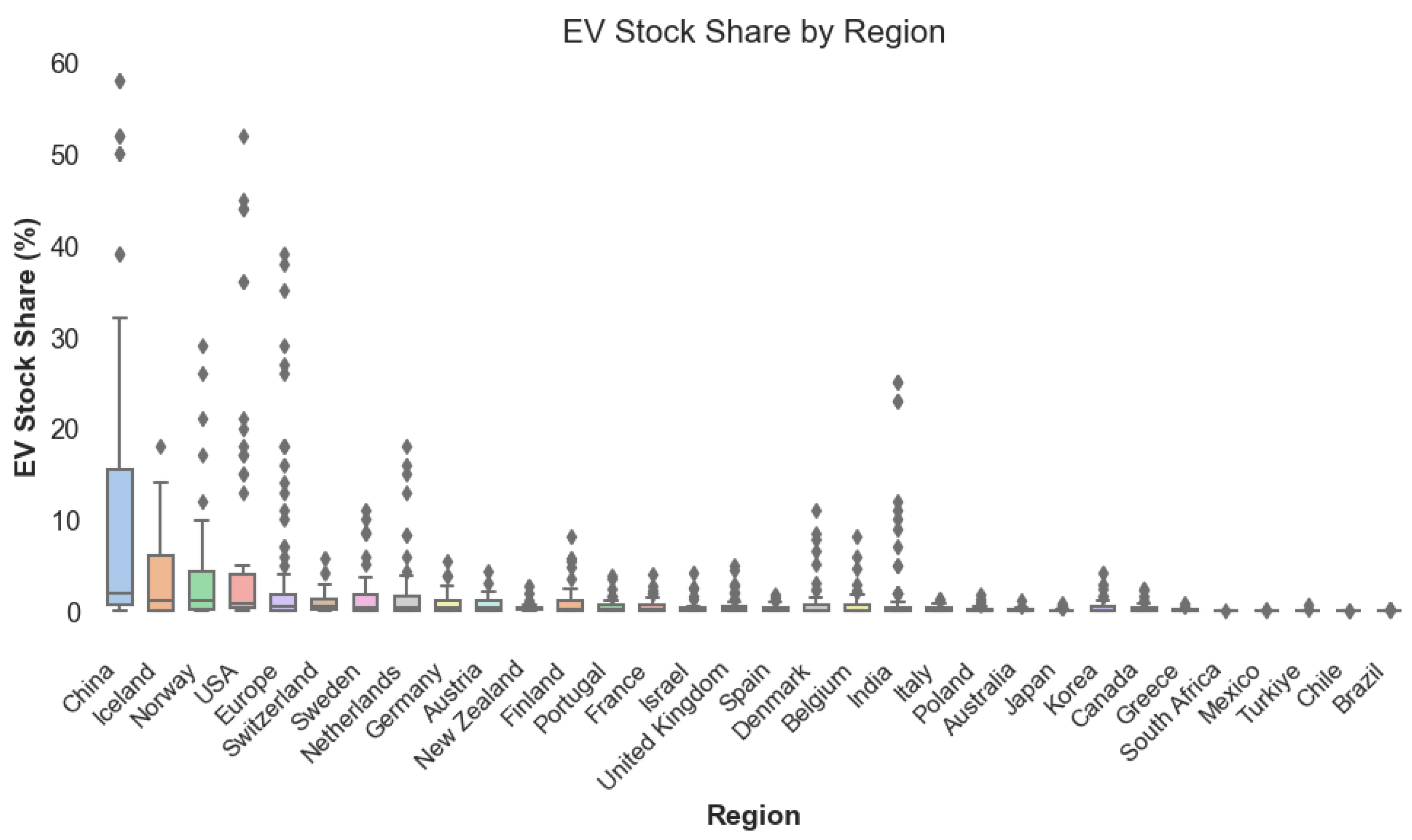
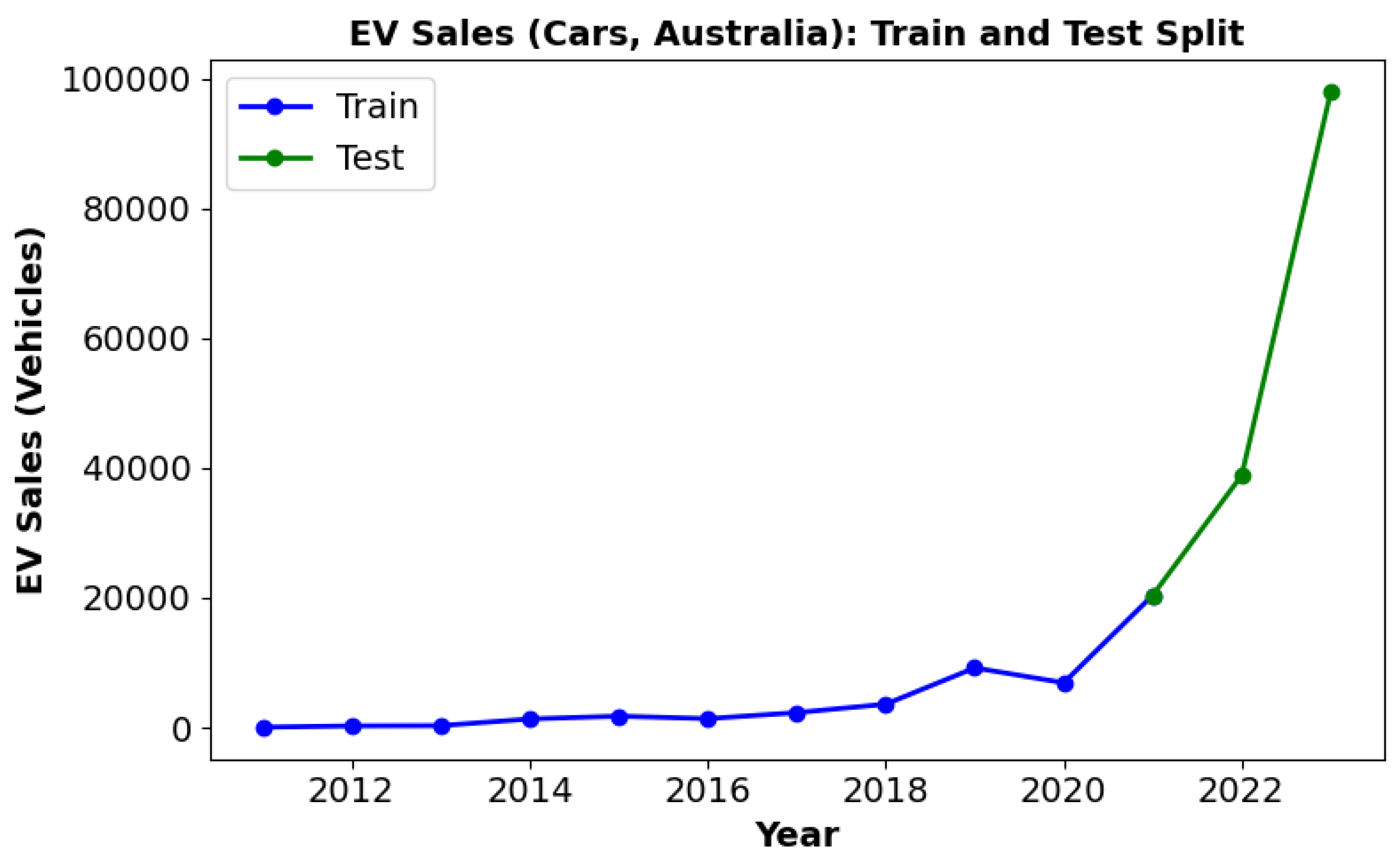
4. Dataset
4.1. Data Structure and Coverage
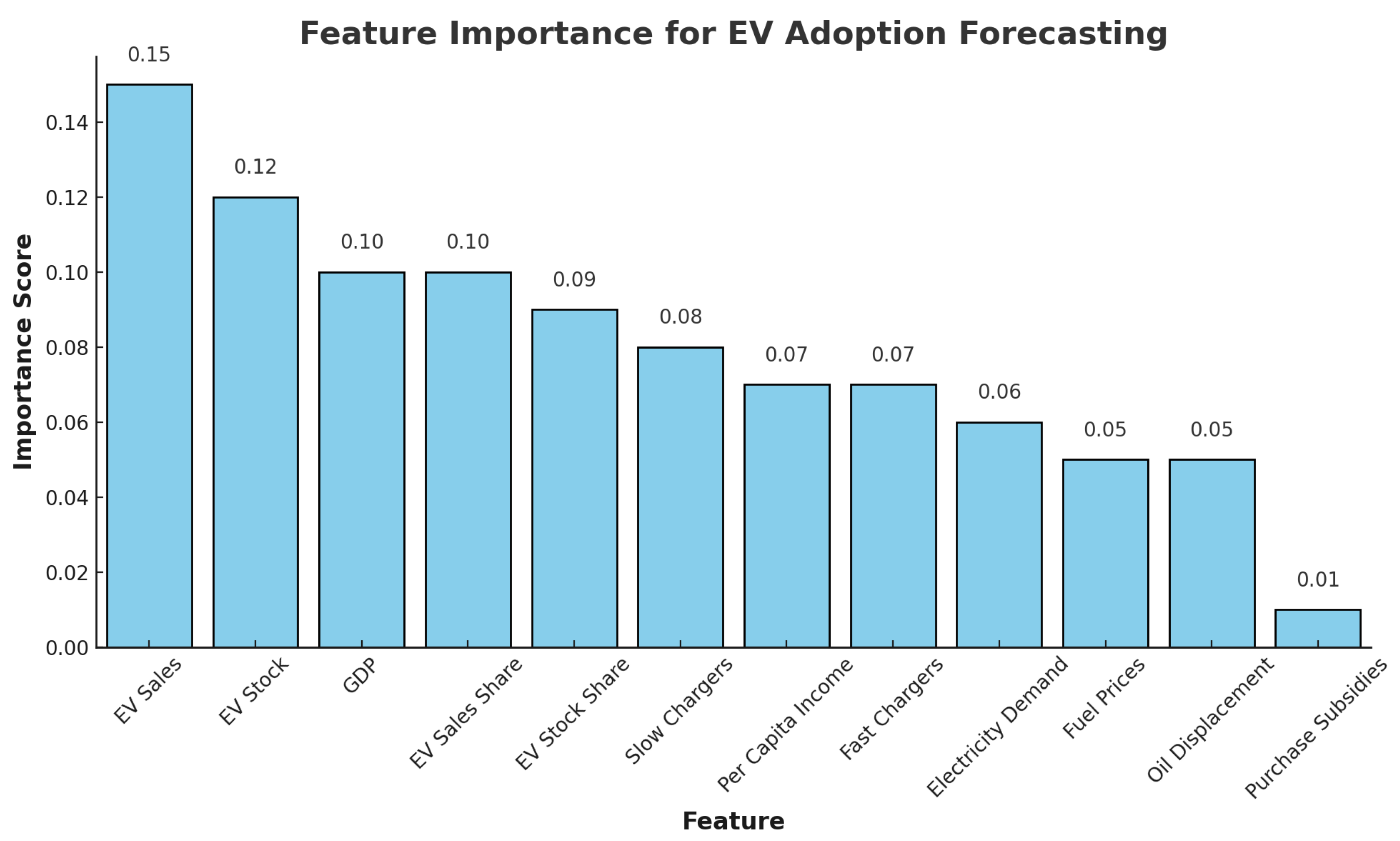
4.2. Principal Variables and Features
4.3. Preprocessing, Feature Engineering, and Model Application
5. Research Scope and Methodology
5.1. Scope and Objectives
- We introduce a novel architecture that integrates multi-branch LSTM networks with an attention mechanism, specifically designed for forecasting technology adoption.
- Our approach leverages multiple data streams to enhance the prediction accuracy of EV adoption.
- The attention mechanism offers improved interpretability, providing insights into the relative importance of various input features and addressing the conventional black-box nature of deep learning models.
- The proposed framework is extensible and can be adapted to other adoption forecasting applications (e.g., solar panel adoption), highlighting its broad applicability.
5.2. Proposed Multi-Branch LSTM Architecture with Attention
5.3. Model Selection Rationale
- Heterogeneous feature streams. EV adoption is driven by multi-scale signals—historical uptake, infrastructure and policy, and macro-economics—that are only weakly correlated with one another. Gong et al. [47] showed that isolating correlated variable groups in separate BiLSTM branches improved MAE by 9% in hydropower monitoring, confirming the benefit of branch-specific recurrent encoders for heterogeneous inputs.
- Data regime and sequence length. Transformers excel on very long sequences given large training corpora, but can underperform on medium-length, noisy energy datasets: Zeng et al. [9] report that a simple linear baseline outperformed six Transformer variants on nine public energy sets. Our weekly EV series contains fewer than 2000 time steps—well within the effective range of LSTM models and below the scale where Transformer depth is usually beneficial. A systematic review likewise notes the data-hungry nature of Transformer forecasting models [48].
- Parameter efficiency and interpretability. Attention-augmented LSTMs retain the recurrent inductive bias while offering 5–15% lower MAPE than Vanilla LSTMs on multivariate energy tasks [49]. Moreover, branch-level attention weights provide transparent importance scores that align with policy questions, whereas CNN-LSTM hybrids tend to form spatial feature maps whose relevance is harder to trace [50,51].
5.4. Methodology for Performance Evaluation
5.4.1. Train/Test Regime
5.4.2. Hyperparameter Tuning
5.4.3. Baseline Comparison
- Single-branch LSTM: An LSTM model that used only historical EV sales, serving to quantify the added value of the additional branches.
- ARIMA model: A traditional ARIMA approach, with parameters selected based on the Akaike information criterion (AIC), acting as a statistical benchmark.
- Feed-forward neural network: A simple fully connected network trained on the same set of inputs, used to test the advantage of sequence modeling offered by LSTM.
6. Results and Limitations
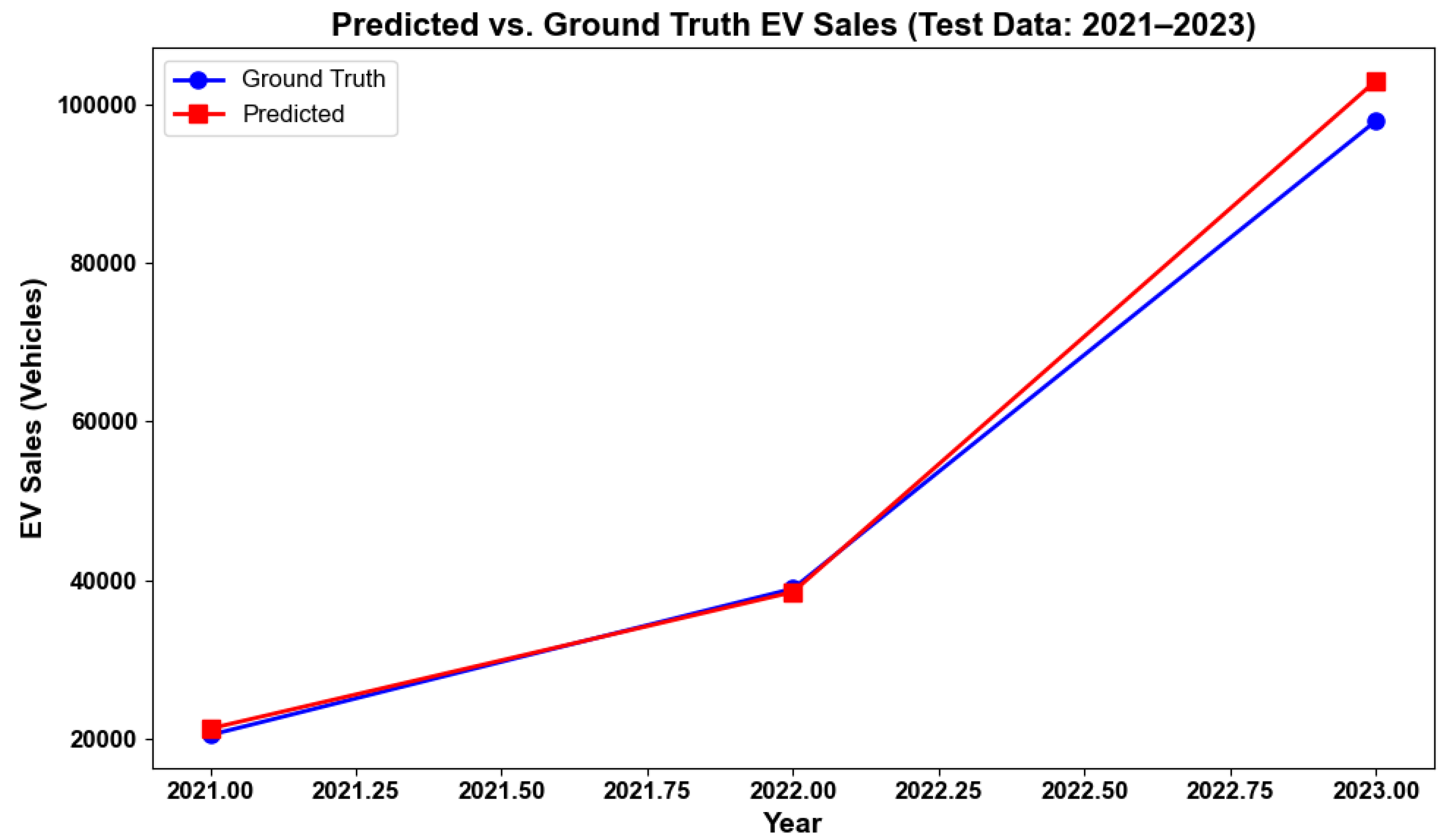
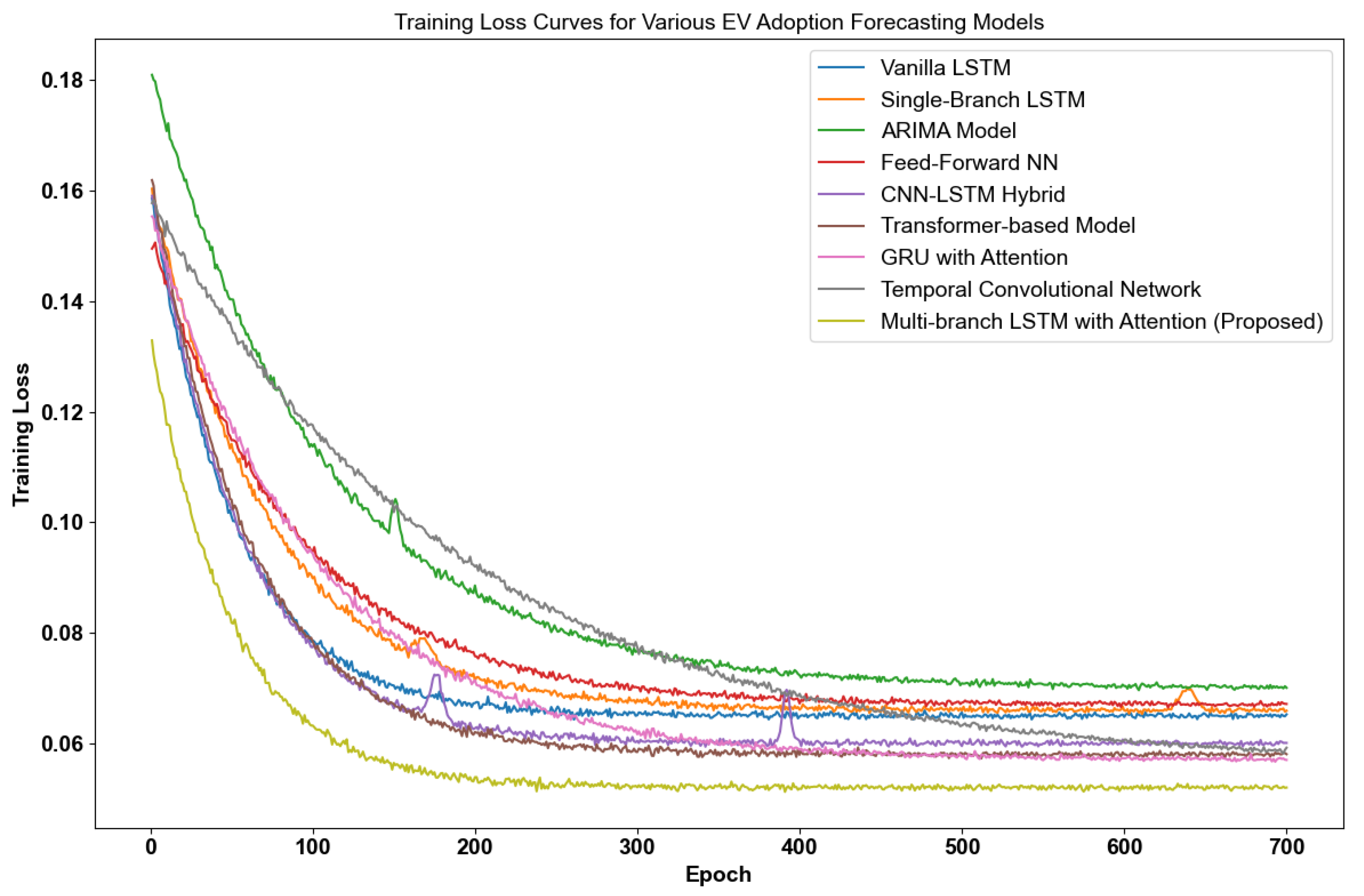
6.1. Overall Results and Comparison
6.2. Limitations and Future Directions
7. Ablation Study
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- International Energy Agency. Electric Vehicles. 2024. Available online: https://www.iea.org/energy-system/transport/electric-vehicles (accessed on 23 March 2025).
- Yang, Y.; Jin, M.; Wen, H.; Zhang, C.; Liang, Y.; Ma, L.; Wang, Y.; Liu, C.; Yang, B.; Xu, Z.; et al. A survey on diffusion models for time series and spatio-temporal data. arXiv 2024, arXiv:2404.18886. [Google Scholar] [CrossRef]
- Zhang, C.; Schmöcker, J.D.; Trépanier, M. Carsharing adoption dynamics considering service type and area expansions with insights from a Montreal case study. Transp. Res. Part C Emerg. Technol. 2024, 167, 104810. [Google Scholar] [CrossRef]
- Dhankhar, S.; Dhankhar, N.; Sandhu, V.; Mehla, S. Forecasting electric vehicle sales with arima and exponential smoothing method: The case of india. Transp. Dev. Econ. 2024, 10, 32. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhong, M.; Geng, N.; Jiang, Y. Forecasting electric vehicles sales with univariate and multivariate time series models: The case of China. PLoS ONE 2017, 12, e0176729. [Google Scholar] [CrossRef]
- Yi, Z.; Liu, X.C.; Wei, R.; Chen, X.; Dai, J. Electric vehicle charging demand forecasting using deep learning model. J. Intell. Transp. Syst. 2022, 26, 690–703. [Google Scholar] [CrossRef]
- Yaghoubi, E.; Yaghoubi, E.; Khamees, A.; Razmi, D.; Lu, T. A systematic review and meta-analysis of machine learning, deep learning, and ensemble learning approaches in predicting EV charging behavior. Eng. Appl. Artif. Intell. 2024, 135, 108789. [Google Scholar] [CrossRef]
- Bampos, Z.N.; Laitsos, V.M.; Afentoulis, K.D.; Vagropoulos, S.I.; Biskas, P.N. Electric vehicles load forecasting for day-ahead market participation using machine and deep learning methods. Appl. Energy 2024, 360, 122801. [Google Scholar] [CrossRef]
- Zeng, A.; Chen, M.; Zhang, L.; Xu, Q. Are transformers effective for time series forecasting? In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 11121–11128. [Google Scholar]
- Giuliari, F.; Hasan, I.; Cristani, M.; Galasso, F. Transformer networks for trajectory forecasting. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 10335–10342. [Google Scholar]
- Mosca, E.; Szigeti, F.; Tragianni, S.; Gallagher, D.; Groh, G. SHAP-based explanation methods: A review for NLP interpretability. In Proceedings of the 29th International Conference on Computational Linguistics, Gyeongju, Republic of Korea, 12–17 October 2022; pp. 4593–4603. [Google Scholar]
- Garreau, D.; Luxburg, U. Explaining the explainer: A first theoretical analysis of LIME. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Online, 26–28 August 2020; PMLR: New York, NY, USA, 2020; pp. 1287–1296. [Google Scholar]
- Zhang, W.; Valencia, A.; Chang, N.B. Synergistic integration between machine learning and agent-based modeling: A multidisciplinary review. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 2170–2190. [Google Scholar] [CrossRef]
- Peng, Z.; Yu, Z.; Wang, H.; Yang, S. Research on industrialization of electric vehicles with its demand forecast using exponential smoothing method. J. Ind. Eng. Manag. (JIEM) 2015, 8, 365–382. [Google Scholar] [CrossRef]
- Duan, Z.; Gutierrez, B.; Wang, L. Forecasting plug-in electric vehicle sales and the diurnal recharging load curve. IEEE Trans. Smart Grid 2014, 5, 527–535. [Google Scholar] [CrossRef]
- Chen, G.; Glen, D.R.; Saad, Z.S.; Hamilton, J.P.; Thomason, M.E.; Gotlib, I.H.; Cox, R.W. Vector autoregression, structural equation modeling, and their synthesis in neuroimaging data analysis. Comput. Biol. Med. 2011, 41, 1142–1155. [Google Scholar] [CrossRef]
- Domarchi, C.; Cherchi, E. Electric vehicle forecasts: A review of models and methods including diffusion and substitution effects. Transp. Rev. 2023, 43, 1118–1143. [Google Scholar] [CrossRef]
- Rasheed, I.; Hu, F.; Zhang, L. Deep reinforcement learning approach for autonomous vehicle systems for maintaining security and safety using LSTM-GAN. Veh. Commun. 2020, 26, 100266. [Google Scholar] [CrossRef]
- Simsek, A.I.; Koç, E.; Desticioglu Tasdemir, B.; Aksöz, A.; Turkoglu, M.; Sengur, A. Deep Learning Forecasting Model for Market Demand of Electric Vehicles. Appl. Sci. 2024, 14, 10974. [Google Scholar] [CrossRef]
- Liu, T.; Meidani, H. End-to-end heterogeneous graph neural networks for traffic assignment. Transp. Res. Part C Emerg. Technol. 2024, 165, 104695. [Google Scholar] [CrossRef]
- Liu, T.; Meidani, H. Multi-Class Traffic Assignment using Multi-View Heterogeneous Graph Attention Networks. arXiv 2025, arXiv:2501.09117. [Google Scholar] [CrossRef]
- Zhou, H.; Dang, Y.; Yang, Y.; Wang, J.; Yang, S. An optimized nonlinear time-varying grey Bernoulli model and its application in forecasting the stock and sales of electric vehicles. Energy 2023, 263, 125871. [Google Scholar] [CrossRef]
- Qu, F.; Wang, Y.T.; Hou, W.H.; Zhou, X.Y.; Wang, X.K.; Li, J.B.; Wang, J.Q. Forecasting of automobile sales based on support vector regression optimized by the grey wolf optimizer algorithm. Mathematics 2022, 10, 2234. [Google Scholar] [CrossRef]
- Ma, J.; Yu, J.; Gong, Z. EV Regional Market Sales Forecast Based On GABP Neural Network. In Proceedings of the IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2019; Volume 252, p. 032098. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Mehdizadeh, M.; Nordfjaern, T.; Klöckner, C.A. A systematic review of the agent-based modelling/simulation paradigm in mobility transition. Technol. Forecast. Soc. Change 2022, 184, 122011. [Google Scholar] [CrossRef]
- Gneiting, T.; Katzfuss, M. Probabilistic forecasting. Annu. Rev. Stat. Its Appl. 2014, 1, 125–151. [Google Scholar] [CrossRef]
- Leutbecher, M.; Palmer, T.N. Ensemble forecasting. J. Comput. Phys. 2008, 227, 3515–3539. [Google Scholar] [CrossRef]
- Chatzimparmpas, A.; Martins, R.M.; Kucher, K.; Kerren, A. StackGenVis: Alignment of data, algorithms, and models for stacking ensemble learning using performance metrics. IEEE Trans. Vis. Comput. Graph. 2020, 27, 1547–1557. [Google Scholar] [CrossRef]
- Rolnick, D.; Donti, P.L.; Kaack, L.H.; Kochanski, K.; Lacoste, A.; Sankaran, K.; Ross, A.S.; Milojevic-Dupont, N.; Jaques, N.; Waldman-Brown, A.; et al. Tackling climate change with machine learning. ACM Comput. Surv. (CSUR) 2022, 55, 1–96. [Google Scholar] [CrossRef]
- Zheng, H.; Yuan, J.; Chen, L. Short-term load forecasting using EMD-LSTM neural networks with a Xgboost algorithm for feature importance evaluation. Energies 2017, 10, 1168. [Google Scholar] [CrossRef]
- Liao, X.; Cao, N.; Li, M.; Kang, X. Research on short-term load forecasting using XGBoost based on similar days. In Proceedings of the 2019 International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS), Changsha, China, 12–13 January 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 675–678. [Google Scholar]
- Paudel, D.; De Wit, A.; Boogaard, H.; Marcos, D.; Osinga, S.; Athanasiadis, I.N. Interpretability of deep learning models for crop yield forecasting. Comput. Electron. Agric. 2023, 206, 107663. [Google Scholar] [CrossRef]
- Hu, T.; Liu, K.; Ma, H. Probabilistic electric vehicle charging demand forecast based on deep learning and machine theory of mind. In Proceedings of the 2021 IEEE Transportation Electrification Conference & Expo (ITEC), Chicago, IL, USA, 21–25 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 795–799. [Google Scholar]
- Rahman, M.W.; Vogl, G.W.; Jia, X.; Qu, Y. Physics-Informed Multi-Task Learning for Material Removal Rate Prediction in Semiconductor Chemical Mechanical Planarization. In Proceedings of the 2024 IEEE International Conference on Prognostics and Health Management (ICPHM), Spokane, WA, USA, 17–19 June 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 385–392. [Google Scholar]
- Rahman, M.W.; Zhao, B.; Pan, S.; Qu, Y. Microstructure-informed machine learning for understanding corrosion resistance in structural alloys through fusion with experimental studies. Comput. Mater. Sci. 2025, 248, 113624. [Google Scholar] [CrossRef]
- Bahdanau, D.; Serdyuk, D.; Brakel, P.; Ke, N.R.; Chorowski, J.; Courville, A.; Bengio, Y. Task Loss Estimation for Sequence Prediction. arXiv 2015, arXiv:1511.06456. [Google Scholar]
- International Energy Agency. Global EV Outlook 2024: Global EV Data. 2024. Available online: https://www.iea.org/reports/global-ev-outlook-2024 (accessed on 24 March 2025).
- World Bank. GDP (Current US$) [Indicator: NY.GDP.MKTP.CD]. 2021. Available online: https://data.worldbank.org/indicator/NY.GDP.MKTP.CD (accessed on 3 April 2025).
- Sikes, K.; Cox, B. Factors Influencing the Adoption of Electric Vehicles: A Review. J. Clean. Prod. 2022, 346, 131123. [Google Scholar] [CrossRef]
- Zhuk, P.; Kraus, M. Macroeconomic Determinants of Electric Vehicle Market Penetration. Energy Econ. 2023, 120, 106963. [Google Scholar] [CrossRef]
- World Bank. World Development Indicators. 2024. Available online: https://databank.worldbank.org/source/world-development-indicators (accessed on 6 July 2025).
- Federal Reserve Bank of St. Louis. Europe Brent Spot Price FOB (DCOILBRENTEU). 2024. Available online: https://fred.stlouisfed.org/series/DCOILBRENTEU (accessed on 6 July 2025).
- U.S. Energy Information Administration. Monthly Electric Power Industry Report—Retail Electricity Prices. 2024. Available online: https://www.eia.gov/electricity/data.php (accessed on 6 July 2025).
- International Council on Clean Transportation. Global EV Incentive Index. 2023. Available online: https://theicct.org/tools-for-policy-and-research/ (accessed on 6 July 2025).
- OECD Centre for Tax Policy and Administration. OECD Taxing Energy Use 2024 Database. 2024. Available online: https://www.oecd.org/tax/tax-policy/taxing-energy-use.htm (accessed on 6 July 2025).
- Gong, Y.; Wu, H.; Zhou, J.; Zhang, Y.; Zhang, L. Hybrid Multi-Branch Attention–CNN–BiLSTM Forecast Model for Reservoir Capacities of Pumped Storage Hydropower Plant. Energies 2025, 18, 3057. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, W.; Liu, C. A Systematic Review of Transformer-Based Long-Term Series Forecasting. Artif. Intell. Rev. 2025, 58, 80. [Google Scholar] [CrossRef]
- Yin, Y.; Li, J.; Shen, Q. Attention-Based Models for Multivariate Time Series Forecasting. Sensors 2023, 23, 987. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, F.; Wang, S. Comparative evaluation of LSTM, CNN, and ConvLSTM for hourly streamflow forecasting. J. Hydrol. 2023, 626, 129073. [Google Scholar] [CrossRef]
- Rajalakshmi, R.; Gupta, S. Hybrid CNN-LSTM for Traffic Flow Forecasting. In Proceedings of the 2nd International Conference on Artificial Intelligence: Advances and Applications, Roorkee, India, 2–3 June 2022. [Google Scholar] [CrossRef]
| Stage | Component | Input Dim | Hidden/Units | Dropout | Output Dim |
|---|---|---|---|---|---|
| Branch 1 | EV-history LSTM (2×) | 64, 64 | 0.2 | 64 | |
| Branch 2 | Infrastructure LSTM (2×) | 64, 64 | 0.2 | 64 | |
| Branch 3 | Macro-economic LSTM (2×) | 64, 64 | 0.2 | 64 | |
| Attention | Scaled dot product | 64 | = 64 | — | 64 |
| Fusion | Concat () | 64 + 64 + 64 | — | — | 192 |
| Dense-1 | FC + ReLU | 192 | 64 | — | 64 |
| Dense-2 | FC (linear) | 64 | 1 | — | 1 |
| Model | RMSE | MAE | MAPE (%) | Params (M) | |
|---|---|---|---|---|---|
| Vanilla LSTM | 0.065 | 0.050 | 0.85 | 9.0 | 2.5 |
| Single-Branch LSTM | 0.066 | 0.051 | 0.84 | 9.2 | 2.0 |
| ARIMA | 0.070 | 0.055 | 0.82 | 10.5 | – |
| Feed-Forward Neural Network | 0.067 | 0.051 | 0.84 | 9.4 | 1.8 |
| CNN-LSTM Hybrid | 0.060 | 0.048 | 0.87 | 8.8 | 3.0 |
| Transformer (6-layer, ) | 0.058 | 0.046 | 0.88 | 8.5 | 4.5 |
| GRU + Attention | 0.057 | 0.045 | 0.89 | 8.3 | 3.2 |
| Temporal Convolutional Network (TCN) | 0.056 | 0.044 | 0.89 | 8.2 | 3.0 |
| Neural-ODE | 0.059 | 0.047 | 0.88 | 8.6 | 3.5 |
| Multi-Branch LSTM + Attn (proposed) | 0.052 | 0.041 | 0.92 | 7.8 | 4.0 |
| Setting | Hidden Dim | Layers | Attention | Learning Rate | Batch Size | Dropout | Epochs | RMSE | Comments |
|---|---|---|---|---|---|---|---|---|---|
| A | 64 | 2 | Bahdanau | 0.001 | 32 | 0.1 | 100 | 12.45 | – |
| B | 128 | 2 | Bahdanau | 0.001 | 64 | 0.1 | 300 | 10.12 | – |
| C | 128 | 3 | Self-Attn | 0.0005 | 64 | 0.2 | 500 | 9.32 | – |
| D | 256 | 3 | Self-Attn | 0.0005 | 64 | 0.2 | 700 | 8.74 | – |
| E | 256 | 4 | Self-Attn | 0.0001 | 128 | 0.2 | 700 | 9.05 | – |
| F (Optimal) | 256 | 4 | Self-Attn | 0.0005 | 64 | 0.3 | 1000 | 8.50 | Best performance |
| Variant | RMSE | MAE | MAPE (%) | |
|---|---|---|---|---|
| Full model (baseline) | 0.052 | 0.041 | 7.8 | — |
| Branch removals | ||||
| w/o infrastructure + policy branch | 0.062 | 0.050 | 8.9 | ↓0.040 |
| w/o macro-economy branch | 0.060 | 0.048 | 8.6 | ↓0.035 |
| w/o EV-history branch | 0.065 | 0.053 | 9.5 | ↓0.063 |
| Attention ablations | ||||
| No time-step attention (mean-pool) | 0.058 | 0.046 | 8.4 | ↓0.028 |
| No branch-level attention | 0.057 | 0.045 | 8.3 | ↓0.024 |
| Feature ablations | ||||
| No lag + rolling features | 0.056 | 0.044 | 8.2 | ↓0.019 |
| All external variables removed | 0.068 | 0.055 | 9.8 | ↓0.071 |
| Structural ablations | ||||
| Single-branch LSTM (concat inputs) | 0.066 | 0.051 | 9.3 | ↓0.057 |
| Equal-weight fusion (no learning) | 0.059 | 0.047 | 8.5 | ↓0.031 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahaman, M.M.; Islam, M.R.; Manik, M.M.T.G.; Aziz, M.M.; Noman, I.R.; Bhuiyan, M.M.R.; Bishnu, K.K.; Bortty, J.C. A Novel Data-Driven Multi-Branch LSTM Architecture with Attention Mechanisms for Forecasting Electric Vehicle Adoption. World Electr. Veh. J. 2025, 16, 432. https://doi.org/10.3390/wevj16080432
Rahaman MM, Islam MR, Manik MMTG, Aziz MM, Noman IR, Bhuiyan MMR, Bishnu KK, Bortty JC. A Novel Data-Driven Multi-Branch LSTM Architecture with Attention Mechanisms for Forecasting Electric Vehicle Adoption. World Electric Vehicle Journal. 2025; 16(8):432. https://doi.org/10.3390/wevj16080432
Chicago/Turabian StyleRahaman, Md Mizanur, Md Rashedul Islam, Mia Md Tofayel Gonee Manik, Md Munna Aziz, Inshad Rahman Noman, Mohammad Muzahidur Rahman Bhuiyan, Kanchon Kumar Bishnu, and Joy Chakra Bortty. 2025. "A Novel Data-Driven Multi-Branch LSTM Architecture with Attention Mechanisms for Forecasting Electric Vehicle Adoption" World Electric Vehicle Journal 16, no. 8: 432. https://doi.org/10.3390/wevj16080432
APA StyleRahaman, M. M., Islam, M. R., Manik, M. M. T. G., Aziz, M. M., Noman, I. R., Bhuiyan, M. M. R., Bishnu, K. K., & Bortty, J. C. (2025). A Novel Data-Driven Multi-Branch LSTM Architecture with Attention Mechanisms for Forecasting Electric Vehicle Adoption. World Electric Vehicle Journal, 16(8), 432. https://doi.org/10.3390/wevj16080432








