A Symmetrical Cross Double-D Coil with Improved Misalignment Tolerance for WPT Systems
Abstract
1. Introduction
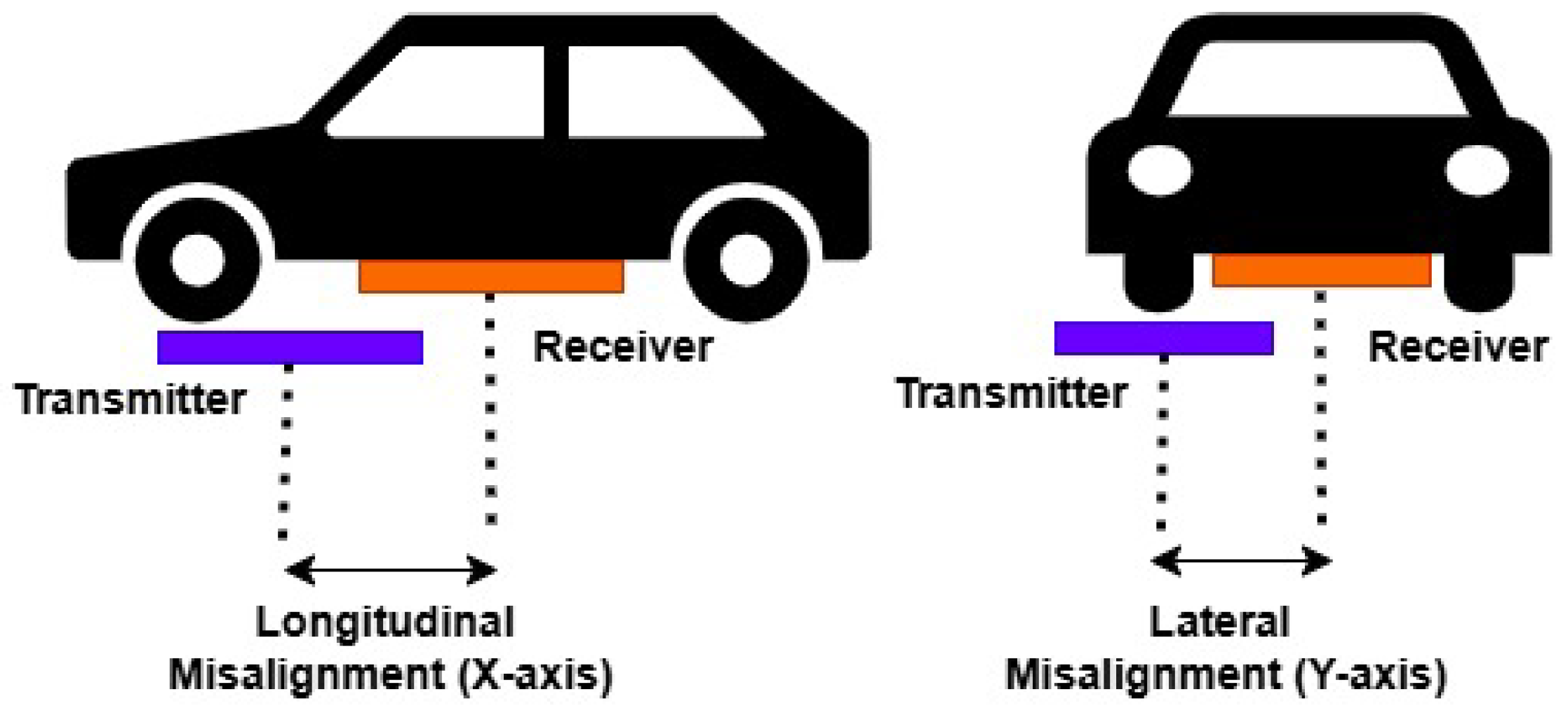
2. Inductive WPT System Development
2.1. Single-D Coupler
2.2. Double -D Coupler
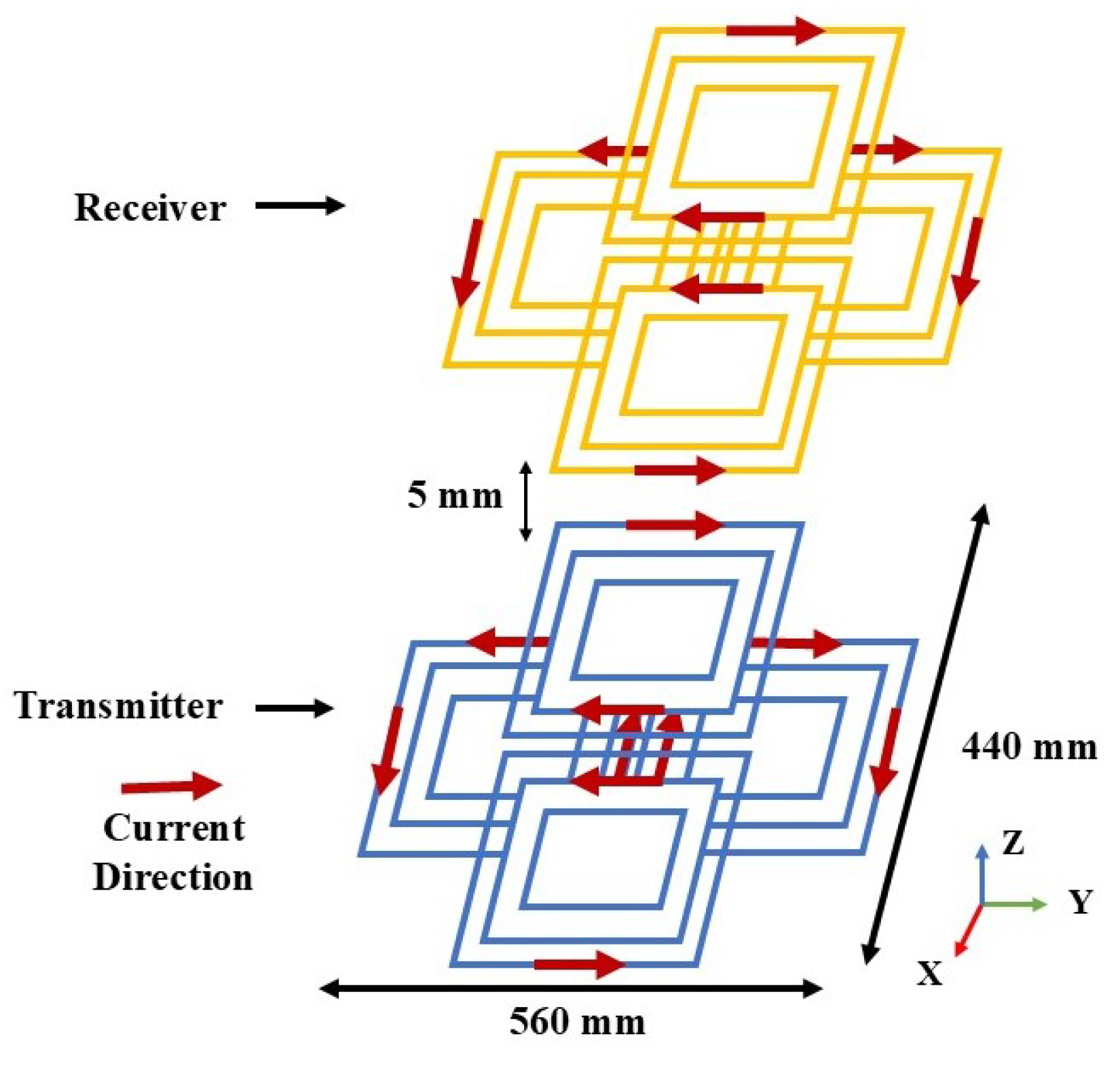
2.3. Symmetrical Cross Double-D Coupler
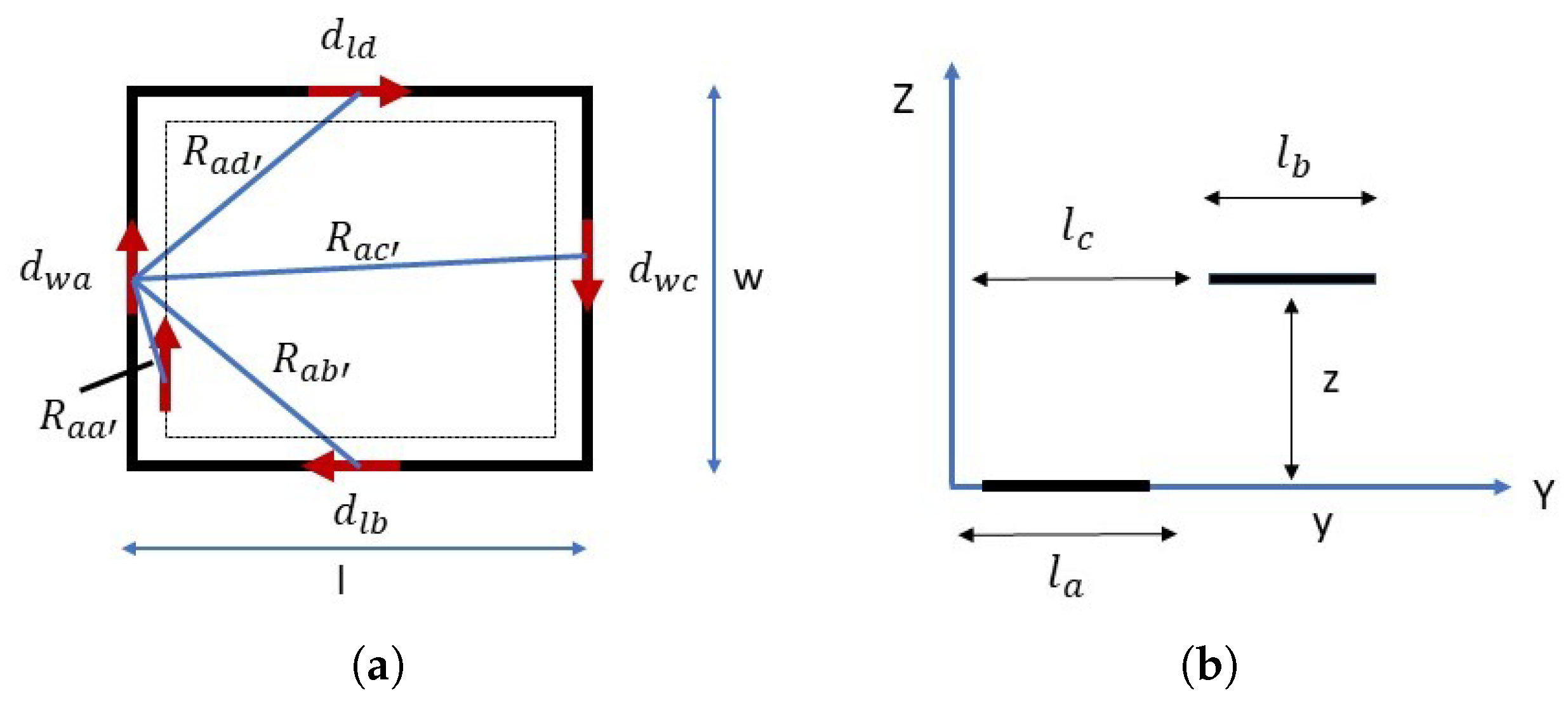
2.4. Self-Inductance Formulation
2.5. Mutual Inductance Formulation
2.6. Circuit Configuration
2.7. System Modeling
3. Results and Discussions
3.1. Simulation Results Based on FEA Analysis
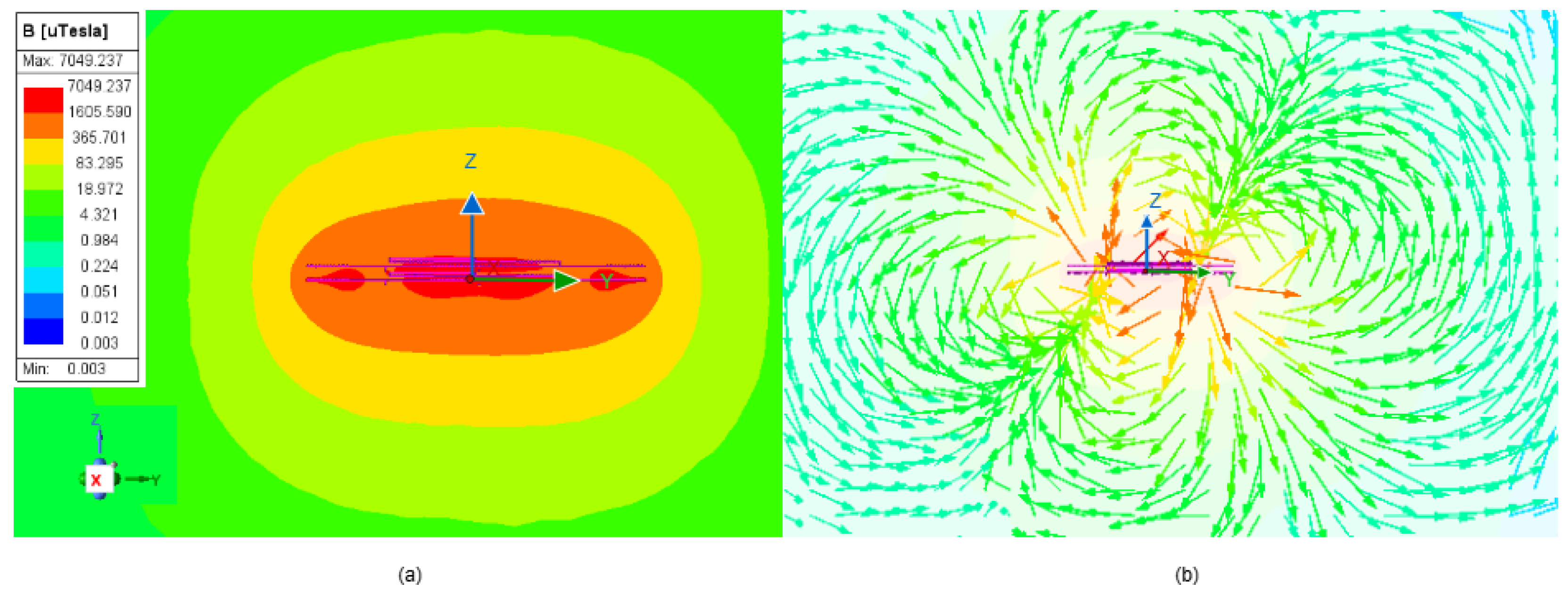
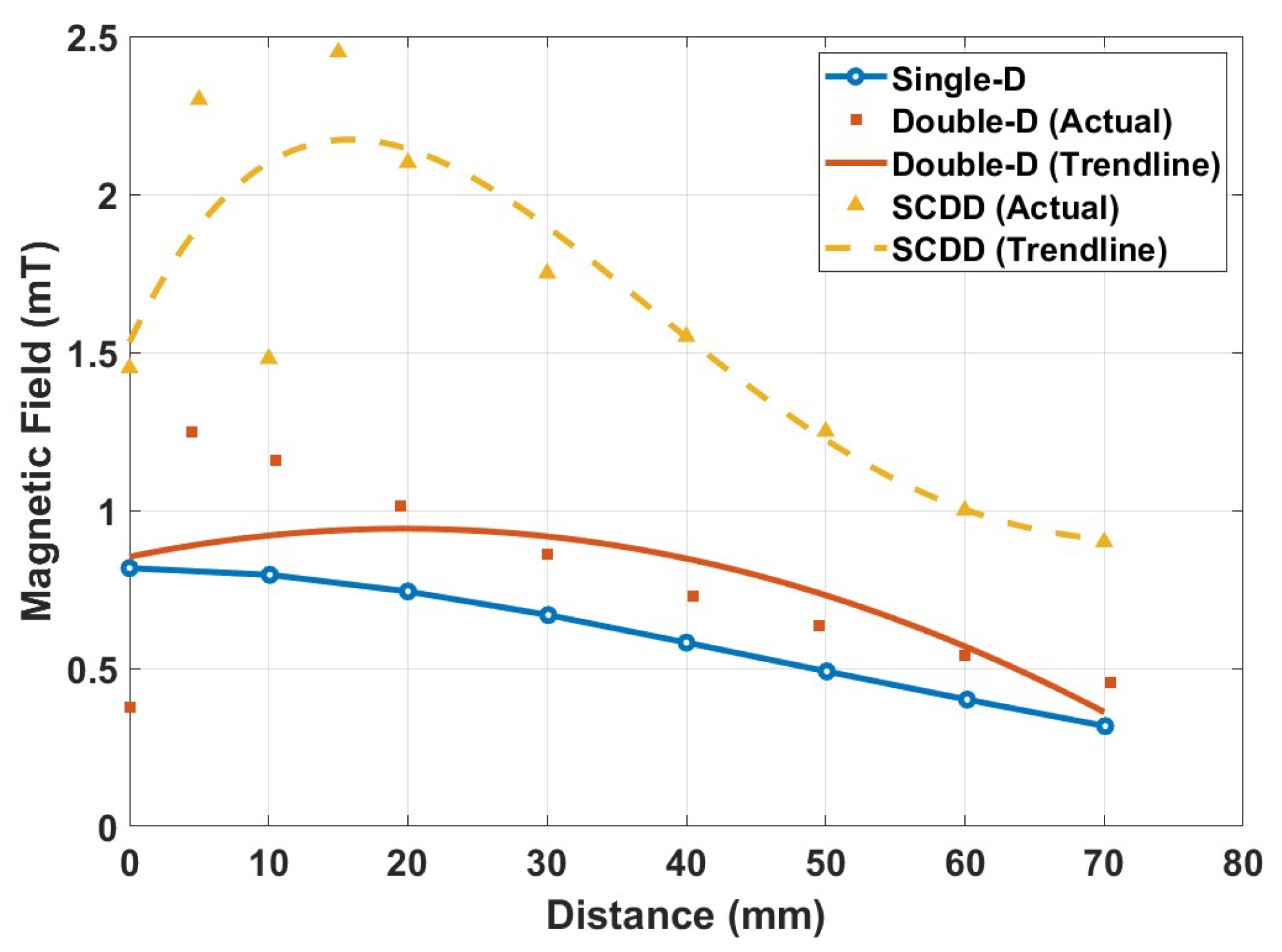
3.1.1. Calculation of the Magnetic Field for Single-D, Double-D and SCDD Along Z-Axis at the Center of the Coil
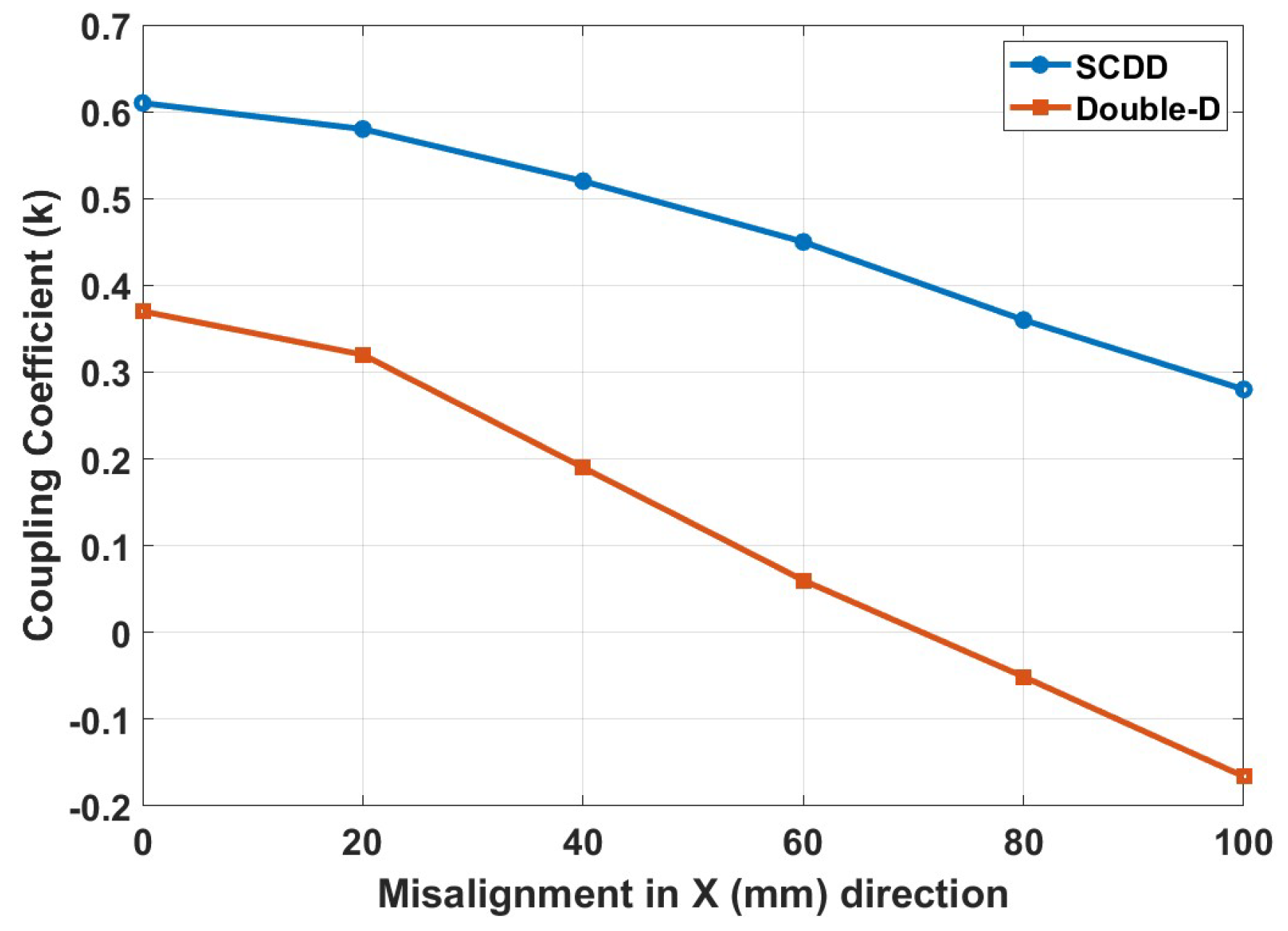
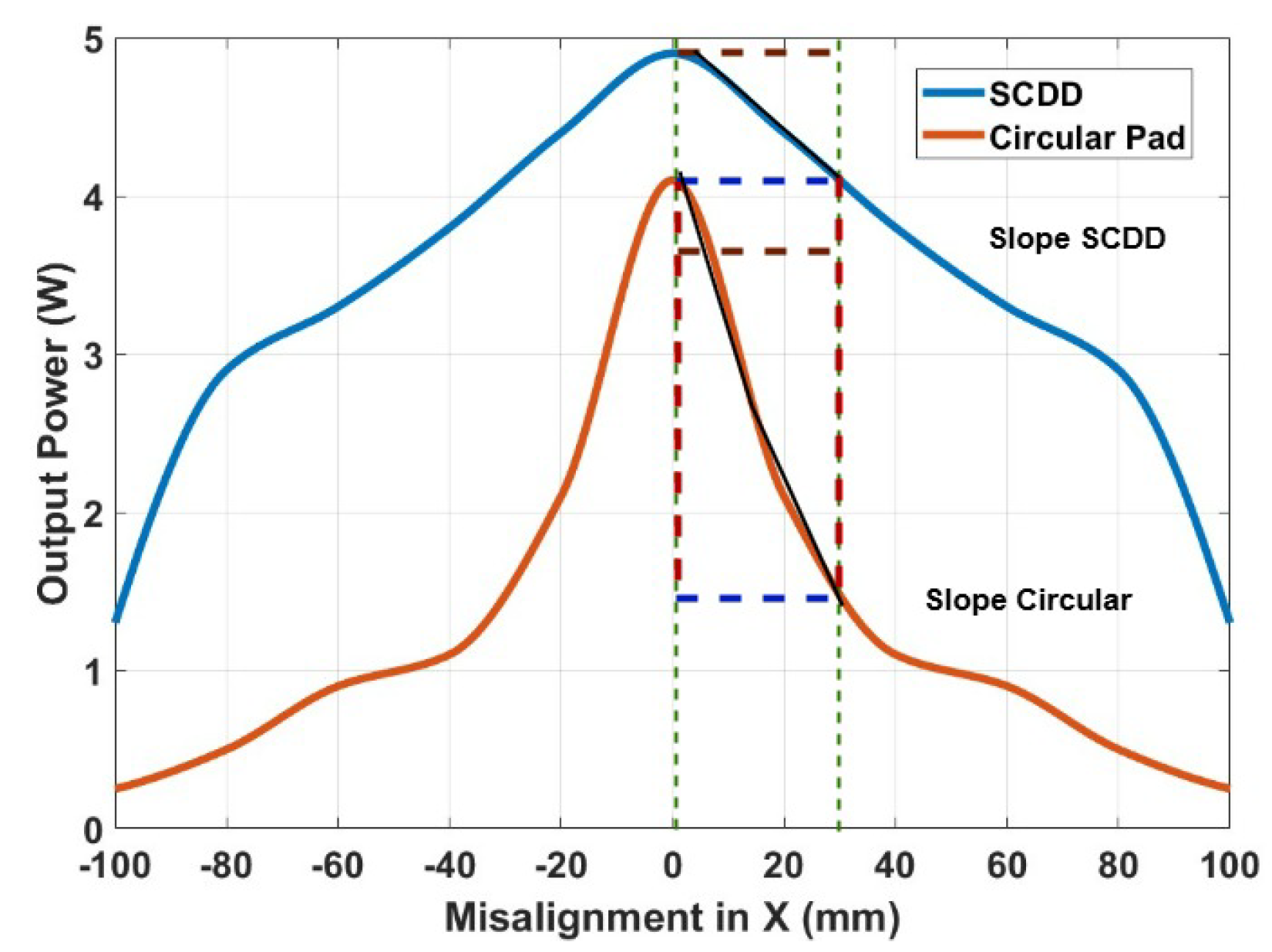
3.1.2. Coupling Coefficient of Double-D and Symmetrical Cross Double-D Coil During Misalignment
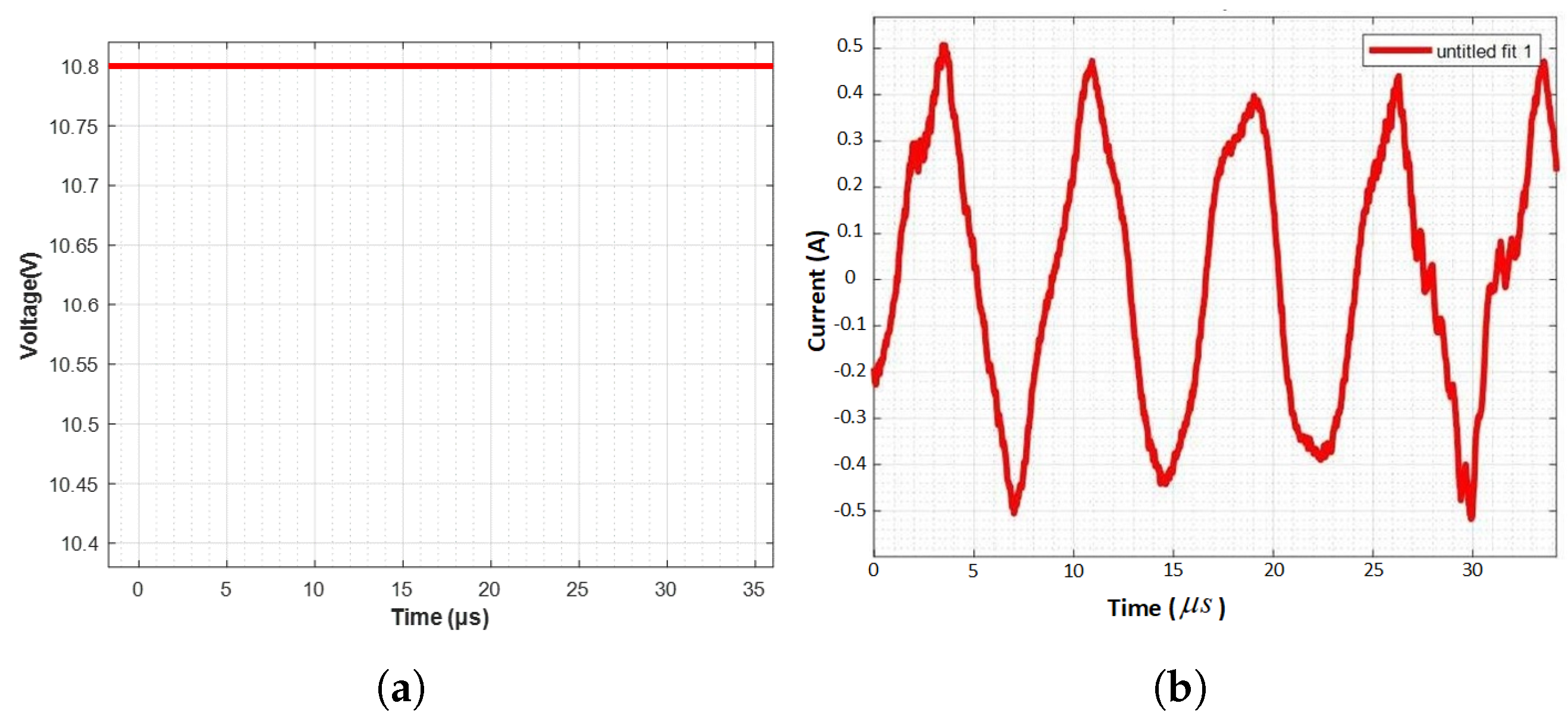
3.2. Experimental Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| WPT | Wireless Power Transfer |
| EV | Electric Vehicle |
| SCDD | Symmetrical Cross Double-D |
| FEA | Finite Element Analysis |
| IPT | Inductive Power Transfer |
| DD | Double-D |
| FOC | Fractional-Order Capacitor |
| DDC | Double-D Circular |
| SAE | Society of Automotive Engineers |
| ICNIRP | International Commission on Non-Ionizing Radiation Protection |
| PWM | Pulse Width Modulation |
References
- López-Alcolea, F.J.; Vázquez del Real, J.; Roncero-Sánchez, P.; Parreño Torres, A. Modeling of a Magnetic Coupler Based on Single- and Double-Layered Rectangular Planar Coils With In-Plane Misalignment for Wireless Power Transfer. IEEE Trans. Power Electron. 2020, 35, 5102–5121. [Google Scholar] [CrossRef]
- Ramezani, A.; Narimani, M. Optimized Electric Vehicle Wireless Chargers With Reduced Output Voltage Sensitivity to Misalignment. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 3569–3581. [Google Scholar] [CrossRef]
- Bosshard, R.; Iruretagoyena, U.; Kolar, J.W. Comprehensive Evaluation of Rectangular and Double-D Coil Geometry for 50 kW/85 kHz IPT System. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1406–1415. [Google Scholar] [CrossRef]
- Luo, Z.; Wei, X.; Pearce, M.G.S.; Covic, G.A. Multiobjective Optimization of Inductive Power Transfer Double-D Pads for Electric Vehicles. IEEE Trans. Power Electron. 2021, 36, 5135–5146. [Google Scholar] [CrossRef]
- Liu, C.; Jiang, C.; Qiu, C. Overview of Coil Designs for Wireless Charging of Electric Vehicle. In Proceedings of the 2017 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW), Chongqing, China, 20–22 May 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Mohammad, M.; Pries, J.; Onar, O.; Anwar, S.; Galigekere, V.P.; Su, G.-J.; Wilkins, J. Comparison of Leakage Magnetic Field from Matched and Mismatched Double-D Coil Based Wireless Charging System for Electric Vehicles. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 5733–5739. [Google Scholar] [CrossRef]
- Barmada, S.; Musolino, A.; Zhu, J.; Yang, S. A Novel Coil Architecture for Interoperability and Tolerance to Misalignment in Electric Vehicle WPT. IEEE Trans. Magn. 2023, 59, 1–5. [Google Scholar] [CrossRef]
- Wang, Q.; Che, W.; Mongiardo, M.; Monti, G. Wireless Power Transfer System With High Misalignment Tolerance for Bio-Medical Implants. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 3023–3027. [Google Scholar] [CrossRef]
- Feng, T.; Sun, Y.; Feng, Y.; Dai, X. A Tripolar Plane-Type Transmitter for Three-Dimensional Omnidirectional Wireless Power Transfer. IEEE Trans. Ind. Appl. 2022, 58, 1254–1267. [Google Scholar] [CrossRef]
- Wang, L.; Sun, P.; Liang, Y.; He, L.; Wu, X.; Deng, Q. Research on the Control Strategy of Communication-Free IPT System Based on Multiparameter Joint Real-Time Identification. IEEE Trans. Power Electron. 2024, 39, 1912–1926. [Google Scholar] [CrossRef]
- Yadav, P.; Veerachary, M. Modified Coupler With Reduced Misalignment Issues for Wireless Power Transfer System. IEEE Trans. Ind. Appl. 2024, 60, 5763–5777. [Google Scholar] [CrossRef]
- Shi, W.; Lan, H.; Li, D.; Guo, D.; Yin, H. Enhancing Simplified Control and Misalignment Tolerance in Autonomous Fractional-Order Wireless Power Transfer System with an Improved Primary-Side Control Strategy. IEEE J. Emerg. Sel. Top. Power Electron. 2025, in press. [Google Scholar] [CrossRef]
- Aurongjeb, M.; Liu, Y.; Ishfaq, M. Design and Simulation of Inductive Power Transfer Pad for Electric Vehicle Charging. Energies 2025, 18, 244. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, S.; Li, X.; Tang, Y. Design of High-Power Static Wireless Power Transfer via Magnetic Induction: An Overview. CPSS Trans. Power Electron. Appl. 2021, 6, 281–297. [Google Scholar] [CrossRef]
- Wang, X.; Leng, M.; Zhang, X.; Tian, Q.; He, L.; Ma, H. An Intermediate Coil for Misalignment Tolerant IPT System with Dual Decoupled Receivers. In Proceedings of the IECON 2023—49th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 16–19 October 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Li, S.; Mi, C.C. Wireless Power Transfer for Electric Vehicle Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 4–17. [Google Scholar] [CrossRef]
- Song, K.; Lee, C.; Kim, H.; Shin, J.; Jung, H. Design of DD Coil With High Misalignment Tolerance and Low EMF Emissions for Wireless Electric Vehicle Charging Systems. IEEE Trans. Power Electron. 2020, 35, 9034–9045. [Google Scholar] [CrossRef]
- Chu, C.-Y.; Lee, Y.-C.; Wu, C.-L.; Lin, Y.-C.; Kuo, Y.-C. Wireless Power Transfer System Design for Electric Vehicle Charging Considering A Wide Range of Coupling Coefficient Variation Depending on the Coil Misalignment. In Proceedings of the 2021 24th International Conference on Electrical Machines and Systems (ICEMS), Gyeongju, Republic of Korea, 31 October–3 November 2021; IEEE: New York, NY, USA, 2021; pp. 732–737. [Google Scholar]
- Lv, X.; Tang, X.; Cheng, K.; Chau, K.T. A cross double-D coil for electric vehicles dynamic wireless transfer system to reduce output power pulsation. In Proceedings of the 2020 8th International Conference on Power Electronics Systems and Applications (PESA), Hong Kong, China, 12–14 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Xiang, L.; Mi, C.; Zhang, M.; Zhao, Z.; Tang, X. A crossed DD geometry and its double-coil excitation method for electric vehicle dynamic wireless charging systems. IEEE Access 2018, 6, 45120–45128. [Google Scholar] [CrossRef]
- Owu, T. A Cross-Double D Coupler for Improved Tolerance to Misalignment Conditions. In Proceedings of the 2024 56th North American Power Symposium (NAPS), San Diego, CA, USA, 8–10 April 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Guru, B.S.; Hiziroglu, H.R. Electric Machinery and Transformers, 3rd ed.; The Oxford Series in Electrical and Computer Engineering; Oxford University Press: New York, NY, USA, 2001. [Google Scholar]
- Bentalhik, I.; Lassioui, A.; El Fadil, H.; Bouanou, T.; Rachid, A.; El Idrissi, Z.; Hamed, A.M. Analysis, Design and Realization of a Wireless Power Transfer Charger for Electric Vehicles: Theoretical Approach and Experimental Results. World Electr. Veh. J. 2022, 13, 121. [Google Scholar] [CrossRef]
- Simonazzi, M.; Campanini, A.; Sandrolini, L.; Rossi, C. Design Procedure Based on Maximum Efficiency for Wireless Power Transfer Battery Chargers with Lightweight Vehicle Assembly. Energies 2022, 15, 70. [Google Scholar] [CrossRef]
- Owu, T.G. Modelling and Optimization of a Cross Double-D Electromagnetic Coupler for Enhanced Misalignment Performance in Wireless Charging Applications. Master’s Thesis, Tennessee Technological University, Cookeville, TN, USA, 2024. [Google Scholar]







| Parameters | Simulation | Experiment |
|---|---|---|
| Self-inductance (μH) | 241.53 | 253.2 |
| Mutual-inductance (μH) (Perfectly aligned) | 138.21 | 151.5 |
| Mutual-inductance (μH) (40 mm misaligned) | 118.36 | 128 |
| Mutual-inductance (μH) (80 mm misaligned) | 82.49 | 74.5 |
| Parameter | Value |
|---|---|
| Primary Coil Inductance (μH) | 253.2 |
| Secondary Coil Inductance (μH) | 253.2 |
| Primary Series Capacitance (nF) | 13.8 |
| Secondary Series Capacitance (nF) | 13.8 |
| Mutual Inductance (Perfectly aligned) (μH) | 151.5 |
| Primary Coil Voltage (V) | 16 |
| System | (W) | (W) | (%) |
|---|---|---|---|
| Inverter | 7.2 | 5.6 | 78 |
| SCDD | 5.6 | 4.9 | 88 |
| Overall | – | – | 68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rathod, A.; Mahajan, S.M.; Owu, T. A Symmetrical Cross Double-D Coil with Improved Misalignment Tolerance for WPT Systems. World Electr. Veh. J. 2025, 16, 405. https://doi.org/10.3390/wevj16070405
Rathod A, Mahajan SM, Owu T. A Symmetrical Cross Double-D Coil with Improved Misalignment Tolerance for WPT Systems. World Electric Vehicle Journal. 2025; 16(7):405. https://doi.org/10.3390/wevj16070405
Chicago/Turabian StyleRathod, Ashwini, Satish M. Mahajan, and Taiye Owu. 2025. "A Symmetrical Cross Double-D Coil with Improved Misalignment Tolerance for WPT Systems" World Electric Vehicle Journal 16, no. 7: 405. https://doi.org/10.3390/wevj16070405
APA StyleRathod, A., Mahajan, S. M., & Owu, T. (2025). A Symmetrical Cross Double-D Coil with Improved Misalignment Tolerance for WPT Systems. World Electric Vehicle Journal, 16(7), 405. https://doi.org/10.3390/wevj16070405







