Physics-Data Fusion Enhanced Virtual Synchronous Generator Control Strategy for Multiple Charging Stations Active Frequency Response

Abstract

In regions where electric vehicles (EVs) are widely adopted and charging stations (CSs) are being built in large numbers, CSs are becoming a critical load-side resource for low-inertia power systems. In this paper, a physics-data fusion enhanced frequency control strategy for multiple CSs is proposed. Firstly, the power grid frequency control architecture is improved, where CSs as multi-agent (MA) can participate in frequency response (FR). Besides, a physics-driven adaptive inertia for CS virtual synchronous generators (VSGs) is proposed to improve system dynamic FR characteristics. Building upon this, the physics-data fusion concept is introduced, wherein the MA-soft-actor-critic (MA-SAC) algorithm dynamically adjusts coordination coefficients with the consideration of CSs’ FR capabilities. To validate the proposed strategy, comparative case studies are conducted on the IEEE 39-node system. The simulation results demonstrate that compared to a single physics-driven method, the proposed control strategy exhibits enhanced adaptability and improved FR characteristics across various scenarios. Under intact MA communication conditions, the proposed strategy reduces the frequency disturbance index to 49.872% and the CS response power oscillation index to 79.542%; Even with MA communication impairments, the strategy maintains significant improvements, reducing these indexes to 48.897% and 86.733% respectively.

1. Introduction

Electric vehicles (EVs) have gradually replaced traditional fuel-powered vehicles, emerging as a crucial mode of transportation [1,2,3]. Besides, the rapid development of vehicle-to-grid (V2G) charging piles enables EVs can function as a critical load-side resource to provide frequency response (FR) [4,5].

Meanwhile, with the large-scale access to renewable energy sources from sustainable energy systems [6], the inertia of the new power system is declining. Therefore, the power system’s frequency is easier to rapidly change in response to disturbances, leading to significant safety risks [7]. Therefore, virtual synchronous generators (VSGs) have become a matter of great concern. VSG can provide inertia support to the new power system, effectively slowing down the rate of frequency change [8,9].

Given the above context, the application of inertia control strategies within CSs to enhance FR performance has emerged as a critical research direction in the energy field [10,11]. The traditional VSG control strategy with constant parameters can provide inertia to the system nodes but loses part of the dynamic regulation ability [12]. Therefore, many scholars have researched in the field of VSG inertia adaptive adjustment. Ref. [13] analyzed the correlation between frequency change and inertia coefficient and proposed a VSG control strategy with adaptive virtual inertia. Refs. [14,15] applied a fuzzy controller to the VSG control strategy to realize adaptive virtual inertia. However, these control strategies only focus on improving frequency dynamic characteristics under a single VSG. The FR capability of an individual CS is insufficient to improve the FR effect. Additionally, for CSs participating in FR, inertia adjustments in the aforementioned strategies do not consider the variations and differences in different CSs’ FR capabilities.

The multi-VSG dynamic characteristics interact with each other, causing frequency and CS response power oscillations of each node [16,17], which seriously depletes EV battery usage life. In recent years, the research about multi-VSG control can be divided into two types: physics-driven and data-driven.

For physics-driven methods, some scholars modified the VSG control strategy with adaptive control, fuzzy control, and optimization algorithms. Ref. [18] used a particle swarm optimization algorithm to optimize VSGs’ control parameters. However, the optimized parameters cannot be changed in real time. Ref. [19] proposed a cooperative virtual inertia control strategy for multiple energy storage stations (ESSs) to coordinate state of charge (SOC) balance and inertia enhancement. Ref. [20] analyzed the relationship between frequency and inertia and proposed a multi-CS control strategy based on adaptive virtual inertia. However, the adaptive inertia in the aforementioned single physics-driven methods relies solely on fixed equations and constant coordination coefficients for CS VSGs. This diminishes the accuracy of inertia adjustments, affecting frequency control performance and adaptability under various FR scenes, particularly in situations involving communication interruptions.

Therefore, for the design of an adaptive VSG control strategy, the deep reinforcement learning (DRL) algorithm which does not depend on specific models has received widespread attention in recent years [21,22]. DRL can achieve effective data accumulation through interaction with the environment to evolve control effects continuously in the training process. It can be divided into two categories. The first category is the value-based method, such as deep Q-network [23]. However, the deep Q-network action space is discrete. When deep Q-network is applied in inertia control, the virtual inertia changing value is discretized, influencing the system FR dynamic performance. The second type is the policy gradient method [24], which is suitable for continuous high-dimensional action space. Ref. [25] took the active power output, angular frequency, and its derivatives as observations, and transformed the optimal VSG adaptive control problem into a deep deterministic policy gradient problem. However, the action selection of deep deterministic policy gradient, as a deterministic strategy algorithm, is limited [26]. Ref. [27] proposed a load frequency control method based on proximal policy optimization to optimize the balance between generation cost and frequency stability in an isolated microgrid. However, proximal policy optimization, as an on-policy algorithm, depends on sample size and its effectiveness.

The soft actor-critic (SAC) algorithm not only introduces action entropy to let action output be dispersed without missing useful actions in the training process but also applies an experience playback pool to enhance sample utilization. Therefore, Ref. [28] introduced SAC to train an agent based on the active power and frequency as state input to output virtual inertia adjustment actions for the optimal FR. However, the above literatures only use a single agent to take a VSG as a single control object. When several CSs are connected to the power system, the training time and dimension under a centralized control architecture will increase exponentially [29]. The multiagent-DRL (MA-DRL) method has good expansibility, and can effectively solve multiple control objects problem through decentralized implementation. Ref. [30] proposed a distributed dynamic inertial droop control strategy based on MA-DRL for multiple ESSs. However, this single physics-driven method focuses on directly adjusting inertia for ESSs and is not suitable for CSs. Firstly, due to the varying EV users’ charging demands, CSs’ FR capabilities vary frequently compared to those of ESSs. Additionally, unlike ESS batteries participating in FR, the service life of EV batteries is more susceptible to degradation from frequent charge and discharge cycles. Consequently, the diversity of CS FR scenes complicates the training environment, which negatively impacts the learning efficiency of single data-driven methods that lack a priori knowledge.

Therefore, unlike previous studies that either rely solely on fixed equations under a single physics-driven method, diminishing the accuracy of inertia adjustments or ignore the complexity of FR scenes involving CS participation, which impacts the learning efficiency of a single data-driven method, this paper proposes a physics-data fusion enhanced VSG control strategy for multiple CSs active FR. The main contributions of this paper are drawn as follows:

(1)

This paper incorporates a power grid frequency control framework with multiple CS VSGs participation based on physics-data fusion driven. Through MA communication of this framework, the application basic of the reinforcement learning method in CS VSG control is constructed, which considers the variations and differences in CS FR capabilities.

(2)

The relationship between the angular velocity changes of multiple CS VSGs and their inertia are integrated into the data-driven method as prior knowledge. The agent learning efficiency, interpretability for FR effect improvement, and generalization for unknown scenes are enhanced under the power grid frequency control framework with multiple CS VSGs participation.

(3)

The proposed control strategy utilizes the MA-SAC algorithm to dynamically adjust the coordination coefficients between CS VSGs. The MA-SAC achieves the cooperative control idea of “centralized training and decentralized execution” to improve adaptability under various FR scenes, including situations with communication interruptions.

2. Power Grid Frequency Control Architecture with Distributed CSs Participation

When power disturbance occurs, the energy control centers (ECCs) in the CSs can change the charging power of EVs through V2G charging piles. To achieve the above process, it is necessary to incorporate multiple CSs into a power grid frequency control framework.

2.1. Frequency Control Architecture of Power Grid with the CS Participation

In recent years, many scholars have researched on CS FR capability evaluation method [10,31] and V2G response model [19,32], making CSs a vital frequency regulation resource in the power grid frequency control architecture. Based on the EV users’ charging demand and EV message, the boundary of the CS response power $P_{\Delta f}^{\mathrm{C}\mathrm{S}}$, including CS equivalent power generation capability Δ$P_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}}^{\mathrm{C}\mathrm{S}}$ and CS equivalent load capability Δ$P_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}^{\mathrm{C}\mathrm{S}}$ can be aggregated by the CS FR capability evaluation method. Furthermore, based on the frequency situation, the CS response power $P_{\Delta f}^{\mathrm{C}\mathrm{S}}$ can be distributed among EVs in the CS by the V2G response model.

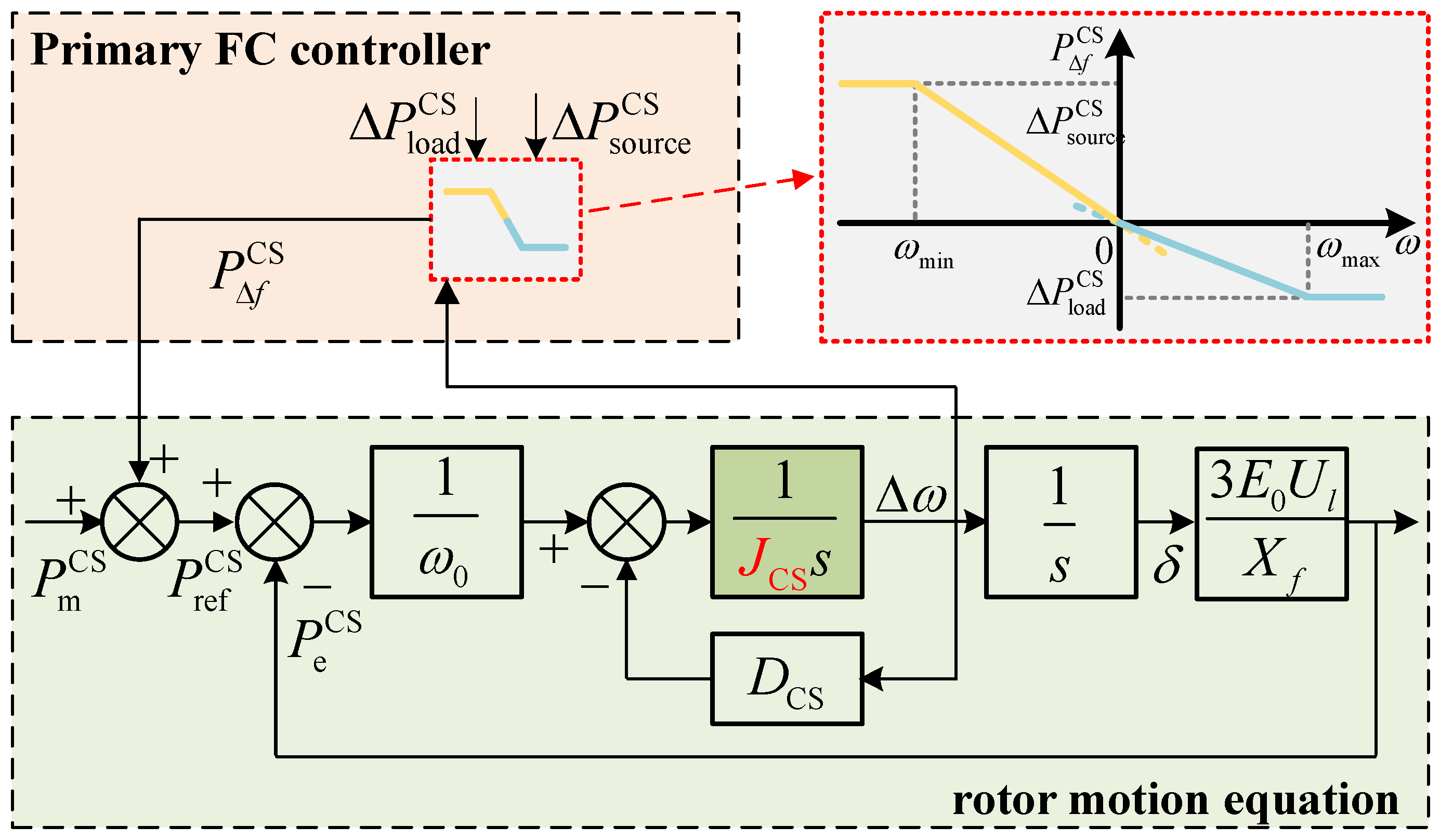
To further improve the power grid frequency control architecture with CS participation based on the above research, this paper focuses on adaptive inertia design for CS VSG. CS participation in frequency response control architecture in this paper is shown in Figure 1, where each CS is equipped with an ECC, a CS VSG controller, and a CS VSG agent. ECC can evaluate each EV’s FR capability based on EV users’ charging demands received from charging piles. Then CS FR capability including CS equivalent power generation capability Δ$P_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}}^{\mathrm{C}\mathrm{S}}$ and equivalent load capability Δ$P_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}^{\mathrm{C}\mathrm{S}}$ can be aggregated. Based on Δ$P_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}}^{\mathrm{C}\mathrm{S}}$, Δ$P_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}^{\mathrm{C}\mathrm{S}}$, rotor angular velocity ω, CS VSG electromagnetic power $P_{\mathrm{e}}^{\mathrm{C}\mathrm{S}}$ received from the corresponding node, and original charging power plan $P_{\mathrm{m}}^{\mathrm{C}\mathrm{S}}$, CS VSGs can respectively output CS response power $P_{\Delta f}^{\mathrm{C}\mathrm{S}}$ to the ECC and the PWM signal to CS grid-connected inverter to provide inertia for the power system. Based on $P_{\Delta f}^{\mathrm{C}\mathrm{S}}$, the ECCs control V2G charging piles to adjust EVs’ charging plans.

2.2. Information Interaction Modeling for Distributed CSs

Based on graph theory knowledge, the communication topology graph of an MA system composed of n agents can be represented by directed graph G = (V, E, A), where V = (V₁, V₂, …, V_n) is a node set; E ⊆ V × V is an edge set; communication topology A = [b_ij]_n×n is an adjacent matrix, and diagonal elements b_ii = 0, i = 1, 2, …, n. When the directed edge E_ij = (V_i, V_j) ∈ E, b_ij = 1; otherwise, b_ij = 0.

In the context of graph theory, a CS equipped with a VSG agent can be modeled as a node within a network [20,30]. Under 5G communication technology, communication delay can be ignored when some CSs’ communication distance is within a certain range [20]. This technological advantage enables CS VSG agents can exchange information.

Assuming that CS_i VSG agent i can receive information from CS_j VSG agent j, CS_j VSG agent j is defined as an adjacent agent (AAG) of CS_i VSG agent i, and CS_i VSG agent i is defined as the leading agent (LAG) of CS_j VSG agent j. If this communication mode is two-way, CS_i VSG agent i and j are an AAG and a LAG to each other, b_ij = b_ji = 1. When the communication channel between CS_i VSG agent i and j is suddenly interrupted, b_ij and b_ji change from 1 to 0.

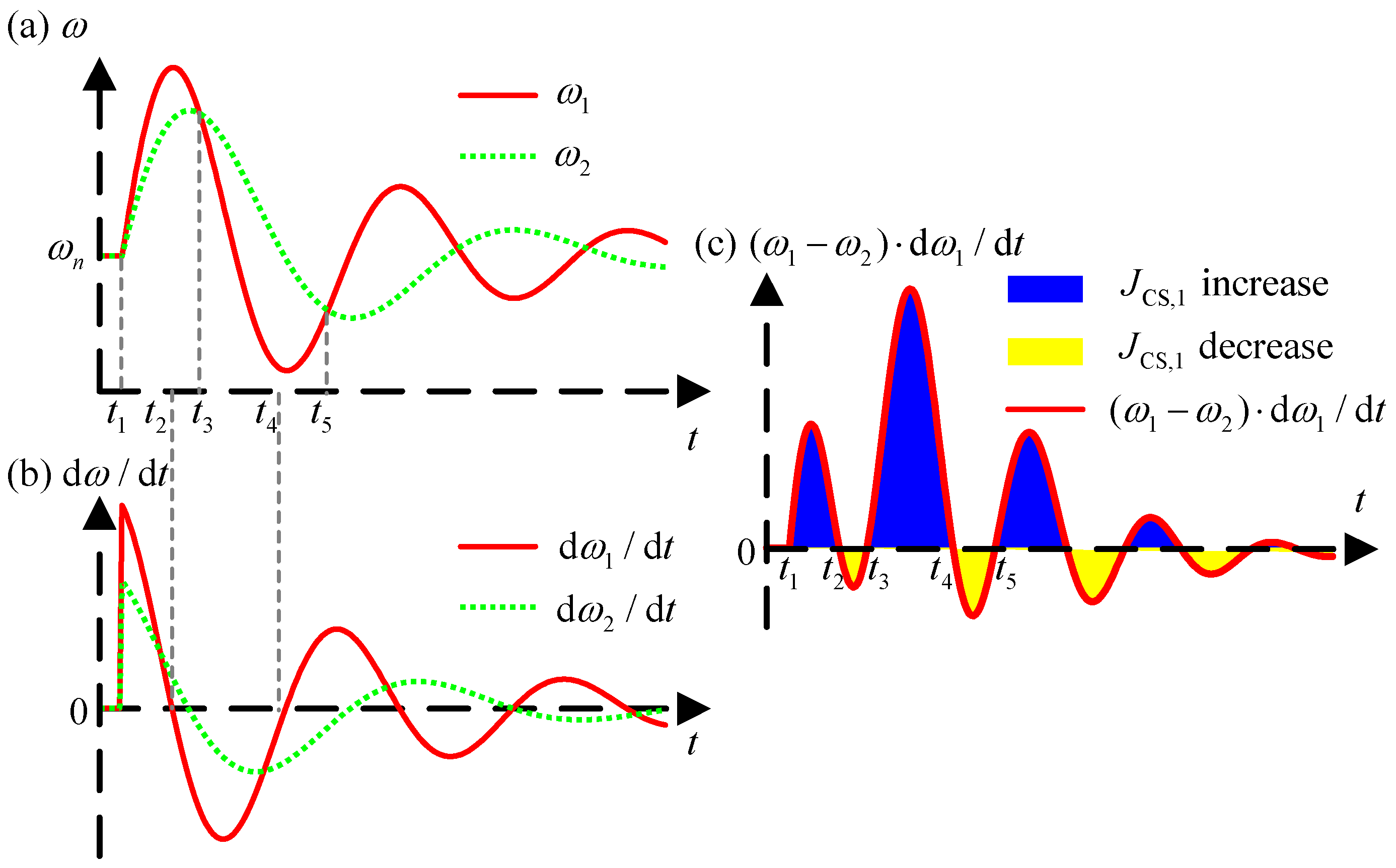
Based on the above background knowledge, the adjustment process of the LAG to the inertia of the local CS VSG can be described in Figure 2. In Figure 2, based on the communication topology A, CS VSG agents can exchange state information. Then, according to the state information received from local CS VSG and AAGs, LAG can reasonably adjust local CS VSG’s inertia to enhance the dynamic adjustment ability of the power system. In the following sections, the relationship between inertia adjustment and state message is specified.

3. Adaptive CS VSGs Control Strategy

VSG control can simulate synchronous generator (SG) inertia characteristics and act on CS grid-connected inverter to provide inertia support for power system nodes to improve FR characteristics. Moreover, adaptive inertia design can enhance the system’s dynamic response performance.

3.1. The Basic Principle of GFM VSG

The grid-connected characteristic of the converter applied VSG technology is determined by its control mode, based on which, it is generally divided into two categories: grid-following (GFL) VSG and grid-forming (GFM) VSG [33]. The converter synchronization mode under GFL VSG is to measure the parallel point’s frequency by a phase-locked loop and adjust the output power to follow the power grid. Therefore, GFL VSG essentially shows current source characteristics, so there is a certain time delay in the control mechanism. For GFM VSG, the electric potential frequency is not determined by power grid frequency, but by active power control loop to realize the synchronization with the power grid. Therefore, GFM VSG shows the voltage source characteristics to construct frequency independently. Its theoretical time delay is almost zero, so GFM VSG is more suitable for CS to participate in FR.

The active power-frequency GFM VSG control equations are listed as follows:

$$J{\omega }_0\cdot \mathrm{d}\omega /\mathrm{d}t=P_{\mathrm{ref}}-P_{\mathrm{e}}-D{\omega }_0(\omega -{\omega }_0)$$

(1)

$$P_{\mathrm{ref}}=P_{\mathrm{m}}+P_{\Delta f}$$

(2)

where J is virtual inertia; D is damping coefficient; ω is rotor angular velocity; ω₀ is synchronous rotor angular velocity; P_e is electromagnetic power; P_m is prime mover power; P_Δf is response power; P_m and P_Δf form active power instruction P_ref.

3.2. A Primary FR Controller Considering CS FR Capability

GFM VSG can be applied in CS to form CS VSG, and a primary FR controller considering CS FR capability is designed to apply in CS VSG, which is shown in Figure 3. In Figure 3, J_CS and D_CS are respectively CS VSG virtual inertia and damping coefficient; $P_{\mathrm{r}\mathrm{e}\mathrm{f}}^{\mathrm{C}\mathrm{S}}$ composed of $P_{\mathrm{m}}^{\mathrm{C}\mathrm{S}}$ and $P_{\Delta f}^{\mathrm{C}\mathrm{S}}$ is CS VSG active power instruction transmitted to ECC to adjust charging plans; E₀ and U_l are CS VSG no-load electric potential and output voltage; X_f is filter reactance; s is Laplace transform operator.

Besides, the proposed primary FR controller can adaptively adjust the droop coefficient based on CS FR capability. $P_{\Delta f}^{\mathrm{C}\mathrm{S}}$ is bound by Δ$P_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}^{\mathrm{C}\mathrm{S}}$ and Δ$P_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}}^{\mathrm{C}\mathrm{S}}$; Δω_max and Δω_min are respectively the corresponding angular velocity offset boundary of ΔPCS source and Δ$P_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}^{\mathrm{C}\mathrm{S}}$. Angular velocity offset Δω = ω−ω₀. The equations of $P_{\Delta f}^{\mathrm{C}\mathrm{S}}$ is established as follows:

$$P_{\Delta f}^{\mathrm{C}\mathrm{S}}=\left\{\begin{array}{l}\Delta P_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}}^{\mathrm{C}\mathrm{S}}\hspace{1em},\Delta \omega <\Delta {\omega }_{\min }\\ K_{\Delta f}\cdot \Delta \omega ,\Delta {\omega }_{\min }\le \Delta \omega \le \Delta {\omega }_{\max }\\ \Delta P_{\mathrm{load}}^{\mathrm{CS}}\hspace{1em} ,\mathrm{else}\end{array}\right.$$

(3)

$$K_{\Delta f}=\left\{\begin{array}{l}\Delta P_{\mathrm{source}}^{\mathrm{CS}}\cdot \Delta \omega \cdot {{\omega }_{\min }}^{-1} ,\Delta {\omega }_{\min }\le \Delta \omega \le 0\\ \Delta P_{\mathrm{load}}^{\mathrm{CS}}\cdot \Delta \omega \cdot {{\omega }_{\max }}^{-1},0<\Delta \omega \le \Delta {\omega }_{\max }\end{array}\right.$$

(4)

$$\Delta {\omega }_{\max }=\Delta f_{\max }\cdot f_{\mathrm{n}}^{-1} , \Delta {\omega }_{\min }=\Delta f_{\min }\cdot f_{\mathrm{n}}^{-1}$$

(5)

where K_Δf is the droop coefficient of CS response power; f_n is rated frequency; Δf_max and Δf_min are the corresponding frequency offset boundary of Δ$P_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}}^{\mathrm{C}\mathrm{S}}$/Δ$P_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}^{\mathrm{C}\mathrm{S}}$, respectively 0.2 Hz/−0.2 Hz. When Δω is between ω_min and ω_max, CS provides appropriate $P_{\Delta f}^{\mathrm{C}\mathrm{S}}$ between Δ$P_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}}^{\mathrm{C}\mathrm{S}}$ and Δ$P_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}^{\mathrm{C}\mathrm{S}}$; when Δω exceeds the boundary of ω_min or ω_max, CS provides Δ$P_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}}^{\mathrm{C}\mathrm{S}}$ or Δ$P_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}^{\mathrm{C}\mathrm{S}}$ to restrain frequency sudden change to reduce maximum frequency offset and reserve time for the secondary FR.

3.3. Physics-Driven Adaptive Inertia

When power disturbance happens, inertia differences lead to the system node dynamic FR difference, including frequency oscillation and CS response power oscillation. Therefore, this paper designs a physics-driven adaptive inertia control strategy.

Based on the Mason equation, Figure 3, and $P_{\Delta f}^{\mathrm{C}\mathrm{S}}$, it can be divided into two cases to analyze the second-order transfer function of CS VSG electromagnetic power by using the small signal model.

Case 1: when Δ$P_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}^{\mathrm{C}\mathrm{S}}$ ≤ $P_{\Delta f}^{\mathrm{C}\mathrm{F}}$ ≤ Δ$P_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}}^{\mathrm{C}\mathrm{S}}$, that is Δω_min ≤ Δω ≤ Δω_max, the transfer function between $P_{\mathrm{e}}^{\mathrm{C}\mathrm{S}}$ and $P_{\mathrm{m}}^{\mathrm{C}\mathrm{S}}$ is as follows:

$$P_{\mathrm{e}}^{\mathrm{C}\mathrm{S}}(s)={\displaystyle \frac{\frac{3E_0{U}_l}{J_{\mathrm{CS}}\omega X_f}}{s^2+(\frac{D_{\mathrm{CS}}}{J_{\mathrm{CS}}}+\frac{K_{\Delta f}}{J_{\mathrm{CS}}\omega })s+\frac{3E_0{U}_l}{J_{\mathrm{CS}}\omega X_f}}}{P}_{\mathrm{m}}^{\mathrm{CS}}(s)$$

(6)

Case 2: when $P_{\Delta f}^{\mathrm{C}\mathrm{S}}$ > Δ$P_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}}^{\mathrm{C}\mathrm{S}}$ or $P_{\Delta f}^{\mathrm{C}\mathrm{S}}$ < Δ$P_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}^{\mathrm{C}\mathrm{S}}$, that is Δω > Δω_max or Δω < Δω_min, the transfer function of $P_{\mathrm{e}}^{\mathrm{C}\mathrm{S}}$ and $P_{\mathrm{r}\mathrm{e}\mathrm{f}}^{\mathrm{C}\mathrm{S}}$ is as follows:

$$P_{\mathrm{e}}^{\mathrm{CS}}(s)={\displaystyle \frac{\frac{3E_0{U}_l}{J_{\mathrm{CS}}\omega X_f}}{s^2+\frac{D_{\mathrm{CS}}}{J_{\mathrm{CS}}}s+\frac{3E_0{U}_l}{J_{\mathrm{CS}}\omega X_f}}}{P}_{\mathrm{ref}}^{\mathrm{CS}}(s)$$

(7)

When Δω < Δω_min, $P_{\mathrm{r}\mathrm{e}\mathrm{f}}^{\mathrm{C}\mathrm{S}}$ = $P_{\mathrm{m}}^{\mathrm{C}\mathrm{S}}$ + Δ$P_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}}^{\mathrm{C}\mathrm{S}}$; when Δω > Δω_max, $P_{\mathrm{r}\mathrm{e}\mathrm{f}}^{\mathrm{C}\mathrm{S}}$ = $P_{\mathrm{m}}^{\mathrm{C}\mathrm{S}}$ + Δ$P_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}^{\mathrm{C}\mathrm{S}}$. It can be seen that Equations (6) and (7) are typical second-order transfer functions. When the error band is ±2%, the natural oscillation angular frequency ω_n, damping ratio ξ, the overshoot σ%, and the adjustment time t_s are obtained in Equations (8) and (9).

$${\omega }_{\mathrm{n}}=\sqrt{{\displaystyle \frac{3E_0{U}_l}{J_{\mathrm{CS}}{\omega }_0{X}_f}}} , \xi ={\displaystyle \frac{D_{\mathrm{CS}}^{\prime }}{2}}\cdot \sqrt{{\displaystyle \frac{{\omega }_0{X}_f}{3J_{\mathrm{CS}}{E}_0{U}_l}}}$$

(8)

$$\sigma \%==e^{-\pi {\displaystyle \frac{1}{\sqrt{\frac{12J_{\mathrm{CS}}{E}_0{U}_l}{{D_{\mathrm{CS}}^{\prime }}^2{\omega }_0{X}_f}-1}}}}\times 100\% , t_s={\displaystyle \frac{4}{\xi {\omega }_n}}={\displaystyle \frac{8J_{\mathrm{CS}}}{D_{\mathrm{CS}}^{\prime }}}$$

(9)

$$D_{\mathrm{CS}}^{\prime }=\left\{\begin{array}{ll}{D}_{\mathrm{CS}}+K_{\Delta f}\cdot {(J_{\mathrm{CS}}\omega )}^{-1} & ,\Delta {\omega }_{\min }\le \Delta \omega \le \Delta {\omega }_{\max }\\ D_{\mathrm{CS}} & ,\mathrm{else}\end{array}\right.$$

(10)

where D’ CS is CS VSG equivalent damping coefficient, which is divided into two cases, as shown in Equation (10). According to Equations (8) and (9), when J_CS increases, ω_n decreases, ξ decreases, σ% increases, and t_s increases, which means the larger J_CS can reduce the dynamic response oscillation for a single CS VSG.

For multiple CS VSGs, the multi-VSG angular velocity oscillation curve is shown in Figure 4, taking CS₁ VSG and CS₂ VSG as examples to analyze J_CS,1 adjustment. The curve can be divided into four intervals: (1) t₁~t₂, (2) t₂~t₃, (3) t₃~t₄, (4) t₄~t₅. In interval (1), if ω₁ − ω₂ > 0, dω₁/dt > 0, and (ω₁ − ω₂)·dω₁/dt > 0, J_CS,1 should increase to slow down the ω₁ increase and decrease ω₁-ω₂; in interval (2), if ω₁ − ω₂ > 0, dω₁/dt < 0, and (ω₁ − ω₂)·dω₁/dt < 0, J_CS,1 should decrease to speed up the ω₁ recovery and decrease ω₁ − ω₂. Similarly, J_CS,1 increases and decreases respectively in intervals (3) and (4). Besides, the change of J_CS,2 should be on the contrary compared with J_CS,1.

The above content only considers two CS VSGs. In multiple CS VSGs, any CS VSG inertia adjustment needs to consider the comprehensive influence of its AAGs. So its adaptive equation and CS VSGs’ coordination matrix K are established as follows:

$$J_{\mathrm{CS},i}=J_{\mathrm{CS},i,0}+{\displaystyle {\sum }_{j=1}^{{\mathrm{Z}}_{i,C_i}}\left[k_{ij}\cdot b_{ij}\left({\omega }_i-{\omega }_j\right)\cdot \mathrm{d}{\omega }_i/\mathrm{d}t\right]}$$

(11)

$$K=\left(\begin{array}{ccc}{k}_{11}\cdot b_{11}& \dots & k_{1n}\cdot b_{1n}\\ ⋮& \ddots & ⋮\\ k_{n1}\cdot b_{n1}& \dots & k_{nn}\cdot b_{nn}\end{array}\right)$$

(12)

where J_CS,i,0 is CS_i VSG initial virtual inertia; k_i,j is coordination coefficient, respecting the influence degree of the CS_j VSG on CS_i VSG’s inertia; C_i is the total number of AAGs for CS_i VSG agent i; Z_i,j is the serial number of jth AAG of CS_i VSG agent i.

4. CS VSGs Control Strategy Based on Physics-Data Fusion Model

The establishment equation of adaptive inertia in Section 3 is not complete. It equates the influence degrees of AAGs to LAGs’ inertia. Therefore, it is necessary to introduce a data-driven method to adjust coordination coefficients, enhancing adaptability to reduce frequency oscillation and CS response power oscillation.

4.1. Physics-Data Fusion Modeling

The physics-driven adaptive inertia has rigidity based on mechanism analysis, but the model construction is too idealized. It is impossible to distinguish the difference in AAGs’ influence on LAGs, reducing inertia adjustment accuracy. Therefore, it is difficult to reduce frequency oscillation and CS response power oscillation. The data-driven model is flexible based on experience playback, which is suitable for complex scenes. However, in the scene where CSs participate in FR, the diversity of CS FR capabilities, communication situation, and power disturbances would lead to low training efficiency when lacking a priori analysis, making actions to adjust virtual inertia confusing.

Given the respective limitations of a physics-driven method and a data-driven method, a physics-data fusion model that integrates mechanistic rules with experience playback can be more effectively applied to CS participation in frequency response control architecture. By applying reinforcement learning to optimize coordination coefficients within the physics-driven adaptive CS VSG inertia, this approach not only enhances the accuracy of inertia adjustments by distinguishing the differential impacts of AAGs on LAGs but also improves MA training efficiency through the incorporation of a priori knowledge.

4.2. SAC Basic Principles

This paper uses the MA-SAC to achieve the cooperative control idea of “centralized training and decentralized execution”, respectively adjusting coordination coefficients between CS VSGs. The SAC discount cumulative reward function M is as follows:

$$M={\displaystyle \sum _t{E}_{(s_t,a_t)\sim {\rho }_{\pi }}\left[r(s_t,a_t)+\alpha H({\pi }_{\beta }(\cdot |s_t))\right]}$$

(13)

$${\pi }^{*}=\underset{{\pi }_{\beta }}{\arg \max }{\displaystyle \sum _t{E}_{(s_t,a_t)\sim {\rho }_{\pi }}\left[r(s_t,a_t)+\alpha H({\pi }_{\beta }(\cdot |s_t))\right]}$$

(14)

$$H({\pi }_{\beta }(\cdot |s_t))=E_{a\sim {\pi }_{\beta }(\cdot |s_t)}[-\ln {\pi }_{\beta }(a_t|s_t)]$$

(15)

where π_β is agent action strategy, reflecting the probability distribution of agent action selection; s_t and a_t are respectively the state and action taken by the agent at t; E[·] is the mathematical expectation; (s_t, a_t)~ρ_π represents the distribution of trajectories (s_t, a_t) under the strategy π; r(s_t, a_t) is the reward value based on a_t and s_t; α is a regularized entropy parameter, determining the entropy importance and the strategy exploratory. H(π_β(|s_t)) is action entropy of strategy π under state s_t; β is the network parameter of π_β.

The SAC actor network is responsible for modeling the action strategy π_β, and the critic network evaluates the strategy by Q-value function Q_θ(s_t,a_t), defined as follows:

$$Q_{\theta }(s_t,a_t)=\epsilon E_{s_{t+1}\sim {\rho }_{\pi }}[V(s_{t+1})]+r(s_t,a_t)$$

(16)

$$V(s_{t+1})=E_{a_t\sim \pi }[Q_{\theta }(s_t,a_t)-\alpha \ln {\pi }_{\beta }(a_t|s_t)]$$

(17)

where Q_θ(s_t,a_t) is the sum of the expected discount reward and the expected action entropy from the state-action (s_t, a_t) to the end; e is the reward discount factor; E_st+1~ρπ represents the sum of the expected values of all states s_t+1 under the trajectory ρ_π.

The SAC algorithm consists of three neural networks, that is actor network, critic network, and target critic network. Their parameters are respectively updated as follows:

$$M_{\pi }(\beta )=E_{s_t\sim D,a_t\sim {\pi }_{\varphi }}\left[\ln {\pi }_{\varphi }(a_t|s_t)-{\displaystyle \frac{1}{\alpha }}{Q}_{\theta }(a_t|s_t)\right]$$

(18)

$$\begin{array}{c}{M}_Q(\theta )=E_{(s_t,a_t,s_{t+1})\sim D,a_{t+1}\sim {\pi }_{\varphi }}({\displaystyle \frac{1}{2}}(Q_{\theta }(a_t|s_t)-R(s_t,a_t)\dots \\ -\epsilon E_{a_{t+1}\sim {\pi }_{\varphi }}[-\alpha \ln {\pi }_{\varphi }(a_{t+1}|s_{t+1})+Q_{\theta \prime }(a_{t+1}|s_{t+1})]{)}^2)\end{array}$$

(19)

$${\theta }^{\prime }=\tau \theta +(1-\tau ){\theta }^{\prime }$$

(20)

where M_π(β) and M_Q(θ) are respectively loss functions with parameters β and θ as the independent variable; D is the experience playback pool; τ is the update coefficient.

4.3. Adaptive Virtual Inertia Modified by Physics-Data Fusion

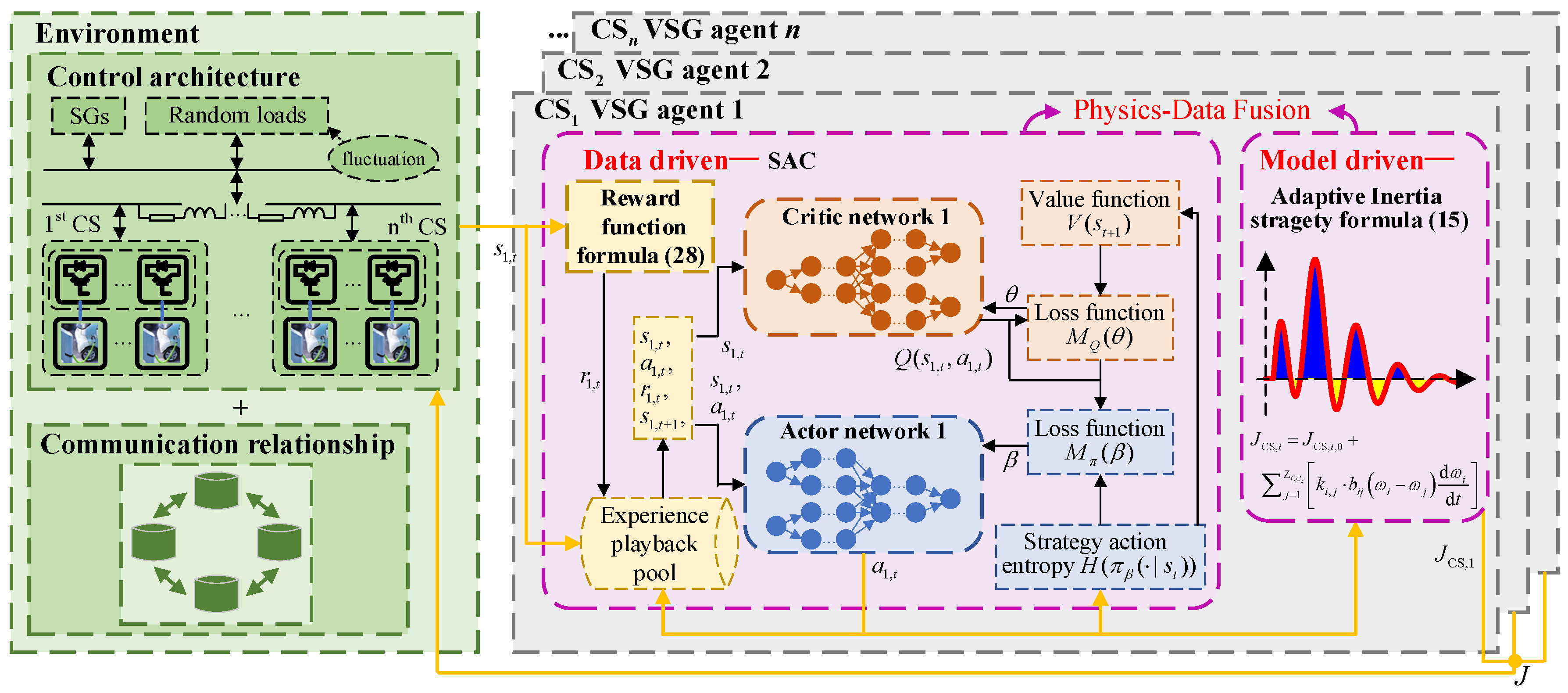
The power grid frequency control framework with multiple CS participation based on physics-data fusion driven is shown in Figure 5, including environment and CS VSG agents. The former includes the power grid frequency control architecture with CS participation and CSs’ communication topology. The latter can interact with the environment and obtain information from AAGs based on the communication topology. s_i,t, a_i,t, and r_i,t, are respectively defined below:

(1)

state:

$$s_{i,t}=(P_{\mathrm{ref},t}^{\mathrm{CS},i},P_{\mathrm{CS},i,t}^{\mathrm{all}},{\omega }_{i,t}^{\mathrm{all}})$$

(21)

$$P_{\mathrm{CS},i}^{\mathrm{all}}=(\Delta P_{\mathrm{source},t}^{\mathrm{CS},i}, \Delta P_{\mathrm{load},t}^{\mathrm{CS},i}, \Delta P_{1,\mathrm{source},t}^{\mathrm{R},\mathrm{CS},i}, \Delta P_{1,\mathrm{load},t}^{\mathrm{R},\mathrm{CS},i},\dots , \Delta P_{C_{i,}\mathrm{source},t}^{\mathrm{R},\mathrm{CS},i}, \Delta P_{C_{i,}\mathrm{load},t}^{\mathrm{R},\mathrm{CS},i})$$

(22)

$${\omega }_{i,t}^{all}=(\Delta {\omega }_{i,t},\mathrm{d}{\omega }_{i,t}/\mathrm{d}t,\Delta {\omega }_{1,t}^{\mathrm{R},i},\mathrm{d}{\omega }_{1,t}^{\mathrm{R},i}/\mathrm{d}t,\dots ,\Delta {\omega }_{C_i,t}^{\mathrm{R},i},\mathrm{d}{\omega }_{C_i,t}^{\mathrm{R},i}/\mathrm{d}t)$$

(23)

where s_i,t is state information for CS_i VSG agent i at the tth step; $P_{\mathrm{r}\mathrm{e}\mathrm{f},t}^{\mathrm{C}\mathrm{S},i}$ is CS_i VSG active power instruction; $P_{\mathrm{C}\mathrm{S},i,t}^{\mathrm{a}\mathrm{l}\mathrm{l}}$ is FR capabilities for CS_i VSG and its AAGs; ${\omega }_{i,t}^{\mathrm{a}\mathrm{l}\mathrm{l}}$ is the angular velocity for CS_i VSG and its AAGs; Δ$P_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e},t}^{\mathrm{C}\mathrm{S},i}$ and Δ$P_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d},t}^{\mathrm{C}\mathrm{S},i}$ are respectively equivalent generation power and equivalent load power from CS_i VSG; Δ$P_{j\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e},t}^{\mathrm{R},\mathrm{C}\mathrm{S},i}$ and Δ$P_{j\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d},t}^{\mathrm{R},\mathrm{C}\mathrm{S},i}$ are respectively equivalent generation power and equivalent load power from its jth AAG; Δω_i,t and dω_i,t/dt are respectively CS_i VSG angular velocity and its derivative; Δ${\omega }_{j,t}^{\mathrm{R},i}$ and d${\omega }_{j,t}^{\mathrm{R},i}$/dt are respectively angular velocity and its derivative from its jth AAG.

(2)

action:

$$a_{i,t}=(k_{i,{\mathrm{Z}}_{i,1},t},\dots k_{i,{\mathrm{Z}}_{i,C_i},t})$$

(24)

where a_i,t is actor network i action at the tth step; k_i,j,t is coordination coefficient between CS_i VSG and CS_j VSG at the tth step. Therefore, the proposed method can adjust CS VSGs’ coordination coefficients to enhance inertia adjustment accuracy.

(3)

reward:

$$r_{i,t}=-q\cdot {{\displaystyle {\sum }_{j=1}^{{\mathrm{Z}}_{i,C_i}}(\Delta {\omega }_{i,t}-\Delta {\omega }_{j,t}^{\mathrm{R},i})}}^2$$

(25)

$$r_{\mathrm{all}}={\displaystyle {\sum }_{t=1}^N{\displaystyle {\sum }_{j=1}^n{r}_{i,t}}}$$

(26)

$$N=T_{\mathrm{f}}/T_{\mathrm{s}}$$

(27)

where r_i,t is the reward value of CS_i VSG agent i at the tth step, reflecting the negative square sum of the angular velocity difference between CS_i VSG agent i and its AAGs; q is the reward weight [30] and is set at 4 × 10⁷ in this paper; r_all is total reward value for MA and control steps; T_s and T_f are respectively each step control time and simulation time per episode; N is the number of control steps.

During the training process, by the interaction with the environment, MA can gradually reasonably adjust corresponding coordination coefficients with consideration of CS FR capabilities to improve inertia adjustment accuracy. Then the rewards are gradually maximized, so different nodes’ frequency oscillation is restrained. Besides, restraining the frequency oscillation can also reduce the response power oscillation, preventing EVs in the CS from switching the states frequently to protect EV battery service life.

4.4. Assessment Index

To compare the control effect with other control strategies, some assessment indexes are designed as follows.

$$R_{\mathrm{all}}={\displaystyle {\sum }_{i=1}^n{R}_i}={\displaystyle {\sum }_{i=1}^n({\displaystyle {\int }_{t_0}^{t_1}[{\displaystyle {\sum }_{j=1}^n{(\Delta f_i(t)-\Delta f_j(t))}^2]\mathrm{d}t}}})$$

(28)

$$V_{\mathrm{all}}={\displaystyle {\sum }_{i=1}^n{V}_i}={\displaystyle {\sum }_{i=1}^n({\displaystyle {\int }_{t_0}^{t_1-\Delta t}(\left|P_{\Delta f}^{\mathrm{CS},i}(t+\Delta t)-P_{\Delta f}^{\mathrm{CS},i}(t)\right|)\mathrm{d}t}})$$

(29)

where R_i is the frequency offset square sum of CS_i VSG node and other CS VSGs nodes; V_i is the sum of CS_i response power oscillation absolute value; R_all/V_all is the sum of R_i/V_i (i = 1, 2, …, n); Δf_i(t) is the frequency offset of CS_i VSG node relative to the rated frequency at the time t; t₀ is simulation start time; t₁ is simulation end time; $P_{\Delta f\left(t\right)}^{\mathrm{C}\mathrm{S},i}$ is CS_i VSG response power at the time t; Δt is the interval time for CS response power comparison. When different control strategies are applied in CSs, the smaller R_i or R_all is, the smaller different nodes’ frequency offsets are; the smaller V_i or V_all is, the less frequently the EV status is switched and the less EV battery loss is.

5. Results and Discussion

The effectiveness of the proposed strategy in this paper is verified by the following simulation. Section 5.1 gives the simulation scene; Section 5.2 gives the MA training situation. Section 5.3 compares the proposed control strategy with traditional CS VSGs and adaptive CS VSGs control strategy.

5.1. Simulation Scene

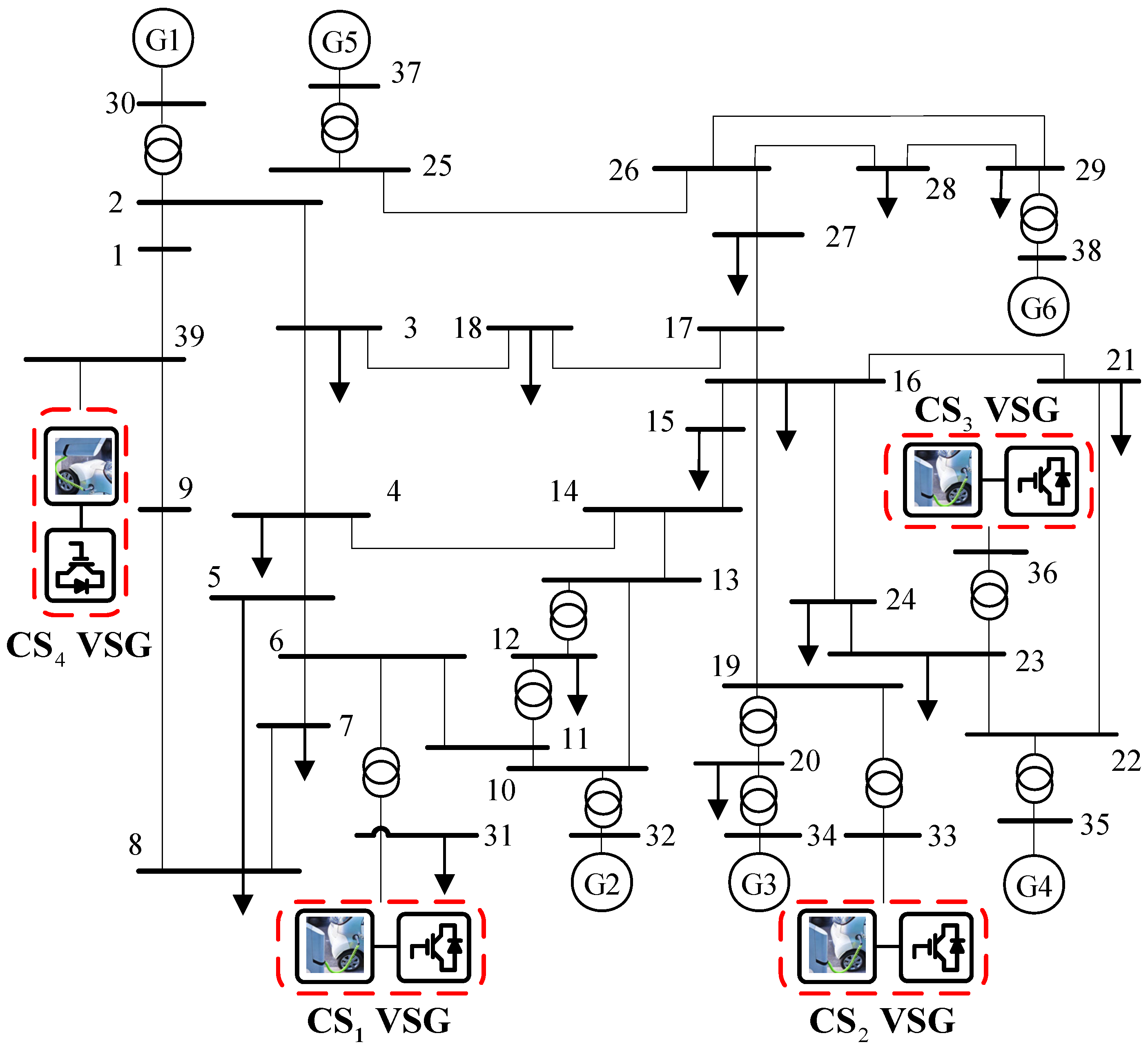
To verify the proposed strategy, four CS VSGs are used to replace the SGs at nodes 31, 33, 36, and 39 in the IEEE 39-node system. The four CS VSGs’ initial inertia information and communication topology are shown in

Table 1. CS VSGs message.

Serial Number	Initial Inertia		Communication
	Variable	Value	Variable	Value
CS1 VSG	JCS,1,0	4	b1,2, b1,3, b1,4	1,0,1
CS2 VSG	JCS,2,0	6	b2,1, b2,3, b2,4	1,1,0
CS3 VSG	JCS,3,0	8	b3,1, b3,2, b3,4	0,1,1
CS4 VSG	JCS,4,0	10	b4,1, b4,2, b4,3	1,0,1

. The IEEE 39-node system after CS VSGs replacement is shown in Figure 6, where 1−39 represent the network nodes.

Besides, disturbance load, communication topology, and CSs’ FR capabilities should be considered to establish random scenes: (1) Load disturbance: load disturbance ranging from −1 MW to 1 MW is randomly generated in load nodes; (2) Communication topology: the communication between CS₂ VSG agent and CS₃ VSG agent is weak, in which there is a 10% probability of interruption, that is b_2,3 and b_3,2 change from 1 to 0; (3) CSs’ FR capabilities: 24 situations are set to simulate four CSs’ FR capabilities’ difference and variability for every hour of one day. Then 200 groups of scenes are randomly generated, and the training set and test set are divided at the proportion of 3:1.

Additionally, the hyperparameter settings for each CS VSG agent are the same, as shown in

Table 2. SAC parameters.

Parameters	Value
Number of layers for actor/critic network	4/3
hidden units per layer for actor/critic network	256/256
Learning rate for actor/critic network	1 × 10−3/1 × 10−3
Each step control time Ts	0.2 s
Simulation time per episode Tf	5.4 s
Control step N	27
Discounted factor	0.99
Entropy parameter α learning rate	1 × 10−3
Replay buffer size	2 × 104
Minimum batch size	128
Training episodes	1800

. The software running the simulation is MATLAB/Simulink 2023a, which is configured on a computer with a 13th Gen Intel (R) Core (TM) i9-13900F CPU (32 GB).

5.2. The MA Training Process

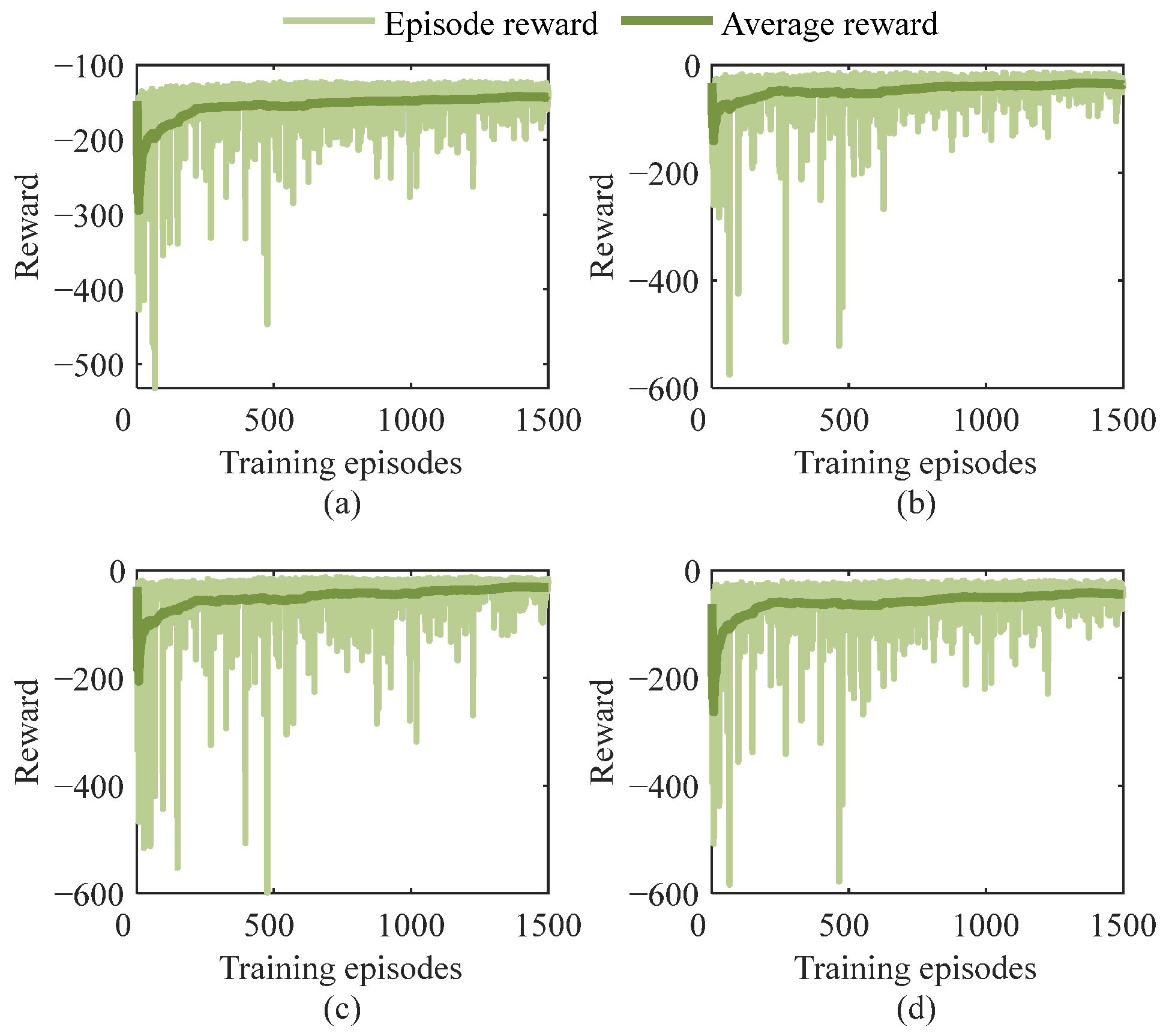
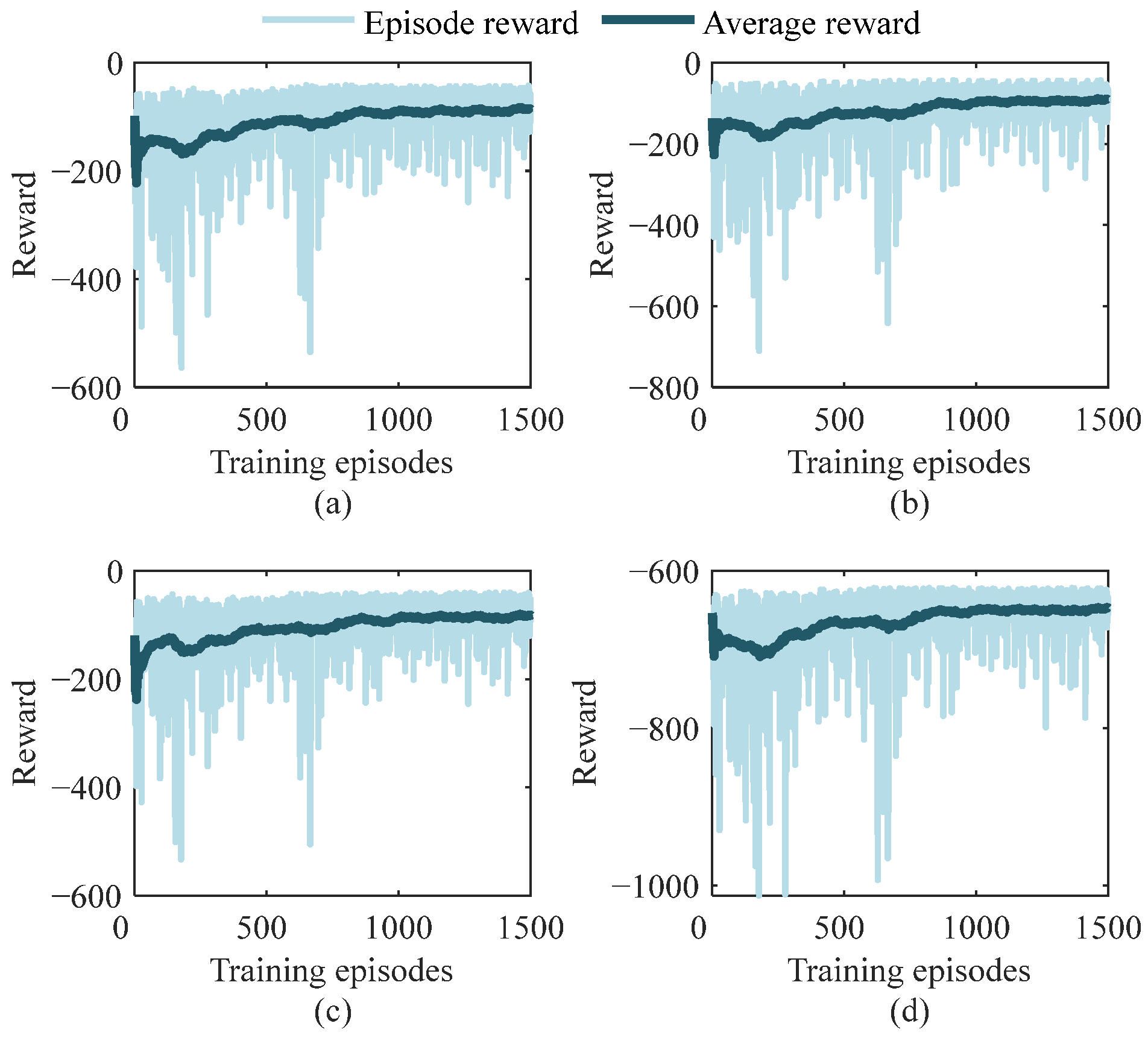
The value range of each parameter in the action a_i,t is set as [0, 6 × 10⁵], and the training set is cycled for four CS VSG agents’ training. The four agents’ reward training curves under the proposed control strategy are shown in Figure 7. The dark green curves represent the average cumulative reward value of nearly 150 training episodes, and the light green curves represent the cumulative reward value in each episode. Besides, to verify the proposed control strategy with prior knowledge has better learning efficiency, the four agents’ reward training curves under a single data-driven method are shown in Figure 8. The SAC parameters of the proposed strategy and a single data-driven method are the same.

In Figure 7, for the proposed control strategy, CS VSGs’ coordination coefficient adjustments are disordered during the first 500 training episodes, leading to inertia adjustment disorder, which makes the reward value small. With the MA-SAC training, CS VSGs’ coordination coefficient adjustments gradually tend to be reasonable, leading the reward value to increase gradually, and the value is stable after 1200 training episodes. In Figure 8, for a single data-driven method, inertia adjustments are still disordered during the first 750 training episodes and the reward value is not stable after 1500 training episodes.

Therefore, the above training results show that for the proposed control strategy, the CS VSG agents can not only achieve effective learning but also have better learning efficiency due to evolution interpretability in the prior knowledge under data-driven. Meanwhile, the power grid frequency control framework with multiple CS VSGs participation based on physics-data fusion driven proposed in this paper provides an application basic for the reinforcement learning method in CS VSG control.

5.3. Control Effect of the Proposed Strategy

The proposed strategy’s control is compared with traditional CS VSGs and adaptive CS VSGs control strategy. The CSs’ initial inertia and communication topology for these control strategies are shown in Table 1. The inertia of traditional CS VSGs control strategy is constant. Adaptive CS VSGs control strategy is established based on Section 3.3, and coordination coefficients are regarded as consistent, setting to 2 × 10⁵.

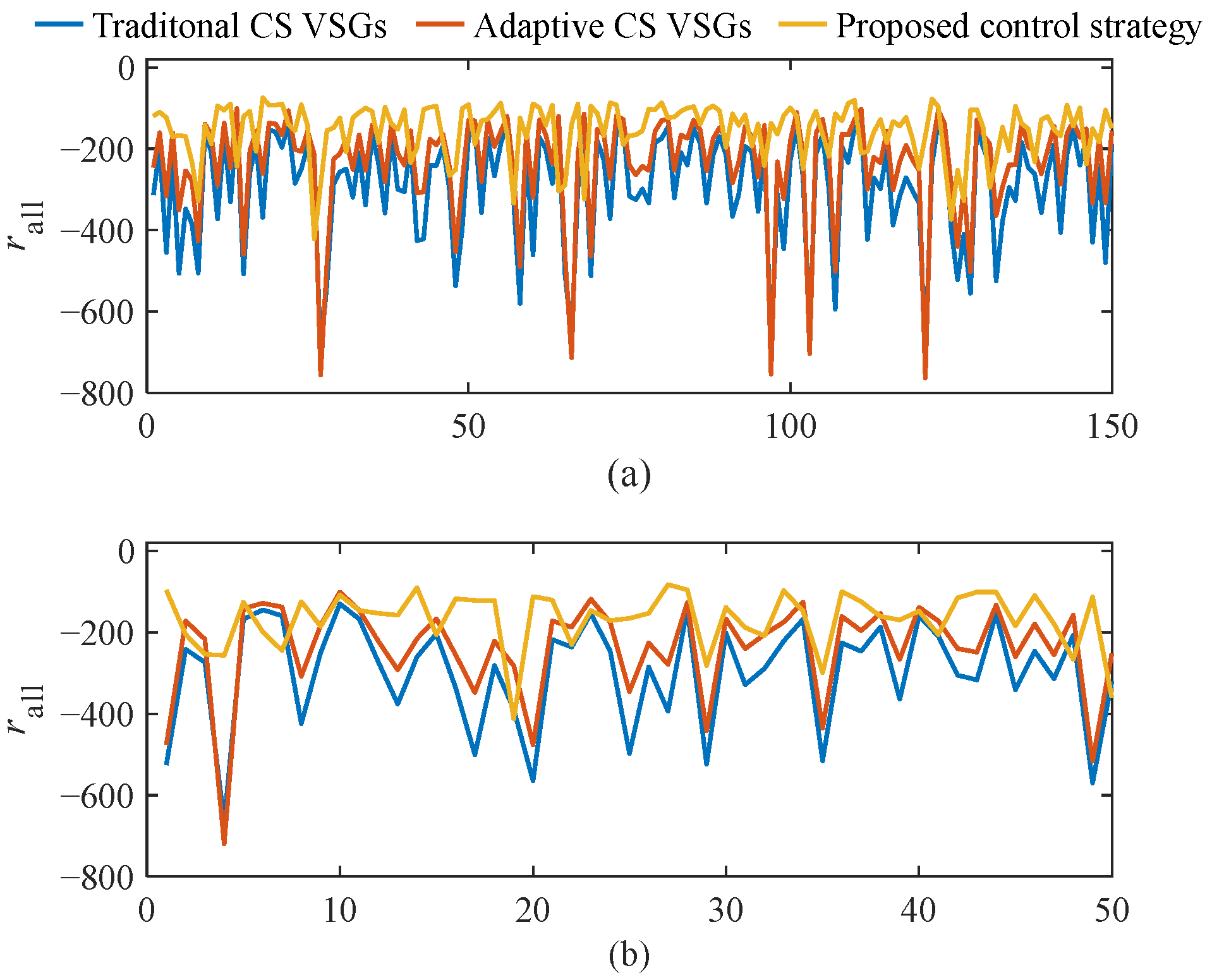
Firstly, 150 training scenes and 50 testing scenes are applied to the above three control strategies, their each scene’s cumulative reward is compared as shown in Figure 9. In Figure 9a, for the training set, the average r_all of traditional CS VSGs control strategy, adaptive CS VSGs control strategy, and the proposed strategy are respectively −292.67, −236.04, and −154.26. In Figure 9b, for the testing set, the average r_all of three strategies are respectively −298.43, −239.08, and −168.00. So average r_all of the proposed strategy are respectively 65.353% and 70.269% of this of the adaptive CS VSGs control strategy for the training set and the testing set, meaning the proposed strategy has better adaptability under various FR scenes and generalization for unknown scenes. This is because the proposed strategy utilizes MA-SAC to adjust coordination coefficients with consideration of CS FR capability to achieve more accurate inertia adjustment.

To specifically reflect the proposed strategy’s validity in improving system FR effect and adaptability under different FR scenes, this paper constructs five cases. The load of 100 MW suddenly increases at node 25, and Δ$P_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}}^{\mathrm{C}\mathrm{S}}$ of CS₁, CS₂, CS₃, and CS₄ are respectively 3.33 MW, 5.38 MW, 1.90 MW, and 5.41 MW. The control strategy applied in CS grid-connected inverters and communication topology for five cases are respectively as follows:

Case 1 applies traditional CS VSGs and the communication is intact as shown in Table 1; Case 2 applies adaptive CS VSGs and the communication is intact as shown in Table 1; Case 3 applies the proposed control strategy and the communication is intact as shown in Table 1; Case 4 applies adaptive CS VSGs and the communication is shown in Table 1 with the exception that the communication between CS₂ VSG agent 2 and CS₃ VSG agent 3 is interrupted; Case 5: applies the proposed control strategy and the communication is shown in Table 1 with the exception that the communication between CS2 VSG agent 2 and CS3 VSG agent 3 is interrupted.

5.3.1. Intact Communication

To verify the proposed control strategy can reduce different nodes’ frequency differences and CS response power oscillation, frequency, inertia, and CS response power for Case 1, Case 2, and Case 3 are shown in Figure 10.

Firstly, from the two red boxes in Figure 10a,d, it can be seen that the frequency offset between different nodes under the adaptive CS VSGs control strategy is less than that of the traditional CS VSGs control strategy. This is because adaptive CS VSGs can adaptively adjust CS VSGs’ inertia based on angular velocity offset and its change rate from its own CS VSG and its AAGs to suppress angular velocity difference, which can be seen in Figure 10e.

Moreover, from the two red boxes in Figure 10d,g, it can be seen that the frequency offset between different nodes under the proposed control strategy is less than that of the adaptive CS VSGs control strategy by further adjusting CS VSGs’ coordination coefficients. Meanwhile, in Figure 10c,f,i, CS response power oscillation of the proposed strategy is the weakest, preventing EVs in the CSs from switching charge state frequently, protecting EV battery service life.

5.3.2. Damaged Communication

To verify the proposed control strategy’s adaptability under a communication interruption. This paper considers Case 4 and Case 5, in which the communication between CS₂ VSG agent 2 and CS₃ VSG agent 3 is interrupted. Frequency, inertia, and CS response power for Case 4 and Case 5 are shown in Figure 11.

Firstly, comparing with Figure 10d Case 2 and Figure 11b Case 4 which both apply adaptive CS VSGs, it can be seen that influenced by the communication interruption, inertia adjustment of CS₂ VSG and CS₃ VSG in Case 4 is reduced. Besides, comparing Figure 10h Case 3 and Figure 11e Case 5 which both apply the proposed control strategy, it can be seen communication interruption influence still exists but is reduced. Because the proposed control strategy can adjust coordination coefficient k₂₁ and k₃₄ respectively to realize compensation.

5.3.3. Assessment Index Comparison Under Different Cases

To further explain the proposed control strategy’s adaptability during a communication interruption,

Table 3. Assessment Index Comparisons of Different Cases.

Cases	Frequency Disturbance Index (1 × 10−4)/Hz2·s					CS Response Power Oscillation Index (1 × 10−1)/MW·s
	R1	R2	R3	R4	Rall	V1	V2	V3	V4	Vall
Case 1	11.361	9.703	15.467	12.790	49.322	7.454	10.458	6.133	11.458	35.503
Case 2	11.113	9.024	9.323	8.855	38.316	9.573	9.706	5.643	10.366	35.287
Case 3	5.988	4.547	3.414	5.160	19.109	6.826	9.496	2.966	8.781	28.068
Case 4	12.081	7.807	11.908	9.967	41.763	8.954	11.909	4.583	10.424	35.870
Case 5	6.433	4.342	4.146	5.500	20.421	7.155	10.514	3.679	9.764	31.111

shows the assessment index results in Cases 1–5.

Firstly, for traditional CS VSGs, no matter whether the communication is interrupted or intact, there is no difference in the control effect. Because traditional CS VSGs’ inertia is constant, leading to the weak dynamic adjustment that R_all and V_all are respectively 49.322 Hz²·s and 35.503 MW·s, relatively large.

Besides, the adaptive CS VSGs control strategy is seriously affected by communication interruption. R_all under Case 4 increases obviously by 8.996% to 41.763 Hz²·s, compared with 38.316 Hz²·s under Case 2. Even V_all of adaptive CS VSGs control strategy under Case 4 increases by 1.023% to 35.870 MW·s compared with 35.503 MW·s of traditional CS VSGs under Case 1. This is because the adaptive CS VSGs control strategy under a single physics-driven method relies solely on fixed equations with constant coordination coefficients for CS VSGs, diminishing the accuracy of inertia adjustments and adaptability under different FR scenes.

Meanwhile, the proposed control strategy is also affected by communication interruption, but not serious. R_all under Case 5 increases slightly by 6.866% to 20.421 Hz²·s compared with 19.109 Hz²·s under Case 3. V_all of the proposed control strategy under Case 5 is 31.111 MW·s, only 87.629% of V_all under Case 1. This is because the proposed control strategy has physics-data fusion modeling advantages by adjusting the coordination coefficients, alleviating the communication interruption influence.

Finally, when the communication is intact, R_all and V_all under Case 4 are respectively 49.872% and 79.542% of those under Case 2; when the communication between CS₂ VSG agent 2 and CS₃ VSG agent 3 is interrupted, R_all and V_all under Case 5 are still respectively 48.897% and 86.733% of those under Case 3. These show that the proposed control strategy has strong adaptability under various FR scenes, including situations with communication interruptions, which can effectively improve the system’s dynamic FR characteristics, that is reducing CS response power oscillation and frequency offset of different nodes.

6. Conclusions

For sustainable development, this paper proposes a physics-data fusion enhanced VSG control strategy for multiple CSs active FR to improve the power system FR characteristics. Firstly, the frequency control architecture with the participation of distributed CSs is constructed as an application basic of the reinforcement learning method in CS VSG control. Besides, the GFM VSG control is applied to the CS grid-connected inverter to form CS VSG with the primary FR controller considering CS FR capability. Then, based on the multiple CS VSGs angular velocity curves, an adaptive CS VSGs inertia is designed as a priori knowledge to enhance interpretability for FR effect improvement and learning efficiency for MA-SAC. Moreover, MA-SAC is used to further modify adaptive CS VSGs by adjusting coordination coefficients with consideration of CS FR capabilities, enhancing inertia adjustment accuracy. Finally, the proposed strategy is verified in the IEEE 39-node system compared with traditional CS VSGs and adaptive CS VSGs. The simulation results show that the proposed strategy has stronger adaptability under different scenes and improves the system’s dynamic FR characteristics; when the MA communication is intact, the frequency disturbance index and the CS response power oscillation index of the proposed control strategy are respectively reduced to 49.872% and 79.542% of the adaptive inertia under a single physics-driven method; when the communication is damaged, these two assessment indexes are still respectively reduced to 48.897% and 86.733%. Future work will focus on implementing this proposed control strategy in engineering practice and collaborating with industry partners to evaluate its performance in different operational environments.