Optimization of Thermoelectric Module Configuration and Cooling Performance in Thermoelectric-Based Battery Thermal Management System
Abstract
1. Introduction
2. Structural Components and Optimization Methods of Thermoelectric Cooling Thermal Management Systems
2.1. Structural Components
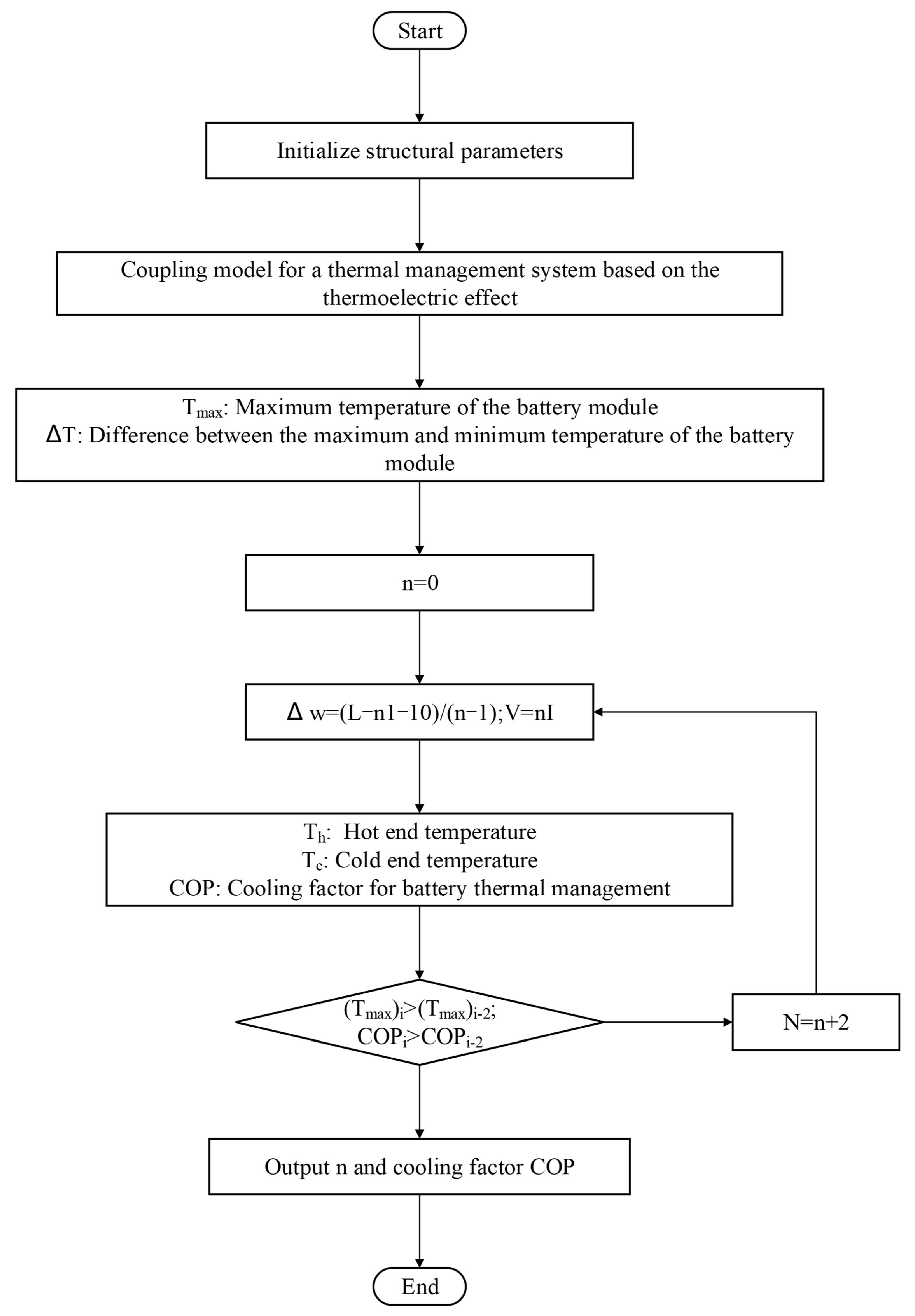
2.2. Optimization Methods
3. Numerical Modeling and Evaluation Indicators
3.1. Numerical Modeling
3.2. Heat Generation Mechanism of Lithium Batteries
3.3. Evaluation Indicators
3.4. Boundary Conditions
3.5. Mesh Independence Verification
4. Results and Discussion
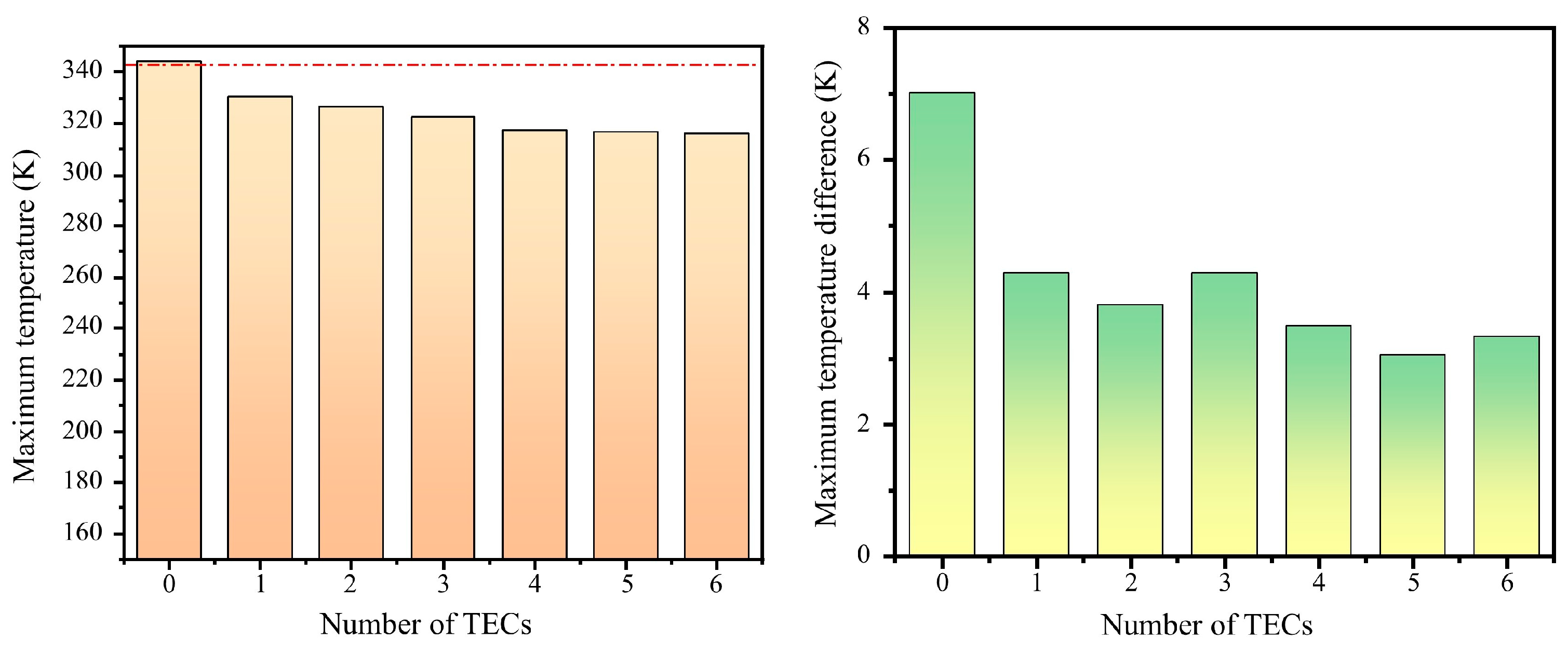
4.1. Optimization of the Number of TECs
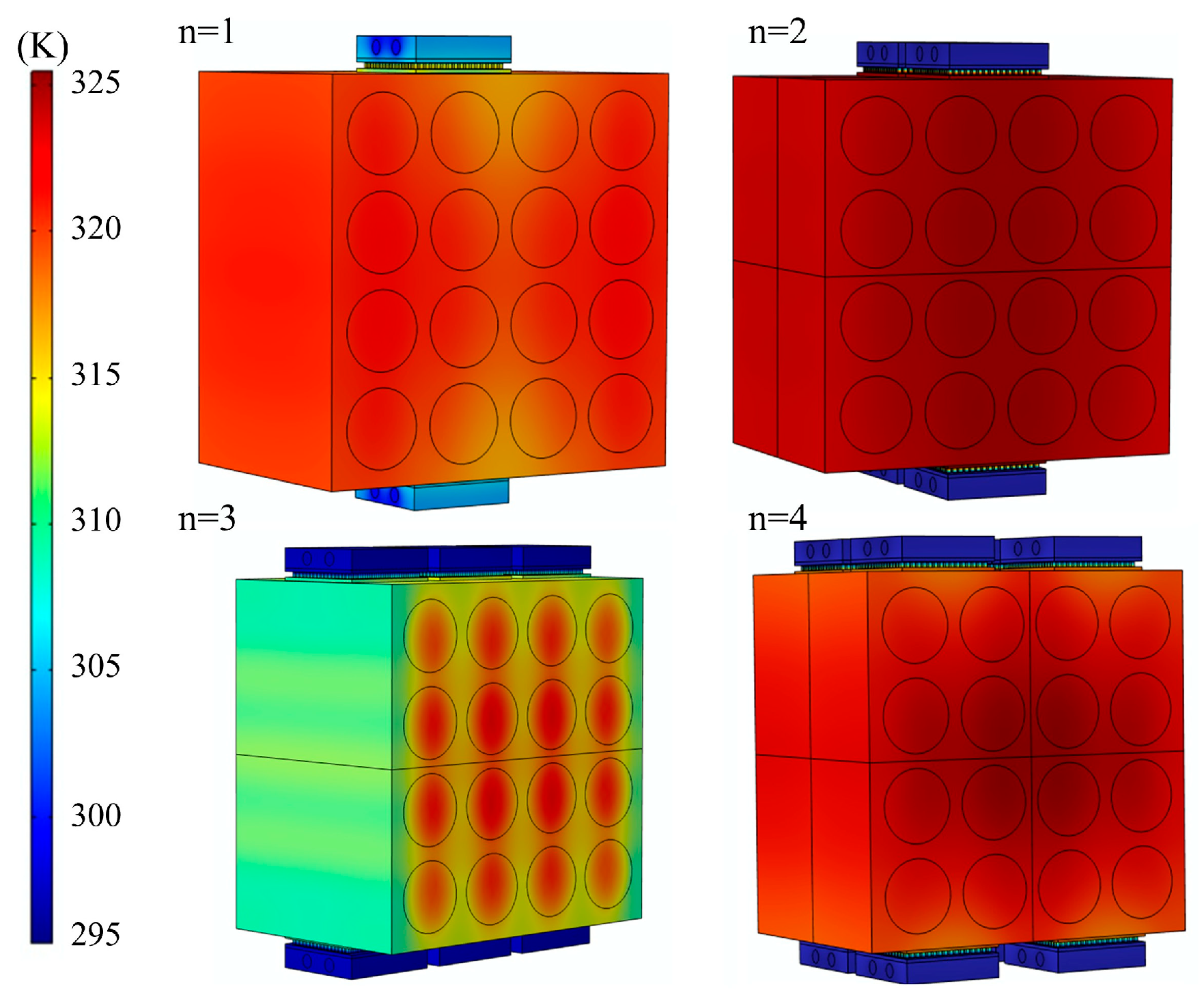
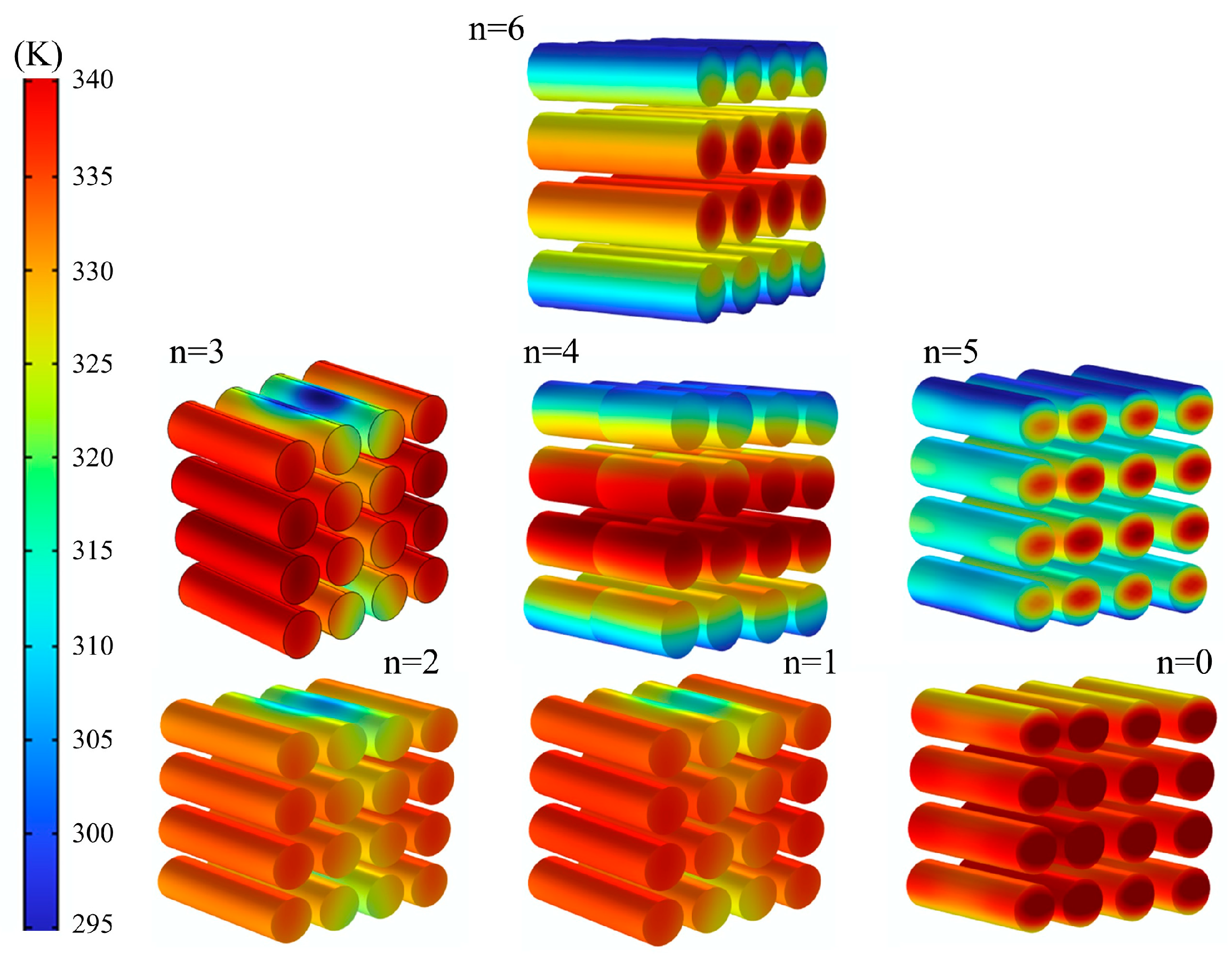
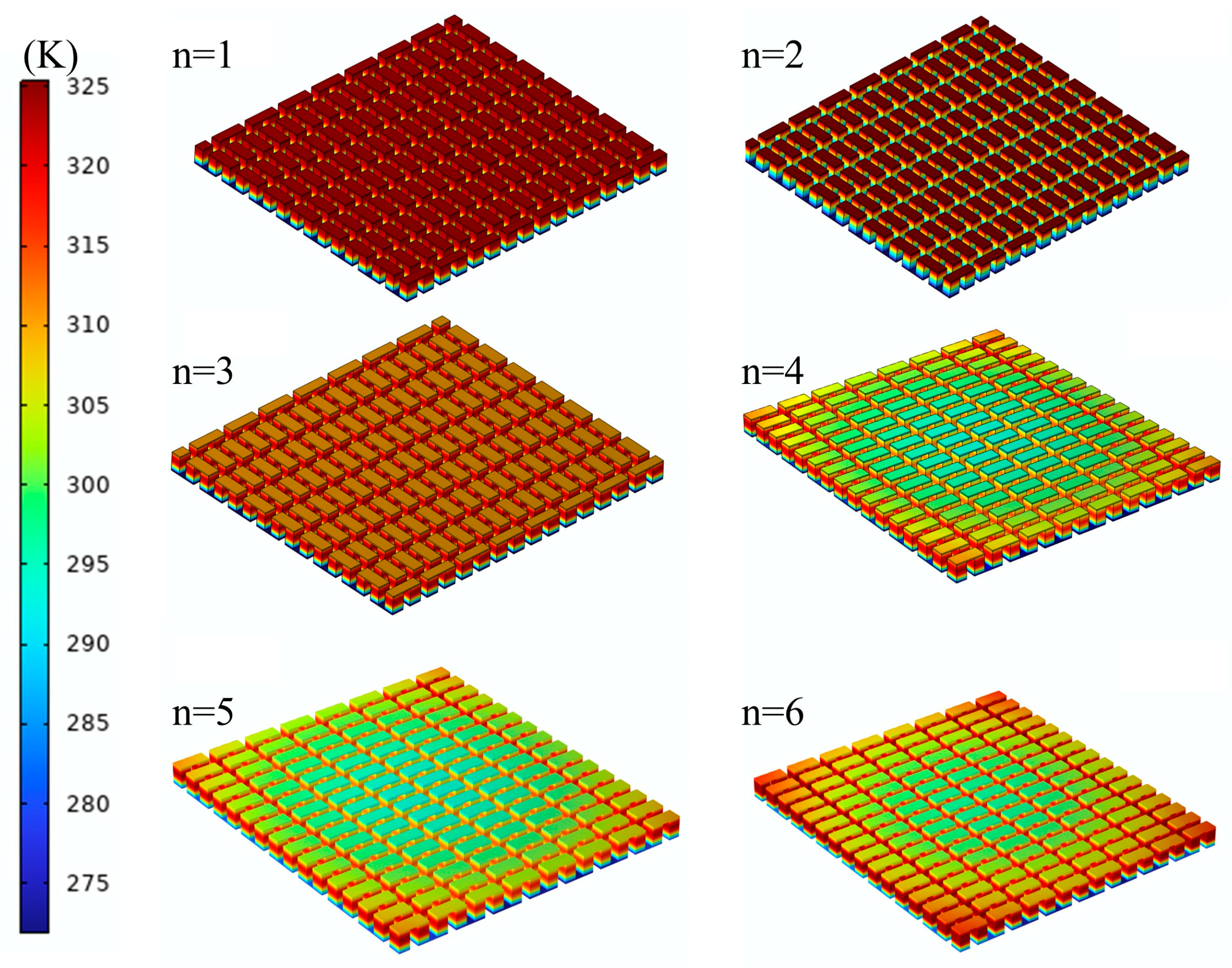
4.1.1. The System Temperature Distribution
4.1.2. Analysis of Temperature Distribution for Thermal Management Systems
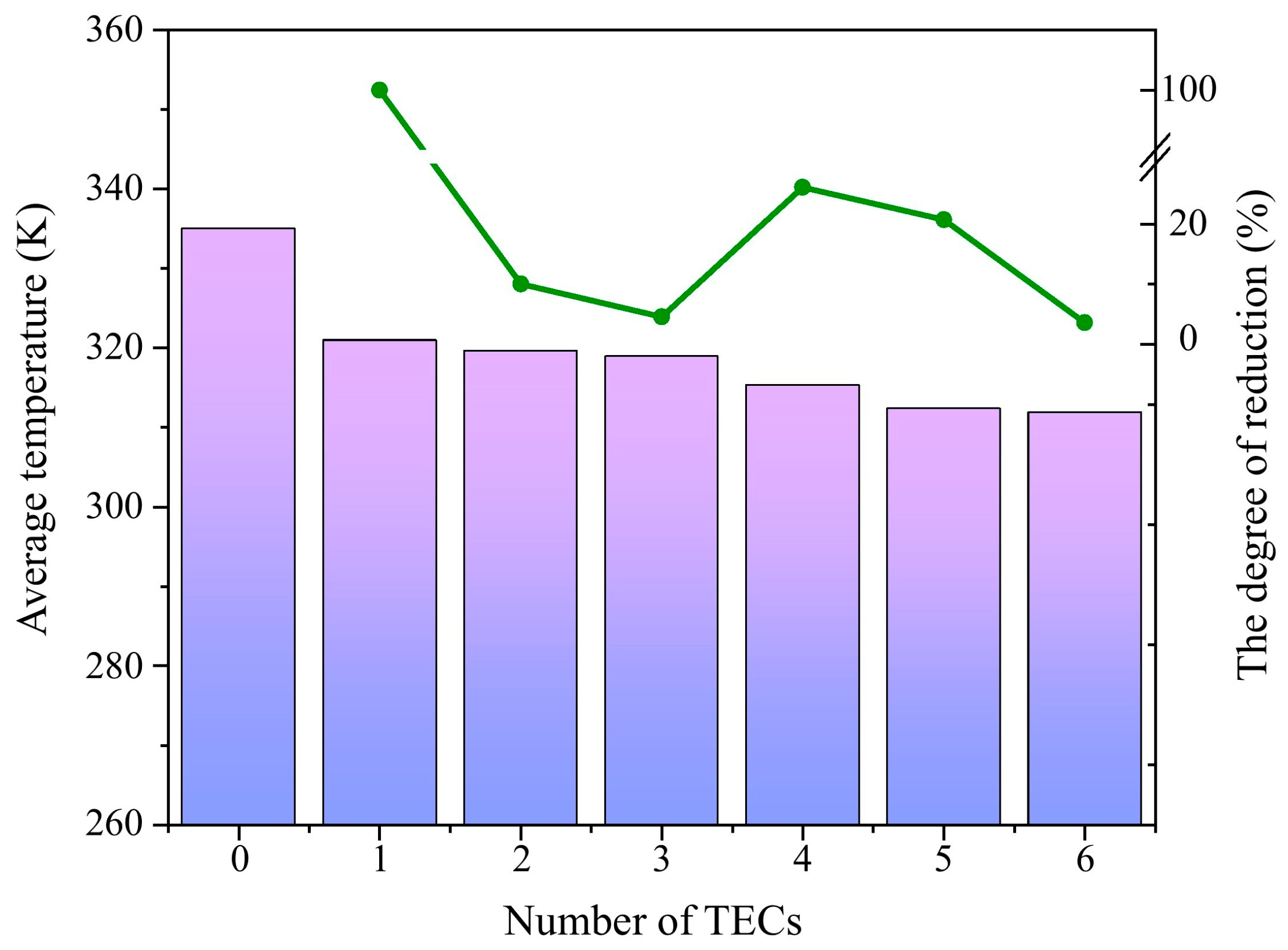
4.1.3. Thermal Management System Battery Temperature Uniformity Analysis
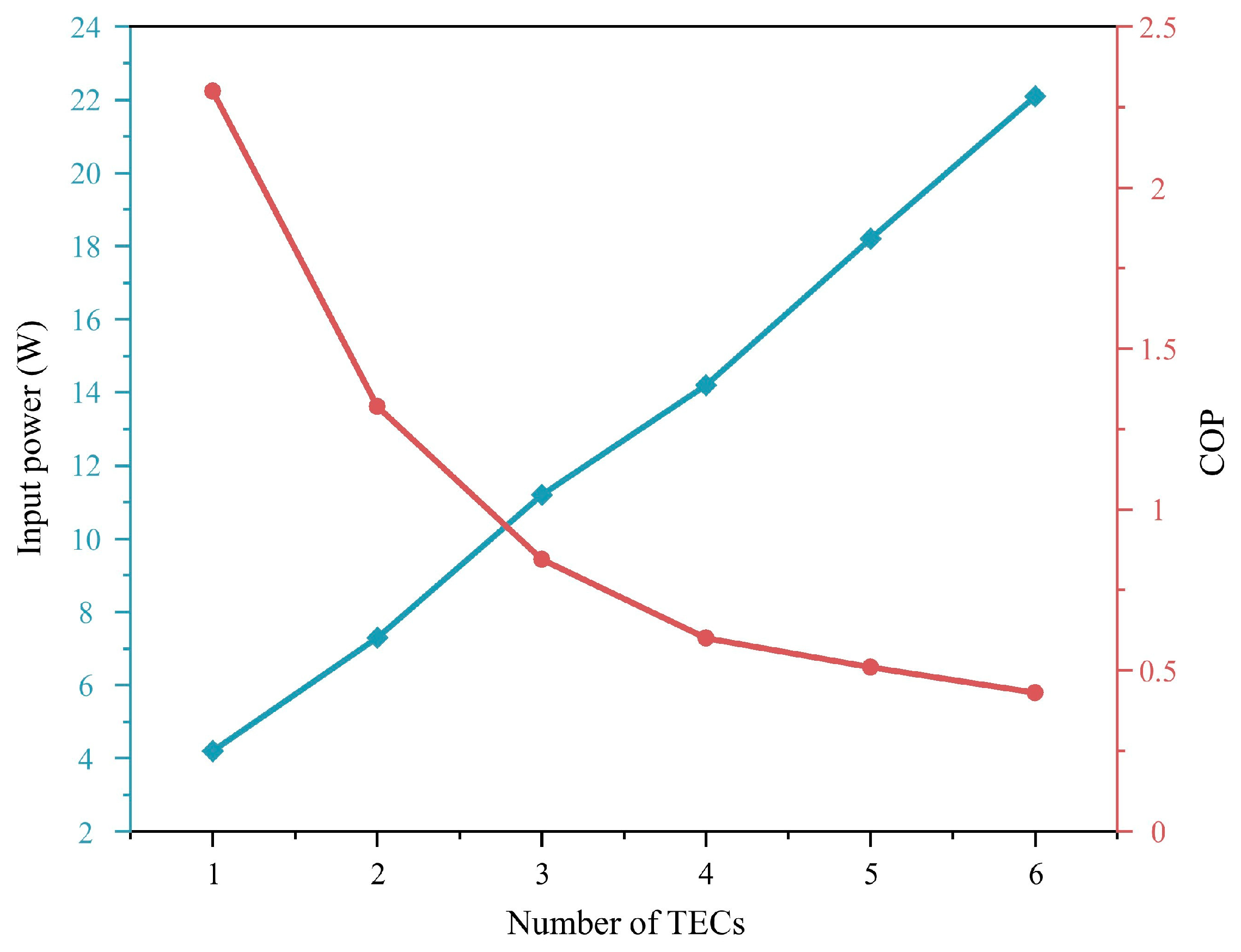
4.1.4. Analysis of Refrigeration Coefficients for Systems
4.2. Analysis of TEC Input Current
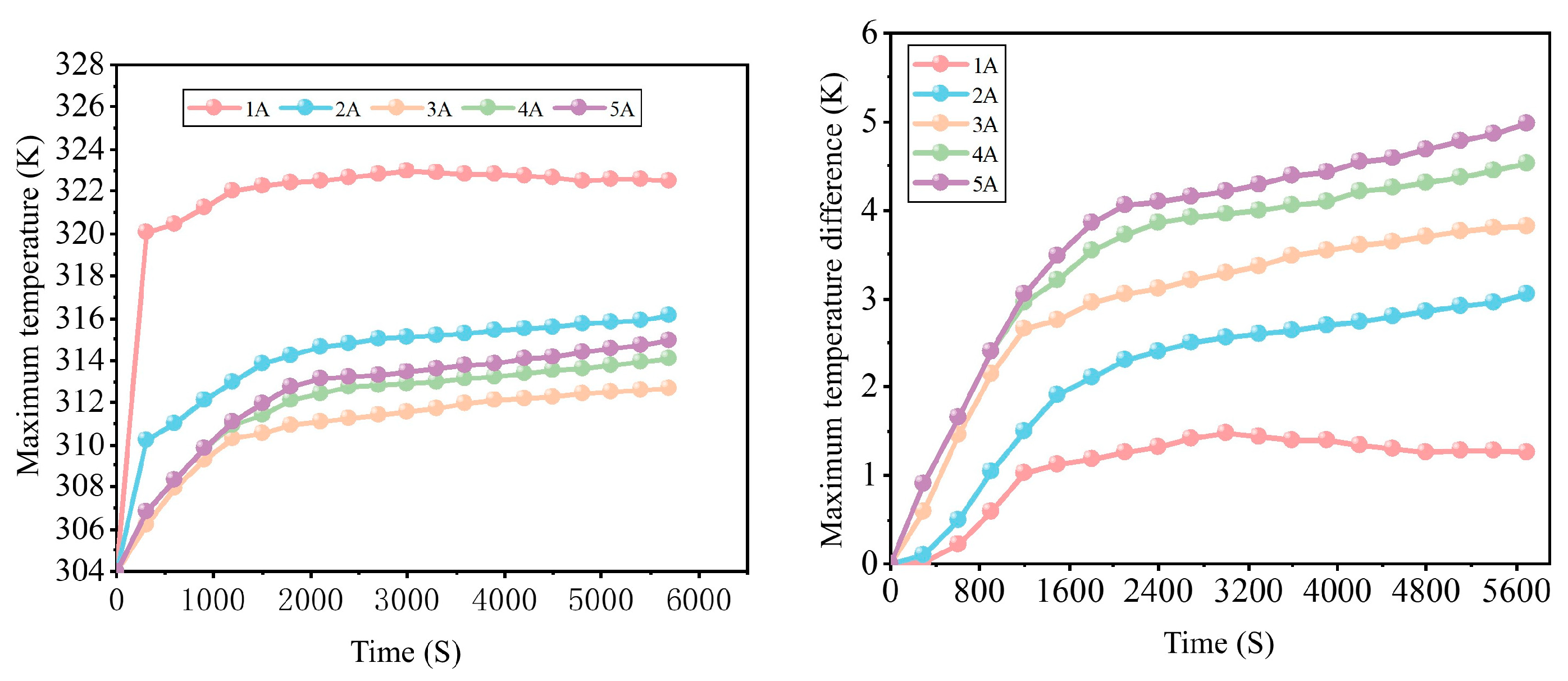
4.2.1. Analysis of Temperature of Battery Under Different Input Currents
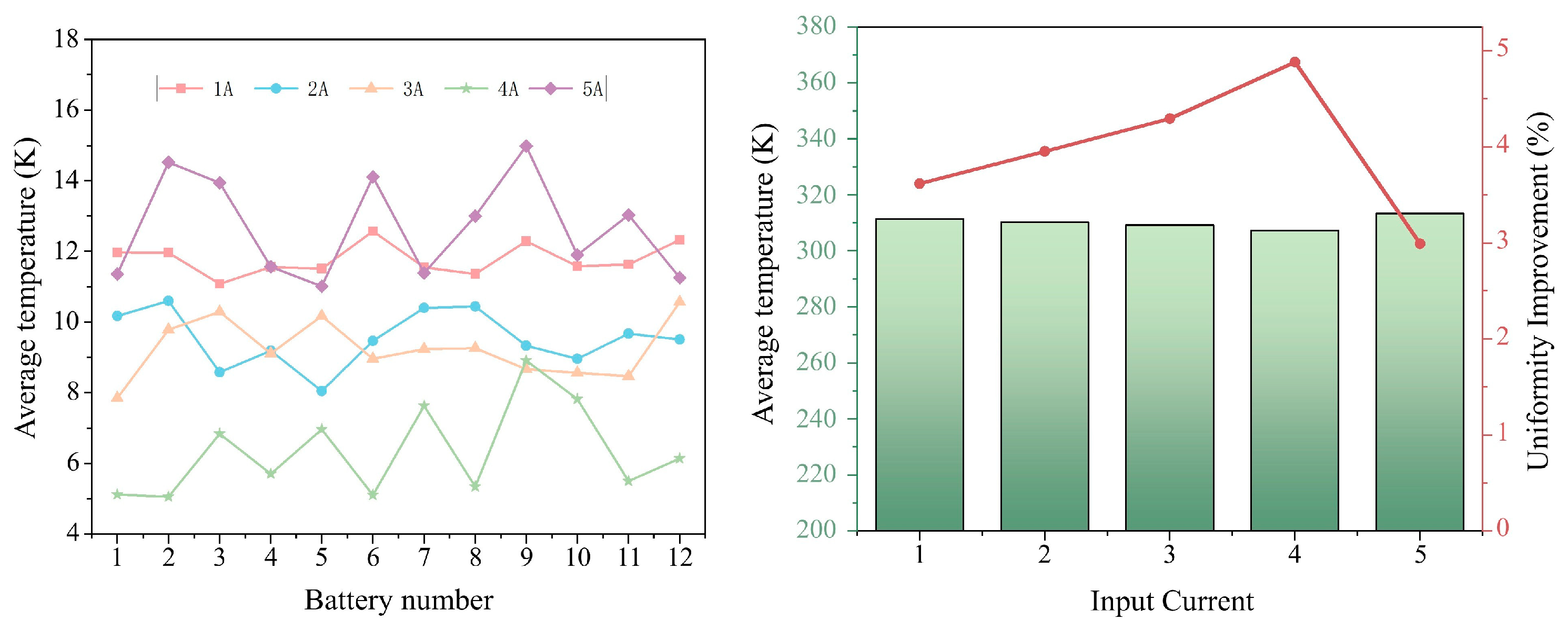
4.2.2. Battery Temperature Uniformity Analysis Under Different Input Currents
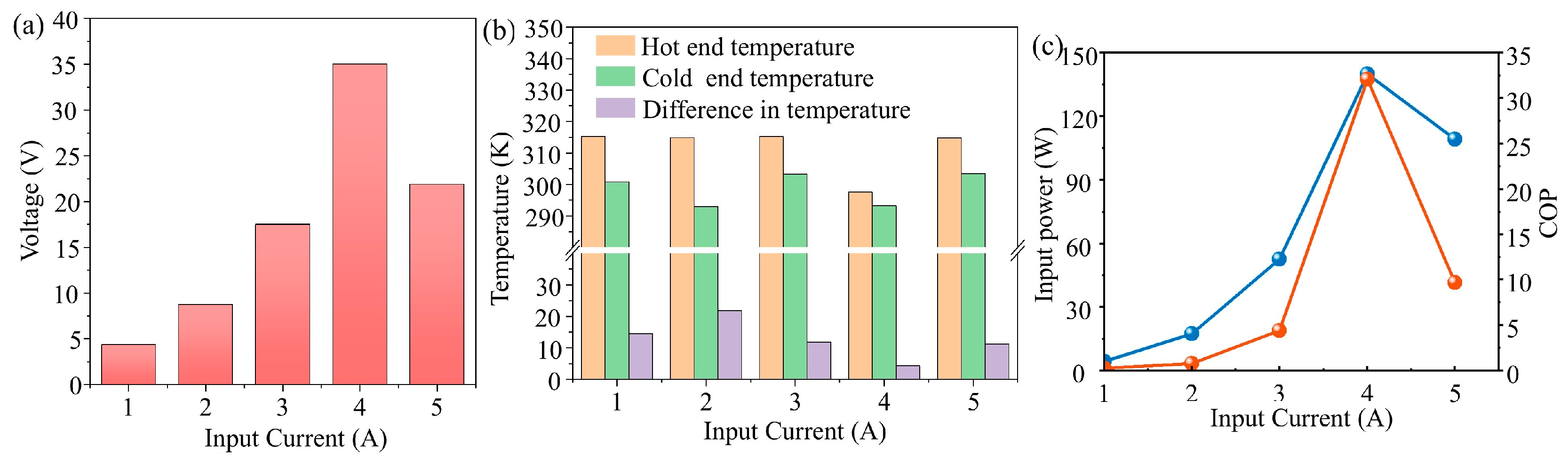
4.2.3. Analysis of Cooling Coefficients of TECs at Different Input Currents
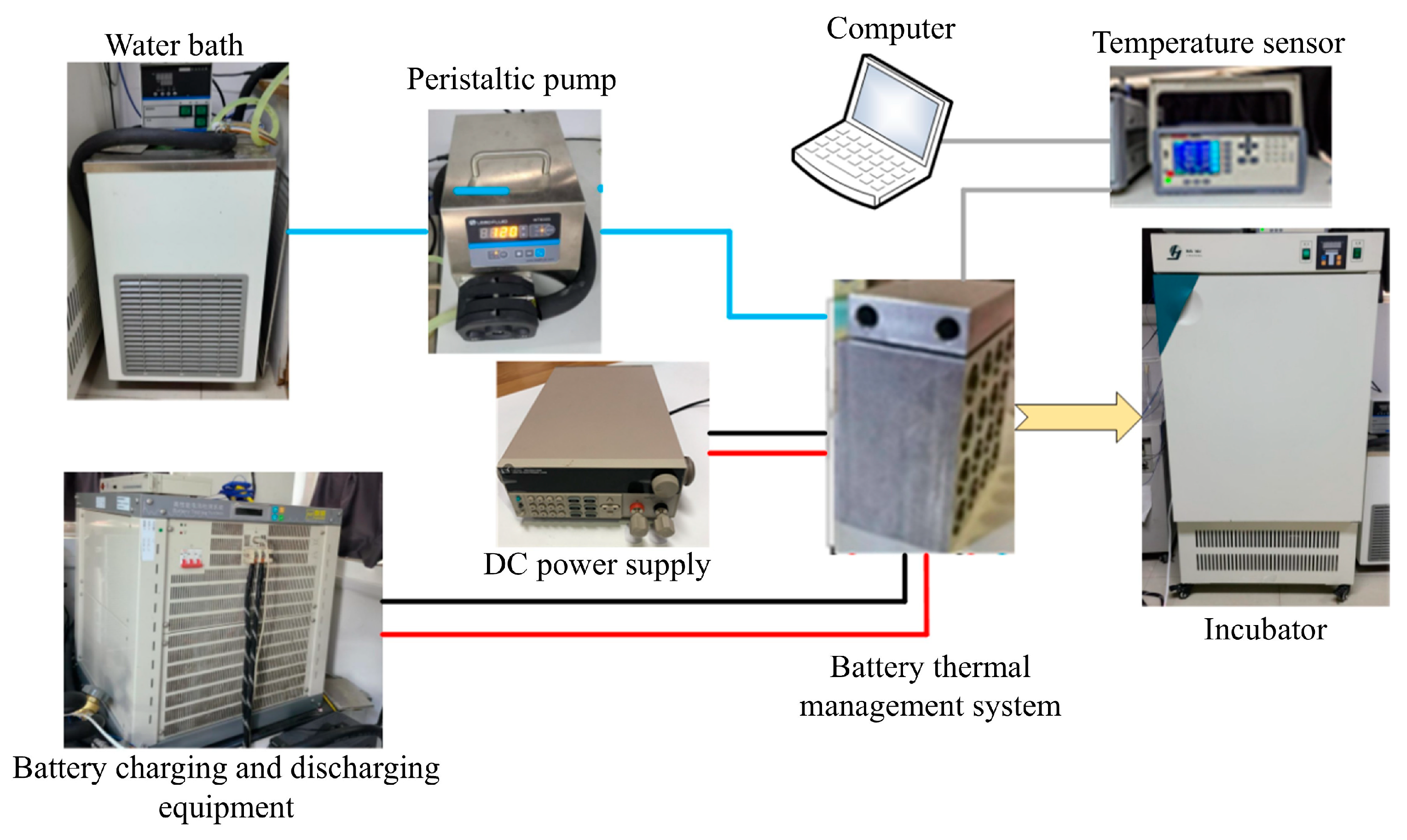
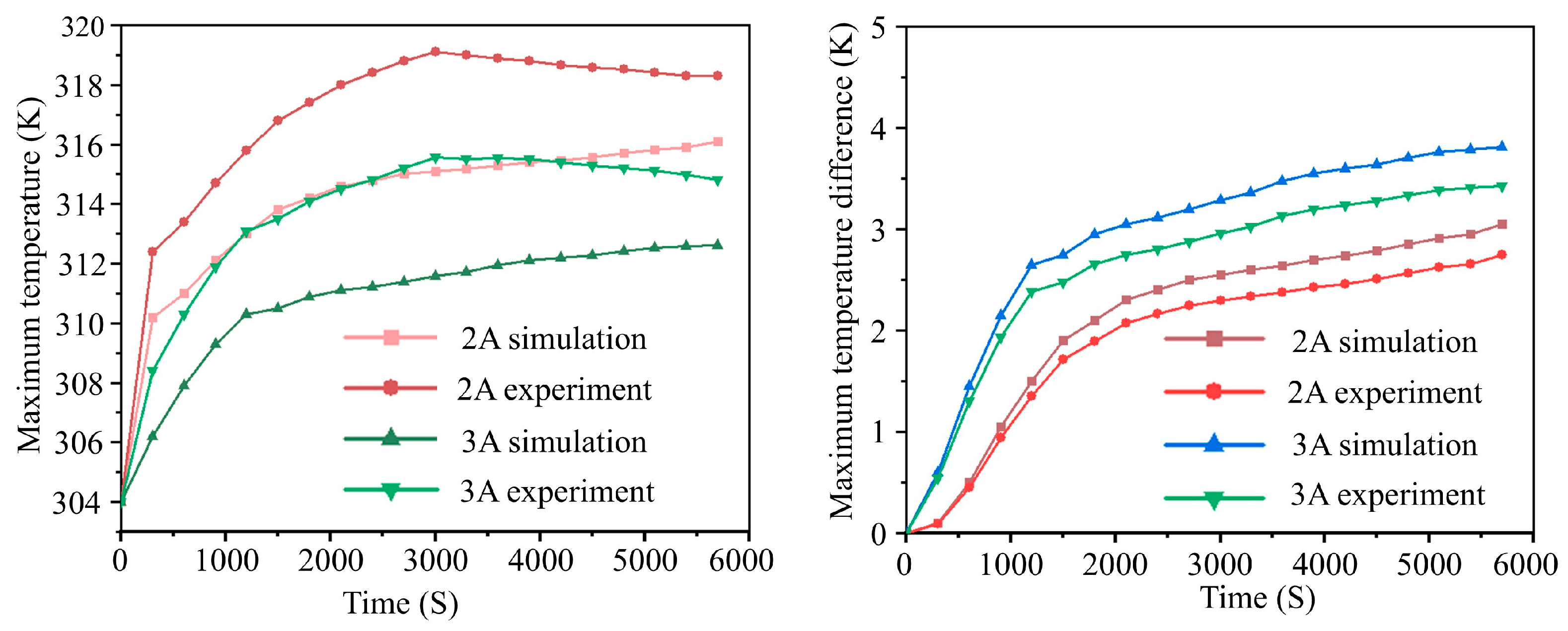
4.3. Experimental Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yan, H.; Ma, X.; Chen, Y.; Tao, Q.; Song, M. Performance analysis of a wet pad assisted air-cooled battery thermal management system with varying number of battery cells. Appl. Therm. Eng. 2025, 259, 124747. [Google Scholar] [CrossRef]
- Na, X.; Kang, H.; Wang, T.; Wang, Y. Reverse layered air flow for Li-ion battery thermal management. Appl. Therm. Eng. 2018, 143, 257–262. [Google Scholar] [CrossRef]
- Su, Q.; Kang, F.; Li, J.; Ma, Q.; Wang, Y.; Duan, J.; Zhang, C. Experimental and numerical investigation of a composite thermal management system for energy storage battery based on air cooling. Appl. Therm. Eng. 2025, 262, 125184. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, X.; Chen, K.; Zhou, D.; Song, M. Experimental and numerical studies on an efficient transient heat transfer model for air-cooled battery thermal management systems. J. Power Sources 2021, 490, 229539. [Google Scholar] [CrossRef]
- Sofi, A.Y.; Qayoum, A. Design optimization and cooling performance assessment of a pulsating Air-Cooled Lithium-Ion battery thermal management System. Therm. Sci. Eng. Prog. 2025, 59, 103391. [Google Scholar] [CrossRef]
- Zhou, H.; Zhou, F.; Xu, L.; Kong, J.; Yang, Q. Thermal performance of cylindrical Lithium-ion battery thermal management system based on air distribution pipe. Int. J. Heat Mass Transf. 2019, 131, 984–998. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, Z.; Wu, Z.; Lu, W.; Yang, Q. Experimental investigation of battery thermal management system based on micro heat pipe array coupled air cooling. Therm. Sci. Eng. Prog. 2025, 60, 103493. [Google Scholar] [CrossRef]
- Al-Zareer, M.; Dincer, I.; Rosen, M.A. Novel thermal management system using boiling cooling for high-powered lithium-ion battery packs for hybrid electric vehicles. J. Power Sources 2017, 363, 291–303. [Google Scholar] [CrossRef]
- Deng, Y.; Feng, C.; Zhu, H.; Chen, J.; Wen, M.; Yin, H. Effects of different coolants and cooling strategies on the cooling performance of the power lithium ion battery system: A review. Appl. Therm. Eng. 2018, 142, 10–29. [Google Scholar] [CrossRef]
- Liu, J.; Yang, Q.; Huang, S.; Wang, H. Optimization of battery thermal management system based on phase change materials coupled with immersion cooling. J. Energy Storage 2025, 127, 117118. [Google Scholar] [CrossRef]
- Tang, Z.; Li, X.; Li, Y.; Cheng, J. Multi-objective optimization of parallel flow immersion cooling battery thermal management system with flow guide plates based on artificial neural network. Appl. Therm. Eng. 2025, 274, 126833. [Google Scholar] [CrossRef]
- Wei, W.; Luo, Z.; Qiao, S.; Zhai, J.; Lei, Z. Analysis and design of module-level liquid cooling system for rectangular Li-ion batteries. Int. J. Heat Mass Transf. 2024, 225, 125435. [Google Scholar] [CrossRef]
- Luo, Y.; Zhu, C.; Zang, M.; Wang, S. Experimental and theoretical study of an immersion battery thermal management system based on synthetic ester fluid. Int. J. Heat Mass Transf. 2025, 250, 127332. [Google Scholar] [CrossRef]
- Keyinci, S.; Ilinčić, P.; Tosun, E.; Uzun, M.; Yakaryilmaz, A.C.; Ozcanli, M. Design and performance analysis of a curved channel liquid cooling system for battery thermal management. Therm. Sci. Eng. Prog. 2025, 63, 103690. [Google Scholar] [CrossRef]
- Bai, F.; Chen, M.; Song, W.; Yu, Q.; Li, Y.; Feng, Z.; Ding, Y. Investigation of thermal management for lithium-ion pouch battery module based on phase change slurry and mini channel cooling plate. Energy 2019, 167, 561–574. [Google Scholar] [CrossRef]
- Bohacek, J.; Raudensky, M.; Karimi-Sibaki, E. Polymeric hollow fibers: Uniform temperature of Li-ion cells in battery modules. Appl. Therm. Eng. 2019, 159, 113940. [Google Scholar] [CrossRef]
- Liu, H.; Chika, E.; Zhao, J. Investigation into the effectiveness of nanofluids on the mini-channel thermal management for high power lithium ion battery. Appl. Therm. Eng. 2018, 142, 511–523. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, Z.; Wu, W.-T. Three-dimensional thermal modeling of Li-ion battery cell and 50 V Li-ion battery pack cooled by mini-channel cold plate. Appl. Therm. Eng. 2019, 147, 829–840. [Google Scholar] [CrossRef]
- Sheng, L.; Zhang, H.; Su, L.; Zhang, Z.; Zhang, H.; Li, K.; Fang, Y.; Ye, W. Effect analysis on thermal profile management of a cylindrical lithium-ion battery utilizing a cellular liquid cooling jacket. Energy 2021, 220, 119725. [Google Scholar] [CrossRef]
- Al-Zareer, M. Numerical Study of Flow and Heat Transfer Performance of 3D-Printed Polymer-Based Battery Thermal Management. Int. J. Heat Mass Transf. 2020, 158, 119995. [Google Scholar] [CrossRef]
- Xie, L.; He, Z.; Zhao, Y.; Vulin, D.; Bhayo, B.A. Research on topology optimization of liquid-cooled plates based on multi-level optimization. Int. Commun. Heat Mass Transf. 2024, 155, 107495. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, B.; Tan, Y.; Li, P. Thermal management of lithium-ion battery pack under demanding conditions and long operating cycles using fin-enhanced PCMs/water hybrid cooling system. Appl. Therm. Eng. 2023, 233, 121214. [Google Scholar] [CrossRef]
- Yu, H.; Zhu, X.; Ma, X.; Yan, H. Cooling performance analysis and sensitivity analysis of thermoelectric cooling for an 18650 battery pack thermal management. Case Stud. Therm. Eng. 2025, 72, 106394. [Google Scholar] [CrossRef]
- Lyu, Y.; Siddique, A.R.M.; Majid, S.H.; Biglarbegian, M.; Gadsden, S.A.; Mahmud, S. Electric vehicle battery thermal management system with thermoelectric cooling. Energy Rep. 2019, 5, 822–827. [Google Scholar] [CrossRef]
- Park, S.J.; Park, J.; Bang, K.M.; Lee, J.M.; Park, W.; Ziolkowski, P.; Jin, H. Thermoelectric hotspot cooling using thermally conductive fillers. Appl. Therm. Eng. 2023, 232, 120994. [Google Scholar] [CrossRef]
- Jiang, L.; Zhang, H.; Li, J.; Xia, P. Thermal performance of a cylindrical battery module impregnated with PCM composite based on thermoelectric cooling. Energy 2019, 188, 116048. [Google Scholar] [CrossRef]
- Zhang, C.-W.; Chen, S.-R.; Gao, H.-B.; Xu, K.-J.; Xia, Z.; Li, S.-T. Study of Thermal Management System Using Composite Phase Change Materials and Thermoelectric Cooling Sheet for Power Battery Pack. Energies 2019, 12, 1937. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, C.-F.; Zhou, J.-G.; Xiong, X.; Zhang, C.-C.; Wang, Y.-P. Numerical simulation of hybrid battery thermal management system combining of thermoelectric cooler and phase change material. Energy Rep. 2022, 8, 1094–1102. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, C.-F.; Zhou, J.-G.; Xiong, X.; Wang, Y.-P. Thermal performance of battery thermal management system using fins to enhance the combination of thermoelectric Cooler and phase change Material. Appl. Energy 2022, 322, 119503. [Google Scholar] [CrossRef]
- Luo, D.; Zhao, Y.; Cao, J.; Chen, W.-H.; Zhao, Y.; Cao, B. Performance analysis of a novel thermoelectric-based battery thermal management system. Renew. Energy 2024, 224, 120193. [Google Scholar] [CrossRef]
- Pan, Y.; Tang, A.; Liu, Z.; Shan, C. Experimental analysis of power battery preheating system based on thermoelectric elements. Appl. Therm. Eng. 2023, 230, 120860. [Google Scholar] [CrossRef]
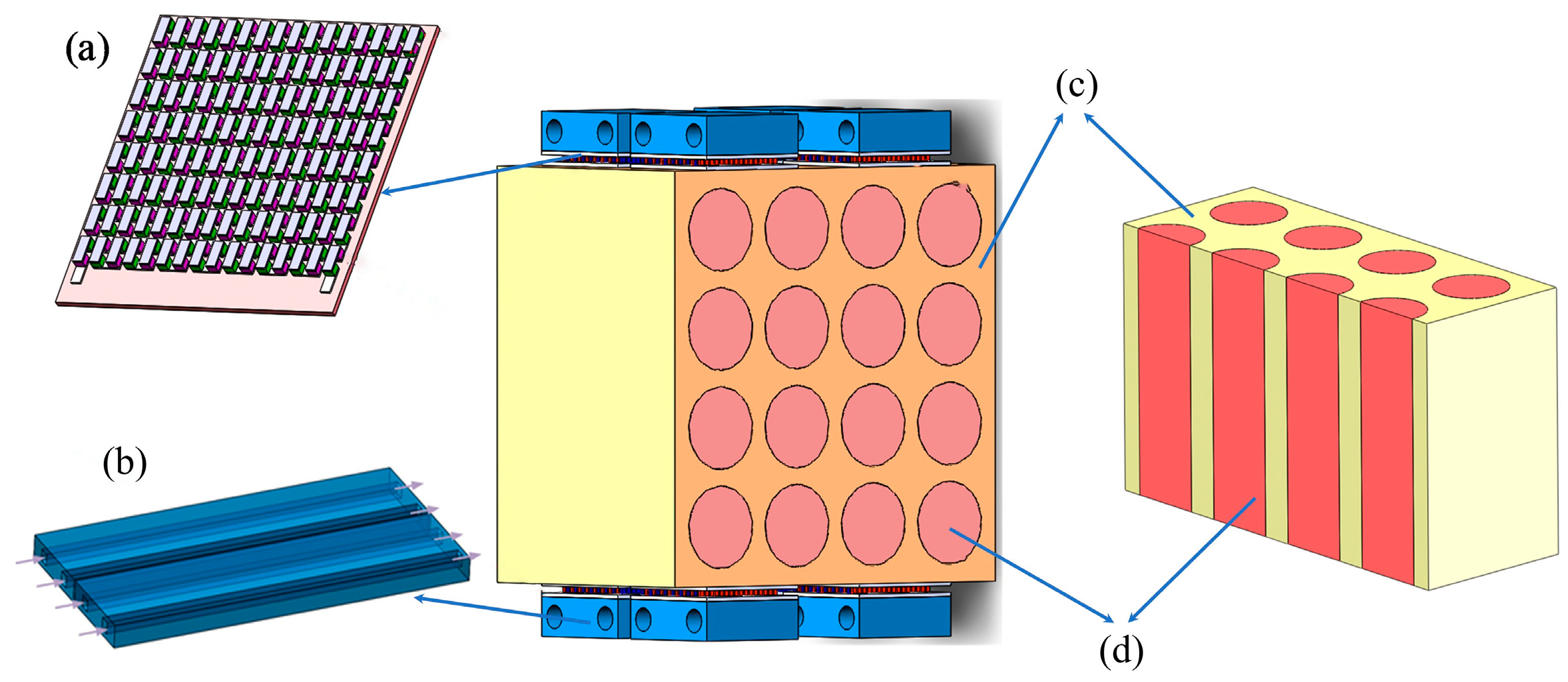


| Parameters | Thermal Conductivity λ (W/m∙k) | Seebeck Coefficient α (μV/K) | Electrical Conductivity σ−1 (10−5 Ω∙m) |
|---|---|---|---|
| Ceramic plates | 20 | NA | NA |
| Copper electrode plates | 397 | NA | 0.00175 |
| P-type semiconductor | |||
| N-type semiconductor |
| Parameters | Value |
|---|---|
| Size (mm) | 18 × 65 |
| Average density (kg·m−3) | 2631.4 |
| Mass (g) | 64 |
| Rated voltage (V) | 3.7 |
| Rated capacity (mAh) | 4000 |
| Discharge cutoff voltage (V) | 2.75 |
| Max. discharge current (A) | 12 |
| Optimum operating temperature during discharge (K) | 293.15–318.15 |
| Anode material | Graphite |
| Cathode material | Lix(Ni0.33Mn0.33Co0.33)O2 |
| Parameters | Value | Unit |
|---|---|---|
| Ambient temperature | 300 | K |
| Environmental heat transfer coefficient | 15 | |
| Specific heat capacity of water | 4.177 | |
| Kinetic energy of turbulent flow | 8.623 | |
| Thermal conductivity of water | 0.612 | |
| Thermal conductivity of aluminum | 217.7 | |
| Air thermal conductivity | ||
| Specific heat of air | ||
| Air turbulence kinetic energy | ||
| Air thermal conductivity |
| Number of Grids | Maximum Temperature (K) | Maximum Temperature Difference (K) |
|---|---|---|
| 420,000 | 315.8 | 3.1 |
| 470,000 | 318.1 | 3.4 |
| 520,000 | 319.2 | 3.5 |
| 570,000 | 319.2 | 3.5 |
| Number of Thermoelectric Components (n) | Maximum Temperature Boosting Capability (%) | Maximum Temperature Lift Capacity (%) |
|---|---|---|
| 0 | - | - |
| 1 | 8.93 | 14.48 |
| 2 | 3.45 | 38.06 |
| 3 | 9.23 | 14.63 |
| 4 | 10.34 | 66.37 |
| 5 | 10.64 | 39.30 |
| 6 | 9.58 | 33.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, S.; Qin, H. Optimization of Thermoelectric Module Configuration and Cooling Performance in Thermoelectric-Based Battery Thermal Management System. World Electr. Veh. J. 2025, 16, 344. https://doi.org/10.3390/wevj16070344
Fu S, Qin H. Optimization of Thermoelectric Module Configuration and Cooling Performance in Thermoelectric-Based Battery Thermal Management System. World Electric Vehicle Journal. 2025; 16(7):344. https://doi.org/10.3390/wevj16070344
Chicago/Turabian StyleFu, Songqiao, and Hongmao Qin. 2025. "Optimization of Thermoelectric Module Configuration and Cooling Performance in Thermoelectric-Based Battery Thermal Management System" World Electric Vehicle Journal 16, no. 7: 344. https://doi.org/10.3390/wevj16070344
APA StyleFu, S., & Qin, H. (2025). Optimization of Thermoelectric Module Configuration and Cooling Performance in Thermoelectric-Based Battery Thermal Management System. World Electric Vehicle Journal, 16(7), 344. https://doi.org/10.3390/wevj16070344






