Design of an Unequal-Teeth Stator Structure for a Low-Vibration Noise Permanent Magnet Synchronous Machine Considering Teeth Modulation
Abstract
1. Introduction
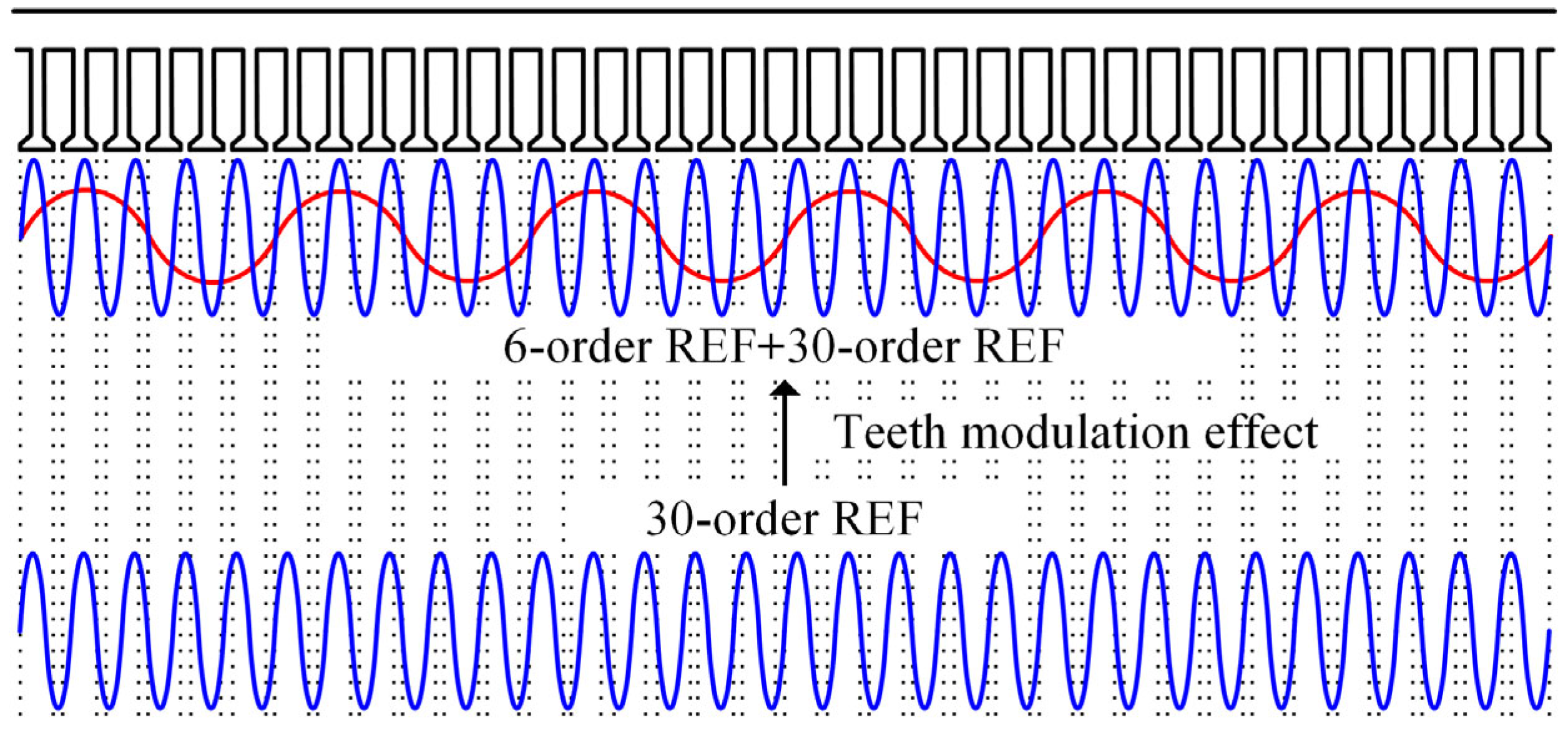
2. Radial Electromagnetic Forces and Teeth Modulation Effect
3. Novel Unequal-Teeth Stator Structure Design Method for Electromagnetic Vibration and Noise Suppression
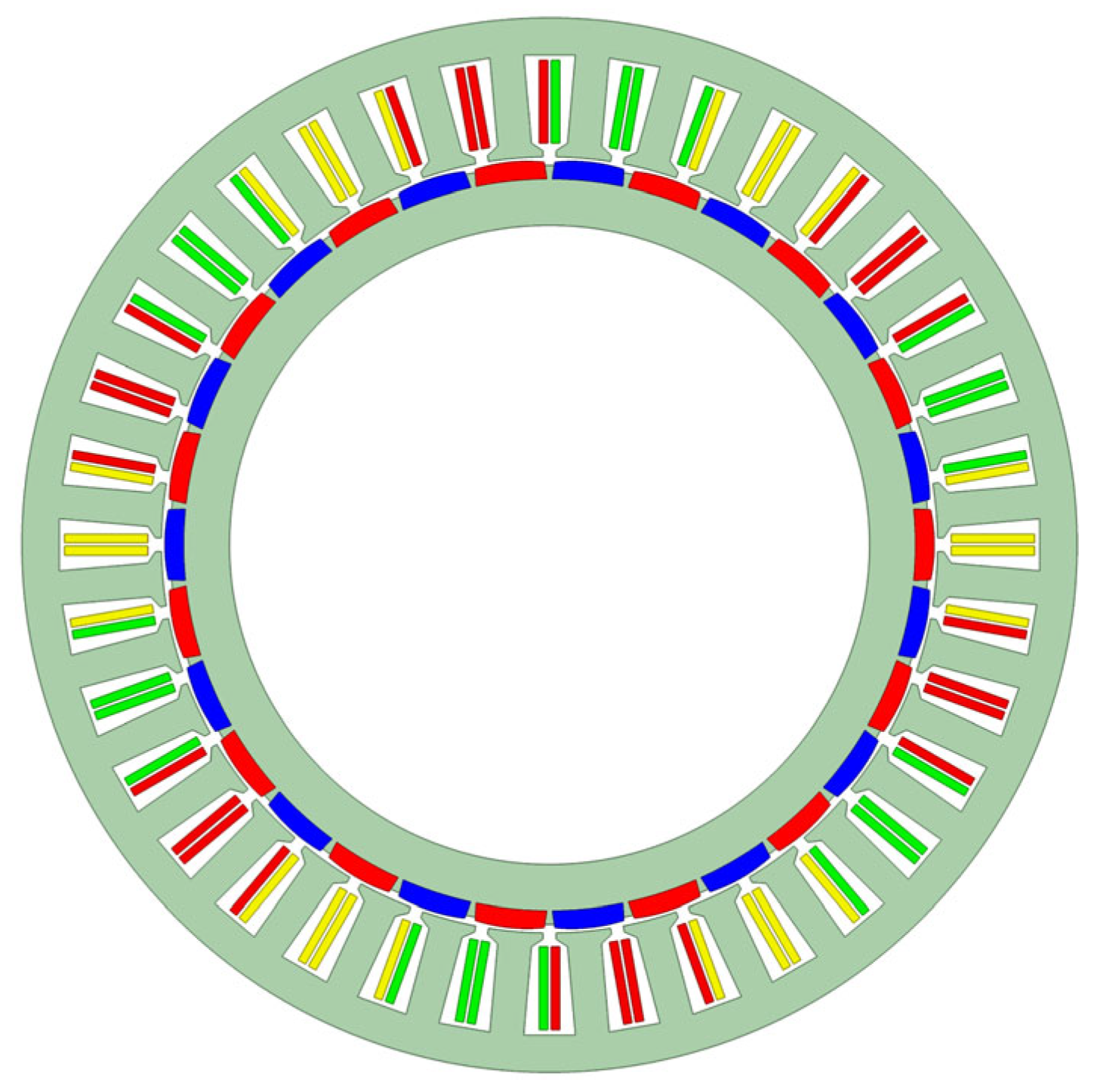
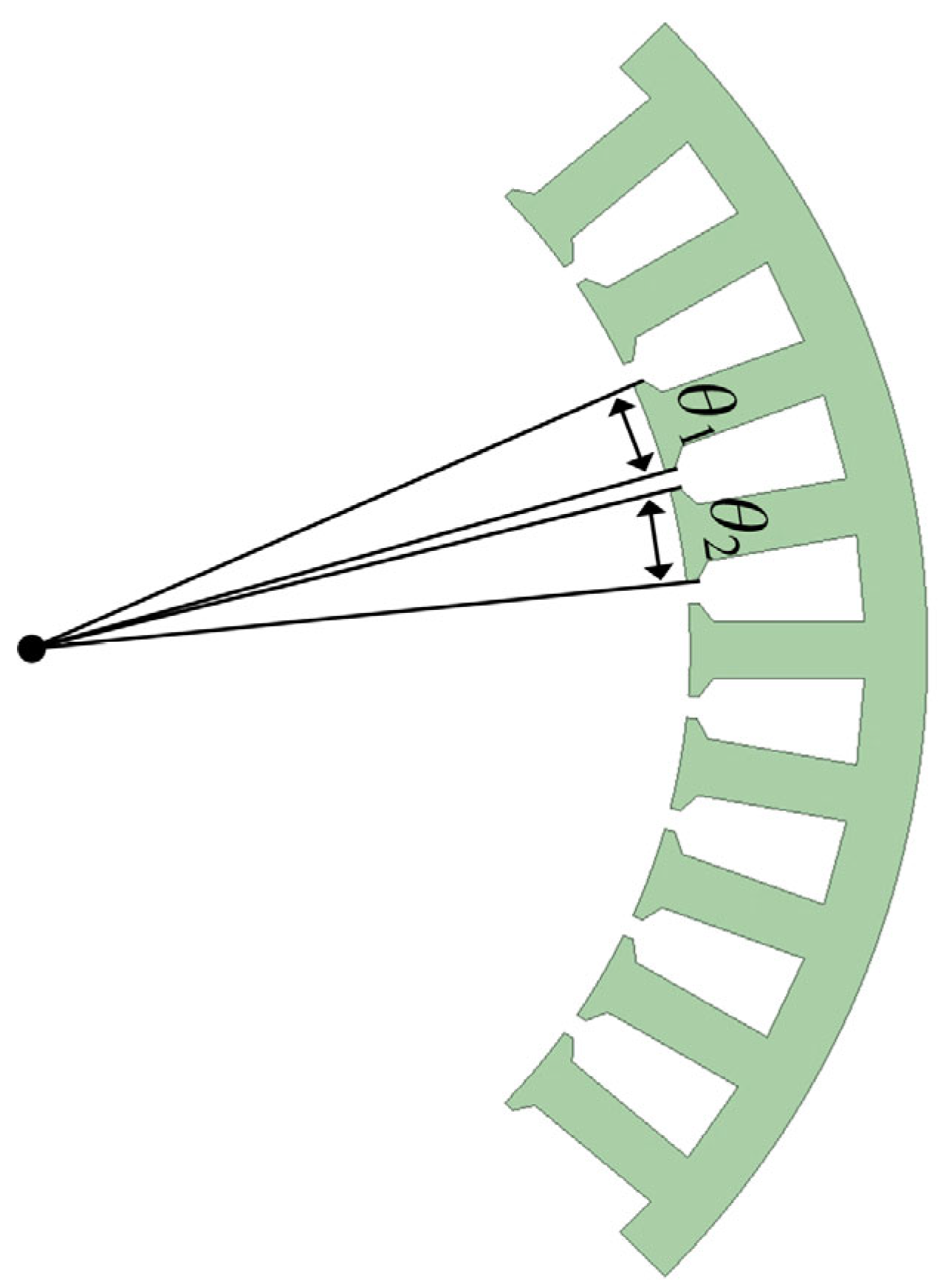
3.1. Design of Unequal-Teeth Stator Structure in FSCW-PMSMs
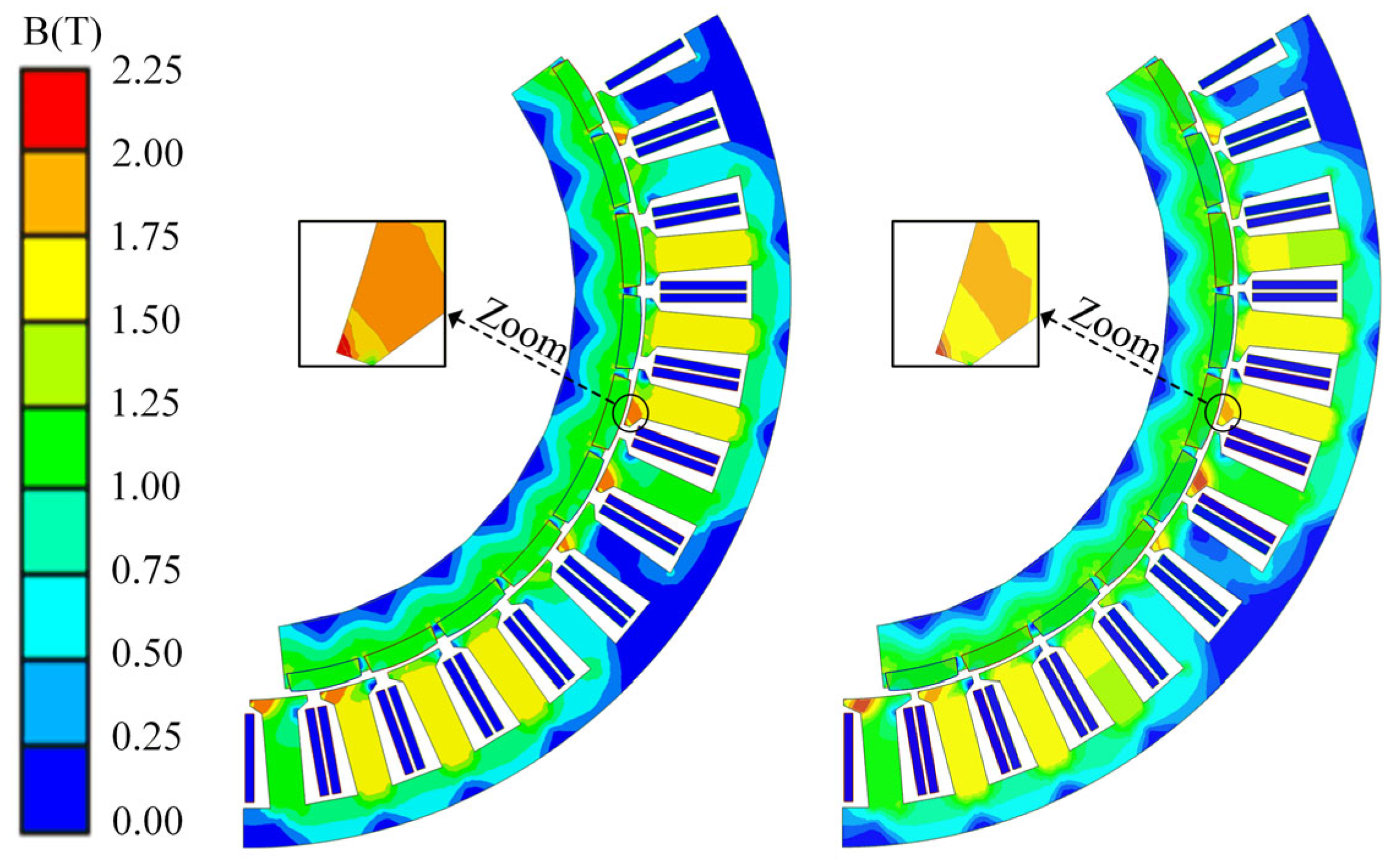
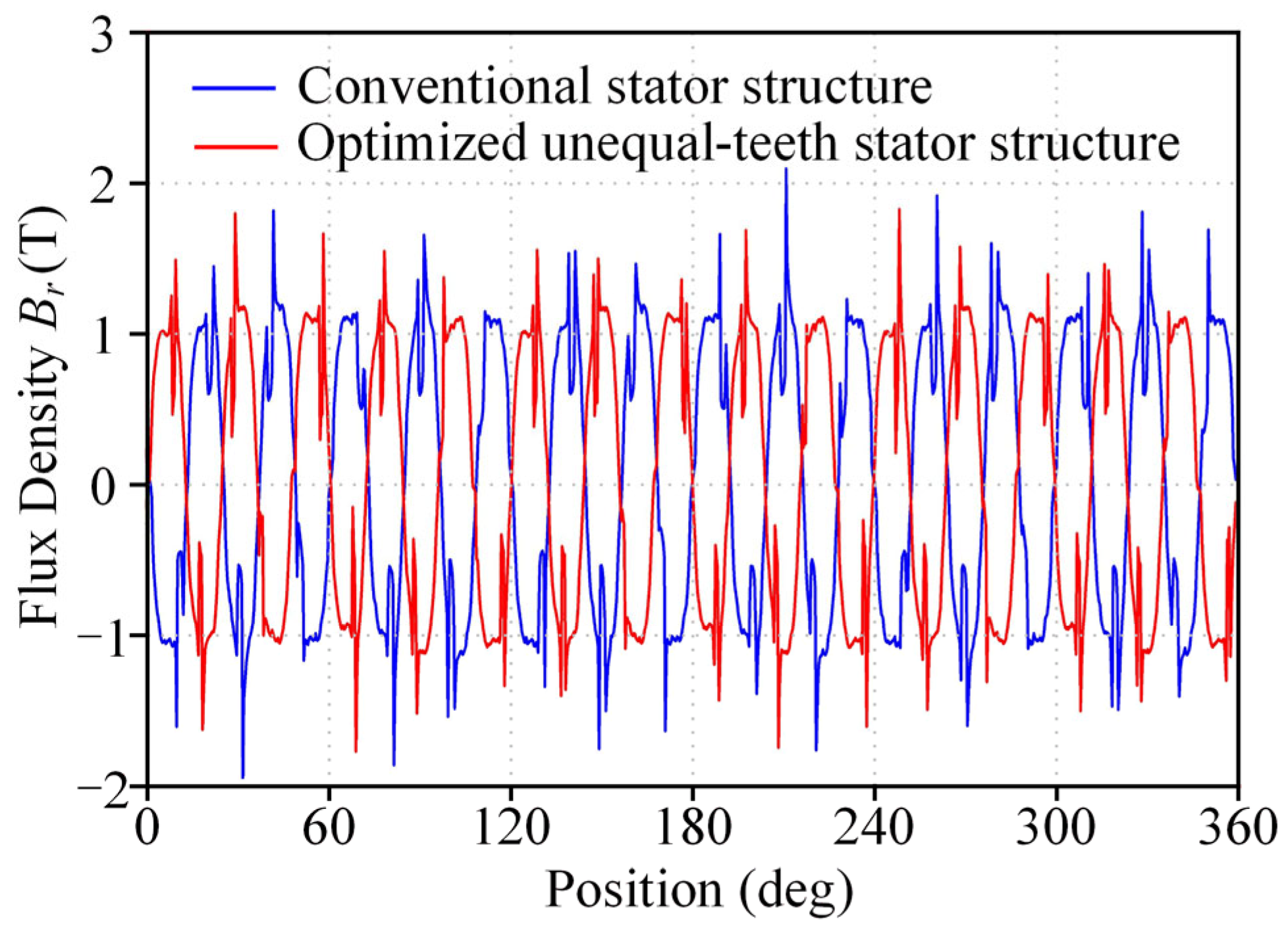
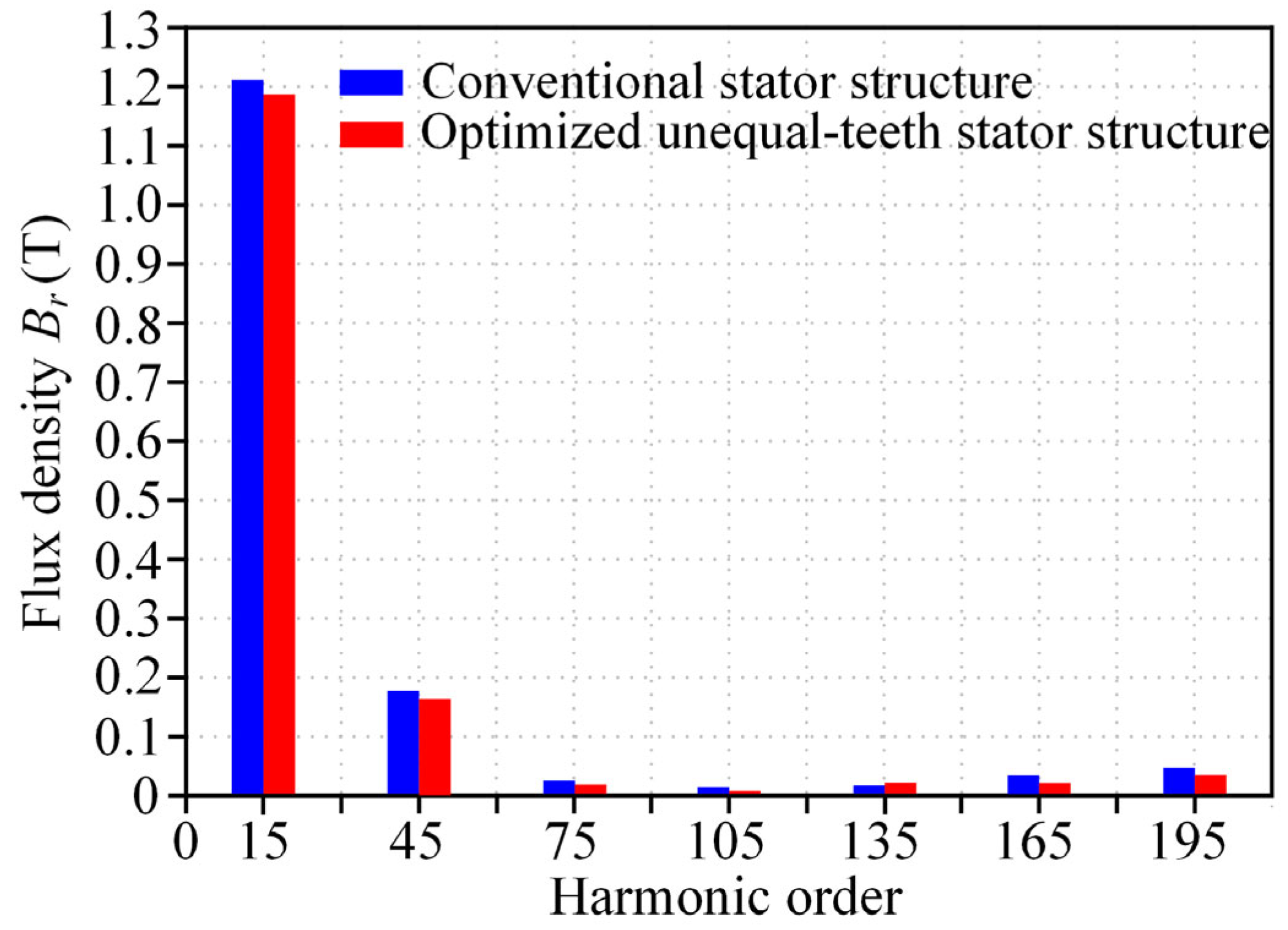
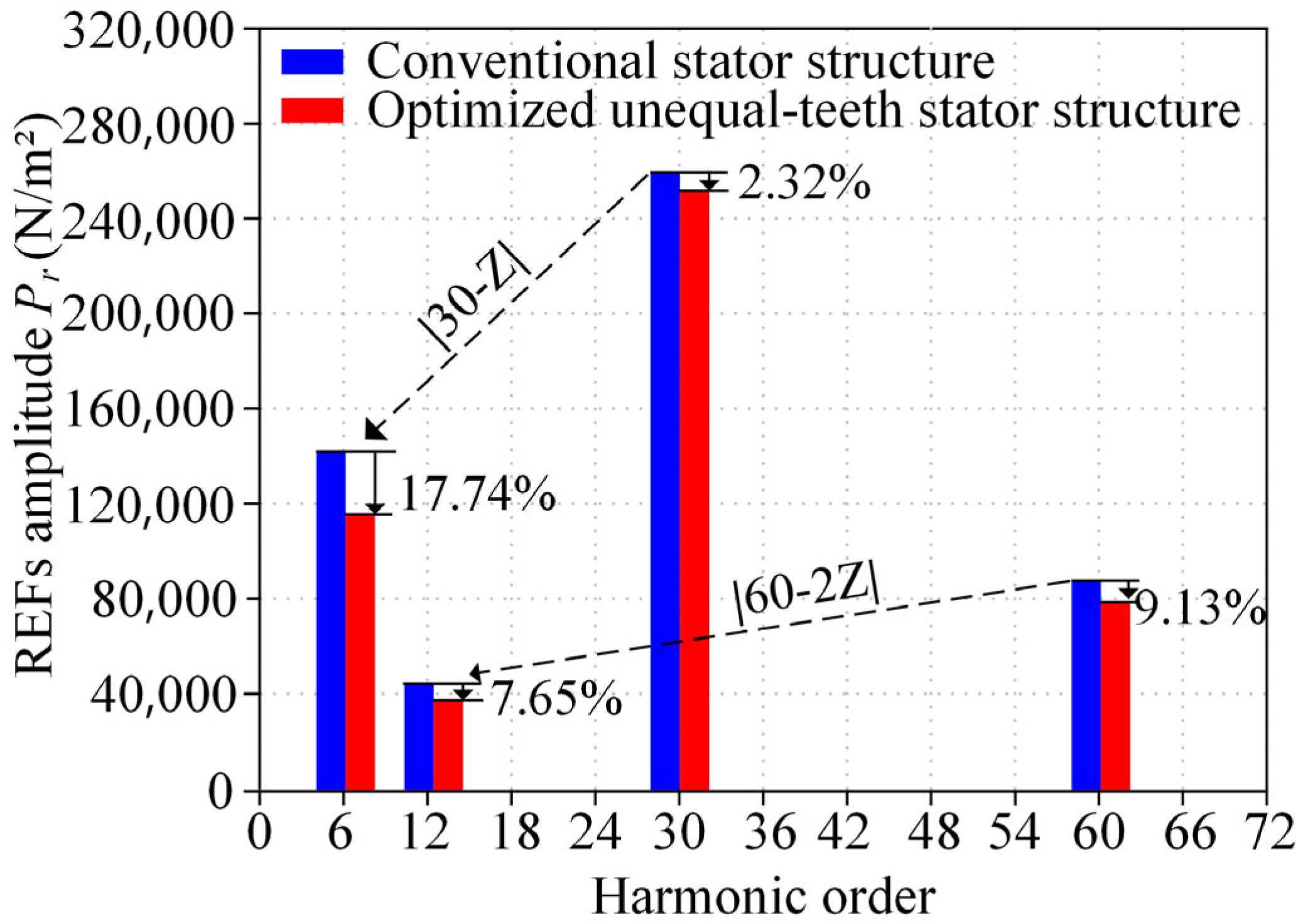
3.2. Electromagnetic Performance Analysis of an FSCW-PMSM with the Optimized Unequal-Teeth Stator Structure Under Rated Operating Conditions
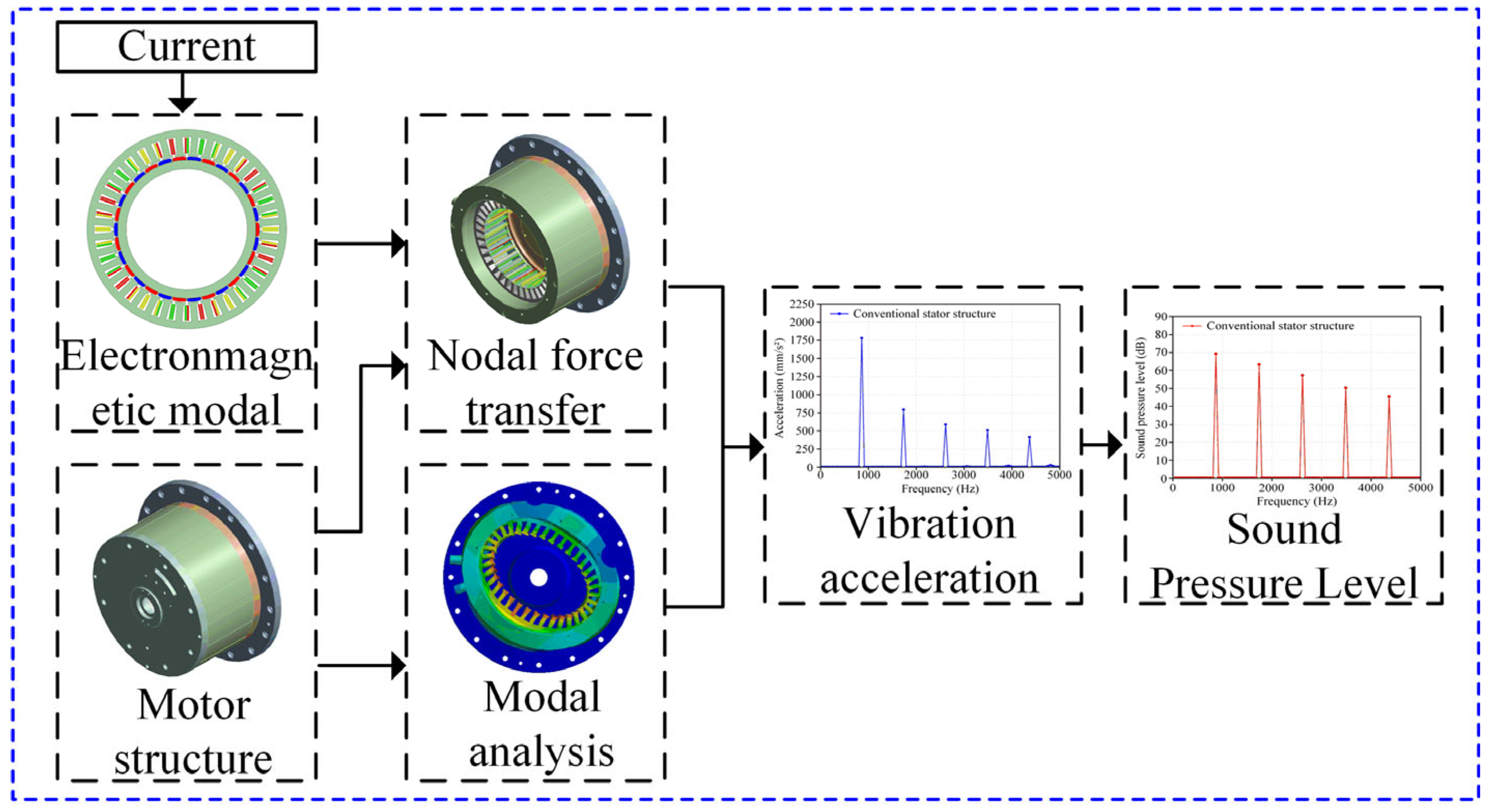
4. Modal and Vibration Noise Analysis of the Machine with Optimized Unequal-Teeth Stator Structure
4.1. Boundary Conditions Setup for Finite Element Simulation
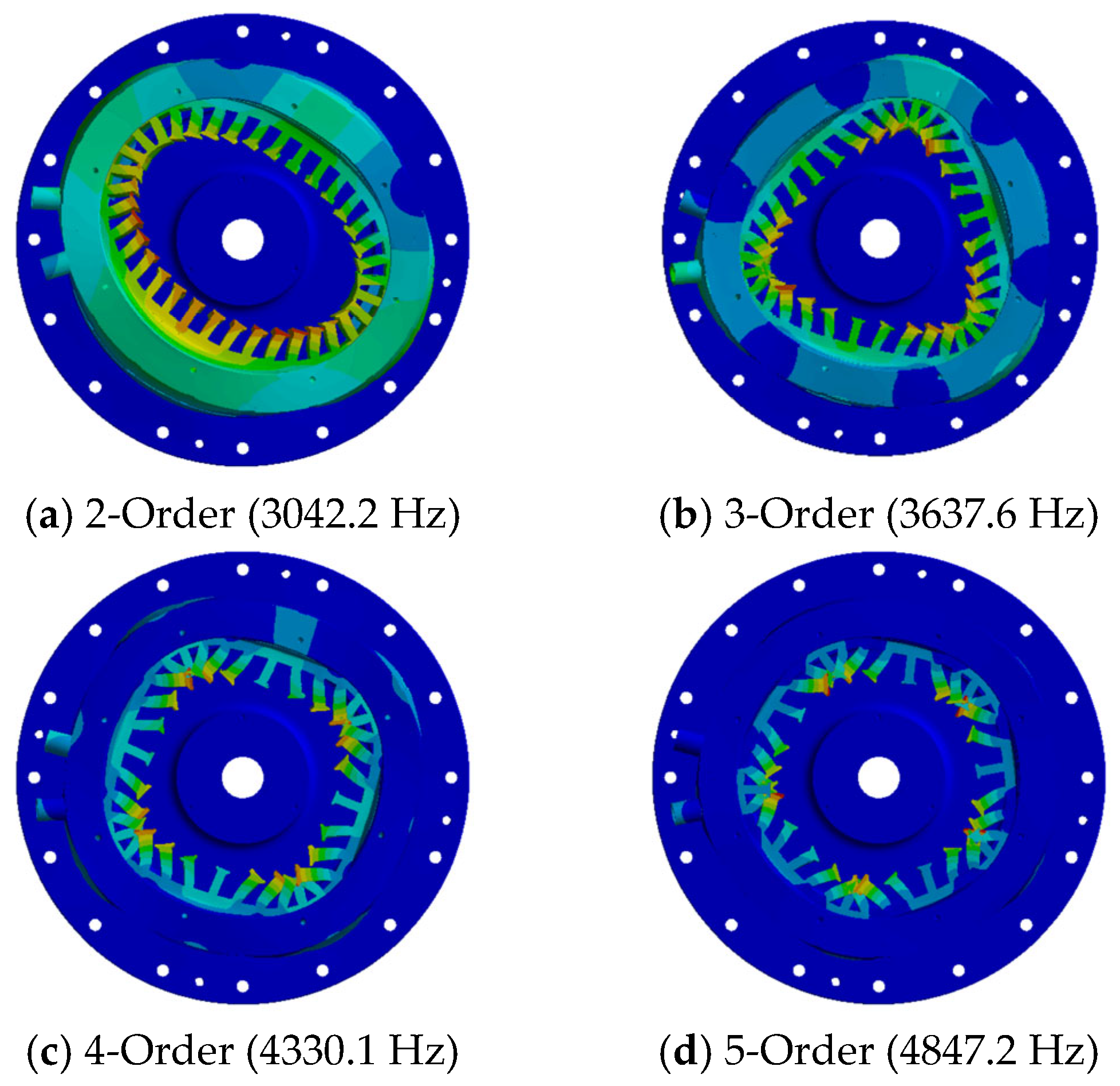
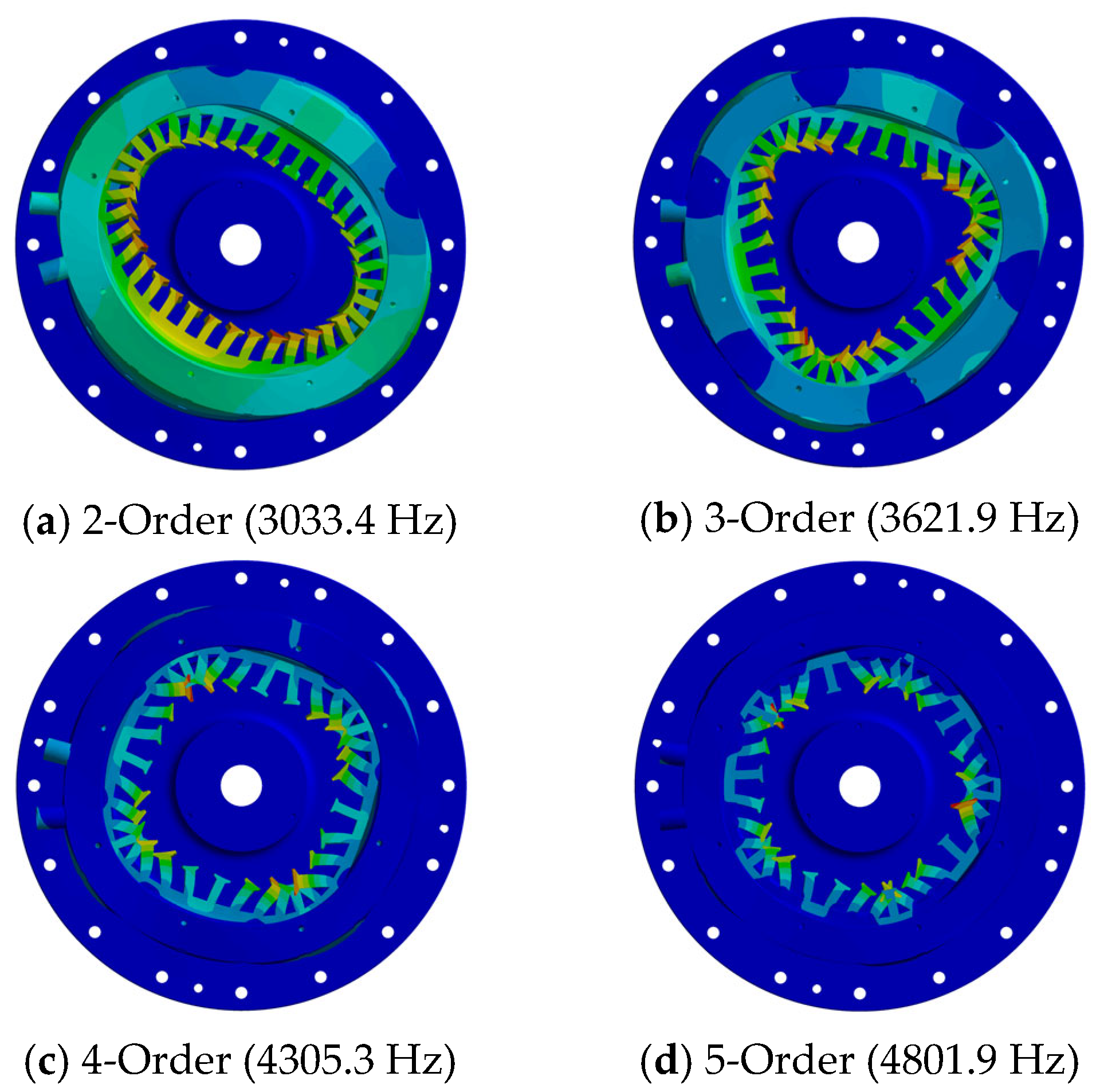
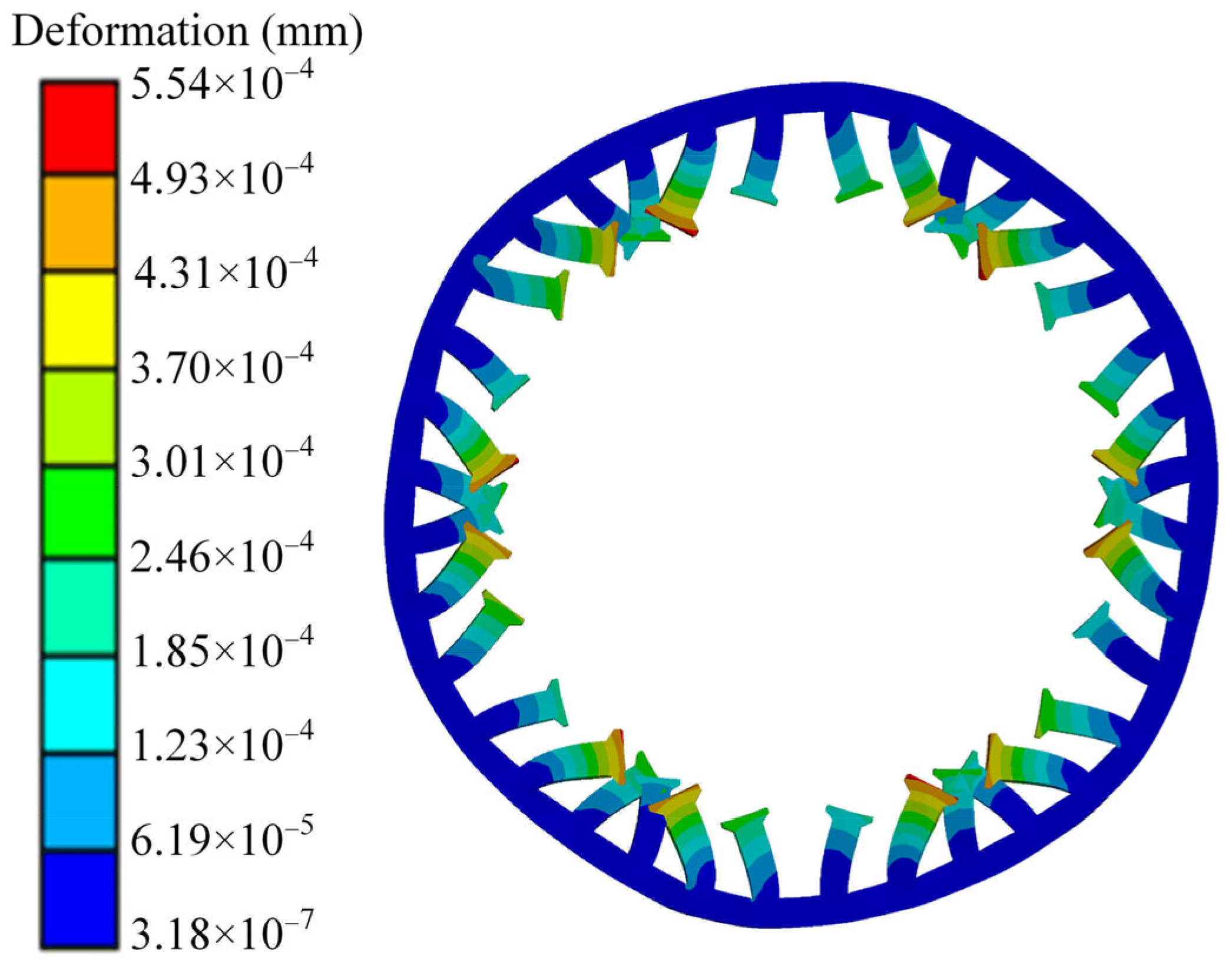
4.2. Modal Analysis of the Optimized Unequal-Teeth Stator Structure
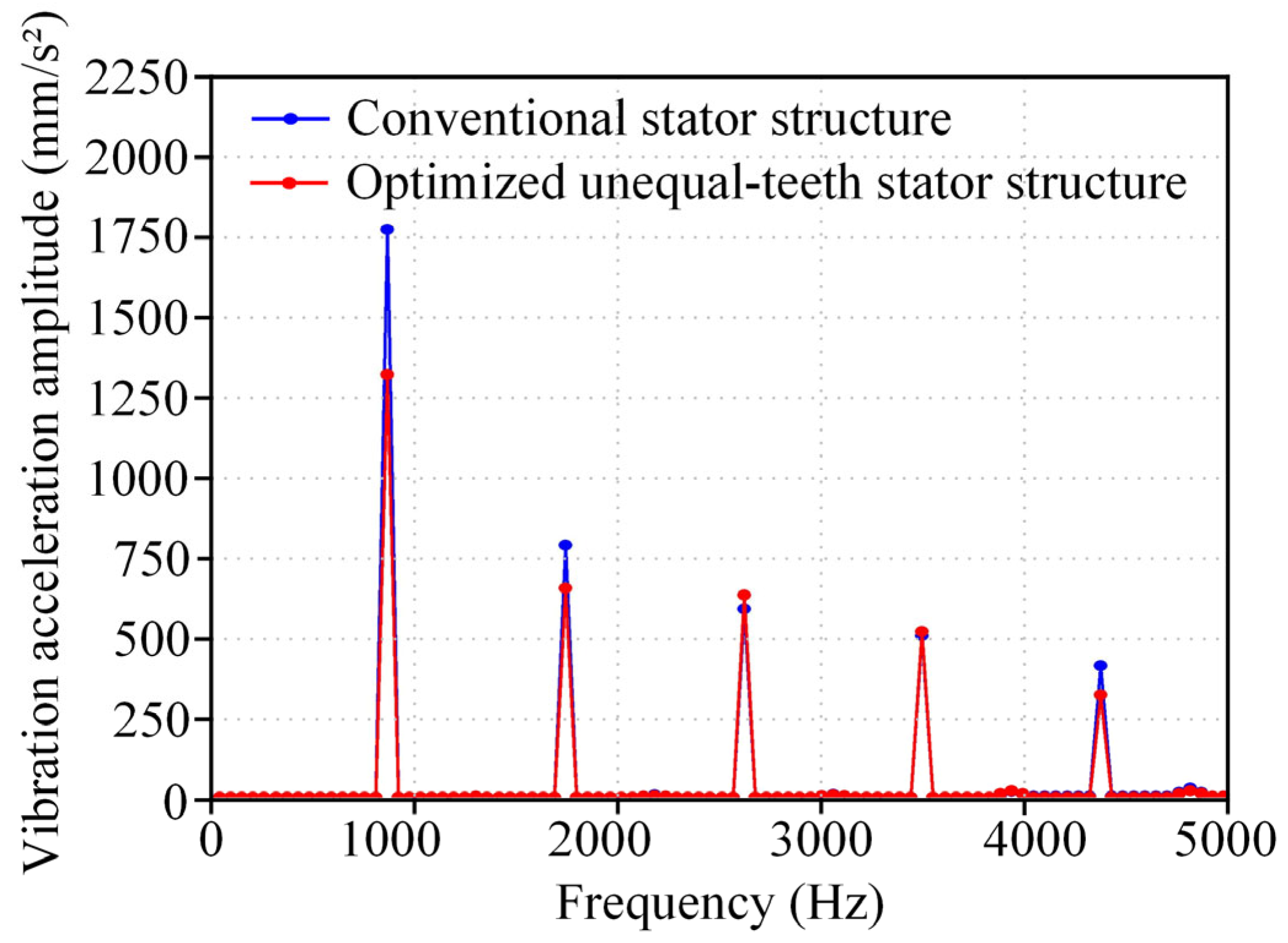
4.3. Vibration and Noise Analysis of the Optimized Unequal-Teeth Stator Structure
5. Conclusions
- This paper proposes a novel low-vibration noise stator structure design methodology. To address variations in machine dimensions, a relative ratio parameter K for the unequal-teeth stator structure is introduced. Finite element simulations are employed to investigate how different stator tooth ratios affect the amplitude of modulated low-order radial electromagnetic forces. By selecting an appropriate unequal-teeth stator ratio, the vibration and noise of the machine can be effectively reduced, demonstrating the potential for broader application in other fractional-slot permanent magnet synchronous machines.
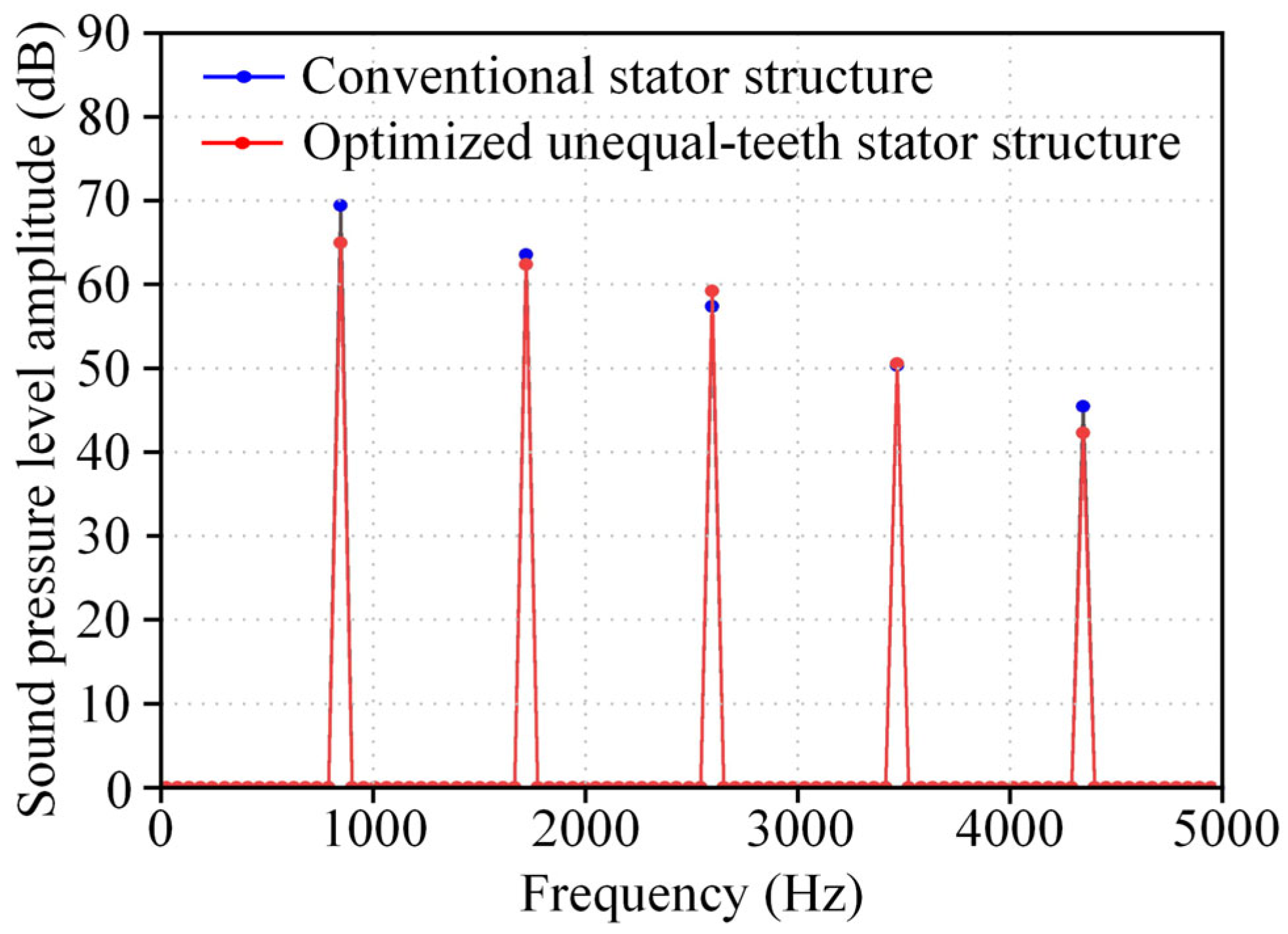
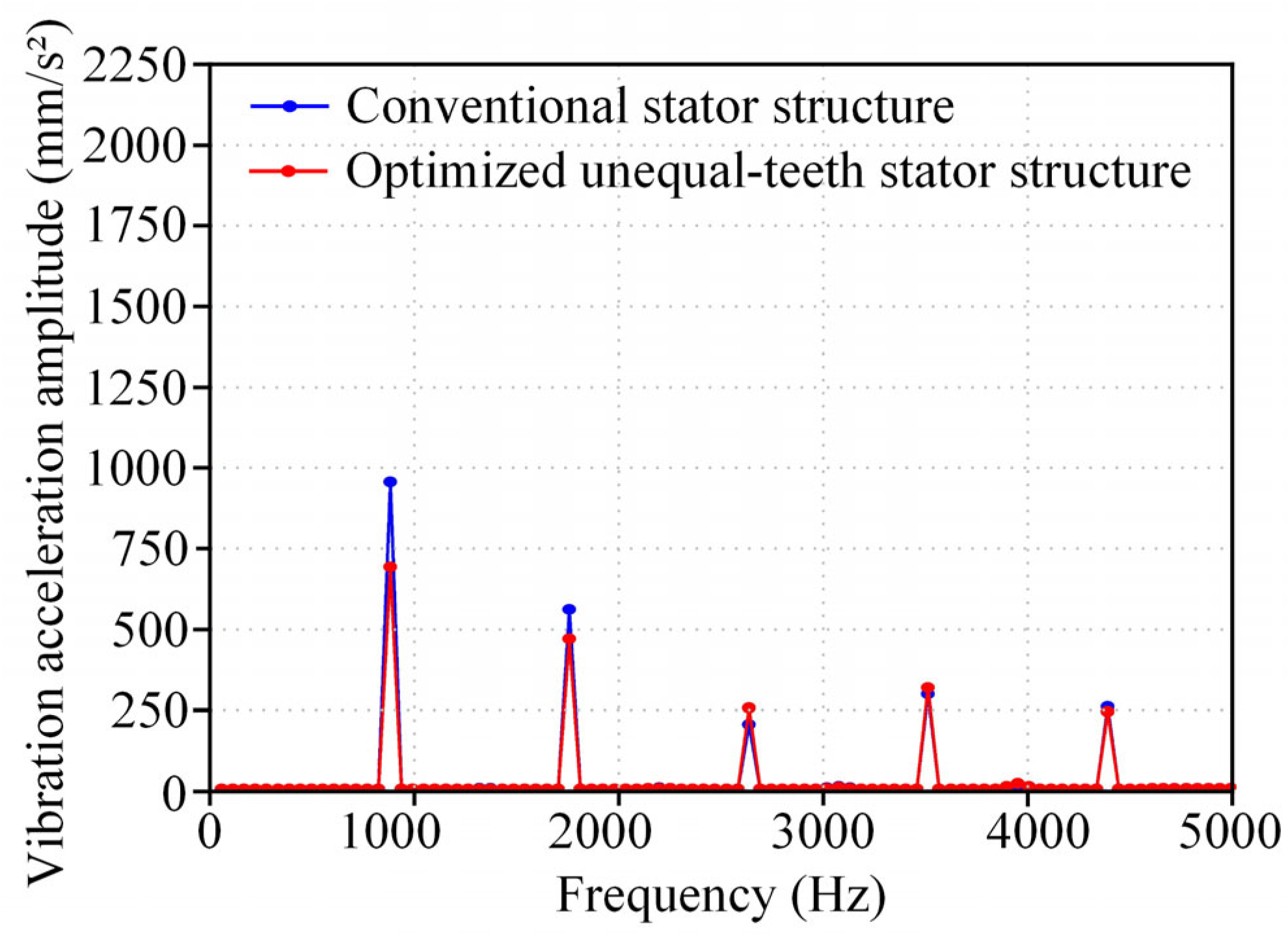
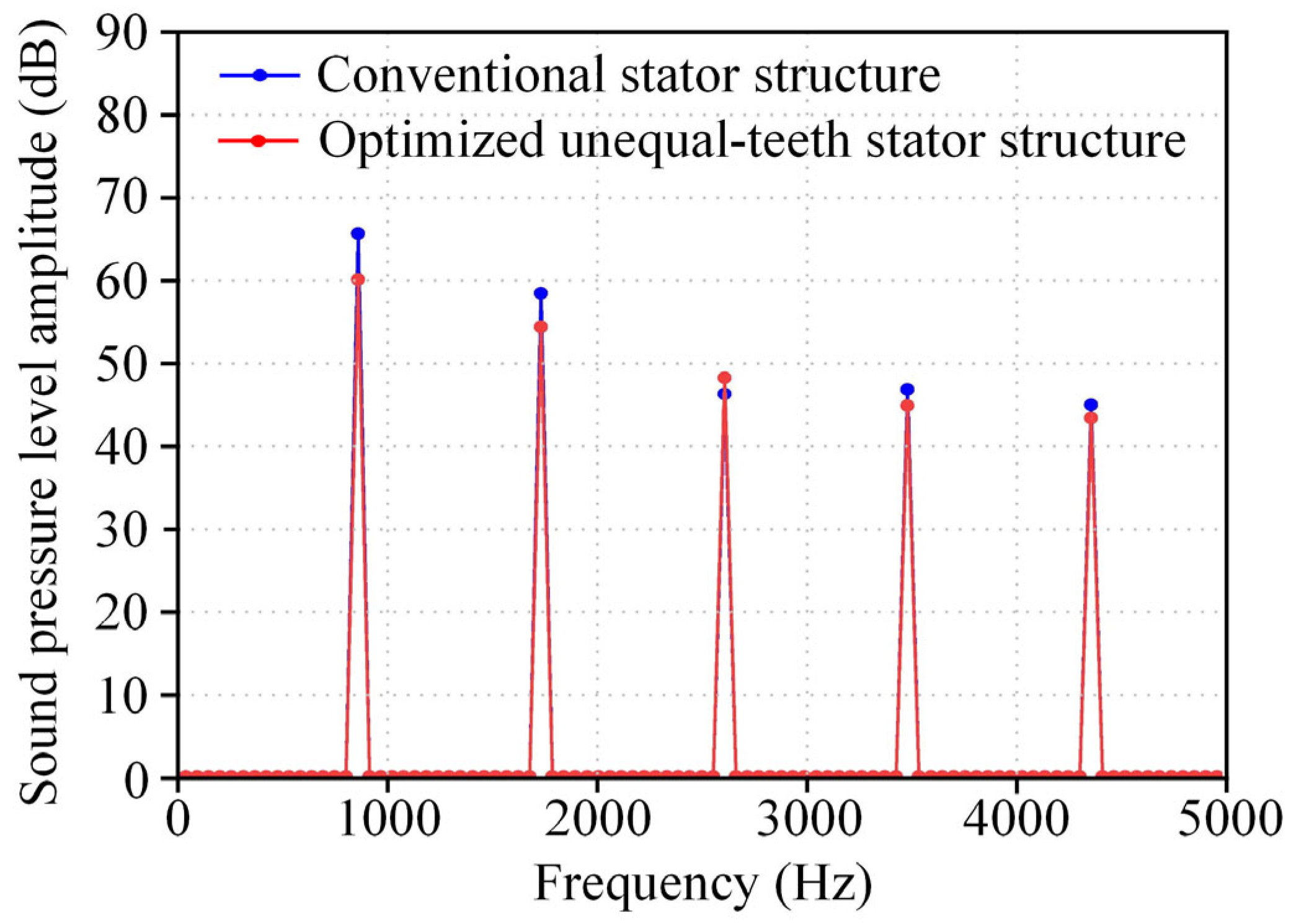
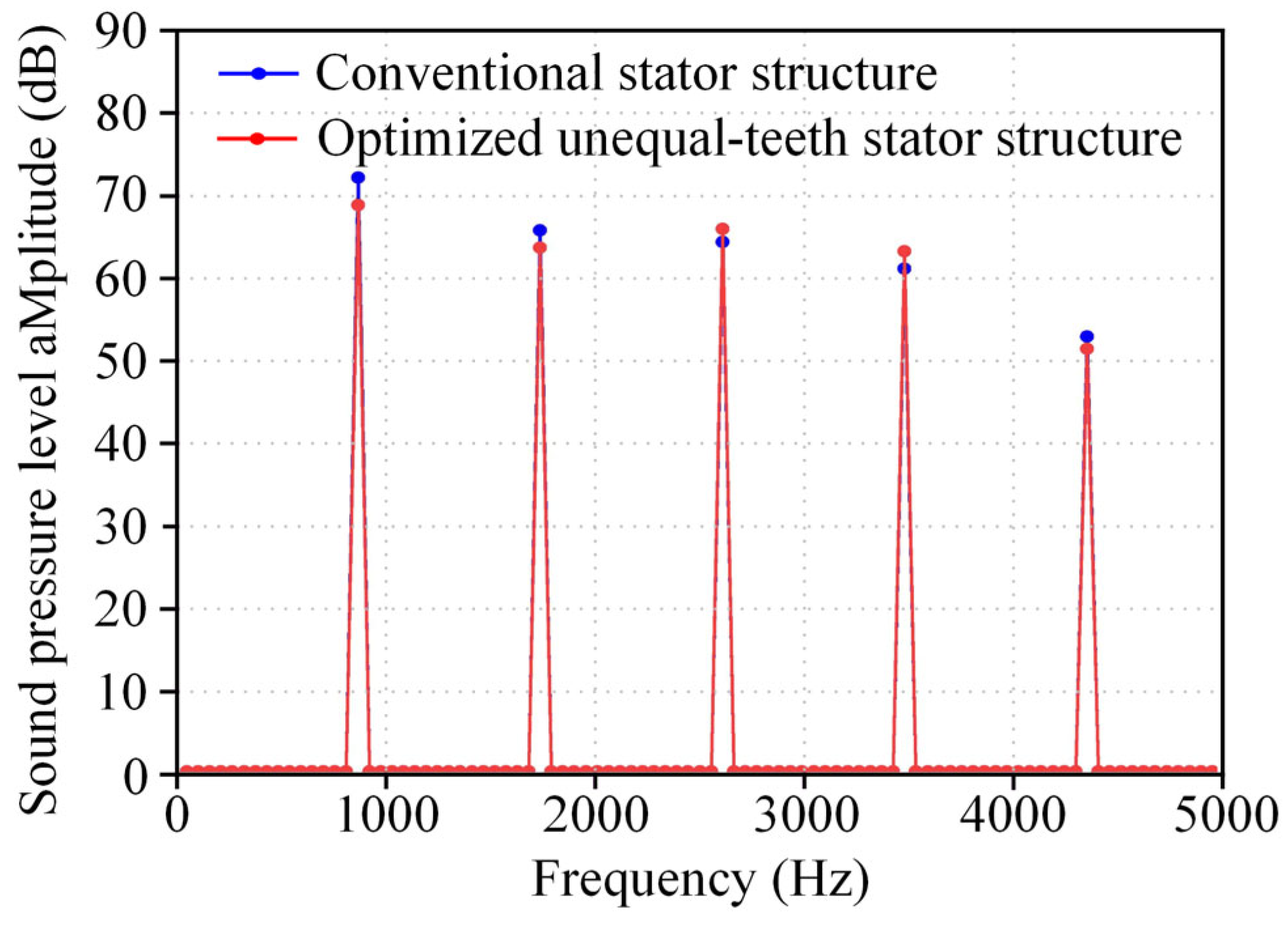
- The proposed method is evaluated under rated, no-load, and peak torque operating conditions. The optimized unequal-teeth stator structure shows a significant reduction in vibration and noise performance. Compared to the conventional stator structure, the optimized unequal-teeth stator structure reduces vibration acceleration by 25.53% and sound pressure level by 6.44% under rated conditions; by 27.88% and 8.50%, respectively, under no-load conditions; and by 21.77% and 4.74%, respectively, under peak torque conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zakri, K.W.; Sarwono, R.S.J.; Santosa, S.P.; Soelami, F.X.N. Modeling and Validation of Acoustic Comfort for Electric Vehicle Using Hybrid Approach Based on Soundscape and Psychoacoustic Methods. World Electr. Veh. J. 2025, 16, 64. [Google Scholar] [CrossRef]
- Dong, J.; Yin, H.; Li, G.; Wang, X.; Luo, M. The Multiphysics Analysis and Suppression Method for the Electromagnetic Noise of Permanent-Magnet Motors Used in Electric Vehicle. World Electr. Veh. J. 2025, 16, 136. [Google Scholar] [CrossRef]
- Wang, J.; Patel, V.I.; Wang, W. Fractional-Slot Permanent Magnet Brushless Machines with Low Space Harmonic Contents. IEEE Trans. Magn. 2013, 50, 1–9. [Google Scholar] [CrossRef]
- Fang, Y.; Zhang, T. Vibroacoustic Characterization of a Permanent Magnet Synchronous Motor Powertrain for Electric Vehicles. IEEE Trans. Energy Convers. 2017, 33, 272–280. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Howe, D.; Bolte, E.; Ackermann, B. Instantaneous magnetic field distribution in brushless permanent magnet DC motors. I. Open-circuit field. IEEE Trans. Magn. 1993, 29, 124–135. [Google Scholar] [CrossRef]
- Zhu, Z.; Howe, D. Instantaneous magnetic field distribution in brushless permanent magnet DC motors. II. Armature-reaction field. IEEE Trans. Magn. 1993, 29, 136–142. [Google Scholar] [CrossRef]
- Zhu, Z.; Howe, D. Instantaneous magnetic field distribution in brushless permanent magnet DC motors. III. Effect of stator slotting. IEEE Trans. Magn. 1993, 29, 143–151. [Google Scholar] [CrossRef]
- Zhu, Z.; Howe, D. Instantaneous magnetic field distribution in permanent magnet brushless DC motors. IV. Magnetic field on load. IEEE Trans. Magn. 1993, 29, 152–158. [Google Scholar] [CrossRef]
- Yang, H.; Chen, Y. Influence of Radial Force Harmonics With Low Mode Number on Electromagnetic Vibration of PMSM. IEEE Trans. Energy Convers. 2013, 29, 38–45. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Xia, Z.P.; Wu, L.J.; Jewell, G.W. Analytical Modeling and Finite-Element Computation of Radial Vibration Force in Fractional-Slot Permanent-Magnet Brushless Machines. IEEE Trans. Ind. Appl. 2010, 46, 1908–1918. [Google Scholar] [CrossRef]
- Dajaku, G.; Xie, W.; Gerling, D. Reduction of Low Space Harmonics for the Fractional Slot Concentrated Windings Using a Novel Stator Design. IEEE Trans. Magn. 2013, 50, 1–12. [Google Scholar] [CrossRef]
- Zhu, X.; Lee, C.H.T.; Chan, C.C.; Xu, L.; Zhao, W. Overview of Flux-Modulation Machines Based on Flux-Modulation Principle: Topology, Theory, and Development Prospects. IEEE Trans. Transp. Electrif. 2020, 6, 612–624. [Google Scholar] [CrossRef]
- Bertoncello, T.; Franceschini, G.; Raghuraman, B.; Diana, M.; Lidbeck, A. Unsymmetrical Pole Design vs Skewing for improving NVH Characteristics and Performance of High Speed PMSM Electric Machines. In Proceedings of the IECON 2022—48th Annual Conference of the IEEE Industrial Electronics Society, Brussels, Belgium, 17–20 October 2022; pp. 1–6. [Google Scholar]
- Ciceo, S.; Raia, R.; Paduraru, F.; Sugiura, K. Fast and Accurate Radial-Flux PMSM Step-Skewing Computation Methodology for NVH Improvements Across the Machine Full Operation Range. In Proceedings of the 2024 27th International Conference on Electrical Machines and Systems (ICEMS), Fukuoka, Japan, 26–29 November 2024; pp. 1–6. [Google Scholar]
- Soresini, F.; Barri, D.; Ballo, F.; Gobbi, M. Numerical modeling of PMSM noise reduction by harmonic current injection. IEEE Access 2025, 13, 60245–60257. [Google Scholar] [CrossRef]
- Ren, M.; Xie, X.; Huang, Z.; Zhang, Z. Novel rubber-electromagnetic composite active/passive vibration isolator. J. Vib. Shock 2021, 40, 32–37. [Google Scholar]
- Wang, R.; Jiang, Y.; Ding, R.; Liu, W.; Meng, X.; Sun, Z. Design and experimental verification of self-powered electromagnetic vibration suppression and absorption system for in-wheel motor electric vehicles. J. Vib. Control 2021, 28, 2544–2555. [Google Scholar] [CrossRef]
- Li, Y.; Su, Z. Active vibration reduction technology of marine motor based on sliding-electromagnetic composite bearing. Ship Sci. Technol. 2023, 45, 114–119. [Google Scholar] [CrossRef]
- Hong, J.; Wang, S.; Sun, Y.; Sun, X.; Cao, H. The Influence of High-Order Force on Electromagnetic Vibration of Permanent Magnet Synchronous Motors. Trans. China Electrotech. Soc. 2022, 37, 2446–2458. [Google Scholar]
- Fang, H.; Li, D.; Qu, R.; Yan, P. Modulation Effect of Slotted Structure on Vibration Response in Electrical Machines. IEEE Trans. Ind. Electron. 2018, 66, 2998–3007. [Google Scholar] [CrossRef]
- Liang, W.; Wang, J.; Luk, P.C.-K.; Fei, W. Analytical Study of Stator Tooth Modulation on Electromagnetic Radial Force in Permanent Magnet Synchronous Machines. IEEE Trans. Ind. Electron. 2020, 68, 11731–11739. [Google Scholar] [CrossRef]
- Pile, R.; Le Menach, Y.; Le Besnerais, J.; Parent, G. Study of the Combined Effects of the Air-Gap Transfer for Maxwell Tensor and the Tooth Mechanical Modulation in Electrical Machines. IEEE Trans. Magn. 2019, 56, 1–4. [Google Scholar] [CrossRef]
- Wang, S.; Hong, J.; Sun, Y.; Cao, H. Analysis of Zeroth-Mode Slot Frequency Vibration of Integer Slot Permanent-Magnet Synchronous Motors. IEEE Trans. Ind. Electron. 2019, 67, 2954–2964. [Google Scholar] [CrossRef]
- Wang, S.; Hong, J.; Sun, Y.; Cao, H. Mechanical and Magnetic Pivot Roles of Tooth in Vibration of Electrical Machines. IEEE Trans. Energy Convers. 2020, 36, 139–148. [Google Scholar] [CrossRef]
- Zhu, S.; Zhao, W.; Ji, J.; Liu, G.; Lee, C.H.T. Design to reduce electromagnetic vibration in integral-slot SPM machine considering force modulation effect. Sci. China Technol. Sci. 2022, 65, 1867–1877. [Google Scholar] [CrossRef]
- Zhu, S.; Zhao, W.; Ji, J.; Liu, G.; Mao, Y.; Liu, T. Investigation of Bread-Loaf Magnet on Vibration Performance in FSCW PMSM Considering Force Modulation Effect. IEEE Trans. Transp. Electrif. 2020, 7, 1379–1389. [Google Scholar] [CrossRef]
- Wang, K.; Guo, Y.; Sun, H.; Zhu, S.; Liu, C. Mitigation of Radial Force for Permanent Magnet Machines With Shifted Notch on Stator Teeth. IEEE Trans. Energy Convers. 2023, 39, 1121–1131. [Google Scholar] [CrossRef]
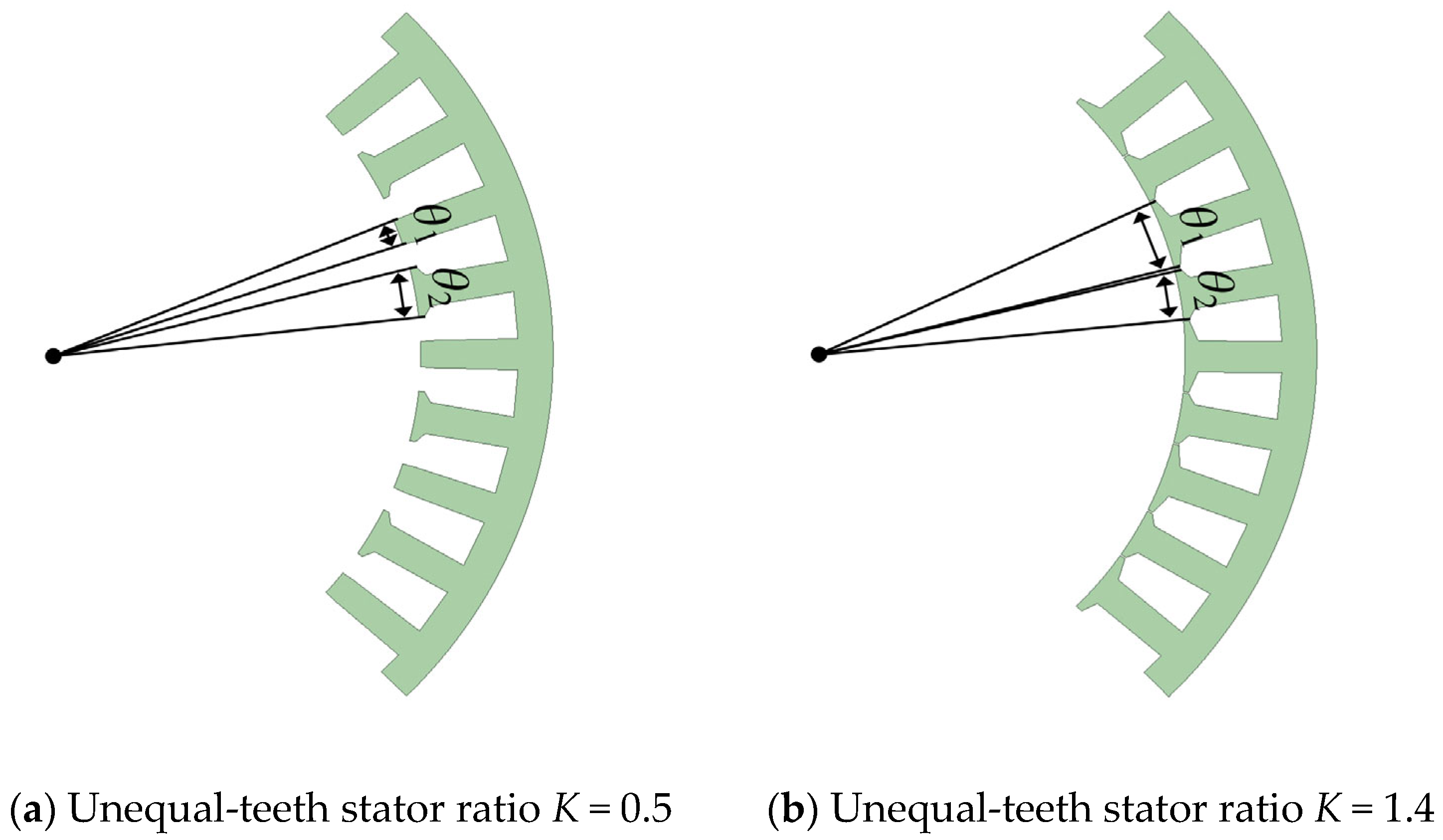





| Source | Spatial Order νr | Frequency fνr |
|---|---|---|
| The magnetic field of a permanent magnet | (μ1 ± μ2)p | (μ1 ± μ2)f |
| The permanent magnet interacts with the stator slots | (μ1 ± μ2)p ± kZ | (μ1 ± μ2)f |
| (μ1 ± μ2)p ± (k1 ± k2)Z | (μ1 ± μ2)f | |
| The permanent magnet interacts with the magnetic field of the armature | (μp ± να) | (μ ± Sν)f |
| The interaction between permanent magnets, armature fields, and stator slots | (μp ± να) ± kZ | (μ ± Sν)f |
| (μp ± να) ± (k1 ± k2)Z | (μ ± Sν)f | |
| The armature field | (ν1 ± ν2)α | (Sν1 ± Sν2)f |
| The armature field interacts with the stator slots | (ν1 ± ν2)α ± kZ | (Sν1 ± Sν2)f |
| (ν1 ± ν2)α ± (k1 ± k2)Z | (Sν1 ± Sν2)f |
| Parameter | Value |
|---|---|
| Pole pairs number | 15 |
| Slot number | 36 |
| Stator out diameter (mm) | 310 |
| Stator inner diameter (mm) | 228 |
| Rotor out diameter (mm) | 223 |
| Air gap (mm) | 1 |
| PM thickness (mm) | 5.5 |
| Pole arc coefficient α | 0.9 |
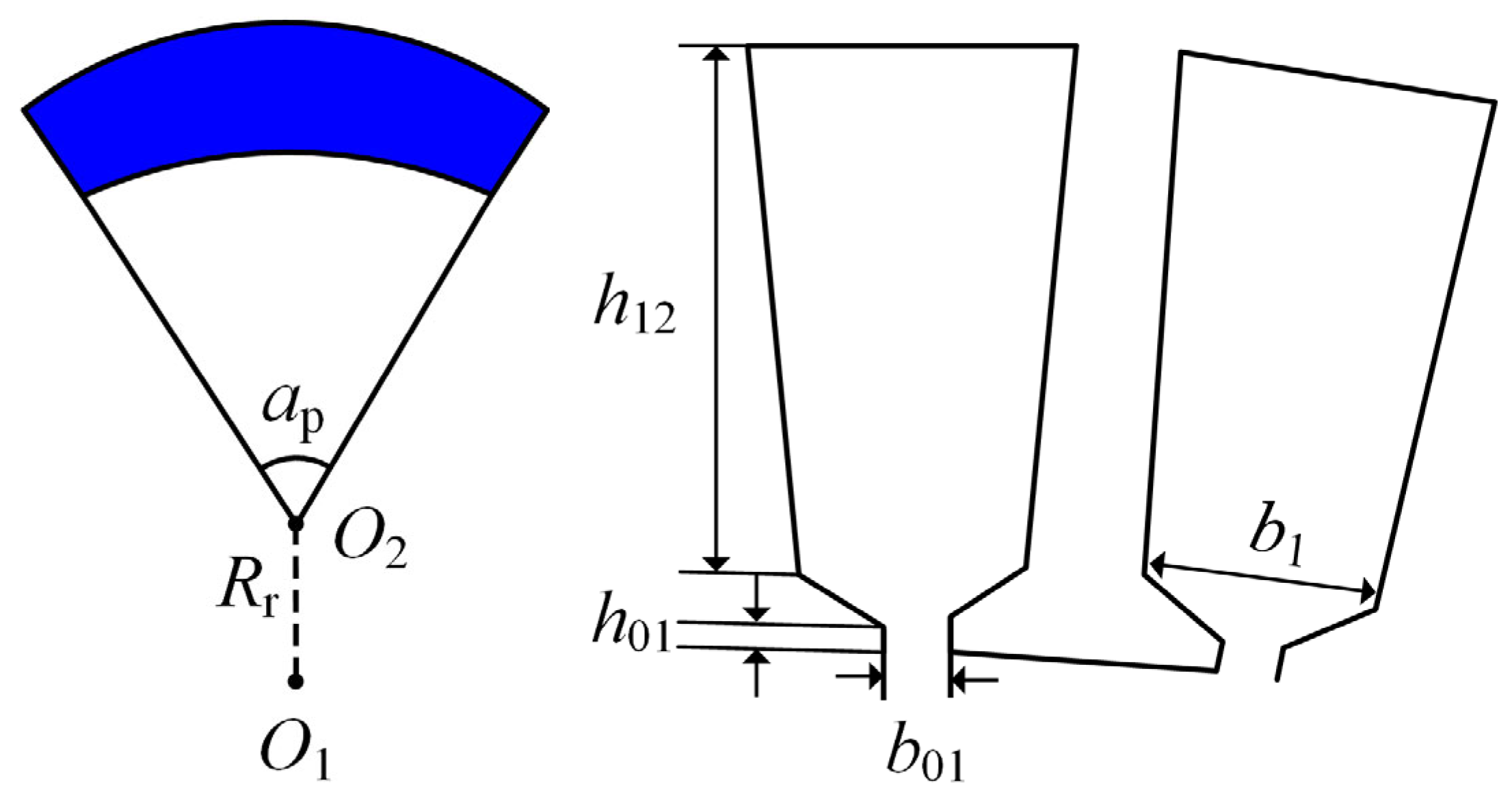
| Eccentricity distance Rr (mm) | 50 |
| Stator slot opening height h01 (mm) | 1.8 |
| Stator slot body height h12 (mm) | 26 |
| Stator slot opening width b01 (mm) | 3.8 |
| Stator slot body height b1 (mm) | 10.6 |
| Rated torque (N·m) | 165 |
| Rated speed (r/min) | 1750 |
| Rated power (KW) | 30 |
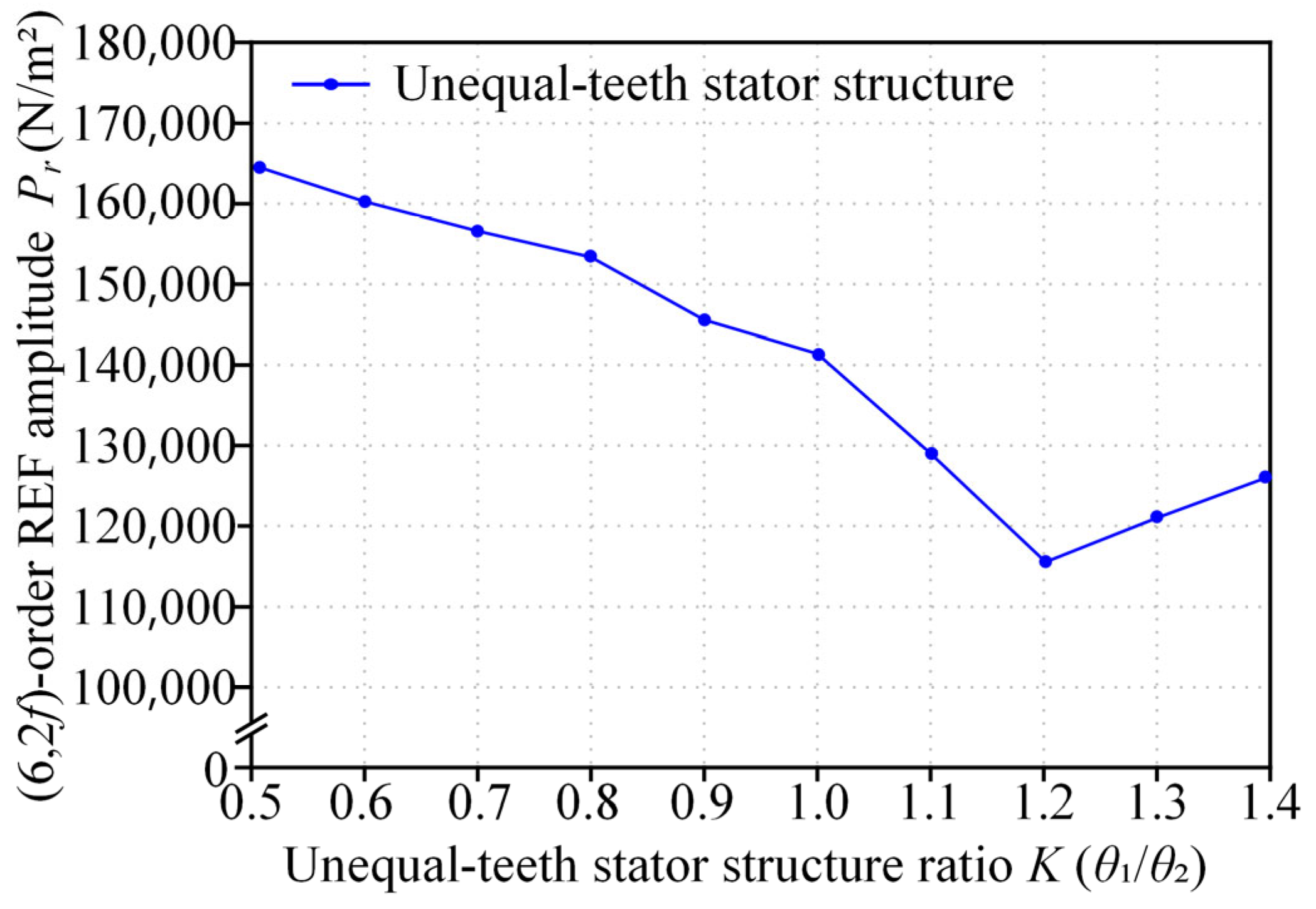
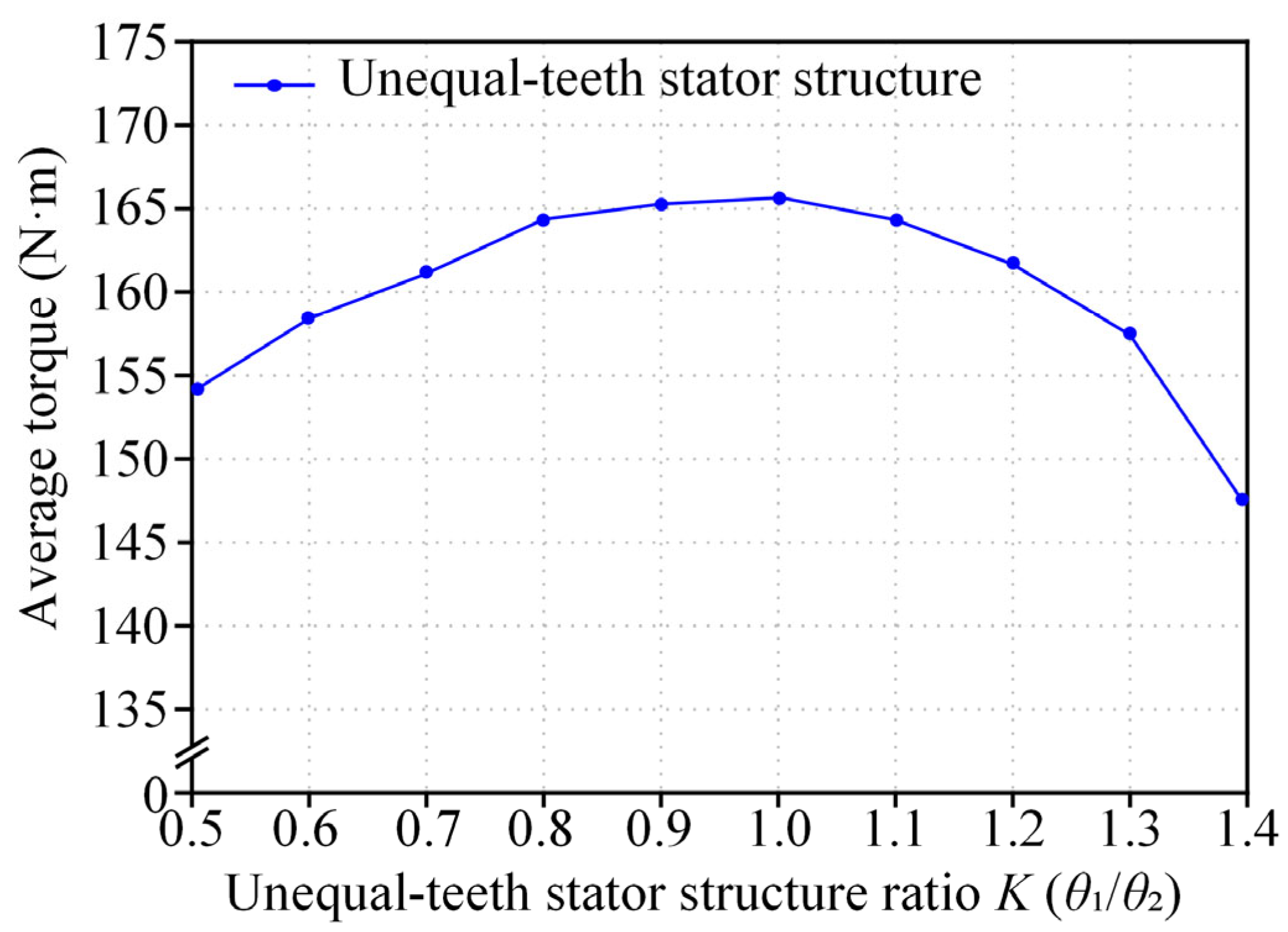
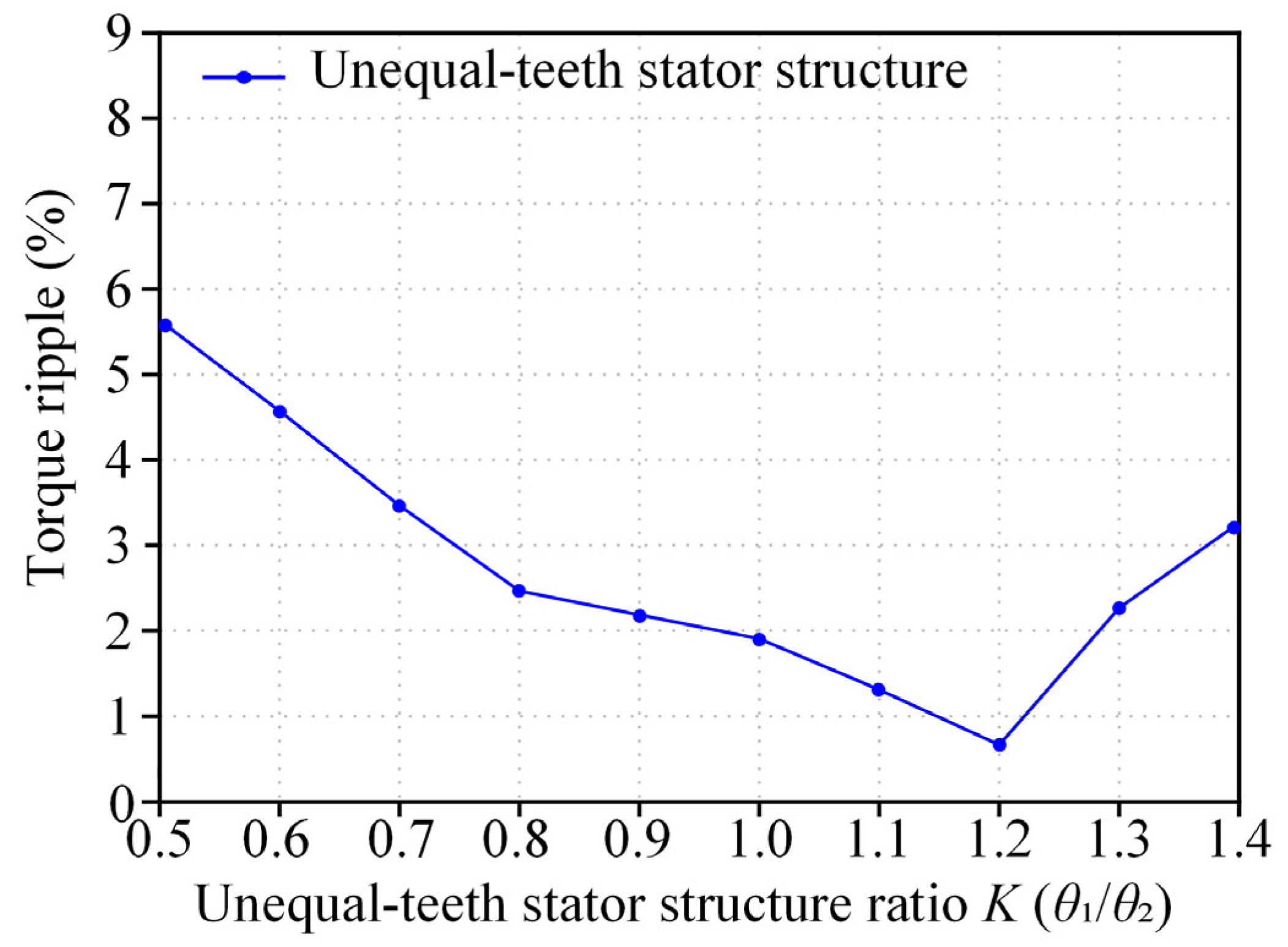
| K | (6, 2f)-Order REF (N/m2) | Torque (N·m) | Torque Ripple (%) |
|---|---|---|---|
| 0.5 | 164,705.54 | 154.15 | 5.54 |
| 0.6 | 160,996.83 | 158.57 | 4.66 |
| 0.7 | 157,336.95 | 161.58 | 3.40 |
| 0.8 | 154,140.16 | 164.43 | 2.38 |
| 0.9 | 146,414.84 | 165.12 | 2.16 |
| 1.0 | 141,477.16 | 165.31 | 1.94 |
| 1.1 | 129,817.72 | 164.41 | 1.31 |
| 1.2 | 116,382.27 | 162.11 | 0.77 |
| 1.3 | 121,044.63 | 157.61 | 2.27 |
| 1.4 | 126,169.52 | 148.20 | 3.12 |
| K | (6, 2f)-Order REF (N/m2) | Torque (N·m) |
|---|---|---|
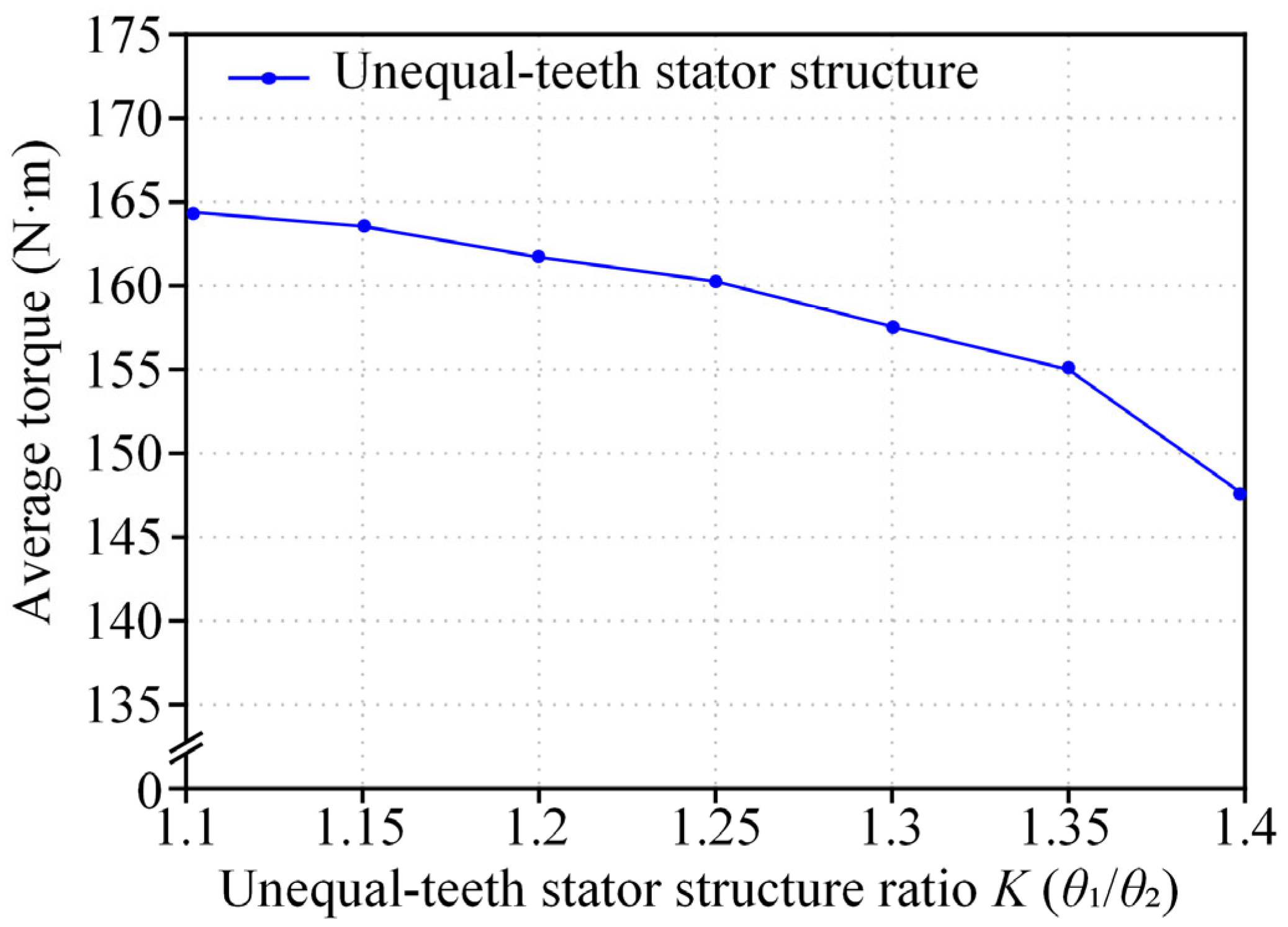
| 1.1 | 129,817.72 | 164.41 |
| 1.15 | 123,854.50 | 163.50 |
| 1.2 | 116,382.27 | 162.11 |
| 1.25 | 118,840.68 | 160.65 |
| 1.3 | 121,044.63 | 157.61 |
| 1.35 | 123,901.79 | 155.03 |
| 1.4 | 126,169.52 | 148.20 |
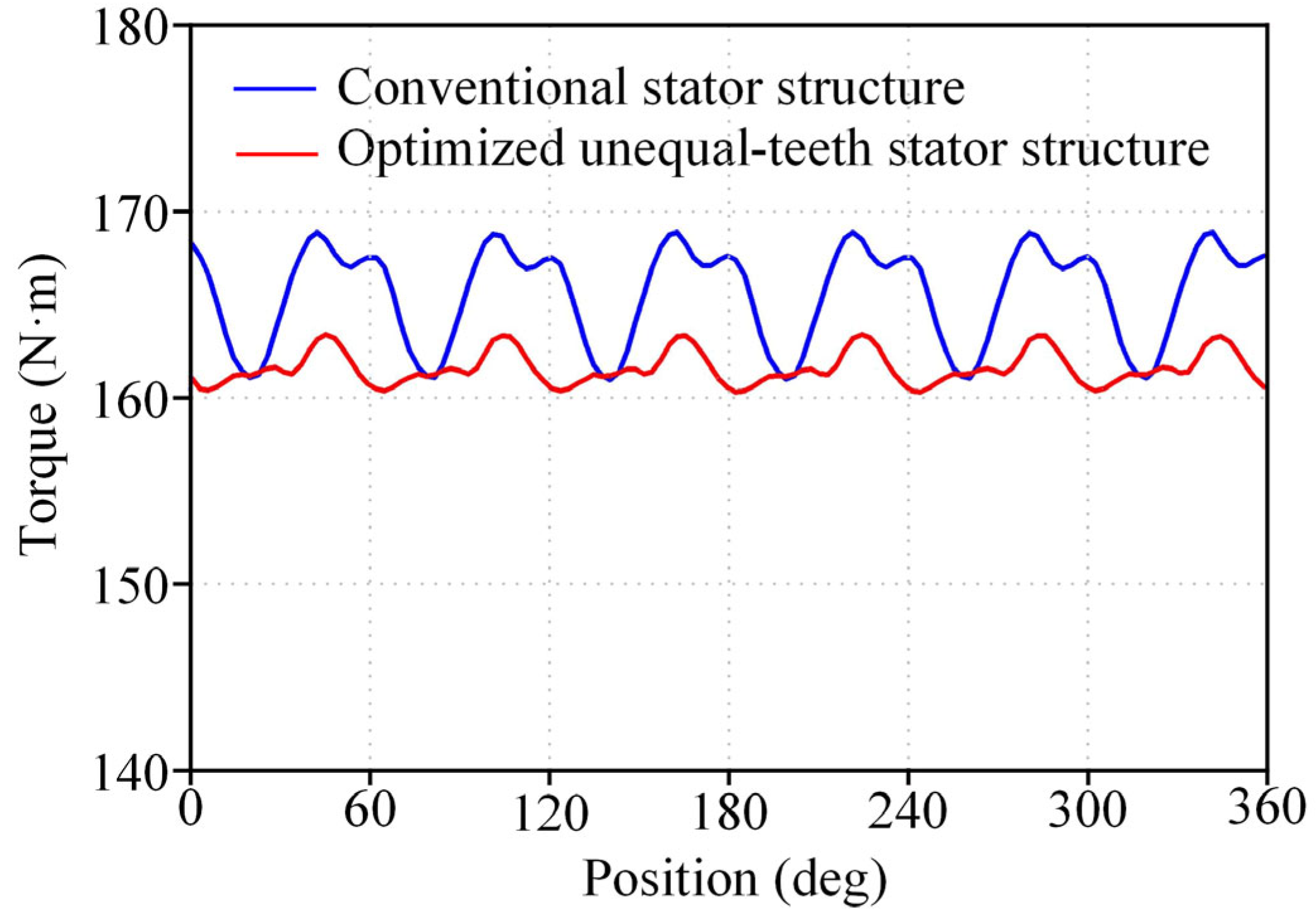
| Spatial Order | REFs of Conventional Stator Structure (N/m2) | REFs of Optimized Unequal-Teeth Stator Structure (N/m2) | Reduction (%) |
|---|---|---|---|
| (6, 2f)-Order | 141,477.16 | 116,382.27 | 17.74 |
| (12, 4f)-Order | 41,206.76 | 38,054.58 | 7.65 |
| (30, 2f)-Order | 256,529.34 | 250,584.83 | 2.32 |
| (60, 4f)-Order | 87,729.93 | 79,719.96 | 9.13 |
| Component | Materials | Density (Kg/m3) | Young’s Modulus (Pa) | Poisson’s Ratio |
|---|---|---|---|---|
| Upper and lower end caps | Aluminum alloy | 2700 | 7 × 1010 | 0.33 |
| Housing | Aluminum alloy | 2700 | 7 × 1010 | 0.33 |
| Flange | Carbon steel | 7890 | 2.09 × 1011 | 0.269 |
| Stator core | Silicon steel | 7600 | 1.6 × 1011 | 0.3 |
| Component | Meshing Method | Element Size (mm) | Number of Nodes | Number of Elements | Mesh Quality |
|---|---|---|---|---|---|
| Upper and lower end caps | Tetrahedrons | 10 | 735,712 | 308,964 | 0.742 |
| Housing | Tetrahedrons | 8 | |||
| Flange | Tetrahedrons | 15 | |||
| Stator core | Multizone | 4 | |||
| Stator teeth Surface | Multizone | 2 |
| Component | Meshing Method | Element Size (mm) | Number of Nodes | Number of Elements | Mesh Quality |
|---|---|---|---|---|---|
| Upper and lower end caps | Tetrahedrons | 10 | 749,869 | 308,490 | 0.744 |
| Housing | Tetrahedrons | 8 | |||
| Flange | Tetrahedrons | 15 | |||
| Stator core | Multizone | 4 | |||
| Stator teeth Surface | Multizone | 2 |
| Machine Type | Conventional Stator Structure | Optimized Unequal-Teeth Stator Structure | Reduction Percentage (%) | |
|---|---|---|---|---|
| Performance | ||||
| Vibration acceleration amplitude (mm/s2) | 1753.40 | 1305.70 | 25.53 | |
| Sound pressure level (dB) | 69.70 | 65.31 | 6.44 | |
| Machine Type | Conventional Stator Structure | Optimized Unequal-Teeth Stator Structure | Reduction Percentage (%) | |
|---|---|---|---|---|
| Performance | ||||
| Vibration acceleration amplitude (mm/s2) | 959.07 | 691.68 | 27.88 | |
| Sound pressure level (dB) | 65.88 | 60.30 | 8.50 | |
| Machine Type | Conventional Stator Structure | Optimized Unequal-Teeth Stator Structure | Reduction Percentage (%) | |
|---|---|---|---|---|
| Performance | ||||
| Vibration acceleration amplitude (mm/s2) | 2663.50 | 2083.74 | 21.77 | |
| Sound pressure level (dB) | 72.60 | 69.16 | 4.74 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, L.; Li, X.; Zhang, H.; Wang, H.; Lin, Z.; Zhang, T. Design of an Unequal-Teeth Stator Structure for a Low-Vibration Noise Permanent Magnet Synchronous Machine Considering Teeth Modulation. World Electr. Veh. J. 2025, 16, 339. https://doi.org/10.3390/wevj16070339
Guo L, Li X, Zhang H, Wang H, Lin Z, Zhang T. Design of an Unequal-Teeth Stator Structure for a Low-Vibration Noise Permanent Magnet Synchronous Machine Considering Teeth Modulation. World Electric Vehicle Journal. 2025; 16(7):339. https://doi.org/10.3390/wevj16070339
Chicago/Turabian StyleGuo, Liyan, Xiangyi Li, Huatuo Zhang, Huimin Wang, Zhichen Lin, and Tao Zhang. 2025. "Design of an Unequal-Teeth Stator Structure for a Low-Vibration Noise Permanent Magnet Synchronous Machine Considering Teeth Modulation" World Electric Vehicle Journal 16, no. 7: 339. https://doi.org/10.3390/wevj16070339
APA StyleGuo, L., Li, X., Zhang, H., Wang, H., Lin, Z., & Zhang, T. (2025). Design of an Unequal-Teeth Stator Structure for a Low-Vibration Noise Permanent Magnet Synchronous Machine Considering Teeth Modulation. World Electric Vehicle Journal, 16(7), 339. https://doi.org/10.3390/wevj16070339






