Multi-Parameter Optimization of Angle Transmission Ratio of Steer-by-Wire Vehicle
Abstract
1. Introduction
2. Steer-by-Wire Vehicle Model
2.1. Differential Formula of Steer-by-Wire System
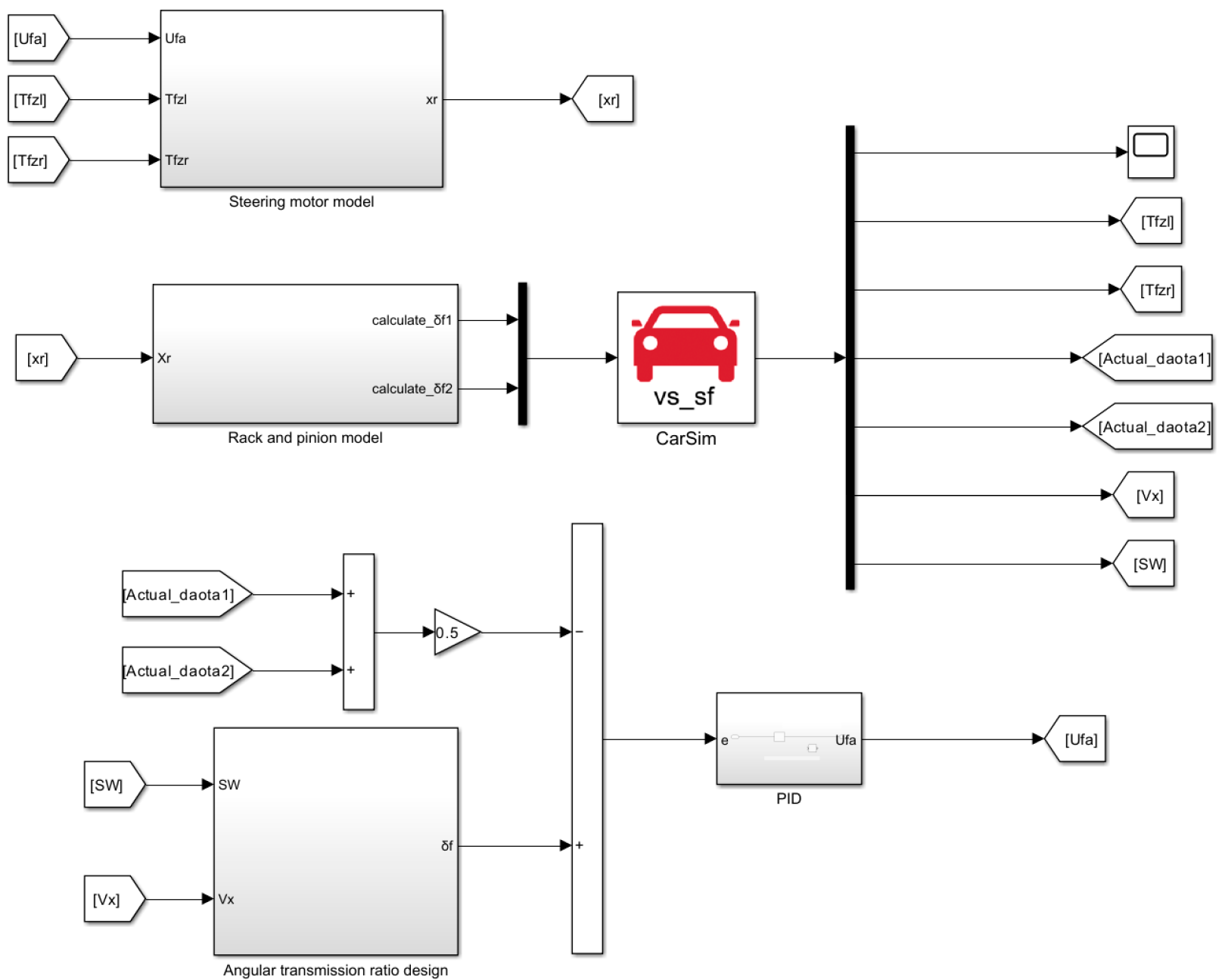
2.2. Establishment of the Steer-by-Wire Vehicle Model
3. Optimization of Unified Model of Steering Angle Transmission Ratio
3.1. Unified Model of Steering Angle Transmission Ratio
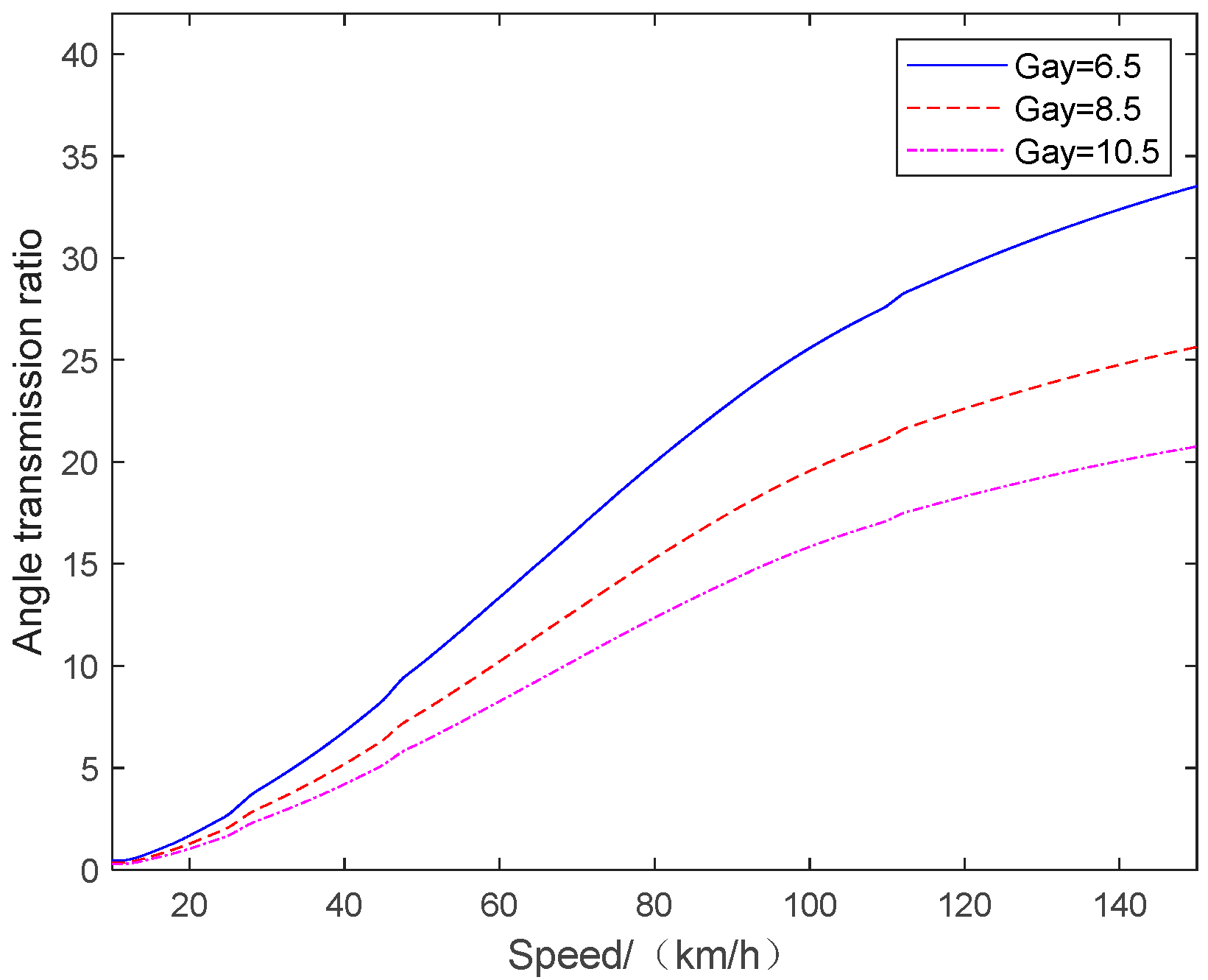
3.2. Different Variable-Angle Transmission Ratio Design of SBW Vehicle
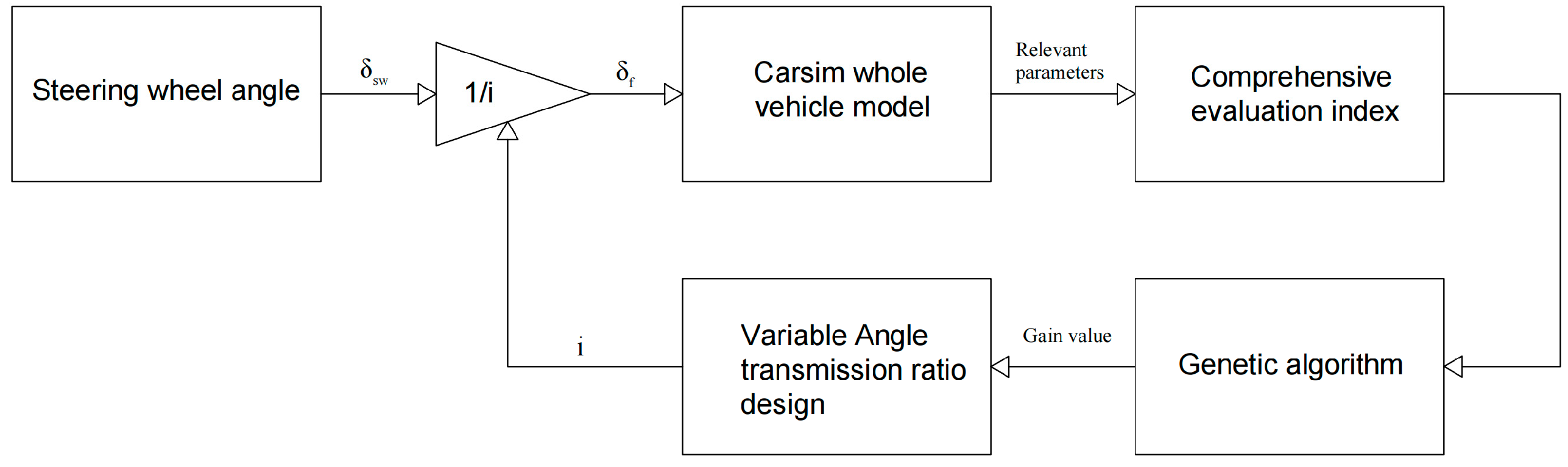
3.3. Variable-Angle Transmission Ratio Design Strategy
4. Optimization of Yaw Rate and Lateral Acceleration Gain Value
4.1. Genetic Algorithm
4.2. Handling Stability Evaluation Index
4.3. Gain Value Optimization
5. Variable-Angle Transmission Ratio Design Method
5.1. Variable Angle Transmission Ratio Control Within Different Speed Ranges
5.1.1. Low-Speed Section
5.1.2. Medium-Speed Section
5.1.3. High-Speed Section
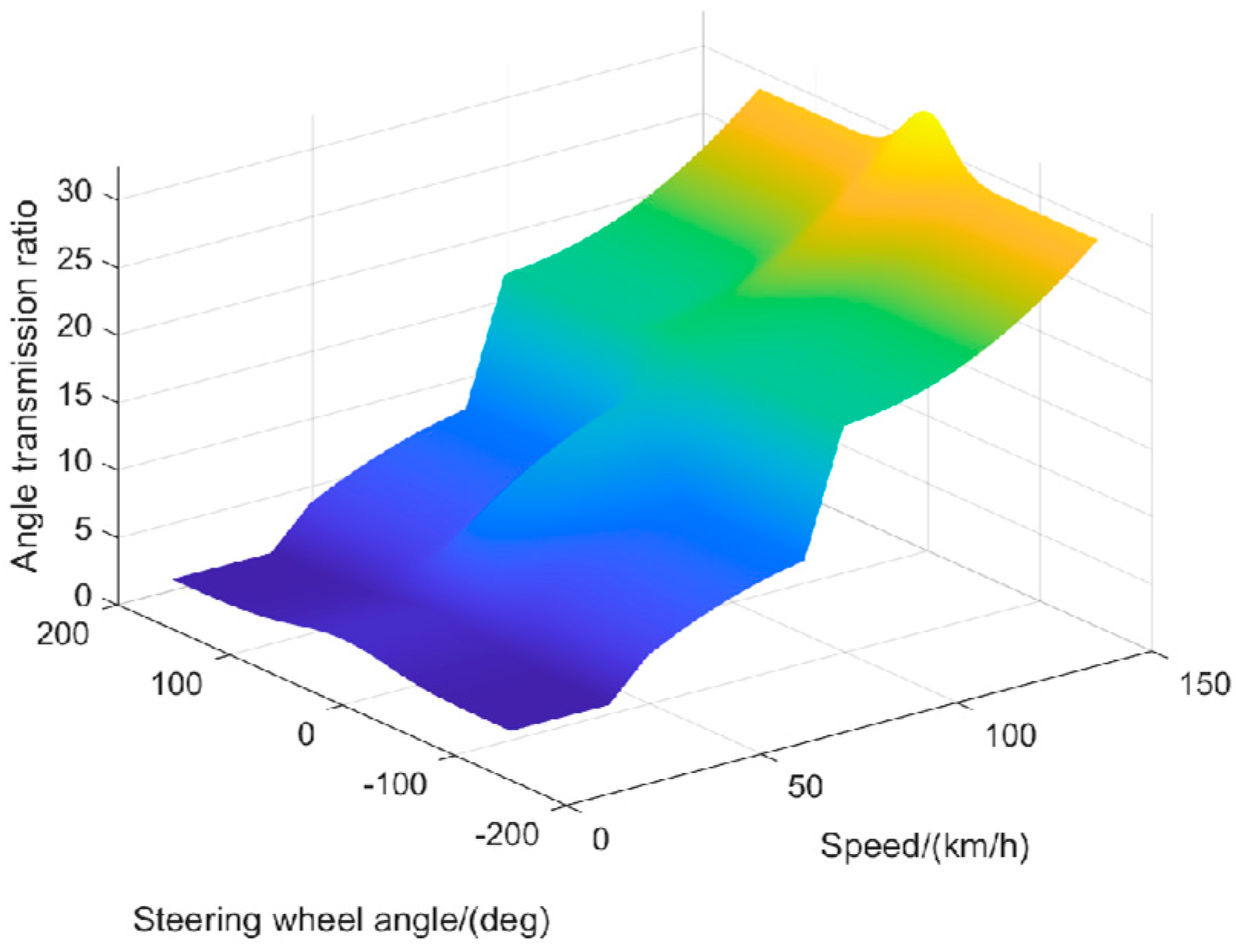
5.2. Variable Angle Transmission Ratio in the Speed Transition Interval
5.3. Full-Speed Variable-Angle Transmission Ratio Control
6. Test Verification
6.1. Low-Speed Section Test Verification
6.2. High-Speed Section Test Verification
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, L. Research on Variable Transmission Ratio and Active Steering Control Strategy of Automotive Steer-by-Wire System. Master’s Thesis, Chongqing University of Technology, Chongqing, China, 2022. [Google Scholar]
- Zhong, C. Research on Variable Transmission Ratio and Stability Control of By-Wire Four-Wheel Steering Electric Vehicles. Master’s Thesis, Chongqing University of Technology, Chongqing, China, 2023. [Google Scholar]
- Chen, Z.; Zhong, C.; Li, H. Design of Fuzzy Controller for Wire-controlled Steering with Variable Angle Transmission Ratio Based on Particle Swarm Optimization. J. Chongqing Univ. Technol. (Nat. Sci.) 2022, 36, 41–49. [Google Scholar]
- Kou, F.; Fang, B.; Zhang, X. Adaptive variable gain ratio of wire control steering system design. J. Zhengzhou Univ. (Eng. Sci.) 2024, 12, 8–15. [Google Scholar]
- Lin, J.; Zhang, F.; Su, L.; Song, G.; Liu, Z.; Zhang, Y. Research on Variable Transmission Ratio Control Method to Improve Vehicle Handling Comfort Based on Steer-by-Wire System. Actuators 2024, 13, 48. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, X.; Xie, J.; Wang, F.; Su, P. Variable transmission ratio design of a steer-by-wire system for intelligent vehicles. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 9341–9353. [Google Scholar] [CrossRef]
- Xu, B.; Xia, C. Research on Variable Angle Transmission Ratio of Vehicle By-wire Steering Based on Fuzzy Control. Pract. Technol. 2024, 49, 15–23. [Google Scholar]
- Feng, X. Research on Control Strategy of Automotive Steer-by-Wire System Based on CarSim. Master’s Thesis, Shandong University of Technology, Qingdao, China, 2019. [Google Scholar]
- Zhang, J. Research on Control Strategy for Handling Stability of By-Wire Steering Vehicles Based on Variable Angle Transmission Ratio. Master’s Thesis, Jilin University, Changchun, China, 2023. [Google Scholar]
- Zhao, B.; Fan, X.; Qi, G. Variable transmission ratio and active steering control for steer-by-wire steering. Int. J. Veh. Syst. Model. Test. 2022, 16, 290–312. [Google Scholar] [CrossRef]
- Yuan, L. Design of Steer-by-Wire Steering Transmission Ratio Based on Particle Swarm Optimization Algorithm. Neijiang Sci. Technol. 2024, 45, 28–30+128. [Google Scholar]
- Qiu, J. Research on Road Sensing Simulation Control of Automotive Steer-by-Wire System. Master’s Thesis, Chongqing University of Technology, Chongqing, China, 2023. [Google Scholar]
- Heathershaw, A. Variable ratio steering development for Formula 1. Auto Technol. 2005, 5, 38–41. [Google Scholar] [CrossRef]
- Wu, X.; Li, W. Variable steering ratio control of steer-by-wire vehicle to improve handling performance. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 774–782. [Google Scholar] [CrossRef]
- Liu, S. Research on Lateral Stability Control Strategy of Passenger Vehicles Based on Steer-by-Wire System. Master’s Thesis, Qingdao Technological University, Qingdao, China, 2022. [Google Scholar]
- Yan, C.; Wang, Y. Research on Ideal Transmission Ratio Control Strategy and Optimization of Steer-by-wire System. J. Chongqing Jiaotong Univ. (Nat. Sci. Ed.) 2024, 43, 106–112+123. [Google Scholar]
- Zong, C.; Guo, K. Objective quantitative evaluation index of vehicle handling stability. J. Jilin Univ. Technol. Sci. 2000, 01, 001. [Google Scholar]
- Gao, S.; Wang, W.; Gao, L. Simulation based on dynamic driving simulator of variable steering ratio and the test evaluation. Sci. Technol. 2025, 9, 106–111. [Google Scholar]
- Pietruch, M.; Wetula, A.; Młyniec, A. Influence of the Accuracy and CAN Frame Period of the Steering Wheel Angle Sensor (SAS) on the Trajectory of a Steer-by-Wire-Equipped Car. IEEE Access 2022, 10, 106110–106116. [Google Scholar] [CrossRef]
- Qu, X.; Chen, H.; Zhang, J. Review on Key Technologies of Vehicle By-wire Steering System. J. Chongqing Univ. Technol. (Nat. Sci.) 2023, 37, 74–84. [Google Scholar]



| Parameter Name | Parameter Value |
|---|---|
| Total mass of the vehicle m/kg | 1110 |
| Distance from front axle to center of mass a/m | 1.04 |
| Distance from rear axle to center of mass b/m | 1.56 |
| Rack quality Mr/kg | 2.25 |
| The radius of the pitch circle of the pinion rp/m | 0.007 |
| The length of the left front wheel’s steering rocker arm lfl/m | 0.132 |
| The length of the right front wheel’s steering rocker arm lfr/m | 0.132 |
| Speed (km/h) | 30 | 50 | 70 | 90 | 110 |
| Optimized Gsw | 0.51 | 0.39 | 0.32 | 0.28 | 0.26 |
| Speed (km/h) | 70 | 90 | 110 |
| Optimized Gay | 6.22 | 7 | 7.95 |
| Control Strategy | Peak Value/(deg) |
|---|---|
| Fixed-angle transmission ratio | 70.42 |
| The control strategy of this article | 23.16 |
| Control Strategy | Peak Yaw Rate/(deg/s) | Peak Lateral Acceleration/(g) | Peak Sideslip Angle/(deg) |
|---|---|---|---|
| Unified model of steering angle transmission ratio | 14.56 | 0.72 | 2.42 |
| The control strategy of this article | 13.55 | 0.68 | 2.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Liu, S.; Che, H.; Liu, X.; Ding, H. Multi-Parameter Optimization of Angle Transmission Ratio of Steer-by-Wire Vehicle. World Electr. Veh. J. 2025, 16, 317. https://doi.org/10.3390/wevj16060317
Liu W, Liu S, Che H, Liu X, Ding H. Multi-Parameter Optimization of Angle Transmission Ratio of Steer-by-Wire Vehicle. World Electric Vehicle Journal. 2025; 16(6):317. https://doi.org/10.3390/wevj16060317
Chicago/Turabian StyleLiu, Wenguang, Suo Liu, Huajun Che, Xi Liu, and Hua Ding. 2025. "Multi-Parameter Optimization of Angle Transmission Ratio of Steer-by-Wire Vehicle" World Electric Vehicle Journal 16, no. 6: 317. https://doi.org/10.3390/wevj16060317
APA StyleLiu, W., Liu, S., Che, H., Liu, X., & Ding, H. (2025). Multi-Parameter Optimization of Angle Transmission Ratio of Steer-by-Wire Vehicle. World Electric Vehicle Journal, 16(6), 317. https://doi.org/10.3390/wevj16060317





