A Review of Control Strategies for Four-Switch Buck–Boost Converters
Abstract
1. Introduction
2. Research of Multi-Mode Control Under Hard Switching
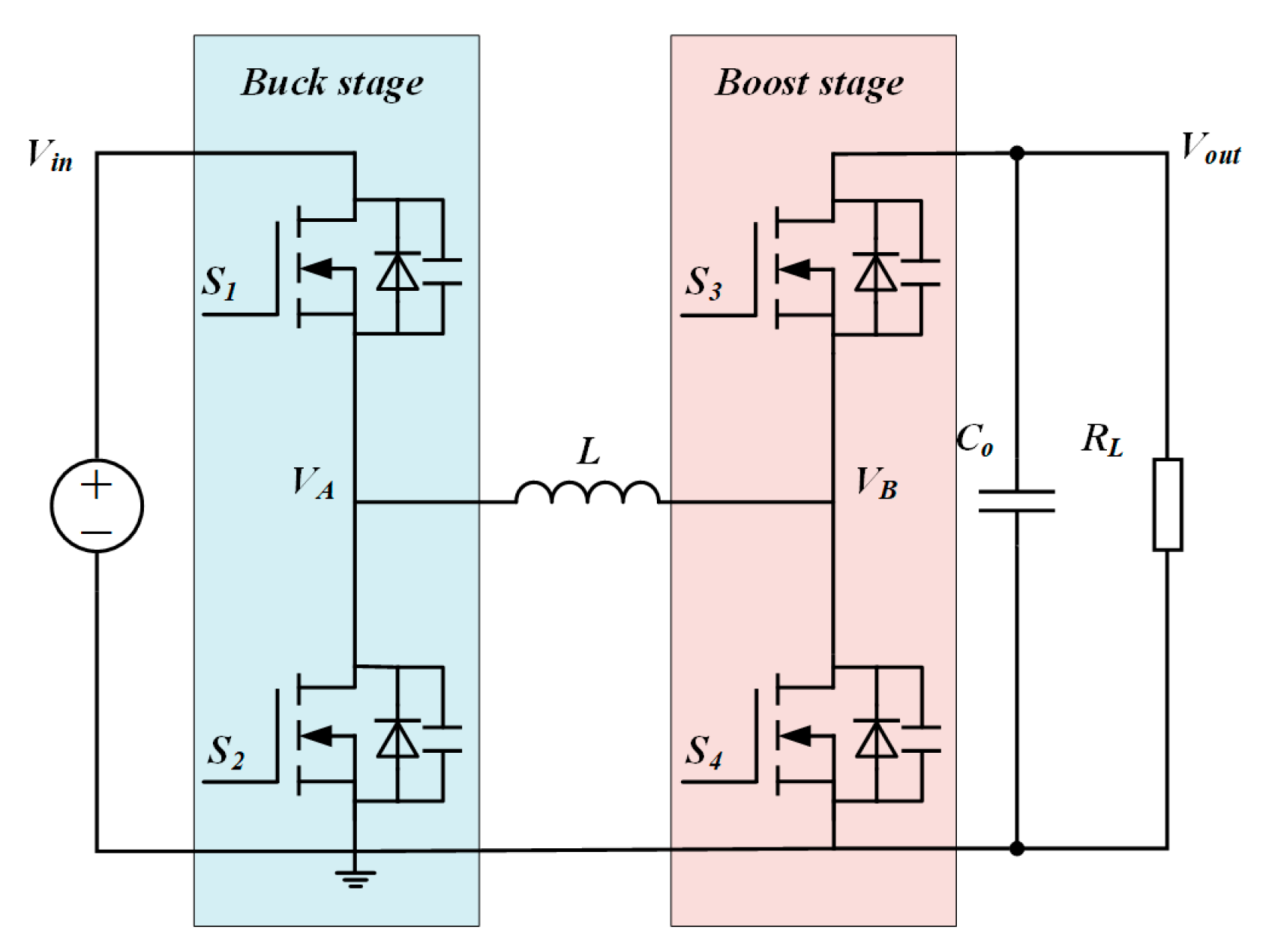
2.1. Principle of Multi-Mode Control
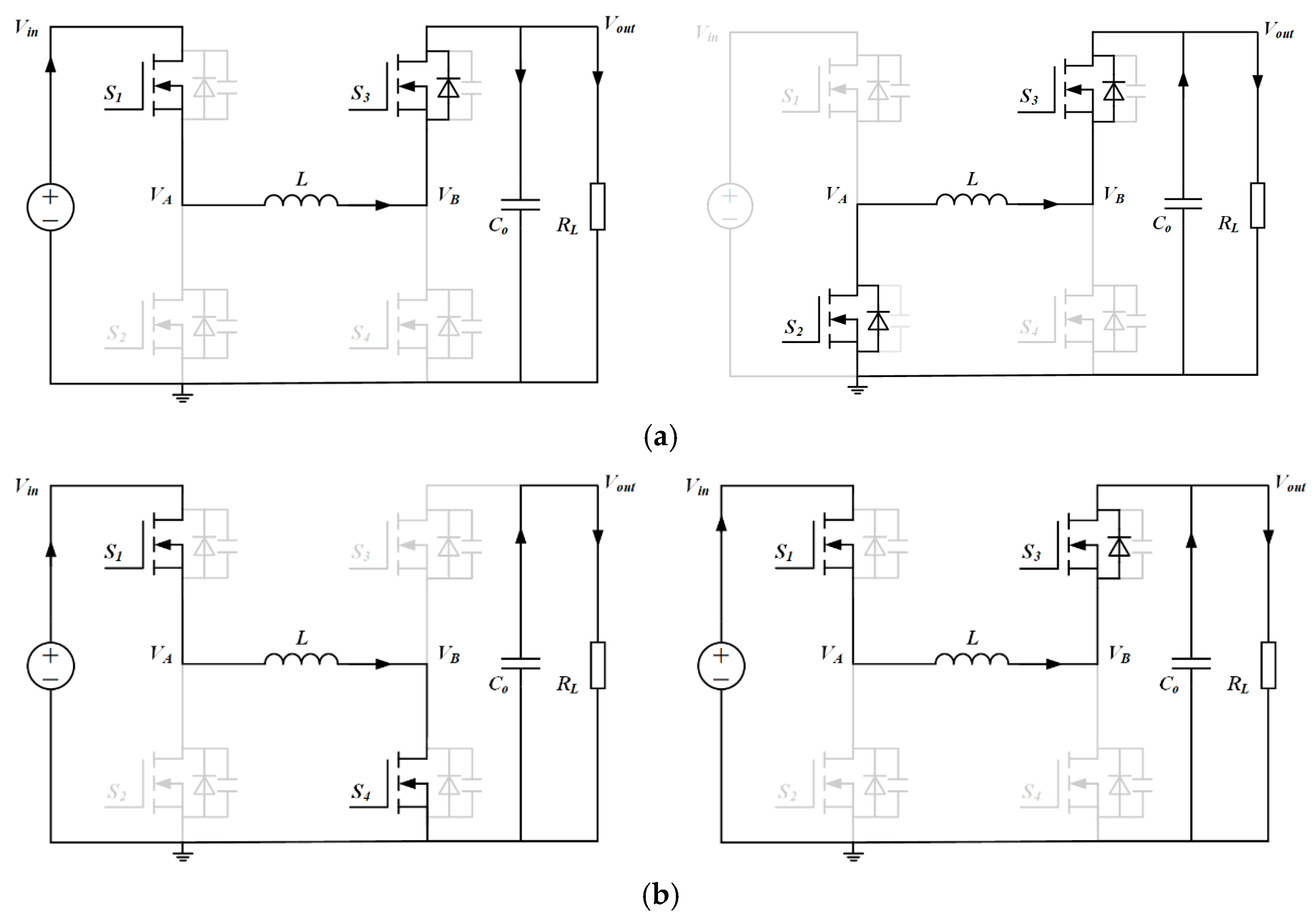
2.1.1. Dual-Mode Control Strategy
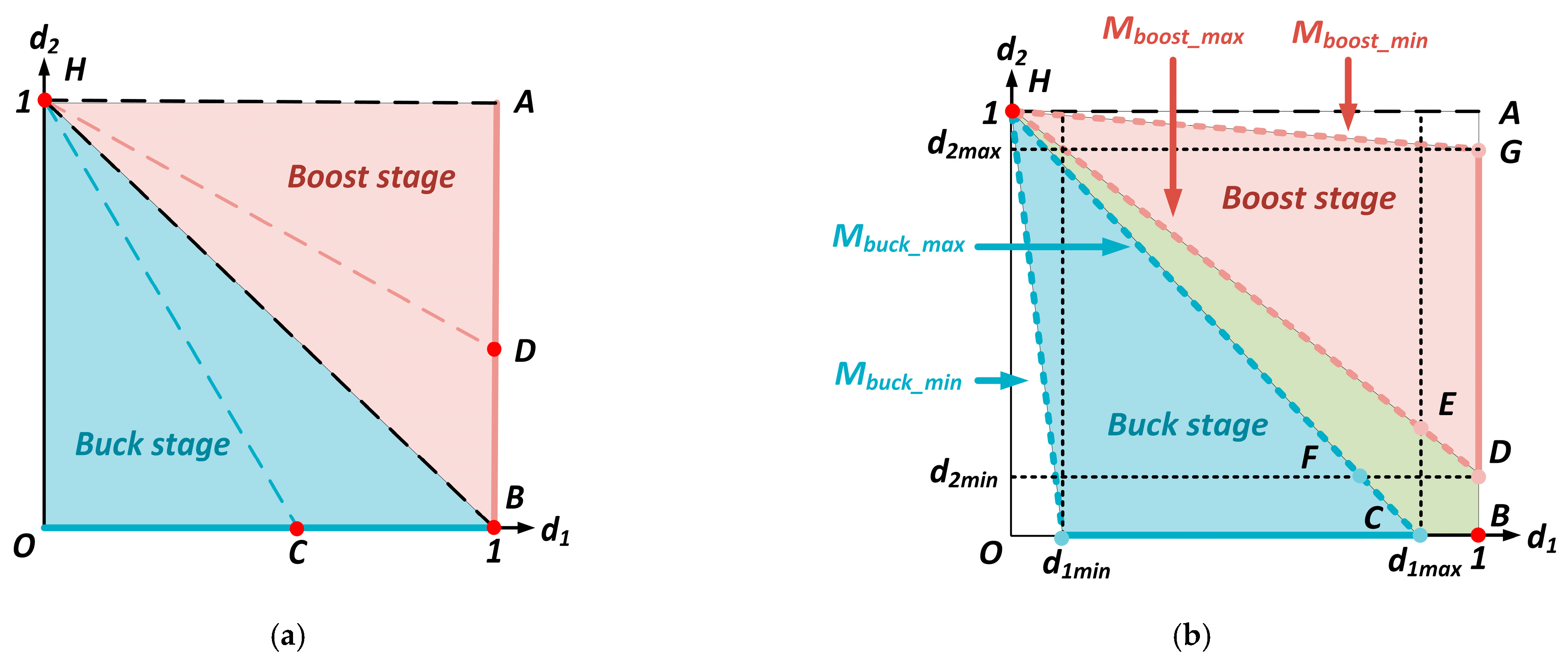
2.1.2. Dead Zone Generated During Mode Switching
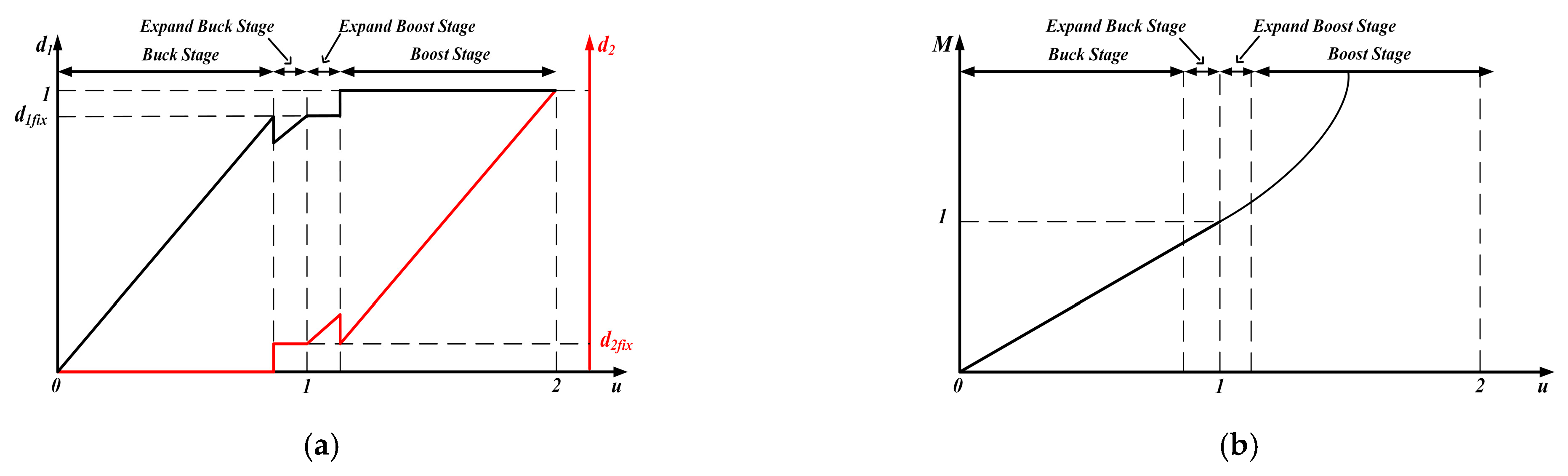
2.1.3. Three-Mode and Four-Mode Control
2.2. Improve Control Algorithms and Control Logic
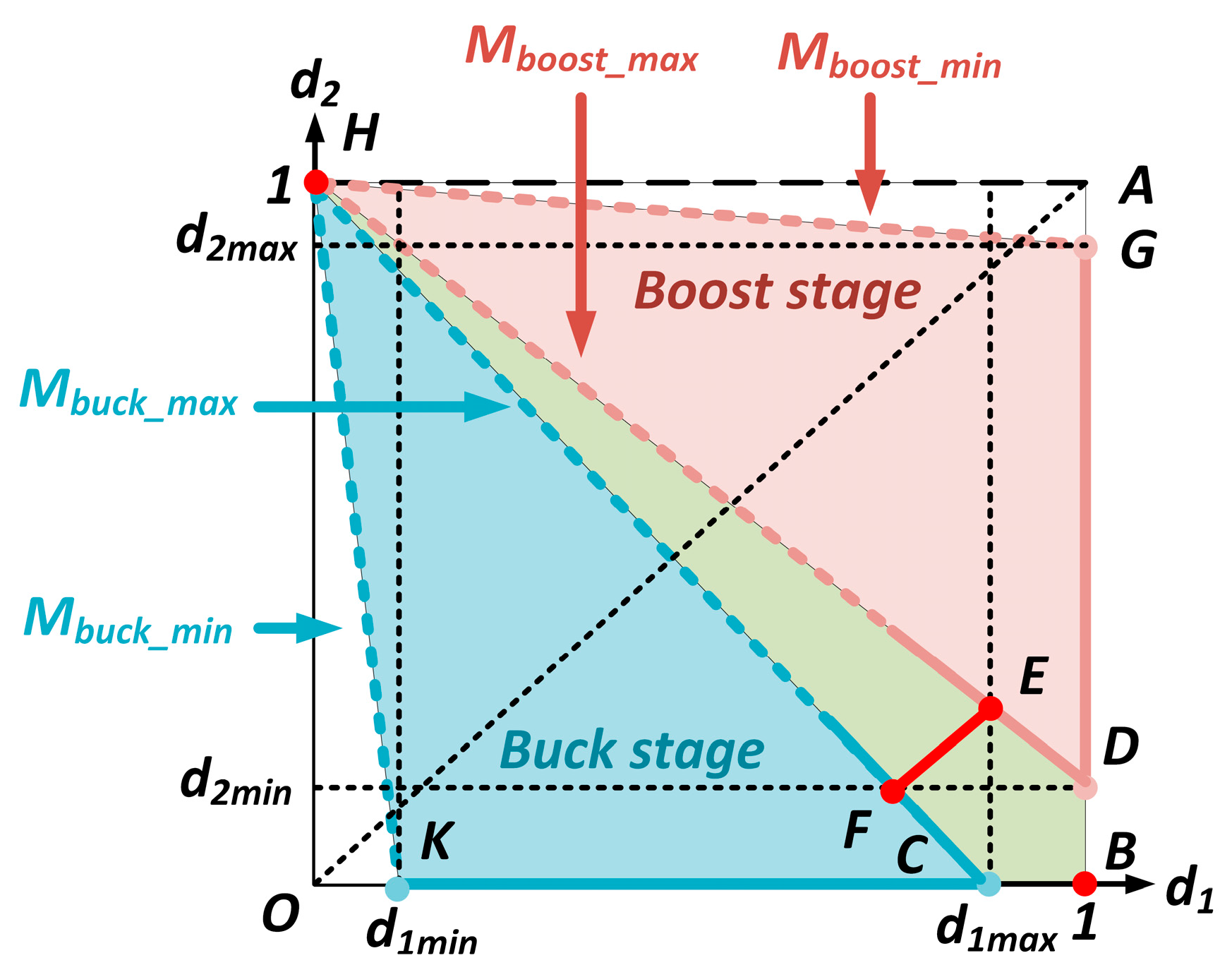
2.2.1. Three-Mode Smooth-Switching Strategy Based on a Graphical Method
2.2.2. Frequency-Varying Loop Selection Control Strategy Based on Four-Mode Control
2.2.3. Model Predictive Control Base on Four-Mode Control
2.3. The Problems of Multi-Mode Control Under Hard Switching
3. Research on a Control Strategy Under Soft Switching
3.1. Process of Implementing Soft Switching in the FSBB
3.1.1. Implementation Principle of ZVS
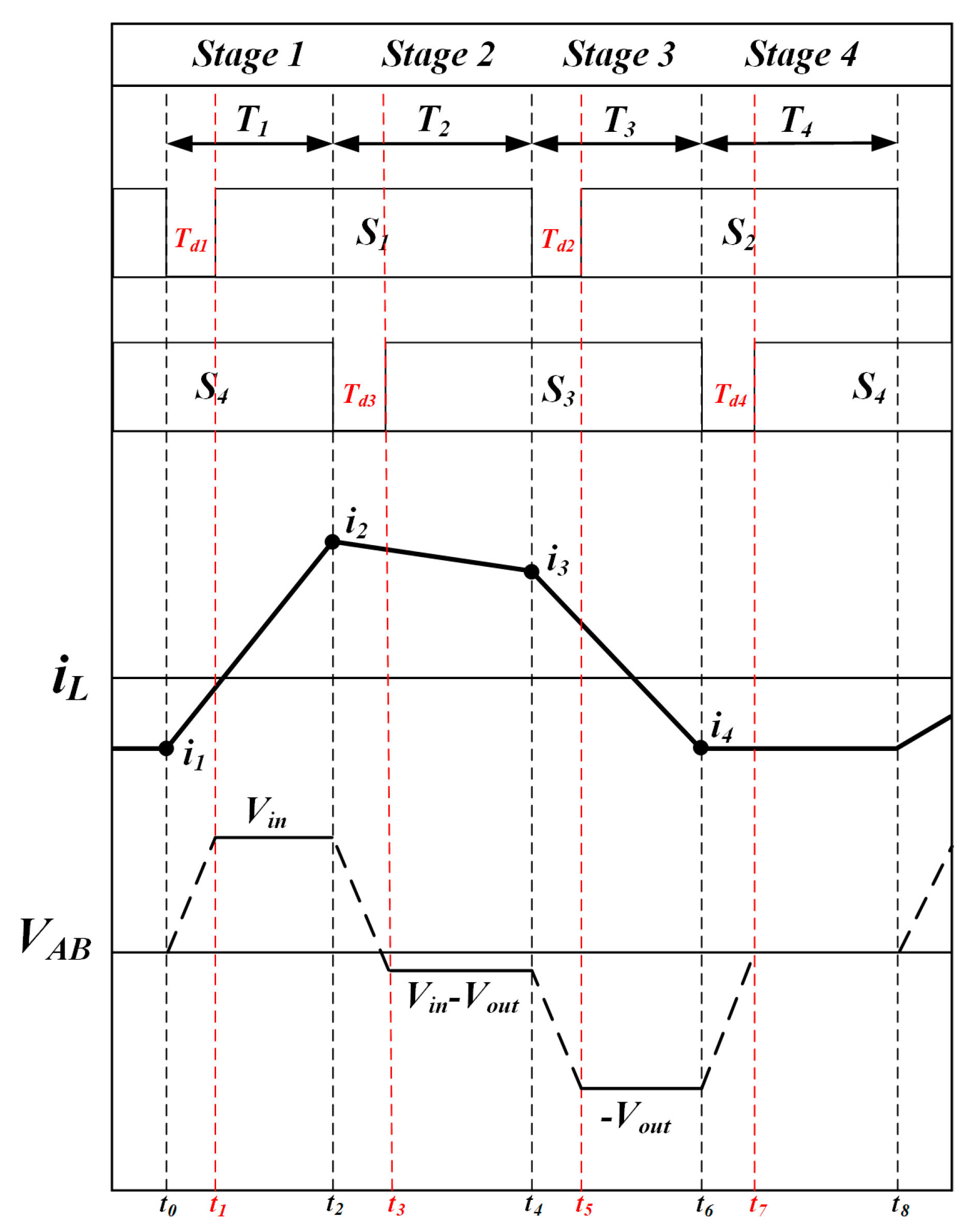
3.1.2. Working Principle of Quadrilateral Inductor Current Control Strategy
3.2. The Main Optimization Directions of Current Research
- (1)
- Potential loss of ZVS under varying operating conditions:
- (2)
- Further Reduction of System Losses:
- (3)
- Challenges in Achieving Good Dynamic Performance and High Computational Demand:
3.3. Optimizing the Implementation of ZVS
3.3.1. Loss of ZVS Due to Small Inductor Current Ripple
3.3.2. Loss of ZVS Due to Reversal of the Power Transfer Direction
3.4. Reducing System Losses
3.4.1. Reducing Losses by Determining Optimal Control Variables Through Mathematical Modelling
3.4.2. Reducing Losses Caused by Current Sensing Resistors
3.5. Improving the Computing Speed and Dynamic Performance
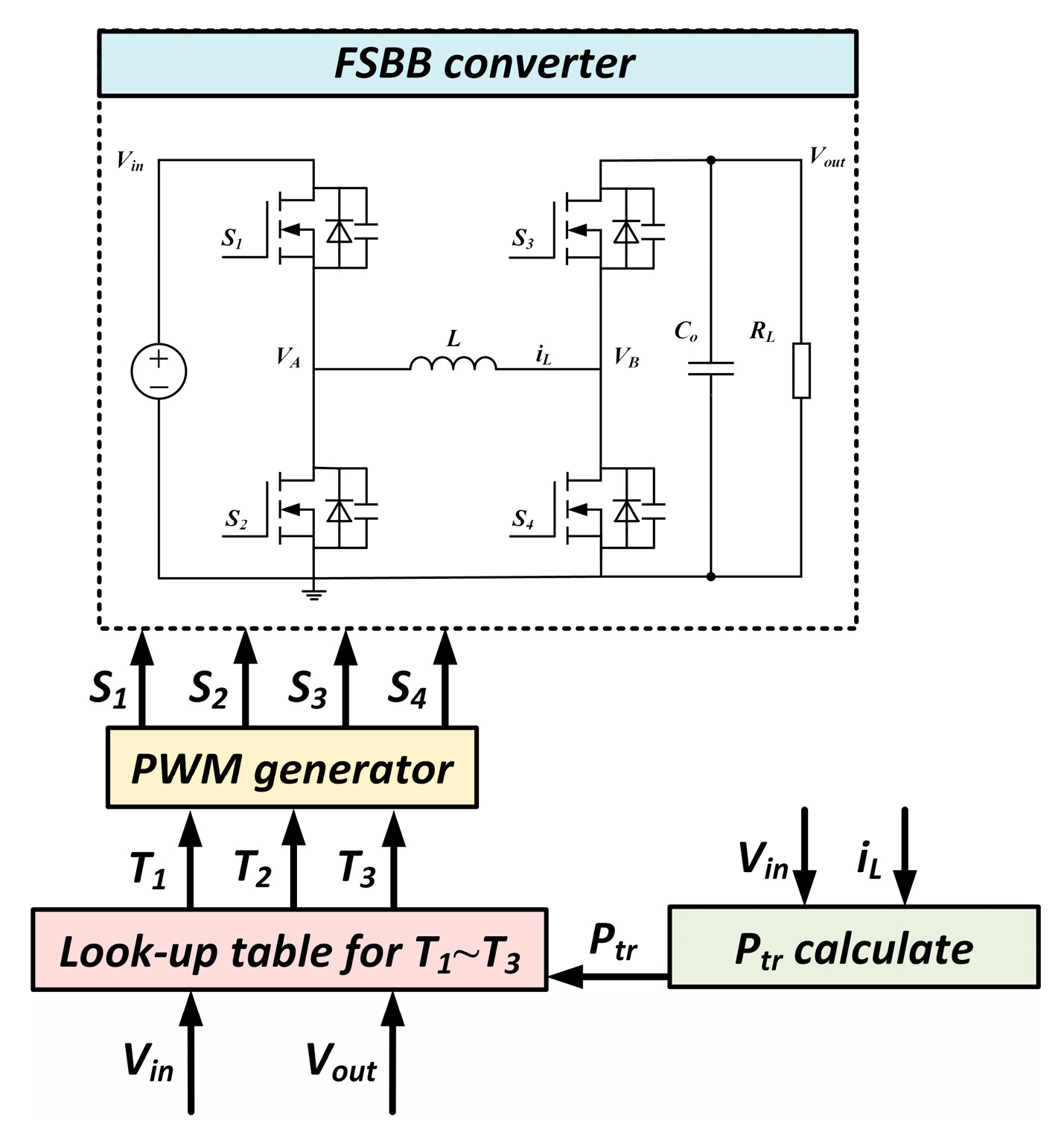
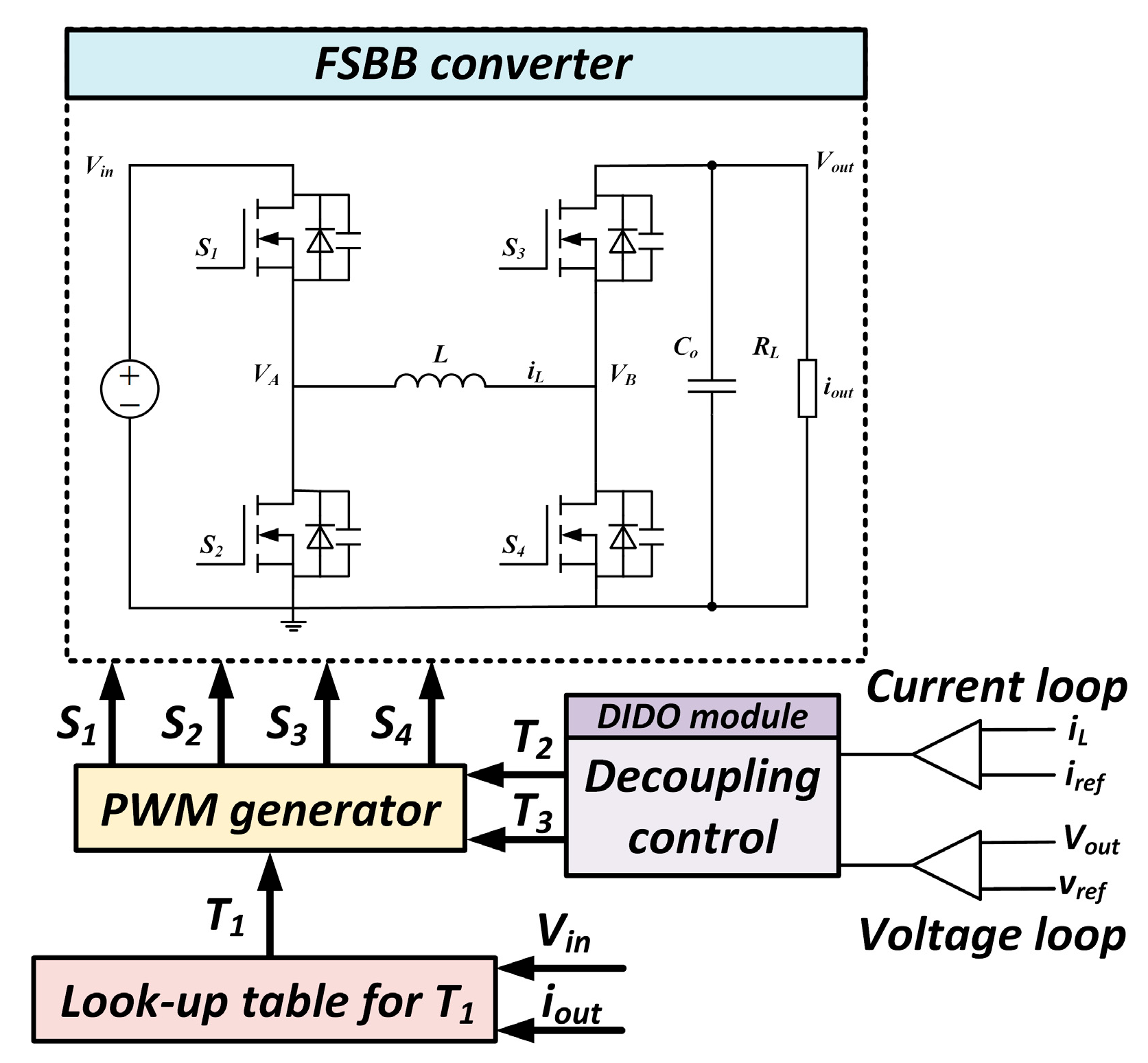
3.5.1. Lookup Table
3.5.2. Simplified Real-Time Calculation Method
3.5.3. Approximate Duty Cycle Phase Shift Method
3.6. Current Issues and Possible Solutions
3.6.1. Destructive Impact of Inductor Parameter Tolerance on ZVS
3.6.2. Impact of Temperature Fluctuations on Critical Current
3.6.3. Other Measures to Improve Dynamic Response
4. Summary and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Grazian, F.; Soeiro, T.B.; Bauer, P. Voltage/Current Doubler Converter for an Efficient Wireless Charging of Electric Vehicles with 400-V and 800-V Battery Voltages. IEEE Trans. Ind. Electron. 2022, 70, 7891–7903. [Google Scholar] [CrossRef]
- Aghabali, I.; Bauman, J.; Kollmeyer, P.J.; Wang, Y.; Bilgin, B.; Emadi, A. 800-V Electric Vehicle Powertrains: Review and Analysis of Benefits, Challenges, and Future Trends. IEEE Trans. Transp. Electrif. 2020, 7, 927–948. [Google Scholar] [CrossRef]
- Jang, Y.J. Survey of the operation and system study on wireless charging electric vehicle systems. Transp. Res. Part C Emerg. Technol. 2018, 95, 844–866. [Google Scholar] [CrossRef]
- Hannan, M.; Hoque, M.; Mohamed, A.; Ayob, A. Review of energy storage systems for electric vehicle applications: Issues and challenges. Renew. Sustain. Energy Rev. 2017, 69, 771–789. [Google Scholar] [CrossRef]
- Manzetti, S.; Mariasiu, F. Electric vehicle battery technologies: From present state to future systems. Renew. Sustain. Energy Rev. 2015, 51, 1004–1012. [Google Scholar] [CrossRef]
- Shimizu, H.; Harada, J.; Bland, C.; Kawakami, K.; Chan, L. Advanced concepts in electric vehicle design. IEEE Trans. Ind. Electron. 1997, 44, 14–18. [Google Scholar] [CrossRef]
- Caricchi, F.; Crescimbini, F.; Di Napoli, A. 20 kW water-cooled prototype of a buck-boost bidirectional DC-DC converter topology for electrical vehicle motor drives. In Proceedings of the 1995 IEEE Applied Power Electronics Conference and Exposition—APEC’95, Dallas, TX, USA, 5–9 March 1995; pp. 887–892. [Google Scholar]
- Xiao, H.; Xie, S.; Chen, W.; Huang, R. An Interleaving Double-switch Buck-Boost Converter for PV Grid-connected Inverter. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 7–12. [Google Scholar] [CrossRef]
- Ren, X.; Tang, Z.; Ruan, X.; Wei, J.; Hua, G. Four Switch Buck-Boost Converter for Telecom DC-DC power supply applications. In Proceedings of the 2008 Twenty-Third Annual IEEE Applied Power Electronics Conference and Exposition, Austin, TX, USA, 24–28 February 2008; Volume 28, pp. 15–19. [Google Scholar] [CrossRef]
- Liang, Y.; Wu, Y.; Ma, Z. Application and Development Prospect of New Generation of LVDC Supply and Utilization System in “New Infrastructure”. Proc. CSEE 2021, 41, 13–24. [Google Scholar] [CrossRef]
- Lee, H.-S.; Yun, J.-J. High-Efficiency Bidirectional Buck–Boost Converter for Photovoltaic and Energy Storage Systems in a Smart Grid. IEEE Trans. Power Electron. 2018, 34, 4316–4328. [Google Scholar] [CrossRef]
- Jia, L.; Sun, X.; Zheng, Z.; Ma, X.; Dai, L. Multimode Smooth Switching Strategy for Eliminating the Operational Dead Zone in Noninverting Buck–Boost Converter. IEEE Trans. Power Electron. 2019, 35, 3106–3113. [Google Scholar] [CrossRef]
- Lintao, R.; Fei, W.; Yangting, X.; Feng, D.; Hui, X.; Chenchen, Y. Review Research on the Four-switch Buck-Boost Converter. J. Electr. Eng. 2023, 18, 52–69. [Google Scholar] [CrossRef]
- Sahu, B.; Rincón-Mora, G.A. A low voltage, dynamic, noninverting, synchronous buck-boost converter for portable applications. IEEE Trans. Power Electron. 2004, 19, 443–452. [Google Scholar] [CrossRef]
- Gaboriault, M.; Notman, A. A high efficiency, noninverting, buck-boost DC-DC converter. In Proceedings of the Nineteenth Annual IEEE Applied Power Electronics Conference and Exposition, 2004. APEC ’04., Anaheim, CA, USA, 22–26 February 2004; pp. 1411–1415. [Google Scholar] [CrossRef]
- Rajarshi, P.; Maksimovic, D. Analysis of PWM nonlinearity in non-inverting buck-boost power converters. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 3741–3747. [Google Scholar] [CrossRef]
- Dey, U.; Veerachary, M. Two-Part Controller Design for Switched-Capacitor Based Buck–Boost Converter. IEEE Trans. Ind. Electron. 2024, 72, 5746–5760. [Google Scholar] [CrossRef]
- Callegaro, L.; Ciobotaru, M.; Pagano, D.J.; Turano, E.; Fletcher, J.E. A Simple Smooth Transition Technique for the Noninverting Buck–Boost Converter. IEEE Trans. Power Electron. 2017, 33, 4906–4915. [Google Scholar] [CrossRef]
- Lee, Y.-J.; Khaligh, A.; Emadi, A. A Compensation Technique for Smooth Transitions in a Noninverting Buck–Boost Converter. IEEE Trans. Power Electron. 2009, 24, 1002–1015. [Google Scholar] [CrossRef]
- Huang, P.-C.; Wu, W.-Q.; Ho, H.-H.; Chen, K.-H. Hybrid Buck–Boost Feedforward and Reduced Average Inductor Current Techniques in Fast Line Transient and High-Efficiency Buck–Boost Converter. IEEE Trans. Power Electron. 2009, 25, 719–730. [Google Scholar] [CrossRef]
- Kim, D.-H.; Lee, B.-K. An Enhanced Control Algorithm for Improving the Light-Load Efficiency of Noninverting Synchronous Buck–Boost Converters. IEEE Trans. Power Electron. 2015, 31, 3395–3399. [Google Scholar] [CrossRef]
- Yao, C.; Ruan, X.; Cao, W.; Chen, P. An Input Voltage Feedforward Control Strategy for Two-switch Buck-Boost DC-DC Converters. Proc. CSEE 2013, 33, 36–44, 191. [Google Scholar] [CrossRef]
- Malcovati, P.; Belloni, M.; Gozzini, F.; Bazzani, C.; Baschirotto, A. A 0.18-µm CMOS, 91%-efficiency, 2-A scalable buck-boost DC–DC converter for LED drivers. IEEE Trans. Power Electron. 2013, 29, 5392–5398. [Google Scholar] [CrossRef]
- Leilei, J.; Xiaofeng, S.; Zhiwen, Z.; Xiaowei, M.; Luming, D. Charge and Discharge Control Strategy for Eliminating the Operational Dead Zone of Noninverting Buck-Boost Converter. Proc. CSEE 2020, 40, 3270–3280. [Google Scholar] [CrossRef]
- Restrepo, C.; Konjedic, T.; Calvente, J.; Giral, R. Hysteretic Transition Method for Avoiding the Dead-Zone Effect and Subharmonics in a Noninverting Buck–Boost Converter. IEEE Trans. Power Electron. 2014, 30, 3418–3430. [Google Scholar] [CrossRef]
- Vermeer, W.; Wolleswinkel, M.; Schijffelen, J.; Mouli, G.R.C.; Bauer, P. Three-Mode Variable-Frequency Modulation for the Four-Switch Buck-Boost Converter: A QR-BCM Versus TCM Case Study and Implementation. IEEE Trans. Ind. Electron. 2024, 72, 1512–1523. [Google Scholar] [CrossRef]
- Cao, Y.; Wu, D.; Zhu, D.; Jiang, Y.; Yang, W. Four-mode Control Strategy Based on Four-switch Buck-Boost Converter. J. Power Supply 2022, 20, 111–118. [Google Scholar] [CrossRef]
- Ren, X.; Ruan, X.; Qian, H.; Li, M.; Chen, Q. Dual-edge modulated four-switch Buck-Boost converter. IEEE Power Electron. Spec. 2009, 16–23. [Google Scholar] [CrossRef]
- Cao, Y.; Zhu, D.; Wu, D. Design of four-switch converter based on three-mode control. Chinese J. Power Sources 2021, 45, 665–668. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, G.; See, K.W. Systematic Derivation of Dead-Zone Elimination Strategies for the Noninverting Synchronous Buck–Boost Converter. IEEE Trans. Power Electron. 2017, 33, 3497–3508. [Google Scholar] [CrossRef]
- Zhang, N.; Batternally, S.; Lim, K.C.; See, K.W.; Han, F. Analysis of the non-inverting buck-boost converter with four-mode control method. In Proceedings of the IECON 2017-43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 876–881. [Google Scholar] [CrossRef]
- Wang, H.; Chen, A.; Xue, Y. Research on Smooth Mode Transition Strategy of FSBB Converter Based on Graphical Method. J. Power Supply 2023, 1–14. Available online: https://kns.cnki.net/kcms/detail/12.1420.TM.20230309.0948.002.html (accessed on 2 June 2024).
- Liu, S. Research on DC/DC Converter with Wide Input Voltage and the Method of Improving Efficiency. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2017. [Google Scholar]
- Jie, S. Research and Design on High Efficiency Non-Isolated Four Switch Buck-Boost Converter. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2018. [Google Scholar]
- Wu, J.; Yang, X.; Wang, D.; Wang, K.; Chen, W. Low Ripple-Variable Frequency Control Strategy for High Efficiency Wide Range Four-Switch Buck-Boost Converter. Trans. China Electrotech. Soc. 2024, 40, 3236–3250. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, F.; Li, H.; Yan, M. High-efficiency four-switch buck-boost converter multi-mode control strategy. Chin. J. Sci. Instrum. 2024, 45, 101–116. [Google Scholar]
- Fang, T.; Wang, Y.; Zhang, H.; Zhang, Y.; Sheng, S.; Lan, J. An Improved Three-Mode Variable Frequency Control Strategy Based on Four-Switch Buck-Boost Converter. Trans. China Electrotech. Soc. 2021, 36, 4544–4557. [Google Scholar] [CrossRef]
- Kang, J.; Chen, X.; Liu, J.; Wang, S. Research on Three-mode Smooth Switching Control Strategy Based on Four Switch Buck-Boost. Sci. Technol. Eng. 2019, 19, 193–199. [Google Scholar]
- Yang, H.; Chao, K.; Sun, X.; Zhang, Q.; Luo, S. Predictive Current Control Method for Bidirectional DC-DC Converter Based on Optimal Operating Time of Vector. Trans. China Electrotech. Soc. 2020, 35, 70–80. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Z.; Li, K.; Zhang, P.; Gao, F. Predictive current control for voltage source inverters considering dead-time effect. CES Trans. Electr. Mach. Syst. 2020, 4, 35–42. [Google Scholar] [CrossRef]
- Wang, Z.; Yin, X.; Chen, Y.; Lai, J.; Sun, G. Arm Current Control Strategy of Modular Multilevel Converter Based on Continuous Control Set Model Predictive Control. Proc. CSU-EPSA 2020, 44, 85–91. [Google Scholar]
- Yan, W.; Wei, W.; Guohong, Z.; Xuezhi, W.; Fen, T. Multi-Mode Model Predictive Control Strategy for the Four-Switch Buck-Boost Converter. Trans. China Electrotech. Soc. 2022, 37, 2572–2583. [Google Scholar] [CrossRef]
- Xia, K.; Li, Z.; Qin, Y.; Yuan, Y.; Yuan, Q. Minimising peak current in boundary conduction mode for the four-switch buck–boost DC/DC converter with soft switching. IET Power Electron. 2019, 12, 944–954. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, H.; Wu, X. A Constant Frequency ZVS Control System for the Four-Switch Buck–Boost DC–DC Converter with Reduced Inductor Current. IEEE Trans. Power Electron. 2018, 34, 5996–6003. [Google Scholar] [CrossRef]
- Liu, Q.; Qian, Q.; Zheng, M.; Xu, S.; Sun, W.; Wang, T. An Improved Quadrangle Control Method for Four-Switch Buck-Boost Converter with Reduced Loss and Decoupling Strategy. IEEE Trans. Power Electron. 2021, 36, 10827–10841. [Google Scholar] [CrossRef]
- Jia, L.; Sun, X.; Pan, Y.; Zhang, M.; Li, X. Three-Segment Zvs Control Strategy for Noninverting Buck-Boost Converter. Acta Energiae Solaris Sin. 2023, 44, 110–119. [Google Scholar] [CrossRef]
- Waffler, S.; Kolar, J.W. A Novel Low-Loss Modulation Strategy for High-Power Bidirectional Buck \bm+\bm+ Boost Converters. IEEE Trans. Power Electron. 2009, 24, 1589–1599. [Google Scholar] [CrossRef]
- Muhammad, F.; Wu, X.; Yang, J.; Tian, L.; Liu, T. Soft-Switching Control for a Resonant Four-Switch Inverting Buck–Boost DC/DC Converter with Wide Voltage Range. IEEE Trans. Power Electron. 2023, 38, 12536–12546. [Google Scholar] [CrossRef]
- Liu, F.; Xu, J.; Chen, Z.; Yang, P.; Deng, K.; Chen, X. A Multi-Frequency PCCM ZVS Modulation Scheme for Optimizing Overall Efficiency of Four-Switch Buck–Boost Converter with Wide Input and Output Voltage Ranges. IEEE Trans. Ind. Electron. 2023, 70, 12431–12441. [Google Scholar] [CrossRef]
- Gallo, E.; Caldognetto, T. A Zero-Voltage Switching Control for Four-Switch Buck–Boost Converters Using the Energy-Based Modeling. IEEE Trans. Power Electron. 2024, 40, 4757–4761. [Google Scholar] [CrossRef]
- Feng, X.; Shao, K.; Cui, X. Control strategy of wide voltage gain LLC resonant converter based on multi-mode switching. Trans. China Electrotech. Soc. 2020, 35, 4350–4360. [Google Scholar]
- Wen, Z.; Tang, W.; Xu, D. Quasi-Peak Current Control Strategy for Four-Switch Buck–Boost Converter. IEEE Trans. Power Electron. 2023, 38, 12607–12619. [Google Scholar] [CrossRef]
- Qiu, G.; Khadkikar, V.; Zahawi, B.; Liao, J. Efficiency Optimization of Four-Switch Buck-Boost Converter Using Frequency-Domain Analysis. IEEE Trans. Transp. Electrif. 2024, 11, 2717–2731. [Google Scholar] [CrossRef]
- Dong, R.; Ruan, X.; Xiao, L. A Simplified Implementation with Improved Dynamic Performance of PWM Plus Phase-Shift Control for Four-Switch Buck–Boost Converter. IEEE Trans. Power Electron. 2023, 39, 3014–3023. [Google Scholar] [CrossRef]
- Liu, F.; Xu, J.; Chen, Z.; Huang, R.; Chen, X. A Constant Frequency ZVS Modulation Scheme for Four-Switch Buck–Boost Converter with Wide Input and Output Voltage Ranges and Reduced Inductor Current. IEEE Trans. Ind. Electron. 2022, 70, 4931–4941. [Google Scholar] [CrossRef]
- Liu, Q.; Qian, Q.; Ren, B.; Xu, S.; Sun, W.; Yang, L. A Two-Stage Buck–Boost Integrated LLC Converter with Extended ZVS Range and Reduced Conduction Loss for High-Frequency and High-Efficiency Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 9, 727–743. [Google Scholar] [CrossRef]
- Xiao, L.; Ruan, X.; Tse, C.K. Smooth Reversal of Power Transfer Direction for ZVS Bidirectional Four-Switch Buck-Boost Converter. IEEE Trans. Ind. Electron. 2024, 72, 600–609. [Google Scholar] [CrossRef]
- Tian, L.; Wu, X.; Jiang, C.; Yang, J. A Simplified Real-Time Digital Control Scheme for ZVS Four-Switch Buck–Boost with Low Inductor Current. IEEE Trans. Ind. Electron. 2021, 69, 7920–7929. [Google Scholar] [CrossRef]
- Liu, Q.; Shi, L.; Xu, Q.; Qian, Q.; Sun, W. The Research and Design of High-Efficiency Control Strategy for Fourswitch Buck-Boost Converter. Proc. CSEE 2025, 45, 690–704. [Google Scholar] [CrossRef]
- Liu, Q.; Xu, Q.; Qian, Q.; Ding, S.; Sun, W. A High-Efficiency Control Method with Lossless Current Sensing and Seamless Transition for Four-Switch Buck–Boost Converter. IEEE Trans. Power Electron. 2025, 40, 8871–8885. [Google Scholar] [CrossRef]
- Gallo, E.; Biadene, D.; Cvejić, F.; Spiazzi, G.; Caldognetto, T. An Energy-Based Model of Four-Switch Buck–Boost Converters. IEEE Trans. Power Electron. 2024, 39, 4139–4148. [Google Scholar] [CrossRef]
- Chowdary, K.; Majetich, S. Frequency-dependent magnetic permeability of Fe10Co90 nanocomposites. J. Phys. D Appl. Physics 2014, 47, 175001. [Google Scholar] [CrossRef]
- Zhou, W.; Zhong, X.; Sheng, K. High Temperature Stability and the Performance Degradation of SiC MOSFETs. IEEE Trans. Power Electron. 2013, 29, 2329–2337. [Google Scholar] [CrossRef]








| u | k | d1 | d2 | M |
|---|---|---|---|---|
| 0 < u < 1 | k > 1 | u | 0 | u |
| u = 1 | k = 1 | 1 | 0 | 1 |
| 1 < u < 2 | 0 < k < 1 | 1 | u − 1 | 1/(2 − u) |
| Strategy | Mode | k | Advantage | Limitation |
|---|---|---|---|---|
| Single-mode | - | - | The simplest control | High switch losses and large ripple in inductor current |
| Dual-mode | Buck Boost | Simple control and improved efficiency | Existence of boundary oscillation and poor dynamic performance | |
| Three-mode | Buck Buck–Boost Boost | Smooth transition | The conduction loss in the intermediate mode is relatively high | |
| Four-mode | Buck Extend Buck Extend Boost Boost | Smoothest transition and reduced ripple | The algorithm is complex and relies on high-precision sensors |
| Control Method | Advantage | Limitation | References | ||
|---|---|---|---|---|---|
| Three-mode | Simultaneous switching of paired transistors | Simple control | The maximum amplitude of the duty cycle jump | [28] | |
| fixing the duty cycle of either the Boost stage or the Buck stage | The control is relatively simple, and the duty cycle jump is reduced | In specific cases, significant duty cycle jumps still exist | [38] | ||
| Smoothly varying duty cycle | The three-mode control with the smoothest mode transition | There is still room for improvement compared to the four-mode control | [32] | ||
| Four-mode | Fixed duty cycle | Smoother mode transition | Large inductor current ripple | [31] | |
| Maximum duty cycle | Frequency conversion control | High efficiency and good dynamic performance | The control process is complex, and the system has a high computational load | [35,36] | |
| Model Predictive Control | Good dynamic performance and the ability to achieve fixed-frequency control | Dependent on model design and sensor accuracy | [42] | ||
| Method of Calculation | Advantage | Limitation | References | |
|---|---|---|---|---|
| lookup table | 3-D | Avoid complex calculations | Requires a large amount of storage resources | [47] |
| 2-D | Decoupling control variables | [56] | ||
| Simplified Real-Time Calculation Method | Fixed control variable | Save costs and reduce computational complexity | Complex EMI design | [58] |
| Using a new mathematical model | Fast dynamic response and reduced computational complexity | Rationality needs further verification through practice | [61] | |
| Approximate duty cycle phase shift method | Fast dynamic response | It will lead to a decrease in efficiency | [54] | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, G.; Li, Y.; Zhang, Z. A Review of Control Strategies for Four-Switch Buck–Boost Converters. World Electr. Veh. J. 2025, 16, 315. https://doi.org/10.3390/wevj16060315
Lin G, Li Y, Zhang Z. A Review of Control Strategies for Four-Switch Buck–Boost Converters. World Electric Vehicle Journal. 2025; 16(6):315. https://doi.org/10.3390/wevj16060315
Chicago/Turabian StyleLin, Guanzheng, Yan Li, and Zhaoyun Zhang. 2025. "A Review of Control Strategies for Four-Switch Buck–Boost Converters" World Electric Vehicle Journal 16, no. 6: 315. https://doi.org/10.3390/wevj16060315
APA StyleLin, G., Li, Y., & Zhang, Z. (2025). A Review of Control Strategies for Four-Switch Buck–Boost Converters. World Electric Vehicle Journal, 16(6), 315. https://doi.org/10.3390/wevj16060315






