Research on Robust Adaptive Model Predictive Control Based on Vehicle State Uncertainty
Abstract
1. Introduction
- Robust MPC (RMPC) incorporates uncertainty modeling to enhance system adaptability to external disturbances (e.g., crosswinds, slippery road surfaces, and adaptive variations in tire cornering stiffness).
- Uncertainty characterization embeds robust optimization strategies into the MPC objective function and constraints, ensuring controller stability across diverse operating conditions.
- The adaptive soft-constraint strategy employs a constraint relaxation optimization method, introducing slack variables and penalty terms into the objective function, which allows for controlled relaxation of constraints within safe boundaries, ensuring MPC feasibility in complex scenarios while significantly improving algorithmic adaptability.
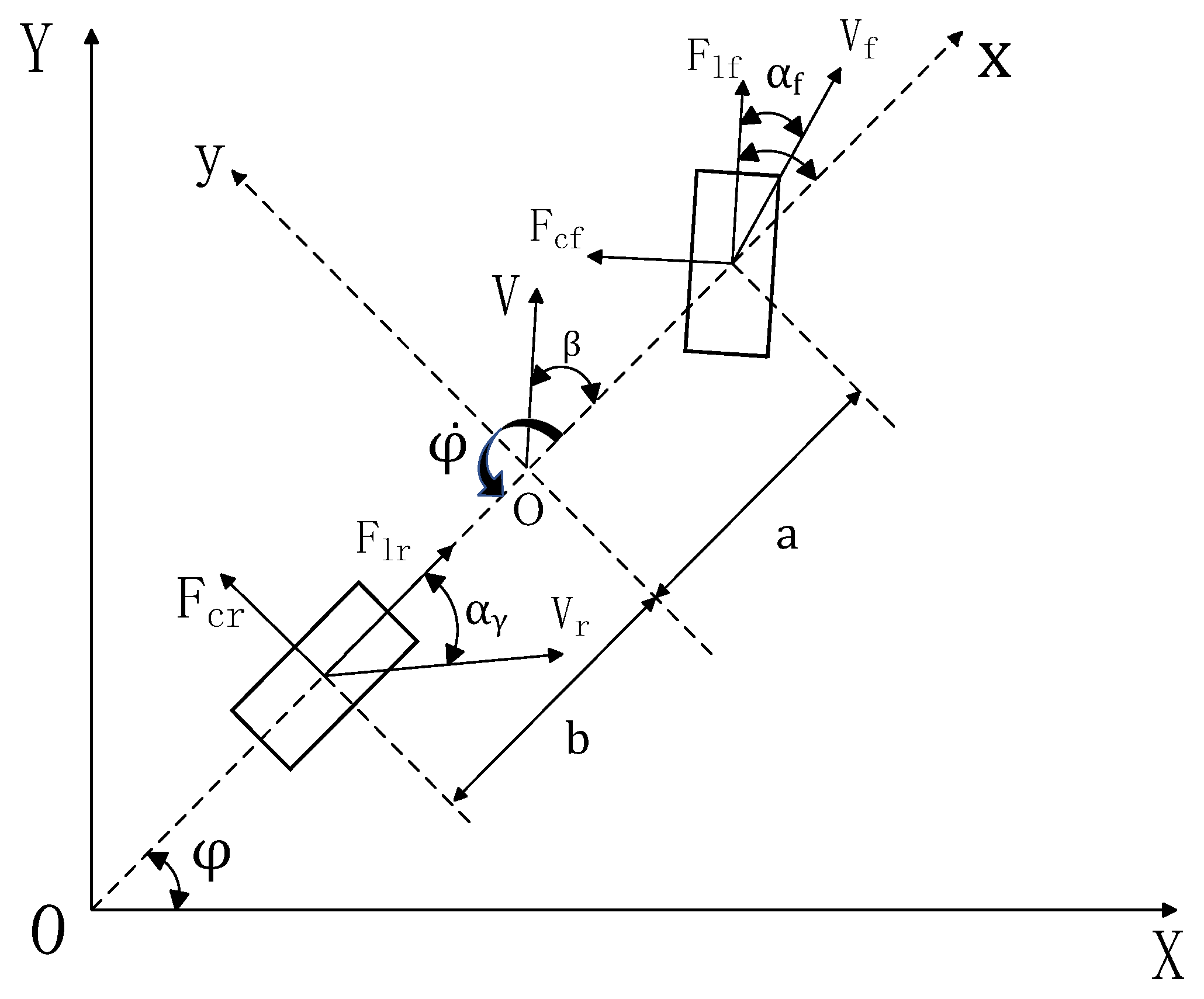
2. Vehicle Uncertainty Modeling
- The influence of vertical motion during vehicle operation can be ignored;
- The influence of the vehicle steering system can be ignored, and the front-wheel angle can be used as the control input;
- The influence of the front-wheel driving force on the vehicle yaw motion can be ignored;
- The influence of aerodynamics on the overall vehicle motion can be ignored.
3. Adaptive Control Strategy for Robust MPC
3.1. Online Estimation and Compensation Strategy for Tire Sideslip Stiffness
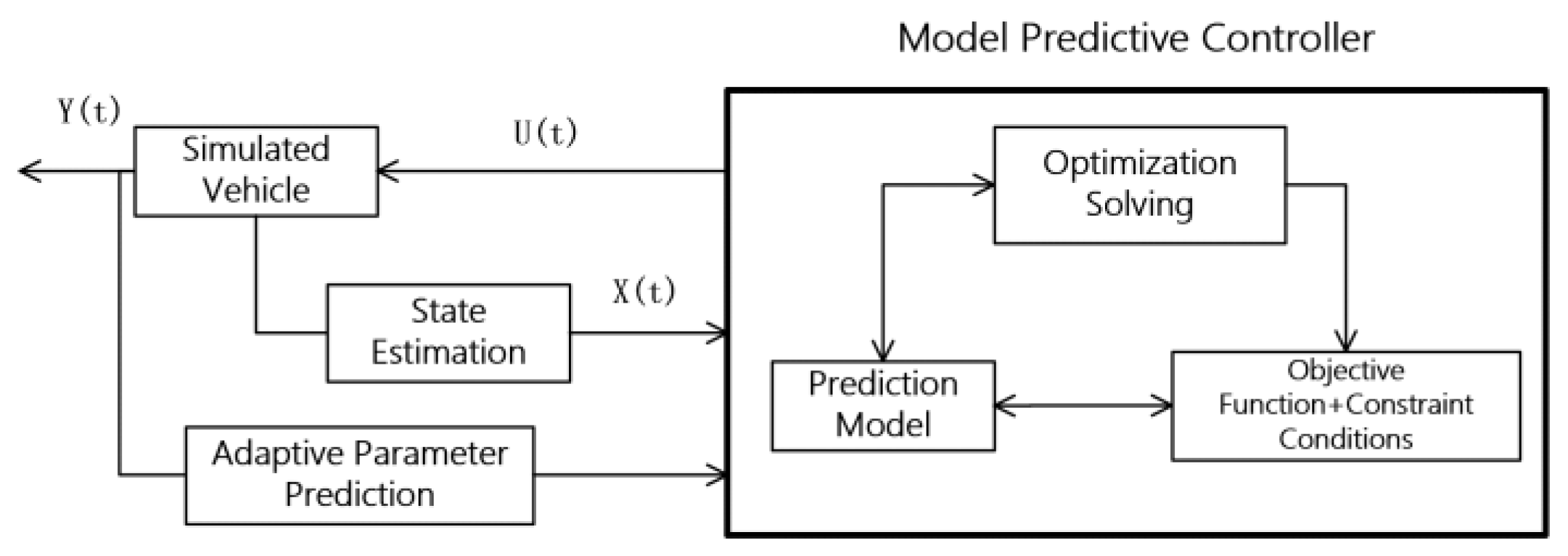
3.2. Design of an MPC Controller
3.3. Adaptive Optimization Objective Construction and Constraint Adjustment Strategy
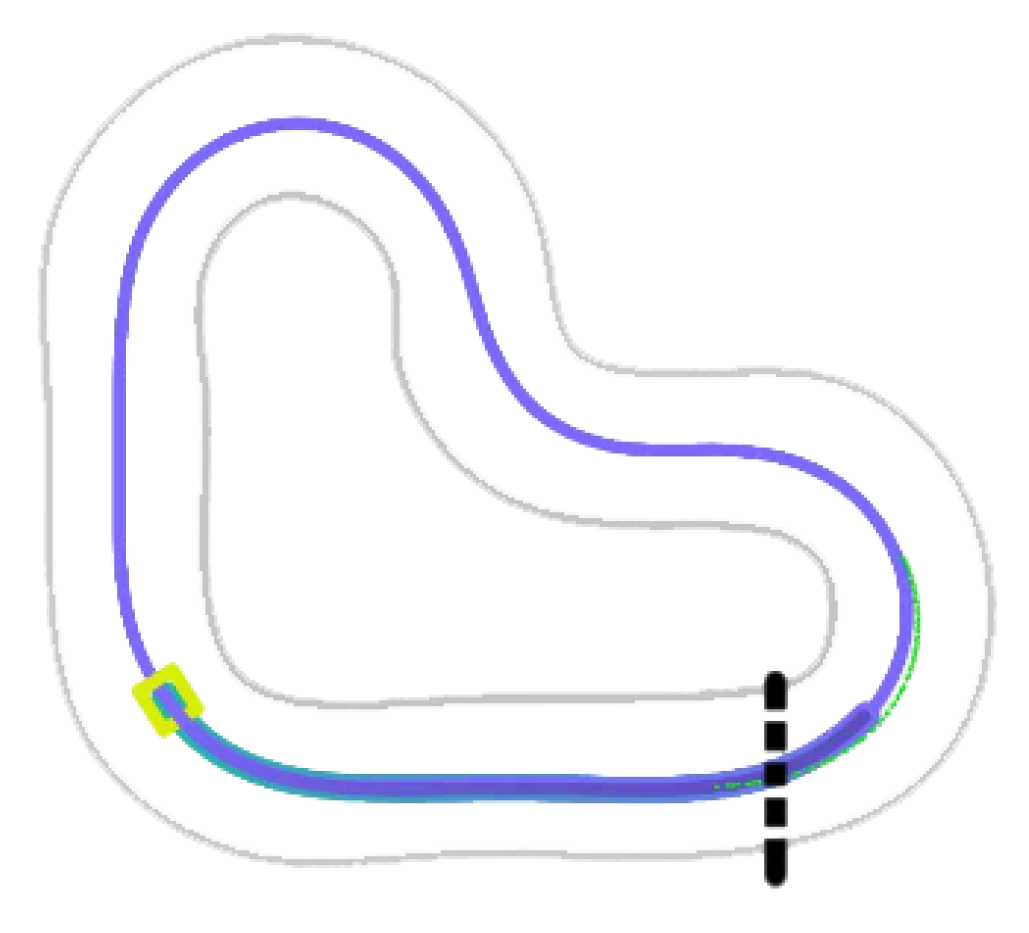
4. Experimental Co-Simulation
5. Results
- Uncertainty modeling and robust optimization: By incorporating uncertainty modeling and robust optimization to characterize state uncertainties and by embedding robust constraints into the MPC framework, the proposed method significantly enhances the system’s resistance to external disturbances (e.g., crosswinds and variations in tire cornering stiffness). This approach reduces the impact of model errors on the control performance and strengthens the system’s robustness against uncertainties.
- Adaptive constraint relaxation optimization mechanism: A flexible constraint conversion method is proposed based on the dynamic adjustment of penalty term weighting factors. By introducing slack variables, hard constraints are transformed into quantifiable soft constraints, resolving the infeasibility issues in traditional MPC caused by rigid constraints. Concurrently, adaptive penalty factors suppress excessive relaxation, achieving a balance between constraint flexibility and control freedom while ensuring system stability.
- The engineering effectiveness of the improved algorithm was validated through an ROS–MATLAB co-simulation platform and real-vehicle tests. Under complex operating conditions involving crosswind disturbances and adaptive variations in tire cornering stiffness, the enhanced MPC algorithm demonstrated significant improvements in control input smoothness and vehicle operational efficiency, further confirming its potential for practical applications. Future research will explore dynamic weight allocation mechanisms in multi-objective optimization frameworks and will integrate online parameter identification techniques to improve adaptability to long-term variations. This study provides novel theoretical tools and practical methodologies for efficient and safe vehicle control.
- Online parameter identification and adaptive optimization: Dynamic real-time calibration of model parameters can be achieved by integrating delayed online estimation technology from the literature and the adaptive weight adjustment strategy proposed in this study.
- Computational efficiency optimization: Aiming to address the computational burden brought about by the extended state MPC algorithm, efficient implementation schemes based on edge computing or sparse optimization algorithms will be studied to further improve the real-time performance of the control system.
- Full-dimensional collaborative control: By combining the advantages of the two MPC algorithms of horizontal trajectory tracking and longitudinal speed control, a global vehicle dynamic coupling model will be constructed, and track–speed collaborative optimization control under complex driving scenarios can finally be achieved.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, W.; Chen, Y.; Lian, C. Integrated Spatial Kinematics-Dynamics Model Predictive Control for Collision-Free Autonomous Vehicle Tracking. Actuators 2024, 13, 153. [Google Scholar] [CrossRef]
- Ji, Y.B.; Zhang, Y.; Liu, Z.L. Design of Follow-up Control in Auto-tracking Smart Car System. In Proceedings of the International Conference on Mechatronics and Industrial Informatics (ICMII 2013), Guangzhou, China, 13–14 March 2013; IEEE: Guangzhou, China, 2013; pp. 234–240. [Google Scholar]
- Jond, H.B.; Platos, J. A Fast Trajectory Tracking Control Design for Autonomous Driving. In Proceedings of the 7th International Conference on Robotics and Mechatronics (ICRoM), Tehran, Iran, 20–21 November 2019; Sharif University of Technology: Tehran, Iran, 2019; pp. 45–52. [Google Scholar]
- Li, Y.; Moreau, J.; Ibanez-Guzman, J. Emergent Visual Sensors for Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2023, 24, 4716–4737. [Google Scholar] [CrossRef]
- Wei, P.; Zeng, Y.; Ouyang, W.; Zhou, J. Multi-Sensor Environmental Perception and Adaptive Cruise Control of Intelligent Vehicles Using Kalman Filter. IEEE Trans. Intell. Transp. Syst. 2024, 25, 3098–3107. [Google Scholar] [CrossRef]
- Tang, X.; Yang, K.; Wang, H.; Yu, W.; Yang, X.; Liu, T.; Li, J. Driving Environment Uncertainty-Aware Motion Planning for Autonomous Vehicles. Chin. J. Mech. Eng. 2022, 35, 120. [Google Scholar] [CrossRef]
- Jeong, Y. Integrated Vehicle Controller for Path Tracking with Rollover Prevention of Autonomous Articulated Electric Vehicle Based on Model Predictive Control. Actuators 2023, 12, 41. [Google Scholar] [CrossRef]
- Subari, M.A.; Hudha, K.; Abd Kadir, Z.; Dardin, S.M.F.S.M.; Amer, N.H. Development of Path Tracking Controller for an Autonomous Tracked Vehicle. In Proceedings of the 16th IEEE International Colloquium on Signal Processing and its Applications (CSPA), Langkawi, Malaysia, 28–29 February 2020; IEEE: Langkawi, Malaysia, 2020; pp. 123–130. [Google Scholar]
- Zhao, W.Q. Real-Time Model Predictive Control of Path-Following for Autonomous Vehicles Towards Model Mismatch and Uncertainty. Control Eng. Pract. 2024, 142, 105678. [Google Scholar] [CrossRef]
- Dong, Z.; Shi, W.; Tong, G.; Yang, K. Collaborative Autonomous Driving: Vision and Challenges. In Proceedings of the International Conferencon Connected and Autonomous Driving (MetroCAD), Detroit, MI, USA, 27–28 February 2020; SAE International: Detroit, MI, USA, 2020; pp. 89–95. [Google Scholar]
- Bhat, V.S.; Kumar, V.; Dayanand, N.; Shettigar, A.; Nikhitha. Comparative Study of PID Control Algorithms for an Electric Vehicle. In Proceedings of the 2nd International Conference on Emerging Trends in Mechanical Engineering (ETIME), Mangaluru, India, 9–10 August 2019; Springer: Mangaluru, India, 2019; pp. 76–85. [Google Scholar]
- Peicheng, S.; Li, L.; Ni, X.; Yang, A. Intelligent Vehicle Path Tracking Control Based on Improved MPC and Hybrid PID. IEEE Access 2022, 10, 94133–94144. [Google Scholar] [CrossRef]
- Li, H.; Li, J.; Wang, R.; Luo, J. Path Planning and Tracking Strategy under Emergency for Vehicle Obstacle Avoidance System. In Proceedings of the 3rd International Conference on Robotics, Control and Automation Engineering (RCAE), Chongqing, China, 5–8 November 2020; IEEE: Chongqing, China, 2020; pp. 112–119. [Google Scholar]
- Yang, T.B.; Li, Z.; Feng, N.; Chen, L. Intelligent Vehicle Lateral Control Method Based on Feedforward+ Predictive LQR Algorithm. Actuators 2021, 10, 228. [Google Scholar] [CrossRef]
- Deng, Z.W.; Zhao, Q.X.; Zhao, Y.Q.; Wang, B.H.; Gao, W.; Kong, X.X. Active LQR Multi-Axle-Steering Method for Improving Maneuverability and Stability of Multi-Trailer Articulated Heavy Vehicles. Int. J. Automot. Technol. 2022, 23, 939–955. [Google Scholar] [CrossRef]
- Zhou, Z.; Bao, Y.; Fan, J. Research on Improving Vehicle Stability Control Using Enhanced LQR Method. In Proceedings of the 3rd International Conference on Energy and Power Engineering, Control Engineering (EPECE), Chengdu, China, 23–25 February 2024; IEEE: Chengdu, China, 2024; pp. 234–241. [Google Scholar]
- Sun, Y.; Dai, Q.; Liu, J.; Zhao, X.; Guo, H. Intelligent Vehicle Path Tracking Based on Feedback Linearization and LQR under Extreme Conditions. In Proceedings of the 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; IEEE: Hefei, China, 2022; pp. 678–685. [Google Scholar]
- Cui, K.; He, J.; Yao, X.; Gu, X. Adaptive Model Predictive Control Based on Stability Index for Path Tracking of Autonomous Vehicles Considering Model Error. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 238, 9372–9396. [Google Scholar] [CrossRef]
- Wang, X.H.; Han, M.; Gao, Z.; Li, L.; Miao, Z. Path Tracking and Obstacle Avoidance Algorithm Based on Model Predictive Control. In Proceedings of the 34th Chinese Control and Decision Conference (CCDC), Hefei, China, 15–17 August 2022; IEEE: Hefei, China, 2022; pp. 102–109. [Google Scholar]
- Jing, Z.Y.; Huang, W.; Ma, H. A Tracking Control Method for Collision Avoidance Trajectory of Autonomous Vehicle Based on Multi-Constraint MPC. Int. J. Veh. Des. 2021, 86, 106–123. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, K.J.; Cheng, M. Optimal Control of Nonlinear Systems with Integer-Valued Control Inputs and Stochastic Constraints. Int. J. Robust Nonlinear Control 2022, 32, 10326–10346. [Google Scholar] [CrossRef]
- Yu, S.; Pan, X.; Georgiou, A.; Chen, B.; Jaimoukha, I.M.; Evangelou, S.A. A Robust Model Predictive Control Framework for Ecological Adaptive Cruise Control Strategy of Electric Vehicles. In Proceedings of the IEEE International Conference on Mechatronics (ICM), Loughborough, UK, 15–17 March 2023; IEEE: Loughborough, UK, 2023; pp. 88–95. [Google Scholar]
- Li, R. Preview Control with Dynamic Constraints for Autonomous Vehicles. Sensors 2021, 21, 5155. [Google Scholar] [CrossRef]
- Bujarbaruah, M.; Nair, S.H.; Borrelli, F. A Semi-Definite Programming Approach to Robust Adaptive MPC under State Dependent Uncertainty. In Proceedings of the 18th European Control Conference (ECC), St. Petersburg, Russia, 12–15 May 2020; IEEE: St. Petersburg, Russia, 2020; pp. 456–463. [Google Scholar]
- Cheng, S.; Li, L.; Chen, X.; Wu, J.; Wang, H.-D. Model-Predictive-Control-Based Path Tracking Controller of Autonomous Vehicle Considering Parametric Uncertainties and Velocity-Varying. IEEE Trans. Ind. Electron. 2021, 68, 8698–8707. [Google Scholar] [CrossRef]
- Iqbal, J. Electric Vehicle Cornering Stiffness & Lateral States Estimation Using Synchronized Adaptive Sliding Mode Observer and Kalman Filter. Int. Trans. J. Eng. Manag. Appl. Sci. Technol. 2021, 12, 234–248. [Google Scholar]
- Qi, G.X. Integrated Control Method for Path Tracking and Lateral Stability of Distributed Drive Electric Vehicles with Extended Kalman Filter-Based Tire Cornering Stiffness Estimation. J. Vib. Control 2024, 30, 567–582. [Google Scholar] [CrossRef]
- Guirguis, J.M.; Hammad, S.; Maged, S.A. Path Tracking Control Based on an Adaptive MPC to Vehicle. Int. J. Mech. Eng. Robot. Res. 2022, 11, 535–541. [Google Scholar]
- Li, H.; Li, B.; Yang, H.; Mu, C. Nonlinear Model Predictive Control for Time-Optimal Turning Around of an Autonomous Vehicle Under Steering Lag. IEEE/ASME Trans. Mechatron. 2025, 30, 577–586. [Google Scholar] [CrossRef]
- Meng, D.; Chu, H.; Tian, M.; Gao, B.; Chen, H. Real-Time High-Precision Nonlinear Tracking Control of Autonomous Vehicles Using Fast Iterative Model Predictive Control. IEEE Trans. Intell. Veh. 2024, 9, 3644–3657. [Google Scholar] [CrossRef]
- Liang, J.; Tian, Q.; Feng, J.; Pi, D.; Yin, G. A Polytopic Model-Based Robust Predictive Control Scheme for Path Tracking of Autonomous Vehicles. IEEE Trans. Intell. Veh. 2024, 9, 3928–3939. [Google Scholar] [CrossRef]
- Tan, W.; Wang, M.F.; Ma, K. Research on Intelligent Vehicle Trajectory Tracking Control Based on Improved Adaptive MPC. Sensors 2024, 24, 2316. [Google Scholar] [CrossRef] [PubMed]
- Widner, A.; Tihanyi, V.; Tettamanti, T. Framework for Vehicle Dynamics Model Validation. IEEE Access 2022, 10, 35422–35436. [Google Scholar] [CrossRef]
- Chen, S.P.; Chen, H.Y.; Negrut, D. Implementation of MPC-Based Path Tracking for Autonomous Vehicles Considering Three Vehicle Dynamics Models with Different Fidelities. Automot. Innov. 2020, 3, 386–399. [Google Scholar] [CrossRef]
- Kanchwala, H.; Viana Í, B.; Ceccoti, M.; Aouf, N. Model Predictive Tracking Controller for a High Fidelity Vehicle Dynamics Model. In Proceedings of the IEEE Intelligent Transportation Systems Conference (IEEE-ITSC), Auckland, New Zealand, 27–30 October 2019; IEEE: Auckland, New Zealand, 2019; pp. 112–120. [Google Scholar]
- Liu, J.; Jayakumar, P.; Overholt, J.L.; Stein, J.L.; Ersal, T. The Role of Model Fidelity in Model Predictive Control-Based Hazard Avoidance in Unmanned Ground Vehicles Using LiDAR Sensors. In Proceedings of the ASME Dynamic Systems and Control Conference (DSCC), Palo Alto, CA, USA, 21–23 October 2013; ASME: Palo Alto, CA, USA, 2013; pp. 234–241. [Google Scholar]
- Thakur, M.B.; Schmid, M. Efficient Uncertainty Mitigation in Automated Vehicles: Combining MPC with Model Reference Adaptive Control. In Proceedings of the 3rd Modeling, Estimation and Control Conference (MECC), Lake Tahoe, NV, USA, 2–5 October 2023; IEEE: Lake Tahoe, NV, USA, 2023; pp. 56–63. [Google Scholar]
- Gao, F.; Hu, Q.; Ma, J.; Han, X. A Simplified Vehicle Dynamics Model for Motion Planner Designed by Nonlinear Model Predictive Control. Appl. Sci. 2021, 11, 9887. [Google Scholar] [CrossRef]
- Kebbati, Y.; Puig, V.; Ait-Oufroukh, N.; Vigneron, V.; Ichalal, D. Optimized Adaptive MPC for Lateral Control of Autonomous Vehicles. In Proceedings of the 9th International Conference on Control, Mechatronics and Automation (ICCMA), Belval, Luxembourg, 11–14 November 2021; pp. 88–95. [Google Scholar]
- Yang, S.; Qian, Y.; Hu, W.; Xu, J.; Sun, H. Adaptive MPC-Based Lateral Path-Tracking Control for Automatic Vehicles. World Electr. Veh. J. 2024, 15, 95. [Google Scholar] [CrossRef]
- Lee, J.; Jo, K. Model Predictive Control with Powertrain Delay Consideration for Longitudinal Speed Tracking of Autonomous Electric Vehicles. World Electr. Veh. J. 2024, 15, 433. [Google Scholar] [CrossRef]
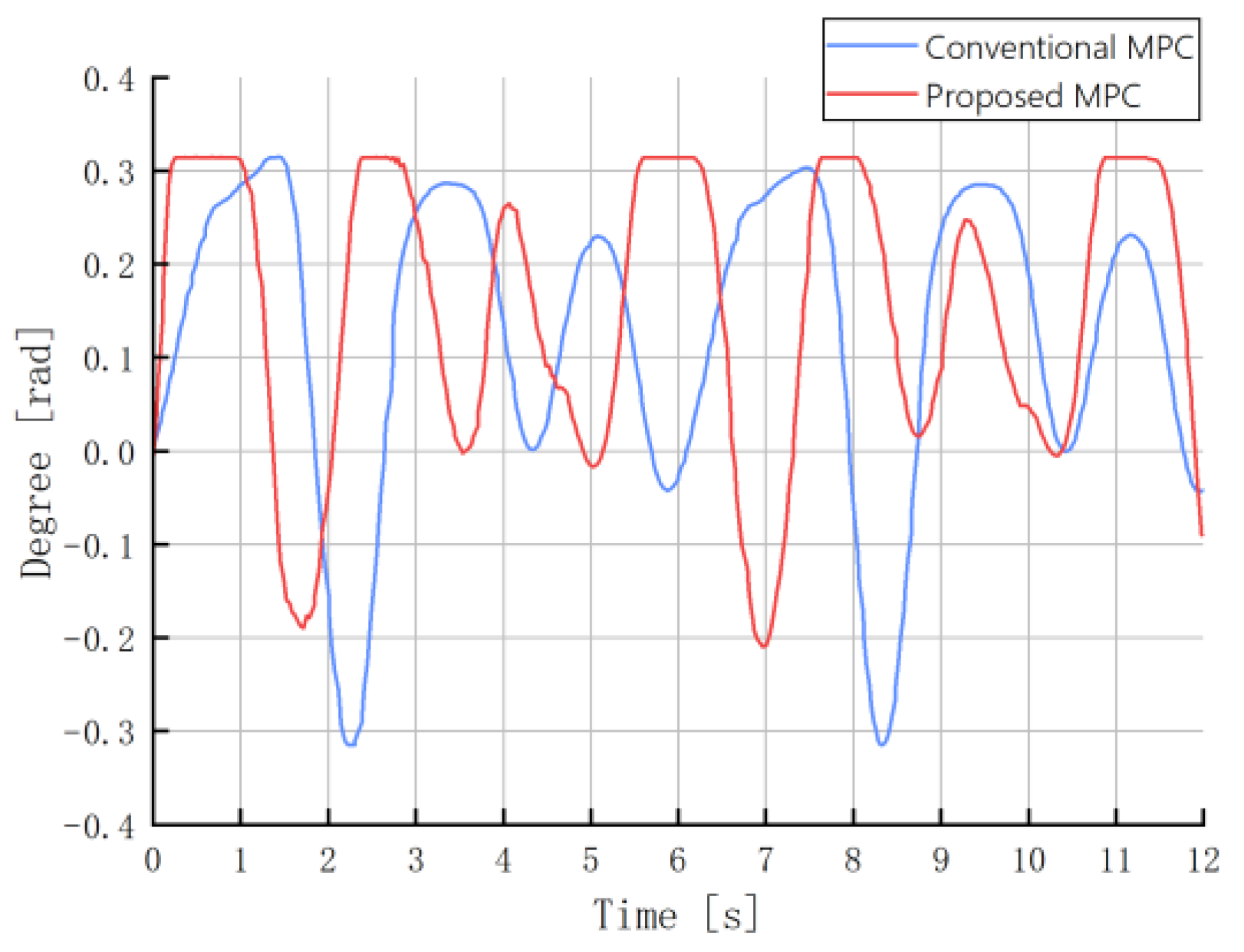
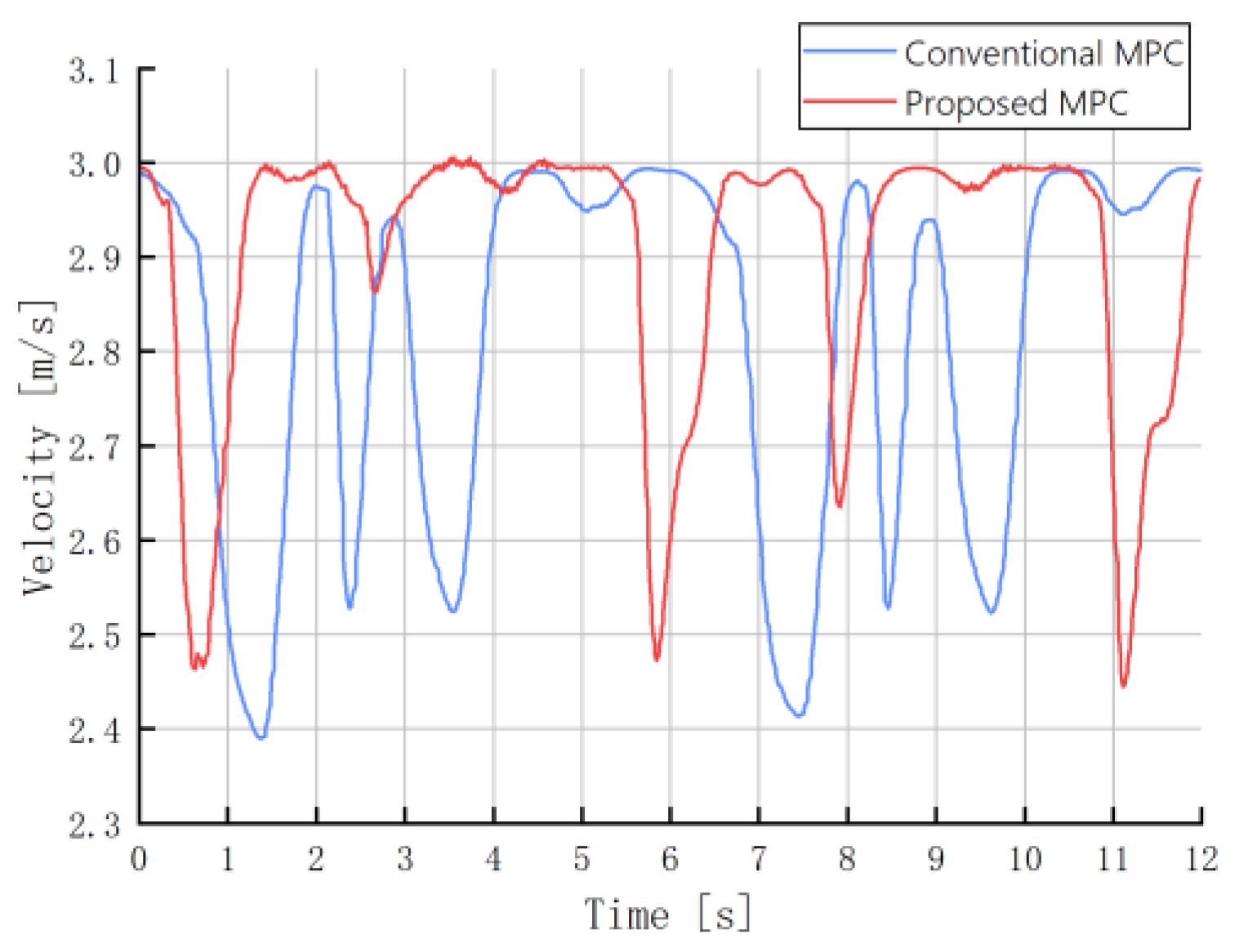
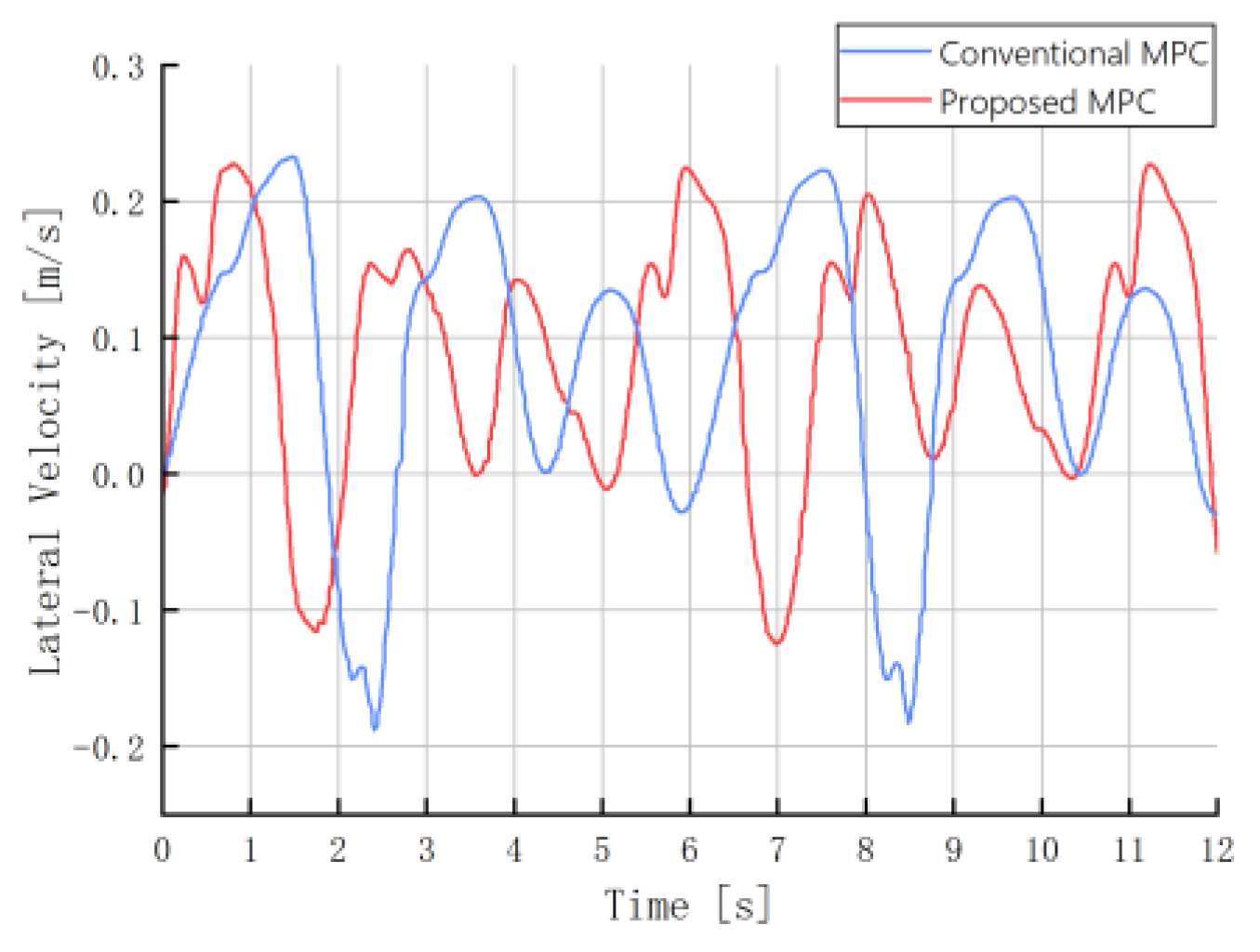
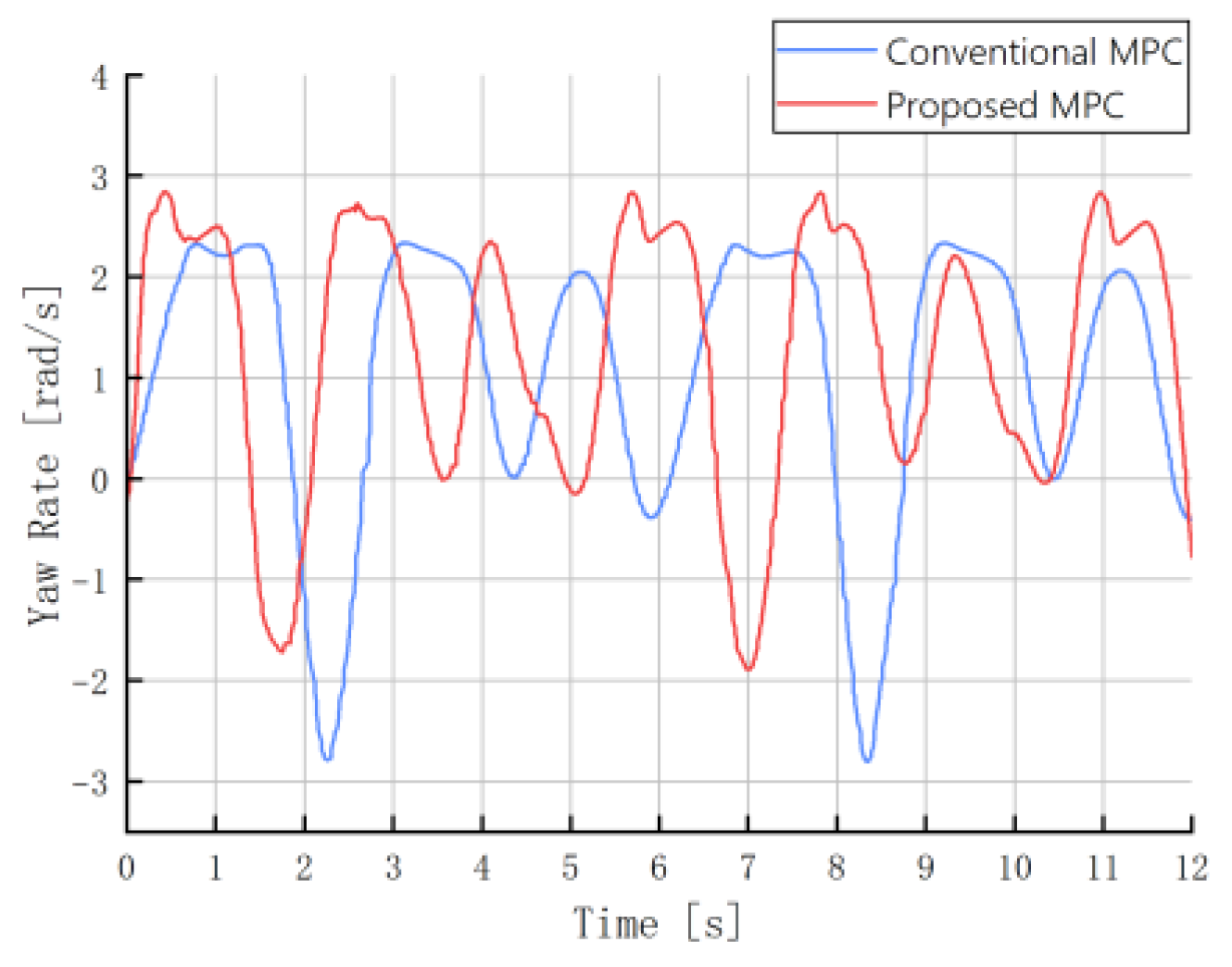
| Max Steering | Max Yaw Rate | Max Lateral Velocity | Max Velocity | |
|---|---|---|---|---|
| Conventional MPC | 0.314 | 2.335 | 0.233 | 2.994 |
| Proposed MPC | 0.020 | 3.102 | 0.227 | 3.006 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Liu, L. Research on Robust Adaptive Model Predictive Control Based on Vehicle State Uncertainty. World Electr. Veh. J. 2025, 16, 271. https://doi.org/10.3390/wevj16050271
Li Y, Liu L. Research on Robust Adaptive Model Predictive Control Based on Vehicle State Uncertainty. World Electric Vehicle Journal. 2025; 16(5):271. https://doi.org/10.3390/wevj16050271
Chicago/Turabian StyleLi, Yinping, and Li Liu. 2025. "Research on Robust Adaptive Model Predictive Control Based on Vehicle State Uncertainty" World Electric Vehicle Journal 16, no. 5: 271. https://doi.org/10.3390/wevj16050271
APA StyleLi, Y., & Liu, L. (2025). Research on Robust Adaptive Model Predictive Control Based on Vehicle State Uncertainty. World Electric Vehicle Journal, 16(5), 271. https://doi.org/10.3390/wevj16050271






