An Improved Finite-Set Predictive Control for Permanent Magnet Synchronous Motors Based on a Neutral-Point-Clamped Three-Level Inverter
Abstract
1. Introduction
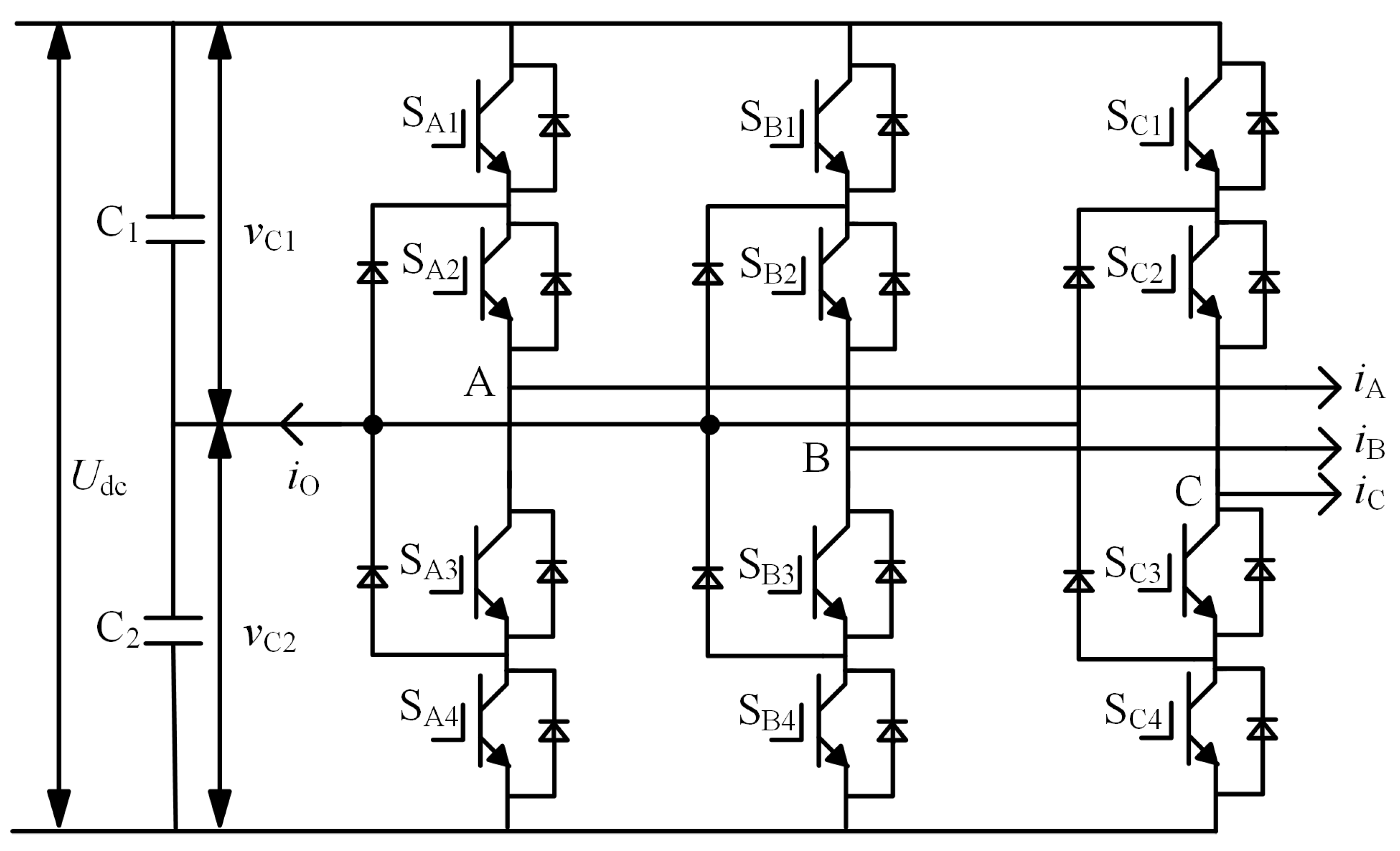
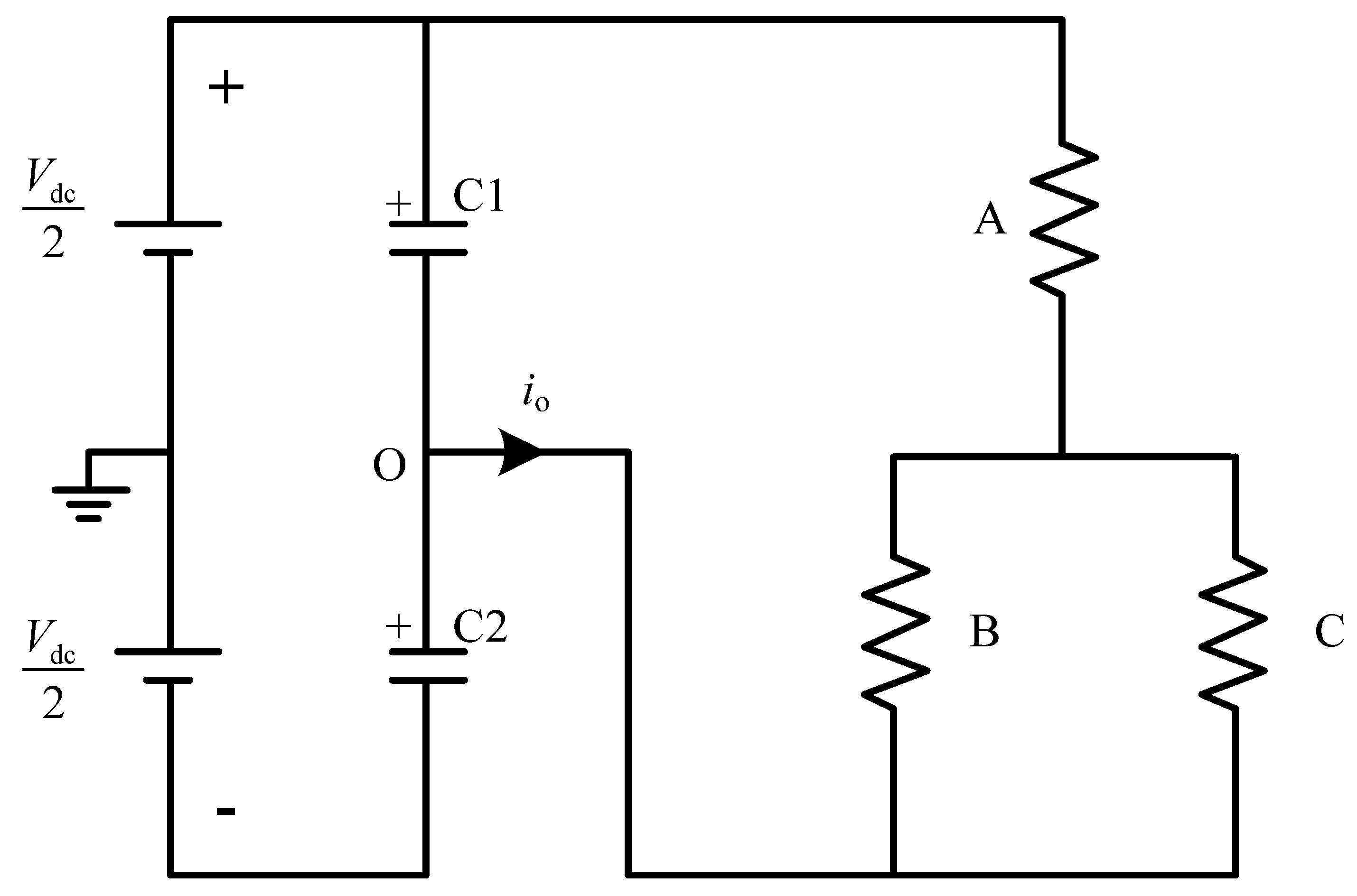
2. NPC Three-Level Inverter Structure
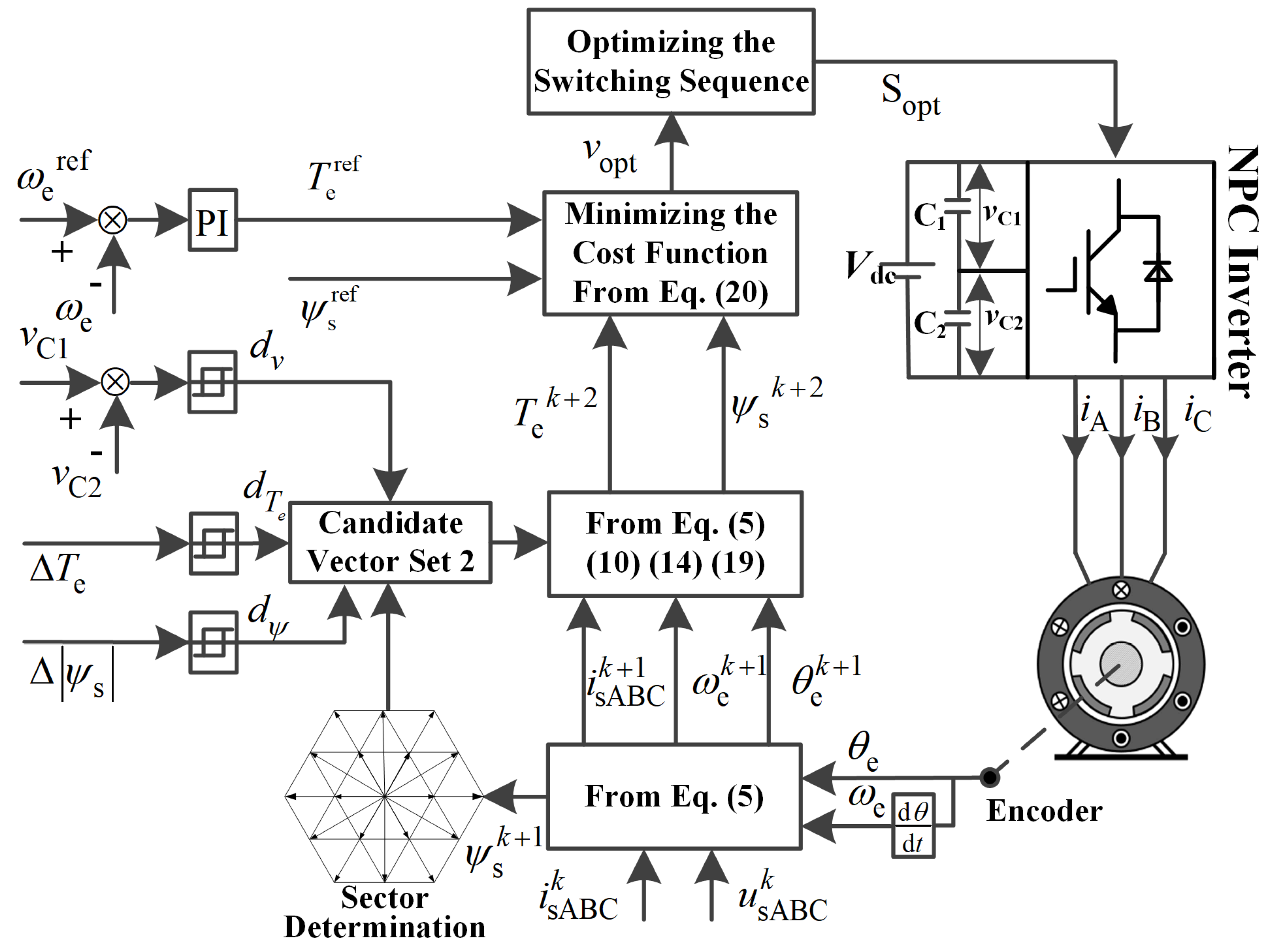
3. Predictive Control Algorithm for PMSM
- (1)
- The three-phase current ia, ib, ic, ωe, and θe and the neutralpoint voltage vo information of the PMSM are obtained at one moment.
- (2)
- Sampling and calculation delay compensation are performed. The collected data from the first step are used to obtain idk+1, iqk+1, and vok+1 at time (k + 1)Ts using Equations (5) and (10), which will serve as the initial values for the next prediction step.
- (3)
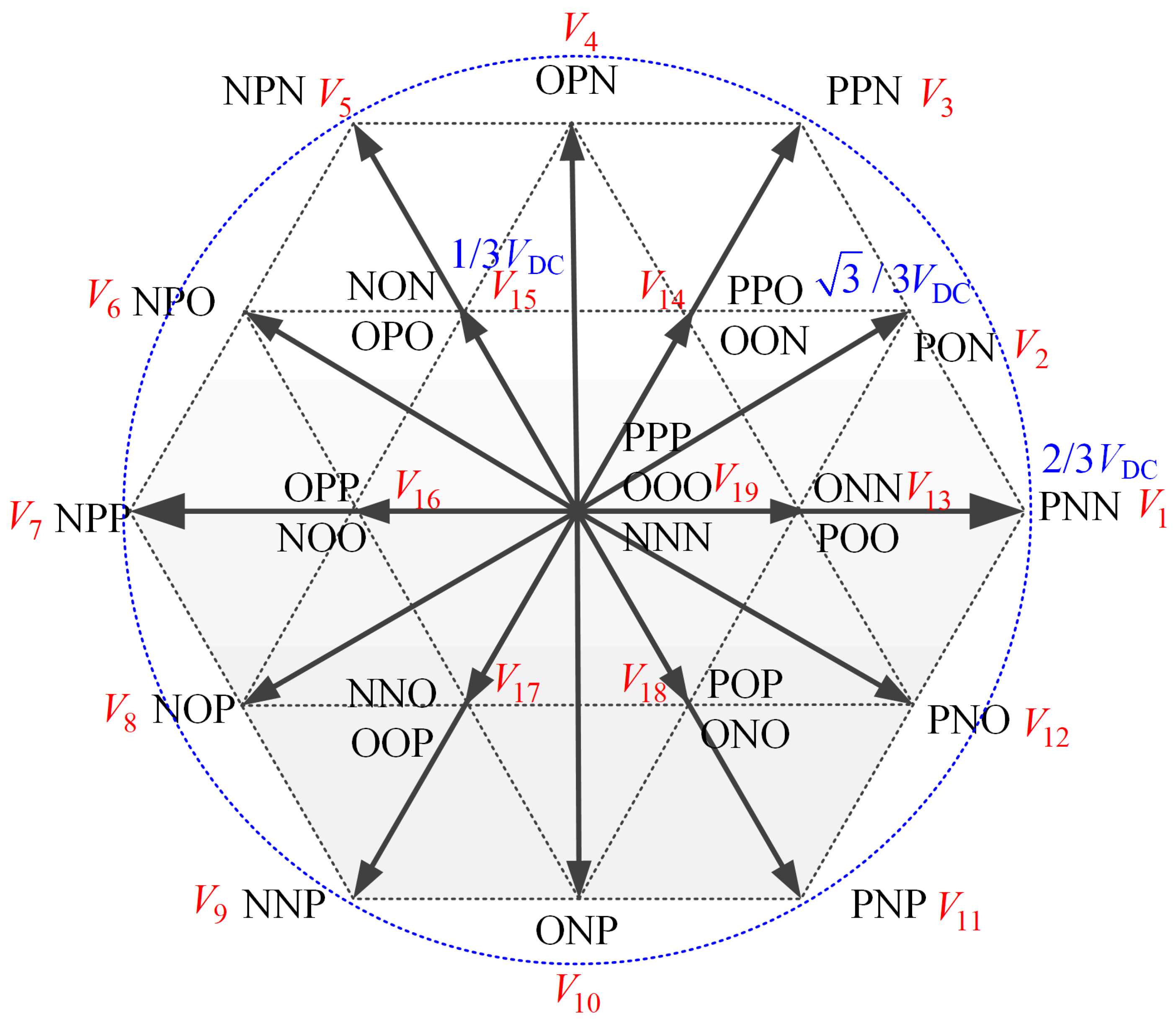
- The sector of the voltage vector from the previous control cycle is determined. The 16 voltage vectors from the 2 adjacent regions are selected as the candidate vector set. These candidate vectors are then substituted into Equations (5)–(7) and (10) to obtain TeNk+2, ψsNk+2, and vONk+2 at the (k + 2)Ts time step, where N is the voltage vector index.
- (4)
- Based on Equation (11), the cost function for each candidate voltage vector in the finite control set is calculated. The voltage vector corresponding to the minimum value of the cost function is then selected and applied to the inverter.
4. Improved Predictive Control
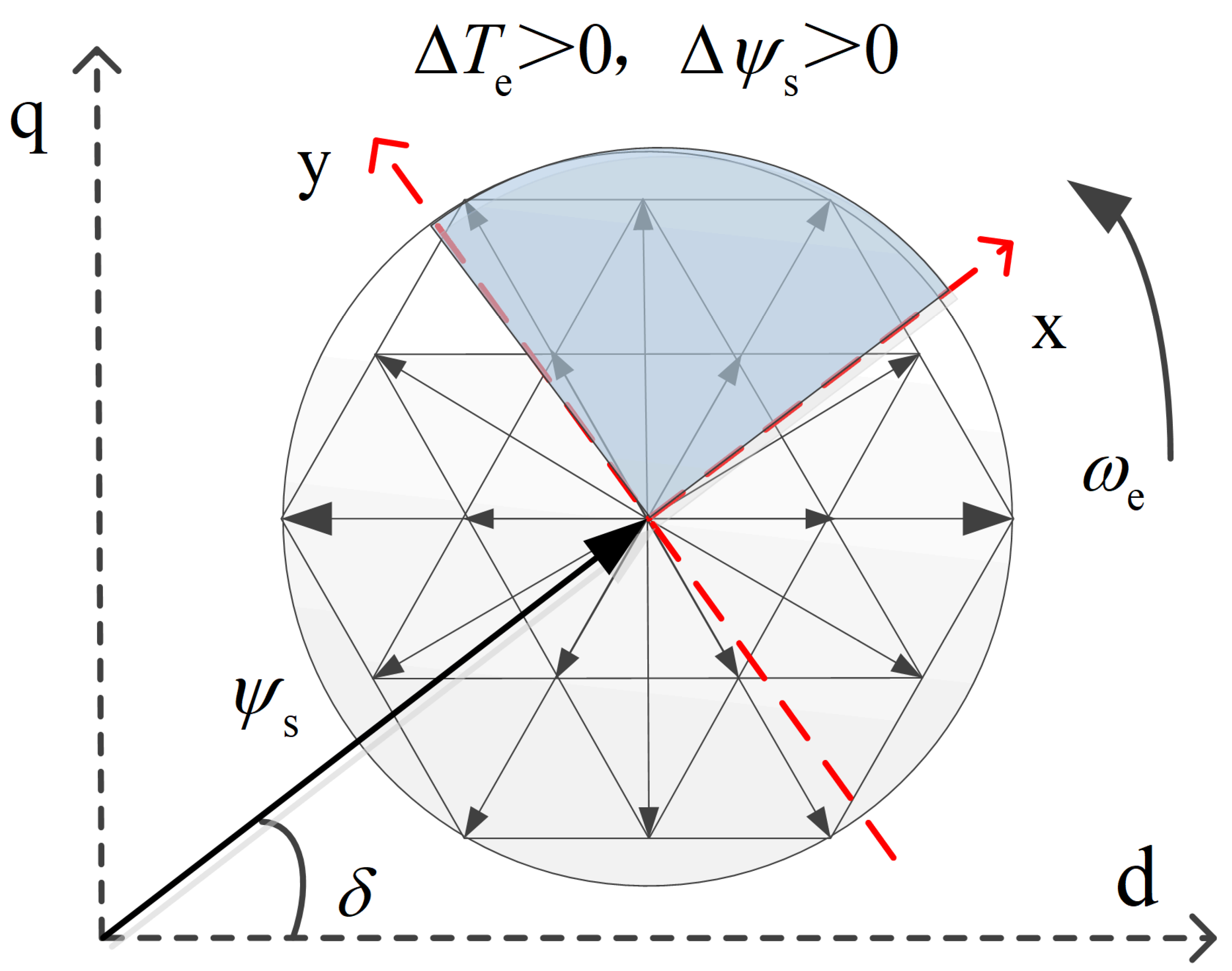
4.1. Vector Sector Selection Strategy
- (a)
- ∆Te > 0, ∆ψs > 0;
- (b)
- ∆Te > 0, ∆ψs < 0;
- (c)
- ∆Te < 0, ∆ψs < 0;
- (d)
- ∆Te < 0, ∆ψs > 0.
4.2. Elimination of the Neutral-Point Voltage Weighting Factor
- (1)
- Information about the three-phase currents iA, iB, iC, ωe, and θe and the neutral-point voltage vO of the PMSM at time (k)Ts is obtained.
- (2)
- Sampling and calculation delay compensation are performed. The data collected in the first step are used, and Equation (5) is applied to obtain idk+1 and iqk+1 at time (k + 1)Ts, which are then used as the initial values for the next prediction step.
- (3)
- The electrical angular speed and its reference value are input into the speed outer loop, which results in the reference torque Teref. The voltage difference between the upper and lower capacitors is input into the neutral-point voltage hysteresis comparator, resulting in ∆vO. The predicted torque value Tek+1 and the reference torque value Teref are input into the torque hysteresis comparator, resulting in ∆Te. The predicted flux linkage value ψsk+1 and the reference flux linkage value ψs ref are input into the flux linkage hysteresis comparator to determine the torque–flux linkage hysteresis, resulting in ∆|ψs|.
- (4)
- The values ∆vO, ∆Te, and ∆|ψs| from the previous steps are input into the candidate voltage vector selection mechanism, resulting in candidate voltage vector set 2. Each candidate voltage vector set 2 contains six basic voltage vectors. By substituting the six basic voltage vectors, along with idk+1, iqk+1, wek+1, and θek+1, into Equations (5), (14), (19), and (10), TeNk+2, TeNk+2, ψsNk+2, and vONk+2 at time (k + 2)Ts are obtained, where N represents the voltage vector index.
- (5)
- Based on Equation (20), the cost function corresponding to each candidate voltage vector in candidate vector set 2 is calculated. The voltage vector corresponding to the minimum value of the cost function is selected and applied to the inverter.
5. Experimental Analysis and Validation
5.1. Comparative Analysis of the Steady-State Performance
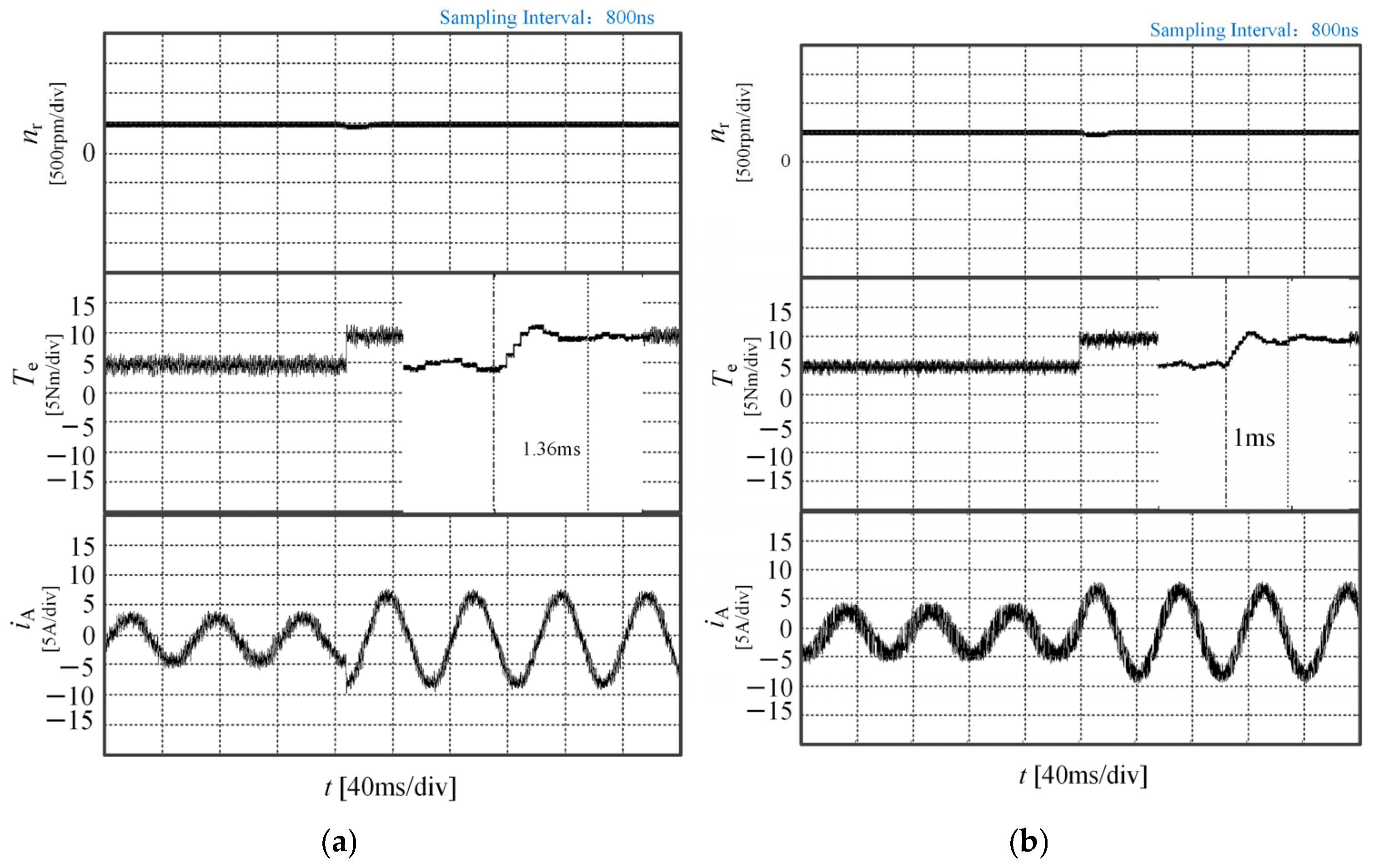
5.2. Comparative Analysis of Dynamic Performance
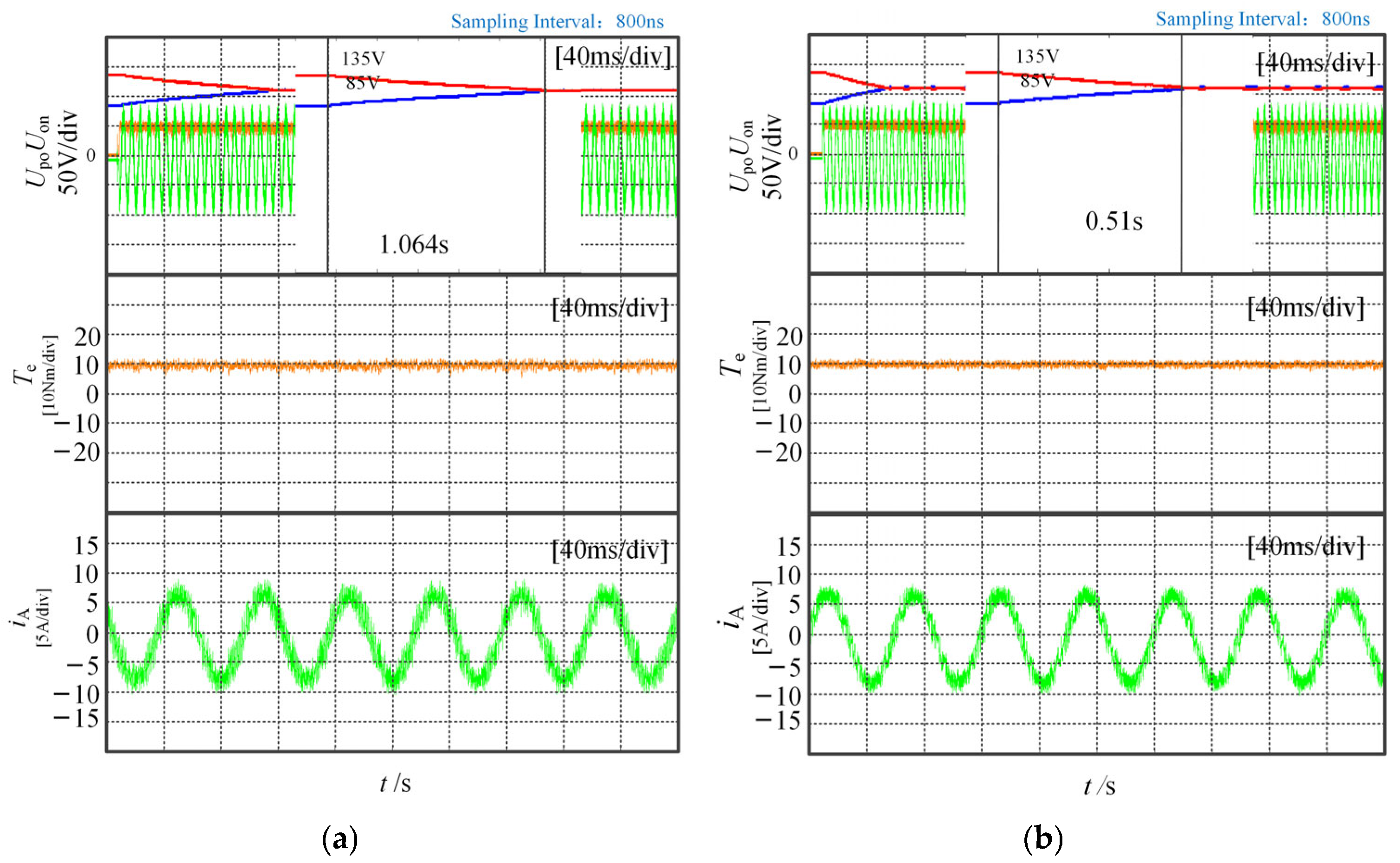
5.3. Neutral-Point Voltage Balancing Capability
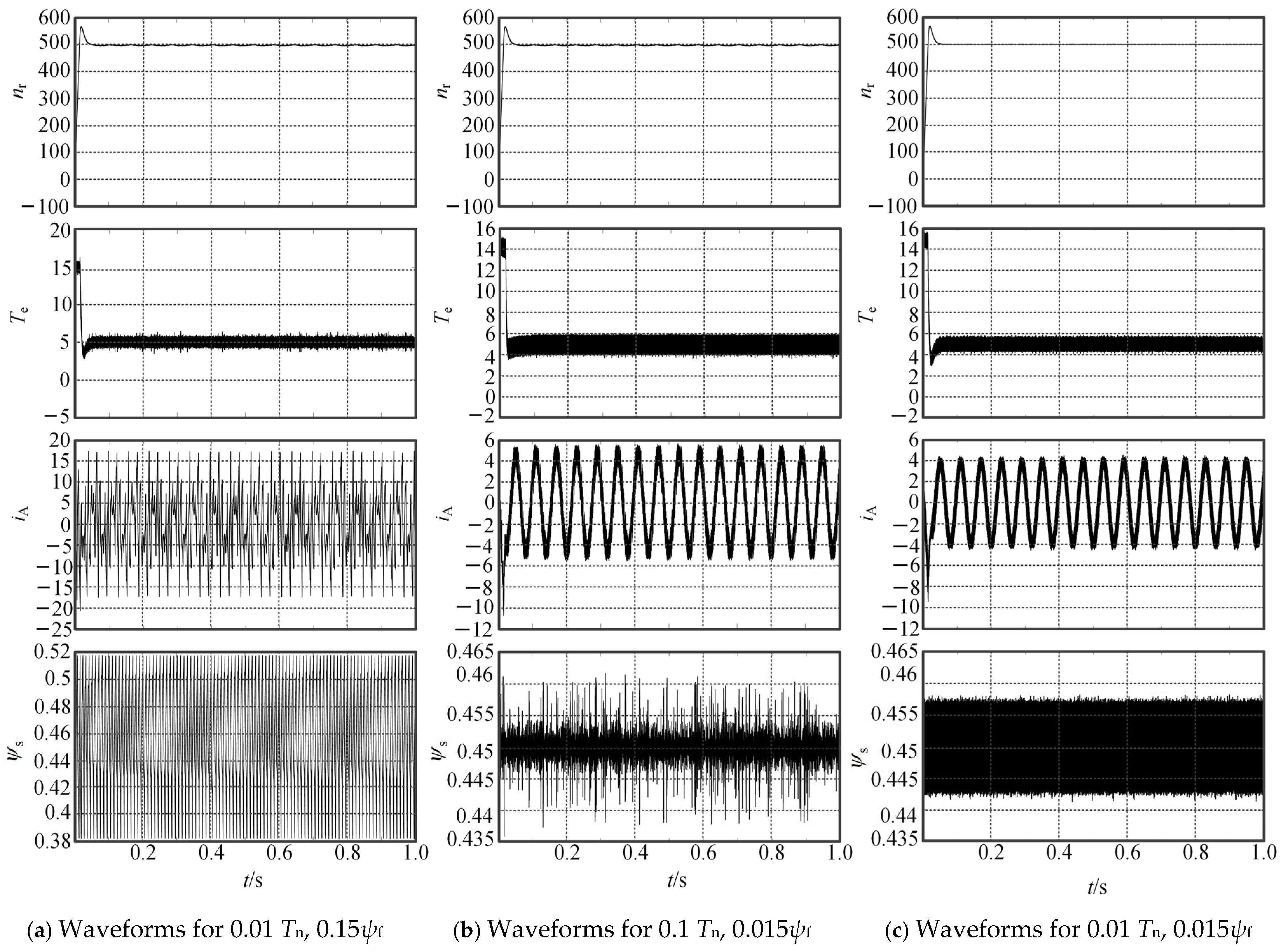
5.4. The Sensitivity Analysis of Hysteresis Thresholds
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Choi, H.H.; Vu, T.T.; Jung, J.W. Digital Implementation of an Adaptive Speed Regulator for a PMSM. IEEE Trans. Power Electron. 2011, 26, 3–8. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, Z.Q.; Mohamed, E.; Fu, Y.; Qi, X. Flux-Weakening Control of Nonsalient Pole PMSM Having Large Winding Inductance, Accounting for Resistive Voltage Drop and Inverter Nonlinearities. IEEE Trans. Power Electron. 2012, 27, 942–952. [Google Scholar] [CrossRef]
- Cho, Y.; Lee, K.; Song, J.; Lee, Y.I. Torque-ripple minimization and fast dynamic scheme for torque predictive control of permanent-magnet synchronous motors. IEEE Trans. Power Electron. 2015, 30, 2182–2190. [Google Scholar] [CrossRef]
- Mourabit, Y.E.; Derouich, A.; Abdelaziz, E.G.; Ouanjli, N.E.; Othmane, Z. Dtc-svm control for permanent magnet synchronous generator based variable speed wind turbine. Int. J. Power Electron. Drive Syst. 2017, 8, 1732–17432. [Google Scholar] [CrossRef]
- Mukherjee, S.; Giri, S.K.; Banerjee, S. A Flexible Discontinuous Modulation Scheme With Hybrid Capacitor Voltage Balancing Strategy for Three-Level NPC Traction Inverter. IEEE Trans. Ind. Electron. 2019, 66, 3333–3343. [Google Scholar]
- Mohammed, E.M.; Badre, B.; Najib, E.O.; Abdelilah, H.; Houda, E.A.; Btissam, M.; Said, M. Predictive Torque and Direct Torque Controls for Doubly Fed Induction Motor: A Comparative Study. In Proceedings of the International Conference on Digital Technologies and Applications, Fez, Morocco, 28 January 2022. [Google Scholar]
- El Daoudi, S.; Lazrak, L.; El Ouanjli, N. New Contributions for Speed Observation of Asynchronous Motor Fed by Multilevel Inverter. Aust. J. Electr. Electron. Eng. 2023, 20, 279–290. [Google Scholar]
- Choundhury, A.; Pillay, P.; Williamson, S.S. Comparative analysis between two-level and three-level DC/AC electric vehicle traction inverters using a novel DC-link voltage balancing algorithm. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 529–540. [Google Scholar]
- Teichmann, R.; Bernet, S. A comparison of three-level converters versus two-level converters for low-voltage drives traction and utility applications. IEEE Trans. Ind. Appl. 2005, 41, 855–865. [Google Scholar]
- Schweizer, M.; Friedli, T.; Kolar, J.W. Comparative evaluation of advanced three-phase three-level inverter/converter topologies against two-level systems. IEEE Trans. Ind. Electron. 2013, 60, 5515–5527. [Google Scholar] [CrossRef]
- Zhang, X.; Hou, B. Double Vectors Model Predictive Torque Control Without Weighting Factor Based on Voltage Tracking Error. IEEE Trans. Power Electron. 2018, 33, 2368–2380. [Google Scholar] [CrossRef]
- Mohan, D.; Zhang, X.; Foo, G.H.B. A Simple Duty Cycle Control Strategy to Reduce Torque Ripples and Improve Low-Speed Performance of a Three-Level Inverter Fed DTC IPMSM Drive. IEEE Trans. Ind. Electron. 2017, 64, 2709–2721. [Google Scholar] [CrossRef]
- Fuentes, E.; Cesar, A.; Silva Kennel, R.M. MPC Implementation of a Quasi-Time-Optimal Speed Control for a PMSM Drive, With Inner Modulated-FS-MPC Torque Control. IEEE Trans. Ind. Electron. 2016, 63, 3897–3905. [Google Scholar] [CrossRef]
- Kakosimos, P.; Abu-Rub, H. Deadbeat Predictive Control for PMSM Drives With 3-L NPC Inverter Accounting for Saturation Effects. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1671–1680. [Google Scholar] [CrossRef]
- Wang, Q.; Yu, H.; Li, C.; Lang, X. A Low-Complexity Optimal Switching Time-Modulated Model-Predictive Control for PMSM With Three-Level NPC Converter. IEEE Trans. Transp. Electrif. 2020, 6, 1188–1198. [Google Scholar] [CrossRef]
- Garcia, G.A.; Keshmiri, S.S.; Stastny, T. Robust and Adaptive Nonlinear Model Predictive Controller for Unsteady and Highly Nonlinear Unmanned Aircraft. IEEE Trans. Control Syst. Technol. 2015, 23, 1620–1627. [Google Scholar] [CrossRef]
- Gao, J.; Gong, C.; Li, W.; Liu, J. Novel Compensation Strategy for Calculation Delay of Finite Control Set Model Predictive Current Control in PMSM. IEEE Trans. Ind. Electron. 2020, 67, 5816–5819. [Google Scholar] [CrossRef]
- Geyer, T. Computationally efficient model predictive direct torque control. IEEE Trans. Power Electron. 2011, 26, 2804–2816. [Google Scholar] [CrossRef]
- Geyer, T.; Quevedo, D.E. Quevedo Multistep finite control set model predictive control for power electronics. IEEE Trans. Power Electron. 2014, 29, 6836–6846. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, Z.; Kennel, R.; Rodriguez, J. Model predictive torque control with an extended prediction horizon for electrical drive systems. Int. J. Control 2015, 88, 1379–1388. [Google Scholar] [CrossRef]
- Habibullah, M.; Lu, D.C.; Rahman, M.F. A simplified finite-state predictive direct torque control for induction motor drive. IEEE Trans. Ind. Electron. 2016, 63, 3964–3975. [Google Scholar] [CrossRef]
- Xia, C.; Liu, T.; Song, Z. A simplified finite-control-set model-predictive control for power converters. IEEE Trans. Ind. Inform. 2014, 10, 991–1002. [Google Scholar]
- Cortes, P.; Wilson, A.; Kouro, S. Model predictive control of multilevel cascaded h-bridge inverters. IEEE Trans. Ind. Electron. 2010, 57, 2691–2699. [Google Scholar] [CrossRef]
- Iqbal, A.; Abu-Rub, H.; Ahmed, S.K.M. Model predictive current control of a three-level five-phase NPC VSI using simplified computational approach. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition (APEC), Fort Worth, TX, USA, 16–20 March 2014. [Google Scholar]
- Zhang, Y.; Xie, W.; Li, Z.; Zhang, Y. Low-complexity model predictive power control: Double-vector-based approach. IEEE Trans. Ind. Electron. 2014, 61, 5871–5880. [Google Scholar] [CrossRef]
- Hu, J.; Zhu, J.; Lei, G.; Platt, G.; Dorrell, D.G. Multi-objective model-predictive control for high-power converters. IEEE Trans. Energy Convers. 2013, 28, 652–663. [Google Scholar]
- Vyncke, T.J.; Thielemans, S.; Melkebeek, J.A. Finite-set model-based predictive control for flying-capacitor converters: Cost function design and efficient FPGA implementation. IEEE Trans. Ind. Inform. 2013, 9, 1113–1121. [Google Scholar] [CrossRef]
- Zhang, Z.; Kennel, R. Novel ripple reduced direct model predictive control of three-level NPC active front end with reduced computational effort. In Proceedings of the 2015 IEEE International Symposium on Predictive Control of Electrical Drives and Power Electronics(precede), Valparaiso, Chile, 5–6 October 2015. [Google Scholar]
- Peng, S.; Zhang, G.; Zhou, Z.; Gu, X.; Xia, C. MPTC of NP-clamped three-level inverter-fed permanent-magnet synchronous motor system for NP potential imbalance suppression. IET Electr. Power Appl. 2020, 14, 658–667. [Google Scholar] [CrossRef]
- Mora, A.; Donoso, F.; Urrutia, M.; Angulo, A.; Cárdenas, R. Predictive Control Strategy for an Induction Machine fed by a 3L-NPC Converter with Fixed Switching Frequency and Improved Tracking Error. In Proceedings of the 2018 IEEE 27th International Symposium on Industrial Electronics (ISIE), Cairns, QLD, Australia, 13–15 June 2018. [Google Scholar]
- Khalilzadeh, M.; Vaez-Zadeh, S. Computation Efficiency and Robustness Improvement of Predictive Control for PMS Motors. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 2645–2654. [Google Scholar] [CrossRef]
- Lewicki, A.; Krzeminski, Z.; Abu-Rub, H. Space-vector pulse-width modulation for three-level NPC converter with the neutral point voltage control. IEEE Trans. Ind. Electron. 2011, 58, 5076–5086. [Google Scholar] [CrossRef]
- Li, C.; Yang, T.; Kulsangcharoen, P.; Calzo, G.L.; Bozhko, S.; Gerada, C. A Modified Neutral Point Balancing Space Vector Modulation for Three-Level Neutral Point Clamped Converters in High-Speed Drives. IEEE Trans. Ind. Electron. 2019, 66, 910–921. [Google Scholar] [CrossRef]
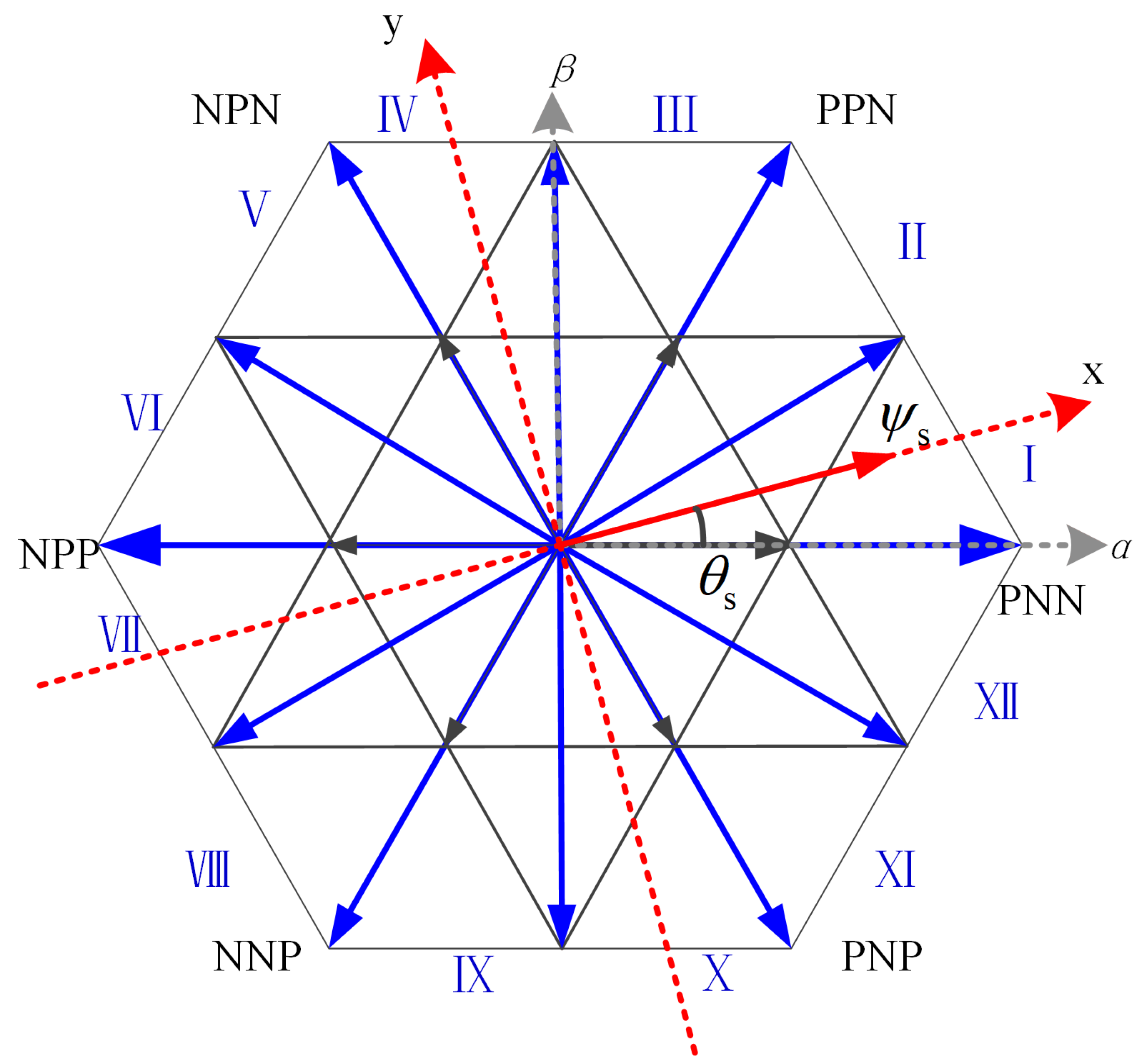



| Section | iA | iB | iC | Section | iA | iB | iC |
|---|---|---|---|---|---|---|---|
| I | >0 | <0 | <0 | VII | >0 | >0 | >0 |
| II | >0 | >0 | <0 | VIII | <0 | <0 | >0 |
| III | >0 | >0 | <0 | IX | <0 | <0 | >0 |
| IV | >0 | >0 | <0 | X | >0 | <0 | >0 |
| V | <0 | >0 | <0 | XI | >0 | <0 | >0 |
| VI | <0 | >0 | >0 | XII | >0 | <0 | <0 |
| Switching state | ||||
| POO, ONN | ONN | POO | POO | ONN |
| OPP, NOO | OPP | NOO | NOO | OPP |
| Switching state | ||||
| OPO, NON | NON | OPO | OPO | NON |
| POP, ONO | POP | ONO | ONO | POP |
| Switching state | ||||
| OOP, NNO | NNO | OOP | OPP | NNO |
| PPO, OON | PPO | OON | OON | PPO |
| Parameters | Symbol | Value | Unit |
|---|---|---|---|
| Number of poles | p | 2 | poles |
| Permanent magnet flux linkage | ψf | 0.45 | Wb |
| Stator resistance | Rs | 0.635 | Ω |
| d/q-axis inductance | Ld/Lq | 4.25 | mH |
| Rated speed | nr | 1500 | r/min |
| Rated torque | TN | 10 | N·m |
| Rated voltage | VN | 220 | V |
| Sampling frequency | Ts | 10 | kHz |
| Strategy | nr (r/min) | TL (N·m) | ITHD | Uripple (V) |
|---|---|---|---|---|
| MPTC1 | 500 | 10 | 27.40% | 7.1 |
| MPTC1 | 1500 | 15 | 32.53% | 6.5 |
| MPTC2 | 500 | 10 | 21.79% | 6.1 |
| MPTC2 | 1500 | 15 | 16.15% | 5.5 |
| MPTC3 | 500 | 10 | 20.63% | 6.6 |
| MPTC3 | 1500 | 15 | 16.67% | 6.6 |
| Strategy | nr (r/min) | TL (N·m) | tbalance (s) |
|---|---|---|---|
| MPTC2 | 500 | 10 | 1.064 |
| MPTC2 | 1000 | 5 | 4.62 |
| MPTC3 | 500 | 10 | 0.51 |
| MPTC3 | 1000 | 5 | 4.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Zhao, J.; Liu, Y.; Gu, X.; Li, C.; Chen, W. An Improved Finite-Set Predictive Control for Permanent Magnet Synchronous Motors Based on a Neutral-Point-Clamped Three-Level Inverter. World Electr. Veh. J. 2025, 16, 254. https://doi.org/10.3390/wevj16050254
Zhang G, Zhao J, Liu Y, Gu X, Li C, Chen W. An Improved Finite-Set Predictive Control for Permanent Magnet Synchronous Motors Based on a Neutral-Point-Clamped Three-Level Inverter. World Electric Vehicle Journal. 2025; 16(5):254. https://doi.org/10.3390/wevj16050254
Chicago/Turabian StyleZhang, Guozheng, Jiangyi Zhao, Yufei Liu, Xin Gu, Chen Li, and Wei Chen. 2025. "An Improved Finite-Set Predictive Control for Permanent Magnet Synchronous Motors Based on a Neutral-Point-Clamped Three-Level Inverter" World Electric Vehicle Journal 16, no. 5: 254. https://doi.org/10.3390/wevj16050254
APA StyleZhang, G., Zhao, J., Liu, Y., Gu, X., Li, C., & Chen, W. (2025). An Improved Finite-Set Predictive Control for Permanent Magnet Synchronous Motors Based on a Neutral-Point-Clamped Three-Level Inverter. World Electric Vehicle Journal, 16(5), 254. https://doi.org/10.3390/wevj16050254







