State of Health Estimation for Lithium-Ion Batteries Using Electrochemical Impedance Spectroscopy and a Multi-Scale Kernel Extreme Learning Machine
Abstract
1. Introduction
- (1)
- To balance the interpretability of the aging mechanism and the performance of the estimated model during LIBs aging, this paper proposes HFs that fuse ECM with DRT characteristics, which also utilize the random forest (RF) for screening the effectiveness of the HFs.
- (2)
- The KELM is used as an estimation model with three radial basis function (RBF) kernel functions and two regularization parameters, which enable to capture of the complex nonlinear relationships of the HFs and battery SOH from multiple scales.
- (3)
- The SSA is used to optimize the parameters of the KELM model to automate the algorithm configuration. The algorithm automatically adjusts the parameters of the model, reducing human effort and avoiding expert experience.
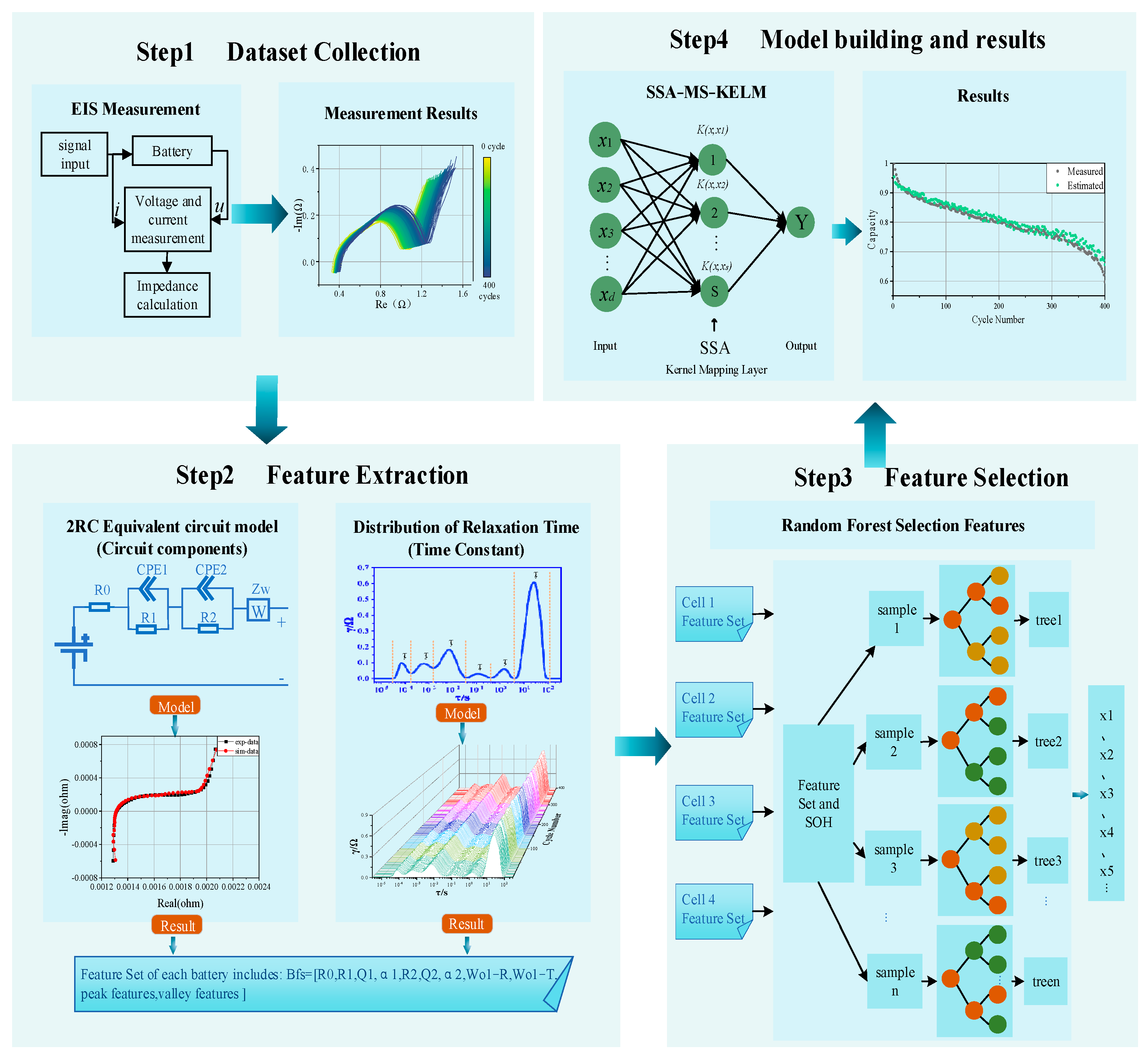
2. EIS-Based HFs Extraction
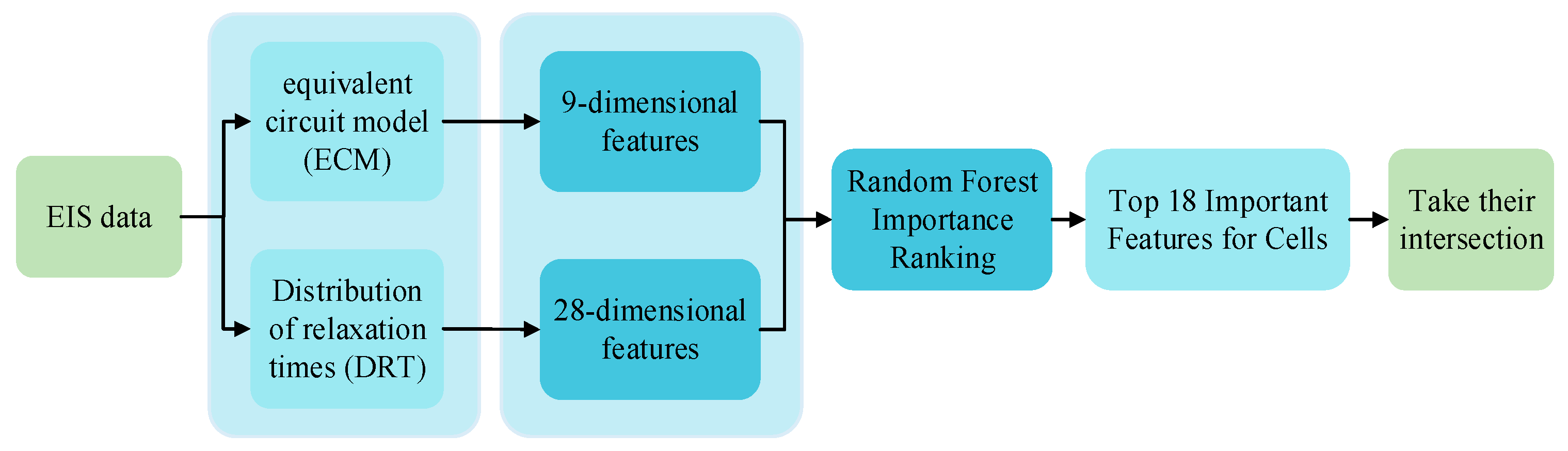
2.1. HFs Extraction and Selection
2.1.1. ECM-Based HFs
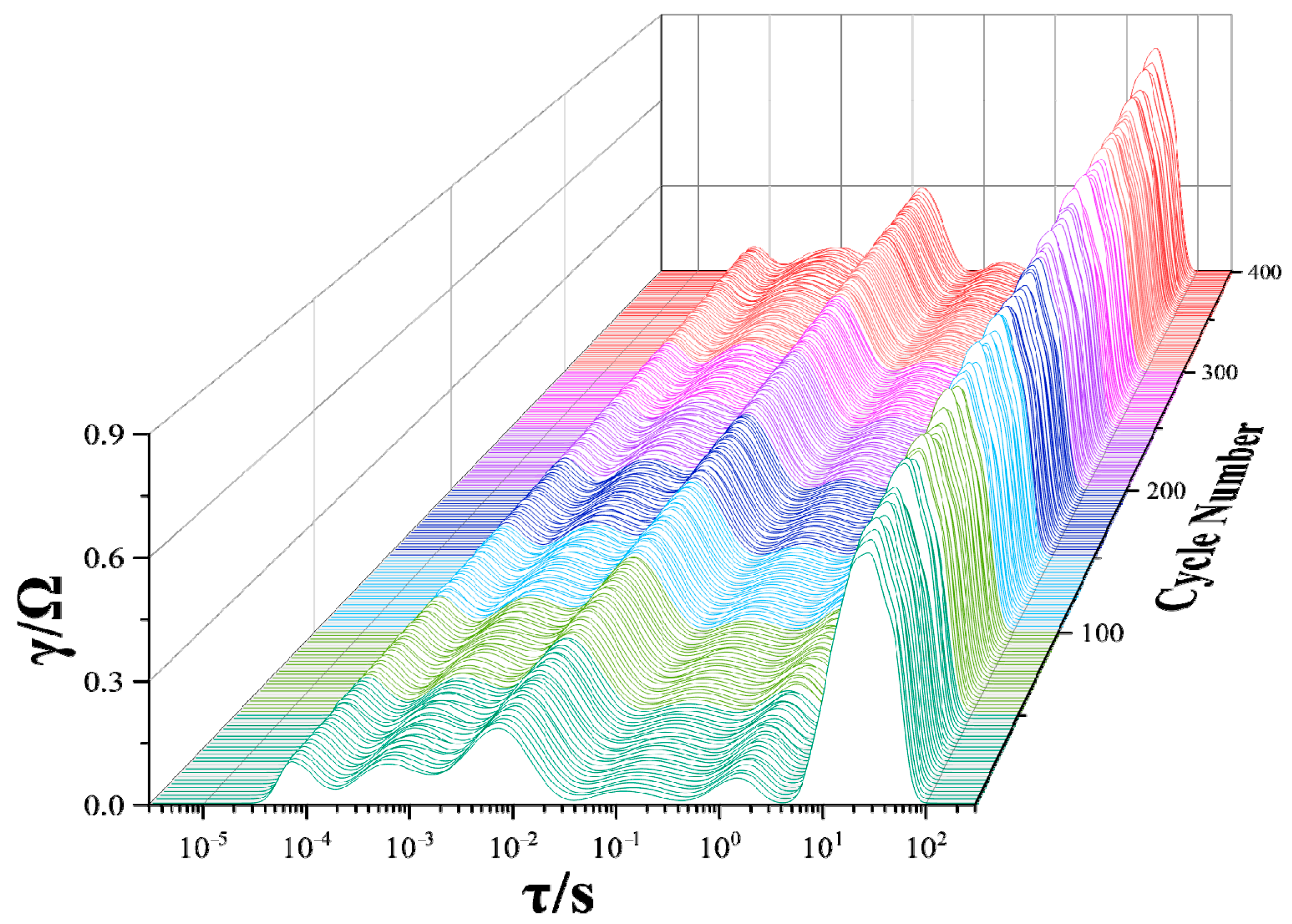
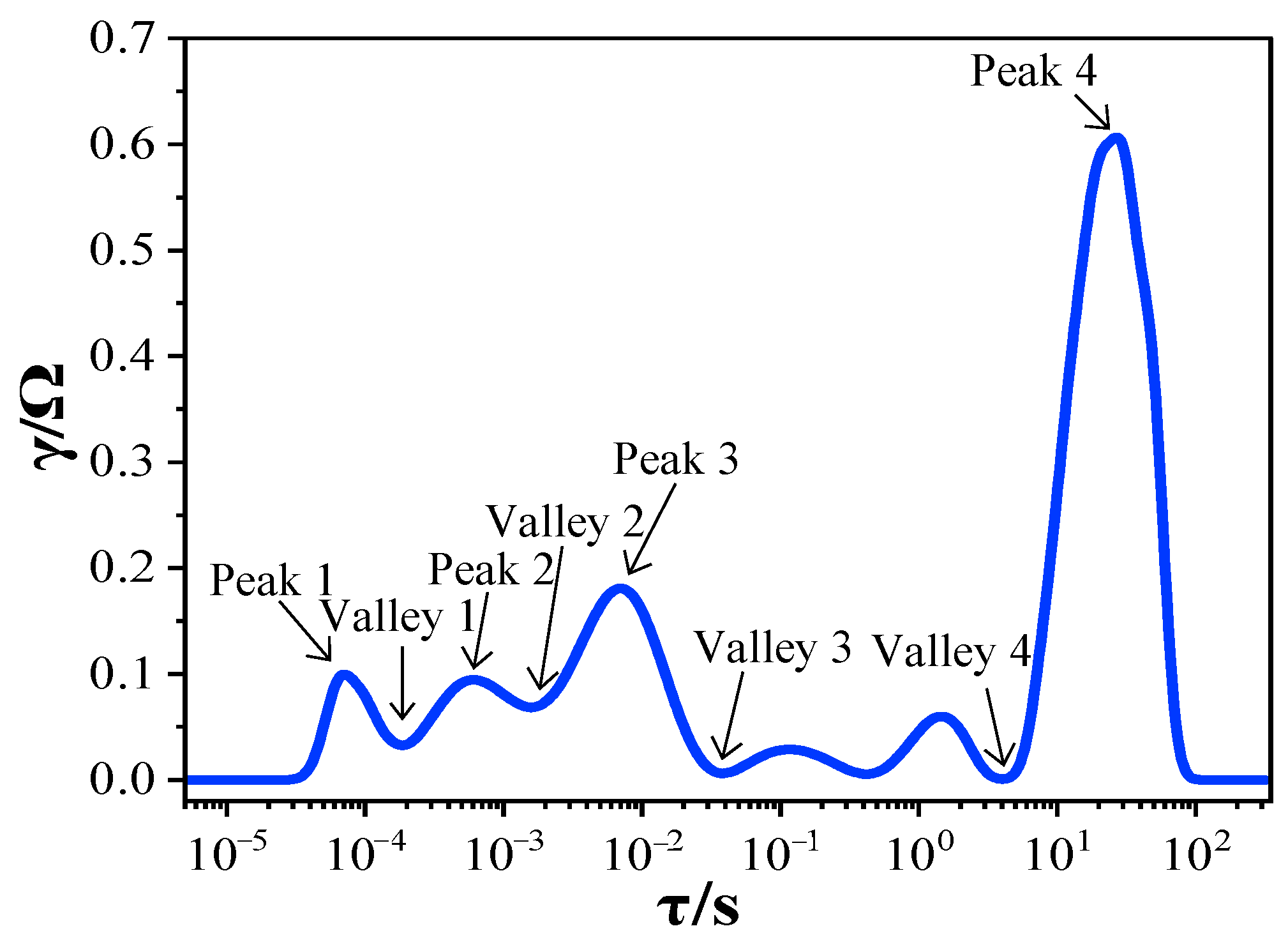
2.1.2. DRT-Based HFs
2.2. Feature Selection Using Random Forest
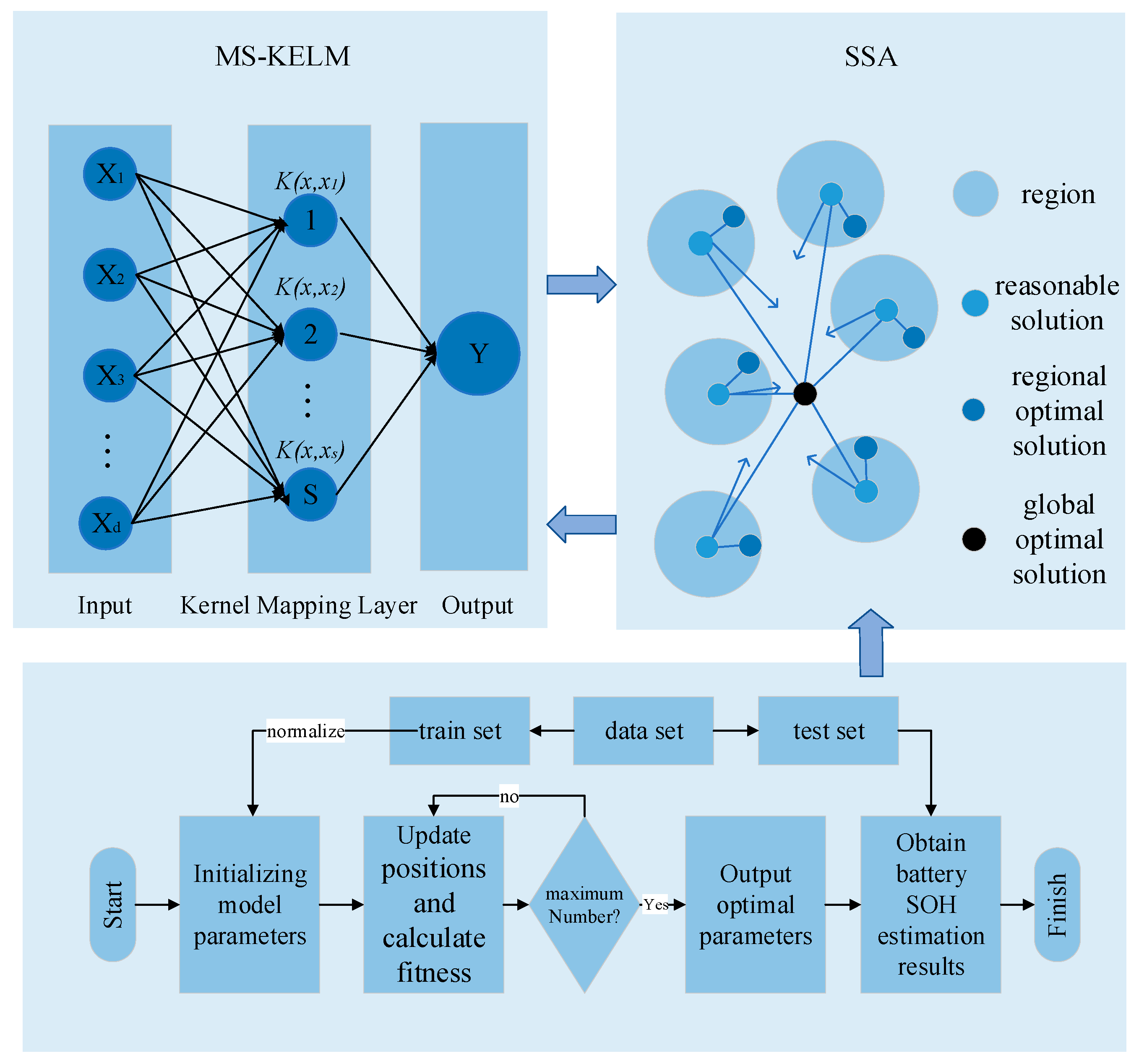
3. SOH Estimation with KELM
3.1. Extreme Learning Machine with Multi-Kernel Functions
3.2. Parameter Optimization Using the Sparrow Search Algorithm
4. Results and Discussion
4.1. Battery Dataset
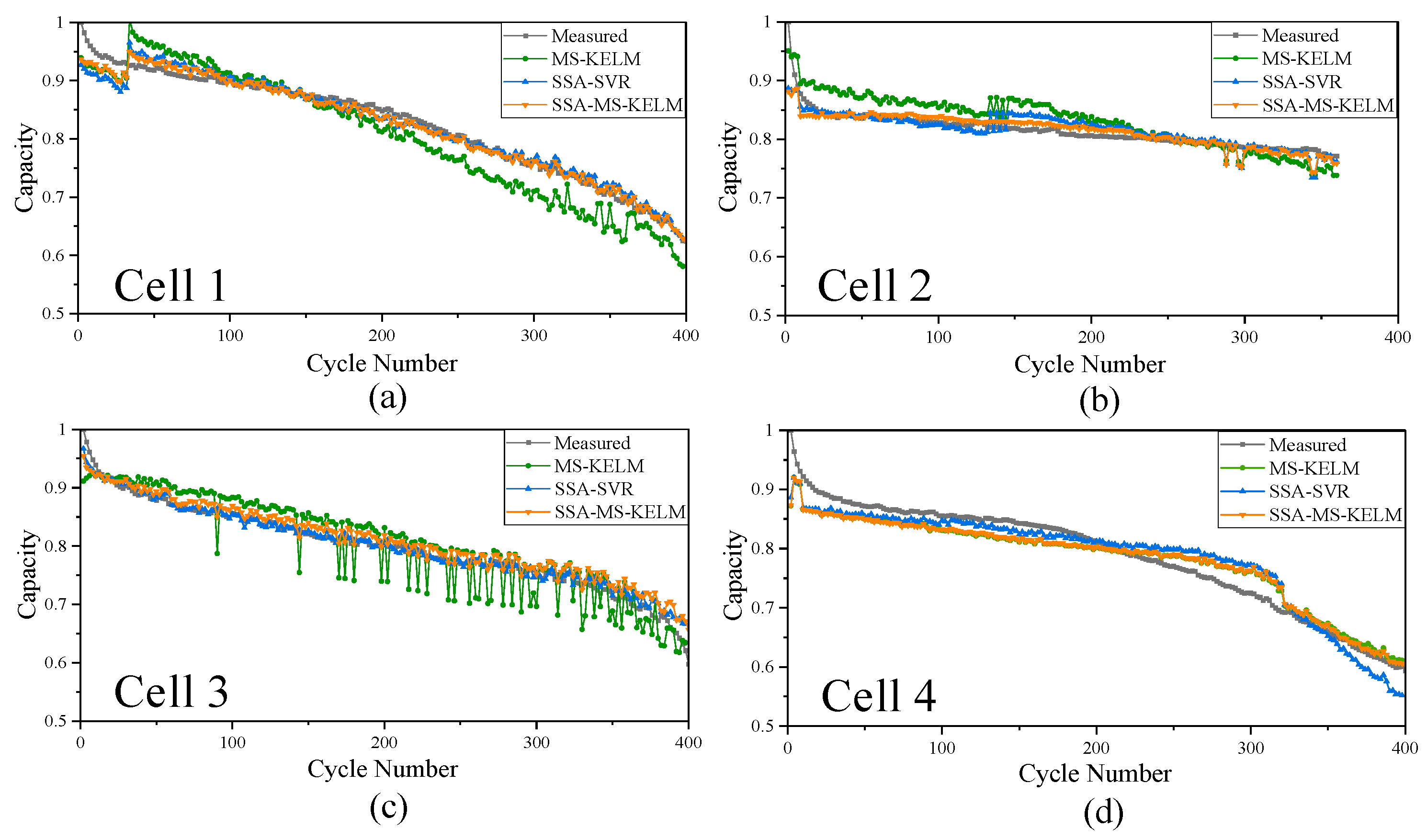
4.2. Results
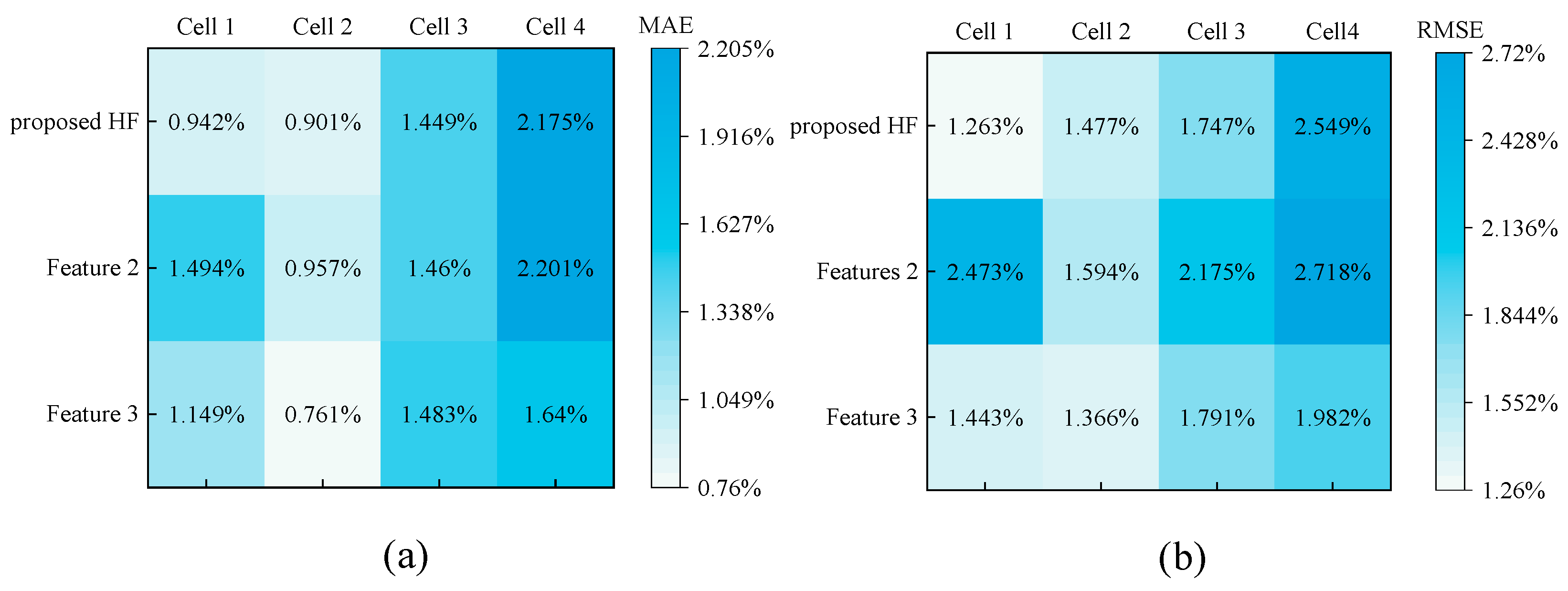
4.3. Comparison of Estimation Results for Different Input Features
4.3.1. Comparison for Different Input Features
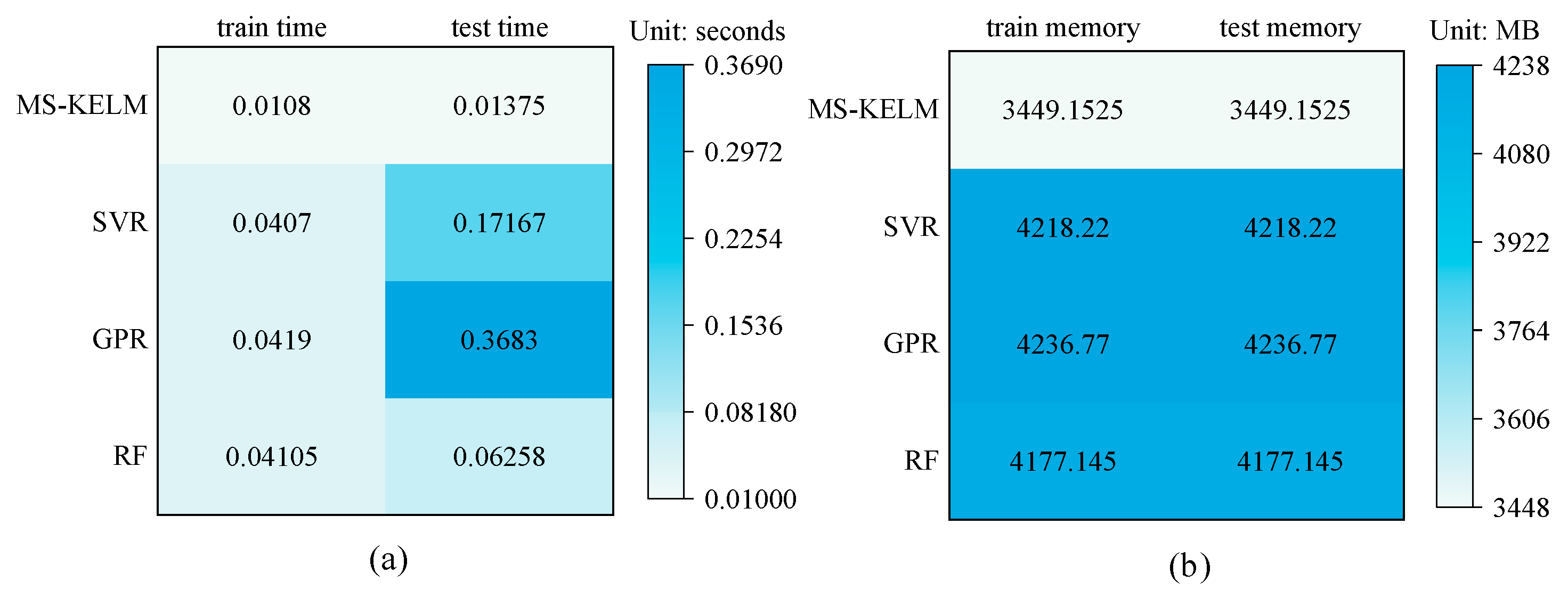
4.3.2. Comparison of Different Estimation Models
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| SOH | State of health |
| LIBs | Lithium-ion batteries |
| EIS | Electrochemical impedance spectroscopy |
| ECM | Equivalent circuit model |
| DRT | Distribution of relaxation times |
| MS-KELM | Multi-scale kernel extreme learning machine |
| SSA | Sparrow Search Algorithm |
| MAE | Mean absolute error |
| RMSE | Root mean square error |
| SVR | Support vector regression |
| GPR | Gaussian process regression |
| EVs | Electric vehicles |
| BMS | Battery management system |
| ICA | Incremental capacity analysis |
| DVA | Differential voltage analysis |
| EIR | Equivalent internal resistance |
| RUL | Remaining useful life |
| SEI | Solid electrolyte interface |
| HFs | Health features |
| ANN | Artificial Neural Networks |
| LSSVR | Least square support vector regression |
| HIs | Health indicators |
| ARD | Automatic relevance determination |
| MRMR | Minimum Redundancy Maximum Relevance |
| KELM | Kernel extreme learning machine |
| RF | Random forest |
| RBF | Radial basis function |
| SSA-MS-KELM | Multi-scale kernel extremum learning machine by the sparrow search algorithm |
| CPE | Constant phase elements |
| PH | Peak Height |
| PP | Peak Position |
| VH | Valley Height |
| VP | Valley Position |
| HPA | Half Peak Area |
| PPR | Peak to Total Peak Ratio |
| VVR | Valley to Total Valley Ratio |
| CC | constant current |
| CV | constant voltage |
| STL | Seasonal and Trend decomposition using Loess |
| SSA-SVR | support vector machine model optimized by the sparrow search algorithm |
| MLM-GPR | Gaussian regression model optimized by the maximized marginal likelihood |
| SSA-RF | random forest model optimized by the sparrow search algorithm |
References
- Ritchie, H.; Roser, M. Sector by Sector: Where Do Global Greenhouse Gas Emissions Come from? Our World in Data. 18 September 2020. Available online: https://ourworldindata.org/ghg-emissions-by-sector (accessed on 8 April 2025).
- Ding, Y.; Cano, Z.P.; Yu, A.; Lu, J.; Chen, Z. Automotive Li-Ion Batteries: Current Status and Future Perspectives. Electrochem. Energy Rev. 2019, 2, 1–28. [Google Scholar] [CrossRef]
- Peng, J.; Meng, J.; Chen, D.; Liu, H.; Hao, S.; Sui, X.; Du, X. A Review of Lithium-Ion Battery Capacity Estimation Methods for Onboard Battery Management Systems: Recent Progress and Perspectives. Batteries 2022, 8, 229. [Google Scholar] [CrossRef]
- Gismero, A.; Schaltz, E.; Stroe, D.-I. Recursive State of Charge and State of Health Estimation Method for Lithium-Ion Batteries Based on Coulomb Counting and Open Circuit Voltage. Energies 2020, 13, 1811. [Google Scholar] [CrossRef]
- Tan, X.; Tan, Y.; Zhan, D.; Yu, Z.; Fan, Y.; Qiu, J.; Li, J. Real-Time State-of-Health Estimation of Lithium-Ion Batteries Based on the Equivalent Internal Resistance. IEEE Access 2020, 8, 56811–56822. [Google Scholar] [CrossRef]
- Guha, A.; Patra, A. State of Health Estimation of Lithium-Ion Batteries Using Capacity Fade and Internal Resistance Growth Models. IEEE Trans. Transport. Electrific. 2018, 4, 135–146. [Google Scholar] [CrossRef]
- Simolka, M.; Heger, J.-F.; Traub, N.; Kaess, H.; Friedrich, K.A. Influence of Cycling Profile, Depth of Discharge and Temperature on Commercial LFP/C Cell Ageing: Cell Level Analysis with ICA, DVA and OCV Measurements. J. Electrochem. Soc. 2020, 167, 110502. [Google Scholar] [CrossRef]
- Nuroldayeva, G.; Serik, Y.; Adair, D.; Uzakbaiuly, B.; Bakenov, Z. State of Health Estimation Methods for Lithium-Ion Batteries. Int. J. Energy Res. 2023, 2023, 4297545. [Google Scholar] [CrossRef]
- Hu, W.; Peng, Y.; Wei, Y.; Yang, Y. Application of Electrochemical Impedance Spectroscopy to Degradation and Aging Research of Lithium-Ion Batteries. J. Phys. Chem. C 2023, 127, 4465–4495. [Google Scholar] [CrossRef]
- Zhou, Y.; Dong, G.; Tan, Q.; Han, X.; Chen, C.; Wei, J. State of Health Estimation for Lithium-Ion Batteries Using Geometric Impedance Spectrum Features and Recurrent Gaussian Process Regression. Energy 2023, 262, 125514. [Google Scholar] [CrossRef]
- Peng, J.; Meng, J.; Du, X.; Cai, L.; Stroe, D.-I. A Fast Impedance Measurement Method for Lithium-Ion Battery Using Power Spectrum Property. IEEE Trans. Ind. Informat. 2023, 19, 8253–8261. [Google Scholar] [CrossRef]
- Jiang, B.; Zhu, J.; Wang, X.; Wei, X.; Shang, W.; Dai, H. A Comparative Study of Different Features Extracted from Electrochemical Impedance Spectroscopy in State of Health Estimation for Lithium-Ion Batteries. Appl. Energy 2022, 322, 119502. [Google Scholar] [CrossRef]
- Meng, J.; Peng, J.; Cai, L.; Song, Z. Rapid Impedance Extraction for Lithium-Ion Battery by Integrating Power Spectrum and Frequency Property. IEEE Trans. Ind. Electron. 2024, 71, 7220–7229. [Google Scholar] [CrossRef]
- Kim, S.; Choi, Y.Y.; Choi, J.-I. Impedance-Based Capacity Estimation for Lithium-Ion Batteries Using Generative Adversarial Network. Appl. Energy 2022, 308, 118317. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, Q.; Zhang, Y.; Wang, J.; Stimming, U.; Lee, A.A. Identifying Degradation Patterns of Lithium Ion Batteries from Impedance Spectroscopy Using Machine Learning. Nat. Commun. 2020, 11, 1706. [Google Scholar] [CrossRef]
- Fu, Y.; Xu, J.; Shi, M.; Mei, X. A Fast Impedance Calculation-Based Battery State-of-Health Estimation Method. IEEE Trans. Ind. Electron. 2022, 69, 7019–7028. [Google Scholar] [CrossRef]
- Loechte, A.; Rojas Ruiz, I.; Gloesekoetter, P. Battery State Estimation with ANN and SVR Evaluating Electrochemical Impedance Spectra Generalizing DC Currents. Appl. Sci. 2022, 12, 274. [Google Scholar] [CrossRef]
- Cai, L.; Meng, J.; Stroe, D.-I.; Peng, J.; Luo, G.; Teodorescu, R. Multiobjective Optimization of Data-Driven Model for Lithium-Ion Battery SOH Estimation with Short-Term Feature. IEEE Trans. Power Electron. 2020, 35, 11855–11864. [Google Scholar] [CrossRef]
- Wang, L.; Xie, L.; Yang, Y.; Zhang, Y.; Wang, K.; Cheng, S. Distributed Online Voltage Control with Fast PV Power Fluctuations and Imperfect Communication. IEEE Trans. Smart Grid 2023, 14, 3681–3695. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, Y.; Li, D.; Cui, X.; Wang, L.; Li, L.; Wang, K. Electrochemical Impedance Spectroscopy: A New Chapter in the Fast and Accurate Estimation of the State of Health for Lithium-Ion Batteries. Energies 2023, 16, 1599. [Google Scholar] [CrossRef]
- Cui, Z.; Wang, L.; Li, Q.; Wang, K. A Comprehensive Review on the State of Charge Estimation for Lithium-Ion Battery Based on Neural Network. Int. J. Energy Res. 2022, 46, 5423–5440. [Google Scholar] [CrossRef]
- Cui, Z.; Kang, L.; Li, L.; Wang, L.; Wang, K. A Combined State-of-Charge Estimation Method for Lithium-Ion Battery Using an Improved BGRU Network and UKF. Energy 2022, 259, 124933. [Google Scholar] [CrossRef]
- Wang, K.; Li, L.; Yin, H.; Zhang, T.; Wan, W. Thermal Modelling Analysis of Spiral Wound Supercapacitor under Constant-Current Cycling. PLoS ONE 2015, 10, e0138672. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, Y.; Zhang, Y.; Wang, L.; Wang, K. Summary of Health-State Estimation of Lithium-Ion Batteries Based on Electrochemical Impedance Spectroscopy. Energies 2023, 16, 5682. [Google Scholar] [CrossRef]
- Yang, D.; Wang, Y.; Pan, R.; Chen, R.; Chen, Z. State-of-Health Estimation for the Lithium-Ion Battery Based on Support Vector Regression. Appl. Energy 2018, 227, 273–283. [Google Scholar] [CrossRef]
- Su, X.; Sun, B.; Wang, J.; Zhang, W.; Ma, S.; He, X.; Ruan, H. Fast Capacity Estimation for Lithium-Ion Battery Based on Online Identification of Low-Frequency Electrochemical Impedance Spectroscopy and Gaussian Process Regression. Appl. Energy 2022, 322, 119516. [Google Scholar] [CrossRef]
- Zhu, Y.; Jiang, B.; Zhu, J.; Wang, X.; Wang, R.; Wei, X.; Dai, H. Adaptive State of Health Estimation for Lithium-Ion Batteries Using Impedance-Based Timescale Information and Ensemble Learning. Energy 2023, 284, 129283. [Google Scholar] [CrossRef]
- Iurilli, P.; Brivio, C.; Wood, V. Detection of Lithium-Ion Cells’ Degradation through Deconvolution of Electrochemical Impedance Spectroscopy with Distribution of Relaxation Time. Energy Technol. 2022, 10, 2200547. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, R.; Huang, Q.-A.; Wang, J.; Fu, Y.; Li, W.; Bai, Y.; Zhao, Y.; Li, X.; Zhang, J. High-Efficient Prediction of State of Health for Lithium-Ion Battery Based on AC Impedance Feature Tuned with Gaussian Process Regression. J. Power Sources 2023, 561, 232737. [Google Scholar] [CrossRef]
- Tröltzsch, U.; Kanoun, O.; Tränkler, H.-R. Characterizing Aging Effects of Lithium Ion Batteries by Impedance Spectroscopy. Electrochim. Acta 2006, 51, 1664–1672. [Google Scholar] [CrossRef]
- Peng, J.; Meng, J.; Wu, J.; Deng, Z.; Lin, M.; Mao, S.; Stroe, D.-I. A Comprehensive Overview and Comparison of Parameter Benchmark Methods for Lithium-Ion Battery Application. J. Energy Storage 2023, 71, 108197. [Google Scholar] [CrossRef]
- Nohl, M.; Raut, G.; Wolf, S.E.; Duyster, T.; Dittrich, L.; Vinke, I.C.; Eichel, R.-A.; Haart, L.G.J.D. Analysis of the DRT as Evaluation Tool for EIS Data Analysis. ECS Trans. 2021, 103, 1403. [Google Scholar] [CrossRef]
- Wang, J.; Huang, Q.; Li, W.; Wang, J.; Zhuang, Q.; Zhang, J. Fundamentals of Distribution of Relaxation Times for Electrochemical Impedance Spectroscopy. J. Electrochem. 2020, 26, 16. [Google Scholar] [CrossRef]
- Xia, J.; Wang, C.; Wang, X.; Bi, L.; Zhang, Y. A Perspective on DRT Applications for the Analysis of Solid Oxide Cell Electrodes. Electrochim. Acta 2020, 349, 136328. [Google Scholar] [CrossRef]
- Wan, T.H.; Saccoccio, M.; Chen, C.; Ciucci, F. Influence of the Discretization Methods on the Distribution of Relaxation Times Deconvolution: Implementing Radial Basis Functions with DRTtools. Electrochim. Acta 2015, 184, 483–499. [Google Scholar] [CrossRef]
- Lu, Y.; Zhao, C.-Z.; Huang, J.-Q.; Zhang, Q. The Timescale Identification Decoupling Complicated Kinetic Processes in Lithium Batteries. Joule 2022, 6, 1172–1198. [Google Scholar] [CrossRef]
- Chen, J.; Liu, Y.; Yong, J.; Yang, C.; Yan, L.; Zheng, Y. State of Health Estimation of Lithium-Ion Batteries Using Fusion Health Indicator by PSO-ELM Model. Batteries 2024, 10, 380. [Google Scholar] [CrossRef]
- Liu, X.; Wang, L.; Huang, G.-B.; Zhang, J.; Yin, J. Multiple Kernel Extreme Learning Machine. Neurocomputing 2015, 149, 253–264. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A Novel Swarm Intelligence Optimization Approach: Sparrow Search Algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Gharehchopogh, F.S.; Namazi, M.; Ebrahimi, L.; Abdollahzadeh, B. Advances in Sparrow Search Algorithm: A Comprehensive Survey. Arch. Comput. Methods Eng. 2023, 30, 427–455. [Google Scholar] [CrossRef]




| References | Feature Selection | Model | Advantage | Disadvantage |
|---|---|---|---|---|
| [15] | EIS data | GPR | Easy to obtain features | It may have limited feature interpretability and involve some redundant computations. |
| [16] | ANN, SVR | Easy to apply | It may have limited feature interpretability. | |
| [26] | Six key health features from EIS data | GPR | High accuracy | It may introduce relatively high complexity. |
| [25] | Battery modeling identification parameters | LSSVR | Interpretable features | The method could be relatively resource-intensive. |
| [29] | Six key health features from DRT curves | GPR | Robust | It may face challenges in feature interpretability and computational complexity. |
| proposed | Nine key health features from ECM and DRT | SSA-MS-KELM | Balanced features, low complexity | / |
| DRT Peaks | ||||||
|---|---|---|---|---|---|---|
| Peak 1 | Peak 2 | Peak 3 | Peak 4 | Peak 5 | Peak 6 | |
| Physical process | Electric and magnetic effects | SEI Growth/decomposition; Li plating | Cathode charge transfer/CEI | Cathode charge transfer | Graphite degradation | Diffusion processes |
| Main reason | Particle–particle and particle–collector interactions | SEI layer of graphite | Cathode | Anode charge transfer | Kinetic slow down | |
| Category | Features | |||
|---|---|---|---|---|
| Height of the four peaks | PH 1 | PH 2 | PH 3 | PH 4 |
| Location of the four peaks | PP 1 | PP 2 | PP 3 | PP 4 |
| Height of the four valleys | VH 1 | VH 2 | VH 3 | VH 4 |
| Location of the four valleys | VP 1 | VP 2 | VP 3 | VP 4 |
| Half-peak area of the four peaks | HPA 1 | HPA 2 | HPA 3 | HPA 4 |
| The ratio of four peak heights to the sum of peak heights | PPR 1 | PPR 2 | PPR 3 | PPR 4 |
| The ratio of four valley heights to the sum of valley heights | VVR 1 | VVR 2 | VVR 3 | VVR 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, J.; Gao, Y.; Cai, L.; Zhang, M.; Sun, C.; Liu, H. State of Health Estimation for Lithium-Ion Batteries Using Electrochemical Impedance Spectroscopy and a Multi-Scale Kernel Extreme Learning Machine. World Electr. Veh. J. 2025, 16, 224. https://doi.org/10.3390/wevj16040224
Peng J, Gao Y, Cai L, Zhang M, Sun C, Liu H. State of Health Estimation for Lithium-Ion Batteries Using Electrochemical Impedance Spectroscopy and a Multi-Scale Kernel Extreme Learning Machine. World Electric Vehicle Journal. 2025; 16(4):224. https://doi.org/10.3390/wevj16040224
Chicago/Turabian StylePeng, Jichang, Ya Gao, Lei Cai, Ming Zhang, Chenghao Sun, and Haitao Liu. 2025. "State of Health Estimation for Lithium-Ion Batteries Using Electrochemical Impedance Spectroscopy and a Multi-Scale Kernel Extreme Learning Machine" World Electric Vehicle Journal 16, no. 4: 224. https://doi.org/10.3390/wevj16040224
APA StylePeng, J., Gao, Y., Cai, L., Zhang, M., Sun, C., & Liu, H. (2025). State of Health Estimation for Lithium-Ion Batteries Using Electrochemical Impedance Spectroscopy and a Multi-Scale Kernel Extreme Learning Machine. World Electric Vehicle Journal, 16(4), 224. https://doi.org/10.3390/wevj16040224








